对称三相电路的计算

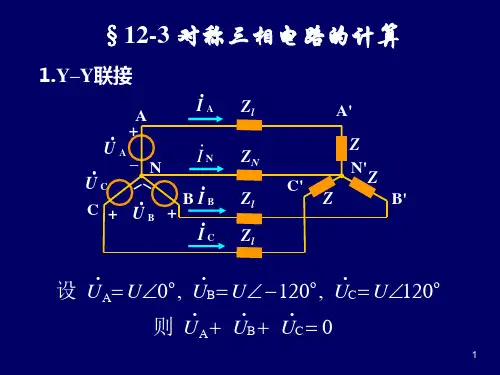
对称三相电路的计算————————————————————————————————作者：————————————————————————————————日期：§7.2 对称三相电路的计算如图7-6（a ）所示，其中l Z 为输电线阻抗，N Z 为中性线阻抗，N 和'N 为中性点，负载阻抗Z Z Z Z C B A ===。

对于这类电路，一般用节点电压法进行分析，以N 参考节点，有)(1)31('C B A l N N l N U U U ZZ U Z Z Z +++=++ 又因为0=++C B A U U U ，所以0'=N N U ，各相电源和负载的相电流等于线电流，即l A l N N A A Z Z U Z Z U U I +=+-= ' A l B B I a Z Z U I 2=+= A lC C I a Z Z U I =+= 由此可见，各线（相）电流独立，0'=N N U 是各线（相）电流独立，彼此无关的充要条件，因此，对称的Y Y -电路可以拆分为三个独立的单相电路，根据三相电源、三相负载和三相输电线路的对称性，分析计算三相中任意一相，而将其他两线(相)可以根据相序关系依次写出，这时对称三相电路可归结为一相的计算方法。

如图7-7所示为一相计算电路(A相)。

注意，在一相计算电路中，联接N 、N '的关系线是0'=N N U 的等效线，与中性线阻抗N Z 无关，此外，中性线的电流为0=++=CB A N I I I I NN '='N N U +-AA 'lZ ZAI图7-7 一相计算电路分析表明，对称的00Y Y -电路在理论上不需要中性线，可以移去，而在任一时刻, A i 、B i 、C i 中至少有一个为负值，对应此负值电流的输电线则作为对称电路系统在该时刻的电流回路。

§7.3 不对称三相电路的概念不对称三相电路主要有两种可能情况：第一，三相电源的大小或角度不相等而使相位有差异；第二，负载阻抗不相等。

简易计算如下：1）三相有功功率P=1.732*U*cosφ2）三相无功功率P=1.732*U*I*sinφ对称负载，φ：相电压与相电流之间的相位差cosφ为功率因数，纯电阻可以看作是1，电容、电抗可以看作是0实际计算如下：⑴有功功率三相交流电路的功率与单相电路一样，分为有功功率、无功功率和视在功率。

不论负载怎样连接，三相有功功率等于各相有功功率之和，即：当三相负载三角形连接时：当对称负载为星形连接时因UL= Up，IL=Ip所以P＝= ULILcosφ当对称负载为三角形连接时因UL=Up，IL= Ip所以P＝= ULILcosφ对于三相对称负载，无论负载是星形接法还是三角形接法，三相有功功率的计算公式相同，因此，三相总功率的计算公式如下。

P＝ULILcosφ⑵三相无功功率：Q＝ULILsinφ（3）三相视在功率S＝ULILP——有功功率，kW；Q——无功功率,kVar；S——视在功率,kV。

A；U——用电设备的额定电压,V；I——用电设备的运行电流.A.有功功率P与视在功率S的比值，称为功率因数cosφ，φ：相电压与相电流之间的相位差。

⑴有功功率三相交流电路的功率与单相电路一样，分为有功功率、无功功率和视在功率。

不论负载怎样连接，三相有功功率等于各相有功功率之和，即：当三相负载三角形连接时：当对称负载为星形连接时因UL= Up，IL=Ip所以P＝= ULILcosφ当对称负载为三角形连接时因UL=Up，IL= Ip所以P＝= ULILcosφ对于三相对称负载，无论负载是星形接法还是三角形接法，三相有功功率的计算公式相同，因此，三相总功率的计算公式如下。

P＝ULILcosφ⑵三相无功功率：Q＝ULILsinφ（3）三相视在功率S＝ULIL有功功率的计算式：P=√3IUcosΦ (W或kw)无功功率的公式: Q=√3IUsinΦ (var或kvar)视在功率的公式：S=√3IU (VA或kVA)同时还可用以下公式计算：在三相对称电路中，各相负载性质相同、大小相等，所以三相总的功率是单相功率的3倍，又因实践中三相电路的线电压、线电流参数获取比较方便，功率表达式其中：P为有功功率；Q为无功功率；S为视在功率,kV；U为用电设备的额定电压；I为用电设备的运行电流不对称三相电路中，因各相负载性质及大小不同，总视在功率不能是三相视在功率的代数和三相电路功率计算公式三相电路的功率分析一般应根据单相负载性质()分别进行计算，然后再求总量。

电功率计算公式电功率计算公式一、电功率计算公式：1、在纯直流电路中：P=UI，P=I²R，P=U²/R；式中：P---电功率（W），U---电压（V），I---电流（A），R---电阻（Ω)。

2、在单相交流电路中：P=UIcosφ式中：cosφ---功率因数，如白炽灯、电炉、电烙铁等可视为电阻性负载，其中cosφ=1则P=UI；U、I---分别为相电压（220V）、相电流。

3、在对称三相交流电路中，不论负载的连接是哪种形式，对称三相负载的平均功率都是：P=√3UIcosφ式中：U、I---分别为线电压（380V）、线电流。

cosφ---功率因数，若为三相阻性负载，如三相电炉，cosφ=1则P=√3UI；若为三相感性负载，如电动机、压缩机、继电器、日光灯等等。

cosφ=0.7～0.85，计算取值0.75。

4、说明：阻性负载：即和电源相比当负载电流负载电压没有相位差时负载为阻性（如负载为白炽灯、电炉等）。

通俗一点讲，仅是通过电阻类的元件进行工作的纯阻性负载称为阻性负载。

感性负载：通常情况下，一般把带电感参数的负载，即符合电压超前电流特性的负载，称为感性负载。

通俗地说，即应用电磁感应原理制作的大功率电器产品。

二、欧姆定律部分1、I=U/R（欧姆定律:导体中的电流跟导体两端电压成正比，跟导体的电阻成反比）2、I=I1=I2=…=In(串联电路中电流的特点：电流处处相等)3、U=U1+U2+…+Un(串联电路中电压的特点：串联电路中，总电压等于各部分电路两端电压之和)4、I=I1+I2+…+In(并联电路中电流的特点：干路上的电流等于各支路电流之和)5、U=U1=U2=…=Un（并联电路中电压的特点：各支路两端电压相等。

都等于电源电压）6、R=R1+R2+…+Rn(串联电路中电阻的特点：总电阻等于各部分电路电阻之和)7、1/R=1/R1+1/R2+…+1/Rn(并联电路中电阻的特点：总电阻的倒数等于各并联电阻的倒数之和)8、R并=R/n（n个相同电阻并联时求总电阻的公式）9、R串=nR(n个相同电阻串联时求总电阻的公式)10、U1:U2=R1:R2（串联电路中电压与电阻的关系：电压之比等于它们所对应的电阻之比）11、I1:I2=R2:R1（并联电路中电流与电阻的关系：电流之比等于它们所对应的电阻的反比）二、电功率部分12、P=UI（经验式，适合于任何电路）13、P=W/t（定义式，适合于任何电路）14、Q=I2Rt(焦耳定律，适合于任何电路)15、P=P1+P2+…+Pn（适合于任何电路）16、W=UIt(经验式,适合于任何电路)17、P=I2R(复合公式，只适合于纯电阻电路)18、P=U2/R(复合公式，只适合于纯电阻电路)19、W=Q（经验式，只适合于纯电阻电路。

三相电路的基本计算方法( 老头儿的博客)目录一.对称三相电路的计算方法 (1)1 计算三相对称电路的基本方法概述 (1)2. Y-Y 结线的三相对称电路的计算 (2)3. Y-Δ 结线的三相对称电路的计算 (3)4. 对称电源的转换和对称负载的转换 (5)5. Δ-Y 结线的三相对称电路的计算 (6)6. ∆-∆结线的三相对称电路的计算 (7)二．非对称三相电路的计算 (8)1. 有中性线的非对称三相四线电路的计算 (8)2. 无中性线的 Y-Y 非对称三相电路的计算 (9)3. ∆-∆结线的非对称三相电路的计算 (12)4．非对称三相负载结线的转换 (14)5. ∆-Y 和Y -∆形不对称三相电路的计算 (14)6．计算非对称三相电路计算方法的小结 (16)三．三相功率的计算方法和测量方法 (16)1. 对称三相电路的功率 (16)2 三相功率和三相电能的测量方法 (17)附：参考文献 (18)一. 对称三相电路的计算方法1．计算三相对称电路的基本方法概述所谓对称电路是指三相电路的各相负载相等、供电的三相电压也对称的情况。

在电力系统中，多数情况下是对称的电力系统。

计算对称的三相电路时，有许多方法可用。

最基本的方法是KVL 、KCL 、网孔法和节点电压法等。

但是，三相电路本身有很强的规律性，当计算对称的三相电路时，如果能善于利用这些规律，将可能使计算过程大为简化。

甚至可以把所有问题都作为单相电路计算。

计算对称的三相电路时，有以下事项需要考虑：① 计算时，首先要审视负载是怎样结线的。

至于电源是怎样结线的，是星形，还是三角形？并不重要。

因为只要知道了电源的线电压，我们都可以根据负载的结线方式对它的结线方式进行假设。

当然，如果在题目中已经明确了电源的结线方式，就没有必要进行假设了。

② 如果负载是星形结线的，可以假设电源的结线也是星形的。

因为计算三相电路时必须首先选定参考电压，选哪个呢？一般都是选线电压ab V ，因为不管是星形结线，还是三角形结线，其线电压的大小和方向都是一致的。

三相电与单相电的负载电流计算：对于单相电路而言，电机功率的计算公式是：P=IUcosφ，相电流I=P/Ucosφ；式中：I为相电流，它等于线电流P为电机功率U为相电压，一般是220Vcosφ是电机功率因素，一般取0.75对于三相平衡电路而言，三相电机功率的计算公式是：P=1.732IUcosφ。

由三相电机功率公式可推出线电流公式：I=P/1.732Ucosφ式中：P为电机功率U为线电压，一般是380Vcosφ是电机功率因素，一般取0.75如果是阻性负载的，可按电路功率公式计算求得。

对称三相交流电路功率：P＝根号3×U×I单相交流电路功率：P＝U×I转换公式求三相电流：I＝P/U×1.732＝1000/380×1.732≈1.52(A)转换公式求单相电流：I＝P/U＝1000/220≈4.55(A)通过上述计算，相同功率在对称三相电路中与单相电路中，三相的每一相电流是单相电流的1/3，即三相总负载1KW的总电流等于单相负载1KW的电流。

三相电路中每千瓦的功率:三相功率P=根号3*电压*电流*功率因素)（三相380电路中的功率P=1.73*380v*I*COSa)单相电路功率P=电压*电流*功率因率（单相220电路的功率P=220V*I*COSa) 其实一只三相电机用一只三相四线电度表计量与使用三只单相电度表计量应该是一样的有台电机,型号YKK5004-6 额定功率800KW 电压6000V 额定电流96.6A 现在知道运行电流是103A 那么实际功率是多少?最佳答案功率=1.732*额定电压*电流p=1.732*6000*103=1070376W=1070.376KW？。

三相功率计算公式P＝1.732×U×I×COSφ(功率因数COSφ一般为0.7～0.85之间，取平均值0.78计算三相有功功率P=1.732*U*I*cosφ三相无功功率P=1.732*U*I*sinφ对称负载，φ：相电压与相电流之间的相位差cosφ为功率因数，纯电阻可以看作是1，电容、电抗可以看作是0有功功率的计算式：P=√3IUcosΦ (W或kw无功功率的公式: Q=√3IUsinΦ (var或kvar视在功率的公式：S=√3IU (VA或kVA⑴有功功率三相交流电路的功率与单相电路一样，分为有功功率、无功功率和视在功率。

不论负载怎样连接，三相有功功率等于各相有功功率之和，即：当三相负载三角形连接时：当对称负载为星形连接时因UL=根号3*Up， IL= Ip所以 P＝= ULILcosφ当对称负载为三角形连接时因UL=Up， IL=根号3*Ip所以 P＝= ULILcosφ对于三相对称负载，无论负载是星形接法还是三角形接法，三相有功功率的计算公式相同，因此，三相总功率的计算公式如下。

P＝根号3*Ip ULILcosφ⑵三相无功功率：Q＝根号3*Ip ULILsinφ（3）三相视在功率S＝根号3*Ip ULIL对于交流电三相四线供电而言，线电压是380，相电压是220，线电压是根号3相电压对于电动机而言一个绕组的电压就是相电压，导线的电压是线电压（指A相B相C相之间的电压，一个绕组的电流就是相电流，导线的电流是线电流当电机星接时：线电流＝相电流；线电压＝根号3相电压。

三个绕组的尾线相连接，电势为零，所以绕组的电压是220伏当电机角接时：线电流＝根号3相电流；线电压＝相电压。

绕组是直接接380的，导线的电流是两个绕组电流的矢量之和功率计算公式 p=根号三UI乘功率因数是对的用一个钳式电流表卡在A B C任意一个线上测到都是线电流电流和相电流与钳式电流表测量无关，与电机定子绕组接线方式有关。

单相、三相交流电路功率计算公式精彩文档相电压：三相电源中星型负载两端的电压称相电压。

用UA、UB、UC 表示。

相电流：三相电源中流过每相负载的电流为相电流，用IAB、IBC、ICA 表示。

线电压：三相电源中，任意两根导线之间的电精彩文档压为线电压，用UAB、UBC、UCA 表示。

线电流：从电源引出的三根导线中的电流为线电流，用IA、IB、IC 表示。

如果是三相三线制，电压电流均采用两个互感器，按V/v接法，测量结果为线电压和线电流；如果是三相四线制：1、电压可采用V/v接法，电流必须采用Y/y 接法，测量结果为线电压和线电流，线电流也等于相电流。

2、电压和电流均采用Y/y接法，测量结果为相电压和相电流，相电流也等于线电流。

Y/y接法时，电压互感器一次接在火线及零线之间，每个电压互感器二次输出接一个独立仪表。

每根火线穿过一个电流互感器，每个电流互感精彩文档器二次输出接一个独立仪表。

电压V/v接法时，电压互感器一次接在火线之间，二次分别连接一个电压表，如需测量另一个线电压，可将两个互感器的二次输出的n端连接在一起，a、b端连接第三个电压表。

电流V/v接法时，两根火线分别穿过一个电流互感器，每个互感器的二次分别接一个电流表，如需测量第三个线电流，可将两个的s2端连接在一起，与两个互感器的s1端一起共三个端子，另外，将三个电流表的负端连在一起，其它三个端子分别与上述三个端子连接在一起。

三相电流计算公式精彩文档I=P/(U*1.732)所以1000W的线电流应该是1.519A。

功率固定的情况下，电流的大小受电压的影响，电压越高，电流就越小，公式是I=P/U 当电压等于220V时，电流是4.545A，电压等于380V时，电流是2.63A，以上说的是指的单相的情况。

380V三相的时候，公式是I=P/(U*1.732)，电流大小是1.519A三相电机的电流计算 I= P/(1.732*380*0.75) 式中： P是三相功率 (1.732是根号3) 380 是三相线电压 (I是三相线电流) 0.75是功率因数，这里功率因数取的是0.75 ，如果功率因数取0.8或者0.9，计算电流还小。

对称三相电路功率的计算
（1）平均功率
设对称三相电路中一相负载汲取的功率等于Pp=UpIpcosφ，其中Up、Ip 为负载上的相电压和相电流。

则三相总功率为：P =3Pp =3UpIpcosφ
留意：
1) 上式中的φ 为相电压与相电流的相位差角( 阻抗角) ；
2) cosφ为每相的功率因数，在对称三相制中三相功率因数：
cosφA=cosφB=cosφC= cosφ；
3) 公式计算的是电源发出的功率( 或负载汲取的功率) 。

当负载为星形连接时，负载端的线电压，线电流，代入上式中有：
当负载为三角形连接时，负载端的线电压，线电流，代入上式中有：
（2）无功功率
对称三相电路中负载汲取的无功功率等于各相无功功率之和：（3）视在功率
（4）对称三相负载的瞬时功率
设对称三相负载A 相的电压电流为：
则各相的瞬时功率分别为：
可以证明它们的和为：
上式表明，对称三相电路的瞬时功率是一个常量，其值等于平均功率，这是对称三相电路的优点之一，反映在三相电动机上，就得到均衡的电磁力矩，避开了机械振动，这是单相电动机所不具有的。

对称三相电路中点电压
对称三相电路是工业和家庭电气系统中常见的一种电路类型。

在这种电路中，三相电源的相位间隔为120度，每个相位都有相同的幅值和频率。

在对称三相电路中，中点电压是一个重要的概念。

中点电压是指三相电路中每相电压的平均值。

在对称三相电路中，每相电压的幅值都相同，所以中点电压等于每相电压的幅值除以根号3。

这样计算的中点电压可以用来驱动对称负载，例如三相电机。

中点电压在对称三相电路中扮演着很重要的角色。

首先，它可以作为对称负载的电源。

对称负载是指负载中每个元件的电阻、电感或电容都是相同的。

通过将中点电压连接到对称负载的中心，可以实现平衡的负载分配，从而确保每个负载元件获得相同的电压和电流。

其次，中点电压还可以用来实现对称三相电路的相序检测。

在三相电路中，相序错误可能会导致电机反向旋转或者烧坏电气设备。

通
过检测中点电压的相位，可以确定三相电路的正确相序，从而确保设备正常运行。

另外，中点电压还可以用来检测对称三相电路中的故障。

如果三相负载中的一个相位出现故障，中点电压的幅值和相位将会发生变化。

通过监测中点电压的变化，可以快速发现故障并及时进行维修。

总之，中点电压在对称三相电路中具有重要的作用。

它不仅可以驱动对称负载，还可以用来实现相序检测和故障检测。

因此，在设计和维护对称三相电路时，我们都需要充分理解并重视中点电压的作用。