最短路线问题-PPT

3
1
最短路线问题
例1：沿着下图所显示的线段，以最短的路线，从A到B有多少种不同 的走法？
1
4
10
20
B
1
3
6
10
1
2
3
4
A11源自1标数法最短路线问题
什么是标数法？
通过在每个点上标记出从起点到此点的 路线数，逐步算出起点到终点路线数的方法！
最短路线问题
欢乐时光
欢乐海洋
最短路线问题
欢乐时光
欢乐海洋
最短路线问题
例1：沿着下图所显示的线段，以最短的路线，从A到B有多少种不同 的走法？
B
A
最短路线问题
例1：沿着下图所显示的线段，以最短的路线，从A到B有多少种不同 的走法？
1
图1
A
2 B1
1
从最简单的情况开始想！
1
图2
1 A
3
2 B1
1
6 B2

问题描述
问题定义
给定一个几何体，如长方体、球体等，求从一个顶点到另一个顶点的最短路线长 度。
问题分析
最短路线问题可以通过几何学中的勾股定理进行求解。勾股定理是直角三角形中 ，直角边的平方和等于斜边的平方。在三维空间中，可以利用勾股定理找到最短 路径。
02
勾股定理简介
勾股定理的定义
勾股定理：在直角三角形中，直角边 的平方和等于斜边的平方。即，如果 直角三角形的两条直角边长度分别为 a和b，斜边长度为c，则有a^2 + b^2 = c^2。
用勾股定理求几何体中的 最短路线长ppt课件
• 引言 • 勾股定理简介 • 几何体的最短路线问题 • 用勾股定理求解最短路线长 • 结论
01
引言
目的和背景
目的
介绍如何使用勾股定理在几何体中寻找最短路线长度。
背景
几何体中的最短路线问题在实际生活中有着广泛的应用，如建筑、工程、机器 人等领域。通过解决这类问题，可以优化设计、提高效率、降低成本等。
THANKS
感谢观看
勾股定理的证明方法
勾股定理的证明方法有多种，其中比较常见的是欧几里得证 明法。该证明方法利用了相似三角形的性质和边长之间的关 系，通过一系列的推导和证明，最终证明了勾股定理。
除了欧几里得证明法外，还有其他的证明方法，如利用代数 方法和微积分方法等。这些证明方法虽然不同，但都能够证 明勾股定理的正确性。
的性质和勾股定理得出的结论。
空间几何体中的最短路线问题
1 2 3
球面几何中的大圆弧最短
在球面几何中，两点之间的大圆弧是最短的路径 。大圆弧是指经过球心并与球面相切的圆弧。
圆柱体或圆锥体中的母线最短
在圆柱体或圆锥体中，从顶点到底面的母线是最 短的路径。母线是与底面平行的线段，也是旋转 轴。

A
a 3、连接PA，PB，由对称轴 的性质知，PA= P1A，
P1
PB=P2B
∴先到点A处吃草，再到点B
处饮水，最后回到营地，
这时的放牧路线总路程最
短，即 (PB+BA+AP)min
• 证明：
P2
b ∵ PA1+A1B1+B1P
B1 B
.P
河
= P1A1+A1B1+B1P2 > P1A+AB+BP2
前面和右面
D D1
③
A 1 A1
C1
2
4
B1
AC1 =√52+22 =√29
左面和上面
• 1、如图是一个长方体木块，已知 AB=5,BC=3,CD=4，假设一只蚂蚁 在点A处，它要沿着木块侧面爬到点D 处，则蚂蚁爬行的最短路径是 7 4 。
D
4
C
A
5
B3
• 2、现要在如图所示的圆柱体侧面A点 与B点之间缠一条金丝带（金丝带的宽 度忽略不计），圆柱体高为6cm，底面 圆周长为16cm，则所缠金丝带长度的 最小值为 10cm 。
在河上建一座桥MN，桥造在何处才能使从A到B
的路径最短？（假设河的两岸是平行的直线，桥
要与河垂直）
.A M
作法： 1、将点B沿垂直与河岸的方
向平移一个河宽到E
N
2、. E连接AE交河对岸与点M,则
.点BM为建桥的位置，MN为 所建的桥。
A C
M ND E
B
• 证明： ∵ AC+CD+DB = AC+CD+CE = AC+CE+CD > AE+CD = AM+ME+CD = AM+NB+MN ∴ AC+CD+DB > AM+NB+MN

第十三章 轴对称
故事引入
导入新课
复习旧知
1.如图，连接A、B两点的所有连线中，哪条最短？
①
为什么？
②
②最短，因为两点之间，线段最短
A ③B
2.如图，点P是直线l外一点，点P与该直线l上各点连
接的所有线段中，哪条最短？为什么？
P
PC最短，因为垂线段最短
A BC
Dl
3.如图，如何作点A关于直线l的对称点？
B
A
C
l
联想旧知
B
A
C
l
B′
用旧知解决新知
A
C
l
B
提示：本题也可作A点关于直线l的对称点
典例精析
例1 如图，已知点D、点E分别是等边三角形ABC
中BC、AB边的中点，AD=5，点F是AD边上的动
点，则BF+EF的最小值为（ B ）
A．7.5
B．5
C．4
D．不能确定
解析：△ABC为等边三角形，点D是BC边的中点，即点B与点 C关于直线AD对称.∵点F在AD上，故BF=CF.即BF+EF的最小 值可转化为求CF+EF的最小值，故连接CE即可，线段CE的长 即为BF+EF的最小值.
l2
l2
2.关键： 作对称点，利用轴对称的性质将线段转化， 从而利用“两点之间，线段最短”来解决
作法及思路分析
1.作点A关于直线 l 的对称点A′ ，连接CA′。
B A
l
C
A′
2.由上步可知AC+CB=B_′_A_C_+_C_B_′ ___
思考：当C在直线 l 的什么位置时AC +CB′最短？
3.如图，如何作点A关于直线l的对称点？

则AC和BC的大小关系是什么？ l
C
A
B
容易得出，AC=BC. 依据“线段垂直平分线上的点到线段两端点的距离相等”.
引出问题
思考：相传古希腊亚历山大里亚城里有一位久负盛名的学者，名叫海伦.有 一天，一位将军专程拜访海伦，求教一个百思不得其解的问题：从图中的A 地出发，到一条笔直的河边l饮马，然后到B地.到河边什么地方饮马可使他 所走的路线全程最短？ 精通数学、物理学的海伦稍加思索，利用轴对称的知识回答了这个问题.这 个问题后来被称为“将军饮马问题”.
B A
l
这是个实际问题，你能用自己理解的语言描述一下吗？ 如图所示：将A，B 两地抽象为两个点，将河l抽象为一条直线.
∙B A∙
l
那你能用数学语言说明这个问题所表达的意思吗？
如图： 点A，B分别在直线l的同侧，点C是直线l上的一个动点，当点C在什么
位置的时候，AC+BC的值最小？
∙B A∙
l
如果点A，B在直线l的两侧，这时该如何求解？
离是（ B ）
A.900
B.1200
C.1500
D.1800
C
D
A
B
谢谢大家
∙B
A∙
你能证明这个结论吗
∙
l
C
∙ B′
容易得出：连接AB′交直线l于点C，则点C即为所求.
证明：在直线l上任意取一点C′（不与点C重合），连接AC′，BC′，B′C′.
由轴对称的性质可得：BC=B′C，BC′=B′C′，
则AC+BC=AC+B′C=AB′，AC′+BC′=AC′+B′C′.
在△AB′C′中，AB′<AC′+B′C′， 所以AC+BC<AC′+B′C′. 由点C′的任意性可知，AC+BC的值是 最小的，故点C的位置符合要求.

12
图论及其应用 作业 用Dijkstra算法求出下图中从顶点a到其它所有 顶点的最短路径及及长度。
13
图论及其应用
有向图中求最短路径的Dijkstra算法
设Sj是带权有向图G中自顶点1到顶点j的最短有向路的长度 步骤1：置P={1}，T={2,3,…,n}且S1=0，Sj=w1j， j=2,3,…,n 。 步骤2：在T中寻找一点k，使得Sk=min{Sj}，置P=P{k}， T=T- {k}。若T=，终止；否则，转向步骤3。 步骤3：对T中每一点j，置Sj=min {Sj ，Sk+ wkj}，然后转向步 骤2。 算法经过n-1 次循环结束。
6
1-6-8-B
6-8-B
13
10
5
图论及其应用
指定点到其它所有点的最短路径
解决这一问题最著名的方法是 Dijkstra算法，这个算法是由荷 兰计算机科学教授Edsger W.Dijkstra在1959年提出的。 他在1972年获得美国计算机协 会授予的图灵奖，这是计算机 科学中最具声望的奖项之一。
最终，起点上方的最短路线及权值即为起点到终点的最 短路线及长度。
3
图论及其应用
例 使用回溯法求下图中结点1到结点10的最短路径
2-6-9-10 600
1-4-6-9-10 650
4-6-9-10 500
6-9-10
300
9-10
100 5-8-10
400
8-10
150
3-5-8-10 600
7-8-10 275
定义2 已知矩阵A=(aij)m n ，B =(bij)mn，规定C=AB=(dij)mn，
其中dij=min(aij, bij)

将A，B 两地抽象为两个点，将河l 抽象为一条直 线．
·B A·
l
探索新知
追问2 你能用自己的语言说明这个问题的意思， 并把它抽象为数学问题吗？
（1）从A 地出发，到河边l 饮马，然后到B 地； （2）在河边饮马的地点有无穷多处，把这些地点与A，
B 连接起来的两条线段的长度之和，就是从A 地 到饮马地点，再回到B 地的路程之和；
若直线l 上任意一点（与点 C 不重合）与A，B 两点的距离 和都大于AC +BC，就说明AC + BC 最小．
A
·
C′ C
B
·
l
B′
探索新知
追问2 回顾前面的探究过程，我们是通过怎样的 过程、借助什么解决问题的？
A
·
C′ C
B
·
l
B′
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
(Ⅰ)两点在一条直线异侧
已知：如图，A，B在直线L的两侧， 在L上求一点P，使得PA+PB最小。
连接AB,线段AB与直线L的交点P ，就是所求。
P
为深入学习习近平新时代中国特色社 会主义 思想和 党的十 九大精 神,贯彻 全国教 育大会 精神,充 分发挥 中小学 图书室 育人功 能
思考？？？
为什么这样做就能得到最短距 离呢？
根据：两点之间线段最短.
引入新知
引言： 前面我们研究过一些关于“两点的所有连线中，线 段最短”、“连接直线外一点与直线上各点的所有线段 中，垂线段最短”等的问题，我们称它们为最短路径问 题．现实生活中经常涉及到选择最短路径的问题，本节 将利用数学知识探究数学史中著名的“将军饮马问题”．

方法点拨：解决“两线两点”型最短路径问题 的方法以两线为对称轴，分别作靠近线的点的 对称点，连接两个对称点，将最短路径转化为 连接两个对称点的线段.
感悟新知
解：如图13 .4 -4，(1)作点A 关于直 线l1 的对称点A′； (2)作点B 关于直线l2 的对称点B′； (3)连接A′B′，分别与直线l1，l2相交 于C，D 两点，连接AC，BD，则沿 路线A → C → D → B 走才能使总路 程最短.
第十三章 轴对称
13.4 课题学习 最短路径问题
感悟新知
知识点 1 最短路径问题
知1－讲
类型
问题
作法
最小值
一 线 两
点 型
两点 在直 线异
侧
在直线l 上找 一点P，使PA
＋PB 最小
连接AB，与直 线l 的交点即为
点P
PA＋PB 的最小值 为AB的
值
感悟新知
类型
问题
作法
知1－讲
最小值
两点
一 线 两
知1－练
ቤተ መጻሕፍቲ ባይዱ
感悟新知
知1－练
3-1.如图，AB 是∠ MON内部的一条线段，在∠ MON 的两 边OM，ON 上分别取点C，D组成四边形ABDC，如何 取点才能使该四边形的周长最小？
感悟新知
知1－练
(1)如果居民小区A，B 在主干线l 的两侧，如图13.4-1，那么 分支点M 在什么地方时总线路最短？
解：如图13 .4 -1，
连接AB，与l 的 交点即为所求的
分支点M.
感悟新知
知1－练
(2)如果居民小区A，B 在主干线l 的同侧，如图13.4-2，那么 分支点M 在什么地方时总线路最短？

多少种情况？ B
(1)经过前面和上底面;
2
(2)经过前面和右面;
1
(3)经过左面和上底面.
A
3
C
B
B
A
3
1 2C
B 2
A
A1
3
C
解:(1)当蚂蚁经过前面和上底面时，如图，最 短路程为
B
B
2
1
A
3
C
A
AB＝ AC2 BC2 ＝ 32 32 ＝ 18
(2)当蚂蚁经过前面和右面时，如图，最短路程 为
B
A
B
B
B"
A
A
A"
2. 如图，有一个圆柱体，它的高等于12厘 米，底面半径等于3厘米，在圆柱下底面的A 点上方1厘米处有一只蚂蚁，它想吃到上底面 C处下方1厘米Q处的食物，需要爬行的最短路 程是多少？
C ．Q
P． A
B
C
．Q
P． A
C B’
A’ D
数学奇闻
葛通藤过是阅自读然以界上中信一息种,聪你明能的设植计物一,种它方自法己解腰决杆下不列硬问,为题了吗享? 受1更.如多果的树阳的光周雨长露为,常3c常m,绕绕着一树圈干升盘高旋4c而m,上则,它它爬还行有一一圈手的绝
B
B
1
A
A
3
2C
AB＝ AC2 BC2 ＝ 52 12 ＝ 26
(3)当蚂蚁经过左面和上底面时，如图，最短路
程为
B
A
AB＝ AC2 BC2 ＝
A1
42 22
B 2
3
C
＝ 20
18 20 26
最短路程为 18即3 2cm

2、连接AB6
则AB6为最短路径
A
由勾股定理得
AB6= 22 12 5
B6
总结
从A到B共有六种最短路径
B
最短路径为 5
a2 (2a)2 5a
A
问题二
1.如图所示的长方体中,长BF=7cm, 宽AB=5cm,高AC=5cm,一只蚂蚁从点A沿着 长方体的外表面爬行到点E的最短路程为( )
（A）12 （B）17 （C）13 （D） 149
在长为5、宽为3、
B
高为4的长方体的右下
角A处有一只蚂蚁，欲
从长方体的外表面爬 4
行去吃右上角B处的食
物，问怎样爬行路径 A 最短，最短路径是多
5
3
少？
思维分析
1、长方体和立方体的情况一样吗？它们 有什么相同和不同点呢？ 和A相连的面是左面、前面和下面；
和B相连的面是上面、右面和后面. 共有六种不同的选择路径
前面右面方法一1展开前面和右面2连接ac?则ac?为最短路径由勾股定理得ac?26前面上面方法二2连接ac?则ab为最短路径ab1展开前面和上面由勾股定理得左面上面方法三2连接ac?则ac?为最短路径ac?261展开左面和上面由勾股定理得方法四2连接ac?则ac?为最短路径ac?261展开左面和后面由勾股定理得方法五2连接ac?则ac?为最短路径ac?1展开下面和右面由勾股定理得方法六2连接ac?则ac?为最短路径ac?1展开下面和后面由勾股定理得10总结从a到b共有六种最短路径最短路径为一只蚂蚁从点沿着长方体的外表面爬行到点的最短路程为a12b17c13问题二14912思维方法和过程前面左面下面上面右面后面13思维方法和过程前面左面下面上面右面后面14思维方法和过程前面左面下面上面右面后面从a到b走最短路径要走几个面

MN=CD,BD∥CE, BD=CE,
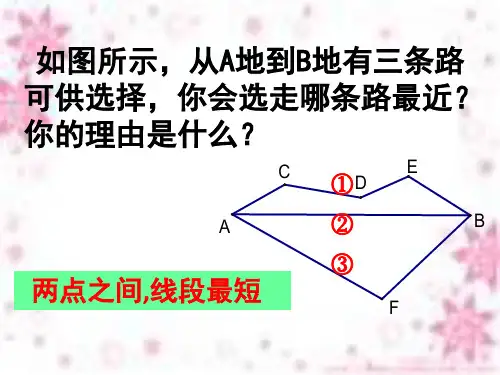
所以A到B地的路程为:AM+MN+BN=AM+MN+EM=AE+MN,
若桥的位置建在CD处，连接AC.CD.DB.CE, 则A到B地的路程为： AC+CD+DB=AC+CD+CE=AC+CE+MN,
A·
MC
在△ACE中，∵AC+CE＞AE, ∴AC+CE+MN＞AE+MN,
关知识，把两点在直线同侧问
题转化为两点在直线异侧问题。
从而用“两点之间，线段最短” A
解决问题。
·
C′
C
B
·
l
B′
如图，OM,ON是两条公路，在两条公路
之间有一油库A，现在想在两条公路分别
建一个加油站，为使运油的车从A出发先
到一个加油站再到另一个加油站，最后
回到油库A的路程最短， 问加油站应如何选址？
∴ AC +C B= AC +C B′= AB′，
AC′+C′B= AC′+C′B′．
A
在△AB′C′中，
·
AB′＜AC′+C′B′， ∴ AC +CB＜AC′+C′B．
C′ C
B
·
l
即 AC +C程，我们是通过怎样的 过程、借助什么解决问题的？
归纳：利用了轴对称的有
D
4.在⊿ABC中，
AB=5cm,BC=12cm ,DE是AC的
B
E
C 垂直平分线，交BC于点
E,⊿ABE的面积为 17cm ；
6、等腰三角形的一边长为3cm,另一边