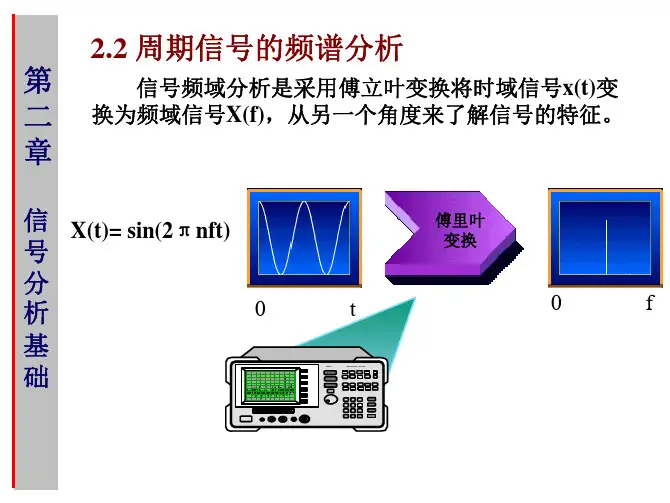
第2章:确定信号的频谱分析
- 格式:ppt
- 大小:2.28 MB
- 文档页数:121


第二章信号的分类及频谱分析信号是指携带有其中一种信息或者表达其中一种含义的波形或者序列。
信号可以被广泛应用于通信、控制、图像处理、声音处理等领域。
信号的分类主要有连续时间信号和离散时间信号、模拟信号和数字信号、周期信号和非周期信号等几种。
连续时间信号是在连续时间轴上定义的信号,它的值在任意时刻都可以取得,通常用x(t)表示。
连续时间信号可以按照时间域特性分为有限长信号和无限长信号。
有限长信号在其中一时间区间内取非零值,而在其他区间内始终为零;无限长信号在无穷远处也存在非零值。
离散时间信号是仅在离散的时间点上定义的信号,它的值仅在离散的时间点上有定义。
离散时间信号通常用x[n]表示,其中n为整数。
离散时间信号可以按照时间域特性分为有限长信号和无限长信号。
有限长离散时间信号仅在有限个点上取非零值,而在其他点上始终为零;无限长离散时间信号在正负无穷远处也存在非零值。
模拟信号是连续时间信号的一种特例,它的取值可以无限细致地变化。
模拟信号通常用x(t)表示。
数字信号是离散时间信号的一种特例,它的取值仅在离散的时间点上有定义且只能取有限个值。
数字信号通常用x[n]表示。
周期信号是在时间轴上以一定的周期性重复出现的信号,它可以表示为x(t)=x(t+T),其中T为周期。
周期信号可以进一步分为连续时间周期信号和离散时间周期信号两种。
非周期信号则是无法用一个固定的周期表示的信号。
通常情况下,任意一个非周期信号都可以用周期信号的加权叠加表示。
频谱分析是研究信号在不同频率上的成分强度分布的方法。
频谱是信号的频率表示,在频谱分析中常用的方法有傅里叶变换、快速傅里叶变换等。
傅里叶变换是将一个信号从时域转换到频域的方法,可以将一个信号拆解成一系列频率成分。
傅里叶变换的结果是一个连续变化的频谱,它可以对信号的频率特性进行详细分析。
快速傅里叶变换是一种高效的傅里叶变换算法,可以在计算机中快速计算傅里叶变换。
它利用了傅里叶变换中的对称性和周期性,大大提高了计算效率。




简单周期信号一般周期信号()⎫⎛k)(t x o m信号的“波形”振动弦(声源)周期性三角波周期性方波1 22 3nn⇒=不存在n1、n2,满足上式。
(a)(b)T’(c)矩形窗信号噪声信号(平稳)噪声信号(非平稳)(a)汽车速度连续信号每日股市的指数变化(离散信号)(d)某地每日的平均气温变化(离散信号)(e)每隔分钟测定开水房锅炉水的温度变化(离散信号)(f)每隔2得的离散信号/t )(C T o水温)um 位移一般周期信号噪声信号信号“域”的不同,是指信号的不同,或描述信号的横坐标物理量不同。
信号的时域描述:以时间为独立变量,其强调信号的值随时间变化的特征。
信号的频域描述:以角频率或频率为独立变量,其强调信号的幅值和相位随频率变化傅里叶变换时域分析频域分析的大小,它能够提供比时域信号波形更直观,丰富的信息。
谱线:按照事物的类别或系统编排记录ωx1(t)=10Sin(2π·3·t+π/6).三角频谱图3ωππ+ =ωω,谱线在横坐标的一边n nb n a ωθ=+=+,2三角波的A-ω幅频和θ-ω相频图=nR 1-0ω2121-实频图虚频图0双边幅频图双边相频图单边幅频图实频图虚频图双边幅频图ϕ双边相频图单边幅频图一般周期函数实频谱总是偶对称的,虚频谱总是奇对称的。
t的频谱图如何借助软件实现呢?——正弦函数sinω实频图虚频图双边幅频图ϕ双边相频图2⋅π2⋅π25.24352|n C 235235-2nϕ。
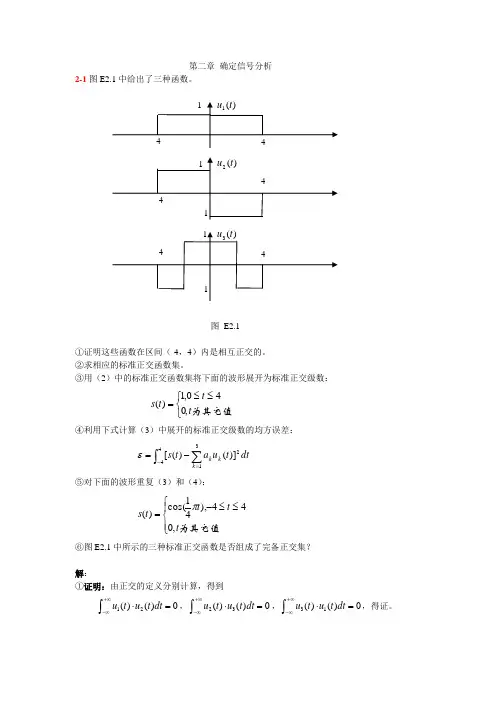
第二章 确定信号分析2-1图E2.1中给出了三种函数。
图 E2.1①证明这些函数在区间(-4,4)内是相互正交的。
②求相应的标准正交函数集。
③用(2)中的标准正交函数集将下面的波形展开为标准正交级数:⎩⎨⎧≤≤=为其它值t t t s ,040,1)(④利用下式计算(3)中展开的标准正交级数的均方误差: ⎰∑-=-=44231])()([dt t u a t s k k k ε⑤对下面的波形重复(3)和(4):⎪⎩⎪⎨⎧≤≤-=为其它值t t t t s ,044),41cos()(π ⑥图E2.1中所示的三种标准正交函数是否组成了完备正交集?解:①证明:由正交的定义分别计算,得到12()()0u t u t dt +∞-∞⋅=⎰,23()()0u t u t dt +∞-∞⋅=⎰,31()()0u t u t dt +∞-∞⋅=⎰,得证。
②解:424()8,k C u t dt k -== =1,2,3⎰,对应标准正交函数应为()(),1,2,3k k q t t k ==因此标准正交函数集为123123{(),(),()}(),()()}q t q t q t t t t =③解:用标准正交函数集展开的系数为4()(),1,2,3k k a s t q t dt k =⋅ =⎰,由此可以得到4110()()a s t t dt ===⎰4220()()a s t t dt ===⎰4330()()0a s t t dt ==⎰。
所以,121211()()()()()22s t t t u t u t ==-④解:先计算得到312111()()()()()()022k k k t s t a u t s t u t u t ε==-=-+=∑ ⑤解:用标准正交集展开的系数分别为441141()())04a s t t dt t dt π--===⎰⎰,44224011()()cos()cos()044a s t t dt t dt t dt ππ--==-=⎰⎰⎰,433422442()()111cos()))444a s t t dtt dt t dt t dt ππππ----= =-+- =⎰⎰⎰⎰。