行列式的几何意义

二阶三阶行列式的几何意义在数学中，行列式是一种用于表示矩阵的数学工具。

本文将探讨二阶和三阶行列式的几何意义，帮助读者更好地理解这一概念。

二阶行列式二阶行列式通常表示一个2x2矩阵的代数表达式。

在几何上，它可以被解释为平行四边形的面积或两点之间的距离。

具体来说，对于一个2x2矩阵A，其行列式可以表示为：| A | = | a11 a12 || :--: | :--: || A | = | a21 a22 |这个行列式的几何意义取决于矩阵A中的元素。

如果a11和a22为正，a12和a21为负，那么这个行列式表示的平行四边形面积就是正的；如果a11和a22为负，a12和a21为正，那么这个行列式表示的平行四边形面积就是负的。

如果a11和a22以及a12和a21的符号相同，那么这个行列式表示的平行四边形面积就是0。

此外，如果A表示一个向量，那么行列式|A|也可以被解释为该向量与其在原点处的反射之间的距离的平方。

三阶行列式三阶行列式通常表示一个3x3矩阵的代数表达式。

在几何上，它可以被解释为三维空间中一个平行六面体的体积或者一个三角形的面积。

具体来说，对于一个3x3矩阵A，其行列式可以表示为：A=a11 a12 a13A=a21 a22 a23A=a31 a32 a33这个行列式的几何意义取决于矩阵A中的元素。

如果a11、a22和a33均为正数，且a12、a13、a21、a23、a31和a32均为负数，那么这个行列式表示的平行六面体的体积就是正的。

如果这些元素的符号不完全相同，那么这个行列式表示的平行六面体的体积就是0。

如果元素的符号出现四种或更多种不同的情况，那么这个行列式表示的平行六面体的体积是负数。

矩阵和行列式的几何意义及其应用矩阵和行列式是数学中重要的概念，它们不仅在代数和线性代数中有着重要的应用，而且在几何中也有着深远的意义和广泛的应用。

本文将从几何角度探讨矩阵和行列式的几何意义以及它们在几何中的应用。

1.1 点、向量和坐标在几何中，我们常常需要描述空间中的点和向量，而矩阵和行列式是描述点和向量的重要数学工具。

在二维空间中，我们可以用一个二维向量来描述点的位置，如(3, 4)表示一个距离原点3个单位向右，4个单位向上的点。

将这个向量表示成一个列向量：```| 3 || 4 |```这个列向量就是一个2×1的矩阵。

同样的，我们也可以用一个2×2的矩阵表示一个二维的旋转或缩放变换。

1.2 点和线性变换在几何中，我们经常需要对空间中的点进行变换，如旋转、缩放、平移等。

这些变换可以用矩阵来表示。

设有一个二维点p(x, y)，我们可以用一个2×2的矩阵A来表示一个线性变换，对点p进行变换得到新的点p'：p' = Ap1.3 向量和矩阵的运算在几何中，我们经常需要对向量进行加法、数乘等运算，这些运算可以用矩阵来表示。

设有向量v和w，其坐标分别为v=(x1, y1, z1)和w=(x2, y2, z2)，则向量的加法和数乘运算可以表示为：v + w = (x1+x2, y1+y2, z1+z2)kv = (kx1, ky1, kz1)这些运算可以用矩阵加法和数乘来表示，即向量(矩阵)的加法和数乘等运算可以用矩阵来表示。

二、矩阵和行列式在几何中的应用2.1 点的映射2.2 向量的投影v' = nv2.3 坐标变换同样的，对于三维空间中的点，我们可以用一个3×3的矩阵来表示一个坐标变换。

这些坐标变换可以表示从一个坐标系变换到另一个坐标系。

三、结语矩阵和行列式不仅在代数和线性代数中有着重要的应用，而且在几何中也有着深远的意义和广泛的应用。

矩阵可以用来描述点、向量和坐标的几何意义，可以用来表示点和线性变换、向量投影和坐标变换等几何应用。

经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的，应 当按照 消费者 的要求 增加赔 偿其受 到的损 失，增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用

矩阵和行列式的几何意义及其应用矩阵和行列式是线性代数中非常重要的概念，它们不仅在数学理论中具有重要意义，而且在各个领域的实际应用中也有着广泛的应用。

本文将对矩阵和行列式的几何意义及其应用进行详细介绍。

一、矩阵的几何意义1. 矩阵的基本概念矩阵是由若干行和若干列组成的数组，通常用大写字母表示。

一个3×3的矩阵可以表示为：A = [a11 a12 a13a21 a22 a23a31 a32 a33]其中a11、a12、a13等是矩阵元素，3×3表示矩阵有3行3列。

矩阵中的元素可以是实数、复数、函数等。

矩阵可以表示线性变换，这种线性变换可以用来描述几何问题。

对于一个二维平面上的点(x, y)，可以用一个2×2的矩阵A进行线性变换，得到新的点(x', y')：[x'] [a11 a12] [x][y'] = [a21 a22] * [y]这个矩阵A实际上描述了一个二维变换，它可以将原来的点(x, y)变换成新的点(x', y')。

这种矩阵向量的几何意义在计算机图形学、物理学、工程学等领域中有着广泛的应用。

3. 矩阵的特征值和特征向量对于一个n阶方阵A，如果存在数λ和非零向量v，使得Av = λv，那么λ称为A 的特征值，v称为A的特征向量。

特征值和特征向量可以描述矩阵的特性，它们在几何上有着重要的意义。

特征向量v描述了矩阵A的特定方向，而特征值λ描述了在这个特定方向上的伸缩比例。

特征值和特征向量的概念在物理学、工程学、统计学等领域中都有着重要的应用，例如在求解振动问题、稳定性分析等方面起着重要作用。

行列式是一个非常重要的概念，它可以用来描述线性变换的伸缩比例和方向。

对于一个n阶方阵A，其行列式的值记作|A|，它用来描述线性变换对空间体积的伸缩情况。

2. 行列式的几何意义行列式的值为正表示线性变换不改变空间的方向和体积，值为负表示线性变换改变了空间的方向，但没有改变体积，值为零表示线性变换将空间压缩成了低维空间。

行列式为1的几何意义行列式是线性代数中的一个重要概念，它具有丰富的几何意义。

行列式的值为1时，代表了一种特殊的变换，让我们一起来探索一下这个几何意义吧。

假设我们有一个二阶行列式，形如：| a b || c d |我们来看行列式的绝对值，即|ad - bc|。

如果行列式的绝对值为1，那么代表着这个二阶行列式的变换将不改变空间的体积。

换句话说，这个变换不会对空间中的任何图形进行缩放或拉伸，而只是对其进行了旋转或镜像。

如果我们将二阶行列式的变换应用到一个平面上的点上，那么这个点将会发生怎样的变化呢？让我们通过一个具体的例子来看一下。

假设有一个点P(x, y)，经过二阶行列式的变换之后，变成了P'(x', y')。

根据行列式的定义，我们可以得到如下的变换公式：x' = ax + byy' = cx + dy假设行列式的值为1，那么我们可以得到如下的方程：x' = x + byy' = cx + y通过观察这个方程组，我们可以发现变换后的点P'相对于原始点P 的位置关系。

例如，如果b的值为0，那么x' = x，意味着变换后的点P'在x轴上与原始点P重合。

同理，如果c的值为0，那么y' = y，意味着变换后的点P'在y轴上与原始点P重合。

除了在坐标轴上发生重合的情况外，行列式为1的变换还可能导致点P'相对于原始点P发生旋转或镜像。

这将取决于a、b、c、d的具体取值。

行列式为1的几何意义是，它代表了一个不改变空间体积的变换。

这种变换可以使点P相对于原始点发生平移、旋转或镜像等操作。

通过行列式的值为1，我们可以更好地理解线性代数中的几何概念，并将其应用于实际问题的解决中。

希望通过以上的描述，读者能够更加直观地理解行列式为1的几何意义，同时也希望读者能够通过自己的实践和思考，进一步深入研究和探索行列式的几何性质。

矩阵和行列式的几何意义及其应用矩阵和行列式是线性代数中非常重要的概念，它们有着广泛的应用，涉及到许多领域，如计算机科学、机器学习、物理学等，本文将介绍它们的几何意义及其应用。

矩阵的几何意义是将几何变换表示为矩阵运算。

在三维空间中，我们可以将向量表示为三个元素的列向量。

例如，一个向量A可以表示为：```（a1）（a2）（a3）``````（cosθ -sinθ 0）（sinθ cosθ 0）（ 0 0 1）```其中cosθ和sinθ是旋转角度θ的cosine和sine。

当我们将一个向量A乘以旋转矩阵时，可以得到一个新的向量B，它对应于旋转后的向量。

具体来说，这个运算可以表示为：```| cosθ -sinθ 0 | |a1| | b1 || sinθ cosθ 0 | x |a2| = | b2 || 0 0 1 | |a3| | b3 |```这里的b1，b2和b3是旋转后的向量A的新坐标。

值得注意的是，矩阵乘法可以表示为向量的内积。

除了旋转矩阵，其他的几何变换（如平移、缩放、投影等）也可以表示为矩阵运算。

这种将几何变换转化为矩阵运算的方法被广泛应用于计算机图形学中，例如在3D建模、动画和游戏开发中。

另一方面，行列式是一个用于计算线性变换区域扩大或缩小程度的数值。

当一个矩阵的行列式为0时，它代表着某些向量之间存在线性相关性。

这种情况下，行列式可用于求解矩阵的逆矩阵，从而求解线性方程组。

除了逆矩阵和线性方程组求解，行列式还有着许多其他的应用。

例如，在微积分中，行列式可以用于计算多元函数导数的雅可比矩阵。

在物理学中，行列式可以用于计算电场和磁场的交互作用。

在概率论中，行列式可以用于计算随机向量的概率密度。

行列式的计算公式是n阶行列式的展开式， 即用代数余子式表示n阶行列式的公式。
性质
行列式的计算公式具有高度的对称性，可以方便地 计算出n阶行列式的值。
计算方法
根据行列式的展开式，将n阶行列式展开成n 个代数余子式的乘积之和。
特殊行列式的计算
01
对角线型行列式
如果一个n阶行列式的主对角线上的元素都是1，其他元素都是0，则该
该行列式称为下三角型行列式。下三角型行列式的值等于副对角线上元
素的乘积的相反数。
03
行列式在几何中的应用
行列式与向量叉积的关系
01
行列式可以表示为三个向量的叉积的线性组合，即行列式值 等于三个向量叉积的代数和。
02
当行列式值为零时，三个向量共面，即它们之间存在线性关 系。
03
行列式可以用来判断向量的叉积是否为零，从而判断三个向 量是否共面。
消元法
将方程组中的系数行列式化为0， 然后利用代数余子式求出方程组 的解。
递推法
利用递推关系式求解方程组，通 过将系数行列式展开，得到一系 列递推关系式，从而求解方程组。
克拉默法则
克拉默法则是一种利用行列 式解线性方程组的方法，其 基本思想是将方程组的解表
示为系数行列式的比值。
1
克拉默法则的前提是系数行列 式不为0，否则方程组无解。
程组无解或有无穷多解。
行列式可以用来判断方程组的解 的情况，也可以用来求解方程组 的解。
03
行列式的性质和计算方法在方程 组的求解过程中具有重要的作用
。
04
05
行列式的应用实例
利用行列式求平面上的点
确定点的位置
通过给定的行列式，我们可以确定平面上的一个点。例如，给 定一个行列式$D$和两个向量$vec{a}$和$vec{b}$，我们可以 使用行列式来找到满足$vec{a} cdot vec{x} = D$和$vec{b} cdot vec{x} = 0$的点$vec{x}$。

3阶行列式的几何意义三阶行列式的几何意义是描述了三个向量的几何特性，通常用于分析三维空间中的几何关系。

在三维空间中，我们可以表示一个向量为一个有序三元组(v1,v2,v3)，其中v1、v2、v3分别表示向量在x、y、z轴上的分量。

将三个向量分别表示为a=(a1,a2,a3)，b=(b1,b2,b3)，c=(c1,c2,c3)，那么这三个向量可以构成一个3x3的矩阵：a1a2a3b1b2b3c1c2c3我们可以通过计算这个矩阵的行列式来获得几何上的一些信息。

行列式的值可以表示这三个向量所构成的平行六面体的有向体积。

具体来说，行列式的值的绝对值等于这个平行六面体的体积，而正负号表示了平行六面体的定向。

如果行列式的值为正，则表示这三个向量按照右手定则指向了空间中的一些方向；如果行列式的值为负，则表示这三个向量按照左手定则指向了空间中的一些方向；如果行列式的值为零，则表示这三个向量共面。

共面意味着这三个向量所在的平面上的所有点都满足一个线性关系，即存在不全为零的实数k1、k2、k3，使得k1a+k2b+k3c=0。

因此，通过计算三阶行列式可以得知三个向量所构成的平行六面体的体积、定向以及共面性。

此外，还可以通过行列式的值和符号来判断三个向量之间的线性关系，例如是否共线、共面以及正交关系等。

接下来，我们将详细讨论这些几何关系。

1.体积：三阶行列式的绝对值等于平行六面体的体积。

当行列式的值非零时，平行六面体存在且具有体积；当行列式的值为零时，平行六面体退化为一个面或一条线，体积为零。

2.定向：行列式的符号表示了平行六面体的定向。

正值表示这三个向量按照右手定则指向了空间中的一些方向；负值表示这三个向量按照左手定则指向了空间中的一些方向。

具体来说，右手定则是指右手的大拇指指向向量a，食指指向向量b，中指指向向量c，如果大拇指的方向指向自己，则行列式的值为正；如果大拇指的方向指向外面，则行列式的值为负。

3.共面性：当三阶行列式的值为零时，表示这三个向量共面。

行列式的几何意义行列式的定义：行列式是由一些数据排列成的方阵经过规定的计算方法而得到的一个数。

当然，如果行列式中含有未知数，那么行列式就是一个多项式。

它本质上代表一个数值，这点请与矩阵区别开来。

矩阵只是一个数表，行列式还要对这个数表按照规则进一步计算,最终得到一个实数、复数或者多项式。

一阶行列式（注意不是绝对值）二阶行列式三阶行列式N阶行列式行列式的几何意义是什么呢？概括说来有两个解释：一个解释是行列式就是行列式中的行或列向量所构成的超平行多面体的有向面积或有向体积；另一个解释是矩阵A的行列式detA就是线性变换A下的图形面积或体积的伸缩因子。

这两个几何解释一个是静态的体积概念，一个是动态的变换比例概念。

但具有相同的几何本质，因为矩阵A表示的（矩阵向量所构成的）几何图形相对于单位矩阵E的所表示的单位面积或体积（即正方形或正方体或超立方体的容积等于1）的几何图形而言，伸缩因子本身就是矩阵矩阵A表示的几何图形的面积或体积，也就是矩阵A的行列式。

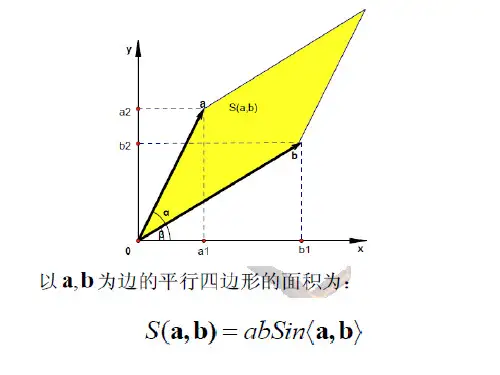
二阶行列式的几何意义：二阶行列式的几何意义是xoy平面上以行向量为邻边的平行四边形的有向面积。

二阶行列式的几何意义就是由行列式的向量所张成的平行四边形的面积。

另外，两个向量的叉积也是这个公式。

二阶行列式的另一个意义就是是两个行向量或列向量的叉积的数值，这个数值是z轴上（在二维平面上，z轴的正向想象为指向读者的方向）的叉积分量。

如果数值是正值，则与z坐标同向；负值就与z坐标反向。

如果我们不强调叉积是第三维的向量，也就是忽略单位向量，那么二阶行列式就与两个向量的叉积完全等价了。

二阶行列式性质的几何解释：两向量在同一条直线上，显然围成的四边形的面积为零，因此行列式为零这个性质由行列式的叉积特性得到，交换行列式的两行，就是改变了向量a和向量b的叉积顺序，根据，因此行列式换号。

把行列式的一行的k倍加到另一行，则行列式值不变，即矩阵的行列式等于其转置矩阵的行列式（根据行列式的定义可证）总结：（1）用一个数k乘以向量a,b中之一的a，则平行四边形的面积就相应地增大了k倍；（2）把向量a,b中的一个乘以数k之后加到另一个上，则平行四边形的面积不变；（3）以单位向量(1，0)，(0，1)构成的平行四边形(即单位正方形)的面积为1。

----图解线性代数----任广千胡翠芳编著2010.06.01《线性代数的几何意义》几何意义名言录没有任何东西比几何图形更容易印入脑际了，因此用这种方式来表达事物是非常有意义的。

-------笛卡尔算术符号是文字化的图形，而几何图形则是图像化的公式；没有一个数学家能缺少这些图像化的公式。

--------希尔伯特“如果代数与几何各自分开发展，那它的进步十分缓慢，而且应用范围也很有限，但若两者互相结合而共同发展，则就会相互加强，并以快速的步伐向着完善化的方向猛进。

”--------拉格朗日不会几何学就不会正确的思考，而不会正确思考的人不过是行尸走肉。

--------柏拉图无论是从事数学教学或研究, 我是喜欢直观的。

学习一条数学定理及其证明, 只有当我能把定理的直观含义和证明的直观思路弄明白了, 我才认为真正懂了。

--------中国当代数学家徐利治第三章 行列式的几何意义在中国古代，用筹算表示联立一次方程未知量的系数时，就有了行列式的萌芽-----排列的方式。

日本吸收了这种思想，在1683年，日本学者关孝和（Seki Takakusu）对行列式的概念和它的展开已有了清楚的叙述。

到18世纪，瑞士数学家克莱姆（G.Gramer）和法国数学家拉普拉斯（place）建立了行列式理论。

行列式的几何意义具有深刻的含义。

它是指行列式的行向量或列向量所构成的平行多面体的有向体积。

这个有向体积是由许多块更小的有向面积或有向体积的累加。

在我们逐步地讨论这个几何意义之前，先来回顾一下行列式的定义。

3.1. 行列式的定义行列式是由一些数据排列成的方阵经过规定的计算方法而得到的一个数。

当然，如果行列式中含有未知数，那么行列式就是一个多项式。

它本质上代表一个数值，这点请与矩阵区别开来。

矩阵只是一个数表，行列式还要对这个数表按照规则进一步计算,最终得到一个实数、复数或者多项式。

行列式分阶，比如二阶行列式、三阶行列式直至n 阶行列式。

行列式的几何意义及多面体体积的计算行列式的几何意义：行列式是线性代数中的一个重要概念，它表示一个矩阵或向量的“大小”或“缩放因子”。

在几何上，行列式的几何意义主要体现在以下几个方面：1. 平行四边形面积：对于一个2x2的矩阵，其行列式的值等于构成该矩阵的两个平行四边形的面积之差。

如果行列式的值为正，则两个平行四边形的面积相等；如果行列式的值为负，则第一个平行四边形的面积大于第二个平行四边形的面积；如果行列式的值为0，则两个平行四边形重叠。

2. 三角形面积：对于一个3x3的矩阵，其行列式的值等于构成该矩阵的三个平行四边形（即三个相邻的矩形）的面积之和减去三个三角形的面积。

3. 体积变换：对于一个n维的超立方体（也称为n-simplex），其行列式的值等于构成该超立方体的n+1个相邻的n维超立方体的体积之和减去n个n维超立方体的体积。

多面体体积的计算：多面体的体积计算通常需要将其分解为更简单的形状，然后分别计算这些形状的体积，最后将这些体积相加。

以下是一些常见多面体的体积计算公式：1. 立方体：V = a³，其中a为立方体的边长。

2. 四面体：V = (a²b + ab²+ b³) / 6，其中a、b为四面体的两条相对棱的长度。

3. 五面体：V = (a²b + ab²+ b³) / 4，其中a、b为五面体的两条相对棱的长度。

4. 六面体：V = (a²b + ab²+ b³) / 3，其中a、b为六面体的两条相对棱的长度。

5. 正八面体：V = 2√2 * a³/ 3，其中a为正八面体的边长。

6. 正十二面体：V = (3 + √5) * a³/ 12，其中a为正十二面体的边长。

7. 正二十面体：V = (3 + √5) * a³/ 10，其中a为正二十面体的边长。

18.1 引言这次课我们考虑行列式的几个应用.我们需要以下定理.定理：行列式某一行(列)的各元素与另一行(列)的对应元素的代数余子式乘积之和等于零. 即18.1 引言理解：18.1 引言综合定理及推论得“代数余子式的重要性质”：例：设计算18.1 引言例：设求和分析：注意到第二、第四行元素的特点，利用行列式按某行展开定理的推论，将与分别看成整体，列方程组求解.解：18.2.1 求逆矩阵公式设可逆，构造如下矩阵，称为的伴随矩阵(adjoint of ).的代数余子式矩阵.18.2.1 求逆矩阵公式例：18.2.1 求逆矩阵公式定理：设可逆，则上例：18.2.1 求逆矩阵公式证明：其中，18.2.1 求逆矩阵公式由引言中定理，故18.2.1 求逆矩阵公式例：若是一个阶阵，求的秩的可能性.解：故的列属于的零空间.而，且存在故的任意阶子矩阵不可逆.18.2.2 线性方程组的公式解设 为可逆方阵， 我们来学习 的解的公式.写成行列式的形式(难于记忆)18.2.2 线性方程组的公式解一般地，不使用行列式，公式将非常复杂.定理(Cramer’s rule)：设可逆，如上，令是将的第列换成向量后的矩阵. 则的唯一解为18.2.2 线性方程组的公式解例：解：18.2.2 线性方程组的公式解定理的证明：可逆，的唯一解是18.2.2 线性方程组的公式解考虑矩阵则的行列式可沿着第列展开，的代数余子式恰好是即因此考虑右图平行四边形的面积为方向：或取决于向量逆(顺)时针转到的有向面积18.3 计算有向长度、面积和体积三维情形：一个三阶矩阵的行列式围成的平行六面体的有向体积.18.3 计算有向长度、面积和体积特别地，若在平面上，则我们有如下推论.推论：平面上三点围成三角形的面积为18.3 计算有向长度、面积和体积证明：令为张成平行四边形面积.18.3 计算有向长度、面积和体积特别地，若和所在平面垂直，则可以通过行列式计算围成平行四边形的面积.设线性无关. 求一个向量使得18.3 计算有向长度、面积和体积设则即令则无关，可逆.18.3 计算有向长度、面积和体积其中，18.3 计算有向长度、面积和体积于是我们有平行四边形面积平行六面体的体积(高 )号：的选取有两种可能.18.3 计算有向长度、面积和体积定义：给定两个向量是一个和均垂直的向量，且形成一个右手系，等于围成的平行四边形的面积. 称为和的叉积(cross product)或外积(exterior product).18.3 计算有向长度、面积和体积定理：记作是轴上单位向量.性质：1.2.18.3 计算有向长度、面积和体积例：验证例：18.3 计算有向长度、面积和体积注：的三个坐标是和在三个坐标平面上的投影向量形成的平行四边形的面积. 例如是在平面上的投影面积.定义：给定三个向量它们的混合积或三重积(triple product)定义为即和的点积.18.3 计算有向长度、面积和体积定理：实际上，18.3 计算有向长度、面积和体积推论一：推论二：形成平行六面体的有向体积.在一个平面上推论三：1.过两点的直线方程为2.过三点的平面方程为18.3 计算有向长度、面积和体积推论三的证明：1. 共线共面.2.在所在平面共面.18.4 和QR分解的联系设可逆.Gram-Schmidt正交化给出是的长度.是平行四边形关于底上的高.是平行六面体在形成的底上的高.平行六面体体积绝对值.18.4 和QR分解的联系给定前面我们使用外积计算了形成的平行四边形的面积. 这里我们使用分解.令设线性无关( 列满秩).高定理：。

矩阵和行列式的几何意义及其应用
矩阵和行列式是线性代数的重要概念，具有广泛的几何意义和应用。

下面将对矩阵和
行列式的几何意义及其应用进行简要介绍。

我们来谈谈矩阵的几何意义。

矩阵可以看作是一个二维数组，其中的元素代表了在二
维空间中的某种量，例如坐标、长度、角度等。

通过矩阵乘法，我们可以进行各种几何变换，例如平移、旋转、缩放等。

具体来说，如果我们用一个矩阵A乘以一个向量x，就可
以得到一个新的向量y，表示将向量x进行某种变换后得到的结果。

这个变换可以表示为：y = A*x。

矩阵可以用来描述几何变换的规律，例如平移矩阵、旋转矩阵、缩放矩阵等。

行列式是矩阵的一个重要性质，它可以用来描述矩阵的行向量或列向量的线性相关性。

行列式的值代表了矩阵所包含的几何信息，例如面积、体积、方向等。

对于二维矩阵来说，行列式的值可以表示平行四边形的面积；对于三维矩阵来说，行列式的值可以表示平行六
面体的体积。

行列式还可以用来判断一个矩阵是否可逆，即是否存在逆矩阵。

如果一个矩
阵的行列式不等于零，那么它是可逆的；反之，如果行列式等于零，则矩阵不可逆。

矩阵和行列式在几何学中有广泛的应用。

其中一个重要的应用是解线性方程组。

通过
将线性方程组转化为矩阵形式，我们可以用矩阵的运算方法求解方程组的解。

对于一个包
含n个未知数和n个方程的线性方程组，可以用一个n阶矩阵表示，通过求解矩阵的逆矩
阵或者行列式等于零的条件，我们可以得到方程组的解。

矩阵和行列式还可以用来进行曲
线拟合、图像处理、数据压缩等各种几何计算。

矩阵和行列式的几何意义及其应用1. 引言1.1 矩阵和行列式的基本概念矩阵和行列式是线性代数中非常重要的概念，也是几何学中不可或缺的工具之一。

矩阵是一个由数字组成的矩形阵列，而行列式则是对一个方阵进行一系列操作得到的一个标量值。

矩阵和行列式的基本概念包括了矩阵的定义、加法和乘法运算，以及行列式的定义和性质。

在矩阵中，每个元素可以表示一个空间中的向量或者点，而矩阵的运算则可以用来描述空间中的变换和关系。

矩阵的平移和旋转应用是其中最常见的几何应用之一，在计算机图形学和机器学习中有着极其广泛的应用。

行列式则可以用来描述空间中的体积和方向，对于线性方程组的求解和空间中的几何问题有着至关重要的作用。

矩阵和行列式在三维空间的表示方法和在计算机图形学中的应用更进一步扩展了它们的应用领域，而在机器学习和人工智能领域，矩阵和行列式更是成为了不可或缺的工具。

它们的重要性不仅体现在几何学中，还体现在理论计算和实际应用中的广泛深入。

通过深入研究和应用矩阵和行列式，我们可以更好地理解和描述空间中的关系和变化，从而推动科学技术的发展和进步。

1.2 矩阵和行列式在几何中的重要性矩阵和行列式在几何中的重要性体现在它们对几何变换的描述和分析中起到至关重要的作用。

几何变换包括平移、旋转、缩放等，而矩阵和行列式可以简洁地表示这些变换。

通过矩阵的乘法运算，可以连续地应用多个变换，实现复杂的几何操作。

行列式则可以用来判断矩阵的行列间关系，比如判断矩阵是否可逆、是否存在逆矩阵等。

在几何中，矩阵和行列式的重要性体现在它们提供了一种便捷且直观的描述几何对象和操作的方式。

平移可以用矩阵的加法表示，旋转可以用矩阵乘法表示。

通过矩阵和行列式，我们可以方便地求解线性方程组、计算多边形的面积、判断平行四边形的性质等几何问题。

矩阵和行列式在几何中的重要性不可替代，它们为我们理解和解决几何问题提供了强大的工具和思维方式。

在接下来的我们将更深入地探讨矩阵和行列式在不同领域的应用，展示它们的广泛性和实用性。

矩阵和行列式的几何意义及其应用矩阵和行列式是线性代数中非常重要的概念，它们不仅在数学理论中有着重要的地位，而且在实际应用中也有着广泛的应用。

本文将介绍矩阵和行列式的几何意义及其应用。

一、矩阵的几何意义矩阵可以被看作是一个数字数组，它由行和列组成。

在几何上，矩阵可以表示一系列的几何变换，比如平移、旋转、缩放等。

1. 平移对于二维平面上的向量来说，一个平移矩阵可以表示向量在平面上的平移。

对于一个向量v=(x, y)，如果我们希望将它在x方向上平移b个单位，在y方向上平移c个单位，那么相应的平移矩阵为：T = | 1 0 || b c |当我们将向量v乘以平移矩阵T时，得到的结果就是平移后的向量。

通过以上例子，我们可以看到，矩阵在几何中有着非常重要的意义，它可以表示各种几何变换，从而帮助我们对几何问题进行分析和计算。

除了在几何中的应用，矩阵在计算机图形学、物理学、工程学等领域也有着广泛的应用。

二、行列式的几何意义行列式是一个非常重要的概念，它可以表示矩阵的“形状”，从而帮助我们理解线性变换的性质。

在几何中，行列式可以理解为表示线性变换对空间的“拉伸”或“压缩”程度。

对于一个二维矩阵A，它可以表示一个线性变换T。

如果我们用矩阵A对一个向量v=(x, y)进行变换，得到的结果就是Av。

对于这个变换，它会使得原来的面积发生改变，而这种改变的程度可以通过A的行列式det(A)来表示。

行列式大于1表示面积被“拉伸”，小于1表示面积被“压缩”，等于1表示面积保持不变。

举个例子来说，如果我们有一个二维矩阵A，它的行列式为2，那么这个矩阵对应的线性变换会使得平面上的面积变为原来的两倍。

而如果行列式为0，表示这个线性变换会把整个平面变为一条线，面积被“压缩”为0。

行列式的几何意义帮助我们理解线性变换对空间的影响，它可以帮助我们分析和理解各种几何问题。

在实际应用中，行列式常常用来判断线性方程组的解的情况，或者用来解决几何问题，比如计算面积、体积等。

《线性代数的几何意义》之三《线性代数的几何意义》之三行列式是线性代数中的一个重要概念，它在几何中有着重要的几何意义。

在本文中，我们将探讨行列式在几何中的三个主要应用。

1.行列式的绝对值表示平行体积行列式的绝对值表示由矩阵的列向量所构成的平行体的体积。

具体来说，对于一个n维空间内的矩阵A，其行列式det(A)的绝对值表示由A的n个列向量所构成的平行体的体积。

这意味着行列式可以用来计算空间中各种几何体的面积、体积等。

举个例子来说明，考虑一个三维空间中的平行四边形，它的两个边长分别由矩阵A的两个列向量表示。

那么这个平行四边形的面积就等于矩阵A的行列式的绝对值。

2.行列式为0表示线性相关行列式的值为0表示矩阵的列向量是线性相关的，也就是说它们在空间中可以表示为一条直线、一个平面或更高维度的超平面。

这是因为当矩阵的列向量线性相关时，它们的平行体会退化成为一个低维的几何体，其体积为0。

因此，行列式为0可以用来判断一个矩阵的列向量是否线性相关，从而确定它们在几何中的几何关系。

例如，考虑一个二维空间中的两个向量，它们可以表示为一个平面上的两条直线。

如果它们的行列式的值为0，那么这两个向量是线性相关的，它们在空间中可以表示为同一条直线。

3.行列式的正负表示方向行列式的正负表示了由矩阵列向量所构成的平行体的方向。

行列式为正表示平行体的方向与参考系的右手定则一致，行列式为负表示平行体的方向与参考系的右手定则相反。

这意味着行列式可以用来确定一个几何体的方向。

举个例子来说明，考虑一个二维空间中的两个向量，它们可以表示为平面上的两条线段。

如果这两个向量按照顺序排列时，它们构成的平行四边形的行列式为正，那么这个平行四边形的方向与参考系的右手定则一致；如果行列式为负，那么这个平行四边形的方向与参考系的右手定则相反。

综上所述，行列式在几何中有着重要的几何意义。

它可以表示平行体的体积，判断向量的线性相关性以及确定几何体的方向。

理解并应用行列式的几何意义，有助于我们更深入地理解线性代数的几何本质，推广到更高维度的几何空间中。

行列式性质及其计算方法
目录页
Contents Page
1. 行列式基本定义与性质 2. 行列式的基本运算规则 3. 行列式的展开定理证明 4. 特殊行列式的计算方法 5. 行列式与矩阵的关系 6. 行列式在线性方程组中的应用 7. 行列式的几何意义解释 8. 行列式计算实例与解析
行列式性质及其计算方法
行列式与矩阵的关系
▪ 行列式与矩阵在计算科学中的实现
1.在计算机中，可以通过编写程序来实现行列式和矩阵的计算 。 2.常用的计算行列式的方法包括：化三角形法、按行（列）展 开法等。 3.对于大型矩阵，可以采用一些高效算法来计算行列式，例如 LU分解法、QR分解法等。
行列式性质及其计算方法
行列式在线性方程组中的应用
行列式的基本运算规则
▪ 拉普拉斯定理
1.在n阶行列式中，取定k行（列），由这k行（列）的元素所 构成的一切k阶子式与其代数余子式的乘积的和等于行列式。 2.拉普拉斯定理亦称按k行展开定理，是行列式计算的重要工 具之一，可以用于化简和计算行列式。在使用拉普拉斯定理时 ，需要选择合适的k行（列）进行展开，并注意计算过程中的 符号变化。 以上内容仅供参考，建议查阅线性代数书籍或咨询专业人士获 取更全面和准确的信息。
行列式性质及其计算方法
行列式的基本运算规则
行列式的基本运算规则
▪ 行列式基本性质
1.行列式与其转置行列式相等。 2.互换行列式的两行（列），行列式变号。 3.行列式的某一行（列）的所有的元素都乘以同一数k，等于 用数k乘此行列式。 行列式的基本性质是行列式计算的基础，必须熟练掌握。这些 性质表明了行列式的一些基本特性和变化规律，为行列式的计 算和化简提供了重要的依据和方法。在利用性质进行计算时， 需要注意性质的适用条件和范围，以及计算过程中的符殊行列式的计算方法