数字图像直方图
- 格式:ppt
- 大小:1.12 MB
- 文档页数:51

数字图像处理作业(第三次)直方图处理第一题第二题(例3.6)1. 问题:1)编写函数Y=MyHisteq(X), 对灰度图象X进行直方图均衡化,得到均衡化后的图像Y,假设X的数据类型为uint8。
2)利用自己编写的直方图均衡化函数,重现例3.6中的实验,即对图3.16中的图像进行直方图均衡化。
2.程序:(1) 函数程序:function Y = MyHisteq(X)%对灰度图象X进行直方图均衡化,得到均衡化后的图像Y[m,n]=size(X);A=zeros(1,256);for k=0:255A(k+1)=length(find(X==k))/(m*n);endS1=zeros(1,256);for i=1:256for j=1:iS1(i)=A(j)+S1(i); %算SkendendS2=round(S1*256);for i=1:256B(i)=sum(A(find(S2==i)));endfigure,bar(0:255,B,'b');title('均衡化后的直方图');xlabel('灰度'),ylabel('出现概率')Y=X;for i=0:255Y(find(X==i))=S2(i+1);endend(2)主程序:X=imread('Fig0316(1)(top_left).tif');figure,imshow(X);Y=MyHisteq(X);figure,imshow(Y);3. 实验结果:第三题(例3.12)1. 问题:编写程序,重现例3.12中的实验,产生图3.27。
2.程序:X=imread('Fig0327(a)(tungsten_original).tif');figure,imshow(X);Y=histeq(X);figure,imshow(Y);E=4.0;k0=0.4;k1=0.02;k2=0.4;[m,n]=size(X);X1=X;Mg=sum(X1(:))/(m*n);Vg=sum(sum((X1-Mg).^2))/(m*n);for i=2:m-1for j=2:n-1X2=X1(i-1:i+1,j-1:j+1);Ms=sum(X2(:))/9;Vs=sum(sum((X2-Ms).^2))/9;if(Ms<=k0*Mg&&k1*Vg<=Vs&&Vs<=k2*Vg)X1(i,j)=E*X1(i,j);endendendfigure,imshow(X1);3. 实验结果:放大了约130倍的钨丝的SME图像:全局直方图均衡的结果:使用局部直方图统计增强后的图像:1. 问题:用自己编写编程实现中值滤波,用96页例3.14的图测试。

【数字图像处理】直⽅图的均衡与规定化很多情况下,图像的灰度级集中在较窄的区间,引起图像细节模糊。
通过直⽅图处理可以明晰图像细节,突出⽬标物体,改善亮度⽐例关系,增强图像对⽐度。
直⽅图处理基于概率论。
直⽅图处理通常包括直⽅图均衡化和直⽅图规定化。
直⽅图均衡化可实现图像的⾃动增强,但效果不易控制,得到的是全局增强的结果。
直⽅图规定化可实现图像的有选择增强,只要给定规定的直⽅图,即可实现特定增强的效果。
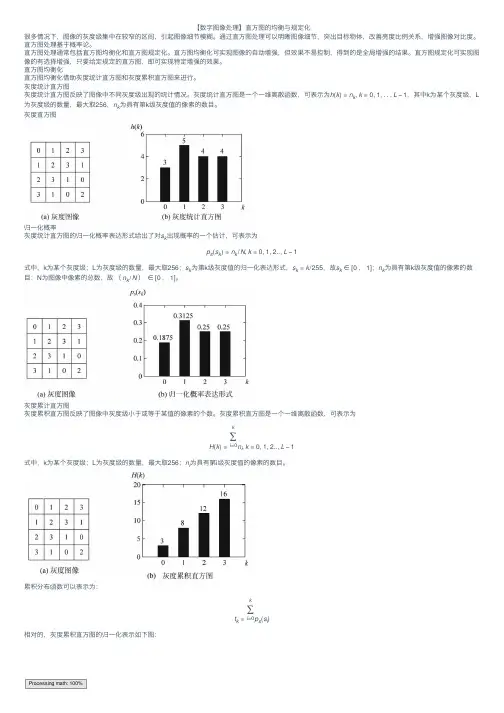
直⽅图均衡化直⽅图均衡化借助灰度统计直⽅图和灰度累积直⽅图来进⾏。
灰度统计直⽅图灰度统计直⽅图反映了图像中不同灰度级出现的统计情况。
灰度统计直⽅图是⼀个⼀维离散函数,可表⽰为h (k )=n k ,k =0,1,...L −1,其中k 为某个灰度级,L 为灰度级的数量,最⼤取256,n k 为具有第k 级灰度值的像素的数⽬。
灰度直⽅图归⼀化概率灰度统计直⽅图的归⼀化概率表达形式给出了对s k 出现概率的⼀个估计,可表⽰为p s (s k )=n k /N ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;s k 为第k 级灰度值的归⼀化表达形式,s k =k /255,故s k ∈[0,1];n k 为具有第k 级灰度值的像素的数⽬;N 为图像中像素的总数,故(n k /N )∈[0,1]。
灰度累计直⽅图灰度累积直⽅图反映了图像中灰度级⼩于或等于某值的像素的个数。
灰度累积直⽅图是⼀个⼀维离散函数,可表⽰为H (k )=k ∑i =0n i ,k =0,1,2..,L −1式中,k 为某个灰度级;L 为灰度级的数量,最⼤取256;n i 为具有第i 级灰度值的像素的数⽬。
累积分布函数可以表⽰为:t k =k ∑i =0p s (s i )相对的,灰度累积直⽅图的归⼀化表⽰如下图:Processing math: 100%原理步骤直⽅图均衡化主要⽤于增强动态范围偏⼩的图像的反差。


图像的点运算图像的点运算是图像处理中相对简单的技术,它主要用于改变一幅图像的灰度分布范围。
点运算通过一个变换函数将图像的像素一一转换,最终构成一幅新的图像。
由于操作对象是图像的一个个像素,故得名为“点运算”。
点运算的最大特点是输出像素值只与当前输入像素值有关。
点运算的图像处理过程可以用以下公式表示:g(x, y)=T[f(x, y)]其中f(x, y)表示输入图像,g(x, y)表示处理后的图像。
函数T 是对f的一种变换操作,在这里它表示灰度变换公式。
可以看到,对于点运算而言,最重要的是确定灰度变换公式。
变换公式一旦确定,点运算对于图像的处理效果就确定了。
本章研究的主要内容包括灰度直方图、线性变换、非线性变换、阈值变换、灰度拉伸及灰度均衡等。
若无特别说明,本章的点运算函数所针对的待处理对象即为8位灰度图。
■ 本章学习地图◆ 学会利用灰度直方图查看图像信息◆ 了解各种灰度变换公式◆ 掌握各种灰度变换的实现方法◆ 进一步了解各种点运算对于图像效果的影响9.1 灰度直方图本节介绍灰度直方图的相关概念和实现原理,它是提取图像信息的重要工具之一。
9.1.1 灰度直方图任何一幅图像都包含着丰富的图像信息,对于图像处理而言,如何提取这些信息并找出其中的特征就显得十分关键。
灰度直方图直观地显示了图像灰度分布的情况,这些信息在图像灰度变换等处理过程中显得十分重要。
在本章随后的内容中,也会经常通过直方图来分析变换后的图像效果。
图9-1显示一幅灰度图及它所对应的灰度直方图。
可以看到,灰度直方图是一个二维图。
从数学上来说,它描绘了图像各灰度值的统计特性,显示了各个灰度级出现的次数或概率。
从图形上来说,其横坐标表示图像的灰度值,取值范围是0到255。
其纵坐标则通过高度来表示出现次数的多少或者概率的高低。
在本章中,纵坐标表示像素出现的次数,最大值为该图像在0至 255阶灰度上分布像素出现次数的最大值。
图9-1 利用灰度直方图显示图像灰度分布需要说明的是,如果没有特别指出,在本章后续内容中的所有变换都是基于图9-1中左侧的图像进行的。

数字图像处理中的直方图均衡化使用注意事项直方图均衡化是一种通过分布调整来改善图像对比度的方法。
它通过重新分布图像的像素值以增强其视觉效果。
在数字图像处理中,直方图均衡化是一项常用的技术,但在使用过程中需要注意以下几个方面。
首先,直方图均衡化可能会导致图像细节丢失的问题。
因为直方图均衡化会根据像素值的分布进行调整,从而扩展像素值的范围,使得亮度范围更广。
但这也可能导致低对比度区域的细节消失,从而影响图像细节。
因此,在进行直方图均衡化时,应该密切关注图像的细节信息,尽量避免过度调整图像的对比度。
其次,直方图均衡化可能引起噪声的增加。
在直方图均衡化的过程中,图像的亮度分布被调整,可能会增加图像的噪声。
这是因为噪声通常与图像的低亮度区域有关,当低亮度区域被调整时,噪声也可能被放大。
为了减少噪声的影响,可以在均衡化之前对图像进行去噪处理,或者采用自适应的直方图均衡化方法,以避免过度增加图像噪声。
另外,直方图均衡化也可能导致图像的颜色失真问题。
因为直方图均衡化是基于像素值的灰度分布进行调整,对彩色图像来说,它可能会改变图像的颜色分布,从而造成颜色失真。
为了避免这种情况,可以在进行直方图均衡化前将图像转换为HSV颜色空间,并只对亮度(Value)通道进行均衡化,这样可以避免颜色的偏移。
此外,直方图均衡化的效果可能受到图像的动态范围限制。
在某些情况下,图像的动态范围可能不足以支持完整的直方图均衡化。
比如,当图像的某些区域非常亮或非常暗时,直方图可能会在动态范围两端产生剧烈的波动,从而导致图像的细节丢失或噪声增加。
为了解决这个问题,可以采用自适应的直方图均衡化方法,以根据图像的局部动态范围来进行调整,减少对整体图像的影响。
最后,直方图均衡化的选择需要根据具体的应用需求来确定。
直方图均衡化可以改善图像的对比度,使图像更加清晰和易于处理。
但对于一些特定的图像处理任务,如目标检测、图像识别等,直方图均衡化可能并不适用。

图像处理:数字图像的灰度直方图均衡化简介在数字图像处理中,灰度直方图均衡化是一种常用的图像增强技术。
它通过重新分配图像中各个灰度级的像素值,使得最终的灰度直方图呈现出更均匀分布的特点,从而提高图像的对比度和视觉效果。
原理灰度直方图是描述一幅图像中每个灰度级出现频次的统计直方图。
在灰度直方图均衡化过程中,首先需要计算原始图像的累积概率密度函数(CDF),然后利用CDF进行线性变换将原始像素值映射到新的像素值上。
这个线性变换可以通过以下公式表示:G' = (G_max - G_min) \times CDF(G) + G_min其中G'是新的像素值,G是原始的像素值,G_max和G_min分别为像素值范围最大和最小值,而CDF(G)则是原始图像中小于或等于G的累积概率密度函数。
实现步骤1.读取待处理的数字图像。
2.将彩色或多通道图转化为灰度图。
3.计算原始灰度图像的像素值的频次统计,得到原始灰度直方图。
4.计算原始灰度直方图的累积概率密度函数。
5.根据累积概率密度函数进行线性变换,将原始像素值映射到新的像素值上。
6.生成处理后得到的均衡化后的图像。
7.输出均衡化后的图像。
应用场景灰度直方图均衡化在许多领域都有广泛应用,例如医学影像分析、计算机视觉和数字摄影等。
其主要作用是增强图像对比度、改善细节和提升视觉效果。
同时,该技术也能够在一些特定场景下帮助识别和检测对象。
总结通过使用灰度直方图均衡化技术,可以使得数字图像中各个灰度级的像素值更加均匀分布,从而提高图像对比度和视觉效果。
这种方法在数字图像处理中具有广泛的应用,并且简单易实现。
然而,需要注意的是,在某些特定情况下,采用该方法可能会产生过度增强或引入噪声等问题,因此在实际应用中需要谨慎使用并结合其他处理方法进行综合处理。



数字图像处理---直⽅图均衡化直⽅图均衡化的英⽂名称是Histogram Equalization. 图像对⽐度增强的⽅法可以分成两类:⼀类是直接对⽐度增强⽅法;另⼀类是间接对⽐度增强⽅法。
直⽅图拉伸和直⽅图均衡化是两种最常见的间接对⽐度增强⽅法。
直⽅图拉伸是通过对⽐度拉伸对直⽅图进⾏调整,从⽽“扩⼤”前景和背景灰度的差别,以达到增强对⽐度的⽬的,这种⽅法可以利⽤线性或⾮线性的⽅法来实现;直⽅图均衡化则通过使⽤累积函数对灰度值进⾏“调整”以实现对⽐度的增强。
直⽅图均衡化处理的“中⼼思想”是把原始图像的灰度直⽅图从⽐较集中的某个灰度区间变成在全部灰度范围内的均匀分布。
直⽅图均衡化就是对图像进⾏⾮线性拉伸,重新分配图像像素值,使⼀定灰度范围内的像素数量⼤致相同。
直⽅图均衡化就是把给定图像的直⽅图分布改变成“均匀”分布直⽅图分布。
缺点: 1)变换后图像的灰度级减少,某些细节消失; 2)某些图像,如直⽅图有⾼峰,经处理后对⽐度不⾃然的过分增强。
直⽅图均衡化是图像处理领域中利⽤图像直⽅图对对⽐度进⾏调整的⽅法。
这种⽅法通常⽤来增加许多图像的局部对⽐度,尤其是当图像的有⽤数据的对⽐度相当接近的时候。
通过这种⽅法,亮度可以更好地在直⽅图上分布。
这样就可以⽤于增强局部的对⽐度⽽不影响整体的对⽐度,直⽅图均衡化通过有效地扩展常⽤的亮度来实现这种功能。
这种⽅法对于背景和前景都太亮或者太暗的图像⾮常有⽤,这种⽅法尤其是可以带来X光图像中更好的⾻骼结构显⽰以及曝光过度或者曝光不⾜照⽚中更好的细节。
这种⽅法的⼀个主要优势是它是⼀个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直⽅图,并且计算量也不⼤。
这种⽅法的⼀个缺点是它对处理的数据不加选择,它可能会增加背景杂讯的对⽐度并且降低有⽤信号的对⽐度。
1.连续灰度值r:待处理图像的灰度。
假设r的取值区间[0,L-1], r = 0表⽰⿊⾊,r = L - 1表⽰⽩⾊。

直方图是一种用于表示数字图像中像素灰度分布的统计图表。
它将图像的灰度范围划分为若干个等级,并统计每个等级中像素的数量,从而形成一个柱状图。
直方图的横坐标表示灰度等级,通常从最暗的黑色(0)到最亮的白色(255)进行划分。
纵坐标表示对应灰度等级的像素数量。
通过观察直方图,可以了解图像中不同灰度级别的像素分布情况。
直方图可以提供以下信息:
1. 图像的整体对比度:直方图的形状可以反映图像的整体对比度。
如果直方图的分布集中在较窄的灰度范围内,说明图像的对比度较低;如果直方图的分布较为分散,说明图像的对比度较高。
2. 像素分布情况:直方图可以显示图像中不同灰度级别的像素数量,从而了解图像的亮度分布。
如果某个灰度级别的像素数量较多,说明该灰度在图像中占据较大的比例。
3. 图像的曝光情况:通过观察直方图的左右端点,可以判断图像的曝光情况。
如果直方图的左侧截断,说明图像可能存在欠曝光;如果右侧截断,说明图像可能存在过曝光。
4. 色彩平衡:对于彩色图像,可以分别查看每个颜色通道的直方图,以评估图像的色彩平衡情况。
在图像处理中,直方图可以用于图像增强、对比度调整、色彩平衡等操作的参考。
它是一种简单而直观的工具,帮助我们了解数字图像的统计特征。
数字图像处理之直⽅图均衡化直⽅图均衡化是图像处理领域中利⽤图像直⽅图对对⽐度进⾏调整的⽅法。
直⽅图均衡化要达到的效果:基本思想:把原始图的直⽅图变换为均匀分布的形式,这样就增加了像素灰度值的动态范围,从⽽达到增强图像整体对⽐度的效果使⽤的⽅法是灰度级变换:s = T(r)原理:s=T(r) 0≤r≤1T(r)满⾜下列两个条件:(1)T(r)在区间0≤r≤1中为单值且单调递增(2)当0≤r≤1时,0≤T(r) ≤1条件(1)保证原图各灰度级在变换后仍保持从⿊到⽩(或从⽩到⿊)的排列次序条件(2)保证变换前后灰度值动态范围的⼀致性Pr(r)是r的概率密度函数,Ps(s)是s的概率密度函数,Pr(r)和T(r)已知,且T-1(s) 满⾜上述条件(1),所以有已知⼀种重要的变换函数:关于上限的定积分的导数就是该上限的积分值(莱布尼茨准则)对于离散值:其中r k 是第k个灰度级,k = 0,1,2,…,L-1. n k是图像中灰度级为r k的像素个数. n是图像中像素的总数.已知变换函数的离散形式为:sk称作直⽅图均衡化将输⼊图像中灰度级为rk(横坐标)的像素映射到输出图像中灰度级为sk (横坐标)的对应像素得到.实现代码:/******************************************************************************* 作⽤: 灰度均衡函数* 参数:* pixel 原始像素数组* tempPixel 保存变换后图像的像素数组* width 原始图像宽度******************************************************************************/void GrayEqualize(BYTE* pixel, BYTE* tempPixel, UINT width, UINT height){// 灰度映射表BYTE map[256];long lCounts[256];memset(lCounts, 0, sizeof(long) * 256);// 计算各灰度值个数for (UINT i = 0; i < width * height; i++){int x = pixel[i * 4];lCounts[x]++;}// 保存运算中的临时值long lTemp;for (int i = 0; i < 256; i++){lTemp = 0;for (int j = 0; j <= i; j++)lTemp += lCounts[j];map[i] = (BYTE)(lTemp * 255.0f / width / height);}// 变换后的值直接在映射表中查找for (UINT i = 0; i < width * height; i++){int x = pixel[i * 4];tempPixel[i*4] = tempPixel[i*4+1] = tempPixel[i*4+2] = pixel[i * 4]; tempPixel[i*4+3] = 255;}}View Code彩⾊图直⽅图均衡化:更清晰:opencv代码:////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////#include "opencv2/highgui/highgui.hpp"#include "opencv2/imgproc/imgproc.hpp"#include <iostream>using namespace cv;using namespace std;int main( int argc, const char** argv ){Mat img = imread("MyPic.JPG", CV_LOAD_IMAGE_COLOR); //open and read the imageif (img.empty()) //if unsuccessful, exit the program{cout << "Image cannot be loaded..!!" << endl;return -1;}vector<Mat> channels;Mat img_hist_equalized;cvtColor(img, img_hist_equalized, CV_BGR2YCrCb); //change the color image from BGR to YCrCb formatsplit(img_hist_equalized,channels); //split the image into channelsequalizeHist(channels[0], channels[0]); //equalize histogram on the 1st channel (Y)merge(channels,img_hist_equalized); //merge 3 channels including the modified 1st channel into one imagecvtColor(img_hist_equalized, img_hist_equalized, CV_YCrCb2BGR); //change the color image from YCrCb to BGR format (to display image properly)//create windowsnamedWindow("Original Image", CV_WINDOW_AUTOSIZE);namedWindow("Histogram Equalized", CV_WINDOW_AUTOSIZE);//show the imageimshow("Original Image", img);imshow("Histogram Equalized", img_hist_equalized);waitKey(0); //wait for key pressdestroyAllWindows(); //destroy all open windowsreturn0;}View Code代码中使⽤的函数:New OpenCV functionscvtColor(img, img_hist_equalized, CV_BGR2YCrCb)This line converts the color space of BGR in 'img' to YCrCb color space and stores the resulting image in 'img_hist_equalized'.In the above example, I am going to equalize the histogram of color images. In this scenario, I have to equalize the histogram of the intensity component only, not the color components. So, BGR format cannot be used because its all three planes represent color components blue, green and red. So, I have to convert the original BGR color space to YCrCb color space because its 1st plane representsthe intensity of the image where as other planes represent the color components.void split(const Mat& m, vector<Mat>& mv )This function splits each channel of the 'm' multi-channel array into separate channels and stores them in a vector, referenced by 'mv'. Argument listconst Mat& m - Input multi-channel arrayvector<Mat>& mv - vector that stores the each channel of the input arrayequalizeHist(channels[0], channels[0]);Here we are only interested in the 1st channel (Y) because it represents the intensity information whereas other two channels (Cr and Cb) represent color components. So, we equalize the histogram of the 1st channel using OpenCV in-built function, 'equalizeHist(..)' and other two channels remain unchanged.void merge(const vector<Mat>& mv, OutputArray dst )This function does the reverse operation of the split function. It takes the vector of channels and create a single multi-channel array. Argument listconst vector<Mat>& mv - vector that holds several channels. All channels should have same size and same depthsOutputArray dst - stores the destination multi-channel arraycvtColor(img_hist_equalized, img_hist_equalized, CV_YCrCb2BGR)This line converts the image from YCrCb color space to BGR color space. It is essential to convert to BGR color space because 'imshow(..)' OpenCV function can only show images with that color space.This is the end of the explanation of new OpenCV functions, found in the above sample code. If you are not familiar with other OpenCV functions, please refer to the previous lessons.参考博客:http://opencv-srf.blogspot.jp/2013/08/histogram-equalization.html。
数字图像处理入门—直方图修正和彩色变换这次,我们主要和调色板打交道。
先从最简单的反色讲起。
1. 反色(invert)反色就是形成底片效果。
如下图所示,图2为图1反色后的结果图1. 原图图2. 图1反色后的结果反色有时是很有用的,比如说,图1中黑色区域占绝大多数,这样打印起来很费墨,我们可以先进行反色处理再打印。
反色的实际含义是将R,G,B值反转。
若颜色的量化级别是256,则新图的R,G,B值为255减去原图的R,G,B值。
这里针对的是所有图,包括真彩图,带调色板的彩色图(又称为伪彩色图),和灰度图。
针对不同种类有不同的处理。
先看看真彩图。
我们知道真彩图不带调色板,每个像素用3个字节,表示R,G,B三个分量。
所以处理很简单,把反转后的R,G,B值写入新图即可。
再来看看带调色板的彩色图,我们知道位图中的数据只是对应调色板中的一个索引值,我们只需要将调色板中的颜色反转,形成新调色板,而位图数据不用动,就能够实现反转。
灰度图是一种特殊的伪彩色图,只不过调色板中的R,G,B值都是一样的而已。
所以反转的处理和上面讲的一样。
这里,我想澄清一个概念。
过去我们讲二值图时,一直都说成黑白图。
二值位图一定是黑白的吗?答案是不一定。
我们安装Windows95时看到的那幅setup.bmp是由蓝色和黑色组成的,但它实际上是二值图。
原来,它的调色板中的两种颜色是黑与蓝,而不是黑与白。
所以说二值图也可以是彩色的,只不过一般情况下是黑白图而已。
实现反色的源程序2. 彩色图转灰度图(color to grayscale)我们在第二讲时提到了YUV的颜色表示方法,知道在这种表示方法中,Y分量的物理含义就是亮度,它含了灰度图的所有信息,只用Y分量就完全能够表示出一幅灰度图来。
YUV和RGB之间有着如下的对应关系。
我们利用上式,根据R,G,B的值求出Y值后,将R,G,B值都赋值成Y,就能表示出灰度图来,这就是彩色图转灰度图的原理。
先看看真彩图。