立体几何基础题题库251-300(有详细答案)
- 格式:doc
- 大小:980.00 KB
- 文档页数:27

立体几何练习题及答案在学习立体几何的过程中,练习题对于巩固知识、提高应用能力起着至关重要的作用。
本文将为大家提供一些立体几何的练习题,并给出详细的答案解析,以帮助读者更好地理解和掌握立体几何的知识。
一、球的表面积和体积1. 某个球的半径为3cm,求其表面积和体积。
解析:球的表面积公式为S = 4πr²,体积公式为V = (4/3)πr³。
将半径r代入公式进行计算即可。
表面积:S = 4π(3)² = 4π(9) ≈ 113.04cm²体积:V = (4/3)π(3)³ = (4/3)π(27)≈ 113.04cm³因此,该球的表面积约为113.04cm²,体积约为113.04cm³。
二、立方体的表面积和体积2. 一个立方体的边长为5cm,求其表面积和体积。
解析:立方体的表面积公式为S = 6a²,体积公式为V = a³。
将边长a代入公式进行计算即可。
表面积:S = 6(5)² = 6(25) = 150cm²体积:V = (5)³ = 5(5)(5) = 125cm³因此,该立方体的表面积为150cm²,体积为125cm³。
三、圆柱的表面积和体积3. 一个圆柱的底面半径为4cm,高度为10cm,求其表面积和体积。
解析:圆柱的表面积公式为S = 2πr² + 2πrh,体积公式为V = πr²h。
将底面半径r和高度h代入公式进行计算即可。
表面积:S = 2π(4)² + 2π(4)(10) = 2π(16) + 2π(40) ≈ 321.2cm²体积:V = π(4)²(10) = π(16)(10) ≈ 502.4cm³因此,该圆柱的表面积约为321.2cm²,体积约为502.4cm³。

立体几何练习题及答案### 立体几何练习题及答案#### 一、选择题1. 在正方体ABCD-A1B1C1D1中,点E是棱CC1的中点,点F是棱BB1上的动点,且BF=1/3BB1,则线段AE与AF所成的角是:- A. 45°- B. 30°- C. 60°- D. 90°答案:C2. 若三棱锥P-ABC的四个顶点不共面,且PA⊥PB,PA⊥PC,PA=PB=PC=1,则三棱锥的体积为:- A. 1/6- B. √2/6- C. √3/6- D. 1/3答案:C#### 二、填空题1. 已知圆锥的底面半径为3,母线长为4,则圆锥的侧面展开图的扇形半径为______。
答案:42. 若球的半径为R,则球的内接正方体的对角线长为______。
答案:√3R#### 三、解答题1. 问题:已知正四面体ABCD的棱长为a,求正四面体的体积。
- 解答:设正四面体的高为h,由正四面体的性质知,底面三角形的高为h',有h' = √3/2 * a。
由勾股定理得,h = √(a^2 - (h'/2)^2) = √(3/4 * a^2)。
正四面体的体积V = (1/3) * 底面积 * 高 = (1/3) * (√3/4 * a^2) * h = (√2/12) * a^3。
2. 问题:已知球的半径为R,求球的内接正四面体的棱长。
- 解答:设正四面体的棱长为l,由球的内接正四面体的性质知,正四面体的高h与球的半径R和棱长l满足关系:h = √3/6 * R,l =√8/3 * h。
将h代入得l = √2R/3。
#### 四、证明题1. 问题:证明正方体中,对角线AC1与棱AB所成的角等于45°。
- 解答:在正方体ABCD-A1B1C1D1中,AC1是体对角线,AB是棱。
由于正方体的对角线AC1平分面A1B1C1D1,所以AC1与面A1B1C1D1垂直。
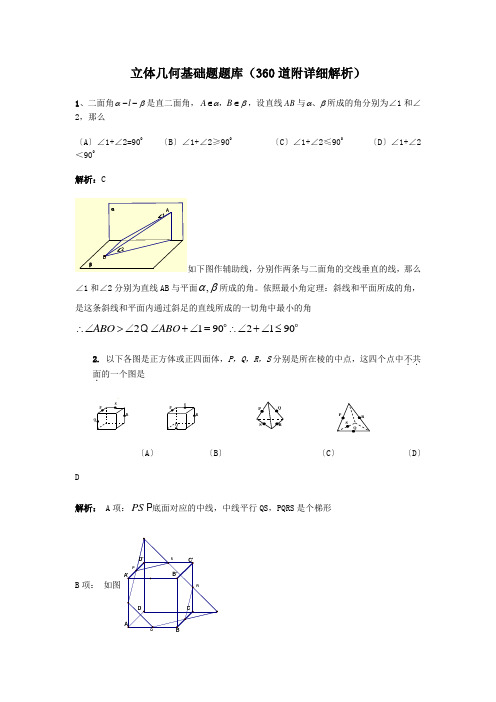
立体几何基础题题库(360道附详细解析)1、二面角βα--l 是直二面角,βα∈∈B A ,,设直线AB 与βα、所成的角分别为∠1和∠2,那么〔A 〕∠1+∠2=900〔B 〕∠1+∠2≥900〔C 〕∠1+∠2≤900〔D 〕∠1+∠2<900解析:C分别作两条与二面角的交线垂直的线,那么∠1和∠2分别为直线AB 与平面,αβ所成的角。
依照最小角定理:斜线和平面所成的角,是这条斜线和平面内通过斜足的直线所成的一切角中最小的角2ABO ∴∠>∠1902190ABO ∠+∠=∴∠+∠≤o o Q2. 以下各图是正方体或正四面体,P ,Q ,R ,S 分别是所在棱的中点,这四个点中不共..面.的一个图是PPQQRSSPPPQQRR RSSSPP PQQQR RS SS PP Q QR RRSS〔A 〕 〔B 〕 〔C 〕 〔D 〕 D解析: A 项:PS P 底面对应的中线,中线平行QS ,PQRS 是个梯形B 项: 如图C 项:是个平行四边形D 项:是异面直线。
〔A 〕假设α,β,γ两两相交,那么有三条交线〔B 〕假设α⊥β,α⊥γ,那么β∥γ〔C 〕假设α⊥γ,β∩α=a ,β∩γ=b ,那么a ⊥b 〔D 〕假设α∥β,β∩γ=∅,那么α∩γ=∅ D解析:A 项:如正方体的一个角,三个平面相交,只有一条交线。
B 项:如正方体的一个角,三个平面互相垂直,却两两相交。
C 项:如图4.如下图,在正方体ABCD -A 1B 1C 1D 1的侧面AB 1内有一动点P 到直线AB 与直线B 1C 1的距离相等,那么动点P 所在曲线的形状为AP A 1B PA 1BPA 1O BP A O ABDP A C 1D 1C解析:11B C ⊥平面AB 111,B C PB ∴⊥,如图:PCD C'D'BB'AA'P 点到定点B 的距离与到定直线AB 的距离相等,建立坐标系画图时能够以点B 1B 的中点为原点建立坐标系。

2023高中数学立体几何复习题集附答案一、立体几何基础知识立体几何是数学中的一个重要分支,主要研究空间内的图形、体积和表面积等相关性质。
掌握立体几何的基础知识对于高中数学学习尤为重要。
下面是一些常见的立体几何概念及其性质:1. 空间中的点、线、面是立体几何中最基本的概念。
点是没有长度、宽度和高度的,线是由无数个点组成的,面是由无数条线组成的。
2. 立体是由许多平面相互连接而成的。
这些平面称为面,每个面都有其特定的几何形状,如三角形面、矩形面等。
3. 空间中的距离有两种:直线距离和曲线距离。
直线距离是两点之间最短的距离,而曲线距离则是沿着曲线的长度。
4. 空间中的体积是指一个物体占据的空间大小。
常见的几何体体积计算公式有:长方体的体积为底面积乘以高,球体的体积为4/3乘以π半径的立方,圆柱体的体积为底面积乘以高等。
5. 表面积是指立体图形外表面的总面积。
计算几何体表面积的公式与计算体积的公式类似,只是不同几何体的取值不同。
二、复习题1. 长方体A的长、宽、高分别为3cm、4cm和5cm,计算长方体A的表面积和体积。
解答:长方体的表面积公式为S = 2(ab + ac + bc),其中a、b和c分别是长方体的三个边长。
代入数据后,可得长方体A的表面积为:S = 2(3*4 + 3*5 + 4*5) = 94cm²长方体的体积公式为V = lwh,其中l、w和h分别是长方体的三个边长。
代入数据后,可得长方体A的体积为:V = 3*4*5 = 60cm³因此,长方体A的表面积为94cm²,体积为60cm³。
2. 一个四棱锥的底面是一个边长为6cm的正方形,其高度为8cm。
计算该四棱锥的体积和表面积。
解答:四棱锥的体积公式为V = 1/3 * 底面积 * 高度。
底面为正方形,因此底面积为6²=36cm²。
代入数据后,可得四棱锥的体积为:V = 1/3 * 36 * 8 = 96cm³四棱锥的表面积公式为S = 底面积 + 侧面积。

立体几何试题及答案一、选择题1. 已知一个正方体的体积为8立方厘米,那么它的棱长为多少厘米?A. 2B. 4C. 3D. 2√2答案:C2. 一个长方体的长、宽、高分别为3厘米、4厘米、5厘米,那么它的表面积是多少平方厘米?A. 62B. 94C. 96D. 100答案:B3. 一个圆锥的底面半径为3厘米,高为4厘米,那么它的体积是多少立方厘米?A. 36πB. 48πC. 72πD. 96π答案:B二、填空题4. 如果一个圆柱的底面半径为5厘米,高为10厘米,那么它的体积是_____立方厘米。
答案:7855. 一个球的体积是4/3π立方厘米,那么它的半径是_____厘米。
答案:16. 一个棱锥的底面是边长为4厘米的正方形,高为5厘米,那么它的体积是_____立方厘米。
答案:32三、解答题7. 已知一个圆锥的底面半径为3厘米,高为5厘米,求圆锥的体积。
解:圆锥的体积公式为V = 1/3πr²h,代入数据得:V = 1/3 × π × 3² × 5 = 15π(立方厘米)答:圆锥的体积为15π立方厘米。
8. 一个正四面体的棱长为a厘米,求它的体积。
解:正四面体的体积公式为V = a³√2/12,代入数据得:V = a³√2/12(立方厘米)答:正四面体的体积为a³√2/12立方厘米。
9. 一个长方体的长、宽、高分别为2a厘米、a厘米、a厘米,求它的体积。
解:长方体的体积公式为V = 长× 宽× 高,代入数据得:V = 2a × a × a = 2a³(立方厘米)答:长方体的体积为2a³立方厘米。

立体几何练习题及解析一、选择题1. 下列哪个是正方体?A. 圆柱体B. 球体C. 锥体D. 正四面体解析:正确答案为D。
正四面体是一个具有四个等边三角形面的多面体,也是一种立体几何体。
2. 以下哪个是圆锥体?A. 立方体B. 正方形C. 圆柱体D. 球体解析:正确答案为C。
圆柱体的两个底面都是同心圆,且高度与底面的半径相等。
3. 以下哪个不是球体的属性?A. 没有棱B. 没有边C. 没有顶点D. 没有底面解析:正确答案为D。
球体没有底面,它是由无数个相同半径的小球面组成的。
二、填空题1. 立方体有多少个面?解析:立方体有6个面。
2. 锥体有多少个顶点?解析:锥体有1个顶点。
3. 正四面体有多少个边?解析:正四面体有6个边。
三、计算题1. 一个圆柱体的底面半径为5 cm,高度为8 cm,计算其体积和表面积。
解析:圆柱体的体积公式为V = πr²h,表面积公式为S = 2πrh + 2πr²。
将底面半径r = 5 cm,高度h = 8 cm代入公式计算得:V = π(5)²(8) = 200π cm³S = 2π(5)(8) + 2π(5)² = 80π + 50π = 130π cm²2. 一个球体的半径为10 cm,计算其体积和表面积。
解析:球体的体积公式为V = (4/3)πr³,表面积公式为S = 4πr²。
将半径r = 10 cm代入公式计算得:V = (4/3)π(10)³ = 4000π/3 cm³S = 4π(10)² = 400π cm²3. 一个正方体的边长为6 cm,计算其体积和表面积。
解析:正方体的体积公式为V = a³,表面积公式为S = 6a²。
将边长a = 6 cm代入公式计算得:V = 6³ = 216 cm³S = 6(6)² = 216 cm²四、解答题1. 画出一个平行六面体,其中底面是边长为4 cm的正方形,高度为6 cm。
2024年数学七年级上册立体几何基础练习题(含答案)试题部分一、选择题:1. 下列哪个图形是正方体?()A. 长方体B. 正六面体C. 圆柱体D. 球体2. 一个长方体的长、宽、高分别为2cm、3cm、4cm,它的对角线长度是多少cm?()A. 5cmB. 6cmC. 7cmD. 9cm3. 下列哪个图形的表面积最小?()A. 正方体B. 长方体C. 球体D. 圆柱体4. 一个正方体的体积是64立方厘米,它的棱长是多少厘米?()A. 2cmB. 4cmC. 6cmD. 8cm5. 下列哪个图形有6个面?()A. 三棱锥B. 四棱锥C. 圆锥D. 球体6. 一个圆柱的底面半径为3cm,高为5cm,它的侧面积是多少平方厘米?()A. 45πcm²B. 54πcm²C. 75πcm²D. 90πcm²7. 下列哪个图形的体积最大?()A. 长方体(长、宽、高分别为2cm、3cm、4cm)B. 正方体(棱长为3cm)C. 球体(半径为2cm)D. 圆柱体(底面半径为2cm,高为3cm)8. 一个圆锥的底面半径为4cm,高为3cm,它的体积是多少立方厘米?()A. 48πcm³B. 64πcm³C. 72πcm³D. 96πcm³9. 下列哪个图形可以展开成一个长方形?()A. 正方体B. 球体C. 圆锥D. 圆柱体10. 一个正方体的棱长为x,它的表面积是多少?()A. 6x²B. 8x²C. 12x²D. 24x²二、判断题:1. 正方体的六个面都是正方形。
()2. 圆柱体的底面和顶面都是圆形。
()3. 球体的表面积和体积相等。
()4. 长方体的对角线长度等于其长、宽、高的和。
()5. 圆锥的体积等于底面积乘以高。
()6. 正方体的体积是棱长的三次方。
()7. 两个相同体积的正方体,它们的表面积也相同。
立体几何练习题及答案立体几何练习题及答案立体几何是数学中的一个重要分支,它研究的是空间中的几何形体。
在我们的日常生活中,立体几何无处不在,比如建筑物、雕塑、家具等。
掌握立体几何的基本概念和解题方法,不仅可以提高我们的空间想象能力,还能帮助我们解决实际问题。
下面,我将给大家提供一些立体几何的练习题及答案,希望能对大家的学习有所帮助。
1. 题目:一个正方体的体积是64立方单位,求它的边长。
解答:设正方体的边长为a,则根据正方体的性质可知,它的体积等于边长的立方,即a³=64。
两边开立方根,得到a=4。
所以,这个正方体的边长是4个单位。
2. 题目:一个圆柱的底面半径为3cm,高为8cm,求它的体积和表面积。
解答:圆柱的体积公式为V=πr²h,其中r是底面半径,h是高。
代入已知条件,可得V=π×3²×8=72π。
所以,这个圆柱的体积是72π立方厘米。
圆柱的表面积公式为A=2πrh+2πr²。
代入已知条件,可得A=2π×3×8+2π×3²=48π+18π=66π。
所以,这个圆柱的表面积是66π平方厘米。
3. 题目:一个球的半径为5cm,求它的体积和表面积。
解答:球的体积公式为V=4/3πr³,其中r是半径。
代入已知条件,可得V=4/3π×5³=500/3π。
所以,这个球的体积是500/3π立方厘米。
球的表面积公式为A=4πr²。
代入已知条件,可得A=4π×5²=100π。
所以,这个球的表面积是100π平方厘米。
4. 题目:一个圆锥的底面半径为6cm,高为10cm,求它的体积和表面积。
解答:圆锥的体积公式为V=1/3πr²h,其中r是底面半径,h是高。
代入已知条件,可得V=1/3π×6²×10=120π。
所以,这个圆锥的体积是120π立方厘米。
立体几何基础题题库251-300(有详细答案)251. 已知两平面α,β相交于直线a ,直线b 在β内与直线a 相交于A 点,直线c 在平面α内与直线a 平行,请用反证法论证b,c 为异面直线.解析:这题规定用反证法,提出与结论相反的假定后,要注意分可能的几种情况讨论. 证:用反证法.假设b,c 共面,则b ∥c 或b,c 相交.(1)若b ∥c,∵ c ∥a, ∴ a ∥b 这与b ∩a =A 的已知条件矛盾;(2)若b ∩c =P,∵ b ⊂β,∴ P ∈β.又∵ c ⊂α,∴ P ∈α. ∴ P ∈α∩β而α∩β=a.∴ P ∈a ,这样c,a 有了公共点P ,这与a ∥c 的已知条件矛盾.综上所述,假设不成立,所以b 、c 为异面直线.说明 本题如不指明用反证法,也可以考虑用平面直线的判定定理来证明.252. 如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,异面直线AA 1和1BD 的中点分别是E 、F.(1)证明EF 是AA 1与BD 1的公垂线段;(2)求异面直线AA 1和BD 1间的距离.解析:(1)连接ED 1、EB ,则显然ED 1=EB =25a 又F 为BD 1之中点.∴ EF ⊥BD 1;连接FA 1,FA.∵ F 为正方体的中心,∴ FA =FA 1,又E 为AA 1之中点,∴ EF ⊥A 1A.故EF 为AA 1与BD 1的公垂线段.(2)在Rt ΔEFD 1中EF =2121FD ED -=a a a 22434522=-. 故AA 1到BD 1间的距离是a 22. 评析:今后学习了线面的位置关系之后,可以利用“转化”的思想求距离.253. 如图所示,正三棱锥S —ABC 的侧棱与底面的边长相等,如果E 、F 分别为SC 、AB 的中点,求异面直线EF 与SA 所成的角.解析:计算EF 、SA 所成的角,可把SA 平移,使其角的顶点在EF 上.为此取SB 之中点G ,连GE 、GF 、BE 、AE ,由三角形中位线定理:GE =21BC ,GF =21SA ,且GF ∥SA ,所以∠GFE 就是EF 与SA 所成的角.若设此正三棱锥棱长为a ,那么GF =GE =21a,EA =EB =23a,EF =22)21(AB EA -=22a ,因为ΔEGF 为等腰直角三角形.∠EFG =45°,所以EF 与SA 所成的角为45°.说明 异面直线所成角的求法:利用定义构造角,可固定一条,平移另一条,或同时平移到某个特殊的位置,顶点选在特殊的位置上,通过证明所作的角就是所求的角或者补角,解三角形,可求.254. 在空间四边形ABCD 中,M 、N 、P 、Q 分别是四边上的点,且满足MB AM =NB CN =QD AQ =PDCP =k. (1)求证:M 、N 、P 、Q 共面.(2)当对角线AC =a,BD =b ,且MNPQ 是正方形时,求AC 、BD 所成的角及k 的值(用a,b 表示) 解析:(1)∵ MB AM =QDAQ =k ∴ MQ ∥BD ,且MB AM AM +=1+k k ∴ BDMQ =AB AM =1+k k ∴ MQ =1+k k BD 又 NB CN =PDCP =k ∴ PN ∥BD ,且NB CN CN +=1+k k ∴ BD NP =CB CN =1+k k 从而NP =1+k k BD ∴ MQ ∥NP ,MQ ,NP 共面,从而M 、N 、P 、Q 四点共面. (2)∵ MABM =k 1,NC BN =k 1 ∴ MABM =NC BN =k 1,MA BM BM +=11+k ∴ MN ∥AC ,又NP ∥BD.∴ MN 与NP 所成的角等于AC 与BD 所成的角.∵ MNPQ 是正方形,∴ ∠MNP =90°∴ AC 与BD 所成的角为90°,又AC =a ,BD =b ,AC MN =BA BM =11+k ∴ MN =11+k a 又 MQ =11+k b,且MQ =MN , 1+k k b =11+k a ,即k =ba . 说明:公理4是证明空间两直线平行的基本出发点.255.已知:直线a 和直线b 是异面直线,直线c ∥a ,直线b 与c 不相交,求证:b 、c 是异面直线.证:因为b,c 不相交,b 、c 的位置关系有b ∥c 或b 、c 异面两种可能.假设b ∥c,∵ c ∥a,∴ a ∥b ,这与已知a,b 是异面直线矛盾.所以b 与c 不能平行,又b 、c 不相交所以b,c 是异面直线.256.分别和两条异面直线AB 、CD 同时相交的两条直线AC 、BD 一定是异面直线,为什么? 证明:假设AC 、BD 不异面,则它们都在某个平面α内,这时A 、B 、C 、D 四点都在α上,由公理1知A 、B 、C 、D ⊂α,这与已知AB 与CD 异面矛盾,所以AC 、BD 一定是异面直线.257. 如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( ) A.1715 B.21 C. 178 D. 23解析:过A 点在平面ABB 1A 1内作AF ,使A 1F =D 1F 1,则ADF 1F 是平行四边形,∴FA ∥DF 1,再过E 1在平面ABB 1A 1内作E 1E ∥FA ,则∠BE 1E 即是BE 1与DF 1所成的角,由已知BE 1=DF 1=411B A ,ABCD —A 1B 1C 1D 1是正方体,∴ E 1E =417A 1B 1, 又DF 1=AF =E 1E ,DF 1=BE 1.∴ E 1E =417A 1B 1,EB =21A 1B 1 在ΔBE 1E 中,cos ∠BE 1E =11221212BE E E BE BE E E ⋅⋅-+=1715. ∴ 应选A.258. 在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( ) A.23 B.1010 C.53 D.52解析:由图所示,AM 与CN 是异面直线,过N 作平行于AM 的平行线NP ,交AB 于P ,由定义可知∠PNC 就是AM 与CN 所成的角.因ΔPBC ,ΔPBN ,ΔCBN 皆为直角三角形,且BP =41,BN =21,BC =1,故PN 2=(41)2+(21)2=165,CN 2=(21)2+12=45,PC 2=(41)2+12=1617,在ΔPCN 中cos ∠PNC =CNPN PC CN PN ⋅-+2222,所以cos ∠PNC =52,因此应选D. 259. 已知异面直线a 与b 所成的角为50°,P 为空间一定点,则过点P 且与a 、b 所成的角都是30°的直线有且仅有( )A.1条B.2条C.3条D.4条解析: 过P 点分别作直线a ′∥a,b ′∥b,则a ′与b ′的夹角为50°,由异面直线所成的角的定义可知,过P 点与a ′,b ′成30°角的条数,就是所求的条数.画图可知,过P 点与a ′、b ′成30°角的直线只有两条.∴ 应选B.260. .若a 、b 为异面直线,P 为空间一点,过P 且与a 、b 所成角均为3π的直线有( ) A.二条B.二条或三条C.二条或四条D.二条、三条或四条 解析:D261. 已知空间四边形ABCD ,E 、H 分别是AB 、AD 的中点,F 、G 分别是边BC 、DC 的三等分点.求证:①对角线AC 、BD 是异面直线,②EF 和HG 必交于一点,且交点在AC 上.解析:①提示:用反证法,或者用判定定理.②提示:先证EH ∥FG ,EH <FG ,设FE ∩GH =0又 0∈GH.GH ⊂平面ADC.∴O ∈平面ADC.同理O ∈平面ABC.∴O 在平面ADC 和平面ABC 的交线AC 上.262.如果直线a 垂直于直线b ,那么直线a 与平行于直线b 的任意一条直线b ′互相垂直 解析:在a 上任取一点A ,过A 作b 1∥b ,则a 与b 1垂直.∵b ∥b ′,b ∥b 1 ∴b 1∥b ′∴直线a 与b 1和a 与b ′所成的角相等.∴a ⊥b ′263. 在一块长方形木块的面上有一点P ,木匠师傅要用锯子从P 和CD 将木块分成两块,问怎样画线.解析:过P 作C 1D 1的平行线EF ,连DE 、CF.264.异面直线l 1、l 2,它们之间的距离为1,所成角是3,它们的公垂线是AB ,A ∈l 1,B ∈l 2.E ∈l 1,F ∈l 2,AE =BF =1,求EF 的长.解析:如图,用异面直线l 1、l 2作为长方体的上、下底面的对角线,公垂线AB 为高. ①EF 的长即是正方形PEE ′F 的对角线长,为2.②侧面G F EE ''的对角线E F ',用勾股定理得E F '=2,即为所求.265.试证:两两相交且不全过同一点的四条直线共面.解析:(1)设a 、b 、c 、d 四条直线两两相交,且不过同一点,并且无三线共点.记 a ∩b =A,a ∩c =C,c ∩b =B,∵ a ∩b =A,∴ a 、b 确定平面α.∴ B ∈b,C ∈a. ∴ B 、C ∈α.∴ BC ⊂α,即c ⊂α,同理d ⊂α从而 a 、b 、c 、d 共面(2)若有三线共点,不妨设b 、c 、d 相交于A ,a ∩b =B ,a ∩c =C,a ∩d =D.∴ a 与A 可确定平面α.∵ B ∈a. ∴B ∈α,于是b ⊂α.同理,c ⊂α,d ⊂α.从而a 、b 、c 、d 共面.266. 正方体的两条体对角线所夹角的正弦值为______________。
立几测001试一、选择题:1.a 、b 是两条异面直线,下列结论正确的是( )A .过不在a 、b 上的任一点,可作一个平面与a 、b 都平行B .过不在a 、b 上的任一点,可作一条直线与a 、b 都相交C .过不在a 、b 上的任一点,可作一条直线与a 、b 都平行D .过a 可以且只可以作一个平面与b 平行2.空间不共线的四点,可以确定平面的个数为 ( )A.0 B.1 C.1或4 D.无法确定3.在正方体1111ABCD A B C D -中,M 、N 分别为棱1AA 、1BB 的中点,则异面直线CM 和1D N 所成角的正弦值为 ( ) A.19 B.2345 254.已知平面α⊥平面β,m 是α内的一直线,n 是β内的一直线,且m n ⊥,则:①m β⊥;②n α⊥;③m β⊥或n α⊥;④m β⊥且n α⊥。
这四个结论中,不正确...的三个是 ( )A.①②③ B.①②④ C.①③④ D.②③④5.一个简单多面体的各个面都是三角形,它有6个顶点,则这个简单多面体的面数是( ) A. 4 B. 5 C. 6 D. 86. 在北纬45°的纬度圈上有甲、乙两地,两地经度差为90°,则甲、乙两地最短距离为(设地球半径为R )( ) A.R π42 B. R 3π C. R 2π D. 3R7. 直线l ⊥平面α,直线m ⊂平面β,有下列四个命题(1)m l ⊥⇒βα// (2)m l //⇒⊥βα (3)βα⊥⇒m l // (4)βα//⇒⊥m l 其中正确的命题是( )A. (1)与(2)B. (2)与(4)C. (1)与(3)D. (3)与(4)8. 正三棱锥的侧面均为直角三角形,侧面与底面所成角为α,则下列不等式成立的是( ) A. 60πα<< B.46παπ<< C.34παπ<< D.23παπ<<9.ABC ∆中,9AB =,15AC =,120BAC ∠=︒,ABC ∆所在平面α外一点P 到点A 、B 、C 的距离都是14,则P 到平面α的距离为( )A.7 B.9 C.11 D.1310.在一个45︒的二面角的一个平面内有一条直线与二面角的棱成角45︒,则此直线与二面角的另一个平面所成角的大小为 ( )A.30︒ B.45︒ C.60︒ D.90︒11. 如图,E, F 分别是正方形SD 1DD 2的边D 1D,DD 2的中点, 沿SE,SF,EF 将其折成一个几何体,使D 1,D,D 2重合,记作 D.给出下列位置关系:①SD ⊥面DEF; ②SE ⊥面DEF;③DF ⊥SE; ④EF ⊥面SED,其中成立的有: ( )A. ①与② B. ①与③ C. ②与③ D. ③与④12. 某地球仪的北纬60度圈的周长为6πcm,则地球仪的表面积为( )A. 24πcm 2B. 48πcm 2C. 144πcm 2D. 288πcm 2二、填空题(本大题共4小题,每小题4分,共16分) 13. 直二面角α—MN —β中,等腰直角三角形ABC 的斜边BC ⊂α,一直角边AC ⊂β,BC 与β所成角的正弦值是46,则AB 与β所成角大小为__________。
立体几何基础题题库2501-300(有详细答案)251. 已知两平面α,β相交于直线a ,直线b 在β内与直线a 相交于A 点,直线c 在平面α内与直线a 平行,请用反证法论证b,c 为异面直线.解析:这题规定用反证法,提出与结论相反的假定后,要注意分可能的几种情况讨论. 证:用反证法.假设b,c 共面,则b ∥c 或b,c 相交.(1)若b ∥c,∵ c ∥a, ∴ a ∥b 这与b ∩a =A 的已知条件矛盾;(2)若b ∩c =P,∵ b ⊂β,∴ P ∈β.又∵ c ⊂α,∴ P ∈α. ∴ P ∈α∩β而α∩β=a.∴ P ∈a ,这样c,a 有了公共点P ,这与a ∥c 的已知条件矛盾.综上所述,假设不成立,所以b 、c 为异面直线.说明 本题如不指明用反证法,也可以考虑用平面直线的判定定理来证明.252. 如图,在棱长为a 的正方体ABCD —A 1B 1C 1D 1中,异面直线AA 1和1BD 的中点分别是E 、F.(1)证明EF 是AA 1与BD 1的公垂线段;(2)求异面直线AA 1和BD 1间的距离.解析:(1)连接ED 1、EB ,则显然ED 1=EB =25a 又F 为BD 1之中点.∴ EF ⊥BD 1;连接FA 1,FA.∵ F 为正方体的中心,∴ FA =FA 1,又E 为AA 1之中点,∴ EF ⊥A 1A.故EF 为AA 1与BD 1的公垂线段.(2)在Rt ΔEFD 1中EF =2121FD ED -=a a a 22434522=-. 故AA 1到BD 1间的距离是a 22. 评析:今后学习了线面的位置关系之后,可以利用“转化”的思想求距离.253. 如图所示,正三棱锥S —ABC 的侧棱与底面的边长相等,如果E 、F 分别为SC 、AB 的中点,求异面直线EF 与SA 所成的角.解析:计算EF 、SA 所成的角,可把SA 平移,使其角的顶点在EF 上.为此取SB 之中点G ,连GE 、GF 、BE 、AE ,由三角形中位线定理:GE =21BC ,GF =21SA ,且GF ∥SA ,所以∠GFE 就是EF 与SA 所成的角.若设此正三棱锥棱长为a ,那么GF =GE =21a,EA =EB =23a,EF =22)21(AB EA -=22a ,因为ΔEGF 为等腰直角三角形.∠EFG =45°,所以EF 与SA 所成的角为45°.说明 异面直线所成角的求法:利用定义构造角,可固定一条,平移另一条,或同时平移到某个特殊的位置,顶点选在特殊的位置上,通过证明所作的角就是所求的角或者补角,解三角形,可求.254. 在空间四边形ABCD 中,M 、N 、P 、Q 分别是四边上的点,且满足MB AM =NB CN =QD AQ =PDCP =k. (1)求证:M 、N 、P 、Q 共面.(2)当对角线AC =a,BD =b ,且MNPQ 是正方形时,求AC 、BD 所成的角及k 的值(用a,b 表示) 解析:(1)∵ MB AM =QDAQ =k ∴ MQ ∥BD ,且MB AM AM +=1+k k ∴ BDMQ =AB AM =1+k k ∴ MQ =1+k k BD 又 NB CN =PDCP =k ∴ PN ∥BD ,且NB CN CN +=1+k k ∴ BD NP =CB CN =1+k k 从而NP =1+k k BD ∴ MQ ∥NP ,MQ ,NP 共面,从而M 、N 、P 、Q 四点共面. (2)∵ MA BM =k1,NC BN =k 1 ∴ MABM =NC BN =k 1,MA BM BM +=11+k ∴ MN ∥AC ,又NP ∥BD.∴ MN 与NP 所成的角等于AC 与BD 所成的角.∵ MNPQ 是正方形,∴ ∠MNP =90°∴ AC 与BD 所成的角为90°,又AC =a ,BD =b ,AC MN =BA BM =11+k ∴ MN =11+k a 又 MQ =11+k b,且MQ =MN , 1+k k b =11+k a ,即k =ba . 说明:公理4是证明空间两直线平行的基本出发点.255.已知:直线a 和直线b 是异面直线,直线c ∥a ,直线b 与c 不相交,求证:b 、c 是异面直线.证:因为b,c 不相交,b 、c 的位置关系有b ∥c 或b 、c 异面两种可能.假设b ∥c,∵ c ∥a,∴ a ∥b ,这与已知a,b 是异面直线矛盾.所以b 与c 不能平行,又b 、c 不相交所以b,c 是异面直线.256.分别和两条异面直线AB 、CD 同时相交的两条直线AC 、BD 一定是异面直线,为什么? 证明:假设AC 、BD 不异面,则它们都在某个平面α内,这时A 、B 、C 、D 四点都在α上,由公理1知A 、B 、C 、D ⊂α,这与已知AB 与CD 异面矛盾,所以AC 、BD 一定是异面直线.257. 如图,ABCD —A 1B 1C 1D 1是正方体,B 1E 1=D 1F 1=411B A ,则BE 1与DF 1所成角的余弦值是( ) A.1715 B.21 C. 178 D. 23解析:过A 点在平面ABB 1A 1内作AF ,使A 1F =D 1F 1,则ADF 1F 是平行四边形,∴FA ∥DF 1,再过E 1在平面ABB 1A 1内作E 1E ∥FA ,则∠BE 1E 即是BE 1与DF 1所成的角,由已知BE 1=DF 1=411B A ,ABCD —A 1B 1C 1D 1是正方体,∴ E 1E =417A 1B 1, 又DF 1=AF =E 1E ,DF 1=BE 1.∴ E 1E =417A 1B 1,EB =21A 1B 1 在ΔBE 1E 中,cos ∠BE 1E =11221212BE E E BE BE E E ⋅⋅-+=1715. ∴ 应选A.258. 在棱长为1的正方体ABCD —A 1B 1C 1D 1中,M 和N 分别为A 1B 1和BB 1的中点,那么直线AM 与CN 所成角的余弦值是( ) A.23 B.1010 C.53 D.52解析:由图所示,AM 与CN 是异面直线,过N 作平行于AM 的平行线NP ,交AB 于P ,由定义可知∠PNC 就是AM 与CN 所成的角.因ΔPBC ,ΔPBN ,ΔCBN 皆为直角三角形,且BP =41,BN =21,BC =1,故PN 2=(41)2+(21)2=165,CN 2=(21)2+12=45,PC 2=(41)2+12=1617,在ΔPCN 中cos ∠PNC =CN PN PC CN PN ⋅-+2222,所以cos ∠PNC =52,因此应选D. 259. 已知异面直线a 与b 所成的角为50°,P 为空间一定点,则过点P 且与a 、b 所成的角都是30°的直线有且仅有( )A.1条B.2条C.3条D.4条解析: 过P 点分别作直线a ′∥a,b ′∥b,则a ′与b ′的夹角为50°,由异面直线所成的角的定义可知,过P 点与a ′,b ′成30°角的条数,就是所求的条数.画图可知,过P 点与a ′、b ′成30°角的直线只有两条.∴ 应选B.260. .若a 、b 为异面直线,P 为空间一点,过P 且与a 、b 所成角均为3π的直线有( ) A.二条B.二条或三条C.二条或四条D.二条、三条或四条 解析:D261. 已知空间四边形ABCD ,E 、H 分别是AB 、AD 的中点,F 、G 分别是边BC 、DC 的三等分点.求证:①对角线AC 、BD 是异面直线,②EF 和HG 必交于一点,且交点在AC 上.解析:①提示:用反证法,或者用判定定理.②提示:先证EH ∥FG ,EH <FG ,设FE ∩GH =0又 0∈GH.GH ⊂平面ADC.∴O ∈平面ADC.同理O ∈平面ABC.∴O 在平面ADC 和平面ABC 的交线AC 上.262.如果直线a 垂直于直线b ,那么直线a 与平行于直线b 的任意一条直线b ′互相垂直 解析:在a 上任取一点A ,过A 作b 1∥b ,则a 与b 1垂直.∵b ∥b ′,b ∥b 1 ∴b 1∥b ′∴直线a 与b 1和a 与b ′所成的角相等.∴a ⊥b ′263. 在一块长方形木块的面上有一点P ,木匠师傅要用锯子从P 和CD 将木块分成两块,问怎样画线.解析:过P 作C 1D 1的平行线EF ,连DE 、CF.264.异面直线l 1、l 2,它们之间的距离为1,所成角是3,它们的公垂线是AB ,A ∈l 1,B ∈l 2.E ∈l 1,F ∈l 2,AE =BF =1,求EF 的长.解析:如图,用异面直线l 1、l 2作为长方体的上、下底面的对角线,公垂线AB 为高. ①EF 的长即是正方形PEE ′F 的对角线长,为2.②侧面G F EE ''的对角线E F ',用勾股定理得E F '=2,即为所求.265.试证:两两相交且不全过同一点的四条直线共面.解析:(1)设a 、b 、c 、d 四条直线两两相交,且不过同一点,并且无三线共点.记 a ∩b =A,a ∩c =C,c ∩b =B,∵ a ∩b =A,∴ a 、b 确定平面α.∴ B ∈b,C ∈a. ∴ B 、C ∈α.∴ BC ⊂α,即c ⊂α,同理d ⊂α从而 a 、b 、c 、d 共面(2)若有三线共点,不妨设b 、c 、d 相交于A ,a ∩b =B ,a ∩c =C,a ∩d =D.∴ a 与A 可确定平面α.∵ B ∈a. ∴B ∈α,于是b ⊂α.同理,c ⊂α,d ⊂α.从而a 、b 、c 、d 共面.266. 正方体的两条体对角线所夹角的正弦值为______________。
232 解析:易知A D BC 11//,故A C BD 11与两条体对角线相交,设交点为O (如图),则∠∠BOC AOB 或即为所成的角。
设正方体棱长为1,则A B A C 1123==,,BC =1,所以tg BA C ∠=122,而∠=∠BOC BA C 21,故 tg BOC ∠=⨯-=222122222(),即cos 221119∠=+∠=BOC tg BOC , s i n s i n 289232∠=∴∠=B O C B O C267.长方体ABCD A B C D -1111中,BC CD DD ===2214251,,,则A C B D 111和所成角的大小为______________。
60︒解析:如图所示,将B D 11平移到A F 1,则在∆A FC 1中A F A C CF FA C FA C 11122212372372231260===∠=+-⨯⨯=∴∠=︒;;,故cos () 268. 根据叙述作图,指出二面角α -l -β 的平面角,并证明.(1)已知α ∩β =l ,A ∈l (图9-39).在α 内作P A ⊥l 于A ,在β 内作QA ⊥l 于A .图9-39(2)已知α ∩β =l ,A ∈α ,l A ∉(图9-40).作AP ⊥β 于P ,在α 内作AQ ⊥l 于Q ,连结PQ .图9-40(3)已知α ∩β =l ,α∉A ,β∉A (图9-41).作AP ⊥α 于P ,AQ ⊥β 于Q ,l ∩平面P AQ =H ,连结PH 、QH .解析:(1)P A α ,QA β ,P A ⊥l ,QA ⊥l ,∴ ∠P AQ 为二面角的平面角.(2)∵ AP ⊥β ,∴ PQ 为AQ 在平面β 内的射影,∵ AQ ⊥l ,根据三垂线定理,有PQ ⊥l ,∴ ∠AQP 为二面角的平面角(如图答9-35).(3)∵ AP ⊥α ,∴ AP ⊥l ,∵ AQ ⊥β ,∴ AQ ⊥l ,∴ l ⊥平面P AQ ,∵ PH ·QH 平面P AQ ,∴ l ⊥PH ,l ⊥QH ,∴ ∠PHQ 为二面角的平面角(如图答9-36).269.如图9-42,立体图形A-BCD中,AC=AD,BC=BD.求作二面角A-CD-B的平面角,并说明理由.解析:取CD中点E,连结AE、BE,∵AC=AD,∴AE⊥CD.∵BC=BD,∴BE⊥CD,∴∠AEB为二面角A-CD-B的平面角.270.若二面角α -l-β 的一个半平面α 上有一个点A,点A到棱l的距离是它到另一个平面β 的距离的2倍,则这个二面角的大小为().A.90°B.60°C.45°D.30°解析:D.作AH⊥β 交β 于H,作HB⊥l于B,连结AB,由三垂线定理,HB⊥l,∴∠ABH 为二面角α -l-β 的平面角,由已知在Rt△ABH中,AB=2AH,∴∠ABH=30°.271.下列命题中正确的是().A.平面α 和β 分别过两条互相垂直的直线,则α ⊥βB.若平面α 内的一条直线垂直于平面β 内的两条平行直线,则α ⊥βC.若平面α 内的一条直线垂直于平面β 内的两条相交直线,则α ⊥βD.若平面α 内的一条直线垂直于平面β 内的无数条直线,则α ⊥β解析:C.α 内的直线l垂直β 内的相交直线a、b,则l⊥β .∵lα ,∴α ⊥β .272. 设两个平面互相垂直,则( ).A .一个平面内的任何一条直线都垂直于另一个平面B .过交线上一点垂直于一个平面的直线必在另一个平面上C .过交线上一点垂直于交线的直线,必垂直于另一个平面D .分别在两个平面内的两条直线互相垂直 解析:B .如图答9-38,在正方体1111D C B A ABCD -中,平面D D AA 11⊥平面ABCD ,其中D A 1平面D D AA 11,但D A 1不垂直平面ABCD ,故A 不正确.点D 在交线AD 上,AD D C ⊥1,但D C 1不垂直平面ABCD ,故C 不正确.1AD 平面D D AA 11,AC 平面ABCD ,但1AD 与AC 不垂直,故D 不正确.273. 如图9-43,∠AOB 是二面角α -CD -β 的平面角,AE 是△AOB 的OB 边上的高,回答下列问题,并说明理由:(1)CD 与平面AOB 垂直吗?(2)平面AOB 与α 、β 垂直吗?(3)AE 与平面β 垂直吗?解析:(1)∵ ∠AOB 是二面角α -CD -β 的平面角,∴ OB ⊥CD ,OA ⊥CD ,∴ CD ⊥平面AOB .(2)∵ CD ⊥平面AOB ,CD α ,∴ α ⊥平面AOB .同理β ⊥平面AOB .(3)∵ CD ⊥平面AOB ,∵ AE ⊂平面AOB ,∴ CO ⊥AE ,又∵ AE ⊥OB ,CD ∩OB =O ,∴ AE ⊥平面BCD ,即AE ⊥β .274. 如图9-44,以等腰直角三角形的斜边BC 上的高AD 为折痕,使△ABD 和△ACD 折成相垂直的两个面.求证:BD ⊥CD ,∠BAC =60°.图9-44解析:∵ AD 是等腰△ABC 底边BC 上的高线,∴ AD ⊥BD ,AD ⊥DC ,∴ ∠BDC 是二面角B -AD -C 的平面角,∵ 平面ABD ⊥平面ACD ,∴ ∠BDC =90°,即BD ⊥DC .连结BC ,设AD =a ,则BD =DC =AD =a ,a AB 2=,a AC 2=,a BC 2=,∴ △ABC是正三角形,∴ ∠BAC =60°275. 直线a 、b 是异面直线,a ⊥平面α,b ⊥平面β,a ⊥b ,求证:α⊥β.证明 过b 上任意一点作直线a ′,使a ∥a ′.∵a ⊥b,∴a ⊥b.设相交直线a ′、b 确定一个平面γ,γ∩β=c.∵b ⊥β,c ⊂β,∴b ⊥c.在平面γ内,b ⊥c,b ⊥a ′,∴a ′∥c.∴a ∥a ′∥c.又∵a ⊥α,∴c ⊥α,c ⊂β,∴β⊥α 276. 在三棱锥S —ABC 中,∠ASB =∠BSC =60°,∠ASC =90°,且SA =SB =SC ,求证:平面ASC ⊥平面ABC.证明 取AC 的中点O ,连SO 、BO ,由已知,得ΔSAB 、ΔSBC 都是正三角形.∴BC =AB =a,SA =SC =a,又SO ⊥AC ,BO ⊥AC ,∴∠SOB 就是二面角S —AC —B 的平面角.又∵SA =AB =a,SC =BC =a,AC =AC,∴ΔACS ≌ΔACB.∴SO =BO =22a.在ΔSOB 中,∵SB =a,∴∠SOB =90°. 即平面SAC ⊥平面ABC.另证:过S 作SO ⊥平面ABC ,垂足是O.∵SA =SB =SC ,∴S 在平面内的射影是ΔABC 的外心,同前面的证明,可知ΔABC 是直角三角形,∴O 在斜边AC 上.又∵平面SAC 经过SO ,∴平面SAC ⊥平面ABC说明 证明“面面垂直”的常用方法是根据定义证明平面角是90°,或利用判定定理证明一个平面经过另一个平面的垂线.277. 如图,四面体ABCD 的棱BD 长为2,其余各棱的长均是2,求:二面角A—BD —C 、A —BC —D 、B —AC —D 的大小.解析:(1)取BD 的中点O ,连AO 、OC.在ΔABD 中,∵AB =AD =2,BD =2,∴ΔABD 是等腰直角三角形,AO ⊥BD ,同理OC ⊥BD.∴∠AOC 是二面角A —BD —C 的平面角又AO =OC =1,AC =2,∴∠AOC =90°.即二面角A —BD —C 为直二面角.(2)∵二面角A —BD —C 是直二面角,AO ⊥BD ,∴AO ⊥平面BCD.∴ΔABC 在平面BCD 内的射影是ΔBOC.∵S ΔOCB =21,S ΔABC =23,∴cos θ=33.即二面角A —BC —D 的大小是arccos 33. (3)取AC 的中点E ,连BE 、DE.∵AB =BC ,AD =DC ,∴BD ⊥AC ,DE ⊥AC ,∴∠BED 就是二面角的平面角.在ΔBDE 中,BE =DE =26,由余弦定理,得cos α=-31 ∴二面角B —AC —D 的大小是π-arccos 31. 评析 本例提供了求二面角大小的方法:先作出二面角的平面角,再利用其所在的三角形算出角的三角函数值,或利用面积的射影公式S ′=S ·cos θ求得.278. 如图所示,在三棱锥S —ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交AC 、SC 于D 、E.又SA =AB ,SB =SC.求以BD 为棱,以BDE 与BDC 为面的二面角的度数.解法一:由于SB =BC ,且E 是SC 中点,因此BE 是等腰三角形SBC 的底边SC的中线,所以SC ⊥BE.又已知SC ⊥DE ,BE ∩DE =E ,∴SC ⊥平面BDE ,∴SC ⊥BD ,又∵SA ⊥底面ABC ,BD 在底面ABC 上,∴SA ⊥BD.而SA ∩SC =S ,所以BD ⊥平面SAC.∵DE =平面SAC ∩平面BDE ,DC =平面SAC ∩平面BDC ,∴BD ⊥DE ,BD ⊥DC.∴∠EDC 是所求二面角的平面角.∵SA ⊥底面ABC ,∴SA ⊥AB ,SA ⊥AC.设SA =a,则AB =a,BC =SB =2a.又AB ⊥BC ,所以AC =3a.在Rt ΔSAC 中tg ∠ACS =AC SA =31,所以∠ACS =30°. 又已知DE ⊥SC ,所以∠EDC =60°,即所求的二面角等于60°.解法二:由于SB =BC ,且E 是SC 的中点,因此BE 是等腰ΔSBC 的底边SC 的中线,所以SC ⊥BE.又已知SC ⊥DE ,BE ∩DE =E.∴SC ⊥平面BDE ,SC ⊥BD.由于SA ⊥底面ABC ,且A 是垂足,所以,AC 是SC 在平面ABC 上的射影,由三垂线定理的逆定理得BD ⊥AC ;又E ∈SC ,AC 是SC 在平面内的射影,所以E 在平面ABC 内的射影在AC 上,由于D ∈AC ,所以DE 在平面ABC 内的射影在AC 上,根据三垂线定理得BD ⊥DE.∵DE ⊂平面BDE ,DC ⊂平面BDC.∴∠EDC 是所求二面角的平面角.以下解法同解法一.279. 在直三棱柱ABC —A ′B ′C ′中,∠BAC =90°,AB =BB ′=1,直线B ′C 与平面ABC 成30°的角.(如图所示)(1)求点C ′到平面AB ′C 的距离;(2)求二面角B -B ′C —A 的余弦值.解析:(1)∵ABC —A ′B ′C ′是直三棱柱,∴A ′C ′∥AC ,AC ⊂平面AB ′C ,∴A ′C ′∥平面AB ′C ,于是C ′到平面AB ′C 的距离等于点A ′到平面AB ′C 的距离,作A ′M ⊥AB ′于M.由AC ⊥平面AB ′A ′得平面AB ′C ⊥平面AB ′A ′,∴A ′M ⊥平面AB ′C ,A ′M 的长是A ′到平面AB ′C 的距离.∵AB =B ′B =1,⊥B ′CB =30°,∴B ′C =2,BC =3,AB ′=2,A ′M =A A A A B A ''⨯''=22.即C ′到平面AB ′C 的距离为22; (2)作AN ⊥BC 于N ,则AN ⊥平面B ′BCC ′,作NQ ⊥B ′C 于Q ,则AQ ⊥B ′C ,∴∠AQN 是所求二面角的平面角,AN =BCAC AB ⨯=36,AQ =C B B A AC ''⨯=1.∴sin ∠AQN =AQ AN =36,cos ∠AQN =33. 说明 利用异面直线上两点间的距离公式,也可以求二面角的大小,如图,AB =BB ′=1,∴AB ′=2,又∠B ′CB =30°,∴BC =3,B ′C =2,AC =2.作AM ⊥B ′C 于M ,BN ⊥B ′C 于N ,则AM =1,BN =23, CN =23,CM =1,∴MN =21.∵BN ⊥B ′C,AM ⊥B ′C ,∴BN 与AM 所成的角等于二面角B —B ′C —A 的平面角.设为θ.由AB 2=AM 2+BN 2+MN 2-2AM ×BN ×cos θ得cos θ=31=33.280 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小.解析:(1)设O 是AC ,BD 的交点,连结EO.∵ABCD 是菱形,∴O 是AC 、BD 的中点,∵E 是PA 的中点,∴EO ∥PC ,又PC ⊥平面ABCD ,∴EO ⊥平面ABCD ,EO ⊂平面BDE ,∴平面BDE ⊥平面ABCD.(2)EO ∥PC ,PC ⊂平面PBC ,∴EO ∥平面PBC ,于是点O 到平面PBC 的距离等于E 到平面PBC 的距离.作OF ⊥BC 于F ,∵EO ⊥平面ABCD ,EO ∥PC ,PC ⊂平面PBC ,∴平面PBC ⊥平面ABCD ,于是OF ⊥平面PBC ,OF 的长等于O 到平面PBC 的距离.由条件可知,OB =2a ,OF =2a ×23=43a ,则点E 到平面PBC 的距离为43a. (3)过O 作OG ⊥EB 于G ,连接AG ∵OE ⊥AC ,BD ⊥AC ∴AC ⊥平面BDE∴AG ⊥EB(三垂线定理) ∴∠AGO 是二面角A —EB —D 的平面角∵OE =21PC =21a,OB =23a ∴EB =a.∴OG =EB OB OE ⋅=43a 又AO =21a. ∴tan ∠AGO =OGAO =332∴∠AGO =arctan 332. 评析 本题考查了面面垂直判定与性质,以及利用其性质求点到面距离,及二面角的求法,三垂线定理及逆定理的应用.281. 如图,矩形ABCD 中,AB =2,BC =23,以AC 为轴翻折半平面,使二平面角B —AC —D 为120°,求:(1)翻折后,D 到平面ABC 的距离;(2)BD 和AC 所成的角.解析:研究翻折问题,通常要画出翻折前的平面图形和翻折后的空间图形,对应点的字母要相同.解 分别过B 、D 作AC 的垂线,垂足是E 、F ,过F 作FB ′∥BE ,过B 作BB ′∥AC ,交点B ′,则四边形EFB ′B 是矩形.∵AC ⊥DF ,AC ⊥B ′F ,∴AC ⊥平面B ′FD ,即∠DF ′B 就是二面角B —AC —D 的平面角,亦即∠DFB ′=120°.过D 作DO ⊥B ′F ,垂足为O.∵DO ⊂平面DFB ′,AC ⊥平面DFB ′.∴DO ⊥AF ,DO ⊥平面ABC. 在Rt ΔADC 中,CD =2,AD =23,∴DF =3,OD =DF ·sin60°=23. (2)在ΔDFB ′中,DB ′=︒⋅'⋅⋅-'+120cos 22F B DF F B DF =3.又由(1)可知,AC ∥BB ′,AC ⊥平面DFB ′⊥平面DFB ′.∴BB ′⊥平面DFB ′,∴ΔDB B ′是直角三角形,又BB ′=EF =2.∴tan ∠DBB ′=23. ∵AC ∥BB ′,∴AC 与BD 所成的角就是∠DBB ′,即为arctan23. 说明 处理翻折问题,只要过不在棱上的点作棱的垂直相交的线段,就可以化成基本题型处理,本题也可以这样考虑,即利用异面直线DF 、BE 上两点B 、D 间的距离,先求出BD 2=EF 2+DF 2+BE 2-2DF ·BE ·cos120°=13,从而得出∠DBB ′=arccos 132. 282. 判断下列命题是否正确,并说明理由.(1)若两个平面有无数个公共点,则这两个平面重合;(2)在一个平面内有三条直线和另一个平面平行,那么这两个平面平行;(3)若两个平面相交,那么分别在这两个平面内的两条直线也相交;(4)如果两个平面平行,那么分别在这两个平面内的两条直线也平行;(5)一条直线与两个平行平面所成的角相等;(6)一条直线与两个平行平面中的一个平行,那么一定平行于另一个平面.解析:(1)不正确.两个平面还可能相交于一条直线;(2)不正确.两个平面可能相交,这三条直线均与交线平行;(3)不正确.分别在两个相交平面内的两条直线也可能平行,它们都平行于交线;(4)不正确.两条直线还可能异面;(5)正确.无论直线与两个平面相对位置如何,直线与两个平面所成的角都相等;(6)不正确.直线可能在另一个平面上.283. 平面α ∥平面β ,a α ,b β ,则a 、b 一定是( ).A .两条平行直线B .异面直线C .相交直线D .无公共点的两条直线解析:D .α ∥β ,则平面α 与β 无公共点,a 、b 一定无公共点.284. 下列命题中,不正确的是( ).A .一直线和两个平面α 、β 所成的角相等,那么α ∥βB .平面α ∥平面β ,则α 内的任意直线平行于平面βC .一个三角形有两条边所在直线平行一个平面,那么三角形所在平面与这个平面平行D .分别在两个平行平面内的两条直线只能是平行直线或异面直线解析:A .直线与两平面所成的角相等,这两个平面可能相交,故A 命题不正确.三角形两边必相交,这两条相交直线平行于一个平面,那么三角形所在平面与这个平面平行,所以C 命题正确,分别在两个平行平面内的两条直线一定没有公共点,它们的位置关系是平行或异面.285. 若a ∥b ,a ⊥α ,b ⊥β ,则α 、β 这两个平面的位置关系是________.解析:平行.. ////βαβαα⇒⎭⎬⎫⊥⊥⇒⎭⎬⎫⊥b b b a a286. 夹在两平行平面α 、β 间的线段AB =8,AB 与α 所成的角为45°,那么α 、β 间的距离等于________. 解析:24.如图答9-27,过A 作AH ⊥α ,交α 于H ,AH 为平面α 与β 间的距离.连结BH ,则BH 是AB 在平面α 内的射影,∴ ∠ABH =45°.∵ AB =8,∴ ︒⋅=45sin AB AH .24228=⨯= 287. .三个不同平面α ,β ,γ 满足α ∥β ,β ∩γ =l ,则α 与γ 的位置关系是________;若三个平面满足α ∥β ,β ∥γ ,则α 与γ 的位置关系是________.解析:相交;平行.作直线l ⊥β ,∵ α ∥β ,∴ l ⊥α ,∵ β ∥γ ,∴ l ⊥γ .∴ α ∥γ .当α ∥β ,β ∩γ =l ,假设α 与γ 不相交,则α ∥γ ,∵ α ∥β ,由前面证明可知β ∥γ ,这与β 、γ 相交矛盾.∴ α 与γ 相交.288. 已知直线a 平面α ,直线b 平面β ,α b ,a ∥β ,b ∥α .求证:α ∥β .解析:如图答9-29,在b 上任取一点P ,由点P 和直线a 确定的平面γ 与平面β 交于直线c ,则c 与b 相交于点P ..//////////βααααγβγβa P cb bc c a ca c a a ⇒⎪⎭⎪⎬⎫=⇒⎪⎭⎪⎬⎫⊆/≠⊂⇒⎪⎭⎪⎬⎫=≠⊂图答9-29289..B.A不正确是因为直线b可以在平面α 内,也可能与α 平行,还可能与α 相交但不成直角,C中的直线b只与β 内的直线a垂直,不能得出垂直β 的结论.D中α 、β 可能相交,α 内的两条直线均与交线平行290.给出以下命题:①平行于同一条直线的两条直线平行;②垂直于同一条直线的两条直线平行;③平行于同一个平面的两条直线平行;④垂直于同一个平面的两条直线平行;⑤平行于同一条直线的两个平面平行;⑥垂直于同一条直线的两个平面平行;⑦平行于同一个平面的两个平面平行.其中正确的命题是________(把你认为正确的命题的序号都写上).解析:①、④、⑥、⑦.由公理4知①正确.由直线与平面垂直的性质定理知④正确.由两个平面平行判定定理可以推导出⑥、⑦正确.垂直于同一条直线的两条直线的位置关系是平行、相交、或异面;平行于同一个平面的两条直线的位置关系是平行、相交、或异面;平行于同一条直线的两个平面的位置关系是平行或相交.291.给出下列命题,错误的命题是().A.若直线a平面α ,且α ∥平面β ,则直线a与平面β 的距离等于平面α 、β 间的距离B.若平面α ∥平面β ,点A∈α ,则点A到平面β 的距离等于平面α 、β 间的距离C .两条平行直线分别在两个平行平面内,则这两条直线间的距离等于这两个平行平面间的距离D .两条异面直线分别在两个平行平面内,则这两条直线间的距离等于这两个平行平面间的距离解析:C .以下按顺序说明,对A 中,在a 上任取一点P ,作PH ⊥β ,PH 为直线a 与平面β 的距离.∵ α ∥β ,PH ⊥α ,∴ PH 又为α 、β 间的距离.对于B ,作AH ⊥β ,AH 的长为点A 到β 的距离.又∵ α ∥β ,∴ AH ⊥α ,于是AH 的长是α 、β 两个平行平面间的距离.对于C ,设a ∥b ,a α ,b β ,过a 上任一点P 作PQ ⊥b 于Q ,则PQ 的长为a 、b 两平行直线间的距离.因为PQ 与α 、β 不一定垂直,所以PQ 的长一般不是α 、β 间的距离,一般地说,a 、b 间的距离不小于α 、β 间的距离.对于D .设1AA 是异面直线a 、b 的公垂线段,A ∈a ,b A ∈',a α ,b β ,过A 和b 的平面与α 相交于b ',则b b //',于是b A A '⊥'.∴ α⊥'A A .同理β⊥'A A .故A A '的长又是α 、β 两个平面间的距离(如图答9-30).292. 设α 、β 是两个平面,l 和m 是两条直线,那么α ∥β 的一个充分条件是( ).A .l α ,m α ,且l ∥β ,m ∥βB .l α ,m β ,且l ∥mC .l ⊥α ,m ⊥β ,且l ∥mD .l ∥α ,m ∥β ,且l ∥m解析:C .可参看图答9-31.图答9-31293. 平面α ∥平面β ,过平面α 、β 外一点P 引直线P AB 分别交α 、β 于A 、B 两点,P A =6,AB =2,引直线PCD 分别交α 、β 于C 、D 两点.已知BD =12,则AC 的长等于( ).A .10B .9C .8D .7解析:B .如图答9-32,平面PBD ∩α =AC ,平面PBD ∩β =BD ,∵ α ∥β ,∴ AC ∥BD .由平面几何知识知,BD AC PD PC PB PA ==.∵ P A =6,AB =2,BD =12,∴ 12266AC =+,∴ AC =9.294. 已知AC ,BD 是夹在两平行平面α 、β 间的线段,A ∈α ,B ∈α ,C ∈β ,D ∈β ,且AC =25cm ,BD =30cm ,AC 、BD 在平面β 内的射影的和为25cm ,则AC 、BD 在平面β 内的射影长分别为________,AC 与平面β 所成的角的正切值为________,BD 与平面β 所成的角的正切值为________.解析:设α 、β 间的距离为h ,AC 在平面β 内的射影x C A =',BD 在平面β 内的射影y D B =',根据已知条件可得②-①得22222530-=-x y ,即222530))((-=-+x y y x ,把③代入得y -x =11,∴ ⎩⎨⎧=-=+.,1125x y y x 解得⎩⎨⎧==.,187y x 即cm 7='C A ,cm 18='D B .又h =24cm ,AC 与平面β 所成的角为A AC '∠,='∠A AC tan 724='C A h ,同理.341824tan =='='∠D B h D BD 295. 已知空间不共面的四个点,与此四个点距离都相等的平面有________个.解析:与不共面的四个点距离相等的平面分为两类,一类是四个点中一个点位于平面的一侧,另外三个点在平面的另一侧,这样的平面有4个;另一类是四个点中的两个点位于平面一侧,另外两个点在平面的另一侧,这样的平面有3个,故一共7个平面到这四个点距离相等. 296. 如图9-35,平面α ∥平面β ,△ABC 、△C B A '''的分别在α 、β 内,线段A A '、B B '、C C '相交于点O ,O 在α 、β 之间.若AB =2,AC =1,∠ABC =60°,OA ∶A O '=3∶2,则△C B A '''的面积为________.解析:图9-35∵ O B B A A ='' ,∴ A A '、B B '确定平面B A AB '',平面B A AB ''∩α =AB ,平面B A B A AB ''=''β ,∵ α ∥β ,∴ B A AB ''//,同理C B BC ''//,A C CA ''//.由于方向相反,∴ △ABC 与△C B A '''的三内角相等,∴ △ABC ∽△C B A '''.且32='=''OA A O AB B A . ∵2360sin 1221=︒⨯⨯⨯=∆ABC S ,∴ .39223322=⋅⎪⎭⎫ ⎝⎛='''∆C B A S 297. 如图9-37,两条异面直线AB 、CD 与三个平行平面α 、β 、γ 分别相交于A 、E 、B ,及C 、F 、D ,又AD 、BC 与平面β 的交点为H 、G .求证:EHFG 为平行四边形.解析:.同理平面平面.HF AC EG ABC AC ABC EG AC ////// ⇒⎪⎭⎪⎬⎫==βαβα 是平行四边形.故同理..EHFG FG EH HF EG HF AC FG AC ////////⇒⎭⎬⎫ 298. 如图9-38,已知平面α ∥平面β ,A 、C ∈α ,B 、D ∈β ,E 、F 分别为AB 、CD 的中点.求证:EF ∥α ,EF ∥β .解析:当AB 、CD 共面时,平面ABCD ∩α =AC ,平面ABCD ∩β =BD .∵ α ∥β ,∴ AC ∥BD .∵ E 、F 分别为AB 、CD 的中点,∴ EF ∥AC .∵AC α ,EF α ,∴ EF ∥α ,同理EF ∥β .当AB 、CD 异面时,∵ CD E ∉,∴ 可在平面ECD 内过点E 作CD D C //'',与α ,β 分别交于C ',D '.平面C A D B C A '=''α ,平面D B D B C A '=''β ,∵ α ∥β ,∴ D B C A ''//.∵ E 是AB 中点,∴ E 也是D C ''的中点.平面C C D D C C '=''α ,平面D D D D C C '=''β ,∵ α ∥β ,∴ D D C C ''//,∵ E 、F 分别为D C ''、CD 中点,∴ C C EF '//,D D EF '//.∵ C C'α ,EF α ,∴ EF∥α ,同理EF∥β .299.已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F(1)求证:AF⊥SC(2)若平面AEF交SD于G,求证:AG⊥SD解析:如图,欲证AF⊥SC,只需证SC垂直于AF所在平面,即SC⊥平面AEF,由已知,欲证SC⊥平面AEF,只需证AE垂直于SC所在平面,即AE⊥平面ABC,再由已知只需证AE⊥BC,而要证AE⊥BC,只需证BC⊥平面SAB,而这可由已知得证证明 (1)∵SA⊥平面AC,BC⊂平面AC,∴SA⊥BC∵矩形ABCD,∴AB⊥BC∴BC⊥平面SAB∴BC⊥AE又SB⊥AE ∴AE⊥平面SBC∴SC⊥平面AEF∴AF⊥SC(2)∵SA⊥平面AC ∴SA⊥DC,又AD⊥DC∴DC⊥平面SAD ∴DC⊥AG又由(1)有SC⊥平面AEF,AG 平面AEF∴SC⊥AG ∴AG⊥平面SDC ∴AG⊥SD300.已知四面体A—BCD,AO1⊥平面BCD,且O1为ΔBCD的垂心.BO2⊥平面ACD,求证:O2是ΔACD的垂心.证明如图所示,连结BO1,AO2,∵AO1⊥平面BCD,O1为ΔBCD的垂心,∴BO1⊥CD,由三垂线定理得AB⊥CD.又BO2⊥平面ACD,由三垂线逆定理得AO2⊥CD.同理连结DO1,CO2可证BC⊥AD,即CO2⊥AD.∴O2是ΔACD垂心.。