1.4解直角三角形课件
- 格式:ppt
- 大小:274.50 KB
- 文档页数:13



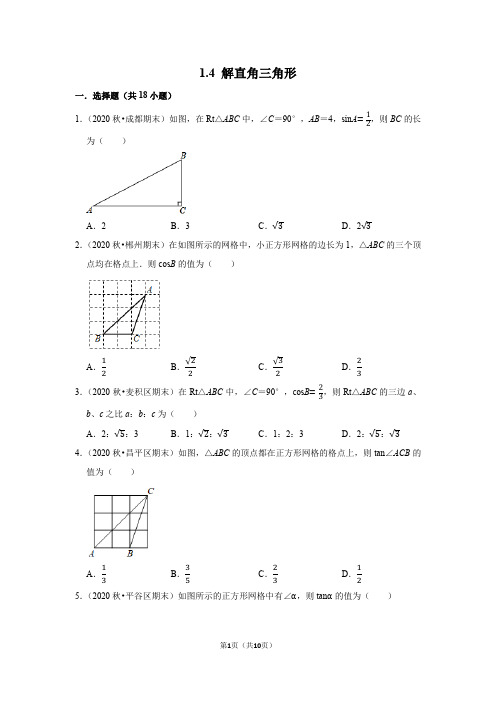
1.4 解直角三角形一.选择题(共18小题)1.(2020秋•成都期末)如图,在Rt △ABC 中,∠C =90°,AB =4,sin A =12,则BC 的长为( )A .2B .3C .√3D .2√32.(2020秋•郴州期末)在如图所示的网格中,小正方形网格的边长为1,△ABC 的三个顶点均在格点上.则cos B 的值为( )A .12B .√22C .√32D .233.(2020秋•麦积区期末)在Rt △ABC 中,∠C =90°,cos B =23,则Rt △ABC 的三边a 、b 、c 之比a :b :c 为( ) A .2:√5:3B .1:√2:√3C .1:2:3D .2:√5:√34.(2020秋•昌平区期末)如图,△ABC 的顶点都在正方形网格的格点上,则tan ∠ACB 的值为( )A .13B .35C .23D .125.(2020秋•平谷区期末)如图所示的正方形网格中有∠α,则tan α的值为( )A .12B .√55C .2√55D .26.(2020秋•长春期末)如图,在平面直角坐标系中,P 是第一象限内的点,其坐标是(3,m ),且OP 与x 轴正半轴的夹角α的正切值是43,则m 的值为( )A .5B .4C .3D .947.(2020秋•蜀山区期末)如图,在平面直角坐标中,点P 的坐标为(3,4),则射线OP 与x 轴正方向所夹锐角α的余弦值为( )A .43B .45C .35D .348.(2020秋•南海区期末)如图,在Rt △ABC 中,∠ACB =90°,CD 是斜边AB 上的高,BC =√7,AC =3,则sin ∠ACD =( )A .√74B .√73C .34D .439.(2020秋•郫都区期末)如图,在正方形网格纸中,△ABC 的三个顶点都在格点上,则tan∠BAC 的值是( )A .34B .45C .43D .3510.(2020秋•余姚市期末)在4×5网格中,A ,B ,C 为如图所示的格点(正方形的顶点),则下列等式正确的是( )A .sin A =√32B .cos A =12C .tan A =√33D .cos A =√2211.(2020秋•虹口区期末)如图,在Rt △ABC 中,∠ACB =90°,D 是边AB 上一点,过D 作DF ⊥AB 交边BC 于点E ,交AC 的延长线于点F ,联结AE ,如果tan ∠EAC =13,S △CEF =1,那么S △ABC 的值是( )A .3B .6C .9D .1212.(2020秋•河南期末)如图,△ABC 的顶点是正方形网格的格点,则cos ∠C =( )A .12B .√22C .√32D .2√5513.(2020秋•齐河县期末)如图,在△ABC 中,∠C =90°,AC =32,AB 的垂直平分线MN 交AC 于点D ,连接BD ,若sin ∠CBD =79,则BC 的长是( )A .16B .8√2C .4√2D .814.(2020秋•平房区期末)在Rt △ABC 中,∠C =90°,∠B =36°,若BC =m ,则AB 的长为( ) A .m cos36°B .m •cos36°C .m •sin36°D .m •tan36°15.(2020秋•河口区期末)如图,在5×4的正方形网格中,每个小正方形的边长都是1,△ABC 的顶点都在这些小正方形的顶点上,则cos ∠BAC 的值为( )A .43B .34C .35D .4516.(2020秋•德江县期末)如图,在平面直角坐标系中,点A 的坐标为(4,3),那么sin α的值是( )A .34B .43C .45D .3517.(2021•碑林区校级模拟)如图在△ABC 中,AC =BC ,过点C 作CD ⊥AB ,垂足为点D ,过D 作DE ∥BC 交AC 于点E ,若BD =6,AE =5,则sin ∠EDC 的值为( )A .35B .725C .45D .242518.(2020秋•肃州区期末)如图,在Rt △ABC 中,∠C =90°,AC =4,tan A =12,则BC 的长度为( )A .2B .8C .4√3D .4√5二.填空题(共14小题)19.(2020秋•成华区期末)如图,在4×4的正方形网格(每个小正方形的边长都是1)中,△ABC 的顶点都在小正方形的顶点上,则sin ∠ACB = .20.(2020•杭州模拟)在△ABC 中,∠C =90°,∠A =30°,BC =4,D 为直线AB 上的一点,若AD =2,则tan ∠BDC 的值为 .21.(2019秋•平房区期末)已知△ABC 中,∠ABC =30°,AB =4√3,AC =√13,则BC 的长为 .22.(2019秋•碑林区校级期末)在△ABC 中,若AB =5,BC =13,AD 是BC 边上的高,AD =4,则tan C = .23.(2020秋•河口区校级月考)已知AD 是△ABC 的高,CD =1,AD =BD =√3,则∠BAC = .24.(2019•南岗区一模)在△ABC 中,AB =2√5,AC =√5,tan ∠B =12,则BC 的长度为 . 25.(2020秋•高邮市期末)如图,CD 是△ABC 的高,若AB =10,CD =6,tan ∠CAD =34,则BD=.26.(2020秋•常州期末)在△ABC中,∠C=90°,AC=3,BC=4,则sin∠ABC=.27.(2020秋•顺义区期末)如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AB=9,AC=6,则cos∠DCB=.28.(2020秋•槐荫区期末)如图所示,∠1是放置在正方形网格中的一个角,则sin∠1的值是.29.(2020秋•松江区期末)如图,△ABC在边长为1个单位的方格纸中,△ABC的顶点在小正方形顶点位置,那么∠ABC的正弦值为.30.(2020秋•瓜州县期末)在△ABC中,sin B=13,tan C=√22,AB=3,则AC的长为.31.(2020秋•香坊区期末)△ABC中,sin∠ABC=513,AD为BC边上的高,∠CAD=45°,BD=12,则BC的长为.32.(2020秋•昆都仑区期末)如图,点D在钝角△ABC的边BC上连接AD,∠B=45°,∠CAD=∠CDA,CA:CB=5:7,则∠CAD的余弦值为.三.解答题(共11小题)33.(2020秋•盐城期末)如图,在△ABC中,∠B=45°,∠C=75°,BC=3√2,求:AB、AC.34.(2020秋•嘉定区期末)如图,在△ABC中,AB=AC=10,sin B=4 5.(1)求边BC的长度;(2)求cos A的值.35.(2020秋•松江区期末)如图,已知在Rt△ABC中,∠C=90°,sin∠ABC=35,点D在边BC上,BD=4,联结AD,tan∠DAC=2 3.(1)求边AC的长;(2)求cot∠BAD的值.36.(2020秋•兰州期末)如图,在△ABC中,cos B=√22,sin C=35,AC=10,求△ABC的面积.37.(2020秋•垦利区期末)如图,在△ABC中,AD是BC上的高,BD=AC=10,tan B=4 5.(1)求AD的长;(2)求cos∠C的值和S△ABC.38.(2020秋•常宁市期末)如图,在△ABC中,AD⊥BC于点D,若AD=6.tan C=32,BC=12,求cos B的值.39.(2020秋•肇源县期末)如图,在Rt△ABC中,∠B=90°,E是BC边上一点,过点E 作ED⊥AC,垂足为D,AB=8,DE=6,∠C=30°,求BE的长.40.(2020秋•周村区期末)如图,在△ABC中,∠C=90°,AB的垂直平分线分别交边AB、BC于点D、E,连接AE.(1)如果∠B=25°,求∠CAE的度数;(2)如果CE=2,sin∠CAE=23,求tan B的值.41.(2020秋•中宁县期末)在Rt△ABC中,∠ACB=90°,D为AB边上的中点,DE⊥AB,AD=2DE.(1)求sin B的值;(2)若CD=√5,求CE的值.42.(2020秋•瓜州县期末)如图,在平面直角坐标系内,点O为原点,点A在x轴的正半轴上,点B在第一象限内,且AO=BO=10,tan∠BOA=3 4.(1)求点B坐标;(2)求cos∠BAO的值.43.(2019秋•新晃县期末)如图,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,sin∠ACB=1 3.(1)求AC的长.(2)求tam∠DAC•cos∠DAC的值.。

