知识点32 洛必达法则求极限

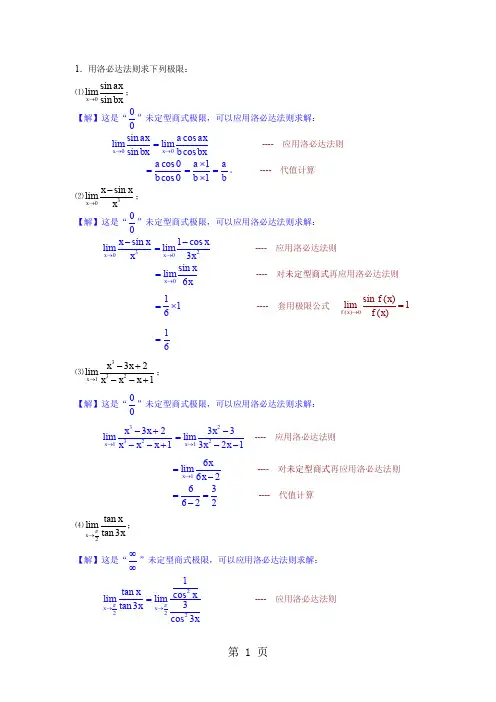
1．用洛必达法则求下列极限：⑴0sin limsin x axbx→；【解】这是“00”未定型商式极限，可以应用洛必达法则求解：0sin lim sin x ax bx →0cos limcos x a axb bx→= ---- 应用洛必达法则 cos 0cos 0a b =11a b ⨯=⨯ab=。

---- 代值计算 ⑵30sin lim x x x x→-； 【解】这是“00”未定型商式极限，可以应用洛必达法则求解：30sin lim x x x x →-201cos lim3x xx →-= ---- 应用洛必达法则 0sin lim6x xx→= ---- 对未定型商式再应用洛必达法则 116=⨯ ---- 套用极限公式 ()0sin ()lim1()f x f x f x →= 16=⑶332132lim 1x x x x x x →-+--+； 【解】这是“”未定型商式极限，可以应用洛必达法则求解： 332132lim 1x x x x x x →-+--+22133lim 321x x x x →-=-- ---- 应用洛必达法则 16lim62x xx →=- ---- 对未定型商式再应用洛必达法则63622==- ---- 代值计算 ⑷2tan limtan 3x xxπ→； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解： 2tan lim tan 3x xx π→2221cos lim 3cos 3x x xπ→= ---- 应用洛必达法则222cos 3lim3cos x xx π→= ---- 整理繁分式 22cos3(sin 3)3lim32cos (sin )x x x x x π→⋅-⋅=⋅⋅- ---- 对未定型商式再应用洛必达法则2sin 6limsin 2x xxπ→= ---- 化简复杂分式 26cos6lim2cos 2x xxπ→= ---- 对未定型商式再应用洛必达法则3cos3cos ππ=---- 代值计算3=⑸2(ln )lim x x x→+∞； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解： 2(ln )limx x x→+∞12ln lim 12x x x x→+∞⋅= ---- 应用洛必达法则 4ln limx xx→+∞= ---- 化简繁分式14lim 12x x x→+∞= ---- 对未定型商式再应用洛必达法则 8limx x→+∞= ---- 化简繁分式 0=⑹2ln()2lim tan x x x ππ+→-； 【解】这是“∞∞”未定型商式极限，可以应用洛必达法则求解：2ln()2lim tan x x x ππ+→-2212lim 1cos x x xππ+→-= ---- 应用洛必达法则 22cos lim 2x x x ππ+→=----- 化简繁分式22cos (sin )lim 1x x x π+→-= ---- 对未定型商式再应用洛必达法则2cossin22ππ=-0= ---- 代入计算⑺212lim x x x e →；【解】这是“0⨯∞”未定型极限，应化为商式极限后应用洛必达法则求解：212lim xx x e →2102lim 1x x e x →= ---- 化为商式后，成为“∞∞”未定型商式极限 212021()'lim1()'x x e x x→= ---- 应用洛必达法则 2211lim x x e →+∞= ---- 化简繁分式 =+∞ ---- 代入计算⑻0lim cot x x x →；【解】这是“0⨯∞”未定型极限，应化为商式极限后应用洛必达法则求解：lim cot x x x →0limtan x xx →= ---- 化为商式后，成为“∞∞”未定型商式极限021lim 1cos x x →= ---- 应用洛必达法则 20limcos x x →= ---- 化简繁分式2cos 01== ---- 代入计算⑼2lim(sec tan )x x x π→-；【解】这是“∞-∞”未定型极限，应化为商式极限后应用洛必达法则求解：2lim(sec tan )x x x π→-21sin lim()cos cos x x x xπ→=- ---- 为通分化为商式作准备 21sin limcos x xx π→-= ---- 成为“00”未定型商式极限2cos limsin x xxπ→-=- ---- 应用洛必达法则cos 20sin2ππ== ---- 代入计算⑽11lim()1ln x x x x→--； 【解】这是“∞-∞”未定型极限，应化为商式极限后应用洛必达法则求解：11lim()1ln x x x x→--1ln (1)lim(1)ln x x x x x x →--=- ---- 通分化为商式，成为“00”未定型 1ln 11lim1ln x x x x x→+-=-+---- 应用洛必达法则1ln limln 1x x xx x x →=+- ---- 化简繁分式，成为“00”未定型 1ln 1limln 11x x x →+=++ ---- 应用洛必达法则 011022+==+ ---- 代入计算 ⑾tan 0lim xx x +→；【解】这是“00”幂指函数未定型极限，应化为商式极限后应用洛必达法则求解： 【解法一】应用对数法，令tan xy x=，则tan ln ln ln tan ln cot xxy xx x x===， 于是，00ln lim ln lim cot x x xy x ++→→= ---- 成为“∞∞”未定型021lim 1sin x x x+→=- ---- 应用洛必达法则20sin lim x x x +→= ---- 化简繁分式，成为“00”未定型 02sin cos lim 1x x x+→= ---- 应用洛必达法则2sin0cos00== ---- 代入计算得到 0l i m l n 0x y +→=，亦即0ln lim 0x y +→=， 从而有 0l i m 1x y e +→==，亦即tan 0lim 1xx x +→=。

32洛必达法则1．用洛必达法则求下列极限：⑴«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...»«Skip Record If...»«Skip Record If...»。

---- 代值计算⑵«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 套用极限公式«Skip Record If...»«Skip Record If...»⑶«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 代值计算⑷«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 整理繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 化简复杂分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 代值计算«Skip Record If...»⑸«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...»⑹«Skip Record If...»；【解】这是“«Skip Record If...»”未定型商式极限，可以应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 对未定型商式再应用洛必达法则«Skip Record If...»«Skip Record If...» ---- 代入计算⑺«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 化为商式后，成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 代入计算⑻«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 化为商式后，成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式«Skip Record If...» ---- 代入计算⑼«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 为通分化为商式作准备«Skip Record If...» ---- 成为“«Skip Record If...»”未定型商式极限«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算⑽«Skip Record If...»；【解】这是“«Skip Record If...»”未定型极限，应化为商式极限后应用洛必达法则求解：«Skip Record If...»«Skip Record If...» ---- 通分化为商式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算⑾«Skip Record If...»；【解】这是“«Skip Record If...»”幂指函数未定型极限，应化为商式极限后应用洛必达法则求解：【解法一】应用对数法，令«Skip Record If...»，则«Skip Record If...»，于是，«Skip Record If...»---- 成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 化简繁分式，成为“«Skip Record If...»”未定型«Skip Record If...» ---- 应用洛必达法则«Skip Record If...» ---- 代入计算得到 «Skip Record If...»，亦即«Skip Record If...»，从而有 «Skip Record If...»，亦即«Skip Record If...»。

洛必达法则
一、洛必达法则的基本形式
洛必达法则是微积分中的一个重要定理，用于解决0/0或无穷/无穷的极限问题。

其基本形式为：如果函数f(x)和g(x)满足以下条件：
1. f(x)和g(x)在某点a的某个邻域内可导；
2. g'(x)不等于0；
3. 存在一个实数点b，使得f(b)=0；
4. 存在一个实数点c，使得g(c)=0。

那么，当x趋近于a时，f'(x)/g'(x)的极限等于f(a)/g(a)。

二、洛必达法则的推导过程
洛必达法则的推导过程涉及到极限、导数和微分的知识。

其证明过程为：根据泰勒公式，f(x)和g(x)都可以展开为泰勒级数，然后通过比较系数，可以证明f'(x)/g'(x)的极限等于f(a)/g(a)。

三、洛必达法则的应用范围
洛必达法则可以应用于解决0/0或无穷/无穷的极限问题。

具体来说，当分母或分子为无穷大时，可以通过求导数的方法来解决极限问题。

此外，洛必达法则还可以应用于一些其他类型的极限问题，例如求定积分、不定积分等。

四、洛必达法则的局限性
虽然洛必达法则是微积分中的一个重要定理，但是它也存在一些局限性。

首先，洛必达法则只适用于0/0或无穷/无穷的极限问题，对于其他类型的极限问题无法应用。

其次，在使用洛必达法则时需要注意满足其前提条件，否则可能导致错误的结果。

此外，洛必达法则也无法应用于一些复杂的极限问题，例如涉及到多个变量或多个函数的极限问题。

因此，在使用洛必达法则时需要结合其他方法来解决复杂的极限问题。

极限的计算方法洛必达法则和泰勒展开洛必达法则和泰勒展开是数学中极限的计算方法，它们在求解复杂函数的极限问题时非常有用。

本文将详细介绍这两种计算方法的原理和应用。

一、洛必达法则洛必达法则是一种计算不定型极限的方法，它是由17世纪法国数学家洛必达提出的。

当我们计算一个函数的极限时，如果得到的是0/0或无穷大/无穷大的形式，就可以运用洛必达法则来求解。

洛必达法则的思想是利用两个函数的导数之商来逼近函数的极限，具体步骤如下：1. 若极限形式为0/0或无穷大/无穷大，先对分子函数和分母函数分别求导；2. 如果导数的极限存在，即可得到原极限的结果。

如果导数的极限不存在，或者求导后的函数仍然为0/0或无穷大/无穷大的形式，就可以继续使用洛必达法则。

以下是一个应用洛必达法则求解极限的示例：设函数f(x) = (sinx - x)/x^3，求lim(x→0) f(x)的极限。

解：首先对函数f(x)分子分母求导，得到f'(x) = (cosx - 1)/x^3 - 3sinx/x^4。

然后计算极限lim(x→0) f'(x)，仍然得到0/0的形式。

再次对f'(x)进行求导，得到f''(x) = (-2sinx - 9cosx)/x^4 +12sinx/x^5。

继续计算极限lim(x→0) f''(x)，仍然得到0/0的形式。

最后再对f''(x)求导，得到f'''(x) = (-16sinx - 4cosx)/x^5 -60cosx/x^6。

继续计算极限lim(x→0) f'''(x)，得到极限值为-4/3。

因此，lim(x→0) f(x)的极限为-4/3。

二、泰勒展开泰勒展开是一种将函数在某点附近进行多项式逼近的方法。

根据泰勒定理，如果一个函数在某点处存在各阶导数，则可以用一个多项式逼近该函数。

泰勒展开的公式如下：f(x) = f(a) + f'(a)(x - a)/1! + f''(a)(x - a)^2/2! + ... + f^n(a)(x - a)^n/n! + R_n(x)其中，f(a)表示函数在点a处的函数值，f^(n)(a)表示函数在点a 处的n阶导数，R_n(x)为余项。

§3.2 洛必达法则教学内容：一．“”型未定式 1.定理:（洛必达法则I ）设)(x f 、()g x 在0x 的某一去心邻域内有定义，如果 (1)0lim ()0→=x x f x ，0lim ()0→=x x g x ；(2))(x f 、()g x 在0x 的某邻域内可导，且()0g x '≠； (3)0()lim()x x f x g x →''存在(或无穷大)，那么00()()lim =lim ()()→→''x x x x f x f x g x g x .2.如果0()lim()→''x x f x g x 还是“0”型未定式，且函数()f x '与()g x '满足洛必达法则I 中应满足的条件，则可继续使用洛必达法则，即有000()()()limlim lim ()()()x x x x x x f x f x f x g x g x g x →→→'''=='''，依此类推，直到求出所要求的极限．3．洛必达法则I 中，极限过程0x x →若换成0x x +→，0x x -→以及x →∞，x →+∞，x →-∞情形的0型未定式，结论仍然成立．二．“∞∞”型未定式 1.定理：（洛必达法则II ）设)(x f 、()g x 在0x 的某一去心邻域内有定义，如果)1(0lim ()→=∞x x f x ，0lim ()→=∞x x g x ；)2()(x f 、()g x 在0x 的某邻域内可导，且()0g x '≠；)3(0()lim()x x f x g x →''存在(或无穷大)，那么00()()lim =lim ()()x x x x f x f x g x g x →→''.2.如果0()lim()→''x x f x g x 还是“∞∞”型未定式，且函数()f x '与()g x '满足洛必达法则II 中应满足的条件，则可继续使用洛必达法则，即有000()()()limlim lim ()()()→→→'''=='''x x x x x x f x f x f x g x g x g x ，依此类推，直到求出所要求的极限．3.洛必达法则II 中，极限过程0x x →若换成0x x +→，0x x -→以及x →∞，x →+∞，x →-∞情形的“∞∞”型未定式，结论仍然成立．三．其它类型的未定式1．“0⋅∞”型未定式设0lim ()0→=x x f x ，0lim ()→=∞x x g x ，则0()lim ()()=lim1()→→⋅x x x x f x f x g x g x （00型）, 或00()lim ()()=lim 1()→→⋅x x x x g x f x g x f x （∞∞型）.2．“∞-∞”型未定式：可以通过通分化简等方式转化为“00”型或“∞∞”型未定式．3．“000 , 1, ∞∞”型未定式：可以通过取对数进行转化,()()ln ()lim ()ln ()lim[()]lim e e g x g x f x g x f x f x ==，无论()[()]g x f x 是上述三种类型中的哪一种，lim ()ln ()g x f x 均为“0⋅∞”型未定式.四．小结利用洛必达法则求未定式的极限，总结如下： 1.洛必达法则只能适用于“00”和“∞∞”型的未定式，其它的未定式须先化简变形成“00”或“∞∞”型才能运用该法则．2.只要条件具备，可以连续使用洛必达法则．3.洛必达法则可以和其它求未定式的方法结合使用．4.洛必达法则的条件是充分的，但不必要．在某些特殊情况下洛必达法则可能失效，此时应寻求其他解法.五．例题讲解例1.计算20e 1lim x x x x →--． 例2.计算33221216lim 248x x x x x x →-+--+．例3.计算20tan lim sin →-x x x x x ． 例4.计算0ln cot limln x xx+→．例5.计算sin lim 1x x xx →∞++． 例6.计算0limln x x x +→．例7.设()f x ''在x a =点附近连续，求极限2()()2()lim→++--h f a h f a h f a h．例8.计算 (1) ln lim (0)a x xa x→+∞>; (2) lim (0)e n xx x n →+∞>.。

第十七讲Ⅰ 授课题目：§3.2 洛必塔法则 Ⅱ 教学目的与要求：1.掌握用罗必塔法则求极限；2.明了使用罗必塔法则的条件；3.了解将罗必塔法则与极限运算性质结合使用常能简化运算。

Ⅲ 教学重点与难点：重点：各种类型的未定式转化为00或∞∞型的未定式 难点：罗必塔法则与极限运算性质的结合使用 Ⅳ 讲授内容：§3.2 洛必塔法则如果当a x →（或∞→x ）时，两个函数)(x f 与)(x F 都趋于零或都趋于无穷大，那末极限)()(lim)(x F x f x a x ∞→→可能存在、也可能不存在．通常把这种极限叫做未定式，并分别简记为00或∞∞.在第一章第六节中讨论过的极限x x x sin lim 0→就是未定式00的一个例子．对于这类极限，即使它存在也不能用“商的极限等于极限的商”这—法则．下面我们将根据柯西中值定理来推出求这类极限的一种简便且重要的方法． 我们着重讨论a x →时的未定式的情形，关于这情形有以下定理： 定理1 设 (1)当a x →时，函数)(x f 及)(x F 都趋于零；(2)在点a 的某去心邻域内，)(x f '及)(x F '都存在且0)(≠'x F ； （3）)()(limx F x f ax ''→存在（或为无穷大）， 那么 )()(lim )()(limx F x f x F x f a x ax ''=→→. 这就是说，当)()(limx F x f ax ''→存在时,)()(lim x F x f a x →也存在且等于)()(lim x F x f a x ''→；当)()(lim x F x f a x ''→为无穷大时，)()(limx F x f ax →也是无穷大．这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必塔（L ’Hospital ）法则 证明 因为求)()(x F x f 当a x →时的极限与)(a f 及)(a F 无关，所以可以假定0)()(==a F a f ，于是由条件(1)、(2)知道，)(x f 及)(x F 在点a 的某一邻域内是连续的．设x 是这邻域内的一点，那么在以x 及a 为端点的区间上，柯西中值定理的条件均满足，因此有)()()()()()()()(ξξF f a F x F a f x f x F x f ''=--= （ξ在x 与a 之间）． 令a x →，并对上式两端求极限，注意到a x →时a →ξ，再根据条件(3)便得说明: 1.如果)()(limx F x f a x ''→仍属于00型, 且)(x f '和)(x F '满足洛必达法则的条件,可继续使用洛必达法则, 即 =''''=''=→→→)()(lim )()(lim )()(limx F x f x F x f x F x f a x a x a x ;2.当∞→x 时, 该法则仍然成立, 有)()(lim )()(lim x F x f x F x f x x ''=∞→∞→;3.对a x →（或∞→x ）时的未定式∞∞，也有相应的洛必达法则;4. 洛必达法则是充分条件，反之不成立；5. 如果数列极限也属于未定式的极限问题，需先将其转换为函数极限，然后使用洛必达法则，从而求出数列极限.（因为数列不连续，不能求导） 例1 求下列极限（1）x x x tan lim 0→, (0型) （2）123lim 2331+--+-→x x x x x x , (00型) 解 原式=)()(tan lim 0''→x x x =11sec lim 20=→x x 原式= 12333lim 221---→x x x x = =-→266lim 1x x x 23注 上式中的266lim1-→x xx 已不是未定式，不能对它应用洛必达法则，否则要导致错误结果．以后使用洛必达法则时应当经常注意这一点，如果不是未定式，就不能应用洛必达法则．（3）xx x 1arctan 2lim -+∞→π, (00型) 原式=22111limxx x -+-+∞→=221lim x x x ++∞→=1 （4）bx ax x sin ln sin ln lim0→, (∞∞型). 原式= ax bx b bx ax a x sin cos sin cos lim0⋅⋅→= ax bx x cos cos lim 0→=1（5）xx x 3tan tan lim 2π→, (∞∞型) 原式=x x x 3sec 3sec lim 222π→= x x x 222cos 3cos lim 31π→= x x x x x sin cos 23sin 3cos 6lim 312--→π= x x x 2sin 6sin lim 2π→= 32cos 26cos 6lim 2=→x xx π注意：洛必达法则是求未定式的一种有效方法，但与其它求极限方法结合使用，效果更好.例2 求下列极限（1）x x xx x tan tan lim 20-→ 原式30tan lim x x x x →-== 22031sec lim x x x -→=220tan lim 31x x x →=31（2）0ln lim ln(1)xx x e +→- 原式0001111lim lim lim 11x x x xx x x x e x x e x e x e e +++→→→-==⋅=⋅=- （3）1ln cos(1)lim 1sin 2x x xπ→-- 原式2111sin(1)2sin(1)4cos(1)cos(1)lim lim lim cos cos sin 2222x x x x x x x x x x ππππππ→→→-----===--24π=-练习：（1）30arcsin lim sin x x xx→- （2）20ln(1)lim sec cos x x x x →+-二．0,1,0,,0∞∞-∞∞⋅∞型未定式的求法关键: 将其它类型未定式化为洛必达法则可解决的类型00型和∞∞型.1．∞⋅0型未定式的求法步骤：,10∞⋅∞⇒∞⋅或0100⋅⇒∞⋅ 例3 求下列极限（1）.lim 2xx e x -+∞→ 原式=2lim x e xx +∞→=x e xx 2lim +∞→2lim xx e +∞→=.+∞=（2）0lim cot x x x → 原式20011limlim tan 22sec 2x x x x x →→===型∞-∞.2步骤：0101-⇒∞-∞.0000⋅-⇒ 例4 求下列极限 （1）).1sin 1(lim 0xx x -→ 原式=x x x x x sin sin lim 0⋅-→x x x x x cos sin cos 1lim 0+-=→.0=（2）011lim ln(1)x x x →⎡⎤-⎢⎥+⎣⎦ 原式200011ln(1)ln(1)1lim lim lim ln(1)2x x x x x x x x x x x x→→→--+-++===+ 011lim2(1)2x x →==+型00,1,0.3∞∞步骤： ⎪⎩⎪⎨⎧∞⋅⋅∞⋅−−→−⎪⎭⎪⎬⎫∞∞ln 01ln 0ln 01000取对数.0∞⋅⇒例3 求下列极限（1）.lim 0xx x +→ 原式=xx x eln 0lim +→xx x eln lim 0+→=xxx e1ln lim 0+→=2011lim xxx e-+→=0e =.1=（2）11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭原式0lnsin ln 1lim1cos 3...x x x xee →---===例4 求下列极限（1）.lim111xx x -→ 原式=x xx eln 111lim -→xx x e-→=1ln lim111lim 1-→=x x e.1-=e（2）10lim(1sin )xx x →+ 原式00cos ln(1sin )1sin lim lim 1x x xx x xeee →→++===例5 求下列极限（1）.)(cot lim ln 10xx x +→ 原式20011ln(cot )cot sin limlim1ln 1/x x x x x x xe ee ++→→-⋅-===（2）()1lim ln xx x →+∞原式11ln(ln )ln lim lim 011x x x x x xeee →+∞→+∞⋅====例6 求)]24([tan lim nnn +→∞π解 设)]24([tan )(x x f x +=π，则)]24([tan )(n n f n +=π因为)]24tan(ln lim exp[)(lim xx x f x x +=+∞→+∞→π=]1)24tan(ln limexp[x x x ++∞→π])24tan(1)2)(24(sec lim exp[222x xx x x +--+=+∞→ππ=4e从而 原式=4)(lim )(lim e x f n f x n ==+∞→∞→练习：1）)1(cot lim 0xx x -→ （2）x x x ln 10)(cot lim +→ （3）xx x tan 0lim +→（4）xx x 2tan 4)(tan lim π→（5）xx x cot 0)sin 1(lim -→Ⅴ 小结与提问：小结：1.使用罗必塔法则之前应该验明其是否满足罗必塔法则条件。

1 引言18世纪数学本身的发展，以及这个世纪后期数学研究活动的扩张和数学教育的改革都为19世纪数学的发展准备了条件．微积分学的深人发展，才有了后面的洛比达法则，而且在英国和欧洲大陆是循着不同的路线进行的．在欧洲大陆，新分析正在莱布尼茨的继承者们的推动下蓬勃发展起来．伯努利家族的数学家们首先继承并推广莱布尼茨的学说. 雅各布·伯努利运用莱布尼茨引用的符号，并称之为积分，莱布尼茨采用他的建议，并列使用微分学与积分学两个术语．雅各布·伯努利的弟弟约. 翰·伯努利在莱布尼茨的协助之下发展和完善了微积分学. 他借助于常量和变量，用解析表达式来定义函数，这比在此之前对函数的几何解释有明显的进步. 他在求“0/0”型不定式的值时，发现了现称为洛必达法则的方法，即用以寻找满足一定条件的两函数之商的极限. 约翰·伯努利的学生、法国数学家洛必达的《无限小分析》(1696)一书是微积分学方面最早的教科书，在十八世纪时为一模范著作，他在书中规范了这一种算法即洛必达法则，之后洛必达法则的也得到了广泛应用，这对传播微分学起到很大的作用.从极限概念的产生到现在已经经历了两千五百多年的发展，漫漫的历史长河，人类在寻求真理和科学的过程中不断探索和总结，对于数学的探索给了人类科学发展以强大的动力．我们应当对任何知识都认真的学习、研究及做出总结．不仅踏寻前人的路迹，同时也要从中开创新的空间．极限是数学分析的基石，是微积分学的基础．不定式极限是一种常见和重要的极限类型，其求法多种多样，变化无穷．本文先介绍了洛必达法则的定义，然后对洛必达法则使用条件及其常见误区进行了详细分析，阐述了该法则适用于解决函数极限的类型并举例说明其应用，总结了洛必达法则的各种形式及使用范围，并介绍了洛必达法则的基本应用，以及在使用洛必达法则解题时应注意的问题．文章还将法则的适用范围推广至求数列极限，然后分析法则的使用过程中容易出现的错误；最后通过具体实例说明了可以将法则和其他求极限方法结合起来使用，使我们对法则有了更深入的理解，进而提高了应用洛必达法则解决问题的能力．2 洛必达法则及使用条件在计算一个分式函数的极限时，常常会遇到分子分母同时趋向于零或无穷大的情况，由于这时无法使用“商的极限等于极限的商”的法则，运算将遇到很大的困难，事实上，这时极限可能存在，也可能不存在，当极限存在时，极限的值也会有各种各样的可能，如当a x →（或∞→x ）时，两个函数)(x f 与)(x g 都趋于零或都趋于无穷大，那么极限第 2 页 共16页)()(lim)(x g x f x ax →∞→可能存在也可能不存在. 通常把这种极限叫做未定式，并分别简记为0型和∞∞型. 未定式极限除了以上两种外，还有∞⋅0型、∞-∞型、0∞型、∞1型、00型等五种，后面几种都可以转换成前面两种类型来进行计算，因此掌握0型和∞∞型极限的计算方法是前提．2.1 洛必达法则型 定理2.1 设函数)(x f ，)(x g 满足：（1）当a x →时，函数)(x f 及)(x g 都趋于零；（2）在点a 的某去心邻域内，)('x f 及)('x g 都存在且0)('≠x g ； （3）)(')('limx g x f ax →存在（或为无穷大）， 那么)(')('lim )()(limx g x f x g x f a x ax →→=. 这就是说，当)(')('limx g x f ax →存在时，)()(lim x g x f a x →也存在且等于)(')('lim x g x f a x →；当)(')('lim x g x f a x →为无穷大时，)()(limx g x f ax →也是无穷大，这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则. 证明 因为)()(x g x f 当a x →时的极限与)(a f 及)(a g 无关，所以可以假定0)()(==a g a f ，于是由条件（1）、（2）知道，)(x f 及)(x g 在点a 的某一邻域内是连续的，设x 是这一邻域内的一点，那么在以x 及a 为端点的区间上，柯西中值定理的条件均满足，因此有)(')(')()()()()()(ξξg f a g x g a f x f x g x f =--= （ξ在x 与a 之间）.令a x →，并对上式两端求极限，注意到a x →时a →ξ，再根据条件（3）便得要证明的结论.如果)(')('x g x f 当a x →时仍属于0型，且这时)('x f ，)('x g 都能满足定理中)(x f ，)(x g 所要满足的条件，那么可以继续使用洛必达法则，从而确定)()(limx g x f ax →，即 )('')(''lim)(')('lim )()(limx g x f x g x f x g x f a x a x ax →→→==. 且可以依次类推.定理2.2 设函数)(x f ，)(x g 满足：（1）当∞→x 时，函数)(x f 及)(x g 都趋于零； （2）当N x >时，)('x f 及)('x g 都存在且0)('≠x g ； （3）)(')('limx g x f x ∞→存在（或为无穷大）， 那么)(')('lim )()(limx g x f x g x f x x ∞→∞→=. 2.2 洛必达法则∞∞型 定理2.3 设函数)(x f ，)(x g 满足：（1）当a x →时，函数)(x f 及)(x g 都趋于∞；（2）在点a 的某去心邻域内，)('x f 及)('x g 都存在且0)('≠x g ； （3）)(')('limx g x f ax →存在（或为无穷大）， 那么)(')('lim )()(limx g x f x g x f a x ax →→=. 定理2.4 设函数)(x f ，)(x g 满足：（1）当∞→x 时，函数)(x f 及)(x g 都趋于∞； （2）当N x >时，)('x f 及)('x g 都存在且0)('≠x g ； （3）)(')('limx g x f x ∞→存在（或为无穷大），第 4 页 共16页那么)(')('lim )()(limx g x f x g x f x x ∞→∞→=. 2.3 其他类型未定式除了上述的00型和∞∞型未定式外，还有∞-∞∞⋅∞∞,0,,0,100等类型的未定式．这几种类型的未定式，都可转化为0型或∞∞型的未定式，即可利用洛必达法则进行求解．如下图所示：具体步骤如下：(1)∞⋅0型未定式可将乘积化为除的形式，即当0x x →或∞时，若0)(→x f ,∞→)(x g ，则()()()()x g x f x g x f x x x x 1limlim 0→→=⋅或()()()()x f x g x g x f x x x x 1lim lim 00→→=⋅， 这样，∞⋅0型未定式就变为00型或∞∞型未定式. (2)∞-∞型未定式可通过通分计算，即当0x x →或∞时，若∞→)(x f ,∞→)(x g ，则型∞∞型 ∞-∞型∞⋅0型0,1,0∞∞型()()()()()()11()lim lim11x x x x f x g x f x g x f x g x →→---=⋅，这样，∞-∞型未定式就变为型未定式. (3)00，1∞，0∞型未定式可先化为以e 为底的指数函数的极限, 再利用指数函数的连续性, 转为直接求指数的极限, 而指数的极限形式为“∞⋅0”型, 再转化为“” 型或“∞∞”型计算.当0x x →或∞时，若0)(→x f (或1)(→x f ，或∞→)(x f )，0)(→x g （或∞→)(x g ）. 则()()ln ()lim ()lim g x g x f x x x x x f x e →→=或000lim ()ln ()()()ln ()lim ()lim x x g x f x g x g x f x x x x x f x e e →→→==，这样就可利用洛必达法则进行求解.2.4 洛必达法则求极限的条件从定理知道, 无论是“0”型还是“∞∞”型,都必须具备一个重要条件, 即在自变量的同一变化过程中，)(')('lim)(x g x f x ax →∞→存在（或为∞）时，才有)()(lim )(x g x f x a x →∞→存在（或为∞），且)(')('lim )()(lim)()(x g x f x g x f x x a x ax →∞→∞→→=，但是此条件却不便先验证后使用，所以连续多次使用法则时，每次都必须验证它是否为“”型或“∞∞”型，其使用程序如下：)()(lim )(x g x f x a x →∞→（“00”），)(')('l i m )(x g x f x a x →∞→（“00”），...，)()(lim )1()1()(x g x f n n a x x --→→∞（“00”），若)()(lim )()()(x g x f n n a x x →∞→存在（或为∞），那么才有式子)()(lim )()(lim ...)(')('lim )()(lim )()()1()1()()()()(x g x f x g x f x g x f x g x f n n a x n n a x a x a x x x x x →∞→∞→∞→∞→--→→→====成 立。

第二节 洛必达法则洛必达法则型未定式解法型及一、:00∞∞.00)()(lim ,)()(,)()(型未定式或称为那末极限零或都趋于无穷大都趋于与两个函数时或定义：如果当∞∞∞→→∞→→x F x f x F x f x a x x a x 例如, ,tan lim 0x x x →)00(，,sin ln sin ln lim 0bx ax x →)(∞∞定理1(1),()();(2)(),()()()0;()(3)lim();()()()lim lim .()()x a x a x a x a f x F x a a f x F x F x f x F x f x f x F x F x →→→→'''≠'''='设当时函数及都趋于零在点的某领域内点本身可以除外及都存在且存在或为无穷大那末 定义 ：这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则.注意 (1)定理表明:如果未定式0型满足罗必塔法则的条件,则未定式的极限可用对分子分母分别求导再求极限来确定未定式的极限.如果)()(lim 0x g x f x x ''→还是00型,可再用一次罗必塔法则,直至不是未定式0型为止.即)()(lim )()(lim )()(lim )()(000x g x f g f x g x f n n x x x x x x →→→==''= ξξ. (2) 罗必塔法则对∞→x 时的未定式0型也适用.对0x x →或∞→x 的未定式∞∞型也适用.即)()(lim )()(lim )()(lim )()(x g x f g f x g x f n n x x x ∞→∞→∞→==''= ξξ. 0型 0型 不是00型)()(lim )()(lim )()(lim )()(000x g x f g f x g x f n n x x x x x x →→→==''= ξξ.∞∞型 ∞∞型 不是∞∞型(3)如果不是未定式,则不能用罗必塔法则. 例1：0sin lim(0).sin x ax b bx →≠求)0( 解：00(sin )cos lim lim (sin )cos x x ax a ax a bx b bx b →→'==='原式1sec lim 20xx →==1 例2：.123lim 2331+--+-→x x x x x x 求)00( 解：12333lim 221---=→x x x x 原式266lim 1-=→x x x .23= 例33sin lim.x x xx→-求 解：2001cos sin 1lim lim 366x x x x x x →→-===原式 例4.1arctan 2lim x x x -+∞→π求)00(解：22111lim xx x -+-=+∞→原式221lim x x x +=+∞→=1 例5 设0>n ,则求ln lim nx xx →∞。