格与布尔代数格与布尔代数万字
- 格式:doc
- 大小:2.83 MB
- 文档页数:37










离散数学--⼗⼀章格与布尔代数格的定义与性质:布尔代数是计算机逻辑设计的基础,它是由格引出的。
格⼜是从偏序集引出的。
所以我们先回顾⼀下偏序集中的⼀些概念。
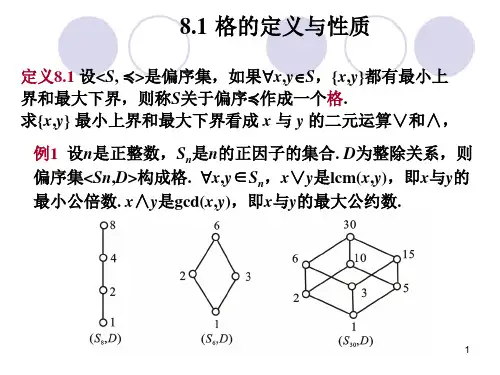
偏序集简单来说就是集合A中有⾃反,反⾃反,传递的关系具体可以看第七章我们结合Hasse图看如下关系:假如 A={1,2,3,6,12,24,36} 且有如下关系如果:B={2,3,6}最⼤|⼩元定义:y是B的最⼩元⇔∃y∈B∧∀x(x∈B→y≤x)y是B的最⼤元⇔∃y∈B∧∀x(x∈B→x≤y)最⼤|⼩元是唯⼀的(类⽐函数的最值)⽽极⼤|⼩元不唯⼀B最⼤元6 ,最⼩元⽆B中Hasse图的最底(顶)层,且这⼀层只有⼀个点才能是最⼩(⼤)元极⼤|⼩元定义:y是B的极⼩元⇔∃y∈B∧¬∃x(x∈B∧x≤y)y是B的极⼤元⇔∃y∈B∧¬∃x(x∈B∧y≤x)这⾥⾯B的极⼩元是 {2,3},极⼤元是 {6}B中Hasse图的最底(顶)层,则是极⼩(⼤)元上下界定义:y是B的下界⇔∃y∈A∧∀x(x∈B→y≤x)y是B的上界⇔∃y∈A∧∀x(x∈B→x≤y)⽐如 B上界 {12,24,36} 下界 {1}Hasse图中B的最底(顶)层,包括这⼀层和这⼀层下⾯(上⾯)的所有元素构成的集合则是下(上)界确界定义:B的上确界(最⼩上界)下确界(最⼤下界)就是上界的min,下界的max结合Hasse 图理解若B={2,3,6} 有如上图的关系格讲这么多终于到格的定义了其实只要⼀个偏序集中任意⼦集都有上下确界就是格了莫名很简洁暗⽰判断格要疯狂枚举格诱导的代数系统交并运算设<A, ≤>是格,在A上定义⼆元运算∨和∧为:∀a,b∈Aa∨b=LUB {a,b} |{a,b}的最⼩上界.Least Upper Bounda∧b=GLB {a,b} |{a,b}的最⼤下界.Greatest Lower Bound称<A,∨,∧>是由格<A,≤>诱导的代数系统. (∨-并,∧-交)就是⽤符号定义了上下确界⽽已并且有:设<L, ≼>是格则有运算∨和∧适合交换律、结合律、幂等律和吸收律<==> 设<S, ∗, ◦ >是代数系统, ∗和◦是⼆元运算, 如果∗和◦满⾜交换律、结合律和吸收律, 则<S, ∗,◦>构成格.注意⼀下吸收率就好了:a∨(a∧b) = a, a∧(a∨b) = a各种格分配格如果交并还满⾜分配率就叫分配格有界格如果B是A时仍有上下确界则此时的格为有界格,这个确界分别称为全上|下界⼀般将全上界记为1 ,全下界记为0,⼀般将有界格L记为<L,∧,∨,0,1>.有限格L={a1,a2,…,an}是有界格, 则a1∧a2∧…∧an是L的全下界, a1∨a2∨…∨an是L的全上界.0是关于∧运算的零元,∨运算的单位元;1是关于∨运算的零元,∧运算的单位元.有补格有补元的格称为有补格a∧b = 0 和 a∨b = 1成⽴, 则称b是a的补元在任何有界格中, 全下界0与全上界1互补对于⼀般元素, 可能存在补元, 也可能不存在补元. 如果存在补元, 可能是惟⼀的, 也可能是多个补元.对于有界分配格, 如果元素存在补元, ⼀定是惟⼀的⼦群格没有特别懂对⼀个群先找出它的所有⼦群⽐如Z12 <0>,<1>,<2>,<3> ,<6>就是所有⼦群|也满⾜格的定义?也是⼦格然后再画所有⼦群(⼦格)的Hasse图就⾏了布尔代数本质上就是⼀个集合如果⼀个格是有补分配格, 则称它为布尔格或布尔代数. 布尔代数标记为<B,∧,∨,′, 0, 1>, ′为求补运算这⾥⾯的 ' 的运算规律相当于 ‘否’(a' )' =a∀a,b∈B, (a∧b)′ = a′∨b′, (a∨b) ′= a′∧b′(0∧b)∨(a∧0) = 0∨0 = 0(1∨b′)∧(a′∨1) = 1∧1 = 1(a∧b)∧(a′∨b′) = (a∧b∧a′)∨(a∧b∧b′)注意⼀下:Sn代表 n的因⼦所构成的集合|别到时候不知道⽐如 s6={1,2,3,6}。
格与布尔代数后述,一部分关于格与一部分关于布尔代数。
关于格格是数学中的一种代数结构,它被广泛用于数学、计算机科学和逻辑学等领域。
在数学中,格是一种偏序集合,它具有两个基本运算:上下拟合和交并运算。
其中,上下拟合是指存在最小上估和最大下估,而交并运算则是指对于任意两个元素都可以求出它们的最大公共上界和最小公共下界。
尽管最初格是在点集拓扑学中发现的,但它们的概念在其他领域中也扮演着重要角色,例如,它们在科学中被用来定义空间,它们被用来解决许多计算机科学问题,例如,程序正确性证明,它们与数据结构有关,在逻辑学中,格被用来理解一些推理系统。
关于布尔代数布尔代数是一种代数结构,它被广泛用于逻辑学、电子工程和计算机科学中。
布尔代数是邓纳-Bier恩论文提出的一种基于命题逻辑的代数系统,其中对于两个命题P和Q,存在两个二元运算,即并(∨)和交(∧)。
这种代数系统可以用0和1表示,其中0表示假,1表示真。
布尔代数中的一些重要性质是:交换律、结合律、分配律等。
尽管在布尔代数中并和交这两个朴素的逻辑运算都不是独立产生的概念,但该理论在数学和计算机科学中有着重要应用。
布尔代数不仅用于设计电路和硬件,还用于在计算机程序和算法中描述逻辑条件,可编程逻辑和任意逻辑等方面。
格与布尔代数的关系虽然格和布尔代数看起来似乎是两种完全不同类型的代数结构,但它们之间有着密切的联系。
一些格配合着一些次区域可以构成布尔代数;同样,对于一个布尔代数而言,它也可以被看作是某个格所描述的偏序集合。
在交集上平凡地定义结构子格也叫布尔子格。
一个布尔代数的子集都可以看做是一种决策支持系统(Decision Support System,DSS)或决策信息系统(Decision Information System,DIS)。
由此可见,布尔代数是格论的一种特例,而格论是布尔代数的一种扩展。
总体而言,格与布尔代数的关系很紧密。
事实上,这种关系已经在数学和计算机科学的广泛应用中得到了充分的体现。
第5章:格与布尔代数格与布尔代数是代数系统中的又一类重要代数系统。
这两个代数系统与第4章讨论的代数系统之间存在着一个重要的区别:在格与布尔代数中,偏序关系具有重要的意义。
为了强调偏序关系的作用,我们将分别从偏序关系和代数系统两个方面引入格的概念。
给格附加一定的限制后,格就转化为布尔代数,即布尔代数是一种特殊的格。
布尔代数最初是作为对逻辑思维法则的研究而出现的,创立者是英国哲学家和数学家布尔(G .Boole )。
自布尔之后,许多数学家对布尔代数的一般化作了许多努力,特别是斯通(M.H.Stone ),他的工作可以说是对现代布尔代数的发展开创了一个新阶段。
1938年,香农(C.E.Shannon )发表了《继电器和开关电路的符号分析》一文,为布尔代数在工艺技术中的应用开创了道路,从而出现了开关代数。
为了给开关代数奠定基础,于是自然形成了二值布尔代数,即逻辑代数。
自香农之后,人们应用布尔代数对电路作了大量研究,并形成了网络理论。
格与布尔代数不仅是代数学的一个分支,而且在近代解析几何、半序空间等方面也都有重要的作用,同时,格与布尔代数在计算机科学中也有十分重要的作用,可直接用于开关理论和逻辑设计、密码学、计算机理论科学等。
§5.1 偏序关系与偏序集 1. 基本概念我们常用关系对集合的某些元素或全体元素进行排序。
例如,使用包含着字对><y x ,的关系对字排序,其中x 按照字典顺序排在y 的前面。
使用包含着任务对><y x ,的关系安排任务,其中任务x 必须在任务y 之前完成。
使用包含着整数对><y x ,的关系安排整数,其中x 小于y 。
当我们再把所有形如><x x ,的序偶加到这些关系中时就得到一个自反的、反对称的和传递的关系,即偏序关系。
定义5.1 设R 是集合X 上的关系,如果R 是自反的、反对称的和传递的,则称R 是X上的偏序关系。
偏序关系通常用符号π表示,π>∈<b a ,通常记为b a π并读着“a 先于b ”。
带有偏序关系π的集合X 叫做偏序集,当我们需要指明时,记作><π,X 。
b a π意为b a π且b a ≠,读着“a 严格先于b ”。
π也是集合X 上的关系,并且是反自反的、反对称的和传递的,叫做X 上的半序。
显然,如果π是偏序,则X I -π为半序π,反之,如果π是半序,则X I Y π为偏序π。
a b φ意为b a π,读着“b 后于a ”。
φ也是集合X 上的偏序关系,叫做π的对偶序,相应的偏序集><φ,X 称为><π,X 的对偶集。
显然对偶序φ是关系π的逆,即1-=πφ。
例5.1 (1)设R 是实数集合,≤为小于或等于关系,则≤是R 上的偏序关系,≤><,R 是偏序集。
(2)设+Z 是正整数集合,a 整除b 记作“b a |”,例如,21|712|34|2,,,等等,则这种整除关系“|”是+Z 上的偏序关系,><+|,Z 是偏序集。
(3)整除关系“|”不是整数集合Z 上的偏序关系。
特别地,“|”在Z 上不是反对称的,例如有2|2-和2|2-,但22-≠。
(注意:说m 整除x 是指存在整数k ,使得m k x ⨯=)(4)在整数集合Z 上,定义关系:aRb 当且仅当存在正整数r 使得ra b =,例如因为328=所以82R 。
则R 是Z 上的偏序关系,><R ,Z 是偏序集。
(5)设)(S p 是集合S 的幂集,⊆是集合的包含于关系,则⊆是幂集)(S p 上的偏序关系,⊆><,)(S p 是偏序集。
■为了更直观地研究偏序关系和偏序集,可借助于哈斯(Hass )图。
哈斯图的画法可描述为:设><π,X 是偏序集,X 中的每个元素用节点表示,若X y x ∈,,且y x π,则节点x 画于节点y 的下面;若y x π且x 与y 之间不存在另一个z 使得z x π和y z π,则x 与y 之间用一线段连接。
显然,哈斯图是关系图的一种简化,它是根据偏序关系的自反和传递特点去掉了关系图中所有环和某些线段后的简化图。
例5.2 (1)集合}362412632{,,,,,=X 在整除关系下构成偏序集,它的哈斯图如图5.1(a )所示。
(2)集合}{c b a S ,,=的幂集)(S p 在集合的包含于关系⊆下构成偏序集,它的哈斯图如图5.1(b )所示。
图5.1偏序集的哈斯图■定义5.2 假设a 和b 是偏序集><π,X 上的两个元素。
如果b a π或a b π。
我们就说a 和b 是可比较的。
否则我们就说a 和b 是不可比较的,并记作b a ||。
“偏”是用来定义偏序集X 的,因为集合X 上某些元素是不可比较的。
若X 的每一对元素都是可比较的,则称X 为全序集,相应的偏序就称为全序。
全序集也叫做线性序集或叫做链。
虽然偏序集可能不是全序集,但它的子集仍有可能是全序集。
很明显,全序集的每一个子集都是全序集。
例5.3 (1)偏序集≤><,R 是全序集,R 的每个子集在偏序关系≤下也都是全序集。
(2)考虑偏序集><+|,Z 。
21和7可比较,因为21|7;但3和5不可比较,因为既没有5|3也没有3|5。
因此><+|,Z 不是全序集,但}361262{,,,=S 是+Z 在整除关系下的全序子集。
(3)对于含有两个或两个以上元素的集合S ,偏序集⊆><,)(S p 不是全序集。
例如,假设a 和b 属于S ,那么)(S p 中的}{a 与}{b 是不可比较的。
而}}{{S a A ,,φ=是)(S p 在偏序关系⊆下的全序子集。
■2. 偏序集中的特殊元素定义5.3 设><π,X 是偏序集,S 是X 的子集。
S 中的一个元素a 叫做S 的极小元,如果S 中没有其它元素严格先于a 。
类似地,S 中的一个元素b 叫做S 的极大元,如果S 中没有其它元素严格后于b 。
极小元、极大元的符号化表示为a 为S 的极小元)(a x a x S x x =→∧∈∀⇔π a 为S 的极大元)(a x x a S x x =→∧∈∀⇔π偏序集的子集S 可以有多于一个的极小元和极大元。
如果S 是无限集合,那么S 可能没有极小元和极大元,例如,偏序集≤><,R 没有极小元和极大元。
如果S 是有限集合,那么S 一定至少有一个极小元和一个极大元。
即有下面的定理。
定理5.1 设><π,X 是偏序集,S 是X 的子集。
如果S 是有限集,那么S 至少有一个极小元和一个极大元。
证明 不妨设}{21n y y y S ,,,Λ=,令1y a =,并且对n i ,,,Λ32=做⎪⎩⎪⎨⎧=ii i i y a a y a aa y y a ||若若若ππ根据偏序关系的传递性知S 中不可能存在元素x 使得a x π,所以a 就是S 的极小元。
同样可以证明存在极大元。
■定义5.4 设><π,X 是偏序集,S 是X 的子集。
S 中的元素a 叫做S 的最小元,如果对于S 中的每一个元素x 有x a π即a 先于S 中的每一个元素。
类似地,S 中的元素b 叫做S 的最大元,如果对于S 中的每一个元素x 有b x π即b 后于S 中的每一个元素。
最小元和最大元的符号化表示为a 为S 的最小元)(x a S x x π→∈∀⇔ a 为S 的最大元)(a x S x x π→∈∀⇔偏序集的子集S 若有最小元则最小元唯一,而且它一定是极小元;若有最大元则最大元唯一,而且它一定是极大元。
反之,如果子集S 为有限集且有唯一的极小元,则它一定就是最小元;若为有限集且有唯一的极大元,则它一定就是最大元。
即有下面的定理。
定理5.2 设><π,X 是偏序集,S 是X 的子集。
如果S 是有限集且a 是其唯一极小元(极大元),那么a 一定是S 的最小元(最大元)。
证明 不妨设}{21n y y y S ,,,Λ=,假设a 是唯一极小元而不是最小元,则在S 中必至少有一个元素j y 使得a y j π。
令j y b =,并且对n i ,,,Λ21=且j i =/做⎪⎩⎪⎨⎧=ii i iy a b y a bb y y b ||若若若ππ根据偏序关系的传递性知S 中不可能存在元素x 使得b x π,所以b 也是S 的极小元且a b ≠,这与极小元的唯一性矛盾,所以a 是最小元。
对极大元和最大元,同样可以证明。
■例5.4 (1)偏序集≤><,R 无极小元、极大元、最小元、最大元。
(2)偏序集><+|,Z 有唯一的极小元1,它也是最小元,但无极大元和最大元。
(3)集合}362412632{,,,,,=X 在整除关系下构成偏序集,它的哈斯图如前面的图5.1(a )所示,2和3是极小元,24和36是极大元,无最小元和最大元。
(4)集合}{c b a S ,,=的幂集)(S p 在集合的包含于关系⊆下构成偏序集,它的哈斯图如前面的图5.1(b )所示,空集φ是唯一的极小元也是最小元,全集}{c b a S ,,=是唯一的极大元也是最大元。
■定义5.5 设><π,X 是偏序集,S 是X 的子集。
X 中的元素a 叫做S 的下界,如果a 先于S 中的每一个元素,即对S 中的每一个元素x 有x a πS 的所有下界组成的集合的最大元称为S 的下确界,记作)inf(S 。
类似地,X 中的一个元素b 叫做S 的上界,如果b 后于S 中的每一个元素,即对S 中的每一个元素x 有b x πS 的所有上界组成的集合的最小元称为S 的上确界,记作)sup(S 。
如果S 是含有元素n a a a ,,,Λ21的有限集,我们也将)inf(S 和)sup(S 记为)inf(21n a a a ,,,Λ和)sup(21n a a a ,,,Λ。
同极小元、极大元、最小元和最大元类似,下界、上界也可以用符号化表示为a 为S 的下界)(x a S x x π→∈∀⇔ a 为S 的上界)(a x S x x π→∈∀⇔下界、上界、下确界和上确界都可能不存在,即使对有限集合也是这样;下界和上界可以有多个,但下确界和上确界如果存在则唯一。
而且如果a 是集合S 的最小(大)元,则a 也是S 的下(上)确界;反之,如果a 是集合S 的下(上)确界且S a ∈,则a 也是S 的最小(大)元。
有些书将下确界叫做最大下界,并记作)glb(S 不不是)inf(S ,将上确界叫做最小上界,并记作)lub(S 不不是)sup(S 。
例5.5 (1)偏序集}{1f e d c b a X ,,,,,=,其哈斯图如图5.2(a )所示,求子集}{1d c b a S ,,,=的下界、上界、下确界、上确界。