当前位置：文档之家 › 第七章格与布尔代数

第七章格与布尔代数

  • 格式：doc
  • 大小：287.51 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

代数结构-布尔代数与格

代数结构-布尔代数与格

布尔代数举例

({0, 1}, +, ⋅ , , 0, 1)为布尔代数 n度布尔函数全体也构成一个布尔代数

布尔和 布尔积 补函数 全取0的函数、全取1的函数

A的幂集也构成一个布尔代数(ρ(A), ⋂, ⋃, ∼, ∅, A）
布尔代数举例

Bn={(x1, …, xn)| xi∈B, i =1, …, n}构成布尔代数 x= (a1 , …, an), y=(b1 , …, bn), ai∈B, bi∈B
111 110
Bn as Product of n B’s

B1, ({0,1}, ∧, ∨, 1, 0, ’), is denoted as B. For any n≥1, Bn is the product B×B×...×B of B, n factors, where B×B×...×B is given the product partial order.
格中的原子
a
a a b c d (1) e (2) b c d b
c 原子 d e (3)
有限布尔代数的表示定理

任一有限布尔代数B 同构于 B中所有的原子构成的 集合A的幂集代数系统P(A)。 即(B, ∧, ∨, ', 0, 1) ≅ (P(A), ⋂, ⋃, ∼, ∅, A)

备注（关于无限布尔代数）

若 x∧y =x，则 x∨y = (x∧y) ∨ y = y //吸收律
若 x∨y =y，则 x∧ y = x∧ (x∨y) = x //吸收律


证明这个关系满足自反性、反对称性、传递性。 这个偏序构成一个格。

lub{x,y} 即为 x∨y。 glb{x,y} 即为 x∧y。

第7章 格和布尔代数

第7章 格和布尔代数
m∨n＝LCM（m,n） m∧n＝gcd（m,n）
另外，若将〈L, 〉中的小于等于关系换成大于等 ，即对于L中任何两个元素a,b定义a b的充
分必要条件是b a,则〈L, 〉也是偏序集。我们把偏 序集〈L, 〉和〈L, 〉称为是相互对偶的。并且它们 所对应的哈斯图是互为颠倒的。关于格我们有同样的 性质。
对偶式。
在上述对偶原理中，“如果命题P在任意格
〈L， 〉上成立”的含义是指当命题P中的变量取值于L 中，且上确界运算为∨，下确界运算为∧，则P对于它 们也成立。现在我们深入地讨论格的性质。
定理7.1.3 设〈L, 〉是一个格，那么对L中任何元 素a,b,c，有
（1） a a∨b，b a∨b a∧b a，a∧b b
定理7.1.1 若〈L, 〉是一个格，则〈L, 〉也是一 个格,且它的并、交运算∨r,∧r对任意a,b∈L满足
a∨rb=a∧b a∧rb=a∨b 于是，我们有下列对偶原理。
定理7.1.2 如果命题P在任意格〈L， 〉上成立，
则将L中符号∨，∧，
∧，∨，
公式P*在任意格〈L， 〉上也成立，这里P*称为P的
（1）a b当且仅当a∧b=a当且仅当a∨b=b。 （2）a∨（b∧c） （a∨b）∧（a∨c）。 （3）a c当且仅当a∨(b∧c) a∨b）∧c。
图 7.1.1
在第四章，对偏序集的任一子集可引入上确界（最 小上界）和下确界（最大下界）的概念，但并非每个 子集都有上确界或下确界，例如在图7.1.1中哈斯图所
示的有序集里，{a，b}没有上确界，{e，f}没有下确界
。不过，当某子集的上、下确界存在时，这个上、下 确界是唯一确定的。
定义7.1.1 如果偏序集〈L 的子集都有上确界和下确界,则称偏序集〈L 格（lattice）。

格与布尔代数

格与布尔代数

对P(S)中任一元素A,S与A的差集S-A是其唯一补元
因为:
(S-A)∪A=S和(S-A)∩A=Φ.
36
7.5 几种特殊的格
定义4(分配格) 格<L, ,*>称作一个分配格,如果对L中 任意元素a,b,c都有: (1) a*(bc)=(a*b)(a*c); (2) a(b*c)=(ab)*(ac). 例：幂集格<P(S),∩,∪>都是分配格. 格<P(S),∩,∪> 的两个二元运算分别是S幂集合上的交和并运算,交 对并和并对交都具有分配律;
M={c,d}
无上确界，下确界为e 上确界为a，下确界为b
12
7.1 偏序集
M={{a},{b}}
上确界{{a,b}}，下确界为
M={{a},{a,b}}
上确界{{a,b}}，下确界为{a}
M={{a},{b,c}}或 M={{a},{b},{c}}或
上确界{{a,b,c}}，下确界为
M={{a,b},{b,c}}
31
7.5 几种特殊的格
定义1 (有界格) 若格<L,≤>存在最大元和最小元，则称该格为有界格。
记最大元为1，最小元为0。记有界格为<L,≤,0,1>。
例： <P(S), , ,S>有界格。
32
7.5 几种特殊的格
定义2 (补元) 有界格<L,≤,0,1>中，如果a*b=0且ab=1. 则称元素b为a的补元。
18
7.2 格的定义
例. 设S是任意集合, 则< P(s), >为偏序格。
|S|=1
|S|=2
|S|=3 两个集合A，B的上确界是A∪B，下确界是A∩B

格与布尔代数课件2

格与布尔代数课件2
= {y | y≤x1} ∩{y | y≤x2} = f(x1) ∧2 f(x2) f (x1∨1x2) = f (max{x1,x2}) = {y | y≤max{x1,x2}}
= {y | y≤x1} ∪ {y | y≤x2} = f(x1) ∨2 f(x2)
存在一个从A1到A2的映射f，使得对 x1,x2 A， 有f(x1∨1x2)=f(x1)∨2f(x2)，f(x1∧1x2)=f(x1)∧2f(x2) ∴f 是 A1 到 A2 的格同态。
吸收律：a∨(a∧b) = a、a∧(a∨b) = a
证明：幂等律 ∵ a≤a，∴ a是a的上界，而a∨a是a的最小上界， ∴a∨a≤a ，又 ∵ a≤a ∨a，
由反对称性得：a∨a = a 由对偶原理得，a∧a = a
第15页，共28页。
证明：吸收律 ∵ a ≤a a ∧b ≤a ∴ a∨(a ∧ b)≤a∨a， a∨(a ∧ b)≤a
解：< I+ , D>是格 ∵整除关系是偏序关系，对a,bI， a、b的最小上界等于a、b的最小公倍数， a、b的最大上界等于a、b的最大公约数。
第3页，共28页。
< P(S) , > 是格
∵子集关系是偏序关系，对a,b P(S)，
a、b的最小上界等于a∪b，
a、b的最大上界等于a∩b。
<<=S{S<n61, ,D,1D>>>,是<2格,2，>,<偏3,序3>关,<系1,6的>,哈<1斯,2>图,<如1,下3>1：,2<2,6>,<3,6>}
{a,b,c}
a
{a,b} {a,c} {b,c}

格和布尔代数

格和布尔代数
a,bL，若a≤b a∧b = a
分三步： 1) 证明’≤’是L上的偏序关系 2）证明 a,bL, {a,b}的下确界存在， 且 a∧b = glb(a,b)。 3）a,bL, {a,b}的上确界存在，且 lub(a,b) a∨b 具体证法见后面
1) 证明’≤’是L上的偏序关系 自反性：aL 由等幂律 a∧a=a, a≤a 反对称性：a,bL, 若a≤b, b≤a 则 a∧b=a, b∧a=b a = a∧b = b∧a = b 传递性：a,b,cL, 若 a≤b,b≤c 则a∧b=a, b∧c=b a∧c=(a∧b)∧c = a∧(b∧c)= a∧b=a a≤c
2、格的对偶原理
① 集合S的偏序关系≤的逆关系≥也是偏序关 系，若AS, 其中 ≤的glb(A) 对应于 ≥的lub(A), ≤的lub(A) 对应于 ≥的glb(A), 所以，若<S,≤>是格，则<S,≥>也是格， 称这两个格互为对偶。
2、格的对偶原理
② 因为<S,≤>的交是<S,≥>的并， <S,≤>的并是<S,≥>的交，
一般格只满足分配不等式： a∨(b∧c)≤(a∨b)∧(a∨c)
一、定义
设<L,∧,∨>是格，若a,b,cL，有： (1) a∧(b∨c)=(a∧b)∨(a∧c), (2) a∨(b∧c)=(a∨b)∧(a∨c), 则称 <L,∧,∨> 为分配格。
注：(1)(2)是互相等价的，由对偶原理，从一式可推
2）证明 a,bL, {a,b}的下确界存在， 且 a∧b=glb(a,b)。
a) 因为 (a∧b)∧a =(a∧a)∧b=a∧b a∧b≤a 同理a∧b≤b a∧b 是a,b的下界。

格与布尔代数

格与布尔代数

例7.12 设B={0，1}，B n=BxBx…xB，B n中的元 素a=＜a1，a2，…，an＞，b=＜b1，b2，…，bn＞, 其中ai与bi取0或1，＜0，0，…，0＞表示为0n， ＜1，1，…，1＞表示为1n，定义*， ⊕ 与┐运算
如下：
a*b=＜a1*b1，a2*b2，…,an*bn＞,a⊕b＜a1⊕b1， a2⊕b2，…， an⊕bn＞, ┐a=＜┐a1， ┐a2，…，┐an ＞,可验证：＜Bn，*，⊕，┐，0n，1n＞符合条件 （H1）至（H4），故可构成布尔代数。
3、分配格的判定 定理7.7 格L是分配格，当且仅当L中不含有与钻 石格或五角格同构的子格。 推论7.1 （1）小于五元的格都是分配格；（2） 任意一条链都是分配格。 证明P130
例7.7 图7.4中哪个是分配格，哪个不是？
f
f
f
d e
e d
b
c
d
b
c c
e b
a
（a)L1
a
（b)L2
图7.4 格的示意图
7.1 格的基本概念
7.1.1 格的定义 1、格定义7.1 设＜A，≤＞是一个偏序集，对于 Ɐa,b∈A,子集{a，b}在A中都有一个最大下界(也 称为下确界，记为inf{a,b})和一个最小上界(也称 为上确界，记为sup{a,b}),则称＜A，≤＞为 格。
2、诱导的代数系统 定义7.2 设＜A，≤＞是一个格，如果在A上定义两 个二元运算，使得对Ɐa,b∈A，a∧b等于a和b的最 大下界，a∨b等于a和b的最小上界。则称＜A，∧， ∨ ＞为由格＜A，≤＞所诱导的代数系统。
⊕0 1 00 0 10 1
x ┐x
01 10
可验证＜B，*，⊕ ，┐，0，1＞是布尔格，也称为 二值布尔代数。

离散数学-格和布尔代数

离散数学-格和布尔代数

的次序图如下
-1 的次序图如下
6 2 1 3 2
1 3 6
若 < L; > 是一个偏序集，则对于任意元素 l1, l2, l3 L，有以 下六个关系式成立： l1 l1 若 l1 l2，l2 l1，则 l1 = l2 若 l1 l2，l2 l3，则 l1 l3 l1 l1 若 l1 l2，l2 l1，则 l1 = l2 (7-1) (7-2) (7-3) (7-1) (7-2)
60以上说明与格一样布尔代数也是一个代数系统该代数系统可取交换律分配律同一律和互补律作为公二元运算是一元运算若这些运算满足交换律分配律同一律和互补律则称称作集合代数它是一个布尔代数
第二部分 抽象代数
0
第七章
格和布尔代数
格是 Birkhoff (1884 - 1944) 在 20 世纪 30 年代提出的，格的提出 以子集为背景。 历史上最初出现的格是英国数学家 George Boole 于 1854 年提出 的，是他在研究命题演算中发现的，通常称为布尔格或布尔代 数。 格和布尔代数的理论成为计算机硬件设计和通讯系统设计中的 重要工具。格论是计算机语言的指称语义的理论基础。格是一 种特殊的偏序集，也可以看作是有两个二元运算的代数系统， 布尔代数是一种特殊的格。在保密学、开关理论、计算机理论 和逻辑设计以及其他一些科学和工程领域中，都直接应用了格 与布尔代数。 1
7.2 格及其性质
一、格的定义
定义7-5 设 < L; > 是一个偏序集，如果 L 中任意两个元素都 存在着最大下界和最小上界，则称 < L; > 是格。 由于每对元素的最大下界和最小上界唯一，故引入记号： l1 l2 = glb(l1, l2)，l1 l2 = lub(l1, l2)， 其中 和 均可看作是集合 L 上的二元运算，分别称为交和并。 注：若 < L; > 是一个格，则意味着 < L; > 也是一个形为 < L; , > 的代数系统，其中 和 是 L 上的两个二元运算， 对于任意 l1, l2 L，l1 l2 表示在偏序 “ ” 意义下，l1 和 l2 的最小上界，l1 l2 表示 l1 和 l2 的最大下界。

离散数学布尔代数

离散数学布尔代数

一个非零元素b，至少存在一个原子a，使得a ≤ b。 1
证明：若b本身就是一个原子，则b ≤ b，得证。c
df
若b不是原子，肯定存在b1，使得0 ≤ b1 ≤ b， a
be
若b1是原子，则定理得证；
0
否则，若b1不是原子，则必存在b2，使得0 ≤ b2 ≤ b1 ≤ b
∵<A, ≤>是一个有全下界的有限格，
定理1：对于布尔代数中任意两个元素 a, b，必定有
(1) ( a ) = a， (2) a∨b = a∧b ， (3) a∧b = a∨b
3
❖ 布尔代数
定义3：设<A,∨1,∧1, - > 和<B,∨2,∧2, ~ >是两个布尔代数， 如果存在A到B的双射 f，对于a,bA，有
f (a∨1b) = f (a) ∨2 f (b)
2、对a,bA，有 f (a∧b) = f (a)∩f (b)
9
❖ 格与布尔代数
定理3 ( Stone表示定理 ) ：
设<A,∨,∧, - >是由有限布尔格<A, ≤>所诱导的一个有 限布尔代数，S是布尔格<A, ≤>中的所有原子的集合，则 < A,∨,∧, - >< P(S),∪,∩, ~ >同构。 分析：要证两个代数系统同构，分为以下几步：
1、找一个双射函数 f: A P(S)
∴a ≤ c ，又∵a ≤ c， ∴a ≤ c ∧ c，即 a ≤ 0，
这与a是原子相矛盾， ∴假设错
∴b ∧ c = 0，由引理1得： b≤c ∴b=c，即：b= a1∨a2∨... ∨ak
7
❖ 格与布尔代数
证明(2)：设b的另一种表示形式为 b = aj1∨aj2∨... ∨ajt 其中aj1,aj2,……,ajt是A中原子。∵b是 aj1,aj2,……,ajt 的最小上界， ∴有aj1≤b, aj2≤b,…,ajt≤b，而a1,a2,……,ak是A中满足 a j ≤b的所有原子， {aj1,aj2,…,ajt}是{a1,a2,…,ak}的子集，即 |{aj1,aj2,…,ajt}|<=|{a1,a2,…,ak}|， 即：t ≤ k。(下面证 t < k 是不可能的)

离散数学格与布尔代数

离散数学格与布尔代数

6
<S15,|>,
2
2019/10/12
30
10
15
3
5
1
§7.1 格
例 判断图中的哈斯图表示的偏序集是否构成格,说明为什么。
d c
b a
(a)

e d
c b
a (b)

f
d
e
d
e
c
b
c
a (c)

a
b
(d)

e
c
d
a
b
(e)

2019/10/12
§7.1 格
例 设Z+为正整数集合，对于a,b Z+，关系“≤”定义为： a≤b当 且仅当a整除b。则偏序集<Z+,≤>构成格，
Input A B Cin
00 0 00 1 01 0 01 1 10 0 10 1 11 0 11 1
Output S Cout
00 10 10 01 10 01 01 11
S A BCin A BCin A BCin A BCin
Cout A B Cin A B Cin A B Cin A B Cin
§7.2 格——代数系统
证〈L，≤〉为要求的格
a，b∈L，（a * b）* a ＝ a*（a * b）＝（a * a）*b＝a*b，
故a*b≤a，
L3
L1
同理a*b≤b，因此a*b是｛a，b｝的下界，
又设c是｛a，b｝的任一下界，即c≤a，c≤b，则a * c＝c，b * c＝c，于是（a * b）* c＝a *（b * c）＝a * c＝c，即c≤a * b， 所以a * b是｛a，b｝的最大下界，即a * b＝inf｛a，b｝，

布 尔 代 数

布 尔 代 数
1.2 布尔代数
➢定义12.10
代数系统< B，∨，∧>
（∨，∧为B上二元运算）称为布尔代数， 如果
B满足下列条：
（1）运算∨，∧满足交换律。
（2）∨运算对∧运算满足分配律，∧运算对∨
运算也满足分配律。
（3）B有∨运算么元和∧运算零元O，∧运算
么元和∨运算零元1。
（4）对B中每一元素a，均存在元素a’，使
✓定理12.5
有补分配格中每一元素的补元都是 唯一的。
✓定理12.16
对有补分配格中每一元素a，有
（a’）’＝ a
.
布尔代数
1.1 有界格和有补格
✓定理12.17
设< L，∨,∧>为有补分配格，那么对
L中任意元素a，b，有
（1） （a∨b）’＝ a’∧ b’ （2）（a∧b）’= a’∨ b’
✓定理12.18
如果 a∨b = 1， a∧b = 0
a的补常用a’来表示。
.
布尔代数
1.1 有界格和有补格
➢定义12.8
有界格< L，∨,∧>称为有补格
（complemented lettice），如果L中每个 元素都有补元。
✓定理12.4
有补格< L，∨,∧>中元素0，1的 补元是唯一的。
.
布尔ቤተ መጻሕፍቲ ባይዱ数
1.1 有界格和有补格
称为 n个变元的极大项，其中 i为变元xi或xi’.
.
布尔代数
1.4 布尔表达式与布尔函数
➢定义12.16
布尔表达式f(x1,x2,…,xn)
所定义的函数f:B→B称为布尔函数
（Booleanl functions）．

格 布尔代数的应用

格 布尔代数的应用

格布尔代数的应用
布尔代数起源于数学领域，是一个用于集合运算和逻辑运算的公式：〈B，∨，∧，¬ 〉。

其中B为一个非空集合，∨，∧为定义在B上的两个二元运算，¬为定义在B上的一个一元运算。

通过布尔代数进行集合运算可以获取到不同集合之间的交集、并集或补集，进行逻辑运算可以对不同集合进行与、或、非。

应用
布尔代数不仅可以在数学领域内实现集合运算，更广泛应用于电子学、计算机硬件、计算机软件等领域的逻辑运算：当集合内只包含两个元素（1和0）时，分别对应{真}和{假}，可以用于实现对逻辑的判断。

常见的应用包括：
•数字电路设计，0和1与数字电路中某个位的状态对应，例如：高电平、低电平。

•计算机的网络设置，利用计算机的二进制特性，将子网掩码与本机IP地址进行逻辑与运算，可以得到计算机的网络地址和主机地址。

•数据库应用，通过SQL语句查询数据库时需要进行逻辑运算，确定具体的查询目标。

离散数学第七章格与布尔代数

离散数学第七章格与布尔代数
离散数学第七章格 与布尔代数
contents
目录
• 格的概述 • 布尔代数 • 格与布尔代数的应用 • 格与布尔代数的关系 • 格与布尔代数的扩展知识
01
CATALOGUE
格的概述
格的定义与性质
定义
格是一个有序的二元组(L,≤)，其中L 是非空集合，≤是L上的二元关系， 满足自反性、反对称性和传递性。
布尔代数性质
布尔代数具有一些基本性质，如交换 律、结合律、吸收律等，这些性质使 得布尔代数成为逻辑推理和电路设计 等领域的重要工具。
布尔代数的运算
逻辑与运算
逻辑与运算用符号"∧"表示，表示两个逻辑量同时 为真时结果才为真。
逻辑或运算
逻辑或运算用符号"∨"表示，表示两个逻辑量至少 有一个为真时结果才为真。
布尔代数的扩展运算
布尔函数的复合
01
通过将两个或多个布尔函数连接在一起，形成更复杂的布尔函
数。
布尔函数的展开
02
将一个复杂的布尔函数分解为简单的布尔函数，以便更好地理
解和分析。
布尔函数的化简
03
通过消除冗余的输入和输出，简化布尔函数的表示。
格与布尔代数在其他领域的应用
计算机科学
01
格与布尔代数在计算机科学中有着广泛的应用，例如
布尔代数用于描述命题逻辑和谓词逻辑中的各种关系和运算，而格理论则用于描述集合论和集合运算。
格与布尔代数的理论框架为逻辑推理提供了数学基础，有助于深入研究和理解逻辑推理的本质和规律。
计算机科学中的应用
01 02 03 04
计算机科学是离散数学的另一个重要应用领域，其中格与布尔代数在 计算机算法、数据结构和程序设计语言等方面有广泛应用。

离散数学格的概念

离散数学格的概念

❖ 代数系统定义的格
定理1:<A,∨,∧>是代数系统，∨,∧都是二元运算且满足交换律、 结合律和吸收律，则A上存在偏序关系≤，使<A, ≤>是一个格。 证明：在A上定义一个二元关系≤为： ≤ ={<a,b> | a,b A, a∧b = a 或 a ∨ b =b} 可以证明a∧b = a 与 a ∨ b =b 是等价的。即a∧b = a a ∨ b =b 首先证明≤是偏序关系 (1) ∵ ∨,∧满足吸收律∴ ∨,∧满足幂等律
d
g
c
h
b
e
f
a
❖格的基本性质
格的性质：设<A,≤>格，对A中的任意元素 a,b,c，有：
(4) 交换律：a∨b = b∨a、a∧b = b∧a 结合律：a∨(b∨c) = (a∨b)∨c、a∧(b∧c) = (a∧b)∧c 幂等律：a∨a = a、a∧a = a 吸收律：a∨(a∧b) = a、a∧(a∨b) = a
❖ 基本概念
例3： B3 = {1,2,3,6,10,15,30} ，显然 < B3, D >是格。
30
30
10
6 15
2
3
10
6 15
2
53
1
1
但∵10∧15 = 5 ≠ 1，即∧运算在B3上不封闭，
∴< B3 , D >不是 < S30 , D >的子格。
说明：
(2) BA 且<B,≤ > 是格，则<B,≤ > 一定是<A,≤ >的子格。
< B, max, min >
< P(A) , > 诱导代数系统是：

第7章 格与布尔代数

第7章 格与布尔代数

第7章 格与布尔代数
7.1―1 格的定义
定义7.1―1设〈L,≤〉是一个偏序集合,如果L中每 一对元素a,b,都有最大下界和最小上界,则称此〈L,≤〉
为格。
通常用ab表示｛a,b｝的最大下界,用ab表示｛a,b｝ 的最小上界。即 a * b=glb｛a,b｝ ab=lub｛a,b｝
第7章 格与布尔代数

(5′)得a≥a
公式(2′)得a
(a*b), 但由公式(4′)有a
(a*b)=a。
(a*b)≥ a,这样,根据
第7章 格与布尔代数
(10)a≤b a*b=a a b=b的证明。
先证a≤b a*b=a,由公式1知a≤a,由假设a≤b,所以,由 公式5得a≤a*b,但a*b≤a。因此,a*b=a。即a≤b a*b=a a≤b。 再证a*b=a a b=b由a*b=a得b (a *b)=a b, 即a b=b。反之,若a b=b,则a*(a b)=a*b,即a*b=a。 公式(10)建立了格中偏序关系和保交,保联间的一种 联系。
f (a*b)=f (a)∧f (b)=f (a)
所以,f (a)≤′f (b)。证毕
第7章 格与布尔代数
在定义7.2―3中,若f是双射函数,则称f是格同构。或
说〈L, *, 〉 和〈S,∧,∨〉两个格同构。由于同构是 相互的,又是保序的,所以对任何a,b∈L有,
a≤bf (a)≤′f (b)
第7章 格与布尔代数
7.2.2 子格,格同态和格的积代数
定义7.2―2 〈L, *, 〉是一个格,S L,如果S对运 算和封闭,那么称〈S, *, 〉是〈L, *, 〉的子格。 子格本身是一个格,因为交换律,结合律,吸收律都是 继承的。显然 , 不是 L 的任意子集都可构成子格。例如 图 7.2―1 所 示 的 格 中 ,〈 ｛ a,b,d ｝ ,≤〉 是 子 格 , 〈｛b,c｝,≤〉不是子格,因为｛b,c｝对运算不封闭。

2017年中国科学技术大学0812计算机科学与技术考研专业目录及考试科目

2017年中国科学技术大学0812计算机科学与技术考研专业目录及考试科目

2017年中国科学技术大学0812计算机科学与技术考研专业目录及考试科目一、报考说明：接收推免生及统考生。

二、专业介绍：本学科培养学生德、智、体全面发展，适合于在高等学校、科研机构、企事业单位从事计算机系统结构相关领域的教学、科研和应用开发等工作的高层次专门人才。

掌握计算机学科方面坚实的基础理论和系统的专门知识，了解本学科的发展方向及前沿动向，具备较强的综合运用所学理论知识从事科学研究工作和独立承担专门技术工作的能力，有严谨求实的科学作风和良好的科研道德，开拓进取的创新精神，团队合作和敬业精神。

熟练掌握一门外国语，能阅读本专业的外文资料并撰写专业领域外文文章。

具有较强的综合能力、语言表达能力及写作能力；具有健康的体魄和良好的心理素质。

本学科点具有计算机系统结构、计算机软件与理论、计算机应用技术以及信息安全4个二级学科。

相应的研究方向如下：1、计算机系统结构计算机系统结构是计算机科学技术最活跃的研究领域之一，特别是最近几年，随着高性能计算机的广泛研究和应用、计算机整体设计关键技术的突破、计算机网络体系结构的迅速发展，计算机系统结构的研究出现了新的热点和重大进展。

在微处理芯片体系结构方面主要研究新型微处理芯片体系结构及其编程技术，可重构的片上并行体系结构，通用微处理芯片设计技术，指令级并行关键技术和嵌入式系统整体设计方法，多处理器体系结构等；在计算机体系结构方面主要研究新型高效能并行计算机体系结构、模型及其关键技术，包括软件技术、超高扩展高密度计算技术、高可用集群中间件技术、可重构计算等，“并行结构-并行算法-并行编程”研究一体化；在网络及分布式计算方面主要研究新型网络体系结构和协议，网格计算平台及应用，对等网络、无线网络和移动计算等。

2、计算机软件与理论计算机软件与理论是指由计算机科学理论和研究、开发计算机软件所涉及的理论、方法、技术所构成的学科，是信息科学的核心研究领域之一，是计算机学科用来为国民经济、国防建设、人民生活服务的工具和基础。

格与布尔代数

格与布尔代数

a∨0＝a 和 a∧1＝a 互为对偶命题。
有界格中的补元
定义 设<L,∧,∨,0,1>是有界格，a∈L， 若存在b∈L 使得 a∧b＝0 和 a∨b＝1 成立，则称b是a的补元。
说明 若b是a的补元，那么a也是b的补元。
换句话说，a和b互为补元。
有界格中补元的说明
在任何有界格中， 全下界0与全上界1互补。 对于其他元素，可能存在补元，也可能不存在补元。 如果存在，可能是唯一的，也可能是多个补元。
格与布尔代数
格的定义与性质
定义 设<S,≤>是偏序集，如果x,y∈S，{x,y}都有最小上界 和最大下界，则称S关于偏序≤作成一个格。
说明：由于最小上界和最大下界的唯一性，可以把求{x,y}的最 小上界和最大下界看成x与y的二元运算∨和∧。
x∨y：表示x与y的最小上界
x∧y：表示x和y的最大下界。
本章出现的∨和∧符号只代表格中的运算，而不再有其它的 含义。
格的实例
例 设n是正整数，Sn是n的正因子的集合。D为整除关系，则 偏序集<Sn,D>构成格。x,y∈Sn， x∨y是lcm(x,y)，即x与y的最小公倍数。 x∧y是gcd(x,y)，即x与y的最大公约数。 下图给出了格<S8,D>，<S6,D>和<S30,D>。
定义 设<L,∧,∨>是格，若a,b,c∈L，有
a∧(b∨c)＝(a∧b)∨(a∧c) a∨(b∧c)＝(a∨b)∧(a∨c)
则称L为分配格。
说明 上面两个等式互为对偶式。 在证明L为分配格时，只须证明其中的一个等式即可。
分配格的判别
定理 设L是格，则L是分配格当且仅当L中不含有与钻石格或 五角格同构的子格。

离散数学第7章 格

离散数学第7章 格

4
2
3
7．2
格及其性质
1．格的定义
定义7-4
设<L；≤>是一个偏序集，如果L中任
意两个元素都存在着最大下界和最小上界，则称<L；≤> 是格. 在格上定义两个二元运算“˄” 和 “˅” 如下：
l1˄ l2=glb(l1, l2), l1˅ l2=lub(l1, l2). 因此 <L；≤>是一个格意味着 <L；≤> 也是一个形为<L； ˄ ,˅>的代数系统，其中˄和˅是L上的两个二元运算， 对于任意l1，l2 L ， l1˅ l2表示在偏序“≤”意义下， l1 和l2的最小上界， l1˄ l2表示l1和l2的最大下界.
l1 ≤ l 1 (7-1) (7-2) (7-3) (7-1')
若 l1 ≤ l2 , l2 ≤ l1, 则 l1= l2 若 l1 ≤ l2 , l2 ≤ l3, 则 l1 ≤ l3 l1 ≥ l1
若 l1 ≥ l2 , l2 ≥ l1 , 则 l1 = l2
若 l1 ≥ l2 , l2 ≥ l3, 则 l1 ≥ l3
非分配格非有补格75布尔代数布尔代数的定义定义710如果一个格是有补分配格则称其为布尔代数一般记作具有如下性质对于b中任意元素上定义的集合的并交和补运算与称作集合代数它是一个布尔代数
第7章 格和布尔代数
7.1 偏序集
7.2 格及其性质 7.3 格是一种代数系统 7.4 分配格和有补格 7.5 布尔代数
可以证明关系 ≤ 是 L 上的自反，反对称和可传递
的关系，因此 ≤ 是 L 上的偏序关系. 进一步还可以证明，对任意 l1 , l2 L ， l1 ∨ l2 是在 偏序关系 ≤ 意义下 l1 和 l2 的最小上界， l1 ∧ l2 是 l1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第七章 格与布尔代数1. 说明什么叫格？2. 给定偏序集<A,≤>、<B,≤>、<C,≤>如下图所示，其中哪些不是格？为什么？3下面图哪些是格？对于不是格的，要说明原因。

4. 填空： <A,≤>是平凡格，当且仅当 ( ).5.证明全序都是格。

6. 填空： 设<A, ≤>是格, <A,∨,∧>是由格<A,≤>诱导的代数系统。

其中∨与∧是在A 上定义二元运算。

: a,b ∈A 则 a ∨b 表示（ ）。

q(a)(b)(c)(d)３２5156<A,≤> <C,≤><B,≤>41 23a ∧b 表示（ ）。

7. 说明什么叫子格？8. 给定偏序集<A,≤>、<B,≤>、<C,≤>如下图所示，其中哪些不是格<A,≤>的子格？ 为什么？9.设<A, ≤>是一个格,任取a,b ∈A,a<b (即a ≤b ∧a ≠b) ,构造集合： B={x| x ∈A 且a ≤x ≤b}, 证明<B, ≤>也是格.10.具有一、二、三个元素的格各有几种不同构形式？请分别请画出它们的哈斯图。

11.具有四个元素的格有几种不同构形式？请分别请画出它们的哈斯图。

12具有五个元素的格有几种不同构形式？请分别请画出它们的哈斯图。

13. 证明格中下面式子成立： (a ∧b)∨(c ∧d)≤(a ∨c)∧(b ∨d)aac<B,≤> <A,≤>a<C,≤>14. 请说出什么叫分配格？15. 指出判定一个格是分配格的充分且必要条件是在该格中没有任何子格与两个五元素非分配格之一同构。

请画出这两个五元素非分配格。

16. 下面具有五个元素的格中，哪些是分配格？17.具有五个元素的格中，有几个不是分配格？请画出这些非分配格的图。

18. 验证下面格不是分配格。

19. 验证下面格不是分配格。

a b c de20.下面图中哪个是分配格？对不是分配格的，说明原因。

21. 给定集合如下：A 1={1,2,4,8,16} A 2={1,2,3,5,6,10,15,30}A 3={1,2,3,5,30} A 4={1,2,3,5,10,15,30} A 5={1,2,3,4,9,36}令≤是上述集合上的整除关系。

1. 请分别画出各个偏序集<A i ,≤>的哈斯图（i=1,2,3,4,5）22. 设<A,≤>是分配格,a,b ∈A, 且a<b, 证明 f(x)=(x ∨a)∧b 是一个从A 到B 的同态映射。

其中 B={x|x ∈A 且a ≤x ≤b}。

(a)34(b)b(c)dac23 给出有界格如图(1)所示。

问 a) 哪些元素有补元? b) 该格是分配格吗? c) 该格是有补格吗?24. 证明具有两个或更多个元素的格中 不存在以自身为补元的元素。

25. 在有界分配格中,证明具有补元的那些元素组成一个子格。

26. 设<A,≤>是有界格, 对于任何x,y ∈A, 证明 a). x ∨y=0 , 则 x=y=0 b). x ∧y=1, 则 x=y=127. 填空1．<A,≤>是布尔格，当且仅当它是 ( ) 格。

28. 下面(a),(b),(c)三个格是布尔格吗？如果是，请指出各个格的原子。

cbdgedaf(1)(2)29.下面的说法是否正确？为什么？ 1．不是所有格都是有界格。

2．少于五个元素的格，都是分配格。

30. 设<A,∨,∧>是由格<A,≤>诱导的代数系统，求证如果∧对∨可分配，则∨对∧也可分配。

31. 设<A,≤>是布尔格，求证，对于任何a,b,c ∈A ，如果有 a ∧b=a ∧c 和 a ∨b=a ∨c 成立，则 b=c 。

32. 判断下面命题的真值，并说明原因。

所有链都不是有补格。

33.判断下面命题的真值，并说明原因。

<A,≤>是格，如果|A|=3，则它不是有补格；如果|A|<5，则它必是分配格。

34.判断下面命题的真值，并说明原因。

d fc1b(a)(b)<A,≤>是有限布尔格，仅当它的元素个数为2n 。

(n 是正整数)35.设<A,∨,∧, ->是布尔代数，* 是A 上的二元运算，定义如下： a *b=a ∨b 其中a,b ∈A1．化简表达式 a b a a b a *****)(())(( 2．<A,*>是否为半群？为什么？36. 设<S,∨,∧,¯>是布尔代数，x,y ∈S, 证明:x ≤y 当且仅当 x y ≤37. 举例说明并非有补格都是分配格。

并非分配格都是有补格。

（画出图说明即可）38. 给定布尔代数<{0,1},∨,∧,―>中的布尔表达式E(x,y,z)如下，请用最简单的方法对它化简。

(提示：考虑析取范式与合取范式的关系))()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧=39.给定布尔代数<{0,1},∨,∧,―>中的布尔表达式E(x,y,z)如下，请用最简单的方法对它化简。

(提示：考虑析取范式与合取范式的关系))()()()()()(),,(z y x z y x z y x z y x z y x z y x z y x E ∧∧∨∧∧∨∧∧∨∧∧∨∧∧∨∧∧=40.给定布尔代数<{0,1},∨,∧, ¯ >上的一个布尔表达式如下：)()()(),,(323221321x x x x x x x x x E ∧∨∧∨∧=分别写出它的析取范式与合取范式。

1.答案：<A,≤>是偏序集，如果任何a,b ∈A,使得{a,b}都有最大下界和最小上界，则称<A,≤>是格。

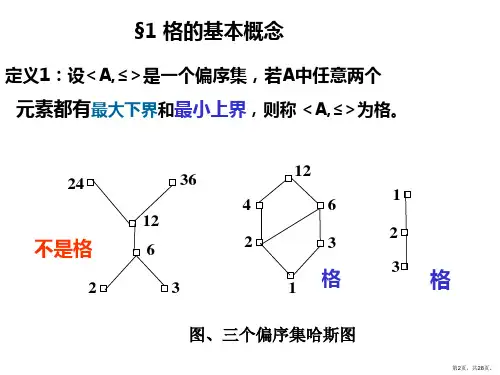
2.答案：<A,≤>不是格。

因为{24,36}无上界，所以无上确界。

所以不是格。

3.(a) 不是格，因为d 和e 没有下确界,也没有上确界.(d) 不是格，因为5和6没有下确界,7和8既没下确界,也没上确界. 4.答案：(<A,≤>是全序 ) 5.答案：设<A,≤>是全序。

所以A 中任何两个元素x,y ，要么有x ≤y, 要么有y ≤x 。

如果x ≤y ，则{x,y}的最大下界为x ，最小上界为y 。

如果y ≤x ，则{x,y}的最大下界为y ，最小上界为 x 。

即{x,y}的最大下界为较小元素，最小上界为较大元素。

所以全序都是格。

6.答案：a ∨b 表示（LUB {a,b}, 或者{a,b}的最小上界）a ∧b 表示（GLB {a,b}, 或者{a,b}的最大下界）7.答案：设<A,≤>是格, <A,∨,∧>是由<A,≤>诱导的代数系统。

B 是A 的非空子集，如果∧和∨在B 上封闭，则称<B, ≤>是<A, ≤>的子格。

8.答案：<B,≤>不是格<A,≤>的子格。

因为在<A,≤>中，b ∧c=d ，而d ∉B,，所以<B,≤>不是格<A,≤>的子格。

9.答案：证明:显然B 是A 的非空子集, (因为a ≤a ≤b,a ≤b ≤b,所以a,b ∈B)。

只要证明∧和∨在B 上封闭即可。

任取x,y ∈B, 由B 的构成得a ≤x ≤b,a ≤y ≤b, 于是由格的性质得,a ≤x ∨y ≤b ，a ≤x ∧y ≤b, 于是有 x ∨y ∈B ,x ∧y ∈B , 说明∨和∧在B 上封闭 。

所以<B, ≤>也是格。

10.答案：含有一、二、三个元素的格都是链。

都各有一种不同构形式。

它们的哈斯图如下：11.答案：具有四个元素的格不同构形式有2钟。

任何一个具有四个元素的格必同构于下面两种格形式之一： 它们的哈斯图如下：∙ aababc12.答案：具有五个元素的格有五种不同构的形式，其图形如下： 设a,b 是格<A, ≤>中的两个元素,证明: a). a ∧b=b 当且仅当a ∨b=a.b). a ∧b<b 和a ∧b<a,当且仅当 a 与b 是不可比较的. 答案：证明:a) 充分性：已知a ∨b=a ，b=b ∧(b ∨a)= b ∧(a ∨b) =b ∧a=a ∧b 必要性：已知a ∧b=b , a=a ∨(a ∧b)=a ∨bb) 充分性:已知a 与b 是不可比较的. 因a ∧b ≤b, a ∧b ≤a,如果a ∧b=b, 则有b ≤a, 如果a ∧b=a, 则有a ≤b,都与a 与b 是不可比较的矛盾. 所以有：a ∧b ≤b ∧ a ∧b ≠b,于是有 a ∧b<b a ∧b ≤a ∧ a ∧b ≠a,于是有 a ∧b<a必要性：已知a ∧b<b 和a ∧b<a, 假设a 与b 是可比较的，则要么a ≤b,要么b ≤a. 于是要么a ∧b=a 要么a ∧b=b. 这与a ∧b<b 和a ∧b<a 矛盾。

所以a 与b 是不可比较的。

13. 答案：证明:∵ (a ∧b)≤a ≤(a ∨c) ∴ (a ∧b)≤(a ∨c) ∵ (c ∧d)≤c ≤(a ∨c) ∴ (c ∧d)≤(a ∨c) ∴ (a ∧b)∨(c ∧d)≤(a ∨c)同理 (a ∧b)≤(b ∨d) (c ∧d)≤(b ∨d) ∴ (a ∧b)∨(c ∧d)≤(b ∨d) ∴(a ∧b)∨(c ∧d)≤(a ∨c)∧(b ∨d)14.答案：<A,∨,∧>是由格<A,≤>诱导的代数系统。

如果对 a,b,c ∈A ，有 a ∨(b ∧c) =(a ∨b)∧(a ∨c) ， a ∧(b ∨c)= (a ∧b)∨(a ∧c)则称<A,≤>是分配格。

15.答案：16.答案：a,d,e 是分配格。

17.答案：有两个。

图形如下：dacdab18.答案：2∧(3∨5)=2∧30=2 (2∧3)∨(2∧5)=1∨1=1 2∧(3∨5)≠ (2∧3)∨(2∧5) 19.答案：c ∧(b ∨d)=c ∧a=c (c ∧b)∨(c ∧d)=e ∨d=d c ∧(b ∨d) ≠(c ∧b)∨(c ∧d) 20.答案：(a)和(b)是分配格。

(c)不是分配格。

因为(c)图等价于下面图(d)，而其中结点bfged 构成的子格就是与五元素非分配格(e)同构的子格。