第三章-湍流模型
- 格式:doc
- 大小:1.12 MB
- 文档页数:19
第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
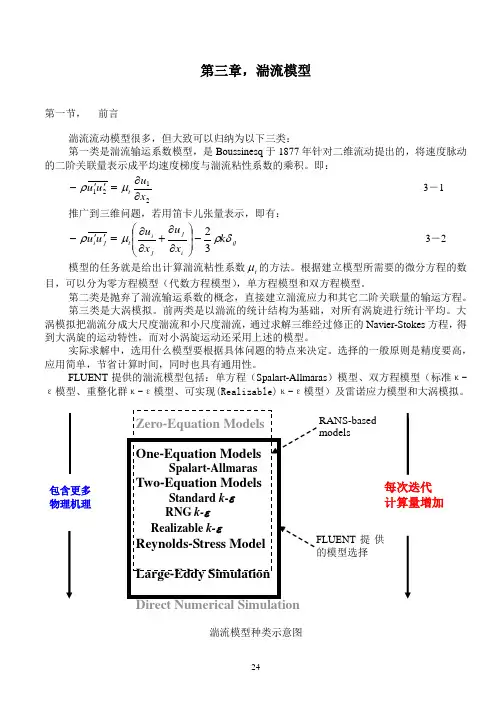
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提供RANS-based models第二节,平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。

第三章 湍流模型第一节 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图Direct Numerical Simulation包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节 平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。


湍流模型概述范文湍流是液体或气体流动中的一种复杂的现象,它包含着三个主要特征:不规则性、不可预测性和多尺度性。
湍流的产生是由于流体内部存在多个尺度的涡旋,它们之间相互作用并且不断地改变尺度和形状。
湍流模型是用来解释和描述湍流现象的一种数学方法。
本文将对湍流模型进行概述。
湍流模型的目的是通过对流场中各个参数的统计平均来描述湍流的性质。
根据湍流模型的复杂程度和适用范围的不同,可以将湍流模型分为三个等级:经验模型、半经验模型和基于数值模拟的模型。
经验模型是最早发展的湍流模型,它基于观察和实验结果,将各个参数之间的关系表示为一些经验公式。
这种模型的优点是简单易用,适用于几乎所有的湍流问题。
然而,由于经验模型只是基于经验规律,对于复杂的湍流现象并不准确,所以它的适用范围有限。
半经验模型是在经验模型的基础上发展而来的一种湍流模型。
它基于一些经验关系,并结合一些理论和模型来提高预测的准确性。
半经验模型通常可以包括一些常见的湍流模型,如k-ε模型、k-ω模型等。
这些模型通过引入一些方程和参数,来描述湍流的速度、压力和湍动能等参数之间的动态平衡。
半经验模型在计算流体力学领域得到了广泛的应用,能够较准确地预测湍流的性质。
基于数值模拟的模型是通过计算流体力学(CFD)方法来模拟湍流现象的模型。
这种模型基于流体的基本方程和湍流模型,通过数值方法进行求解并得到流场的数值解。
基于数值模拟的模型具有较高的计算精度和更大的适用范围,能够模拟各种复杂的湍流流动现象。
然而,基于数值模拟的模型需要较大的计算资源和时间,并且对于湍流模型的选择和设定需要一定的经验。
湍流模型的开发和改进是一个长期而具有挑战性的研究领域。
目前,湍流模型的研究主要集中在发展更准确、更适用于特定流动条件的模型。
研究人员通过理论推导、实验验证和数值模拟等方法,不断改进湍流模型的参数设定和方程形式,以提高湍流模型的准确性和适用性。
总之,湍流模型是描述和解释湍流现象的数学方法。




流体的湍流模型和湍流模拟流体力学是研究流体的运动规律和性质的学科,其中湍流模型和湍流模拟是其中非常重要的研究方向。
湍流是流体力学中一种复杂而普遍存在的现象,它具有不规则、无序和随机性等特点。
湍流模型和湍流模拟的发展,对于理解和预测真实世界中的湍流现象,以及涉及湍流的工程设计和应用具有重要意义。
一、湍流模型湍流模型是描述湍流现象的数学模型,在流体力学中起着扮演着非常重要的作用。
根据流体力学理论,湍流是由于流体中微小尺度的速度涡旋突然出现和消失所导致的现象。
由于湍流涡旋的尺度范围很广,从而难以直接模拟和计算。
因此,使用湍流模型来近似描述湍流现象,成为了一种常用的方法。
常见的湍流模型包括雷诺平均湍流模型(Reynolds-averaged Navier-Stokes equations, RANS)和大涡模拟(large eddy simulation, LES)等。
雷诺平均湍流模型是基于平均流场的统计性质,通过求解雷诺平均速度和湍流应力来评估湍流效应。
而大涡模拟是将湍流现象分解为不同尺度的涡旋,并通过直接模拟大涡旋来研究湍流运动。
二、湍流模拟湍流模拟是利用计算机来模拟湍流现象的方法,通常基于数值方法对流体力学方程进行求解。
湍流模拟分为直接数值模拟(direct numerical simulation, DNS)、雷诺平均湍流模拟和大涡模拟等。
直接数值模拟是将流场划分为网格,并通过离散化流体力学方程和湍流模型来求解湍流流场的详细信息。
由于该方法需要计算微小尺度的细节,计算量非常大,限制了其在实际工程中的应用。
因此,直接数值模拟主要用于湍流现象的基础研究和理论验证。
相比之下,雷诺平均湍流模拟和大涡模拟能够更有效地模拟湍流现象。
雷诺平均湍流模拟通过对湍流参数进行求解,来描述平均的湍流效应。
而大涡模拟则将湍流现象分为大涡旋和小涡旋,通过模拟大涡旋来捕获湍流流场的主要特征。
三、湍流模型与湍流模拟的应用湍流模型和湍流模拟在工程设计和应用中有着广泛的应用。


流体力学中的流体流动的湍流模型在流体力学中,流体流动是一个复杂而广泛的研究领域。
湍流作为流体流动的一种重要模型,具有不可忽视的影响。
本文将讨论湍流模型在流体力学中的应用和意义。
一、湍流的概念和特点湍流是指在流体中存在不规则、混乱的流动现象。
与之相对的是层流,层流是指流体以平行且有序的路径运动。
湍流的主要特点包括:不规则性、三维性、旋转性和不可预测性。
湍流具有广泛的应用领域,如气象学、航空航天、工程流体力学等。
二、湍流模型的分类湍流模型主要用于描述湍流流动的数学和物理特性,有多种分类方法。
根据直接数值模拟(DNS)、雷诺平均模拟(RANS)和大涡模拟(LES)等,湍流模型可分为直接模拟模型、统计模型和动态模型等。
1. 直接模拟模型直接模拟模型是基于流体力学方程的解析解,通过数值方法模拟流体流动的全过程。
这种模型能够精确描述湍流的数学和物理特性,但计算量大,适用范围有限。
2. 统计模型统计模型是通过对湍流流动的统计数据进行建模,以得到平均场变量的表达式。
常见的统计模型包括雷诺平均模型(RANS)、湍动能方程模型和湍流动能理论模型等。
这些模型适用于工程实际,计算量相对较小。
3. 动态模型动态模型是指结合统计模型和直接模拟模型的模型。
它能够根据流动状态自适应地调整模型参数,以提高模型的准确性。
动态模型适用于大尺度流动和高雷诺数流动的模拟。
三、湍流模型的应用湍流模型在流体力学研究和工程实践中有着广泛的应用。
以下是一些典型的应用案例:1. 空气动力学湍流模型在飞行器气动性能研究中起到了重要作用。
通过模拟湍流的生成和演化过程,可以预测飞行器在不同工况下的气动特性。
这对于飞机设计、空气动力学优化和飞行安全都具有重要意义。
2. 水力学湍流在水动力学中的应用同样不可忽视。
例如,在水坝设计中,湍流模型可以用来预测水体在溢流过程中的流速、压力和能量损失等参数。
这对于保证水坝的安全性和有效性至关重要。
3. 工业应用湍流模型在工业领域中的应用十分广泛。
流体的湍流模型湍流是流体力学中一个重要的概念,指的是流体运动过程中的混乱无序的状态。
湍流现象普遍存在于自然界中,例如大气中的风、海洋中的波浪以及河流中的涡流等。
湍流模型是用来描述湍流运动的数学模型,它通过建立流体的动量和能量传输方程,来揭示湍流形成和演化的规律。
一、湍流模型的基本原理湍流的形成是由于流体运动过程中存在的各种非线性的物理过程,比如惯性力、摩擦力和压力梯度等。
湍流模型的基本原理是基于雷诺平均导出的方程式,其中雷诺平均是指对流体宏观属性进行时间平均运算。
通过平均之后,湍流运动可以被看作是均匀流动和湍流脉动两个部分的叠加。
二、湍流模型的分类湍流模型可以分为两大类:一类是基于统计理论的湍流模型,另一类是基于运动方程的湍流模型。
基于统计理论的湍流模型通常使用统计学中的概率密度函数和相关函数等概念来描述湍流运动中的各种参数。
而基于运动方程的湍流模型则是通过对流体动量和能量传输方程进行进一步的分析和求解,从而得到流体湍流运动的演化规律。
三、湍流模型的应用湍流模型在工程领域中有着广泛的应用。
例如在空气动力学研究中,湍流模型可以用来评估飞机的气动性能,优化机体的设计。
在流体力学领域,湍流模型可以用于预测和模拟液体的流动,帮助优化流体管道的设计和运行。
湍流模型还可以应用于天气预报、水利工程和环境保护等领域。
四、湍流模型的发展趋势随着计算机科学和数值模拟技术的发展,湍流模型也在不断地完善和演进。
近年来,随着大规模计算能力的提升,湍流模型的数值模拟能力得到了显著的提高,可以更准确地描述湍流现象和湍流的演化规律。
另外,机器学习和人工智能等新兴技术的引入,也为湍流模型的发展带来了新的机遇和挑战。
五、结语湍流模型是流体力学研究中的重要工具,通过对湍流现象的建模和仿真,可以帮助我们更好地理解和预测流体运动的行为。
随着科学技术的不断发展,湍流模型将继续完善和更新,为人类的科学研究和工程应用提供更准确、可靠的支持。
我们相信,在不久的将来,湍流模型将在更多领域发挥出重要的作用,促进科学技术和工程领域的进步和发展。
第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models第二节,平均量输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。
第三章 湍流模型第一节 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量(笛卡尔坐标系)表示,即有:ij i j j i t j i k x u x u u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 ij δ为DELT 函数,一般i=j 时为1,否则为0.模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
(模拟大空间建筑空气流动)μt=0.038 74ρvl (模拟通风空调室内的空气流动)比例系数由直接数值模拟的结果拟合而得,其中:v 为当地时均速度,l 为当地距壁面最近的距离。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
参见:湍流模型的选择资料。
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图大涡模拟启动需要用命令:(rpsetvar 'les-2d? #t)Direct Numerical Simulation包含更多物理机理 每次迭代计算量增加 提的模型选RANS-based models第二节 平均量输运方程输运过程的粘滞系数、扩散系数和热传导率,故称为输运方程雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
第三章,湍流模型第一节, 前言湍流流动模型很多,但大致可以归纳为以下三类:第一类是湍流输运系数模型,是Boussinesq 于1877年针对二维流动提出的,将速度脉动的二阶关联量表示成平均速度梯度与湍流粘性系数的乘积。
即:2121x u u u t ∂∂=''-μρ 3-1 推广到三维问题,若用笛卡儿张量表示,即有:ij ijj i t j i k x u xu u u δρμρ32-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-2 模型的任务就是给出计算湍流粘性系数t μ的方法。
根据建立模型所需要的微分方程的数目,可以分为零方程模型(代数方程模型),单方程模型和双方程模型。
第二类是抛弃了湍流输运系数的概念,直接建立湍流应力和其它二阶关联量的输运方程。
第三类是大涡模拟。
前两类是以湍流的统计结构为基础,对所有涡旋进行统计平均。
大涡模拟把湍流分成大尺度湍流和小尺度湍流,通过求解三维经过修正的Navier-Stokes 方程,得到大涡旋的运动特性,而对小涡旋运动还采用上述的模型。
实际求解中,选用什么模型要根据具体问题的特点来决定。
选择的一般原则是精度要高,应用简单,节省计算时间,同时也具有通用性。
FLUENT 提供的湍流模型包括:单方程(Spalart-Allmaras )模型、双方程模型(标准κ-ε模型、重整化群κ-ε模型、可实现(Realizable)κ-ε模型)及雷诺应力模型和大涡模拟。
湍流模型种类示意图第二节,平均量输运方程包含更多 物理机理每次迭代 计算量增加提的模型选RANS-based models雷诺平均就是把Navier-Stokes 方程中的瞬时变量分解成平均量和脉动量两部分。
对于速度,有:i i i u u u '+= 3-3其中,i u 和i u '分别是平均速度和脉动速度(i=1,2,3)类似地,对于压力等其它标量,我们也有:φφφ'+= 3-4 其中,φ表示标量,如压力、能量、组分浓度等。
把上面的表达式代入瞬时的连续与动量方程,并取平均(去掉平均速度i u 上的横线),我们可以把连续与动量方程写成如下的笛卡儿坐标系下的张量形式:0)(=∂∂+∂∂i iu x t ρρ 3-5 ()j i jl l ij i j j i ji i u u x x u x u x u x x p Dt Du ''-∂∂+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂-∂∂+∂∂∂∂+∂∂-=ρδμρ32 3-6 上面两个方程称为雷诺平均的Navier-Stokes (RANS )方程。
他们和瞬时Navier-Stokes 方程有相同的形式,只是速度或其它求解变量变成了时间平均量。
额外多出来的项j i u u ''-ρ是雷诺应力,表示湍流的影响。
如果要求解该方程,必须模拟该项以封闭方程。
如果密度是变化的流动过程如燃烧问题,我们可以用法夫雷(Favre )平均。
这样才可以求解有密度变化的流动问题。
法夫雷平均就是出了压力和密度本身以外,所有变量都用密度加权平均。
变量的密度加权平均定义为:ρρ/~Φ=Φ 3-7符号~表示密度加权平均;对应于密度加权平均值的脉动值用Φ''表示,即有:Φ''+Φ=Φ~。
很显然,这种脉动值的简单平均值不为零,但它的密度加权平均值等于零,即:0≠Φ'', 0=Φ''ρBoussinesq 近似与雷诺应力输运模型为了封闭方程,必须对额外项雷诺应力j i u u ''-ρ进行模拟。
一个通常的方法是应用Boussinesq 假设,认为雷诺应力与平均速度梯度成正比,即:ij i i t ijj i t j i x u k x u xu u u δμρμρ)(32∂∂+-⎪⎪⎭⎫ ⎝⎛∂∂+∂∂=''- 3-8 Boussinesq 假设被用于Spalart-Allmaras 单方程模型和ε-k 双方程模型。
Boussinesq 近似的好处是与求解湍流粘性系数有关的计算时间比较少,例如在Spalart-Allmaras 单方程模型中,只多求解一个表示湍流粘性的输运方程;在ε-k 双方程模型中,只需多求解湍动能k 和耗散率ε两个方程,湍流粘性系数用湍动能k 和耗散率ε的函数。
Boussinesq 假设的缺点是认为湍流粘性系数t μ是各向同性标量,对一些复杂流动该条件并不是严格成立,所以具有其应用限制性。
另外的方法是求解雷诺应力各分量的输运方程。
这也需要额外再求解一个标量方程,通常是耗散率ε方程。
这就意味着对于二维湍流流动问题,需要多求解4个输运方程,而三维湍流问题需要多求解7个方程,需要比较多的计算时间,对计算机内存也有更高要求。
在许多问题中,Boussinesq 近似方法可以得到比较好的结果,并不一定需要花费很多时间来求解雷诺应力各分量的输运方程。
但是,如果湍流场各向异性很明显,如强旋流动以及应力驱动的二次流等流动中,求解雷诺应力分量输运方程无疑可以得到更好的结果。
第三节, 湍流模型3.3.1 单方程(Spalart-Allmaras )模型Spalart-Allmaras 模型的求解变量是ν~,表征出了近壁(粘性影响)区域以外的湍流运动粘性系数。
ν~的输运方程为: ννννρννρμσνρY x C x x G Dt D j b j j -⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∂∂+∂∂+=~~)~(1~2~ 3-9 其中,νG 是湍流粘性产生项;νY 是由于壁面阻挡与粘性阻尼引起的湍流粘性的减少;νσ~和2b C 是常数;ν是分子运动粘性系数。
湍流粘性系数用如下公式计算:1~ννρμf t = 其中,1νf 是粘性阻尼函数,定义为:31331ννχχC f +=,并且ννχ~≡。
湍流粘性产生项,νG 用如下公式模拟:νρν~~1S C G b = 3-10 其中,222~~ννf dk S S +≡,而1211ννχχf f +-=。
其中,1b C 和k 是常数,d 是计算点到壁面的距离;S ij ij ΩΩ≡2。
ij Ω定义为:⎪⎪⎭⎫⎝⎛∂∂-∂∂=Ωji i j ij x u x u 21 3-11 由于平均应变率对湍流产生也起到很大作用,FLUENT 处理过程中,定义S 为:),0min(ij ij prod ij S C S Ω-+Ω≡ 3-12其中,0.2=prod C ,ij ij ij ΩΩ≡Ω,ij ij ij S S S 2≡,平均应变率ij S 定义为:⎪⎪⎭⎫⎝⎛∂∂+∂∂=j i i j ij x u x u S 21 3-13 在涡量超过应变率的计算区域计算出来的涡旋粘性系数变小。
这适合涡流靠近涡旋中心的区域,那里只有“单纯”的旋转,湍流受到抑止。
包含应变张量的影响更能体现旋转对湍流的影响。
忽略了平均应变,估计的涡旋粘性系数产生项偏高。
湍流粘性系数减少项νY 为:21~⎪⎭⎫ ⎝⎛=d f C Y w w νρν 3-14其中,6/1636631⎥⎦⎤⎢⎣⎡++=w w w C g C g f 3-15 )(62r r C r g w -+= 3-1622~~dk S r ν≡ 3-17其中,1w C ,2w C ,3w C 是常数,222~~ννf dk S S +≡。
在上式中,包括了平均应变率对S的影响,因而也影响用S ~计算出来的r 。
上面的模型常数在FLUENT 中默认值为:1335.01=b C ,622.02=b C ,3/2~=νσ,1.71=νC ,νσ~2211/)1(/b b w C k C C ++=,3.02=w C ,0.23=w C ,41.0=k 。
壁面条件在壁面,湍流运动粘性ν~设置为零。
当计算网格足够细,可以计算层流底层时,壁面切应力用层流应力-应变关系求解,即:μρττy u u u= 3-18 如果网格粗错不能用来求解层流底层,则假设与壁面近邻的网格质心落在边界层的对数区,则根据壁面法则:⎪⎪⎭⎫ ⎝⎛=μρττy u E k u u ln 13-19 其中,k=0.419,E=9.793。
对流传热传质模型在FLUENT 中,用雷诺相似湍流输运的概念来模拟热输运过程。
给出的能量方程为:h eff ij j i t p i i i S u x T t c k x p E u x E t +⎥⎥⎦⎤⎢⎢⎣⎡+∂∂⎪⎪⎭⎫ ⎝⎛+∂∂=+∂∂+∂∂)(Pr )]([)(τμρρ 3-20 式中,E 是总能量,eff ij )(τ是偏应力张量,定义为:ij ii eff j i ij eff eff ij x u x u x u δμμτ∂∂-∂∂+∂∂=32)()( 3-21 其中,eff ij )(τ表示粘性加热,耦合求解。
如果默认为分开求解,FLUENT 不求解处eff ij )(τ。
但是可以通过变化“粘性模型”面板上的湍流普朗特数(Prt ),其默认值为0.85。
湍流质量输运与热输运类似,默认的Schmidt 数是0.7,该值同样也可以在“粘性模型”面板上调节。
标量的壁面处理与动量壁面处理类似,分别选用合适的壁面法则。
综上所述,Spalart-Allmaras 模型是相对简单的单方程模型,只需求解湍流粘性的输运方程,并不需要求解当地剪切层厚度的长度尺度。
该模型对于求解有壁面影响流动及有逆压力梯度的边界层问题有很好模拟效果,在透平机械湍流模拟方面也有较好结果。
Spalart-Allmaras 模型的初始形式属于对低雷诺数湍流模型,这必须很好解决边界层的粘性影响区求解问题。
在FLUENT 中,当网格不是很细时,采用壁面函数来解决这一问题。
当网格比较粗糙时,网格不满足精确的湍流计算要求,用壁面函数也许是最好的解决方案。
另外,该模型中的输运变量在近壁处的梯度要比ε-k 中的小,这使得该模型对网格粗糙带来数值误差不太敏感。
但是,Spalart-Allmaras 模型不能预测均匀各向同性湍流的耗散。
并且,单方程模型没有考虑长度尺度的变化,这对一些流动尺度变换比较大的流动问题不太适合。
比如,平板射流问题,从有壁面影响流动突然变化到自由剪切流,流场尺度变化明显。
3.3.2 标准ε-k 模型标准ε-k 模型需要求解湍动能及其耗散率方程。
湍动能输运方程是通过精确的方程推导得到,但耗散率方程是通过物理推理,数学上模拟相似原形方程得到的。
该模型假设流动为完全湍流,分子粘性的影响可以忽略。
因此,标准ε-k 模型只适合完全湍流的流动过程模拟。
标准ε-k 模型的湍动能k 和耗散率ε方程为如下形式:M b k i kt iY G G x k x Dt Dk --++⎥⎦⎤⎢⎣⎡∂∂⎪⎪⎭⎫⎝⎛+∂∂=ρεσμμρ3-22 k C G C G k C x x Dt D b k i k t i2231)(ερεεσμμερεεε-++⎥⎦⎤⎢⎣⎡∂∂⎪⎪⎭⎫ ⎝⎛+∂∂= 3-23在上述方程中,k G 表示由于平均速度梯度引起的湍动能产生,b G 是用于浮力影响引起的湍动能产生;M Y 可压速湍流脉动膨胀对总的耗散率的影响。