概率论一二章习题详解

概率论第二章习题答案习题1：离散型随机变量及其分布律设随机变量X表示掷一枚公正的六面骰子得到的点数。

求X的分布律。

解答：随机变量X的可能取值为1, 2, 3, 4, 5, 6。

由于骰子是公正的，每个面出现的概率都是1/6。

因此，X的分布律为：\[ P(X=k) = \frac{1}{6}, \quad k = 1, 2, 3, 4, 5, 6 \]习题2：连续型随机变量及其概率密度函数设随机变量Y表示从标准正态分布中抽取的数值。

求Y的概率密度函数。

解答：标准正态分布的概率密度函数为高斯函数，其形式为：\[ f(y) = \frac{1}{\sqrt{2\pi}} e^{-\frac{y^2}{2}}, \quad -\infty < y < \infty \]习题3：随机变量的期望值已知随机变量X的分布律为：\[ P(X=k) = p_k, \quad k = 1, 2, ..., n \]求X的期望值E(X)。

解答：随机变量X的期望值定义为：\[ E(X) = \sum_{k=1}^{n} k \cdot p_k \]习题4：随机变量的方差继续使用习题3中的随机变量X，求X的方差Var(X)。

解答：随机变量X的方差定义为期望值的平方与每个值乘以其概率之和的差：\[ Var(X) = E(X^2) - (E(X))^2 \]其中，\( E(X^2) = \sum_{k=1}^{n} k^2 \cdot p_k \)习题5：二项分布设随机变量X表示n次独立伯努利试验中成功的次数，每次试验成功的概率为p。

求X的分布律和期望值。

解答：X服从参数为n和p的二项分布。

其分布律为：\[ P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}, \quad k = 0, 1, ..., n \]X的期望值为：\[ E(X) = np \]结束语：以上是概率论第二章的一些典型习题及其解答。

习题一（A ）1. 用三个事件,,A B C 的运算表示下列事件：（1）,,A B C 中至少有一个发生； （2）,,A B C 中只有A 发生； （3）,,A B C 中恰好有两个发生； （4）,,A B C 中至少有两个发生； （5）,,A B C 中至少有一个不发生； （6）,,A B C 中不多于一个发生. 解：（1）A B C （2）ABC (3) ABC ABC CAB(4) ABBC CA (5) A B C (6) ABBC CA2. 在区间[0,2]上任取一数x ， 记 1{|1},2A x x =<≤ 13{|}42B x x =≤≤，求下列事件的表达式： （1）AB ； （2）AB ； (3) AB .解：（1）{|1412132}x x x ≤≤<≤或 （2）∅（3）{|014121x x x ≤<<≤或3. 已知()0.4,()0.2,()0.1P A P BA P CAB ===，求()P A B C .解：0.2()()P A P AB =-,0.1()(())()()()()()()P CAB P C A B P C P CA CB P C P CA P CB P ABC -=-=-=--+()()()()()()()()P A B C P A P B P C P AB P BC P CA P ABC =++---+=0.40.20.10.7++=4. 已知()0.4,()0.25,()0.25P A P B P A B ==-=，求()P B A -与()P AB .解：()()()0.25P A B P A P AB -=-=, ()0.15P AB =, ()()()0.250.150.1P B A P B P AB -=-=-=, ()()1()()()P AB P AB P A P B P AB ==--+10.40.250.150.5=--+=5.将13个分别写有,,,,,,,,,,,,A A A C E H I I M M N T T 的卡片随意地排成一行，求恰好排单词“MATHEMATICIAN ”的概率.解：232224813!13!p ⨯⨯⨯⨯==6. 从一批由45件正品、5件次品组成的产品中任取3件产品，求其中恰好有1件次品的概率.解：1254535099392C C p C == 7. 某学生研究小组共有12名同学，求这12名同学的生日都集中在第二季度（即4月、5月和6月）的概率.解： 1212312p =:8. 在100件产品中有5件是次品，每次从中随机地抽取1件，取后不放回，求第三次才取到次品的概率.解：设i A 表示第i 次取到次品，1,2,3i =， 12395945()0.0461009998P A A A ==9. 两人相约7点到8点在校门口见面，试求一人要等另一人半小时以上的概率.解：1112122214p ⨯⨯⨯== 10. 两艘轮船在码头的同一泊位停船卸货，且每艘船卸货都需要6小时.假设它们在一昼夜的时间段中随机地到达，求两轮船中至少有一轮船在停靠时必须等待的概率.解：22246371()1()24416p -=-=-=11. 任取两个不大于1的正数，求它们的积不大于29，且它们和不大于1的概率. 解：29xy ≤ ， 1x y +≤ ，所以 13x =，23x =23131212ln 23939p dx x =+=+⎰12. 设(),(),P A a P B b == 证明：1(|)a b P A B b+-≥. 证明： ()()()()()()()P AB P A P B P A B P A B P B P B +-==()()11()P A P B a b P B b+-+-≥≥13. 有朋自远方来，他坐火车、坐船、坐汽车和坐汽车的概率分别为0.3, 0.2,0.1,0.4 .若坐火车来，迟到的概率是0.25；若坐船来，迟到的概率是0.3；若坐汽车来，迟到的概率是0.1；若坐飞机来，则不会迟到.求他迟到的概率.解：0.30.250.20.30.10.10.145⨯+⨯+⨯=14. 设10个考题签中有4个难答，3人参加抽签，甲先抽，乙次之，丙最后.求下列事件的概率：（1）甲抽到难签；（2）甲未抽到难签而乙抽到难签； （3）甲、乙、丙均抽到难签.解；（1）42105p == （2）64410915p == （3） 4321109830p ==15. 发报台分别以概率0.6和0.4发出信号“＊”和“-” .由于通信系统受到干扰，当发出信号“＊”时，收报台未必收到信号“＊”，而是分别以概率0.8和0.2收到信号“＊”和“-”；同样，当发出信号“-”时，收报台分别以0.9和0.1收到信号“-”和“＊”.求：（1）收报台收到信号“＊”的概率；（2）当收到信号“＊”时，发报台确实是发出信号“＊”的概率.解：（1）0.60.80.40.10.52⨯+⨯= （2）0.48120.5213= 16. 设,A B 相互独立，()0.6,()0.4P A B P B ==，求()P A .解：()0.6()()()0.4()()P AB P A P B P AB P A P AB ==+-=+-0.2()0.4()P A P A =-, 1()3P A =17. 两两独立的三事件,,A B C 满足,ABC =∅并且1()()()2P A P B P C ==<.若9()16P AB C =，求()P A . 解：293()3()16P A P A =- ,216()16()30P A P A -+= 21()(,()34P A P A ==舍） 18、证明：（1）若(|)()P A B P A >，则(|)()P B A P B >.（2）若(|)(|)P A B P A B =，则事件A 与B 相互独立.证明：（1）()()()P AB P A P B > ,()()()P AB P A P B > ()()()()()()()P AB P A P B P B A P B P A P A >= (2) ()()P A B P A B =,()()()1()P AB P A B P B P B -=-()()()P AB P A P B =19. 甲、乙、丙三人独立地向一架飞机射击.设甲、乙、丙的命中率分别为0.4，0.5，0.7.又飞机中1弹，2弹，3弹而坠毁的概率分别为0.2，0.6，1. 若三人各向飞机射击一次，求：（1）飞机坠毁的概率；（2）已知飞机坠毁，求飞机被击中2弹的概率.解：（1）0.2(0.40.50.30.60.50.30.60.50.7)0.6(0.40.50.30.40.50.70.60.50.7)0.40.50.70.20.360.60.410.140.458⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=⨯+⨯+=（2）0.60.410.540.458⨯=20. 三人独立破译一密码，他们能独立译出的概率分别为0.25，0.35，0.4.求此密码能被译出的概率.解： 0.250.350.40.250.650.60.750.350.60.750.650.40.250.350.60.250.650.40.750.350.4⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯0.0350.09750.15750.1950.05250.0650.1050.7075=++++++=21. 在试验E 中，事件A 发生的概率为()P A p =，将试验E 独立重复进行三次，若在三次试验中“A 至少出现一次的概率为1927”，求p . 解：00333191(1)1(1)27C p p p =--=--，13p = 22. 已知某种灯泡的耐用时间在1000小时以上的概率为0.2，求三个该型号的灯泡在使用1000小时以后至多有一个坏掉的概率.解：31230.20.80.20.0830.80.040.104C +⋅=+⨯⨯=23. 设有两箱同种零件，在第一箱内装50件，其中有10件是一等品；在第二箱内装有30件，其中有18件是一等品.现从两箱中任取一箱，然后从该箱中不放回地取两次零件，每次1个，求：（1）第一次取出的零件是一等品的概率； （2）已知第一次取出的零件是一等品，，第二次取出的零件也是一等品的概率.解： （1） 1011810.4502302+= (2) 5110911817519117[][]225049230294549529+=+ 19512612499()0.4856449295684+=+==（B ）1.箱中有α个白球和β个黑球，从中不放回地接连取1(1)k k αβ++≤+次球，每次1个.求最后取出的是白球的概率.解：(1)(2)()()(1)()k k αβαβαβαααβαβαβαβ+-+-+-=++-+-+2. 一栋大楼共有11层，电梯等可能地停在2层至11层楼的每一层，电梯在一楼开始运行时有6位乘客，并且乘客在2层至11层楼的每一层离开电梯的可能性相等，求下列事件的概率：（1）某一层有两位乘客离开；（2）没有两位及以上的乘客在同一层离开； （3）至少有两位乘客在同一层离开.解：（1）42242666199()()101010C C = （2） 61010!P(3) 610110!P -3.将线段(0,)a 任意折成3折，求此3折线段能构成三角形的概率. 解：{}(,)0,0,0x y x a y a x y a Ω=<<<<<+<，(,)0,0,222a a a A x y x y x y a ⎧⎫=<<<<<+<⎨⎬⎩⎭， 21122242a a p a ==4. 设平面区域D 由四点(0,0),(0,1),(1,0),(1,1)围成的正方形，现向D 内随机投10个点，求这10个点中至少有2个落在由曲线2y x =和直线y x =所围成的区域1D 的概率.解： 1201()6p x x dx =-=⎰， 001019101015151()()()()6666C C --91091051055151()()166662929687510.5260466176⨯=--=-=-= 5. 设有来自三个地区的10名、15名、25名考生的报名表，其中女生的报名表分别为3份、7份、5份. 随机地取一个地区的报名表，从中先后抽取两份.（1）求先抽到的一份是女生表的概率；（2）已知后抽到的一份是男生表，求先抽到的是女生表的概率.解：（ 1） 1317152931031532590++= （2） 13717815202020310931514325243029616119030++==-6. (Banach 问题)某数学家有两盒火柴，每盒装有N 根，每次使用时，他在任一盒中取一根，问他发现一空盒，而另一盒还有k 根火柴的概率是多少.解：222211112()(1)()2222N k N N N k N NN k N k p C C -----=-=习题二（ A ）1．同时抛掷3枚硬币，以X 表示出现正面的枚数，求X 的分布律。

第一章 事件与概率1.1 写出下列随机试验的样本空间及表示下列事件的样本点集合。

(1)10件产品中有1件是不合格品，从中任取2件得1件不合格品。

(2)一个口袋中有2个白球、3个黑球、4个红球，从中任取一球，(ⅰ)得白球，(ⅱ)得红球。

解 (1)记9个合格品分别为 921,正正正，， ，记不合格为次，则，，，，，，，，，)()()(){(1913121次正正正正正正正 =Ω，，，，，，，，，)()()()(2924232次正正正正正正正 ，，，，，，，)()()(39343次正正正正正 )}()()(9898次正次正正正，，，，，，=A ){(1次正，，，，)(2次正)}(9次正，，(2)记2个白球分别为1ω，2ω，3个黑球分别为1b ，2b ，3b ，4个红球分别为1r ，2r ，3r ，4r 。

则=Ω{1ω，2ω，1b ，2b ，3b ，1r ，2r ，3r ，4r } (ⅰ) =A {1ω，2ω} (ⅱ) =B {1r ，2r ，3r ，4r }1.2 在数学系的学生中任选一名学生，令事件A 表示被选学生是男生，事件B 表示被选学生是三年级学生，事件C 表示该生是运动员。

(1) 叙述C AB 的意义。

(2)在什么条件下C ABC =成立？(3)什么时候关系式B C ⊂是正确的？(4) 什么时候B A =成立？解 (1)事件C AB 表示该是三年级男生，但不是运动员。

(2) C ABC = 等价于AB C ⊂，表示全系运动员都有是三年级的男生。

(3)当全系运动员都是三年级学生时。

(4)当全系女生都在三年级并且三年级学生都是女生时`。

1.3 一个工人生产了n 个零件，以事件i A 表示他生产的第i 个零件是合格品（n i ≤≤1）。

用i A 表示下列事件：(1)没有一个零件是不合格品；(2)至少有一个零件是不合格品；(3)仅仅只有一个零件是不合格品；(4)至少有两个零件是不合格品。

解 (1) n i i A 1=; (2) n i i n i i A A 11===; (3) n i n ij j j i A A 11)]([=≠=;(4)原事件即“至少有两个零件是合格品”，可表示为 nj i j i j i A A ≠=1,；1.4 证明下列各式：(1)A B B A ⋃=⋃;(2)A B B A ⋂=⋂(3)=⋃⋃C B A )()(C B A ⋃⋃;(4)=⋂⋂C B A )()(C B A ⋂⋂(5)=⋂⋃C B A )(⋃⋂)(C A )(C B ⋂ (6) ni i n i i A A 11===证明 （1）—（4）显然，（5）和（6）的证法分别类似于课文第10—12页（1.5）式和(1.6)式的证法。

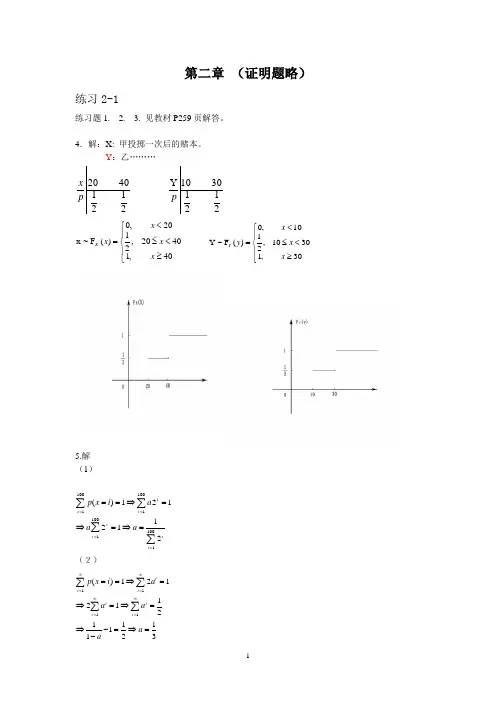
第二章 （证明题略）练习2-1练习题1. 2. 3. 见教材P259页解答。

4．解：X: 甲投掷一次后的赌本。

Y ：乙……… 21214020p x 21213010Y p⎪⎩⎪⎨⎧≥<≤<=40,14020,2120,0)(F ~x x x x x X ⎪⎩⎪⎨⎧≥<≤<=30,13010,2110,0)(F ~Y x x x y Y5.解（1）∑∑∑∑=====⇒=⇒=⇒==10011001100110012112121)(i ii i i i ia a a i x p（２）31211112112121)(1111=⇒=--⇒=⇒=⇒=⇒==∑∑∑∑∞=∞=∞=∞=a a a a ai x p i i i i i i i6.解 21 51 101512 0 25X --p 7．解（１）X:有放回情形下的抽取次数。

P （取到正品）＝107C C 11017=P （取到次品）＝103 107)103( 107)103( 107103,107i 3 2 1X 1-i 2 ⋅p（２）Y:无放回情形下。

778192103 87 92103 97 103 1074 3 2 1 Y ⋅⋅⋅⋅⋅⋅p8．解54511)5(1)3(1)3P(=-=-=-=-≤-=->X p X p X 542)P(X 0)P(X )2()33()3X P(==+=+-==<<-=<X p X p 107)5()2()3()1()21P(2)1()21X P(=-=+==-<+>=-<++>+=>+X p X p X p X p X X p9．解（１）根据分布函数的性质11)1()(2lim 1lim 1=⇒=⇒=++→→A Ax F x F x x(2))5.0()8.0()8.05.0(F F X P -=≤<225.08.0-=＝0.3910．解：依据分布满足的性质进行判断： （１）+∞<<∞-x单调性：+∞<<<⇒<x x F x F x x 0).()(2121在时不满足。

一、习题详解：1.1 写出下列随机试验的样本空间：(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解：连续5 次都命中，至少要投5次以上，故}{ ,7,6,51=Ω；(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解：}{12,11,4,3,22 =Ω；(3) 观察某医院一天内前来就诊的人数;解：医院一天内前来就诊的人数理论上可以从0到无穷，所以}{,2,1,03=Ω； (4) 从编号为1，2，3，4，5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解：属于不放回抽样，故两件产品不会相同，编号必是一大一小，故：()}{;51,4≤≤=Ωj i j i(5) 检查两件产品是否合格;解：用0 表示合格, 1 表示不合格，则()()()()}{1,1,0,1,1,0,0,05=Ω；(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解：用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间，故： ()}{216,T y x T y x ≤≤=Ω ；(7) 在单位圆内任取两点, 观察这两点的距离;解：}{207 x x =Ω；(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解：()}{l y x y x y x =+=Ω,0,0,8 ；1.2 设A ，B ，C 为三事件, 用A;B;C 的运算关系表示下列各事件：(1) A 与B 都发生, 但C 不发生; C AB ；(2) A 发生, 且B 与C 至少有一个发生;)(C B A ⋃；(3) A,B,C 中至少有一个发生; C B A ⋃⋃；(4) A,B,C 中恰有一个发生;C B A C B A C B A ⋃⋃；(5) A,B,C 中至少有两个发生; BC AC AB ⋃⋃；(6) A,B,C 中至多有一个发生;C B C A B A ⋃⋃； (7) A;B;C 中至多有两个发生;ABC ；(8) A,B,C 中恰有两个发生.C AB C B A BC A ⋃⋃ ；注意：此类题目答案一般不唯一，有不同的表示方式。

第一章习 题1．写出下列试验下的样本空间：（1）将一枚硬币抛掷两次答：样本空间由如下4个样本点组成{(,)(,)(,)(,)Ω=正正，正反，反正，反反 （2）将两枚骰子抛掷一次答：样本空间由如下36个样本点组成{(,),1,2,3,4,5,6}i j i j Ω==（3）调查城市居民（以户为单位）烟、酒的年支出答：结果可以用（x ，y ）表示，x ，y 分别是烟、酒年支出的元数.这时，样本空间由坐标平面第一象限内一切点构成 .{(,)0,0}x y x y Ω=≥≥2．甲，乙，丙三人各射一次靶，记-A “甲中靶” -B “乙中靶” -C “丙中靶” 则可用上述三个事件的运算来分别表示下列各事件：(1) “甲未中靶”： ;A(2) “甲中靶而乙未中靶”： ;B A(3) “三人中只有丙未中靶”： ;C AB(4) “三人中恰好有一人中靶”： ;C B A C B A C B A(5)“ 三人中至少有一人中靶”： ;C B A(6)“三人中至少有一人未中靶”： ;C B A 或;ABC(7)“三人中恰有两人中靶”： ;BC A C B A C AB(8)“三人中至少两人中靶”： ;BC AC AB(9)“三人均未中靶”： ;C B A(10)“三人中至多一人中靶”： ;C B A C B A C B A C B A(11)“三人中至多两人中靶”： ;ABC 或;C B A3 .设,A B 是两随机事件，化简事件 (1)()()A B A B (2) ()()A B A B解:(1)()()A B A B AB AB B B == , (2) ()()A B A B ()AB AB B A A B B ==Ω= .4．某城市的电话号码由5个数字组成，每个数字可能是从0-9这十个数字中的任一个，求电话号码由五个不同数字组成的概率. 解：51050.302410P P ==. 5．n 张奖券中含有m 张有奖的，k 个人购买，每人一张，求其中至少有一人中奖的概率。

概率统计第一章教材习题选解习题1-21．已知B A ⊂，()4.0=A P ，()6.0=B P .求：（1）()A P ，()B P ；（2）()AB P ；（3）()B A P +；（4）()B A P ；（5）()B A P ⋅，()A B P .解：（1）()()6.01=-=A P A P ，()()4.01=-=B P B P ；（2）()()4.0====⊂A P AB P B A ；（3）()()6.0====+⊂B P B A P B A ；（4）()()()()()()2.0=-=-=-=A P B P AB P B P A B P B A P ；（5）()()()()4.011=-=+-=+=⋅B P B A P B A P B A P ，()()()0=-=AB P A P A B P .2．设B A ,是两事件，且()6.0=A P ，()7.0=B P .问分别在什么条件下，()AB P 取得最大值和最小值？最大值和最小值各为多少？解：因为()()()()B A P B P A P AB P +-+=，所以要使()AB P 最大，只要()B A P +最小；要使()AB P 最小，只要()B A P +最大. 而()B A A +⊆，()B A B +⊆，则()()B A P A P +≤，()()B A P B P +≤.于是B A ⊃或A B ⊃.又因为()()A P B P <，则B A ⊃不合题意.故，当A B ⊃时，()()()()()()()()6.0==-+=+-+=A P B P B P A P B A P B P A P AB P 最大；当Ω=+B A 时，()B A P +最大，()()()()3.0=+-+=B A P B P A P AB P 最小.3．已知B A ,是二事件，且()5.0=A P ， ()7.0=B P ，()8.0=+B A P .试求()A B P -与()B A P -. 解：因为()()()()4.0=+-+=B A P B P A P AB P ，所以()()()3.0=-=-AB P B P A B P , ()()()1.0=-=-AB P A P B A P .4．已知()()41==B P A P ，()21=C P ，()81=AB P ，()()0==CA P BC P .试求C B A ,,中有一个发生的概率. 解：()()()()()()()()ABC P AC P BC P AB P C P B P A P C B A P +---++=++因为()()()0==CA B P CA P ABC P ，而ABC AC ⊇，所以()()0=≥ABC P AC P ，即()0=AC P . 故，()()()()()()()()ABC P AC P BC P AB P C P B P A P C B A P +---++=++()()()()()87=-++=++AB P C P B P A P C B A P . 5．书架上有一部五卷册的文集，求各册自左至右或自右至左排成自然顺序的概率. 解：设A 表示“一部五卷册的文集，各册自左至右或自右至左排成自然顺序”，则()601!5!2==A P . 6．从一批由45件正品、5件次品组成的产品中任取3件产品，求其中恰有一件次品的概率.解：设A 表示“任取3件产品，求其中恰有一件次品”，则()3929935024515==C C C A P . 7．n 个朋友随机地围绕圆桌就座，求其中两人一定坐在一起（即座位相邻）的概率.解：首先必须搞清楚，这是一个环状排列问题.这种排列是无首尾之分的，而我们所熟悉的是线状排列问题.环状排列一种，相当于线状排列n 种.设A 表示“n 个朋友随机地围绕圆桌就座，其中甲，乙两人一定坐在一起”，则按线状排列时，首先考虑将甲，乙两人排在一起，有!2种排法，然后把这两人视为一个元素，再与其它的()1-n 的元素作全排列，共有()!1!2-n 种，而对应的环状排列有()()1!1!2--n n 种，于是()()()12!1!1!2-=--=n n n n n A P . 8．某油漆公司发出17桶油漆，其中白油漆10桶，黑油漆4桶，红油漆3桶，在搬运过程中所有的标签脱落，交货人随机地将这些油漆发给顾客，问一个订货为4桶白油漆，3桶黑油漆和2桶红油漆的顾客，能按所订颜色如数得到订货的概率是多少？解：设A 表示“能按所订颜色如数得到订货”，则()24312529172334410==C C C C A P . 9．设有N 件产品，其中M 件次品，今从中任取n 件，（1）求其中恰有()()n M k k ,m in ≤件次品的概率；（2）求其中至少有两件次品的概率.解：（1）设A 为“从N 件产品中任取n 件，其中恰有()()n M k k ,m in ≤件次品”，则()n Nk n M N k M C C C A P --=. （2）设B 为“从N 件产品中任取n 件，其中至少有两件次品”，则考虑逆事件的概率有：()()B P B P -=1，其中：B 表示“从N 件产品中任取n 件，其中次品件数不多于两件”.于是，()()n N n M N M n M N M C C C C C B P B P 11011---+-=-=. 10．将一枚骰子重复地掷n 次，试求掷出的最大点数为5的概率.解：设k A “n 次投掷中恰有k 次掷出5点，且其他各次小于5点”，则所求概率为：()⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=+++--0222112164616461646161n n n n n n n n n C C C A A A P ΛΛ. 点评：本题不管是直接计算还是从对立事件着手都是困难的，但利用减法公式是简洁的. 设A “最大点数为5”，B “最大点数不超过5”，C “最大点数不超过4”，则B C ⊂，且C B A -=，于是()()()()n nn n n n n C P B P C B P A P 6456465-=-=-=-=. 11．甲乙两艘轮船驶向一个不能同时停泊两艘轮船的码头，它们在一昼夜内到达的时间是等可能的，如果甲船的停泊时间是一小时，乙船的停泊时间是两小时，求它们中任何一艘都不需要等候码头空出的概率.解：设甲乙两船到达的时刻为y x ,，则(){}240;240,≤≤≤≤=Ωy x y x .(){}y x x y y x A +≥+≥=21,或.显然，()11521013=A P . 点评：若甲船先到，则乙船必须晚到一小时x y +≥1；若乙船先到，则甲船必须晚两小时到达y x +≥2.12．（91数1-3）随机地向半圆a x ax y (202-<<为正常数）内掷一点，点落在半圆内任何区域的概率与区域的面积成正比，试求原点和该点的连线与x 轴的夹角小于4π的概率.解：.1212cos 20402πθπθπ+===⎰⎰a D rdr d a S S P 半圆 点评：此题求面积时可用定积分或二重积分.习题1-31．已知()3.0=A P ，()4.0=B P ，()5.0=B A P ，求条件概率()B A B P +. 解：()()()()()()()()()()()()B A P B P A P AB P B A P B P A P B B P AB P B A P B B AB P B A B P --+=-++=++=+1 因为()()()()5.0=-=-=AB P A P B A P B A P ，所以()()()B A P A P AB P -=. 故，()B A B P +()()()()()()()()()4111=--+-=--+=B A P B P A P B A P A P B A P B P A P AB P . 2．已知()5.0=A P ，()6.0=B P ，()8.0=A B P ，求()AB P 及()B A P ⋅.解：()()()4.0==A B P A P AB P ； ()()()()()()3.011=+--=+-=+=⋅AB P B P A P B A P B A P B A P . 3．某种动物由出生活到20岁的概率为8.0，活到25岁的概率为4.0，这种动物已经活到20岁，再活到25岁的概率是多少？解：设A “这种动物由出生活到20岁”，B “这种动物由出生活到25岁”，则A B ⊂， 故所求概率为：()()()()()218.04.0====A PB P A P AB P A B P .4．掷两颗骰子，已知两颗骰子的点数之和为7，求其中有一颗为1点的概率（分别用条件概率的定义计算和条件概率的含义（即用缩减后的样本空间）计算）.解法（一）：设A 表示“两颗骰子的点数之和为7”，B 表示“其中有一颗为1点”，则所求概率为：()()()31666222===A P AB P A B P . 解法（二）：考虑缩减后的样本空间（即两颗骰子的点数之和为7）：()()()()()(){}4,3,5,2,6,1,3,4,2,5,1,6=Ω，()(){}6,1,1,6=A ，故()31=A P . 点评：缩减后的样本空间只含有6个基本事件，而原样本空间含有36个基本事件.5．某人有一笔资金，他投入基金的概率为58.0，购买股票的概率为28.0，两项同时都投资的概率为19.0，（1）已知他已经投入基金，再购买股票的概率是多少？（2）已知他已购买股票，再投入基金的概率是多少？解：设A “投入基金”，B “购买股票”，则()58.0=A P ，()28.0=B P ，()19.0=AB P ，于是，已知他已经投入基金，再购买股票的概率是：()()()581958.019.0===A P AB P A B P . 已知他已购买股票，再投入基金的概率是：()()()281928.019.0===B P AB P B A P . 6．袋中有r 只红球，t 只白球，每次从袋中任取一只球，观察颜色后放回，并再放入a 只与取出的那只球同色的球，若在袋中连续取球四次，试求第一、二次取到红球且第三、四次取到白球的概率（此题为波利亚模型，它是一个包含了许多重要的随机现象的模型，请读者思考一下，什么样的现象可以归结于这一模型）.解：设()4,3,2,1=i A i 表示“第i 次取到红球”，则所求概率为：()4321A A A A P ⋅⋅⋅()()()()()()a t r a t r a t r t r a t a r rt 32+++++++++=. 7．已知10只产品中有2只次品，在其中取两次，每次任取一只，作不放回抽样.求下列事件的概率：（1）两只都是正品；（2）两只都是次品；（3）一只正品，一只次品. 解：设21,A A 分别表示“第1，2次取的是正品”，则（1）()()()45289710812121=⋅==A A P A P A A P . （2）()()()4519110212121=⋅==⋅A A P A P A A P . （3）()()()()()()()12112121212121A A P A P A A P A P A A P A A P A A A A P +=+=+45169810292108=⋅+⋅=. 8．已知()3.0=A P ，()5.0=B P ，()15.0=AB P ，验证()()B P A B P =，()()B P A B P =，()()A P B A P =，()()A P B A P =. 证明：()()()()B P A P AB P A B P ===5.0；()()()()()()()()A P AB P B P A P A B P A P A B P A B P --=--==11 ()B P ==-=5.07.015.05.0.同理可证其他. 9．第一个盒子中有5只红球，4只白球；第二个盒子中有4只红球，5只白球.先从第一个盒子中任取2只球放入第二个盒子中去，然后从第二个盒子中任取一球，求取到白球的概率.解：设1B “从第一只盒子中取得2 只红球”，2B “从第一只盒子中取得2 只白球”，3B “从第一只盒子中取得一只红球，一只白球”，A “从第二只盒子中取到一只白球”. 由全概率公式得：()()()9953116951176111518531=⨯+⨯+⨯==∑=i i i B A P B P A P . 10．某产品主要由三个厂家供货. 甲、乙、丙三个厂家的产品分别占总数的%15，%80，%5.其次品率分别为02.0，01.0，03.0. 试计算：（1）从这批产品中任取一件是合格品的概率；（2）已知从这批产品中随机地取出的一件是不合格品，问这件产品由哪家生产的可能性大？解：设1B ，2B ，3B 分别表示“任取一件产品是甲，乙，丙厂生产的”，A 表示“从这批产品中任取一件是合格品”则()()()0125.003.005.001.08.002.015.031=⨯+⨯+⨯==∑=i i i B A P B P A P .11．将两信息分别编码为X 和Y 后传送出去，接收站接收时，X 被误收作Y 的概率为02.0，而Y 被误收作X 的概率为01.0.信息X 与信息Y 传送的频繁程度之比为1:2.若接收站收到的信息是X ，问原发信息也是X 的概率是多少？解：设A “发出信号X ”，B “收到信号X ”，则由Bayes 公式可知：()()()()()()()19719601.03198.03298.032=⨯+⨯⨯=+=A B P A P A B P A P A B P A P B A P . 12．设有两箱同类零件，第一箱内装有50件，其中10件是一等品；第二箱内装有30件，其中18件是一等品，现从两箱中任选一箱，然后从该箱中依次随机地取出两个零件（取出的零件不放回），试求：（1）第一次取出的零件是一等品的概率；（2）在第一次取出的零件是一等品的条件下，第二次取出的零件仍是一等品的概率.解：设21,A A 分别表示“第一，二次取得一等品”，21,B B 分别表示“取到第一箱，第二箱中的零件”.（1）由全概率公式得：()()()4.02130182*********=⨯+⨯==∑=i i i B A P B P A P . （2）由全概率公式得：4856.0=.习题1-41．设()7.0=A P ，()8.0=B P ，()8.0=A B P .问事件A 与B 是否相互独立？解：因为()()()56.0==A B P A P AB P ，而()()56.0=B P A P ，即()()()B P A P AB P =，所以事件A 与B 是相互独立的.2．设C B A ,,是三个互相独立的随机事件，且()10<<C P ，问AC 与C 是否相互独立？ 解：因为()()()()()()01>-==+⋅=+=⋅C P C P C C A P C A C P C AC P ， ()()()[]()()()[]()C P C P A P C P AC P C P AC P C B A -=====-=11,,独立，所以当()0=A P 时，()()()()C P C P AC P C AC P ==⋅，故AC 与C 是相互独立的.否则，AC 与C 是不相互独立的. 点评：因为C AC ⊂，所以C AC ⊃，从而()()C P C AC P =⋅.3．已知()a A P =，()3.0=B P ，()7.0=+B A P .（1）若事件A 与B 互不相容，求a ；（2）若事件A 与B 相互独立，求a .解：（1）若事件A 与B 互不相容，则()()()()A B P B P A P B A P -+=+ ()()()()()()()()()AB P A P AB P B P B P A P A B P B P A P +-=+-+-=--+=11，因为A 与B 互不相容，所以()0=AB P ，从而()()3.0117.0=⇒-=-==+a a A P B A P .（2）若事件A 与B 相互独立，则()()()()A B P B P A P B A P -+=+ ()()()B P A P A P +-=1，从而()()()()a a B P A P A P B A P 3.0117.0+-=+-==+，故73=a . 4．设A 与B 相互独立，且()α=A P ，()β=B P ，求下列事件的概率：（1）()B A P +；（2）()B A P +；（3）()B A P +. 解：（1）()αββα-+=-+=+)()()()(B P A P B P A P B A P ；（2）()()()B A P B P A P B A P -+=+)(，当A 与B 相互独立时，A 与B 也是独立的，则 αββ+-=1；（3）()()()()()αβ-=-=-==+111B P A P AB P AB P B A P . 5．已知事件A 与B 相互独立，且()91=⋅B A P ，()()B A P B A P =，求()A P ，()B P . 解：()()()()()()()()AB P B P AB P A P A B P B A P B A P B A P -=-⇔-=-⇔= ()()B P A P =⇔，从而有()()B P A P =. 当事件A 与B 相互独立时，事件A 与B 也独立，则()()()9191=⇔=⋅B P A P B A P ，于是()()31==B P A P ，()()32==B P A P .6．三个人独立地破译一份密码，已知各人能译出的概率分别为51，31，41，问三人中至少有一人能将此密码译出的概率为多少？解：设C B A ,,分别表示“甲，乙，丙能独立地译出此密码”，则()()()()()()4332541111⨯⨯-=-=⋅⋅-=++-=++C P B P A P C B A P C B A P C B A P 53=.7．对同一目标进行三次独立射击，第一次、第二次、第三次射击的命中率分别是7.0,5.0,4.0，求：（1）在这三次射击中，恰好有一次击中目标的概率；（2）在这三次射击中，至少有一次命中目标的概率.解：设C B A ,,分别表示“第一，二，三次射击时命中目标”.（1）()()()()()()()()()()C P B P A P C P B P A P C P B P A P C B A C B A C B A P ++=⋅⋅+⋅⋅+⋅⋅36.07.05.06.03.05.06.03.05.04.0=⨯⨯+⨯⨯+⨯⨯=.（2）()()()()()()C P B P A P C B A P C B A P C B A P -=⋅⋅-=++-=++11191.03.05.06.01=⨯⨯-=.8．一个元件（或系统）能正常工作的概率称为元件（或系统）的可靠性，设4个独立工作的元件4,3,2,1，求这一系统的可靠性.解：设i A 表示“第i 个元件可靠”)4,3,2,1(=i ，则所求概率为：()()()413214321A A A A A P A A A A P +=+ ()()()432141321432141321p p p p p p p p p A A A A P A A P A A A P -+=-+=.9．设第一只盒子中装有3只兰球，2只绿球，2只白球；第二个盒子中装有2只兰球，3只绿球，4只白球，独立地分别在两个盒子中各取一只球.（1）求至少有一只兰球的概率；（2）求有一只兰球，一只白球的概率；（3）已知至少有一只兰球，求有一只兰球一只白球的概率.解：设111,,C B A 分别表示“从第一只盒子中取出的球为兰，绿，白色的”，设222,,C B A 分别表示“从第二只盒子中取出的球为兰，绿，白色的”.（1）()()()()()959774111121212121=⨯-=-=⋅-=+-=+A P A P A A P A A P A A P ;（2）()()()()()()()212121212121A P C P C P A P A C P C A P A C C A P +=+=+631692729473=⨯+⨯=. （3）()()()()()21212121212121A A P A A A C C A P A A A C C A P +++=++，因为()()212121A A A C C A +⊂+，所以()()()()2121212121A C C A P A A A C C A P +=++.故，()()()()()()()3121212121212121212121=++=+++=++A A P A C C A P A A P A A A C C A P A A A C C A P .10．（先下手为强）甲、乙两人射击水平相当，于是约定比赛规则：双方对同一目标轮流射击，若一方失利，另一方可以继续射击，直到有人命中目标为止.命中一方为该轮的获胜者.你以为先射击者是否一定沾光？为什么？解：设i A 表示“第i 次射击时命中目标”()Λ,2,1=i ，B 表示“甲获胜”，假设由甲先发第一枪，又设甲，乙两人每次射击时的命中率为p ，未命中的概率为q ，则1=+q p .qq p +=-=1112，于是乙获胜的概率为：()()q qB P B P +=-=11.因为10<<q ，故()()B P B P >.即，先下手为强.第一章总习题1．填空题（1）假设B A ,是两个随机事件，且B A AB ⋅=，则()=+B A ，()=AB ；解：()()Ω=+⇔+=+++⇔B A B A B B A A .Φ=Φ⋅=⇔⋅⋅=⇔⋅=A AB B B A ABB B A AB .（2）假设B A ,是任意两个事件，则()()()()[]()=++++B A B A B A B A P .解：()()()()[]()()()()[]B A B A B A B A P B A B A B A B A P ++++=++++()()[]()0=Φ=++=P B B A B B A P .2．选择题（1）设8.0)(=A P ，7.0)(=B P ，()8.0=B A P ，则下列结论正确的是().（A ）事件A 与事件B 相互独立；（B ）事件A 与事件B 互逆； （C ）A B ⊃；（D ）())()(B P A P B A P +=+.解：因为()56.0)()(==B A P B P AB P ，而56.0)()(=B P A P ，即)()()(B P A P AB P =，所以事件A 与事件B 相互独立，选（A ）.（2）设B A ,为两个互逆的事件，且0)(>A P ，0)(>B P ，则下列结论正确的是().（A ）()0>A B P ；（B ）())(A P B A P =；（C ）()0=B A P ；（D ）)()()(B P A P AB P =. 解：因为B A ,为两个互逆的事件，所以当事件B 发生时，事件A 是不会以生的，故()0=B A P .选（C ）.（3）设1)(0<<A P ，1)(0<<B P ，()()1=+B A P B A P ，则下列结论正确的是().（A ）事件A 与事件B 互不相容；（B ）事件A 与事件B 互逆；（C ）事件A 与事件B 不互相独立；（D ）事件A 与事件B 互相独立.解：因为()()()()()()()()()()1111=-++⇔=⋅+⇔=+B P BA PB P AB P BP B A P B P AB P B A P B A P )()()(B P A P AB P =，所以事件A 与事件B 互相独立.选（D ）.3．从五双不同的鞋子中任取四只，求取得的四只鞋子中至少有两只配成一双的概率.解：此题考虑逆事件求解比较方便，即取得的四只鞋子中不能配成一双.设A 表示“取得的四只鞋子中至少有两只配成一双”，则()4101212124511)(C C C C C A P A P -=-= 2113=. 4．（找次品问题）盒中有4只次品晶体管，6只正品晶体管，随机地抽取一只进行测试，直到4只次品晶体管都找到为止，求第4次品晶体管在第五次测试中被发现的概率.解：设i A 表示“第i 次找到次品晶体管”()5,4,3,2,1=i ，则所求概率为：1052617283941064=⎪⎭⎫⎝⎛⨯⨯⨯⨯=.5．（讨论奖金分配的公平性问题）在一次羽毛球比赛中，设立奖金1000元.比赛规定：谁先胜三盘，谁获得全部奖金.设甲、乙两人的球技相当，现已打了三盘，甲2胜1负.由于特殊原因必须中止比赛.问这1000元应如何分配才算公平?解：应以预期获胜的概率为权重来分配这笔奖金，于是求出甲、乙两人获胜的预期概率即可.比赛采取的应是五局三胜制，比赛已打三盘，甲胜两盘，甲若再胜一盘即可获胜. 甲获胜的预期概率为：()()()()43212121544544=⨯+=+=+A P A P A P A A A P . 于是，甲应分得1000元奖金中的750100043=⨯元，乙分得250元.6．4张卡片标着1到4，面朝下放在桌子上，一个自称有透视能力的人将用他超感觉的能力说出卡片上的号码.如果他是冒者而只能随机地猜一下，他至少猜中一个的概率p 是多少？解：由古典概型下概率的定义可知：85!41!40444342414=-=+++=C C C C C p . 7．甲从10,8,6,4,2中任取一个数，乙从9,7,5,3,1中任取一个数，求甲取得的数大于乙取得的数的概率.解：设i A 表示“甲取的数为()10,8,6,4,2=i i ”，k B 表示“乙取的数为()9,7,5,3,1=k k ”，则所求概率为：由于甲、乙取数是相互独立的，则由独立性的性质可知：()()()k i k i B P A P B A P =，且()51=i A P ，()51=k B P ，()9,7,5,3,1;10,8,6,4,2==k i . 以上概率为：5315251=⨯. 8．从数字9,,,3,2,1Λ中可重复地任取n 次，每次取一个数，求n 次所取数的乘积能被10整除的概率.解：n 次取得的数的乘积能被10整除，相当于取得的n 个数中至少有一个是偶数，另一个是5.设A 表示“所取的数是5”，B 表示“所取的数中至少有一个是偶数”，则所求概率为：nnn n 94581-+-=.9．向正方形区域(){}1,1,≤≤=Ωy x y x 中随机地投一个点，如果()y x ,是所投点M 的坐标，试求：（1）02=++y xt t 有两个实根的概率；（2）方程02=++y xt t 有两个正实根的概率.解：（1）设A 表示“02=++y xt t 有两个实根”，02=++y xt t 有两个实根的充要条件是 042≥-y x ， 即(){}04,2≥-=y x y x A .故()24134242102=+=⎰dx x A P .⎝⎛x（2）设B 表示“方程02=++y xt t 有两个正实根”，则方程02=++y xt t 有两个正实根的条件是：042≥-y x ，0>-x ，0>y ，即(){}0,0,04,2><≥-=y x y x y x B .故()48144012==⎰-dx x B P . 10．将四个球任意地放到四个盒子中去，每个盒子中容纳球的个数不限，如果已知前两个球放在不同的盒子中，试求有一个盒子中恰好放有三个球的概率.解：设A 表示“前两个球放在不同的盒子中”，B 表示“有一个盒子中恰好有两个球”，则所求概率为：()()()8114141224121224===C C C C C C C A P AB P A B P .11．设M 件产品中有m 件不合格品，从中任取两件.（1）在所取的两件产品中有一件是不合格品的条件下，求另一件也是不合格品的概率；（2）在所取产品中有一件是合格品的条件下，求另一件也是合格品的概率.解：设i A 表示“取出的两件产品中有i 件合格品”，则()22Mi mi m M i C C C A P --=()2,1,0=i . （1）()()()()()()12112222010010100100---=-=+=++=+--m M m C CC C C A A P A P A A P A A A P A A A P MmM M mm M . 或()()()()()()()()()10010010100100A P A P A P A A P A P A A P A A A P A A A P +=+=++=+121211220220---=+=---m M m C C C C C C C C C Mmm M M m m M M mm M . （2）()()()()()()()()1221121211211-+=+=++=+m M mA P A P A P A P A P A A A P A A A P .12．口袋中有20个球，其中两个是红球，现从袋中取球三次，每次取一个，取后不放回，求第三次才取到红球的概率.解：设i A 表示“第i 次取得红球()3,2,1=i ”，则所求概率为：()()()()089.011812119117120118213121321=⨯⨯=⋅=⋅⋅C C C C C C A A A P A A P A P A A A P .13．12个乒乓球全是新的，每次比赛时取出3个用完后放回去.（1）求第三次比赛时取到的三个球都是新球的概率；（2）问在第三次取到的三个球都是新球的条件下，第二次取到几个新球的概率最大？解：设事件i i i C B A ,,分别表示第一、二、三次比赛时取到i 个新球()3,2,1,0=i .（1）由全概率公式，()()()∑==333i i i B C P B P C P .其中：()()3,2,1,0312339==-i C C C B P i i i ，()()3,2,1,0312393==-i C C B C P i i . 故()()()146.03312393123393033≈⋅==∑∑=--=i ii i i i i C C C C C B C P B P C P .（2）容易求得，()70568430=C B P ，()7056151231=C B P ，()7056378032=C B P ，()7056168033=C B P . 故在第三次取到的三个球都是新球的条件下，第二次取到两个新球的概率最大.14．（有关经济的忠告）美国总统常常从经济顾问委员会寻求各种建议.假设有三种不同经济理论的顾问C B A ,,，总统正在考虑采取一项关于工资和价格控制的新政策，并关注这项政策对失业率的影响，每位顾问就这种影响给总统一个个人预测，预测是以失业率将减少、保持不变或上升的概率来给出的，见下表.用字母C B A ,,分别表示顾问C B A ,,的经济理论是正确的事件，根据以往总统与这些顾问一起工作的经验，总统已经形成了关于每位顾问正确的经济理论可能的一个估计，分别为：()61=A P ，()31=B P ，()21=C P .假设总统采取了所提出的新政策，一年后，失业率上升了，总统应如何调整他对其经济顾问的理论的正确的估计？解：设I 表示“失业率上升”，则()()()()()()()C I P C P B I P B P P A I P A P I P ++=3.02.0212.0318.061=⨯+⨯+⨯=.由Bayes 公式得：()()()()943.08.061=⨯==I P A I P A P I A P ， ()()()()923.02.031=⨯==I P B I P B P I B P ，()()()()933.02.021=⨯==I P C I P C P I C P .总统调整他对其经济顾问的理论的正确的估计为：()94=I A P ，()92=I B P ，()93=I C P . 15．设一枚深水炸弹击沉一艘潜水艇的概率为31，击伤的概率为21，击不中的概率为61，并设击伤两次会导致潜水艇下沉，求施放4枚深水炸弹能击沉潜水艇的概率.（提示：先求出击不沉的概率.）解：设A 表示“施放4枚深水炸弹击沉潜水艇”，则()()43344613121616111-=⎥⎥⎦⎤⎢⎢⎣⎡⨯⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-=-=C A P A P .16．设有五个独立工作的元件,5,4,3,2,1（称为桥式系统），试求出该系统的可靠性. 解：设i A 表示“第i 个元件可靠()5,4,3,2,1=i ”，则所求概率为：()()()54325432154321543225224p p p p A A A A A P A A A A A P A A A A P +-+=-+-.17．（下赌注问题）17世纪未，法国的De Mere 爵士与人打赌，在“一颗骰子连续掷四次至少出现一次六点”的情况下他赢了钱，可是在“两颗骰子连续掷二十四次至少出现一次双六点”的情况下却输了钱，从概率论的角度解释这是为什么？5解：应分别求出“一颗骰子连续掷四次至少出现一次六点”和“两颗骰子连续掷二十四次至少出现一次双六点”的概率，比较这两个概率的大小即可作出解释.设A “一颗骰子连续掷四次至少出现一次六点”，B “两颗骰子连续掷二十四次至少出现一次双六点”；再设i A “第i 次抛掷时出现六点()4,3,2,1=i ”，k B “第k 次抛掷时出现双六点”，则()()()()518.0651144321≈⎪⎭⎫ ⎝⎛-=-=A P A P A P A P . 此概率大于5.0，故赢钱的可能性大.()()()491.0363511242421≈⎪⎭⎫ ⎝⎛-=-=B P B P B P Λ.此概率小于5.0，故赢钱的可能性小.请注意，在“两颗骰子连续掷二十四次至少出现一次双六点”的情形中，当抛掷次数25>n 时，这时的概率大于5.0，且抛掷次数超过25次越多越有利，这是因为136351lim =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-∞→n n . 18．要验收一批100件的乐器，验收方案如下：自该乐器中随机地取3件测试（设3件乐器的测试是相互独立的），如果3件中至少有一件被认为音色不纯，则这批乐器就被拒绝接收.设一件音色不纯的乐器经测试查出其为音色不纯的概率为95.0，而一件音色纯的乐器经测试被误认为不纯的概率为01.0，如果已知这100件乐器中恰好有4件音色不纯的，试问这批乐器被接收的概率是多少？解：设i H 表示“随机取出的三件乐器中有i 件音色不纯()3,2,1,0=i ”，A 表示“这批乐器被接收”，则()31003960C C H P =，()3100296131C C C H P =，()3100196242C C C H P =，()3100343C C H P =，()()3099.0=H A P ，()()05.099.021⨯=H A P ，()()2205.099.0⨯=H A P ，()()3305.0=H A P . 于是，由全概率公式得：()()()6829.030==∑=i i i H A P H P A P .。

概论论与数理统计习题参考解答习题一8. 掷3枚硬币, 求出现3个正面的概率.解: 设事件A ={出现3个正面}基本事件总数n =23, 有利于A 的基本事件数n A =1, 即A 为一基本事件, 则125.08121)(3====n n A P A . 9. 10把钥匙中有3把能打开门, 今任取两把, 求能打开门的概率.解: 设事件A ={能打开门}, 则A 为不能打开门基本事件总数, 有利于210C n =A 的基本事件数27C n A =, 467.0157910212167)(21027==××⋅××==C C A P 因此, 533.0467.01)(1)(=−=−=A P A P .10. 一部四卷的文集随便放在书架上, 问恰好各卷自左向右或自右向左的卷号为1,2,3,4的概率是多少?解: 设A ={能打开门},基本事件总数2412344=×××==P n ,有利于A 的基本事件数为,2=A n 因此, 0833.0121)(===n n A P A . 11. 100个产品中有3个次品,任取5个, 求其次品数分别为0,1,2,3的概率.解: 设A i 为取到i 个次品, i =0,1,2,3,基本事件总数, 有利于A i 的基本事件数为5100C n =3,2,1,0,5973==−i C C n i i i 则00006.09833512196979697989910054321)(006.0983359532195969739697989910054321)(138.09833209495432194959697396979899100543213)(856.0334920314719969798991009394959697)(51002973351003972322510049711510059700=××==××⋅××××××××====××=×××××⋅××××××××====×××=×××××××⋅××××××××=×===××××=××××××××===C C n n A P C C C n n A P C C n n A P C C n n A P12. N 个产品中有N 1个次品, 从中任取n 个(1≤n ≤N 1≤N ), 求其中有k (k ≤n )个次品的概率. 解: 设A k 为有k 个次品的概率, k =0,1,2,…,n ,基本事件总数, 有利于事件A k 的基本事件数,k =0,1,2,…,n , n N C m =kn N N k N k C C m −−=11因此, n k C C C m m A P n Nk n N N k N k k ,,1,0,)(11L ===−− 13. 一个袋内有5个红球, 3个白球, 2个黑球, 计算任取3个球恰为一红, 一白, 一黑的概率. 解: 设A 为任取三个球恰为一红一白一黑的事件,则基本事件总数, 有利于A 的基本事件数为,310C n =121315C C C n A =则25.0412358910321)(310121315==×××××××===C C C C n n A P A 14. 两封信随机地投入四个邮筒, 求前两个邮筒内没有信的概率以及第一个邮筒内只有一封信的概率.解: 设A 为前两个邮筒没有信的事件, B 为第一个邮筒内只有一封信的事件,则基本事件总数,1644=×=n 有利于A 的基本事件数422=×=A n ,有利于B 的基本事件数632=×=B n , 则25.041164)(====n n A P A 375.083166)(====n n B P B .15. 一批产品中, 一, 二, 三等品率分别为0.8, 0.16, 0.04, 若规定一, 二等品为合格品, 求产品的合格率.解: 设事件A 1为一等品, A 2为二等品, B 为合格品, 则P (A 1)=0.8, P (A 2)=0.16,B =A 1+A 2, 且A 1与A 2互不相容, 根据加法法则有P (B )=P (A 1)+P (A 2)=0.8+0.16=0.9616. 袋内装有两个5分, 三个2分, 五个一分的硬币, 任意取出5个, 求总数超过一角的概率. 解: 假设B 为总数超过一角,A 1为5个中有两个5分, A 2为5个中有一个5分三个2分一个1分,A 3为5个中有一个5分两个2分两个1分, 则B =A 1+A 2+A 3, 而A 1,A 2,A 3互不相容, 基本事件总数252762354321678910510=×××=××××××××==C n 设有利于A 1,A 2,A 3的基本事件数为n 1,n 2,n 3,则5.0252126252601056)(,60214532,1052,563216782523123153312238221==++==××××===×===××××==B P C C C n C C C n C C n 17. 求习题11中次品数不超过一个的概率.解: 设A i 为取到i 个次品, i =0,1,2,3, B 为次品数不超过一个,则B =A 0+A 1, A 0与A 1互不相容, 则根据11题的计算结果有P (B )=P (A 0)+P (A 1)=0.856+0.138=0.99419. 由长期统计资料得知, 某一地区在4月份下雨(记作事件A )的概率为4/15, 刮风(用B 表示)的概率为7/15, 既刮风又下雨的概率为1/10, 求P (A |B ), P (B |A ), P (A +B ).解: 根据题意有P (A )=4/15, P (B )=7/15, P (AB )=1/10, 则633.03019303814101154157)()()()(275.08315/410/1)())|(214.014315/710/1)()()|(==−+=−+=−+=+========AB P B P A P B A P A P PAB A B P B P AB P B A P 20. 为防止意外, 在矿内同时设有两种报警系统A 与B , 每种系统单独使用时, 其有效的概率系统A 为0.92, 系统B 为0.93, 在A 失灵的条件下, B 有效的概率为0.85, 求(1) 发生意外时, 这两个报警系统至少有一个有效的概率(2) B 失灵的条件下, A 有效的概率解: 设A 为系统A 有效, B 为系统B 有效, 则根据题意有P (A )=0.92, P (B )=0.93, 85.0)|(=A B P(1) 两个系统至少一个有效的事件为A +B , 其对立事件为两个系统都失效, 即B A B A =+, 而15.085.01)|(1)|(=−=−=A B P A B P , 则988.0012.01(1)(012.015.008.015.0)92.01(|()((=−=−=+=×=×−==B A P B A P A B P A P B A P(2) B 失灵条件下A 有效的概率为|(B A P , 则 829.093.01012.01)()(1|(1)|(=−−=−=−=B P B A P B A P B A P 21. 10个考签中有4个难签, 3人参加抽签考试, 不重复地抽取, 每人一次, 甲先, 乙次, 丙最后, 证明3人抽到难签的概率相等.证: 设事件A ,B ,C 表示甲,乙,丙各抽到难签, 显然P (A )=4/10,而由903095106|()((902496104)|()((902494106|()()(901293104)|()()(=×===×===×===×==A B P A P B A P A B P A P B A P A B P A P B A P A B P A P AB P 由于A 与A 互不相容,且构成完备事件组, 因此B A AB B +=可分解为两个互不相容事件的并, 则有1049036902412)()()(==+=+=A P AB P B P 又因B A B A B A AB ,,,之间两两互不相容且构成完备事件组, 因此有B A B A A ABC C +++=分解为四个互不相容的事件的并,且720120849030)|(()(72072839024|(()(72072839024)|()()(72024829012)|()()(=×===×===×===×==B A C P B A P B A P B A C P B A P B A P B A C P B A P BC A P AB C P AB P ABC P则104720288720120727224()()()()(==+++=+++=CB A PC B A P BC A P ABC P C P 因此有P (A )=P (B )=P (C ), 证毕.22. 用3个机床加工同一种零件, 零件由各机床加工的概率分别为0.5, 0.3, 0.2, 各机床加工的零件为合格品的概率分别等于0.94, 0.9, 0.95, 求全部产品中的合格率.解: 设A 1,A 2,A 3零件由第1,2,3个机床加工, B 为产品合格,A 1,A 2,A 3构成完备事件组.则根据题意有P (A 1)=0.5, P (A 2)=0.3, P (A 3)=0.2,P (B |A 1)=0.94, P (B |A 2)=0.9, P (B |A 3)=0.95,由全概率公式得全部产品的合格率P (B )为93.095.02.09.03.094.05.0)|()()(31=×+×+×==∑=i i i A B P A P B P23. 12个乒乓球中有9个新的3个旧的, 第一次比赛取出了3个, 用完后放回去, 第二次比赛又取出3个, 求第二次取到的3个球中有2个新球的概率.解: 设A 0,A 1,A 2,A 3为第一次比赛取到了0,1,2,3个新球, A 0,A 1,A 2,A 3构成完备事件组. 设B 为第二次取到的3个球中有2个新球. 则有22962156101112321)|(,552132101112789321)(,442152167101112321)|(,55272101112389321)(,552842178101112321)|(,2202710111239321)(,552732189101112321)|(,2201101112321)(3121626331239331215272312132923121428131223191312132********=⋅××⋅××××===×××××××××===⋅××⋅××××===××××××××===⋅××⋅××××===××××××===⋅××⋅××××===××××==C C C A B P C C A P C C C A B P C C C A P C C C A B P C C C A P C C C A B P C C A P 根据全概率公式有455.01562.02341.00625.00022.022955214421552755282202755272201)|()()(30=+++=⋅+⋅+⋅+⋅==∑=i i i A B P A P B P 24. 某商店收进甲厂生产的产品30箱, 乙厂生产的同种产品20箱, 甲厂每箱100个, 废品率为0.06, 乙厂每箱装120个, 废品率是0.05, 求:(1)任取一箱, 从中任取一个为废品的概率;(2)若将所有产品开箱混放, 求任取一个为废品的概率.解: (1) 设B 为任取一箱, 从中任取一个为废品的事件.设A 为取到甲厂的箱, 则A 与A 构成完备事件组056.005.04.006.06.0)|()()|()()(05.0|(,06.0)|(4.05020)(,6.05030)(=×+×=+=======A B P A P A B P A P B P A B P A B P A P A P(2) 设B 为开箱混放后任取一个为废品的事件.则甲厂产品的总数为30×100=3000个, 其中废品总数为3000×0.06=180个,乙厂产品的总数为20×120=2400个, 其中废品总数为2400×0.05=120个,因此...055555555.0540030024003000120180)(==++=B P 25. 一个机床有1/3的时间加工零件A , 其余时间加工零件B , 加工零件A 时, 停机的概率是0.3, 加工零件B 时, 停机的概率是0.4, 求这个机床停机的概率.解: 设C 为加工零件A 的事件, 则C 为加工零件B 的事件, C 与C 构成完备事件组. 设D 为停机事件, 则根据题意有P (C )=1/3, P (C )=2/3,P (D |C )=0.3, P (D |C )=0.4,根据全概率公司有367.04.0323.031)|(()|()()(=×+×=+=C D P C P C D P C P D P 26. 甲, 乙两部机器制造大量的同一种机器零件, 根据长期资料总结, 甲机器制造出的零件废品率为1%, 乙机器制造出的废品率为2%, 现有同一机器制造的一批零件, 估计这一批零件是乙机器制造的可能性比它们是甲机器制造的可能性大一倍, 今从该批零件中任意取出一件, 经检查恰好是废品, 试由此检查结果计算这批零件为甲机器制造的概率.解: 设A 为零件由甲机器制造, 则A 为零件由乙机器制造, A 与A 构成完备事件组. 由P (A +A )=P (A )+P (A )=1并由题意知P (A )=2P (A ),得P (A )=1/3, P (A )=2/3.设B 为零件为废品, 则由题意知P (B |A )=0.01, P (B |A )=0.02,则根据贝叶斯公式, 任抽一件检查为废品条件下零件由甲机器制造的概率为2.005.001.002.03201.03101.031)|()()|()()|()()|(==×+××==+=A B P A P A B P A P A B P A P B A P 27. 有两个口袋, 甲袋中盛有两个白球, 一个黑球, 乙袋中盛有一个白球两个黑球. 由甲袋中任取一个球放入乙袋, 再从乙袋中取出一个球, 求取到白球的概率.解: 设事件A 为从甲袋中取出的是白球, 则A 为从甲袋中取出的是黑球, A 与A 构成完备事件组. 设事件B 为从乙袋中取到的是白球.则P (A )=2/3, P (A )=1/3,P (B |A )=2/4=1/2, P (B |A )=1/4,则根据全概率公式有417.012541312132)|()()|()()(==×+×=+=A B P A P A B P A P B P28. 上题中若发现从乙袋中取出的是白球, 问从甲袋中取出放入乙袋的球, 黑白哪种颜色可能性大?解: 事件假设如上题, 而现在要求的是在事件B 已经发生条件下, 事件A 和A 发生的条件概率P (A |B )和P (A |B )哪个大, 可以套用贝叶斯公式进行计算, 而计算时分母为P (B )已上题算出为0.417, 因此2.0417.04131)()|()()|(8.0417.02132)()|()()|(=×===×==B P A B P A P B A P B P A B P A P B A PP (A |B )>P (A |B ), 因此在乙袋取出的是白球的情况下, 甲袋放入乙袋的球是白球的可能性大.29. 假设有3箱同种型号的零件, 里面分别装有50件, 30件和40件, 而一等品分别有20件, 12件及24件. 现在任选一箱从中随机地先后各抽取一个零件(第一次取到的零件不放回). 试求先取出的零件是一等品的概率; 并计算两次都取出一等品的概率.解: 称这三箱分别为甲,乙,丙箱, 假设A 1,A 2,A 3分别为取到甲,乙,丙箱的事件, 则A 1,A 2,A 3构成完备事件组.易知P (A 1)=P (A 2)=P (A 3)=1/3.设B 为先取出的是一等品的事件. 则6.04024)|(,4.03012)|(,4.05020)|(321======A B P A B P A B P 根据全概率公式有 467.036.04.04.0)|()()(31=++==∑=i i i A B P A P B P 设C 为两次都取到一等品的事件, 则38.039402324)|(1517.029301112)|(1551.049501920)|(240224323021222502201=××===××===××==C C A C P C C A C P C C A C P 根据全概率公式有22.033538.01517.01551.0)|()()(31=++==∑=i i i A C P A P C P 30. 发报台分别以概率0.6和0.4发出信号“·”和“—”。

第一章《随机事件及概率》练习题一、单项选择题1、设事件A 与B 互不相容，且P (A )＞0，P (B )＞0，则一定有（ ）（A ）()1()P A P B =-； （B ）(|)()P A B P A =；（C ）(|)1P A B =； （D ）(|)1P A B =。

2、设事件A 与B 相互独立，且P (A )＞0，P (B )＞0，则（ ）一定成立 （A ）(|)1()P A B P A =-； （B ）(|)0P A B =；（C ）()1()P A P B =-； （D ）(|)()P A B P B =。

3、设事件A 与B 满足P (A )＞0，P (B )＞0，下面条件（ ）成立时，事件A 与B 一定独立（A ）()()()P AB P A P B =； （B ）()()()P A B P A P B =；（C ）(|)()P A B P B =； （D ）(|)()P A B P A =。

4、设事件A 和B 有关系B A ⊂，则下列等式中正确的是（ ）（A ）()()P AB P A =； （B ）()()P AB P A =；（C ）(|)()P B A P B =； （D ）()()()P B A P B P A -=-。

5、设A 与B 是两个概率不为0的互不相容的事件，则下列结论中肯定正确的是（ ） （A ）A 与B 互不相容； （B ）A 与B 相容；（C ）()()()P AB P A P B =； （D ）()()P A B P A -=。

6、设A 、B 为两个对立事件，且P (A )≠0，P (B ) ≠0，则下面关系成立的是（ ） （A ）()()()P AB P A P B =+； （B ）()()()P A B P A P B ≠+；（C ）()()()P AB P A P B =； （D ）()()()P AB P A P B =。

7、对于任意两个事件A 与B ，()P A B -等于（ ）（A ）()()P A P B - （B ）()()()P A P B P AB -+； （C ）()()P A P AB -； （D ）()()()P A P B P AB +-。

第1章 概率论的基本概念§1 .8 随机事件的独立性1. 电路如图，其中A,B,C,D 为开关。

设各开关闭合与否相互独立，且每一开关闭合的概率均为p,求L 与R 为通路（用T 表示）的概率。

A B L R C D1. 甲，乙,丙三人向同一目标各射击一次，命中率分别为0.4,0.5和0.6，是否命中，相互独立， 求下列概率: (1) 恰好命中一次,(2) 至少命中一次。

第1章作业答案§1 .8. 1： 用A,B,C,D 表示开关闭合，于是 T = AB ∪CD, 从而，由概率的性质及A,B,C,D 的相互独立性P(T) = P(AB) + P(CD) - P(ABCD)= P(A)P(B) + P(C)P(D) – P(A)P(B)P(C)P(D)424222p p p p p -=-+=2： (1) 0.4(1-0.5)(1-0.6)+(1-0.4)0.5(1-0.6)+(1-0.4)(1-0.5)0.6=0.38； (2) 1-(1-0.4)(1-0.5)(1-0.6)=0.88.第2章 随机变量及其分布§2.2 10-分布和泊松分布1 某程控交换机在一分钟内接到用户的呼叫次数X 是服从λ=4的泊松分布，求(1)每分钟恰有1次呼叫的概率；(2)每分钟只少有1次呼叫的概率； (3)每分钟最多有1次呼叫的概率；2 设随机变量X 有分布律： X 23 , Y ～π(X), 试求： p 0.4 0.6（1）P(X=2,Y ≤2)； (2)P(Y ≤2)； (3) 已知 Y ≤2, 求X=2 的概率。

§2.3 贝努里分布2 设每次射击命中率为0.2，问至少必须进行多少次独立射击，才能使至少击中一次的概率不小于0.9 ？§2.6 均匀分布和指数分布2 假设打一次电话所用时间（单位：分）X 服从2.0=α的指数分布，如某人正好在你前面走进电话亭，试求你等待：（1）超过10分钟的概率；（2）10分钟 到20分钟的概率。

第1章 随机变量及其概率1，写出下列试验的样本空间：连续投掷一颗骰子直至6个结果中有一个结果出现两次，记录投掷的次数。

连续投掷一颗骰子直至6个结果中有一个结果接连出现两次，记录投掷的次数。

连续投掷一枚硬币直至正面出现，观察正反面出现的情况。

抛一枚硬币，若出现H 则再抛一次；若出现T ，则再抛一颗骰子，观察出现的各种结果。

解：（1）}7,6,5,4,3,2{=S ；（2）},4,3,2{ =S ；（3）},,,,{ TTTH TTH TH H S =；（4）}6,5,4,3,2,1,,{T T T T T T HT HH S =。

2，设B A ,是两个事件，已知,125.0)(,5.0)(,25.0)(===AB P B P A P ，求)])([(),(),(),(______AB B A P AB P B A P B A P ⋃⋃。

解：625.0)()()()(=-+=⋃AB P B P A P B A P ，375.0)()(])[()(=-=-=AB P B P B A S P B A P ，875.0)(1)(___--=AB P AB P ，5.0)(625.0)])([()()])([()])([(___=-=⋃-⋃=-⋃=⋃AB P AB B A P B A P AB S B A P AB B A P5，袋中有5只白球，4只红球，3只黑球，在其中任取4只，求下列事件的概率。

（1）4只中恰有2只白球，1只红球，1只黑球。

（2）4只中至少有2只红球。

（3）4只中没有白球。

解: （1）所求概率为338412131425=C C C C ； （2） 所求概率为165674952014124418342824==++C C C C C C ； （3）所求概率为16574953541247==C C 。

8，（1）设,1.0)(,3.0)(,5.0)(===AB P B P A P ，求)|(),|(),|(B A A P A B P B A P ⋃, )|(),|(AB A P B A AB P ⋃.（2）袋中有6只白球，5只红球，每次在袋中任取1只球，若取到白球，放回，并放入1只白球；若取到红球不放回也不放入另外的球。

概率论与数理统计课后习题集及解答第一章 随机事件和概率一. 填空题1. 设A, B, C 为三个事件, 且=-=⋃⋃=⋃)(,97.0)(,9.0)(C AB P C B A P B A P 则____. 解.)(1)(1)()()()(ABC P AB P ABC P AB P ABC AB P C AB P +--=-=-=-=)(C B A P ⋃⋃－)(B A P ⋃= 0.97－0.9 = 0.072. 设10件产品中有4件不合格品, 从中任取两件, 已知所取两件产品中有一件是不合格品, 另一件也是不合格品的概率为_______.解. }{合格品二件产品中有一件是不=A , }{二件都是不合格品=B511)()()()()|(2102621024=-===c c c c A P B P A P AB P A B P 注意: }{合格品二件产品中有一件是不=}{不合格品二件产品中恰有一件是 +}{二件都是不合格品 所以B AB B A =⊃,; }{二件都是合格品=A 3. 随机地向半圆a x ax y (202-<<为正常数)内掷一点, 点落在半圆内任何区域的概率与区域的面积成正比, 则原点和该点的连线与x 轴的夹角小于4π的概率为______. 解. 假设落点(X, Y)为二维随机变量, D 为半圆. 则121)),((2==∈a kD Y X P π, k 为比例系数. 所以22ak π= 假设D 1 = {D 中落点和原点连线与x 轴夹角小于4π的区域}πππ121)2141(2)),((22211+=+=⨯=∈a a a D k D Y X P 的面积. 4. 设随机事件A, B 及其和事件A ⋃B 的概率分别是0.4, 0.3, 0.6, 若B 表示B 的对立事件, 则积事件B A 的概率)(B A P = ______.解. =+-+=)()()()(B A P B P A P AB P 0.4 + 0.3－0.6 = 0.13.01.04.0)()()(=-=-=AB P A P B A P .5. 某市有50%住户订日报, 有65%住户订晚报, 有85%住户至少订这两种报纸中的一种, 则同时订这两种报纸的住户的百分比是________. 解. 假设A = {订日报}, B = {订晚报}, C = A + B. 由已知 P(A) = 0.5, P(B) = 0.65, P(C) = 0.85.所以 P(AB) = P(A) + P(B)－P(A + B) = 0.5 + 0.65－0.85 = 0.3.6. 三台机器相互独立运转, 设第一, 第二, 第三台机器不发生故障的概率依次为0.9, 0.8, 0.7, 则这三台机器中至少有一台发生故障的概率________. 解. 设A i 事件表示第i 台机器运转不发生故障(i = 1, 2, 3). 则 P(A 1) = 0.9, P(A 2) = 0.8, P(A 3) = 0.7,)()()(1)(1)()(321321321321A P A P A P A A A P A A A P A A A P -=-==++ =1－0.9×0.8×0.7=0.496.7. 电路由元件A 与两个并联元件B, C 串联而成, 若A, B, C 损坏与否相互独立, 且它们损坏的概率依次为0.3, 0.2, 0.1, 则电路断路的概率是________. 解. 假设事件A, B, C 表示元件A, B, C 完好.P(A) = 0.7, P(B) = 0.8, P(C) = 0.9. 事件线路完好 = A(B + C) = AB + AC.P(A(B + C) ) = P(AB + AC) = P(AB)+P(AC)－P(ABC) = P(A)P(B) + P(A)P(C)－P(A)P(B)P(C) = 0.7×0.8 +0.7×0.9－0.7×0.8×0.9 = 0.686. 所以 P(电路断路) = 1－0.686 = 0.314.8. 甲乙两人投篮, 命中率分别为0.7, 0.6, 每人投三次, 则甲比乙进球多的概率______. 解. 设X 表示甲进球数, Y 表示乙进球数.P(甲比乙进球多) = P(X = 3, Y = 2) +P(X = 3, Y = 1) + P(X = 3, Y = 0) + P(X = 2, Y = 1) +P(X = 2, Y = 0) + P(X = 1, Y = 0) = P(X = 3)P(Y = 2) +P(X = 3)P(Y = 1) + P(X = 3)P(Y = 0) + P(X = 2)P(Y = 1) +P(X = 2)P(Y = 0) + P(X = 1)P(Y = 0)=+⋅⋅⋅21336.04.07.0c +⋅⋅⋅6.04.07.02233c 334.07.0⋅++⋅⋅⋅⋅⋅2132134.06.07.03.0c c +⋅⋅⋅32134.07.03.0c 32134.03.07.0⋅⋅⋅c= 0.148176 + 0.098784 +0.021952 + 0.127008 + 0.028224 + 0.012096 = 0.43624.9. 三人独立破译一密码, 他们能单独译出的概率分别为41,31,51, 则此密码被译出的概率_____.解. 设A, B, C 表示事件甲, 乙, 丙单独译出密码., 则41)(,31)(,51)(===C P B P A P . P(A + B + C) = P(A) + P(B) + P(C)－P(AB)－P(AC)－P(BC) + P(ABC)= P(A) + P(B) + P(C)－P(A)P(B)－P(A)P(C)－P(B)P(C) + P(A)P(B)P(C) =53413151413141513151413151=⋅⋅+⋅-⋅-⋅-++.二．单项选择题.1. 以A 表示“甲种产品畅销, 乙种产品滞销”, 则对立事件A 为(A) “甲种产品滞销, 乙种产品畅销” (B) “甲、乙产品均畅销”(C) “甲种产品滞销” (D) “甲产品滞销或乙产品畅销” 解. (D)是答案.2. 设A, B, C 是三个事件, 与事件A 互斥的事件是(A) C A B A + (B) )(C B A + (C) ABC (D) C B A ++ 解. ==++C B A A )C B A A(φ, 所以(D)是答案. 3. 设A, B 是任意二个事件, 则(A) P(A ⋃B)P(AB)≥P(A)P(B) (B) P(A ⋃B)P(AB)≤P(A)P(B) (C) P(A －B)P(B －A)≤P(A)P(B)－P(AB) (D)41)()(≥--A B P B A P . 解. P(A + B)P(AB)－P(A)P(B) = (P(A) + P(B)－P(AB))P(AB)－P(A)P(B) =－P(A)(P(B)－P(AB)) + P(AB)(P(B)－P(AB) =－(P(B)－P(AB))(P(A)－P(AB)) =－P(B －A)P(A －B) ≤ 0 所以(B)是答案 .4. 事件A 与B 相互独立的充要条件为(A) A + B = Ω (B) P(AB) = P(A)P(B) (C) AB = φ (D) P(A + B) = P(A) + P(B) 解. (B)是答案.5. 设A, B 为二个事件, 且P(AB) = 0, 则(A) A, B 互斥 (B) AB 是不可能事件 (C) AB 未必是不可能事件 (D) P(A) = 0或P(B) = 0. 解. 概率理论中 P(A) = 0不能推出A 为不可能事件(证明超出大纲要求). 所以(C)是答案. 6. 设A, B 为任意二个事件, 且A ⊂B, P(B) > 0, 则下列选项必然成立的是 (A) P(A) < P(A|B) (B) P(A) ≤ P(A|B) (C) P(A) > P(A|B) (C) P(A) ≥ P(A|B) 解. )()()()()()|(A P B P A P B P AB P B A P ≥==(当B = Ω时等式成立). (B)是答案.7. 已知 0 < P(B) < 1, 且P[(A 1 + A 2)|B] = P(A 1|B) + P(A 2|B), 则下列选项必然成立的是 (A))B |P(A )B |P(A ]B |)A P[(A 2121+=+ (B) P(A 1B +A 2B) = P(A 1B) +P(A 2B)(C) P(A 1 +A 2) = P(A 1|B) +P(A 2|B)(D) P(B) = P(A 1)P(B|A 1) + P(A 2)P(B|A 2)解. 由P[(A 1 + A 2)|B] = P(A 1|B) + P(A 2|B)得到)()()()()(])[(2121B P B A P B P B A P B P B A A P +=+, 所以P(A 1B +A 2B) = P(A 1B) +P(A 2B). (B)是答案.三. 计算题1. 某厂生产的产品次品率为0.05, 每100个产品为一批, 抽查产品质量时, 在每批中任取一半来检查, 如果发现次品不多于1个, 则这批产品可以认为合格的, 求一批产品被认为是合格的概率.解. P(该批产品合格) = P(全部正品) + P(恰有1个次品)=2794.050100154995*********=+c cc c c2. 书架上按任意次序摆着15本教科书, 其中有5本是数学书, 从中随机地抽取3本, 至少有一本是数学书的概率.解. 假设A={至少有一本数学书}. A ={没有数学书}P(A ) =9124315310=c c , P(A) = 1－P(A ) = 91673. 全年级100名学生中有男生80名, 来自北京的20名中有男生12名. 免修英语的40名学生中有男生32名, 求出下列概率: i. 碰到男生情况不是北京男生的概率;ii. 碰到北京来的学生情况下是一名男生的概率; iii. 碰到北京男生的概率;iv. 碰到非北京学生情况下是一名女生的概率; v. 碰到免修英语的男生的概率.解. 学生情况: 男生 女生 北京 12 8 免修英语 32 8 总数 80 20i. P(不是北京|男生) =20178068=ii. P(男生|北京学生) =532012=iii. P(北京男生) =10012iv. P(女生|非北京学生) =8012v. P(免修英语男生) =100324． 袋中有12个球, 其中9个是新的, 第一次比赛时从中取3个, 比赛后任放回袋中, 第二次比赛再从袋中任取3个球, 求: i. 第二次取出的球都是新球的概率;ii. 又已知第二次取出的球都是新球, 第一次取到的都是新球的概率.解. i. 设B i 表示第一次比赛抽到i 个新球(i = 0, 1, 2, 3). A 表示第二次比赛都是新球. 于是312339)(c c c B P i i i -=, 31239)|(c c B A P i i -=)()(1)()|()()(3603393713293823193933092312323123933930c c c c c c c c c c c c c c c c c B A P B P A P i i i i i i i +++===∑∑=--=146.0484007056)201843533656398411()220(12==⨯⨯+⨯⨯+⨯⨯+⨯⨯=ii. 215484007056)220(20184)()()|()|(2333=⨯⨯==A P B P B A P A B P5. 设甲、乙两袋, 甲袋中有n 个白球, m 个红球, 乙袋中有N 个白球, M 个红球, 今从甲袋中任取一只放入乙袋, 再从乙袋中任取一球, 问取到白球的概率. 解. 球的情况: 白球 红球 甲袋 n m 乙袋 N M假设 A = {先从甲袋中任取一球为白球} B = {先从甲袋中任取一球为红球} C = {再从乙袋中任取一球为白球} P(C) = P(C|A)P(A) + P(C|B)P(B)nm mM N N m n n M N N +⋅++++⋅+++=111 ))(1()1(n m M N NmN n +++++=第二章 随机变量及其分布一. 填空题1. 设随机变量X ～B(2, p), Y ～B(3, p), 若P(X ≥ 1) =95, 则P(Y ≥ 1) = _________. 解. 94951)1(1)0(=-=≥-==X P X P 94)1(2=-p , 31=p 2719321)0(1)1(3=⎪⎭⎫⎝⎛-==-=≥Y P Y P2. 已知随机变量X 只能取－1, 0, 1, 2四个数值, 其相应的概率依次为cc c c 162,85,43,21, 则c = ______. 解. 2,16321628543211==+++=c cc c c c 3. 用随机变量X 的分布函数F(x)表示下述概率:P(X ≤ a) = ________. P(X = a) = ________.P(X > a) = ________. P(x 1 < X ≤ x 2) = ________.解. P(X ≤ a) = F(a) P(X = a) = P(X ≤ a)－P(X < a) = F(a)－F(a －0) P(X > a) = 1－F(a) P(x 1 < X ≤ x 2) = F(x 2)－F(x 1)4. 设k 在(0, 5)上服从均匀分布, 则02442=+++k kx x 有实根的概率为_____.解. k 的分布密度为⎪⎩⎪⎨⎧=051)(k f 其它50≤≤kP{02442=+++k kx x 有实根} = P{03216162≥--k k } = P{k ≤－1或k ≥ 2} =535152=⎰dk 5. 已知2}{,}{kbk Y P k a k X P =-===(k = 1, 2, 3), X 与Y 独立, 则a = ____, b = ____, 联合概率分布_____, Z = X + Y 的概率分布为_____. 解. 116,132==++a a a a . 4936,194==++b b b b(X, Y)的联合分布为ab = 216α, 539=α α249)3()1()3,1()2(==-===-===-=abY P X P Y X P Z P α66)2,1()3,2()1(=-==+-===-=Y X P Y X P Z Pα251)1,1()2,2()3,3()0(=-==+-==+-====Y X P Y X P Y X P Z P α126)2,3()1,2()1(=-==+-====Y X P Y X P Z Pα723)1()3()1,3()2(==-===-====abY P X P Y X P Z P6. 已知(X, Y)联合密度为⎩⎨⎧+=0)sin(),(y x c y x ϕ 其它4,0π≤≤y x , 则c = ______, Y 的边缘概率密度=)(y Y ϕ______.解.12,1)sin(4/04/0+==+⎰⎰c dxdy y x c ππ所以⎩⎨⎧++=0)sin()12(),(y x y x ϕ 其它4,0π≤≤y x当 40π≤≤y 时))4cos()(cos 12()sin()12(),()(4y y dx y x dx y x y Y +-+=++==⎰⎰∞+∞-πϕϕπ所以⎪⎩⎪⎨⎧+-+=0))4cos()(cos 12()(y y y Y πϕ 其它40π≤≤y7. 设平面区域D 由曲线2,1,01e x x y xy ====及直线围成, 二维随机变量(X, Y)在D 上服从均匀分布, 则(X, Y)关于X 的边缘密度在x = 2处的值为_______. 解. D 的面积 =2121=⎰e dx x. 所以二维随机变量(X, Y)的密度为: ⎪⎩⎪⎨⎧=021),(y x ϕ 其它D y x ∈),(下面求X 的边沿密度:当x < 1或x > e 2时 0)(=x X ϕ 当1 ≤ x ≤ e 2时 ⎰⎰===∞+∞-x X x dy dy y x x 102121),()(ϕϕ, 所以41)2(=X ϕ. 8. 若X 1, X 2, …, X n 是正态总体N(μ, σ2)的一组简单随机样本, 则)(121n X X X nX +++=服从______. 解. 独立正态分布随机变量的线性函数服从正态分布.μ==⎪⎭⎫ ⎝⎛∑∑==n i i n i i X E n X n E 11)(11, nX D nX n D ni in i i 2121)(11σ==⎪⎭⎫ ⎝⎛∑∑==所以 ),(~2nN X σμ9. 如果(X, Y)的联合分布用下列表格给出,且X 与Y 相互独立, 则α = ______, β = _______.解.213161)1(,18)3(,9)2(,31)2(=+==+==+==++==Y P Y P Y P X P βαβα 132)3()2()1(=++==+=+=βαY P Y P Y P⎪⎪⎩⎪⎪⎨⎧+++=======+++=======)181)(31()3()2()3,2()91)(31()2()2()2,2(ββαβαβααY P X P Y X P Y P X P Y X P两式相除得βαβα=++18191, 解得 βα2=, 92,91==αβ.10. 设(X, Y)的联合分布律为3122 0 122 则 i. Z = X + Y 的分布律 ______. ii. V = X －Y 的分布律______.iii. U= X 2 + Y －2的分布律_______. 解.二. 单项选择题1. 如下四个函数哪个是随机变量X 的分布函数(A)⎪⎪⎩⎪⎪⎨⎧=221)(x F 0022≥<≤--<x x x , (B) ⎪⎩⎪⎨⎧=1sin 0)(x x F ππ≥<≤<x x x 00(C) ⎪⎩⎪⎨⎧=1sin 0)(x x F 2/2/00ππ≥<≤<x x x , (D) ⎪⎪⎩⎪⎪⎨⎧+=1310)(x x F 212100≥<≤<x x x解. (A)不满足F(+∞) = 1, 排除(A); (B)不满足单增, 排除(B); (D)不满足F(1/2 + 0) = F(1/2), 排除(D); (C)是答案. 2. ),4,2,0(!/)( ===-k k ec k X P kλλ是随机变量X 的概率分布, 则λ, c 一定满足(A) λ > 0 (B) c > 0 (C) c λ > 0 (D) c > 0, 且 λ > 0 解. 因为),4,2,0(!/)( ===-k k ec k X P kλλ, 所以c > 0. 而k 为偶数, 所以λ可以为负.所以(B)是答案.3. X ～N(1, 1), 概率密度为ϕ(x), 则(A)5.0)0()0(=≥=≤X P X p (B)),(),()(+∞-∞∈-=x x x ϕϕ (C) 5.0)1()1(=≥=≤X P X p (D) ),(),(1)(+∞-∞∈--=x x F x F 解. 因为E(X) = μ = 1, 所以5.0)1()1(=≥=≤X P X p . (C)是答案.4. X, Y 相互独立, 且都服从区间[0, 1]上的均匀分布, 则服从区间或区域上的均匀分布的随机变量是(A) (X, Y) (B) X + Y (C) X 2 (D) X －Y 解. X ～⎩⎨⎧=01)(x ϕ其它10≤≤x , Y ～⎩⎨⎧=01)(y ϕ其它10≤≤y . 所以(X, Y)～⎩⎨⎧=01),(y x ϕ其它1,0≤≤y x .所以(A)是答案.5. 设函数⎪⎪⎩⎪⎪⎨⎧=120)(xx F 1100>≤<≤x x x 则(A) F(x)是随机变量X 的分布函数. (B) 不是分布函数.(C) 离散型分布函数. (D)连续型分布函数.解. 因为不满足F(1 + 0) = F(1), 所以F(x)不是分布函数, (B)是答案.6. 设X, Y 是相互独立的两个随机变量, 它们的分布函数为)(),(y F x F Y X , 则Z = max(X, Y)的分布函数是(A) )(z F Z = max{)(),(z F z F Y X } (B) )(z F Z = max{|)(||,)(|z F z F Y X } (C) )(z F Z = )()(z F z F Y X (D) 都不是解. }{}),{m ax ()()(z Y z X P z Y X P z Z P z F Z ≤≤=≤=≤=且 )()()()(z F z F z Y P z X P Y X =≤≤因为独立. (C)是答案.7. 设X, Y 是相互独立的两个随机变量, 其分布函数分别为)(),(y F x F Y X , 则Z = min(X, Y)的分布函数是(A) )(z F Z = )(z F X (B) )(z F Z = )(z F Y(C) )(z F Z = min{)(),(z F z F Y X } (D) )(z F Z = 1－[1－)(z F X ][1－)(z F Y ] 解. }{1}),{m in(1)(1)()(z Y z X P z Y X P z Z P z Z P z F Z >>-=>-=>-=≤=且 )](1)][(1[1)](1)][(1[1z F z F z Y P z X P Y X ---=≤-≤--因为独立 (D)是答案.8. 设X 的密度函数为)(x ϕ, 而,)1(1)(2x x +=πϕ 则Y = 2X 的概率密度是 (A))41(12y +π (B) )4(22y +π (C) )1(12y +π (D)y arctan 1π解. )2()2(}2{)()(y F y X P y X P y Y P y F X Y =≤=≤=≤= )4(2)2(112121)2()2()]([)(22''y y y y F y F y X X Y Y +=⎪⎭⎫ ⎝⎛+⋅=⋅=⎪⎭⎫ ⎝⎛==ππϕϕ (B)是答案.9. 设随机变量(X, Y)的联合分布函数为⎩⎨⎧=+-0),()(y x e y x ϕ 其它0,0>>y x , 则2YX Z +=的分布密度是(A) ⎪⎩⎪⎨⎧=+-021)()(y x Z e Z ϕ 其它0,0>>y x (B) ⎪⎩⎪⎨⎧=+-0)(2y x Z e z ϕ 其它0,0>>y x(C) ⎩⎨⎧=-04)(2z Z ze Z ϕ 00≤>z z (D) ⎪⎩⎪⎨⎧=-021)(zZ eZ ϕ 00≤>z z解. 2YX Z +=是一维随机变量, 密度函数是一元函数, 排除(A), (B). 21210=⎰∞+-dz e z , 所以(D)不是答案. (C)是答案.注: 排除法做单项选择题是经常使用而且很有效的方法. 该题也可直接计算Z 的密度: 当z < 0时0)(=z F Z当z ≥ 0时⎰⎰≤+=≤+=≤+=≤=zy x Z dxdy y x z Y X P z YX P z Z P z F 2),()2()2()()(ϕ =12222020+--=⎥⎦⎤⎢⎣⎡-----⎰⎰z z z xz y x e ze dx dy e e ==)()('z F z ZZ ϕ⎩⎨⎧-042z ze 00≤>z z , (C)是答案.10. 设两个相互独立的随机变量X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 则下列结论正确的是(A) P{X + Y ≤ 0} = 1/2 (B) P{X + Y ≤ 1} = 1/2 (C) P{X －Y ≤ 0} = 1/2 (D) P{X －Y ≤ 1} = 1/2解. 因为X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 且X 和 Y 相互独立, 所以 X + Y ～ N(1, 2), X －Y ～ N(－1, 2) 于是P{X + Y ≤ 1} = 1/2, (B)是答案.11. 设随机变量X 服从指数分布, 则Y = min{X, 2}的分布函数是(A) 是连续函数 (B) 至少有两个间断点 (C) 是阶梯函数 (D) 恰好有一个间断点 解. 分布函数:))2,(m in(1))2,(m in()()(y X P y X P y Y P y F Y >-=≤=≤= 当y ≥ 2时101))2,(m in(1)(=-=>-=y X P y F Y 当0 ≤ y < 2时)2,(1))2,(m in(1)(y y X y X P y F Y >>-=>-= ye y X P y X P λ--=≤=>-=1)()(1当y < 0时)2,(1))2,(m in(1)(y y X y X P y F Y >>-=>-= 0)()(1=≤=>-=y X P y X P于是 ⎪⎩⎪⎨⎧-=-011)(yY e y F λ 0202<<≤≥y y y 只有y = 2一个间断点, (D)是答案.三. 计算题1. 某射手有5发子弹, 射击一次的命中率为0.9, 如果他命中目标就停止射击, 不命中就一直到用完5发子弹, 求所用子弹数X 的分布密度. 解. 假设X 表示所用子弹数. X = 1, 2, 3, 4, 5.P(X = i) = P(前i －1次不中, 第i 次命中) = 9.0)1.0(1⋅-i , i = 1, 2, 3, 4.当i = 5时, 只要前四次不中, 无论第五次中与不中, 都要结束射击(因为只有五发子弹). 所以 P(X = 5) = 4)1.0(. 于是分布律为2. 设一批产品中有10件正品, 3件次品, 现一件一件地随机取出, 分别求出在下列各情形中直到取得正品为止所需次数X 的分布密度.i. 每次取出的产品不放回; ii. 每次取出的产品经检验后放回, 再抽取; iii. 每次取出一件产品后总以一件正品放回, 再抽取.解. 假设A i 表示第i 次取出正品(i = 1, 2, 3, …) i.1310)()1(1===A P X P 1331210)()|()()2(11212⋅====A P A A P A A P X P 1331221110)()|()|()()3(11223321⋅⋅====A P A A P A A P A A A P X P 1331221111)()|()|()|()4(1122334⋅⋅⋅===A P A A P A A P A A P X Pii. 每次抽取后将原产品放回1310133)()()()()(11111---⎪⎭⎫⎝⎛====k k k k k A P A P A P A A A p k X P , (k = 1, 2, …)iii.13)()1(1===A P X P 1331311)()|()()2(11212⋅====A P A A P A A P X P1331321312)()|()|()()3(112123321⋅⋅====A P A A P A A A P A A A P X P 1331321311)()|()|()|()4(1121231234⋅⋅⋅===A P A A P A A A P A A A A P X P3. 随机变量X 的密度为⎪⎩⎪⎨⎧-=01)(2x cx ϕ 其它1||<x , 求: i. 常数c; ii. X 落在)21,21(-内的概率. 解. πππϕ1,22|arcsin 21)(110112====-==⎰⎰-∞+∞-c c c x c dx xc dx x3162|arcsin 211))2/1,2/1((2/102/12/12=⋅==-=-∈⎰-ππππx x dx X P 4. 随机变量X 分布密度为i. 2102)(x x -⎪⎩⎪⎨⎧=πϕ 其它1||<x , ii. ⎪⎩⎪⎨⎧-=02)(x x x ϕ 其它2110≤≤<≤x x求i., ii 的分布函数F(x).解. i. 当x ≤ 1时 ⎰⎰∞-∞-===x xdt dt t x F 00)()(ϕ当－1< x < 1时 ⎰⎰∞--++-=-==x x x x xdt t dt t x F 21arcsin 1112)()(212πππϕ 当x ≥ 1时 ⎰⎰∞--=-==x dt t dt t x F 112)()(112πϕ所以 ⎪⎪⎩⎪⎪⎨⎧++-=121arcsin 110)(2x x xx F ππ 1111≥<<--≤x x xii. 当x < 0时 ⎰⎰∞-∞-===x xdt dt t x F 00)()(ϕ当0 ≤ x < 1时 ⎰⎰∞-===x x x tdt dt t x F 2)()(2ϕ当1 ≤ x < 2时 122)2()()(2110-+-=-+==⎰⎰⎰∞-x x dt t tdt dt t x F x x ϕ当2 ≤ x 时 1)2()()(2110⎰⎰⎰∞-=-+==x dt t tdt dt t x F ϕ所以 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+-=112220)(22x x x x F 221100≥<≤<≤<x x x x5. 设测量从某地到某一目标的距离时带有的随机误差X 具有分布密度函数⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, －∞ < x < +∞试求: i. 测量误差的绝对值不超过30的概率;ii. 接连独立测量三次, 至少有一次误差的绝对值不超过30的概率.解. 因为⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, －∞ < x < +∞, 所以X ～N(20, 402). i. {}⎭⎬⎫⎩⎨⎧<-<-=<<-=<25.0402025.13030)30|(|X P X P X P )25.1()25.0(-Φ-Φ=1)25.1()25.0()25.1(1()25.0(-Φ+Φ=Φ--Φ= 18944.05987.0-+== 0.4931.(其中Φ(x)为N(0, 1)的分布函数)ii. P(至少有一次误差的绝对值不超过30) = 1－P(三次误差的绝对值都超过30) =88.012.01)4931.0(13=-=- 6. 设电子元件的寿命X 具有密度为⎪⎩⎪⎨⎧=0100)(2x x ϕ 100100≤<x x问在150小时内, i. 三只元件中没有一只损坏的概率是多少? ii. 三只电子元件全损坏的概率是多少? iii. 只有一个电子元件损坏的概率是多少?解. X 的密度⎪⎩⎪⎨⎧=0100)(2x x ϕ 100100≤<x x . 所以31100)150(1501002==<⎰dx x X P . 令p = P(X ≥ 150) = 1－31= 32.i. P(150小时内三只元件没有一只损坏) =2783=p ii. P(150小时内三只元件全部损坏) =271)1(3=-piii. P(150小时内三只元件只有一只损坏) =943231213=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛c 7. 对圆片直径进行测量, 其值在[5, 6]上服从均匀分布, 求圆片面积的概率分布.解. 直径D 的分布密度为⎩⎨⎧=01)(d ϕ 其它65≤≤d假设42D X π=, X 的分布函数为F(x).)()()(2x D P x X P x F ≤=≤=π当x ≤ 0时, F(x) = 0 当x > 0时⎭⎬⎫⎩⎨⎧≤≤-=≤=≤=πππx D xP x D P x X P x F 44)()()(2 当时即425,54ππ<<x xF(x) = 0 当时即πππ925,645≤≤≤≤x x⎭⎬⎫⎩⎨⎧≤≤-=≤=≤=πππx D xP x D P x X P x F 44)()()(2 =54145-=⎰ππxdt x当 x > 9π时 1)()(65===⎰⎰∞-dt dt t x F x ϕ所以 ⎪⎪⎩⎪⎪⎨⎧-=1540)(πxx F ππππ99425425>≤≤<x x x 密度⎪⎩⎪⎨⎧==01)(')(x x F x πϕ 其它ππ9425≤≤x8. 已知X 服从参数 p = 0.6的0－1分布在X = 0, X = 1下, 关于Y 的条件分布分别为表1、表2所示表1 表2Y 1 2 3 Y 1 2 3 P(Y|X = 0)41 21 41 P(Y|X = 1) 21 61 31 求(X, Y)的联合概率分布, 以及在Y ≠ 1时, 关于X 的条件分布.解. X 的分布律为(X, Y)3.05321)1()1|1()1,1(=⋅=======X P X Y P Y X P 1.05361)1()1|2()2,1(=⋅=======X P X Y P Y X P2.05331)1()1|3()3,1(=⋅=======X P X Y P Y X P1.05241)0()0|1()1,0(=⋅=======X P X Y P Y X P2.05221)0()0|2()2,0(=⋅=======X P X Y P Y X P1.05241)0()0|3()3,0(=⋅=======X P X Y P Y X P所以Y 的分布律为5.06.03.0)1()1,0()1|0(==≠≠==≠=Y P Y X P Y X P5.06.03.0)1()1,1()1|1(==≠≠==≠=Y P Y X P Y X P所以9. 设随机变量X 与Y 相互独立, 并在区间[0, 9]上服从均匀分布, 求随机变量YXZ =的分布密度.解. X ～⎪⎩⎪⎨⎧=091)(x X ϕ 其它90≤≤x , Y ～⎪⎩⎪⎨⎧=091)(x Y ϕ 其它90≤≤y因为X, Y 相互独立, 所以(X, Y)联合密度为(X, Y)～⎪⎩⎪⎨⎧=0811),(y x ϕ 其它9,0≤≤y x , )()()(z X Y P z Z P z F Z ≤=≤=当 z ≤ 0时0)(=z F Z 当 0 < z < 1时D 1z z dxdy Xz Y P z X Y P z Z P z F D Z 219921811811)()()()(1=⋅⋅==≤=≤=≤=⎰⎰ 当z ≥ 1时⎰⎰=≤=≤=≤=2811)()()()(D Z dxdy Xz Y P z X Y P z Z P z F zz 211)992181(811-=⋅-⋅=所以 ⎪⎪⎩⎪⎪⎨⎧==2'21210)()(zz F z Z Z ϕ 1100≥<<≤z z z 10. 设(X, Y)的密度为⎩⎨⎧--=0)1(24),(y x y y x ϕ 其它1,0,0<+>>y x y x 求: i.)21|(),|(),(=x y x y x X ϕϕϕ, ii. )21|(),|(),(=y x y x y Y ϕϕϕ 解. i.⎰∞+∞-=dy y x x X ),()(ϕϕ当x ≤ 0 或 x ≥ 1时0),()(==⎰∞+∞-dy y x x X ϕϕ当0 < x < 1时310)1(4)1(24),()(x dy y x y dy y x x x X -=--==⎰⎰-∞+∞-ϕϕ所以 ⎩⎨⎧-=0)1(4)(3x x X ϕ 其它10<<x所以 ⎪⎩⎪⎨⎧---==0)1()1(6)(),()|(3x y x y x y x x y X ϕϕϕ 其它1,0,0<+>>y x y x 所以 ⎩⎨⎧-==0)21(24)21|(y y x y ϕ 其它210<<yii.⎰∞+∞-=dx y x y Y ),()(ϕϕ当y ≤ 0 或 y ≥ 1时0),()(==⎰∞+∞-dx y x y Y ϕϕ当0 < y < 1时210)1(12)1(24),()(y y dx y x y dx y x y y Y -=--==⎰⎰-∞+∞-ϕϕ所以 ⎩⎨⎧-=0)1(12)(2y y y Y ϕ 其它10<<y所以 ⎪⎩⎪⎨⎧---==0)1()1(2)(),()|(2y y x y y x y x Y ϕϕϕ其它1,0,0<+>>y x y x所以 ⎩⎨⎧-==0)21(4)21|(x y x ϕ 其它210<<x第三章 随机变量的数字特征一. 填空题1. 设随机变量X 与Y 相互独立, D(X) = 2, D(Y) = 4, D(2X －Y) = _______. 解. D(2X －Y) = 4D(X) + D(Y) = 122. 已知随机变量X ～N(－3, 1), Y ～N(2, 1 ), 且X 与Y 相互独立, Z = X －2Y + 7, 则Z ～____. 解. 因为Z = X －2Y + 7, 所以Z 服从正态分布. E(Z) = E(X)－2E(Y) + 7 = 0. D(Z) = D(X －2Y + 7) = D(X) + 4D(Y) = 1+4 = 5. 所以Z ～N(0, 5)3. 投掷n 枚骰子, 则出现点数之和的数学期望______. 解. 假设X i 表示第i 颗骰子的点数(i = 1, 2, …, n). 则 E(X i ) = 27616612611=⋅++⋅+⋅(i = 1, 2, …, n) 又设∑==ni i X X 1, 则27)()()(11nX E X E X E ni i ni i ===∑∑== 4. 设离散型随机变量X 的取值是在两次独立试验中事件A 发生的次数, 如果在这些试验中事件发生的概率相同, 并且已知E(X) = 0.9, 则D(X) = ______. 解. ),2(~p B X , 所以E(X) = 0.9 = 2p. p = 0.45, q = 0.55 D(X) = 2pq = 2×0.45×0.55 = 0.495.5. 设随机变量X 在区间[－1, 2]上服从均匀分布, 随机变量⎪⎩⎪⎨⎧-=101Y 000<=>X X X , 则方差D(Y) = _______.解. X ～⎪⎩⎪⎨⎧=031)(x ϕ 其它21≤≤-xY因为 33)0()1(20==>==⎰dx X P Y P 0)0()0(====X P Y P3131)0()1(01==<=-=⎰-dx X P Y P于是 313132)(=-=Y E , 13132)(2=+=Y E , 98)]([)()(22=-=Y E Y E Y D6. 若随机变量X 1, X 2, X 3相互独立, 且服从相同的两点分布⎪⎪⎭⎫ ⎝⎛2.08.010, 则∑==31i i X X 服从_______分布, E(X) = _______, D(X) = ________.解. X 服从B(3, 0.2). 所以E(X) = 3p = 3×0.2= 0.6, D(X) = 3pq = 3×0.2×0.8 = 0.487. 设X 和Y 是两个相互独立的随机变量, 且X ～N(0, 1), Y 在[－1, 1]上服从均匀分布, 则),cov(Y X = _______.解. 因为X 和Y 是两个相互独立的随机变量, 所以),cov(Y X = 0.8. 设X 和Y 是两个相互独立的随机变量, 其概率密度分别为:⎩⎨⎧=02)(x x ϕ 其它10≤≤x , ⎩⎨⎧=--0)()5(y e y ϕ 其它5>y , 则E(XY) = ________. 解. 322)()(1=⋅==⎰⎰∞+∞-xdx x dx x x X E ϕ 6)()(5)5(=⋅==⎰⎰∞+--∞+∞-dy e y dy y y Y E y ϕ因为X 和Y 是两个相互独立的随机变量, 所以E(XY) = E(X)E(Y) = 49. 若随机变量X 1, X 2, X 3相互独立, 其中X 1在[0, 6]服从均匀分布, X 2服从正态分布N(0, 22), X 3服从参数λ = 3的泊松分布, 记Y = X 1－2X 2 + 3X 3, 则D(Y) = ______. 解. )(9)(4)()32()(321321X D X D X D X X X D Y D ++=+-==4639441262=⨯+⨯+二. 单项选择题1. 设随机变量X 和Y 独立同分布, 记U = X －Y , V = X + Y , 则U 和V 必然 (A) 不独立 (B) 独立 (C) 相关系数不为零 (D) 相关系数为零 解. 因为X 和Y 同分布, 所以E(U) = E(X)－E(Y) = 0, E(U)E(V) = 0. 0)()()(22=-=Y E X E UV E .所以 cov(X,Y) = E(UV)－E(U)E(V) = 0. (D)是答案. 2. 已知X 和Y 的联合分布如下表所示, 则有(A) X 与Y 不独立 (B) X 与Y 独立 (C) X 与Y 不相关 (D) X 与Y 彼此独立且相关 解. P(X = 0) = 0.4, P(Y = 0) = 0.3.0.1 = P(X = 0, Y= 0) ≠ P(X = 0)×P(Y = 0). (A)是答案.3. 设离散型随机变量X 可能取值为: x 1 = 1, x 2 = 2, x 3 = 3, 且E(X) = 2.3, E(X 2) = 5.9, 则x 1, x 2, x 3所对应的概率为(A) p 1 = 0.1, p 2 = 0.2, p 3 = 0.7 (B) p 1 = 0.2, p 2 = 0.3, p 3 = 0.5 (C) p 1 = 0.3, p 2 = 0.5, p 3 = 0.2 (D) p 1 = 0.2, p 2 = 0.5, p 3 = 0.3解. 3.223)1(32)(212121332211=--=--++=++=p p p p p p p x p x p x X E 7.0221=+p p9.5)1(94)(21213232221212=--++=++=p p p p p x p x p x X E 1.35821=+p p解得 p 1 = 0.2, p 2 = 0.3, p 3 = 0.5. (B)是答案.4. 现有10张奖券, 其中8张为2元, 2张为5元, 今每人从中随机地无放回地抽取3张, 则此人抽得奖券的金额的数学期望(A) 6 (B) 12 (C) 7.8 (D) 9解. 假设X 表示随机地无放回地抽取3张, 抽得奖券的金额. X 的分布律为157)()6(31038====c c P X P 三张都是二元157),()9(3101228====c c c P X P 一张五元二张二元151),()9(3102218====c c c P X P 二张五元一张二元8.71511215791576)(=⋅+⋅+⋅=X E . (C)是答案. 5. 设随机变量X 和Y 服从正态分布, X ～N(μ, 42), Y ～N(μ, 52), 记P 1 =P{X ≤ μ－4}, P 2 = P{Y≥ μ + 5}, 则(A) 对任何μ, 都有P 1 = P 2 (B) 对任何实数μ, 都有P 1 < P 2 (C) 只有μ的个别值, 才有P 1 = P 2 (D) 对任何实数μ, 都有P 1 > P 2 解. P 1 = {X ≤ μ－4} =)1(1)1(14Φ-=-Φ=⎭⎬⎫⎩⎨⎧-≤-μX PP 2 = {Y ≥ μ + 5} =)1(115115Φ-=⎭⎬⎫⎩⎨⎧≤--=⎭⎬⎫⎩⎨⎧≥-μμY P Y P(其中Φ(x)为N(0, 1)的分布函数). 所以(A)是答案.6. 随机变量ξ = X + Y 与η = X －Y 不相关的充分必要条件为(A) E(X) = E(Y) (B) E(X 2)－E 2(X) = E(Y 2)－E 2(Y) (C) E(X 2) = E(Y 2) (D) E(X 2) + E 2(X) = E(Y 2) + E 2(Y) 解. cov(ξ, η) = E(ξη)－E(ξ)E(η)E(ξη) =)()()])([(22Y E X E Y X Y X E -=-+ E(ξ)E(η) = [E(X)+E(Y)][E(X)－E(Y)] = )()(22Y E X E - 所以(B)是答案.三. 计算题1. 设X 的分布律为1)1()(++==k ka a k X P , k = 0, 1, 2, …, a > 0, 试求E(X), D(X).解. ∑∑∑∞=+∞=+∞=⎪⎭⎫⎝⎛+=+===1111011)1()()(k k k k k k a a k a a ka k X kP X E令 22'2'1211201)1(1)(x x x x x x x kx x kxx f k k k k k k -=⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛===∑∑∑∞=∞=-∞=+ 2222)11()1()1(a aa a a a a f =+-+=+, 所以a a a X E =⋅=21)(.∑∑∑∞=+∞=+∞=+-+=+===11112022)1()11()1()()(k k kk k k k a a k k a a k k X P k X E∑∑∑∞=∞=+∞=+-+++=+-++=11111)1()1(11)1()1()1(k kkk k k k k k a a a k k a a a k a a k k 令 3''2''1111)1(21)1()1()(x x x x x x x kx k x kxk x f k k k k k k-=⎪⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=+=+=∑∑∑∞=+∞=-∞= 23)1(2)11(12)1(a a a a a aa a f +=+-+=+,所以2222)1(211)(a a a a a aX E +=-+⋅+=.222222)]([)()(a a a a a X E X E X D +=-+=-=.2. 设随机变量X 具有概率密度为⎪⎩⎪⎨⎧=0cos 2)(2xx πϕ 其它2||π≤x , 求E(X), D(X).解. 0cos 2)()(222===⎰⎰-∞+∞-πππϕxdx xdx x x X E⎰-=-=222222cos 2)]([)()(πππxdx x X E X E X D211222cos 122222-=+=⎰πππdx x x 3.求⎥⎦⎤⎢⎣⎡+2)(sin Y X E π. 解. 2)(sinY X +π的分布律为 25.015.0)1(40.0145.002)(sin =⨯-+⨯+⨯=⎥⎦⎤⎢⎣⎡+Y X E π 4. 一汽车沿一街道行驶需要通过三个设有红绿信号灯路口, 每个信号灯为红或绿与其它信号灯为红或绿相互独立, 且红绿两种信号显示的时间相等, 以X 表示该汽车首次遇到红灯前已通过的路口的个数, 求: i. X 的概率分布, ii. ⎪⎭⎫⎝⎛+XE 11 解. 假设X 为该汽车首次遇到红灯已通过的路口数P(X = 0) = P{第一个路口为红灯} =2P(X = 1) = P{第一个路口为绿灯, 第二个路口为红灯} =2212121=⋅ P(X = 0) = P{第一,二路口为绿灯, 第三个路口为红灯} =321P(X = 0) = P{第一, 二, 三路口为绿灯} =3219667214121312121211111332=⋅+⋅+⋅+⋅=⎪⎭⎫⎝⎛+X E 5. 设(X, Y)的分布密度⎩⎨⎧=+-04),()(22y xxye y x ϕ其它0,0>>y x求)(22Y X E +. 解. ⎰⎰⎰⎰>>+-∞+∞-∞+∞-+=+=+00)(222222224),()(y x y xdxdy xye y x dxdy y x y x Y X E ϕ434sin cos 02202πθθθπ=⋅⋅⋅⋅=⎰⎰∞+-rdr e r r d r 6. 在长为l 的线段上任选两点, 求两点间距离的数学期望与方差.解. 假设X, Y 为线段上的两点. 则它们都服从[0, l ]上的均匀分布, 且它们相互独立.X ～⎪⎩⎪⎨⎧=01)(l x ϕ 其它l x ≤≤0, Y ～⎪⎩⎪⎨⎧=01)(l y ϕ 其它l y ≤≤0(X, Y)的联合分布为⎪⎩⎪⎨⎧=01)(2l x ϕ 其它l y x ≤≤,0.又设Z = |X －Y|, D 1={(x, y): x > y, 0 ≤ x, y ≤ l }, D 2={(x, y): x ≤ y, 0 ≤ x, y ≤ l }⎰⎰⎰⎰⎰⎰-+-=-=∞+∞-∞+∞-21221)(1)(),(||)(D D dxdy l x y dxdy l y x dxdy y x y x Z E ϕ⎰⎰⎰⎰-+-=l y lxdy dx x y l dx dy y x l2002])([1])([13212122022ldy y l dx x ll l=+=⎰⎰ 6)(1),()()(2002222l dxdy y x ldxdy y x y x Z E ly lx =-=-=⎰⎰⎰⎰∞+∞-∞+∞-≤≤≤≤ϕ 1896)]([)()(22222l l l Z E Z E Z D =-=-=7. 设随机变量X 的分布密度为)(,21)(||+∞<<-∞=--x e x x μϕ, 求E(X), D(X). 解. ⎰⎰⎰∞+∞--∞+∞---∞+∞-+-===dt e t x t dx e x dx x x X E t x ||||)(2121)()(μμϕμ=⎰∞+∞--dt te t ||21+μμμ==⎰⎰∞+-∞+∞--0||21dt e dt e tt⎰⎰⎰∞+∞--∞+∞---∞+∞-+-===dt e t x t dx e x dx x x X E t x ||2||222)(2121)()(μμϕμ=⎰∞+-02dt e t t+20022μμμ+==⎰⎰∞+-∞+-dt e dt e t t所以 22)]([)()(2222=-+=-=μμX E X E X D8. 设(X, Y)的联合密度为⎪⎩⎪⎨⎧=01),(πϕy x 其它122≤+y x , 求E(X), D(Y), ρ(X, Y).解. 01),()(122===⎰⎰⎰⎰+∞∞-+∞∞-≤+y x xdxdy dxdy y x x X E πϕ01),()(122===⎰⎰⎰⎰+∞∞-+∞∞-≤+y x ydxdy dxdy y x y Y E πϕ41cos 11),()(20132122222====⎰⎰⎰⎰⎰⎰∞+∞-∞+∞-≤+πθθππϕdr r d dxdy x dxdy y x x X E y x 41sin 11),()(20132122222====⎰⎰⎰⎰⎰⎰∞+∞-∞+∞-≤+πθθππϕdr r d dxdy y dxdy y x y Y E y x 01),()(122===⎰⎰⎰⎰∞+∞-∞+∞-≤+y x xydxdy dxdy y x xy XY E πϕ41)]([)()(22=-=X E X E X D , 41)]([)()(22=-=Y E Y E Y D0)()()()()(=-=Y D X D Y E X E XY E XY ρ.9. 假设一部机器在一天内发生故障的概率为0.2, 机器发生故障时全天停止工作. 若一周5个工作日里无故障, 可获利润10万元, 发生一次故障仍可获利润5万元; 发生二次故障所获利润0元; 发生三次或三次以上故障就要亏损2万元. 求一周内期望利润是多少? 解. 假设X 表示一周内发生故障的天数. 则X ～B(5, 0.8)33.0)8.0()0(5===X P , 41.0)8.0(2.05)1(4=⨯⨯==X P20.0)8.0(2.0)2(3225=⨯⨯==c X P , 06.020.041.033.01)3(=---=≥X P又设YE(Y) = 10×0.33 + 5×0.41 + 0×0.20 + (－2)×0.06 = 5.23(万元)10. 两台相互独立的自动记录仪, 每台无故障工作的时间服从参数为5的指数分布; 若先开动其中的一台, 当其发生故障时停用而另一台自行开动. 试求两台记录仪无故障工作的总时间T 的概率密度)(t f 、数学期望和方差.解. 假设X 、Y 分别表示第一、二台记录仪的无故障工作时间, 则X 、Y 的密度函数如下:⎩⎨⎧<≥=-05)(~,5x x e x f Y X xX 、Y 相互独立, 且 T = X + Y .X 、Y 的联合密度: ⎩⎨⎧≥≥=+-,00,0,25),()(5y x e y x f y x关于T 的分布函数: ⎰⎰≤+=≤+=≤=ty x T dxdy y x f t Y X P t T P t F ),(}{}{)(当 0<t 时⎰⎰⎰⎰≤+≤+===≤+=≤=ty x ty x T dxdy dxdy y x f t Y X P t T P t F 00),(}{}{)(当 0≥t 时⎰⎰⎰⎰≥≥≤++-≤+==≤+=≤=0,0)(525),(}{}{)(y x t y x y x ty x T dxdy edxdy y x f t Y X P t T P t Ft t tx t y x x t y t x te e dx e e dy e dx e 550055050551|)(525----------=-==⎰⎰⎰所以 ⎩⎨⎧<≥--=--0,00,51)(55t t te e t F t t T所以T 的概率密度: ⎩⎨⎧<≥==-0,00,25)]'([)(5t t e t t F t f t T T 所以 ⎰⎰∞+∞-∞+-===5225)()(052dt e t dt t f t T E t T 所以⎰⎰∞+∞-∞+-=-=-=-=25225425)52()()]([)()(0532222dt e t dt t f t T E T E T D tT第四章 大数定律和中心极限定理一. 填空题1. 设Y n 是n 次伯努利试验中事件A 出现的次数, p 为A 在每次试验中出现的概率, 则对任意 ε > 0, 有=⎪⎭⎫⎝⎛≥-∞→ε||lim p n Y P n n __________. 解. =⎪⎭⎫⎝⎛≥-∞→ε||lim p n Y P n n 1－011||lim =-=⎪⎭⎫ ⎝⎛<-∞→εp n Y P n n2. 设随机变量X 和Y 的数学期望是2, 方差分别为1和4, 而相关系数为0.5, 则根据切比雪夫不等式P(|X －Y| ≥ 6) ≤ _______. 解. E(X －Y) = E(X)－E(Y) = 2－2 = 0 D(X －Y) = D(X) + D(Y)－)()(2Y D X D XY ρ= 1 + 4－2×0.5×1×2 = 3所以 1213636)()6|(|2==-≤≥-Y X D Y X P二. 选择题1. 设随机变量n X X X ,,,21 相互独立, n n X X X S +++= 21, 则根据列维－林德伯格(Levy-Lindberg)中心极限定理, n S 近似服从正态分布, 只要n X X X ,,,21 ( A ) 有相同的数学期望 ( B ) 有相同的方差( C ) 服从同一指数分布 ( D ) 服从同一离散型分布解. 列维－林德伯格(Levy-Lindberg)中心极限定理要求n X X X ,,,21 既有相同的数学期望, 又有相同的方差, 因此( A ) 、( B )、 ( D )都不是答案, ( C )为答案.三. 计算题1. 某厂有400台同型机器, 各台机器发生故障的概率均为0,02, 假如各台机器相互独立工作, 试求机器出现故障的台数不少于2台的概率.解. 假设X 表示400台机器中发生故障的台数, 所以X ～B(400, 0.02) 由棣莫佛－拉普拉斯定理:。

第二章作业题解:2.1 掷一颗匀称的骰子两次, 以X 表示前后两次出现的点数之和, 求X 的概率分布, 并验证其满足(2.2.2) 式.解：由表格知X 的可能取值为2,3,4,5,6,7,8,9,10,11,12。

并且，361)12()2(====X P X P ；362)11()3(====X P X P ； 363)10()4(====X P X P ；364)9()5(====X P X P ； 365)8()6(====X P X P ；366)7(==X P 。

即 36|7|6)(k k X P --== (k =2,3,4,5,6,7,8,9,10,11,12)2.2 设离散型随机变量的概率分布为,2,1,}{Λ===-k ae k X P k 试确定常数a . 解：根据1)(0==∑∞=k k X P ，得10=∑∞=-k kae，即1111=---e ae 。

故 1-=e a2.3 甲、乙两人投篮时, 命中率分别为0.7 和0.4 , 今甲、乙各投篮两次, 求下列事件的概率：(1) 两人投中的次数相同; (2) 甲比乙投中的次数多. 解：分别用)2,1(,=i B A i i 表示甲乙第一、二次投中，则12121212()()0.7,()()0.3,()()0.4,()()0.6,P A P A P A P A P B P B P B P B ========两人两次都未投中的概率为：0324.06.06.03.03.0)(2121=⨯⨯⨯=B B A A P ， 两人各投中一次的概率为：2016.06.04.03.07.04)()()()(1221211212212121=⨯⨯⨯⨯=+++B B A A P B B A A P B B A A P B B A A P 两人各投中两次的概率为：0784.0)(2121=B B A A P 。

所以：（1）两人投中次数相同的概率为3124.00784.02016.00324.0=++ (2) 甲比乙投中的次数多的概率为：12121221121212121212()()()()()20.490.40.60.490.3620.210.360.5628P A A B B P A A B B P A A B B P A A B B P A A B B ++++=⨯⨯⨯+⨯+⨯⨯=2.4 设离散型随机变量X 的概率分布为5,4,3,2,1,15}{===k kk X P ，求)31()1(≤≤X P )5.25.0()2(<<X P 解：(1)52153152151)31(=++=≤≤X P (2) )2()1()5.25.0(=+==<<X P X P X P 51152151=+= 2.5 设离散型随机变量X 的概率分布为,,3,2,1,21}{Λ===k k X P k，求 };6,4,2{)1(Λ=X P }3{)2(≥X P解：31)21211(21212121}6,4,2{)1(422642=++⨯=++==ΛΛΛX P41}2{}1{1}3{)2(==-=-=≥X P X P X P2.6 设事件A 在每次试验中发生的概率均为0.4 , 当A 发生3 次或3 次以上时, 指示灯发出信号, 求下列事件的概率：(1) 进行4 次独立试验, 指示灯发出信号; (2) 进行5 次独立试验, 指示灯发出信号.解：(1))4()3()3(=+==≥X P X P X P1792.04.06.04.04334=+⨯=C(2) )5()4()3()3(=+=+==≥X P X P X P X P31744.04.06.04.06.04.054452335=+⨯+⨯=C C .2.7 某城市在长度为t (单位：小时) 的时间间隔内发生火灾的次数X 服从参数为0.5t 的泊 松分布, 且与时间间隔的起点无关, 求下列事件的概率： (1) 某天中午12 时至下午15 时未发生火灾; (2) 某天中午12 时至下午16 时至少发生两次火灾. 解：(1) ()!kP X k e k λλ-==，由题意，0.53 1.5,0k λ=⨯==，所求事件的概率为 1.5e -.(2) 0(2)110!1!P X e e e e λλλλλλλ----≥=--=--, 由题意，0.54 1.5λ=⨯=，所求事件的概率为213e --.2.8 为保证设备的正常运行, 必须配备一定数量的设备维修人员. 现有同类设备180 台, 且各台设备工作相互独立, 任一时刻发生故障的概率都是0.01，假设一台设备的故障由一人进行修理,问至少应配备多少名修理人员, 才能保证设备发生故障后能得到及时修理的概率不小于0.99？解：设应配备m 名设备维修人员。

概率论第二版习题答案概率论是一门研究随机现象的数学分支，它在统计学、金融学、工程学等多个领域都有广泛的应用。

第二版的概率论教材通常会在第一版的基础上进行修订和补充，以反映最新的研究成果和教学方法。

以下是一些概率论习题的答案示例，这些答案仅供参考，具体习题的答案可能会根据教材的不同而有所变化。

第一章：概率空间1. 习题1：描述一个概率空间的基本元素。

- 答案：一个概率空间由三个基本元素组成：样本空间(Ω)，事件集合(F)，以及概率测度(P)。

样本空间包含了所有可能的结果，事件集合是样本空间的子集，概率测度为每个事件分配一个介于0和1之间的实数，表示事件发生的可能性。

2. 习题2：证明如果事件A和事件B互斥，那么P(A∪B) = P(A) +P(B)。

- 答案：由于A和B互斥，即A∩B = ∅，根据概率测度的性质，P(A∪B) = P(A) + P(B) - P(A∩B)。

由于A和B互斥，P(A∩B) = 0，因此P(A∪B) = P(A) + P(B)。

第二章：随机变量及其分布1. 习题1：定义离散型随机变量和连续型随机变量。

- 答案：离散型随机变量是其取值可以列举的随机变量，其概率分布可以用概率质量函数来描述。

连续型随机变量是其取值无法一一列举的随机变量，其概率分布可以用概率密度函数来描述。

2. 习题2：如果X是一个随机变量，求E(X)和Var(X)。

- 答案：期望E(X)是随机变量X的平均值，定义为E(X) = ∑x *P(X = x)（对于离散型随机变量）或E(X) = ∫x * f(x) d x（对于连续型随机变量）。

方差Var(X)是随机变量X的离散程度的度量，定义为Var(X) = E[(X - E(X))^2]。

第三章：多维随机变量及其分布1. 习题1：描述联合分布函数和边缘分布函数的关系。

- 答案：联合分布函数给出了两个或多个随机变量同时取特定值的概率，而边缘分布函数是通过对联合分布函数进行积分或求和得到的，它给出了单个随机变量的分布。