下载文档原格式
数学必修二直线方程知识点假如想要提高数学成果，可以在做数学题的过程中多商量规律。
不要总是硬套公式，试着进行思维的转换，这样有助于数学思维的开发。
下面是我整理的数学必修二直线方程学问点，仅供参考希望能够关怀到大家。
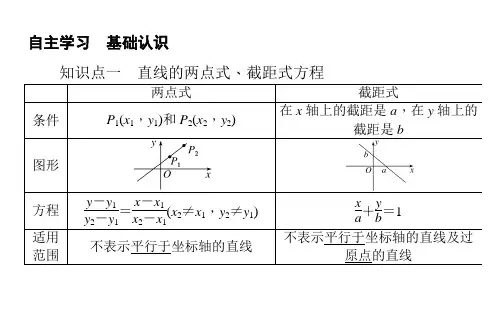
数学必修二直线方程学问点1直线方程形式一般式：Ax+By+C=0(AB≠0)斜截式：y=kx+b(k是斜率b是x轴截距)点斜式：y-y1=k(x-x1)(直线过定点(x1,y1))两点式：(y-y1)/(x-x1)=(y-y2)/(x-x2)(直线过定点(x1,y1)，(x2,y2))截距式：x/a+y/b=1(a是x轴截距,b是y轴截距)做题过程中，点斜式和斜截式用的最多(两种合占90%以上)，一般式属于中间过渡形态。
在与圆及圆锥曲线结合的过程中，还要用到点到直线距离公式。
2直线方程的局限性各种不同形式的直线方程的局限性：(1)点斜式和斜截式都不能表示斜率不存在的直线;(2)两点式不能表示与坐标轴平行的直线;(3)截距式不能表示与坐标轴平行或过原点的直线;(4)直线方程的一般式中系数A、B不能同时为零。
数学集合间的基本关系1.“包含”关系—子集留意：有两种可能(1)A是B的一部分，;(2)A与B是同一集合。
反之:集合A不包含于集合B,或集合B不包含集合A,记作AB或BA2.“相等”关系：A=B(5≥5，且5≤5，则5=5)实例：设A={x|x2-1=0}B={-1,1}“元素相同则两集合相等”即：①任何一个集合是它本身的子集。
AíA②真子集:假如AíB,且A1B那就说集合A是集合B的真子集，记作AB(或BA)③假如AíB,BíC,那么AíC④假如AíB同时BíA那么A=B3.不含任何元素的集合叫做空集，记为Φ规定:空集是任何集合的子集，空集是任何非空集合的真子集。
4.子集个数：有n个元素的集合，含有2n个子集，2n-1个真子集，含有2n-1个非空子集，含有2n-1个非空真子集学数学的好方法第一，兴趣。
2.2直线的方程9题型分类一、直线的点斜式方程直线的点斜式方程和斜截式方程：y－y＝k(x－x)y＝kx＋b二、直线的两点式方程直线的两点式方程和截距式方程：y－y x－x x y三、直线的一般式方程1．直线的一般式方程：关于x和y的二元一次方程都表示一条直线．我们把关于x，y的二元一次方程Ax＋By＋C＝0(其中A，B不同时为0)叫做直线的一般式方程，简称一般式．2．直线的五种形式的方程：3．直线各种形式方程的互化：（一）直线的点斜式方程1．直线的点斜式方程：过点P (x 0，y 0)且斜率为k 的直线的方程：y －y 0＝k (x －x 0).2．两种特殊的直线：(1)垂直于x 轴的直线：如图，过定点()00,P x y ，倾斜角为90°，斜率不存在，没有点斜式，其方程为00-=x x 或0=x x .(2)平行于x 轴（或与x 轴重合）的直线：如图，过定点()00,P x y ，倾斜角为0°，斜率为0，其点斜式方程为0=y y .3.求直线的点斜式方程的步骤及注意点(1)求直线的点斜式方程的步骤：定点(x 0，y 0)→定斜率k →写出方程y －y 0＝k (x －x 0)．(2)点斜式方程y －y 0＝k (x －x 0)可表示过点P (x 0，y 0)的所有直线，但x ＝x 0除外．题型1：求直线的点斜式方程（二）直线的斜截式方程1．直线的斜截式方程:斜率为k 且在y 轴上的截距为b 的直线方程：y ＝kx ＋b.2．(1)直线的斜截式=+y kx b 是直线点斜式()00-=-y y k x x 的特例.(2)一条直线与y 轴的交点为()0,b 的纵坐标叫做直线在y 轴上的截距.特别的，倾斜角为直角的直线没有斜截式方程.3.求直线的斜截式方程的策略:(1)斜截式方程的应用前提是直线的斜率存在．(2)直线的斜截式方程y ＝kx ＋b 中只有两个参数，因此要确定直线方程只需两个独立条件即可．题型2：求直线的斜截式方程(3)倾斜角为60°，与y 轴的交点到坐标原点的距离为3.2-4．（2024高一下·上海杨浦·期末）直线l ：21y x =-绕着点()1,1A 逆时针旋转π4与直线1l 重合，则1l 的斜截式方程是.2-5．（2024高二·全国·课后作业）若直线l 的方程a cy x b b=--中，0ab >，0ac <，则此直线必不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限2-6．（2024高二·全国·课后作业）已知直线l 与直线142y x =+互相垂直，直线l 与直线6y x =+在y 轴上的截距相等，则直线l 的方程为.2-7．（2024高二·全国·课后作业）已知R k Î，223b k k =-+，则下列直线的方程不可能是y kx b =+的是（ ）A ．B ．C ．D ．（三）直线的两点式方程1．直线的两点式方程：过两点P 1(x 1，y 1)，P 2(x 2，y 2)的直线方程：y －y 1y 2－y 1＝x －x 1x 2－x 1.2．(1)与坐标轴垂直的直线没有两点式方程.(2)两点式变形为()()()()121211--=--y y x x y y x x ,其可以表示任何直线.3.利用两点式求直线的方程：(1)首先要判断是否满足两点式方程的适用条件，然后代入两点式．(2)若满足即可考虑用两点式求方程．在斜率存在的情况下，也可以先应用斜率公式求出斜率，再用点斜式写方程．题型3：求直线的两点式方程3-1．（2024高二上·浙江温州·期末）过两点()3,5A -，()5,5B -的直线在y 轴上的截距为（ ）A ．54-B ．54C ．25-D ．253-2．（2024高二上·浙江）已知A (－3，2)，B (5，－4)，C (0，－2)，在△ABC 中，(1)求BC 边所在的直线方程；(2)求BC 边上的中线所在直线的方程．3-3．（2024高二·江苏·课后作业）已知直线分别经过下面两点，用两点式方程求直线的方程：(1)A (3, 1), B (2, －3)；(2)A (2, 1), B (0, －3)；(3)A (0, 5), B (4, 0).3-4．（2024高一·全国·课后作业）已知点A(3,2)，B(－1,4)，则过点C(2,5)且过线段AB 的中点的直线方程为（四）直线的截距式方程1．直线的截距式方程：在x ，y 轴上的截距分别为a ，b （其中a≠0，b≠0）的直线方程：xa ＋y b＝1.2．截距的概念：(1)横截距：直线与x 轴交点的横坐标；在直线方程中，令y=0，解出x ；(2)纵截距：直线与y 轴交点的横坐标；在直线方程中，令x=0，解出y.3.截距式方程应用的注意事项(1)如果问题中涉及直线与坐标轴相交，则可考虑选用截距式直线方程，用待定系数法确定其系数即可．(2)选用截距式直线方程时，必须首先考虑直线能否过原点以及能否与两坐标轴垂直．(3)要注意截距式直线方程的逆向应用．题型4：求直线的截距式方程4-1．（2024高三·全国·专题练习）过点(2，1)且在x 轴上截距与在y 轴上截距之和为6的直线方程为.4-2．（2024高二上·全国·课后作业）过点(3,4)-且在两坐标轴上的截距相等的直线方程是（ ）A ．=1y x --B ．43y x =C ．43y x =-D ．43y x =-或=1y x --4-3．（2024高二·全国·课后作业）求过点(5,2)A ，且在y 轴上的截距是x 轴上的截距的2倍的直线l 的方程．（五）直线的一般式方程1.直线的一般式方程：关于x 和y 的二元一次方程都表示一条直线．我们把关于x ，y 的二元一次方程Ax ＋By ＋C ＝0(其中A ，B 不同时为0)叫做直线的一般式方程，简称一般式．2.求直线一般式方程的策略在求直线方程时，设一般式方程有时并不简单，常用的还是根据给定条件选出四种特殊形式之一求方程，然后转化为一般式．3.含参直线方程的研究策略(1)若方程Ax ＋By ＋C ＝0表示直线，则需满足A ，B 不同时为0.(2)令x ＝0可得在y 轴上的截距．令y ＝0可得在x 轴上的截距．若确定直线斜率存在，可将一般式化为斜截式．(3)解分式方程要注意验根．4.利用一般式解决直线平行与垂直问题的策略直线l 1：A 1x ＋B 1y ＋C 1＝0，直线l 2：A 2x ＋B 2y ＋C 2＝0，(1)若l 1∥l 2⇔A 1B 2－A 2B 1＝0且B 1C 2－B 2C 1≠0(或A 1C 2－A 2C 1≠0)．(2)若l 1⊥l 2⇔A 1A 2＋B 1B 2＝0.题型5：求直线的一般式方程5-1．（2024高一·全国·课后作业）△ABC 的三个顶点分别为A (0,4)、B (－2,6)、C (－8,0).(1)分别求边AC 和AB 所在直线的方程；(2)求AC 边上的中线BD 所在直线的方程；(3)求AC 边的中垂线所在直线的方程；(4)求AC 边上的高所在直线的方程；(5)求经过两边AB 和AC 的中点的直线方程．5-2．（2024高二上·辽宁锦州·阶段练习）根据下列各条件分别写出直线的方程，并化成一般式．(1)斜率是12-，且经过点()8,6A -；(2)在x 轴和y 轴上的截距分别是32和3-；(3)经过点()13,2P -，()25,4P-；(4)经过点()2,3-，且一个方向向量为()2,4a =r．5-3．（2024高二下·上海宝山·期末）若0ab <，0bc <，则直线0ax by c ++=不经过第象限（ ）A ．一B ．二C ．三D ．四5-4．（2024高二下·上海）如果0AB >且0BC <，那么直线0Ax By C ++=不经过第（ ）象限A ．一B ．二C ．三D ．四5-5．（2024高二上·全国·课后作业）已知直线0Ax By C ++=在x 轴的截距大于在y 轴的截距，则A 、B 、C 应满足条件（ ）A ．A B>B ．A B<C ．0C C A B+>D ．0C C A B-<题型6：由一般式方程判断直线的平行、垂直6-1．（湖北省宜昌市部分示范高中教学协作体2023-2024学年高二上学期期中理科数学试题）若直线()120x m y ++-=和直线240mx y ++=平行，则m 的值为（ ）A ．1B ．2-C ．1或2-D ．23-6-2．（2024高二下·海南·学业考试）若直线210x y +-=与220mx y -+=平行，则实数m 的值为（ ）A ．3-B ．1-C ．1D ．26-3．（2024高二下·湖北孝感·期中）“2m =-”是“直线()110m x y +++=与直线()2420x m y +++=互相垂直”的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件6-4．（2024高二上·福建福州·期末）若直线1:340l mx y ++=与直线2:2(1)40l x m y +++=平行，则m 的值为（ ）A ．2B ．3-C ．2或3-D ．2-或3-6-5．（2024高二上·福建）“3a =”是“直线230ax y a ++=和直线3(1)(7)0x a y a +---=平行且不重合”的（ ）.A ．充分非必要条件B ．必要非充分条件C ．充要条件D ．既非充分又非必要条件6-6．（2024高二下·上海黄浦·阶段练习）直线1:310l px y ++=与直线2:6250l x y --=垂直，则p 的值为（ ）A ．1-B ．1C ．9-D ．96-7．（2024高二上·安徽·阶段练习）已知直线420mx y +-=与直线250x y n -+=互相垂直，垂足为()1,p .则m n p +-等于（）A ．24B ．20C ．4D ．0题型7：由两条直线平行、垂直求直线方程7-1．（2024高二·贵州贵阳·阶段练习）过点(1,2)且垂直于直线3250x y -+=的直线方程为（ ）A ．2380x y +-=B ．2340x y -+=C ．3210x y -+=D ．2380x y ++=7-2．（2024高二下·上海浦东新·期中）过点()1,1且与直线210x y +-=平行的直线方程为.7-3．（2024高二上·四川凉山·期末）已知直线l 过点3(2,)A -，且与直线1y x =+平行，则直线l 的方程为（ ）A ．20x y -+=B ．10x y ++=C ．20x y --=D ．50x y --=7-4．（2024高二下·新疆伊犁·期中）过点(1,3)P -且垂直于直线230x y +-= 的直线方程为（ ）A ．250x y ++=B ．250x y -+=C ．250x y +-=D ．250x y --=题型8：直线与坐标轴围成三角形的面积问题8-1．（2024高二·全国·课后作业）求过点(5,2)Q ，且与两坐标轴围成的三角形的面积是92的直线l 的方程．8-2．（2024高一下·江苏扬州·期中）如图所示，已知ABC V 是以AB 为底边的等腰三角形，点()14A ，，()32B ，，点C 在直线：260x y -+=上．（1）求AB 边上的高CE 所在直线的方程；（2）设直线CD 与y 轴交于点()03D ，，求ACD V 的面积．8-3．（2024高二·全国·课后作业）在平面直角坐标系xOy 内，经过点()2,3P 的直线分别与x 轴、y 轴的正半轴交于A ，B 两点，则OAB △面积最小值为 ．8-4．（2024高一下·湖南长沙·期末）过点P （1，1）作直线l ，与两坐标轴相交所得三角形面积为1，则直线l 有（ ）A ．1条B ．2条C ．3条D ．4条8-5．（2024高三·全国·对口高考）已知直线l ：3470x y +-=，则与已知直线l 平行且与两坐标轴围成的三角形的面积为6的直线方程为．（六）直线过定点问题解决直线过定点问题的思路，把平面上过定点的直线的全体称为中心直线系.定点的确定方法：把含参直线方程化为(,)(,)0f x y kg x y +=直线系过定点问题:解含参数的直线恒过定点问题的策略:(1)方法一：任给直线中的参数赋两个不同的值，得到两条不同的直线，然后验证这两条直线的交点就是题目中含参数直线所过的定点，从而问题得解．(2)方法二：含有一个参数的二元一次方程若能整理为A 1x ＋B 1y ＋C 1＋λ(A 2x ＋B 2y ＋C 2)＝0，其中λ是参数，这就说明了它表示的直线必过定点，其定点可由方程组{A 1x ＋B 1y ＋C 1＝0，A 2x ＋B 2y ＋C 2＝0 解得．若整理成y －y 0＝k (x －x 0)的形式，则表示的所有直线必过定点(x 0，y 0)．,求解(,)0(,)0f x y g x y =⎧⎨=⎩，即可得出定点坐标.题型9：直线的恒过定点问题9-1．（2024高一下·浙江宁波·期中）已知点()()1,3,2,1A B --.若直线():21l y k x =-+与线段AB 相交,则k 的取值范围是（ ）A ．12k ³B ．2k £-C ．12k ³或2k £-D ．122k -££9-2．（2024高二上·全国·课后作业）不论m 取何值，直线(1)210m x y m --+-=都过定点（ ）A ．11,2æö-ç÷èøB ．(2,1)-C ．(2,3)D ．(2,3)-9-3．（2024高二上·全国·课后作业）直线13kx y k -+=，当k 变动时，所有直线恒过定点坐标为（ ）A ．()0,0B ．()0,1C ．()3,1D ．()2,19-4．（2024·吉林通化·模拟预测）若直线210kx y k -+-=恒过点A ，点A 也在直线20mx ny ++=上，其中,m n 均为正数，则mn 的最大值为（ ）A ．14B ．12C ．1D ．29-5．（2024高二上·福建福州·期中）已知直线l 方程：220(R)kx y k k -+-=Î，若l 不经过第二象限，则k 的取值范围为（ ）A ．1k £B ．0k ³C ．01k ££D ．0k ³9-6．（2024高一上·河南周口·阶段练习）不论k 为何实数，直线()()()213110k x k y k --+--=恒通过一个定点，这个定点的坐标是（ ）A ．()5,2B ．()2,3C ．()5,9D ．1,32æö-ç÷èø一、单选题1．（2024高二上·全国·课后作业）过两点()()0,3,2,1的直线方程为( )A ．30x y --=B ．30x y +-=C ．30x y ++=D ．30x y -+=2．（2024高二上·广西河池·阶段练习）过点()1,2A 在两坐标轴上的截距相等的直线方程是（ ）A ．2y x =B ．30x y +-=C ．x y =或30x y +-=D ．2y x =或30x y +-=3．（2024高二上·湖南·阶段练习）已知直线l 过点()1,3G -，()2,1H -，则直线l 的方程为（ ）A ．470x y ++=B ．23110x y --=C ．4350x y ++=D ．43130x y +-=4．（2024高二·江苏·课后作业）过两点()2,4-和()41-,的直线在y 轴上的截距为（ ）A ．145B ．145-C ．73D ．73-5．（2024高二·全国·课后作业）过12(2,0),(0,3)P P 两点的直线方程是（ ）A ．032x y+=B ．132xy-=C ．123x y+=D ．123xy-=6．（2024高二上·全国·课后作业）直线l 过点(1,1),(2,4)A B -，则直线l 的方程为（ ）A ．2y x =-B ．2y x =--C ．2y x =-+D ．2y x =+7．（2024高二上·山东枣庄·期末）过点()2,3A 且与直线:2470l x y -+=平行的直线方程是（ ）A ．240x y -+=B ．270x y +-=C ．210x y --=D ．280x y +-=8．（2024高二下·湖北·阶段练习）直线4210x y +-=与直线40ax y +=垂直，则a 等于（ ）A ．2B ．2-C ．1D ．1-9．（广西南宁市第二十六中学等3校2023-2024学年高二下学期开学联合调研测试数学试题）直线l 过点()1,2-且与直线2340x y -+=垂直，则l 的方程是（ ）A ．2350x y -+=B ．3270x y ++=C ．3210x y +-=D ．2380x y -+=10．（2024高二上·全国·课后作业）经过点(1,2)，且与直线2100x y +-=垂直的直线方程为（ ）A ．230x y -+=B ．230x y +-=C ．230x y --=D ．230x y +-=11．（2024高二下·天津北辰·阶段练习）过点()1,3-且平行于直线2310x y -+=的直线方程为（ ）A ．23110x y -+=B ．3230x y +-=C ．2370x y --=D ．3230x y ++=12．（2024高三上·江西新余·期末）已知直线1l ：()2310m x y ---=与直线2l ；()210mx m y +++=相互平行，则实数m 的值是（ ）A ．4-B ．1C ．1-D ．4-或113．（2024高二上·广东肇庆·期末）“12a =”是“直线210x ay +-=与直线()110a x ay ---=平行”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件14．（2024高二上·河北唐山·期中）直线l ：230x y -+=的斜率和在x 轴上的截距分别为（ ）A ．12，3B ．12，3-C ．12-，3D ．12-，3-15．（2024高二上·江苏苏州·期末）直线40x +=的倾斜角是（ ）A ．π3B ．π6C ．2π3D ．π16．（2024高二下·新疆塔城·开学考试）过点(1,1)-且斜率为12的直线l 的方程是（ ）A ．3270x y +-=B ．240x y +-=C ．230x y --=D ．230x y -+=17．（2024高二上·广东江门·期末）直线0Ax By C ++=（,A B 不同时为0），则下列选项正确的是（ ）A ．无论,AB 取任何值，直线都存在斜率B ．当0A =，且0B ¹时，直线只与x 轴相交C ．当0A ¹，或0B ¹时，直线与两条坐标轴都相交D ．当0A ¹，且0B =，且0C =时，直线是y轴所在直线18．（2024高二上·全国·课后作业）经过点(1,2)，且平行于直线2350x y -+=的直线方程为（ ）A ．2340x y -+=B ．2320x y -+=C ．3240x y -+=D ．3220x y -+=19．（2024·北京丰台·二模）“1a =”是“直线10x ay +-=与直线10ax y -+=相互垂直”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件20．（2024高二上·上海宝山·期末）已知)(111,P a b 与)(222,Pa b 是直线2y kx =+（k 为常数）上两个不同的点，则关于111:20l a x b y +-=和222:20l a x b y +-=的交点情况是（ ）A ．无论k ，1P ，2P 如何，总有唯一交点B ．存在k ，1P ，2P 使之有无穷多个交点C ．无论k ，1P ，2P 如何，总是无交点D ．存在k ，1P ，2P 使之无交点二、多选题21．（2024高一下·江苏盐城·阶段练习）下列说法错误的是（ ）A ．过定点()000,P x y 的直线都可用方程()00y y k x x -=-表示B ．过定点()0,A b 的直线都可用方程y kx b =+表示C ．过任意两个点()111,P x y ，()222,P x y 的直线都可用方程()()()()121121y y x x x x y y --=--表示D ．不过原点的直线都可用方程1x ya b +=表示22．（2024高二上·全国·专题练习）下列说法正确的是（ ）A ．11y y x x --＝k 不能表示过点M （x 1，y 1）且斜率为k 的直线方程B ．在x 轴，y 轴上的截距分别为a ，b 的直线方程为1x ya b +=C ．直线y ＝kx +b 与y 轴的交点到原点的距离为bD ．过两点A （x 1，y 1）B （x 2，y 2）的直线方程为212212()()()()0x x y y y y x x -----=23．（2024高二上·江苏扬州·期中）下列说法正确的是（ ）A ．直线30x y --=与两坐标轴围成的三角形的面积是92B ．若三条直线0,0,3x y x y x ay a +=-=+=-不能构成三角形，则实数a 的取值集合为{}1,1-C ．经过点(1,2)且在x 轴和y 轴上截距都相等的直线方程为30x y +-=或10x y -+=D ．过1122(,),(,)x y x y 两点的直线方程为121121()()()()y y x x x x y y --=--24．（2024高二上·江苏徐州·阶段练习）下列说法正确的是（ ）A ．点斜式()11y y k x x -=-可以表示任何直线B ．过()11,x y 、()22,x y 两点的直线方程为112121y y x xy y x x --=--C ．直线240x y --=与直线210x y ++=相互垂直．D ．直线42y x =-在y 轴上的截距为2-三、填空题25．（2024高三·全国·课后作业）经过点()3,1-和点()2,2-的直线方程是 .26．（2024高二·江苏·假期作业）不论a 取何值时，直线()3260a x ay -++=恒过第 象限．27．（2024高二上·全国·课后作业）倾斜角为30°，且过点(2,0)-的直线斜截式方程为 ．28．（2024高二上·全国·专题练习）若直线过点()1,1且与两坐标轴所围成的三角形的面积为2，则这样的直线有 条.29．（2024高二·全国·课后作业）若直线l 与两坐标轴围成一个等腰直角三角形，且此三角形的面积为18，则直线l 的方程为 .30．（2024高一上·广东广州·期末）求过点()2,3P ，并且在两轴上的截距相等的直线方程 ．31．（2024高二下·上海闵行·阶段练习）过点()5,2，且在两坐标轴上截距相等的直线一般式方程是 ．32．（2024高二下·上海普陀·期中）若1122341,341x y x y +=+=，且12x x ¹，则经过()()1122,,A x y B x y 、的直线l 的一般方程为33．（2024高二上·重庆长寿·期末）经过点(1,2)且与直线210x y -+=垂直的直线方程是 ．（用一般式表示）34．（2024·黑龙江齐齐哈尔·二模）已知直线:120l kx y k -++=，若直线l 在两坐标轴上的截距相等，则实数k 的值为；若直线l 不经过第三象限，则k 的取值范围是 .四、解答题35．（2024高二·全国·专题练习）根据下列条件写出直线方程，并化为一般式：在x y ，轴上的截距分别为3-，1-.36．（2024高二上·山东济宁·期中）已知ABC V 的顶点分别为(2,4),(0,2),(2,3)A B C --，求：(1)直线AB 的方程;(2)AB 边上的高所在直线的方程;37．（2024高二上·全国·课后作业）已知直线l 经过点(2,1)A -，(3,3)B -，求直线l 的方程，并求直线l 在y 轴上的截距.38．（2024高二下·湖北宜昌·阶段练习）设直线的方程为(1)20,a x y a a R +++-=Î.（1）若在两坐标轴上的截距相等，求直线的方程；（2）若与两坐标轴围成的三角形的面积为1，求a 的值.39．（2024高二下·上海·课后作业）直线l 过点(2,3)P -，且与两轴围成的三角形面积为4，求直线l 的方程.40．（2024高二上·全国·课后作业）已知直线l 的斜率为－1，且它与两坐标轴围成的三角形的面积为12，求直线l 的方程．41．（2024高一下·安徽·阶段练习）已知点A （5，1）关于x 轴的对称点为B （x 1，y 1），关于原点的对称点为C （x 2，y 2）.(1)求△ABC 中过AB ，BC 边上中点的直线方程；(2)求△ABC 的面积.42．（2024高二·全国·专题练习）ABC V 的三个顶点是()4,0A ，()6,7B ，()0,3C ，求：边BC 上的中线所在直线的方程；43．（2024高二上·湖北·阶段练习）已知直线():120l kx y k k R -++=Î.（1）若直线l 不经过第四象限，求k 的取值范围；（2）若直线l 交x 轴负半轴于点A ，交y 轴正半轴于点B ，求AOB V 面积的最小值；（3）已知()1,5P ，若点P 到直线的距离为d ，求d 最大时直线的方程.44．（2024高二上·河北邢台·阶段练习）已知直线l ：()()231370a x a y a +--++=，a ÎR .(1)证明直线l 过定点A ，并求出点A 的坐标；(2)在（1）的条件下，若直线l ¢过点A ，且在y 轴上的截距是在x 轴上的截距的12，求直线l ¢的方程；(3)若直线l 不经过第四象限，求a 的取值范围.45．（2024高一下·山东滨州·阶段练习）已知直线()1:34110l x m y +-+=与2:70l x my +-=垂直，求m .46．（2024高二上·福建福州·期中）已知直线l 过点()3,2M ．(1)若直线l 在两坐标轴上的截距相等，求直线l 的方程；(2)若l 与x 轴正半轴的交点为A ，与y 轴正半轴的交点为B ，求AOB V （O 为坐标原点）面积的最小值．47．（2024高二上·湖北武汉·期末）已知直线方程为()21y k x +=+．(1)若直线的倾斜角为135o ，求k 的值；(2)若直线分别与x 轴、y 轴的负半轴交于A 、B 两点，O 为坐标原点，求AOB V 面积的最小值及此时直线的方程．48．（2024高一上·内蒙古呼和浩特·期末）已知一条动直线():31640l m x my m ++--=，(1)求证：直线l 恒过定点，并求出定点P 的坐标；(2)若直线l 与x 、y 轴的正半轴分别交于A 、B 两点，O 为坐标原点，是否存在直线l 同时满足下列条件：①AOB V 的周长为12；②AOP V 的面积为4.若存在，求出方程；若不存在，请说明理由.49．（2024高三·全国·专题练习）已知直线l 过点(2,1)M ，且分别与x 轴的正半轴、y 轴的正半轴交于,A B 两点，O 为原点，当AOB V 面积最小时，求直线l 的方程．50．（2024高二上·全国·专题练习）已知直线l 的方程为：()()()212430m x m y m ++-+-=．(1)求证：不论m 为何值，直线必过定点M ；(2)过点M 引直线1l ，使它与两坐标轴的负半轴所围成的三角形面积最小，求1l 的方程．51．（2024高二·全国·课后作业）过点()2,1P 作直线l 分别交x 轴、y 轴的正半轴于A ，B 两点.(1)求||||OA OB ×的最小值，及此时直线l 的截距式方程；(2)求||||PA PB ×的最小值，及此时直线l 的截距式方程.52．（2024高二下·上海金山·期中）已知直线l ：120kx y k -++=，k ÎR（1）直线过定点P ，求点P 坐标；（2）若直线l 交x 轴负半轴于点A ，交y 轴正半轴于点B ，O 为坐标原点，设三角形OAB 的面积为4，求出直线l 方程．53．（2024高二下·湖南常德·期中）已知直线l 的方程为()()1520R a x y a a ++--=Î．(1)求直线l 过的定点P 的坐标；(2)直线l 与x 轴正半轴和y 轴正半轴分别交于点A ，B ，当AOB V 面积最小时，求直线l 的方程；54．（2024高二上·全国·课后作业）当直线方程0Ax By C ++=的系数A ，B ，C 满足什么条件时，该直线分别具有以下性质？(1)过坐标原点；(2)与两条坐标轴都相交；(3)只与x 轴相交；(4)是x 轴所在直线；(5)设()00,P x y 为直线0Ax By C ++=上一点，证明：这条直线的方程可以写成()()000A x x B y y -+-=．55．（2024高二·江苏·假期作业）已知直线1110a x b y ++=和直线2210a x b y ++=都过点(2,1)A ，求过点111()P a b ,和点222()P a b ,的直线方程.。
