自己整理的必修二直线方程的几种形式

求直线的方程.
y y1 y2 y1
x x1 x2 x1
, x1
x2 ,
y1
y2
§2.2.2.1直线的点斜式方程和两点式方程
1.已知直线在x轴上的截距是a，在y轴
上的截距是b，且a≠0，b≠0，
y
求证直线的方程可写为 x y 1 ab
(这种形式的直线方程，
叫做直线的截距式方程)
b
a
O
x
§2.2.2.1直线的点斜式方程和两点式方程
例二 根据下列直线方程，分别写出各直线经过的 一点和直线斜率
1 y 2 x 1 2 y 4 3x 2;
3 y 4x 3
点评：
4 y 2 x 3
5
逆用直线方程，即由方程可看出经过的点和 直线的斜率.
§2.2.2.1直线的点斜式方程和两点式方程
§2.2.2.1直线的点斜式方程和两点式方程
总结与反思
点斜式y y0 k x x 0
1.四种直线方程： 斜截式y kx+b
体会形与数之间
两点式 y y1 x x1
的转化. 2.四种直线方程的应
截距式yx2
yy1
x2
1
x1
ab
用及其注意事项和适
用条件.
3.方程的思想；数形结合的思想；分 类讨论的思想；求动点轨迹的方法和 思路.
§2.2.2.1直线的点斜式方程和两点式方程
课后作业
1. 通读教材内容，熟记所学四种方程，完 成课后练习.
2. 基训.
3. 学案.
方程.
x-y+1=0
2.求经过点A（1，2）与点B（3，2）的直
线方程.
y=2
3.求经过点A（1，2）与点B（1，4） 的直线方程. x=1

解析几何直线方程的五种形式一、点斜式方程点斜式方程是解析几何中直线方程的一种形式，它由直线上已知一点的坐标和直线的斜率决定。

点斜式方程的一般形式为y - y1 = k(x - x1)，其中(x1, y1)为直线上已知的一点的坐标，k为直线的斜率。

例如，给定直线上的一点A(2, 3)和斜率k = 2，我们可以得到该直线的点斜式方程为y - 3 = 2(x - 2)。

二、斜截式方程斜截式方程是解析几何中直线方程的另一种常见形式，它由直线上的截距和直线的斜率决定。

斜截式方程的一般形式为y = kx + b，其中k为直线的斜率，b为直线与y轴的截距。

例如，给定直线的斜率k = -3和截距b = 4，我们可以得到该直线的斜截式方程为y = -3x + 4。

三、一般式方程一般式方程是解析几何中直线方程的标准形式，它由直线的斜率和截距的比值决定。

一般式方程的一般形式为Ax + By + C = 0，其中A、B、C为常数，且A和B不同时为0。

例如，给定直线的斜率k = 1/2和截距 b = 3，我们可以得到该直线的一般式方程为2x - y - 6 = 0。

四、两点式方程两点式方程是解析几何中直线方程的一种形式，它由直线上的两个已知点的坐标决定。

两点式方程的一般形式为(x - x1)/(x2 - x1) = (y - y1)/(y2 - y1)，其中(x1, y1)和(x2, y2)为直线上的两个已知点的坐标。

例如，给定直线上的两个点A(1, 2)和B(3, 4)，我们可以得到该直线的两点式方程为(x - 1)/(3 - 1) = (y - 2)/(4 - 2)。

五、截距式方程截距式方程是解析几何中直线方程的一种形式，它由直线与x轴和y轴的截距决定。

截距式方程的一般形式为x/a + y/b = 1，其中a 和b分别为直线与x轴和y轴的截距。

例如，给定直线与x轴和y轴的截距分别为a = 2和b = 3，我们可以得到该直线的截距式方程为x/2 + y/3 = 1。

2 x 5 y 10 0
五.直线方程的一般式
在平面直角坐标系中 , 对于任何一条直线 , 都有一
个表示这条直线的关于 x, y的二元一次方程 形式为 证明: 关于x, y的二元一次方程的一般
Ax By C 0( A, B不同时为 0)
A C A 1)当B 0时, 有y x , 这 是 斜 率 为 , BC B B 在y轴 上 的 斜 距 为 的直线方程 . B C 2)当B 0时,因A, B不 同 时 为 0, 故A 0, x . A 它表示一条与 y轴平行或重合的直线 .
求这个三角形三边所在 的直线方程 .
解: 把A, B代入两点式 ,得
y0 x (5) 3 0 3 (5)
3x 8 y 15 0
把B, C代入两点式 ,得
y 3 x 3 23 03
5x 3 y 6 0
A(5,0), B(3,3), C (0,2) 例3三角形的顶点是
二
名称
直线方程的五种形式
方程 说明 不包括y轴和平行于y轴 的直线 不包括y轴和平行于y轴 的直线
已知条件
点斜式 点P1(x1,y1)和斜率 y-y1=k(x-x1) k 斜截式 斜率k和y轴上截 距 两点式 点P1(x1,y1)和点 P2(x2,y2) 截距式 在x轴上的截距a 在y轴上的截距b 一般式 A、B不同时为零 y=kx+b
已知直线 l的 斜 率 为 k , 与y轴 的 交 点 是 (0, b), 求直线的方程 . 解: 由直线的点斜式,得 y b k ( x 0)
即y kx b
y
l
方程 y kx b叫做直线方程的斜截式 .

03
然后，将斜率k代入一般 形式的直线方程 y=kx+b中，得到yy1=k*(x-x1)。
04
最后，将k的具体值代入 上式，得到两点式方程。
谢谢观看
04
法线式
法线式的定义
法线式方程是形如 (y - y_1 = m(x x_1)) 的直线方程，其中 (m) 是直线 的斜率，((x_1, y_1)) 是直线上的一 点。
VS
法线式方程表示的是通过点 ((x_1, y_1)) 且斜率为 (m) 的直线。
法线式的应用场景
当已知直线上的一点和斜率时，可以使用法线式方程来表示该直线。
进一步变形，得到 (y - y_1 = frac{A}{B}(x - x_1))，这就是法
线式方程。
05
点向式
点向式的定义
点向式是指通过直线上的一点和直线的方向 向量来表示直线方程的一种形式。具体地， 点向式方程可以表示为 (x - x_1 = m(y y_1))，其中 ((x_1, y_1)) 是直线上的一个点， (m) 是直线的方向向量。
详细描述
在几何问题中，如果已知直线上的一点和斜率，就可以使用点斜式来求解直线的方程。 例如，在解析几何、物理和工程领域中，点斜式被广泛应用于解决与直线相关的问题。
点斜式的推导过程
要点一
总结词
点斜式可以通过直线上两点的坐标来推导得出。
要点二
详细描述
设直线上的两点为 (x1, y1) 和 (x2, y2)，其中 x1 ≠ x2。根据 两点式，直线的斜率 m = (y2 - y1) / (x2 - x1)。将这个斜率 和一点 (x1, y1) 代入点斜式方程，即可得到直线的方程为 y y1 = m(x - x1)。

1经过点(3,2),斜率为 ；
②过点(0,2),斜率为-1；
③过点(-3,1),平行于x轴；
④经过点(-2,0)且垂直于x轴
⑤在y轴上的截距为2，且与x轴平行
⑥经过A(-1,8),B(4,-2)两点
⑦在x，y轴上的截距分别是4，-3
【小结】
探究二：直线 经过点P(2,3),且在x,y轴上的截距相等，试求该直线的方程。
A. y=kx+b B. y=k(x-b) C. y=k(x+b) D. y=kx-b
3.下列说法中不正确的是( )
A.点斜式 适用于不垂直于x轴的任何直线；
B.斜截式 适用于不垂直于x轴的任何直线
C.两点式 适用于不垂直于坐标轴的任何直线
D.截距式 适用于不过原点的任何直线
【我的疑惑】
探究案
探究一：写出满足下列条件的直线的方程。
【拓展】在直线y-1=k(x+1)中，k取遍所有的实数，可得无数条直线，这无数条直线都过定点_________
【小结】
【课堂小结】
1.知识方面
2.数学思想方法
课题：2.2.2直线方程的几种形式
【学习目标】
1.熟练掌握直线方程的几种形式(点斜式、斜截式、两点式、截距式)，提高求直线方程的能力。
2.自主学习、合作探究，学会各种直线方程的运用方法。
3.激情投入，高效学习，体会数形结合的魅力。
【使用说明及学法指导】
1.先精读一遍教材必修二课本P77-81，用红色笔进行勾画；再针对预习自学二次阅读并回答；
2.推导过 ,且 的直线的两点式方程（提示：利用点斜式）
3.已知直线 在x轴上的截距为a,在y轴上截距为b,且 ，求证直线 的方程可写为 （这种形式的直线方程叫做直线的截距式方程）

y - y0 = k(x - x0 )
(1)经过点(2, 1)，且倾斜角是150 °； y - 1 = - 3 ( x - 2 ) 3
(2)经过点(3, 2), 且垂直于 y轴的直线； y = 2
(3)经过点(2,1), 且斜率是 -1的直线. y - 1 = -( x - 2)
6.已知直线的方程是y+7=-x-3,则（ ）C A.直线经过点（-3,7），斜率为-1;
：
(1)l1
// l2
kb11
k2 b2
(2)l1 ⊥l2 ⇔k1 • k2 = -1
2.已知直线y = ax - 2和y = - a x+1互相垂直，
2
则a =
. 2
3.若直线l1 :
2
y
=
-
2 a
x
-
1 a
与直线l2
:
y
=
3x
-1互相平行，
则a =
3
.
4.当a为何值时，直线l1 : y = -x+2a与直线 l2：y = (a2 - 2)x+2平行？
直线的点斜式方程 y - y0 = k(x - x0 )
：
2.直线的点斜式方程能否表示坐标平面 上所有的直线？
直线的点斜式y：- y0 = k(x - x0 )
点P0 (x0 , y0 )+斜率k
3.思考：过点P0(x0,y0) (1)平行于x轴或与x轴重合的直线方程是什么？ (2)平行于y轴或与y轴重合的直线方程是什么？
直线的点斜式方程得：
y -b = k(x - 0)
即：y = kx+b 直线的斜
截距不是距离，
k:直线的斜率 b:直线在y轴上的截距

2：一条直线经过点A（0，5），倾斜角为00， ），倾斜角为 例2：一条直线经过点A（0，5），倾斜角为00，求这直线 方程 y
解：这条直线经过点A（0，5） 斜率是k=tan00=0 代入点斜式，得 y - 5 = 0 O x 5
②直线的斜截式方程： 直线的斜截式方程：
已知直线l的斜率是 ， 轴的交点是P（ ， ）， ），求 已知直线 的斜率是k，与y轴的交点是 （0，b），求 的斜率是 轴的交点是 求这条直线的方程。 求这条直线的方程。 代入点斜式方程， 的直线方程 的直线方程： 代入点斜式方程，得l的直线方程：y - b =k （ x - 0） ） 即 y = kx + b。 (2)
3
BP95
㈣总结： ①直线的点斜式，斜截式方程在 直线斜率存在时才可以应用。 ②直线方程的最后形式应表示成 二元一次方程的一般形式。
③两种形式都有限制条件
直线方程的五种形式之： 直线方程的五种形式之： 点斜式方程和 斜截式方程
新课： 新课： 1、直线的点斜式方程：
已知直线l经过已知点 ），并且它的斜率是 并且它的斜率是k 已知直线l经过已知点P1（x1，y1），并且它的斜率是 求直线l的方程 的方程。 求直线 的方程。 设点P（ ， ）是直线l上 设点 （x，y）是直线 上 不同于P 的任意一点。 不同于 1的任意一点。 l 根据经过两点的直线斜率 y P 公式， 公式，得
k
=
可化为
y y 1 = k (x x 1 )
y y1 x x1
. .
P1
O
x
由直线上一点和直线的斜率确定的直线方程，叫直 由直线上一点和直线的斜率确定的直线方程， 线的点斜式方程。 线的点斜式方程。
小结： 小结： 为直线上的任意一点， ⑴P为直线上的任意一点，它的 为直线上的任意一点 位置与方程无关 直线上任意一点P与这条直线上 直线上任意一点 与这条直线上 一个定点P 所确定的斜率都相等。 一个定点 1所确定的斜率都相等。

直线方程(直线方程完美总结归纳)一、倾斜角与斜率直线的倾斜角是指直线与x轴正方向的夹角。

当直线与x 轴平行或重合时，其倾斜角规定为0度。

倾斜角的范围是小于等于α，且α小于180度。

直线的斜率是指直线倾斜角的正切值，记作k=tanα（α不等于90度）。

当直线与x轴平行或重合时，斜率为0；当直线与x轴垂直时，斜率不存在。

经过两点P的直线的斜率公式是k=(y2-y1)/(x2-x1)。

每条直线都有倾斜角，但并不是每条直线都有斜率。

求斜率的一般方法有两种：已知直线上两点，根据斜率公式k=(y2-y1)/(x2-x1)求斜率；已知直线的倾斜角α或α的某种三角函数，根据k=tanα来求斜率。

利用斜率证明三点共线的方法：已知A(x1,y1),B(x2,y2),C(x3,y3)，若x1=x2=x3或kAB=kBC，则有A、B、C三点共线。

考点一：斜率与倾斜角。

例1.已知直线l的斜率的绝对值等于3，则直线的倾斜角为30度或150度。

例2.已知过两点A(m2+2,m2-3),B(3-m2-m,2m)的直线l的倾斜角为45度，求实数m的值。

考点二：三点共线。

已知三点A(a,2)、B(3,7)、C(-2,-9a)在一条直线上，求实数a的值。

考点三：斜率范围。

例1.已知两点A(-2,-3),B(3,0),过点P(-1,2)的直线l与线段AB始终有公共点，求直线l的斜率k的取值范围。

例2.已知实数x、y满足2x+y=8，当2≤x≤3时，求y的最大值与最小值。

二、直线方程直线方程有四种形式：点斜式、斜截式、两点式和截距式。

其中，点斜式的形式为y-y1=k(x-x1)，斜截式的形式为y=kx+b，两点式的形式为(y-y1)/(x-x1)=(y2-y1)/(x2-x1)，截距式的形式为xy+a+b=0.点斜式的局限性是不包括垂直于x轴的直线，斜率k为斜率。

斜截式的局限性是不包括垂直于x轴和y轴的直线，k为斜率，b是直线在y轴上的截距。

直线的五种方程形式直线是数学的基础概念，它有多种表示方式，其中最常见的形式是直线的方程形式。

它是将定义直线所需的知识组合起来的一种数学表达方式。

本文将重点介绍直线的五种方程形式，以便更好地了解这种概念。

首先，我们介绍标准形式。

标准形式由原点和一条斜率m组成，其中m称为斜率，可以通过求出斜率m的值来确定一条直线的斜率。

当m>0时，直线从原点向右上方延伸；当m<0时，直线从原点向左下方延伸；当m=0时，直线与x轴平行。

标准形式的方程为：y=mx+b，其中m表示斜率，b表示直线上任意一点的y坐标。

其次，我们介绍斜截式。

斜截式由斜率m和直线上任意一点组成，可以用y-y1=m(x-x1)来表示。

其中m表示斜率，(x1,y1)表示直线上任意一点坐标。

第三，我们介绍斜截式第二形式。

斜截式第二形式是直线的一种另类表示形式，其方程为：y-y1=m(x-x1)/(x2-x1)，其中m为斜率，(x1,y1)为直线上某一点，(x2,y2)为直线上另一点。

接下来，我们介绍点斜式。

点斜式也是直线的一种表示形式，其标准点斜式方程为：(y-y1)/(y2-y1)=(x-x1)/(x2-x1)，其中(x1,y1)和(x2,y2)分别为直线上的两点。

最后，我们介绍参数方程式。

参数方程式是由直线的曲线方程式推导出来的，可以用x=at+b和y=ct+d表示，其中a、c分别表示斜率，b、d分别表示来自原点的偏移量。

参数方程式可以用于表示任意直线，甚至垂直于某一直线的直线也可以用参数方程式表示。

以上就是直线的五种方程形式。

它们的表达形式各不相同，但实质都是一样的，都是表示一条直线的数学形式。

只要了解了它们之间的联系，就可以轻松掌握它们，进一步学习数学知识。

直线的方程知识点总结1. 直线的一般方程直线的一般方程一般形式为：Ax + By + C = 0，其中 A、B、C 为常数。

例如，2x + 3y - 5 = 0就是直线2x + 3y = 5的一般方程。

2. 直线的斜率截距方程直线的斜率截距方程形式为：y = mx + c，其中 m 表示直线的斜率，c 表示直线与 y 轴的截距。

斜率（m）可以通过两点之间的坐标差值来求得。

假设两点的坐标分别为(x1, y1)和(x2, y2)，则斜率m = (y2 - y1) / (x2 - x1)。

例如，过点 (2, 5) 和 (4, 9) 的直线的斜率为(9 - 5) / (4 - 2) = 2，截距可以通过取其中一个点的坐标代入方程来求得。

3. 直线的点斜式方程直线的点斜式方程形式为：y - y1 = m(x - x1)，其中 (x1, y1) 是直线上的已知点，m 是直线的斜率。

通过已知斜率和一个点，可以得到直线的方程。

例如，已知直线的斜率为 3，通过点 (2, 4)，直线的点斜式方程为y - 4 = 3(x - 2)。

4. 直线的截距式方程直线的截距式方程形式为：x/a + y/b = 1，其中 a 和 b 分别为 x 轴和 y 轴的截距。

通过截距式方程可以直接得到直线的截距。

例如，直线过 x 轴的截距为 4，过y 轴的截距为 6，直线的截距式方程为x/4 + y/6 = 1。

5. 两条直线的相交性判断两条直线相交的条件是它们的斜率不相等。

如果两条直线的斜率相等，则它们平行或重合。

如果两条直线的斜率为 m1 和m2，且 m1 = m2，则它们重合；如果两条直线的斜率分别为 m1 和 m2，且m1 ≠ m2，则它们平行。

6. 直线的垂直性判断两条直线垂直的条件是它们的斜率的乘积为 -1。

如果两条直线的斜率分别为 m1 和 m2，且 m1 * m2 = -1，则它们垂直于彼此。

7. 通过两点确定直线的方程已知两点 (x1, y1) 和 (x2, y2)，可以通过这两点来确定一条直线的方程。

直线的表达式有哪些直线是一种在数学中经常研究的基本几何概念。

在平面几何中，直线由一对相互垂直的轴线确定。

直线的表达式是描述直线的数学方程或式子，可以用于确定直线在平面上的位置和性质。

在数学和物理学等领域中，直线的表达式有多种形式，下面将介绍其中几种常见的表达方式。

1. 一般式方程直线的一般式方程可以表示为 Ax + By + C = 0 的形式，其中 A、B 和 C 是常数，x 和 y 是变量。

这种表达方式也被称为标准式方程。

一般式方程可以用于表示任意的直线，包括水平线、垂直线和倾斜线。

通过给定的 A、B 和 C 的值，可以唯一确定一条直线。

2. 斜截式方程斜截式方程是直线的另一种常见表达方式，它可以表示为 y = mx + b 的形式，其中 m 是直线的斜率，b 是直线与 y 轴的交点。

斜截式方程可以直观地表示直线的斜率和截距信息，因此在实际问题中常常使用。

3. 点斜式方程点斜式方程是通过直线上的一点和直线的斜率来表示直线的方程。

它可以表示为 y - y1 = m(x - x1) 的形式，其中 (x1, y1) 是直线上的一点，m 是直线的斜率。

点斜式方程可以通过给定的点和斜率来唯一确定一条直线。

4. 截距式方程截距式方程是直线的一种特殊表达方式，可以表示为 x/a + y/b = 1 的形式，其中 a 和 b 是直线与 x 轴和 y 轴的截距。

截距式方程可以方便地表示直线与坐标轴的交点，因此在计算问题中常常使用。

5. 向量方程直线的向量方程是使用向量来表示直线的方程。

它可以表示为 r = a + tb 的形式，其中 r 是直线上的任意一点，a 是直线上的已知点， t 是一个参数，b 是直线的方向向量。

向量方程可以表示出直线上任意一点的位置，因此在向量计算和解析几何中非常有用。

这些是直线的几种常见表达式，每种表达方式都有其独特的特点和适用范围。

了解不同的直线表达式形式，有助于我们在解决数学和科学问题时能够灵活运用直线的数学模型，准确描述直线的性质和特征。

高中数学 知识与方法必修二 第二章 直线的方程1、直线的倾斜角与斜率：（1）直线的倾斜角：x 轴正向与直线l 向上方向之间所成的角。

当直线l 与x 轴平行或重合时，倾斜角为0． 直线l 的倾斜角α的范围：[)0π，． （2）斜率：[)tan ,0k ααπ=∈， 当2πα=时，直线的斜率k 不存在。

直线经过两点()()111222P x y P x y ，，，，其斜率为： ()211221y y k x x x x -=≠- 倾斜角α 0 02πα<<2π 2παπ<< 斜率k 0 0k >，递增 不存在 0k <，递增横截距：直线与x 轴交点(),0a 的横坐标a 纵截距：直线与y 轴交点()0,b 的纵坐标b注意：①截距不是距离，而是实数．可以大于0，可以小于0，也可以等于0。

②令0x =，求出y 即为纵截距；令0y =求出x 即为横截距；当直线过原点时，0a b ==。

名称 方程常数的几何意义适用范围点斜式 00()y y k x x -=-()0,x y 是直线上一定点，k 是斜率与x 轴不垂直的直线 斜截式 y kx b =+ k 是斜率，b 为纵截距与x 轴不垂直的直线 两点式 112121y y x x y y x x --=-- ()()1122,,,x y x y 是直线上两定点与x 轴、y 轴都不垂直的直线截距式 1x y a b+=,a b 分别是直线的非零横截距，非零纵截距 与x 轴、y 轴都不垂直且不过原点的直线 一般式()2200Ax By C A B ++=+≠ A B C 、、为系数坐标平面内任意直线几种特殊直线的方程：①当斜率k 不存在时：0x x =，特别的y 轴所在直线0x = ②当斜率0k =时：0y y =，特别的x 轴所在直线0y = ③过原点的直线：y kx =(k 存在) 求直线的方程（待定系数法）：①过点00(,)P x y 的直线，可设点斜式方程：()00y y k x x -=-（注意讨论k 是否存在）； ②斜率为k 的直线，可设为斜截式：y kx b =+； ③与直线y kx b =+平行的直线可设为：y kx m =+;与直线0Ax By C ++=平行的直线可设为：0Ax By C ++=’④与y kx b =+垂直的直线可设为：1y x m k=-+;与0Ax By C ++=垂直的直线可设为：0Bx Ay C -+=’⑤过两直线1110Ax B y C ++=与2220A x B y C ++=的交点的直线可设为：111Ax B y C +++2220)A x B y C R λλ++=∈（），（（不含直线2220A x B y C ++=） 3、中点与距离公式：①中点坐标公式：11(,)M x y ，22(,)N x y ，则线段MN 的中点1122,22x y x y P ++⎛⎫⎪⎝⎭； ②两点间的距离：11(,)M x y ，22(,)N x y，MN 原点O(0，0)与任一点P(x ，y)的距离|OP|＝x 2＋y 2.； ③点到直线距离： 00(,)P x y ，:0l Ax By C ++=，则d ；④两平行直线间的距离：11:0l Ax By C ++=，22:0l Ax By C ++=，则d =；4、两条直线的位置关系（1）111222:,:l y k x b l y k x b =+=+①121212,l l k k b b ⇔=≠∥；②12121l l k k ⊥⇔=-注意：利用斜率判断直线的平行与垂直时，要注意斜率的存在与否。

直线方程的五种形式直线方程的五种形式，从不同的侧面反映了直线的几何与数量特性.由于它们有各自不同的适用范畴和隐性约束，因此，我们在根据条件求直线方程时，要特别注意不同形式直线方程的适用性，千万不要漏掉了特殊情形.【直线方程的五种基本形式】①点斜式方程：y-y0=k(x-x0).适用于点P(x0，y0)和斜率k为已知.注意：此种形式不包含垂直于x轴的直线.当斜率不存在时，直线方程应为x=x0.②斜截式方程：y=kx+b.适用于点(0，b)和斜率k为已知.其中b叫做直线l在y轴上的截距.截距不是距离，它可以取任意实数.斜截式是点斜式过点(0，b)时的特例. 此种形式也不包含垂直于x轴的直线.③两点式：y−y1y2−y1=x−x1x2−x1(x1≠x2，y1≠y2).适用于两点(x1，y1)，(x2，y2)的坐标为已知.注意：此种形式不包含垂直于x轴和y轴的直线.③截矩式：xa +yb=1.适用于直线l与x轴、y轴的交点(a，0)和(0，b)为已知.注意：此种形式不包含垂直于x轴和y轴及过原点的直线.③一般式：Ax+By+c=0 (A，B不全为0).例1(1)设直线ax+by+c=0的倾斜角为α，且sinα+cosα=0，则a、b满足( ).A.a+b=1.B.a-b=1.C.a+b=0.D.a-b=0.(2)已知ab<0，bc<0.则直线ax+by=c通过( ).A.第一，二，三象限.B.第一，二，四象限.C.第一，三，四象限.D.第二，三，四象限.(3)若方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线，则实数m满足( ).A.m≠0.B.m≠−32. C. m≠1. D. m≠1且m≠−32.解:(1)③ 直线ax+by+c=0的倾斜角为α，且sinα+cosα=0③ k=tanα=-1，又③直线ax+by+c=0的斜率为k= −ab，③ a-b=0. 故应选D.(2)将直线ax+by=c化为截距式y= −ab x+cb，③ ab<0，bc<0，③ 此直线的斜率k>0,在y轴上的截距为负，故应选C.(3)要方程(2m2+m-3)x+(m2-m)y-4m+1=0表示一条直线，则必须满足m2+m-3与m2-m不能同时为0. ③ m≠1. 故应选C.例2.(1)经过点A(1，2)并且在两个坐标轴上截距的绝对值相等的直线有几条？请求出这些直线的方程.(2)已知直线l在y轴上的截距为-4，且它与两坐标轴围成的三角形的面积为8，求l的方程.解:(1)当截距为0时，设y=kx，过点A(1，2)，则得k=2，即y=2x；当截距不为0时，设x+y=a或x-y=a.将点A(1，2)代入所设方程中，得a=3，或a= -1，故这样的直线有3条：y=2x，x+y-3=0，或x-y+1=0.(2)由已知可设直线l的方程为xa +y−4=1.∵直线l与两坐标轴围成的三角形面积为8，③ 12|a ||−4|=8，解得a=±4，故x -y -4=0或x+y+4=0为所求.想一想①：1.过点(1，5)且在两轴上截距相等的直线有几条？分别是怎样的？2.求在x 轴上的截距为1，且倾斜角的正弦为45的直线方程.3.过点A(-5，-4)作一直线l ，使它与两坐标轴相交且与两轴所围成的三角形面积为5．说明：求满足一定条件的直线方程时，若条件中含有“在两坐标轴上的截距相等、互为相反数、绝对值相等或与两坐标轴围成的三角形面积有关”时，均可将直线方程设为截距式，且不要忽略了特例——过原点的直线y=kx.例3(1)已知两点A(3，0)、B(0，4)，动点P 在线段AB 上运动，求xy 的最大值.(2)过点P(4，3)作直线l 与x 、y 的正半轴分别交于A 、B 两点，O 为原点，当|OA|+|OB|最小时，求直线l 的方程.解:(1)设线段AB 所对应的直线方程为x a +yb =1，∵ 点A 、B 在其上， ∴ x3+y4=1 (x>0，y>0).由均值不等式可得1≥2√xy 12,⇒xy ≤3.∴ (xy)max =3.(2)设直线l 的方程为xa +yb =1，∵ 直线l 过点P(4，3)，∴ 4a +3b =1. 又∵ (a+b)(4a +3b)=7+4b a+3a b≥7+4√3，∴ (a+b)max =7+4√3.当且仅当{4b a=3ab,4a +3b=1,即{a =4+2√3,b =3+2√3.时|OA|+|OB|最小. 此时直线l 的方程为√3x +2y −6=0.例4.(1)若方程x 2-my 2+2x+2y=0表示两条直线，则m= ． (2)方程(2x ＋3y －1)(x －3－1)＝0表示的曲线是( ).A.两条直线.B.两条射线.C.两条线段.D.一条直线和一条射线. 解:(1)法1.③ 方程x 2-my 2+2x+2y=0表示两条直线，则关于x 的一元二次方程：x 2+2x+(-my 2+2y)=0根的判别式4842+-=∆y my 一定是完全平方式， ③ .1,06482=⇒=-=∆'m m法2.③ 方程x 2-my 2+2x+2y=0表示两条直线，③x 2-my 2+2x+2y ))((b my x a y x +++-≡.即x 2-my 2+2x+2y=x 2-my 2+(m -1)xy+(a+b)x+(am -b)y+ab=0，比较对应项的系数可得，m=1，a=2，b=0.(2)∵ (2x ＋3y －1)(x －3－1)＝0，∴ {2x +3y −1=0,√x −3有意义,或√x −3−1=0.解得2x+3y -1=0(x≥3)或x=4，故应选D.想一想①：1.过点P(2，1)作直线l 与x 、y 的正半轴分别交于A 、B 两点，O 为原点，求当|PA||PB|最 小时直线l 的方程.2.方程x 2-xy -2y 2+x+y=0表示的两条直线方程分别是 .习题3.2.1.已知集合M={(x ，y)|123+=--a x y }，N={(x ，y)|y -3=(a+1)(x -2)}.则有( ).A.M=N.B.M③N=M.C. M∩N=ND.M ⊆N. 2.若方程x+y -4√x +y +2m=0表示一条直线，则实数m 满足( ) ． A.m=0. B.m=2. C.m=2或m ＜0.D.m≥2.3.直线l 与两直线y=1交于A ，B 两点，若线段AB 的中点为M(1，-1)，则直线l 的斜率为( ).A.32. B. 23. C.− 32. D.−23.4.一直线过点M(-3，4)，并且在两坐标轴上截距之和为12，这条直线方程是_ .5.已知关于x ，y 的方程x 2-4xy+my 2-x+(3m -10)y -2=0表示两条直线，则m= ．6.当a 为何值时，直线(a -1)x+(3-a)y+a=0在两坐标轴上的截距相等.7.把函数y=f(x)在x=a 及x=b 之间的一段图象近似地看作直线，设a ≤c ≤b ， 证明：f(c)≈f (a )+c−ab−a [f (b )−f(a)].8.求经过点A(-2，2) 被两坐标轴围成的三角形的面积是1的直线方程.【参考答案】想一想①：1.两条；5x-y=0，x+y-6=0.2.4x-3y-4=0或4x+3y-4=0.3.2x-5y-10=0或8x-5y+20=0.想一想①：1.x+y-3=0.如图D4.2—1.设∠BAO=θ,θ∈(0,π2).则|PA|=1sinθ,|PB|=2cos θ,⇒|PA||PB|=4sin2θ,当且仅当θ=π4,即k=-1时，|PA||PB|取得最小值4.2.x+y=0或x-2y+1=0.习题3.2.1.D.2.C.令√x+y=t，则问题转换为t2-4t+2m=0的两根相等且非负，或有一正根和一负根.3.A.4.4x-y+16=0或x+3y-9=0.5.3或4.6.若直线过原点，则a=0；直线不过原点，则a=2.7.A，B，C三点共线，∴k AC=k AB, 即y c−f(a)c−a =f(b)−f(a)b−a,∴y c−f(a)=c−ab−a [f(b)−f(a)], 即y c=f(a)+c−ab−a[f(b)−f(a)],∴f(c)≈f(a)+c−ab−a[f(b)−f(a)].8. x+3y-2=0或2x+y+2=0.x yO ABP(2.1)图D3.2—1。

1．直线方程的几种基本形式及适用条件：(1)点斜式： ，注意斜率k 是存在的．(2)斜截式： ，其中b 是直线l 在 上的截距．(3)两点式： (x 1≠x 2且y 1≠y 2)，当方程变形为(y 2－y 1)(x －x 1)－(x 2－x 1)(y －y 1)＝0时，对于一切情况都成立．(4)截距式： ，其中a ·b ≠0，a 为l 在x 轴上的截距，b 是l 在y 轴上的截距．(5)一般式： ，其中A 、B 不同时为0.1．判定两条直线的位置关系(1)两条直线的平行①假设l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则l 1∥l 2⇔ 且 ，l 1与l 2重合⇔ .②当l 1，l 2都垂直于x 轴且不重合时，则有 .③假设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，则l 1∥l 2⇔A 1B 2＝A 2B 1且B 1C 2≠B 2C 1，l 1与l 2重合⇔A 1＝λA 2，B 1＝λB 2，C 1＝(2)两条直线的垂直①假设l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则l 1⊥l 2⇔ . ②假设两条直线中，一条斜率不存在，同时另一条斜率等于零，则两条直线 ．③假设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，则l 1⊥l 2⇔ .(3)直线l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2相交的条件是 . 直线l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0相交的条件是 .自测题1．过点M (－1，m )，N (m ＋1,4)的直线的斜斜角为45° ，则m 的值为2. 以下四个命题中真命题是( )A ．经过定点P 0(x 0，y 0)的直线都可以用方程y －y 0＝k (x －x 0)表示B ．经过任意两个不同点P 1(x 1，y 1)，P 2(x 2，y 2)的直线可以用方程(y －y 1)(x 2－x 1)－(x －x 1)(y 2－y 1)＝0表示C ．不过原点的直线都可以用x a ＋y b ＝1表示D ．经过定点A (0，b )的直线都可以用方程y ＝kx ＋b 表示3．假设三点A (2,3)，B (3，－2)，C (12，m )共线，则m 的值是________．4．已知直线x ＋a 2y ＋6＝0与直线(a －2)x ＋3ay ＋2a ＝0平行，则a 的值为________．5．已知两条直线y ＝ax －2和y ＝(a ＋2)x ＋1互相垂直，则a 等于________．例题例1.已知两点A (－1,2)，B (m,3)，求：(1)求直线AB 的斜率； (2)求直线AB 的方程；例2．已知直线l ：ax ＋y －2－a ＝0在x 轴和y 轴上的截距相等，则a 的值是______例3.已知直线：l 1：ax ＋2y ＋6＝0和直线l 2：x ＋(a －1)y ＋a 2－1＝0.(1)试判断l 1与l 2是否平行；(2)l 1⊥l 2时，求a 的值例4.已知两直线l 1：mx ＋8y ＋n ＝0和l 2：2x ＋my －1＝0.试确定m 、n 的值，使：(1)l 1与l 2相交于点P (m ，－1)； (2)l 1∥l 2； (3)l 1⊥l 2，且l 1在y 轴上的截距为－1.练习题1．以下命题中，正确的选项是( )A ．假设直线的斜率为tan α，则直线的倾斜角是αB ．假设直线的倾斜角为α，则直线的斜率为tan αC ．假设直线的倾斜角越大，则直线的斜率就越大D ．直线的倾斜角α∈[0，π2)∪(π2，π)时，直线的斜率分别在这两个区间上单调递增2.．假设直线l 1，l 2关于x 轴对称，l 1的斜率是－7，则l 2的斜率是( ) A.7B ．－77 C.77 D ．－7 3.．两直线x m －y n ＝1与x n －y m ＝1的图像可能是图中的哪一个( )4.．假设点A (a,0)，B (0，b )，C (1，－1)(a >0，b <0)三点共线，则a －b 的最小值等于______5.．过点M (1，－2)的直线与x 轴、y 轴分别交于P 、Q 两点，假设M 恰为线段PQ 的中点，则直线PQ 的方程为______6.．已知直线l 的斜率为16，且和坐标轴围成面积为3的三角形，求直线l 的方程．7.．已知点M 是直线l ：3x －y ＋3＝0与x 轴的交点，将直线l 绕点M 旋转30°，求所得到的直线l ′的方程．8.．在△ABC 中，已知A (1,1)，AC 边上的高线所在直线方程为x －2y ＝0，AB 边上的高线所在直线方程为3x ＋2y －3＝0.求BC 边所在直线方程．9.．设直线l 的方程为(a ＋1)x ＋y ＋2－a ＝0(a ∈R )．(1)假设l 在两坐标轴上截距相等，求l 的方程；(2)假设l 不经过第二象限，求实数a 的取值范围．高中数学必修二直线和圆练习一、选择题1．过点(1,3)P -且垂直于直线032=+-y x 的直线方程为〔 〕A ．012=-+y xB ．052=-+y xC ．052=-+y xD ．072=+-y x2．已知过点(2,)A m -和(,4)B m 的直线与直线012=-+y x 平行，则m 的值为〔 〕A ．0B ．8-C ．2D ．103．已知0,0ab bc <<，则直线ax by c +=通过〔 〕A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限 4．直线l 与两直线1y =和70x y --=分别交于,A B 两点，假设线段AB 的中点为 (1,1)M -，则直线l 的斜率为〔 〕A ．23B ．32C ．32-D ． 23-. 5. 圆C 1:x 2+y 2+4x-4y+7=0和圆C 2:x 2+y 2-4x-10y+13=0的公切线有( )条条条 D.以上均错6. 已知空间两点A(1,3,5)、B(-3,1,3),则线段AB 的中点坐标为( )A.(-1,2,4)B.(2,1,1)C.(1,0,4)D.(3,3,-1)7.假设直线(1+a)x+y+1=0与圆x 2+y 2-2x=0相切，则a 的值为( )、、8.已知圆C ：(x-a)2+(y-2)2=4(a>0)及直线l ：x-y+3=0，当直线l 被圆C 截得的弦长为32时，则a 等于( ) A.2 B.22- C.12- D.12+二、填空题1．点(1,1)P - 到直线10x y -+=的距离是________________.2.经过点P(1,2)与圆x 2+y 2=1相切的直线方程为______________.3. 与两平行直线x+3y-5=0和x+3y-3=0相切,圆心在直线2x+y+3=0上的圆的方程是________.4. 已知圆x 2+y 2-4x+6y-12=0的内部有一点A(4，-2)，则以A 为中点的弦所在的直线方程为______________________.三、解答题1．求经过点(2,2)A -并且和两个坐标轴围成的三角形的面积是1的直线方程。

已知直线 l的 斜 率 为 k , 与y轴 的 交 点 是 (0, b), 求直线的方程 . 解: 由直线的点斜式,得 y b k ( x 0)
即y kx b
y
方程y kx b叫做直线方程的斜截式 .方程
b叫做直线 l在y轴上的截距 .
b

l
斜---斜率 截---y轴上的截距
y y1 x x1 方程 叫做 直线的两 点式 y 2 y1 x 2 x 1
练习 已知直线经过两点 P1 (2,1), P2 (0,3)
则直线的方程为
y 1 x2 即2 x y 3 0 31 0 2
四.直线的截距式方程
已知直线 l与x轴的交点为 (a,0),与y轴的交点为 (0, b),其中a 0, b 0, 求直线 l的方程 .
求这个三角形三边所在 的直线方程 .
解: 把A, C代入两点式 ,得 y 0 x (5) 2 0 0 (5)
2 x 5 y 10 0
AC在x, y轴 另解: 由A, C两点的坐标得直线
上的截距为 a 5, b 2. 由 截 距 式 得
x y 1 5 2
化成一般式得 : 4 x 3 y 12 0
例5:
把直线方程 2 x 3 y 6 0化成斜截式 , 截距 式, 求出它的斜率和它在 x, y轴上的截距 .
2 y x 2. 解: 斜 截 式 为 3 x y 2 截距式为 1斜 . 率k . 3 2 3 x轴上的截距为 a 3, y轴上的截距为 b 2.
解: 把点 (a,0),(0, b)代入两点式方程 ,得
y0 xa b0 0a
x y 1 a b

直线方程公式大全直线是数学中最基本的几何图形之一，研究直线在平面上的性质和表示方法对于解决许多实际问题具有重要意义。

直线方程公式是表示直线的数学表达式，可以根据直线的特征和已知条件求解直线方程。

在本文中，我们将介绍常见的直线方程公式，包括点斜式、两点式、截距式和一般式。

1. 点斜式点斜式是直线方程表示的一种常用形式，它利用直线上的一点及其斜率来表示直线。

假设直线上有一点P(x₁, y₁)，直线的斜率为k，则直线的点斜式为：y - y₁ = k(x - x₁)其中，(x, y)为直线上的任意一点。

2. 两点式两点式是直线方程表示的另一种常见形式，它利用直线上的两个点来表示直线。

假设直线上有两个点P₁(x₁, y₁)和P₂(x₂, y₂)，则直线的两点式为：(y - y₁)/(x - x₁) = (y₂ - y₁)/(x₂ - x₁)3. 截距式截距式是直线方程表示的一种常用形式，它利用直线在x轴和y轴上的截距表示直线。

假设直线与x轴交点为A(a, 0)，与y轴交点为B(0, b)，则直线的截距式为：x/a + y/b = 14. 一般式一般式是直线方程表示的一种标准形式，它利用直线的一般方程来表示直线。

假设直线的一般方程为Ax + By + C = 0，其中A、B、C为常数且A和B不同时为0，则直线的一般式为：Ax + By + C = 05. 总结这些直线方程公式是数学中常见的描述直线的方式。

根据已知的线段、斜率、截距等条件，我们可以使用这些方程公式来表示和求解直线。

•点斜式：利用直线上的一点及其斜率来表示直线。

•两点式：利用直线上的两个点来表示直线。

•截距式：利用直线在x轴和y轴上的截距表示直线。

•一般式：利用直线的一般方程来表示直线。

根据不同的问题和已知条件，选择合适的直线方程公式可以简化问题的求解过程，并帮助我们更好地理解和应用直线的性质。

希望本文介绍的直线方程公式对您有所帮助！。

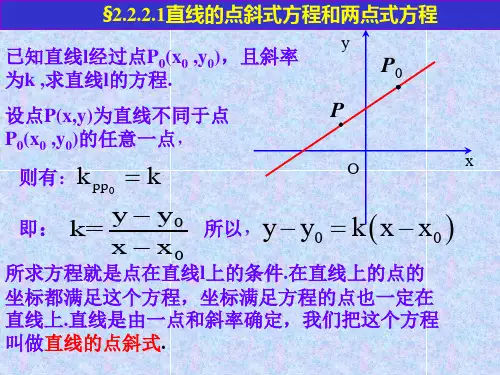
直线方程的几种形式（一）教学目标：掌握直线方程的点斜式、两点式教学重点：掌握直线方程的点斜式、两点式教学过程： (一)1,点斜式已知直线l 的斜率是k ，并且经过点P 1(x 1，y 1)，求直线l 的方程？设点P(x ，y)是直线l 上不同于P 1的任意一点，根据经过两点的斜率公式得11x x y y k --=(1) )(11x x k y y -=-(2)注意方程(1)与方程(2)的差异：点P 1的坐标不满足方程(1)而满足方程(2)，因此，点P 1不在方程(1)表示的图形上而在方程(2)表示的图形上，方程(1)不能称作直线l 的方程．重复上面的过程，可以证明直线上每个点的坐标都是方程(2)的解；对上面的过程逆推，可以证明以这个方程的解为坐标的点都在直线l 上，所以这个方程就是过点P 1、斜率为k 的直线l 的方程．这个方程是由直线上一点和直线的斜率确定的，叫做直线方程的点斜式．当直线的斜率为0°时，k=0，直线的方程是y=y 1．当直线的斜率为90°时，直线的斜率不存在，它的方程不能用点斜式表示．但因l 上每一点的横坐标都等于x 1，所以它的方程是x=x 1．2,斜截式已知直线l 在y 轴上的截距为b ，斜率为b ，求直线的方程．这个问题，相当于给出了直线上一点(0，b)及直线的斜率k ，求直线的方程，是点斜式方程的特殊情况，代入点斜式方程可得：y -b=k(x-0)也就是b kx y +=上面的方程叫做直线的斜截式方程．当k ≠0时，斜截式方程就是直线的表示形式，这样一次函数中k 和b 的几何意义就是分别表示直线的斜率和在y 轴上的截距．（二）两点式已知直线l上的两点P1(x1，y1)、P2(x2，y2)，(x1≠x2)，求直线的方程当y1≠y2时，为了便于记忆，我们把方程写成这个方程是由直线上两点确定的，叫做直线的两点式．（三）例子见书上小结：直线方程的点斜式、两点式。