下载文档原格式
高速流水线浮点加法器的FPGA实现
0 引言
现代信号处理技术通常都需要进行大量高速浮点运算。
由于浮点数系统
操作比较复杂，需要专用硬件来完成相关的操作(在浮点运算中的浮点加法运算
几乎占到全部运算操作的一半以上)，所以，浮点加法器是现代信号处理系统中
最重要的部件之一。
FPGA 是当前数字电路研究开发的一种重要实现形式，它
与全定制ASIC 电路相比，具有开发周期短、成本低等优点。
但多数FPGA 不
支持浮点运算，这使FPGA 在数值计算、数据分析和信号处理等方面受到了限制，由于FPGA 中关于浮点数的运算只能自行设计，因此，研究浮点加法运算
的FPGA 实现方法很有必要。
1 IEEE 754 单精度浮点数标准
浮点数可以在更大的动态范围内提供更高的精度，通常，当定点数受其
精度和动态范围所限不能胜任时，浮点数标准则能够提供良好的解决方案。
IEEE 协会制定的二进制浮点数标准的基本格式是32 位宽(单精度)和64
位宽(双精度)，本文采用单精度格式。
图1 所示是IEEE754 单精度浮点数格式。
图中，用于单精度的32 位二进制数可分为三个独立的部分，其中第0 位到22
位构成尾数，第23 位到第30 位构成指数，第31 位是符号位。
实际上，上述格式的单精度浮点数的数值可表示为：
上式中，当其为正数时，S 为0；当其为负数时，S 为1；(-1)s 表示符号。
指数E 是ON255 的变量，E 减127 可使指数在2-127 到2128 变化。
尾数采用科学计算法表示：M=1．m22m21m20……m0。
m22，m21，…，m0，mi 为Mp。
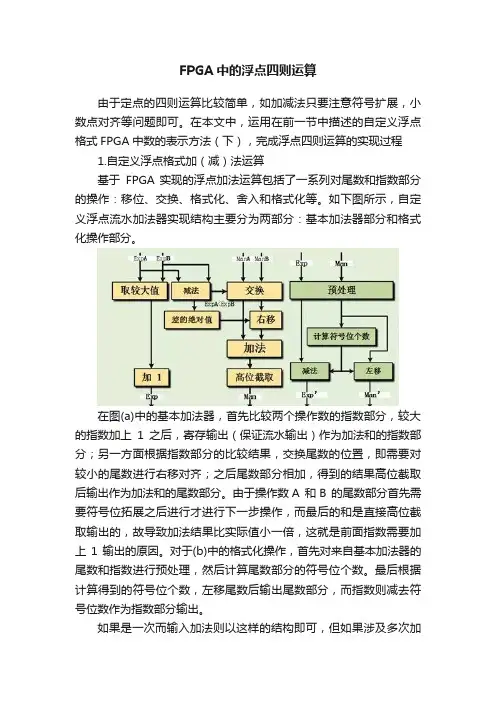
FPGA中的浮点四则运算由于定点的四则运算比较简单，如加减法只要注意符号扩展，小数点对齐等问题即可。
在本文中，运用在前一节中描述的自定义浮点格式FPGA中数的表示方法（下），完成浮点四则运算的实现过程1.自定义浮点格式加（减）法运算基于FPGA 实现的浮点加法运算包括了一系列对尾数和指数部分的操作：移位、交换、格式化、舍入和格式化等。
如下图所示，自定义浮点流水加法器实现结构主要分为两部分：基本加法器部分和格式化操作部分。
在图(a)中的基本加法器，首先比较两个操作数的指数部分，较大的指数加上1之后，寄存输出（保证流水输出）作为加法和的指数部分；另一方面根据指数部分的比较结果，交换尾数的位置，即需要对较小的尾数进行右移对齐；之后尾数部分相加，得到的结果高位截取后输出作为加法和的尾数部分。
由于操作数A 和B 的尾数部分首先需要符号位拓展之后进行才进行下一步操作，而最后的和是直接高位截取输出的，故导致加法结果比实际值小一倍，这就是前面指数需要加上1输出的原因。
对于(b)中的格式化操作，首先对来自基本加法器的尾数和指数进行预处理，然后计算尾数部分的符号位个数。
最后根据计算得到的符号位个数，左移尾数后输出尾数部分，而指数则减去符号位数作为指数部分输出。
如果是一次而输入加法则以这样的结构即可，但如果涉及多次加法，以流水形式完成，则在结构上可以作更好的优化。
如下是四输入和八输入加法器的结构：如上所示的情况，可知，这样的方法可以减少格式化操作，而格式化操作在整个运算过程中消耗相对比较多的资源，因此这样的实现结构可以有效的减少硬件资源的消耗。
3. 乘加运算浮点乘法运算较为简单，对应的尾数部分进行相乘，指数部分进行相加。
尾数相乘部分采用XILINX 乘法器IP即可。
需要注意的是，乘法结果输出的位宽指定，在乘法器IP中，按一般流程下来，乘完之后的结果是保留两位符号位（假设乘数都是一个符号的情况），即多出一个符号位，按小数乘法分析的话，值的情况是比实际结果小一倍，在截位输出的时候需要做一定的取舍（是从最高位开始截位输出，还是次高位开始截位输出；如果从最高位截位输出，则结果比实际值小一倍，如果从次高位截位输出只有一种情况会溢出，即两个乘数都为-1的情况，这种情况如果从次高位截位输出则会错误，其余情况都是正确的）。
基于FPGA的全流水浮点乘累加器的设计及实现作者：李世平陈铠来源：《电子技术与软件工程》2016年第02期摘要为提升浮点乘累加的流水性能，本文提出了一种基于FPGA全流水浮点乘累加器的设计和实现方法。
通过无阻赛流水累加和串形全加等技术，实现了任意长度单精度浮点复向量的乘累加计算，且相邻两个向量之间无流水间隙。
该累加器在Xilinx的XC7VX690T FPGA上实现，乘法器和逻辑资源消耗不到1%，最高运行频率可达279MHz。
【关键词】FPGA 浮点乘累加全流水1 引言随着半导体技术的不断发展，FPGA的功能和性能显著提升，正逐渐成为雷达、通信等诸多领域数字系统设计的重点，通常被用做复杂信号处理算法的硬件加速。
浮点乘累加作为信号处理算法中的常用基本单元，在矩阵乘、矩阵协方差、FIR等计算过程中都有着广泛应用。
传统累加器是通过将加法器的输出反馈到输入端来实现，对于浮点运算而言，由于浮点加法计算较复杂，需要经历对阶、尾数运算、结果规格化、舍入处理和溢出判断五个步骤，一般会有7～14级的流水延迟，进而会导致流水线阻塞，因此需要研究采用合理的累加结构来提高流水性能。
Ling Zhuo等人提出了一种面向矩阵运算的流水累加结构，提高了流水性能，但该结构控制机制复杂，且缓存资源消耗大，正比于流水延迟量的平方；袁松等人采用了分级流水线方法，缓存消耗较小，但在中小规模矩阵累加时会出现流水线暂停，而且输出时延较大，与矩阵总数据个数成正比。
本文提出了一种基于FPGA的全流水浮点乘累加器结构，能够实时完成任意长度单精度浮点复向量的乘累加计算，且相邻两个向量之间无流水间隙，该累加器在Xilinx的XC7VX690T FPGA上实现，乘法器和逻辑资源消耗不到1%，最高运行频率可达279MHz，目前已成功在矩阵协方差、求逆等算法实现过程中推广应用。
2 方案设计基于FPGA的全流水乘累加器结构如图1所示。
A和B为两个等长度的浮点向量，valid 表示输入数据有效，last表示当前处理向量的最后一个数据；Q为输出累加结果，Qvalid为累加结果的有效标志。
国防科技大学学报第26卷第6期JOURNAL OF NATIONAL UNIVERSITY OF DEFENSE TECHNOLOGY Voi.26No.62004文章编号：1001-2486（2004）06-0061-04用FPGA实现浮点FFT处理器的研究*王远模，赵宏钟，张军，付强（国防科技大学电子科学与工程学院，湖南长沙410073）摘要：针对定点FFT处理器精度不高的缺点，提出了浮点格式FFT处理器的FPGA硬件实现方案。
详细阐述了FFT处理器的自定制浮点格式确定、算法选择和浮点加法实现等关键技术。
该处理器已投入使用，工作性能稳定，系统时钟80MHz，完成1024点FFT/IFFT运算只需64!s，误差小于-80dB。
关键词：FPGA；FFT；蝶形运算中图分类号：TN47 文献标识码：AThe Realization of Flolating-point FFT Processor with FPGA ChipWANG Yuan-mo，ZHAO Hong-zhong，ZHANG Jun，FU Oiang（Coiiege of Eiectronic Science and Engineering，Nationai Univ.of Defense Technoiogy，Changsha410073，China）Abstract：The FPGA reaiization of a fioating-point FFT processor is proposed to get over the poor precision of the fixed-point FFT processor.The definition of the fioating-point format，the seiection of arithmetic and the key technigues of the FPGA reaiization are discussed.Such a processor has been put into service and has stabie performance.Its operating freguency is 80MHz and it can finish1024point FFT/IFFT in64!s with an error iess than-80dB.Key words：FPGA；FFT；butterfiy computation在现代雷达、通信、图像处理等领域中，数字信号处理系统经常要进行高速、高精度的FFT运算。
基于FPGA的浮点运算器IP核的设计与实现摘要
本文介绍了基于FPGA的浮点运算器IP核的设计与实现。
在实现过程中，我们采用Verilog HDL实现了一个32位浮点运算器的IP核，它能提
供执行加法、减法、乘法、除法以及规范化的功能，并具有很高的精确度。
在Xilinx FPGAs上实现，该IP核实现了高性能和可靠性。
实验结果表明，这种FPGA浮点运算器IP核的性能可以满足各种应用需求。
关键词：FPGA；浮点运算；IP核；Verilog HDL
1. Introduction
随着技术的发展，浮点运算在计算机体系结构中越来越重要。
它不仅
可以提高运算精度，而且可以准确表达计算机的结果。
为了实现高质量的
数字信号处理（DSP）系统，FPGA浮点运算器IP核变得越来越重要。
FPGA的浮点运算器IP核提供了一个高性能、可靠的实现环境，使得
浮点运算器在DSP系统中得以良好的应用。
此外，基于FPGA的浮点运算
器IP核还具有可编程性、低功率、灵活性和低成本等优势。
本文讨论了使用Verilog HDL实现基于FPGA的浮点运算器IP核的设
计与实现。
它包括浮点运算器的功能、实现及性能等方面的介绍。
2. Design and Implementation of FPGA Floating Point Unit
2.1 Floating Point Unit Design
在本文中，我们采用Verilog HDL实现了一个具有32位数据宽度的
浮点运算器IP核。
此外，它还具有加法、减法、乘法、除法以及规范化
的功能。
—202— 快速浮点加法器的FPGA 实现郭天天，张志勇，卢焕章（国防科技大学ATR 实验室，长沙 410073）摘 要：讨论了3种常用的浮点加法算法，并在VirtexII 系列FPGA 上实现了LOP 算法。
实验结果表明在FPGA 上可以实现快速浮点加法器，最高速度可达152MHz ，资源占用也在合理的范围内。
关键词：浮点加法器；移位器；前导1预测；FPGAFPGA Implementation of Fast Floating-point AdderGUO Tiantian, ZHANG Zhiyong, LU Huanzhang(ATR Lab, NUDT, Changsha 410073)【Abstract 】Three commonly used Floating-point addition algorithms are discussed, and the LOP algorithm is implemented on VirtexII series FPGA. The implementing results show that the fast floating-point adder can be implemented on FPGA, the highest running frequency is 152MHz and the area cost is rational compare to the entire resources.【Key words 】Floating point adder ；Shifter ；Leading-one predicator ；FPGA计 算 机 工 程Computer Engineering 第31卷 第16期Vol.31 № 16 2005年8月August 2005·开发研究与设计技术·文章编号：1000—3428(2005)16—0202—03文献标识码：A中图分类号：TP302浮点加/减法是数字信号处理中的一个非常频繁并且非常重要的操作。
基于FPGA的浮点运算器IP核的设计与实现摘要浮点运算作为数字信号处理的最基本的运算，具备动态范围大的特点，不仅成为衡量微处理器性能的主要指标之一，而且广泛适用于复杂的数学计算、科学应用和工程设计中，随着多媒体技术的蓬勃发展，浮点运算单元的应用范围越来越广泛，它已经走入了千家万户，用来解决复杂的数字图像处理，移动物体模型的建立，三维动画设计与演示等等。
随着FPGA的出现以及EDA技术的成熟，采用FPGA实现数字信号处理的方法已经显示出巨大的潜力，利用FPGA技术设计浮点乘法器可以缩短产品的开发周期。
本设计提出了一种基于VHDL语言的浮点乘法器的硬件实现方法，就是用VHDL 语言描述设计文件和原理图方式设计，以Altera公司的Cyclone系列产品为硬件平台，以Quartus为软件工具进行模拟仿真，实现了任意以IEEE754标准表示的23位单精度浮点数的乘法运算。
设计中对阶码的溢出进行了研究并进行了处理，同时对结果进行了规格化处理，通过利用FPGA在线可编程的技术，设计出的浮点乘法器更加方便灵活，克服了专用乘法器的不足，更能广泛的应用到各个领域。
关键词：IEEE754，单精度浮点数，乘法器，硬件描述语言，FPGA，QuartusTHE DESIGN AND IMPLEMENTATION OF FLOATING-POINT UNIT IP CORE BASED ON FPGAABSTRACTAs the most basic operation of digital signal processing, floating-point calculation is equipped with the characteristic of dynamic range, it is not only the main measure of microprocessor performance indexes, but also is widely used in complex mathematical calculation, science applications and engineering design. with the vigorous development of multimedia technology, floating point arithmetic unit has been widely used, and it has come home, been used to solve complex problems, such as digital image processing, the establishment of the moving object model, 3-d animation design and demonstrate, etc. With the maturity of FPGA presence and EDA technology, it has shown great potential to realize digital signal processing by the method of using FPGA, it can cut short the development cycle by using the FPGA technology design floating-point on time-multiplier. The design is proposed based on VHDL language of floating on time-multiplier, the hardware realization method is described with VHDL language schematic design documents and Altera design, by the way the Cyclone series products for hardware platform, with Quartus for software tools for simulation,it realized any twenty-three single precision floating-point multiplication which is in the IEEE754 standard. Design of order yards was studied and spill the processing, and the results are the normalized processing, by using the on-line programmable FPGA technology, design the floating-point greater flexibility on time-multiplier, overcome the deficiency of special on time-multiplier, more can widely used in various fields.KEY WORDS：IEEE754，float，multiplier unit，VHDL，FPGA，Quartus目录前言 (1)第1章绪论 (3)§1.1 引言 (3)§1.2 浮点数的格式 (3)§1.2.1 一般浮点数表示方法 (3)§1.2.2 IEEE754标准表示的浮点数 (4)§1.2.3 浮点数的规格化 (5)§1.2.4 特殊浮点数 (5)§1.3 浮点乘法器的原理 (6)第2章EDA工具介绍 (8)§2.1 EDA技术及其发展 (8)§2.2 EDA设计流程及其工具 (8)§2.2.1 设计流程 (8)§2.2.2 HDL简介 (10)§2.2.3 Quartus II简介 (10)第3章整体框架设计及功能模块介绍 (11)§3.1 设计思路 (11)§3.2 预处理模块 (11)§3.3 定点乘法器 (12)§3.3.1 IEEE754舍入模式 (12)§3.3.2 定点乘法器原理 (13)§3.3.3 定点乘法器模块 (13)§3.4 计算尾数模块 (15)§3.5 计算阶码及溢出处理 (16)§3.5.1 定点加减法原理 (16)§3.5.2 溢出概念与检测方法 (17)§3.5.3 阶码运算原理 (18)§3.5.4 补码模块 (18)§3.5.5 阶码相加模块 (19)§3.5.6 溢出模块 (20)§3.6 数据显示模块 (21)§3.6.1 数据模块 (21)§3.6.2 显示模块 (22)第4章仿真结果及实验验证 (24)§4.1 顶层原理图 (24)§4.2 顶层仿真 (25)§4.2.1 一般情况 (25)§4.2.2 特殊情况 (25)§4.2.3 显示情况 (26)§4.3 引脚锁定 (26)§4.4 硬件平台 (27)§4.4.1 FPGA简介 (27)§4.4.2 芯片选择 (28)§4.5 下载验证 (28)结论 (30)参考文献 (31)致谢 (33)附录 (34)前言21世纪是信息化的时代，信息产业已经成为衡量一个国家经济科技实力的重要标志，集成电路则是信息技术与信息产业的基础，是电子信息产业的命脉。
—202— 快速浮点加法器的FPGA 实现郭天天，张志勇，卢焕章（国防科技大学ATR 实验室，长沙 410073）摘 要：讨论了3种常用的浮点加法算法，并在VirtexII 系列FPGA 上实现了LOP 算法。
实验结果表明在FPGA 上可以实现快速浮点加法器，最高速度可达152MHz ，资源占用也在合理的范围内。
关键词：浮点加法器；移位器；前导1预测；FPGAFPGA Implementation of Fast Floating-point AdderGUO Tiantian, ZHANG Zhiyong, LU Huanzhang(ATR Lab, NUDT, Changsha 410073)【Abstract 】Three commonly used Floating-point addition algorithms are discussed, and the LOP algorithm is implemented on VirtexII series FPGA. The implementing results show that the fast floating-point adder can be implemented on FPGA, the highest running frequency is 152MHz and the area cost is rational compare to the entire resources.【Key words 】Floating point adder ；Shifter ；Leading-one predicator ；FPGA计 算 机 工 程Computer Engineering 第31卷 第16期Vol.31 № 16 2005年8月August 2005·开发研究与设计技术·文章编号：1000—3428(2005)16—0202—03文献标识码：A中图分类号：TP302浮点加/减法是数字信号处理中的一个非常频繁并且非常重要的操作。
在现代数字信号处理应用中，浮点加减运算几乎占到全部浮点操作的一半以上。
浮点算法比定点算法更复杂，占用更多资源。
目前在大多数数字信号处理系统中，一般都是由DSP 芯片来完成浮点运算。
用DSP 芯片完成浮点运算的好处是容易实现，精度高，缺点是加重DSP 芯片的负担，系统速度可能会受到影响。
在某些情况下需要使用专门的浮点处理部件才能满足系统要求。
FPGA 具有可编程、资源丰富、开发周期短、小批量成本低等优点，它已经成为数字电路研究开发的一种重要实现形式，并广泛应用于各种数字信号处理系统当中。
原来在FPGA 中实现浮点处理部件是很困难的，主要是由于早期的FPGA 速度较慢，资源较少，浮点算法对它来说过于复杂。
例如一个32位的浮点加法器就要占用Altera 8188 72%的资源，时钟频率最大只有10MHz [1]，这样的效果当然不能令人满意。
近年来随着集成电路工艺水平的不断提高，以及体系结构方面的发展，FPGA 的容量、速度、资源等方面都有了很大的提高。
例如Xilinx 公司最新的FPGA 已经采用90nm 工艺，最高时钟频率达到420MHz ，容量达到1 000万逻辑门以上，内部还包括处理器、数字锁相环、块RAM 、大量的寄存器等多种资源，支持多种I/O 接口标准[6]。
FPGA 的速度和容量已经不再是瓶颈了，所以研究浮点处理部件的FPGA 实现具有很强的实际意义。
本文将介绍在Xilinx 公司的VirtexII 系列FPGA 上快速浮点加法器的一种实现形式。
1 浮点格式常用的浮点格式为IEEE 754标准，IEEE 754标准有单精度浮点数、双精度浮点数和扩展双精度浮点数3种，单精度为32位，双精度为64位，扩展双精度为80位以上，位数越多精度越高，表示范围也越大。
在通常的数字信号处理应用中，单精度浮点数已经足够用了，本文将以它为例来设计快速浮点加法器。
单精度浮点数如图1所示。
图1 IEEE 754单精度浮点数格式其中s 为符号位，s 为1时表示负数，s 为0时表示正数；e为指数，取值范围为[1，254]，0和255表示特殊值；f 有22位，再加上小数点左边一位隐含的1总共23位构成尾数部分。
由它表示的浮点数v 的值如下式所示。
(127)(1)2(1.)s e v f −=−•• 32位浮点数可以表示的范围为38381.210 3.410−+±×−±×。
在某些情况下可能不需要32位的精度，那么可以用24位或者16位来表示浮点数，如16位浮点数表示如图2所示。
图2 16位浮点数格式16位浮点数v 的值如下式所示。
(31)(1)2(1.)s e v f −=−••16位浮点数可以表示的范围为9108.581510 6.98510−±×−±×。
2 浮点加法器算法浮点加法一般包括求阶差、对阶、尾数求和、规格化和舍入等步骤，具体的算法在各种文献[1,2]上都有详细的叙述，这里就不再一一介绍了。
目前比较常用的浮点加法有3种[3]，如图3所示。
图中用到的符号描述如下：a E ，b E ：加数a 和加数b 的指数；aM，b M ：加数a 和加数b 的尾数；diff ：两个指数的绝对差，diff＝b a M M −；作者简介：郭天天(1974—)，男，博士生，主研方向为ASIC 与实时系统、DSP 与FPGA 应用等；张志勇，博士生；卢焕章，教授、博导 定稿日期：2004-07-08 E-mail ：ttguo0452@位数位数—203—bmans：指数较小的加数通过移位器后的尾数；SUM ：尾数和；aexp：较大的那个指数。
e mbe m（a ）标准算法 （b ）LOP 算法（c ）双通道算法图3 3种常用的浮点加法算法图3(a)所示为标准的浮点加法算法，a E ，b E 送入指数比较器进行比较，得到阶差diff ，前移位器将指数较小的那个数的尾数右移diff 位，得到新的尾数b mans ，然后送入定点加法器进行尾数相加。
如果尾数相加产生了进位，那么把和右移一位，指数加一。
规格化单元对结果进行规格化。
在规格化单元里有一个前导1检测电路（Leading-One- Detector ），可以检测出尾数中第一个1的位置，后移位器根据此位置对尾数进行左移，同时指数减去相应的值。
图3(b)为LOP 算法，它与标准算法的区别在于用前导1预测电路（Leading-One-Predicator ）代替了前导1检测电路（Leading-One-Detector ）。
LOP 电路可以与尾数加法并行执行，这样可以减少整个系统的延迟。
图3(c)为双通道算法。
它有两个并行的数据通道，当指数差大于1时，选择far 通道，指数对阶时分配较长的时间，尾数运算结果规范化时的移位分配较少的时间；否则选择close 通道，此时尾数最多移一位，甚至不用移位，这样可以去掉前移位器。
在上述3种算法中，标准算法延迟最大，占用资源最少；双通道算法延迟最小，占用资源最多；而LOD 算法介于两者中间。
本文将以LOD 算法为例，实现32位的浮点加法器。
为了专注于算法的实现，下面讨论的都是无符号浮点数相加。
3 浮点加法器的实现选用Xilinx 公司的VirtexII 系列FPGA 来实现32位浮点加法器，具体器件为XC2V1000-5。
下面本文将根据器件的特点介绍，浮点加法器中几个关键部件的实现方案。
3.1 移位器实现移位器的方法有很多，例如用选择器来实现，在VirtexII 器件中也可以用内置的块乘法器实现移位[4]，也可以用3态缓冲器来实现移位。
用选择器实现移位时，如果采用2选1选择器，则所需级数太多；如果采用4选1、8选1选择器则延时比较大。
在VirexII 系列FPGA 中内置了一些18位的硬件乘法器，这些乘法器可以用来实现移位器[4]，但通常的做法是把这些乘法器留给乘法运算用。
所以本文选用3态缓冲器来实现移位器。
具体实现如图4所示。
I I I I 321上图所示为一个由3态缓冲器构成的4位移位器，可以看出整个移位器的延时基本固定，即只有1级3态缓冲器的延时，不随位数的增加而增加，这给流水操作增加了不少方便，有一点要注意，移位位数是one-hot 编码。
这种实现方式需要内置的3态缓冲器，不过对于本文使用的FPGA 来说不成问题。
本文设计的24位深度移位器占用资源为24个slices ，最大延时为2.685ns 。
3.2 加法器VirtexII 系列FPGA 中有专用的超前进位逻辑，可以构成快速行波进位加法器。
虽然行波进位加法器结构由于速度比较慢一般不被专用IC 采用，但在可编程逻辑器件上，行波进位加法器由于结构最为工整，且速度能满足大多数应用的要求，是用得最多的加法器结构。
VirtexII 系列FPGA 的每个slice 可以实现两个如图5所示的全加器。
其中i i i s ds c =⊕，1i i i i i c ds b ds c +=+，i i i ds a b =⊕。
此全加器与普通全加器不同，它有专用的快—204—速进位逻辑，可以在低级进位到达时，更快速地输出该位的运算结果；此外在FPGA 内部同一列的两个slice 之间专门为进位信号保留了一条最短连线。
本文使用Xilinx 公司的开发工具ISE5.1中的Core Generator 生成24位的行波进位加法器，占用资源为12个slices ，最大延时为3.089ns 。
3.3 前导1预测电路前导1预测电路包括预编码模块和前导1检测模块。
预编码模块的原理是：首先通过执行一个有效位的二进制符号－数字（signed-digit ）减法获得O=A-B ，然后根据Oi 串决定前导1的位置。
具体算法请看文献[5]。
前导1检测模块一般采用真值表的方式实现，具体算法参见文献[7]。
前导1预测n A n B A B n A n B n B n A图6 VirtexII 中的前导1预测电路其中A 是被减数，B 是减数，LUT 实现的函数是11()&(&)i i i i F A B A B −−=⊕。
这种实现方式也需要用到FPGA 中的快速行波进位，进位依次从最高位到最低位。
LOP 电路的延时和行波加法器的延时大致相当。
这种实现方案可能会产生一位的误差，需要在规格化单元中进行修正，修正的操作可以通过移位完成。
3.4 实验平台实验平台是自制的DSP-FPGA 实验板，如图7所示。
图7 实验平台板上有一片XC2V1000FPGA ，一片C6701-150DSP ，以及各种存储器资源等。
