25.1.3列举法、列表法、画树状图法求概率
- 格式:ppt
- 大小:749.00 KB
- 文档页数:30








25.3 列举法求概率(3)---------------用树形图求概率一、教学目标1、知识与技能目标:①会借助列表法计算涉及两步试验的随机事件发生的概率②会借助树状图计算涉及两步或三步试验的随机事件发生的概率。
2、方法与过程目标:合作探究,培养合作交流的意识和良好思维习惯。
3、情感态度价值观积极参与数学活动, 提高自身的数学交流水平,经历成功与失败,获得成功感,提高学习数学的兴趣.发展学生初步的辩证思维能力.二、教学重点:借助树状图和列表法计算涉及两步或三步试验的随机事件发生的概率.三、教学难点:能根据实验要求正确画出树形图并利用树形图找出随机事件所有的可能和该事件的可能从而正确求出该事件发生的概率。
四、教学过程:( 一) 复习旧知,引入新课等可能事件的特征,如何求等可能事件的概率?(先分析1、事件发生的总的可能性是有限个,记为几个。
2、每个结果发生的可能性相等。
事件A发生的结果有m个,则P(A)=)2、做一做:小明和小亮做扑克游戏,桌面上放有两堆牌,分别是红桃和黑桃的1,2,3,4,5,6,小明建议:”我从红桃中抽取一张牌,你从黑桃中取一张,当两张牌数字之积为奇数时,你得1分,为偶数我得1分,先得到10分的获胜”。
如果你是小亮,你愿意接受这个游戏的规则吗?你能求出小亮得分的概率吗?(学生思考:本次游戏分几步完成,可以用什么方法来列举出所有可能?)学生合作用列表法求出小亮得分的概率。
(教师巡视检查)想一想:本题还有其他的方法列举出所有可能吗?(引入新课,板书课题------用树形图求概率。
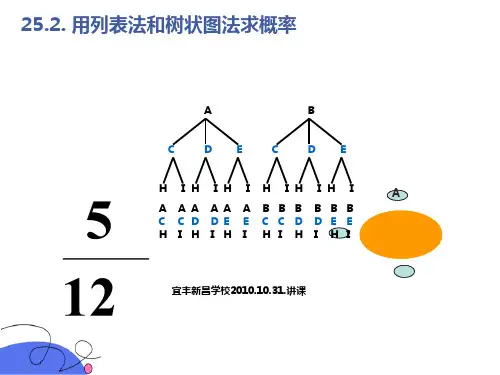
)(二)自主学习探究新知例4:甲口袋中装有2个相同的小球,它们分别写有字母A和B;乙口袋中装有3个相同的小球,它们分别写有字母C.D和E;丙口袋中装有2个相同的小球,它们分别写有字母H和I,从3个口袋中各随机地取出1个小球.取出的3个小球上,恰好有1个,2个和3个元音字母的概率分别是多少?取出的3个小球上全是辅音字母的概率是多少?出示自学指导1、这次实验分步完成,所以用法不能完成,为列出所有可能结果通常采用法完成;2、这次活动是步实验,第一步有种结果即和;第二步有种结果即和;第三步有种结果即和;此时活动完成要用法完成。
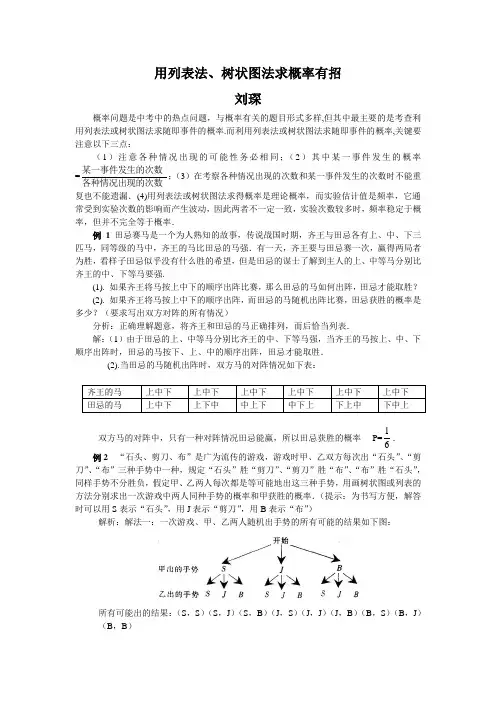
用列表法、树状图法求概率有招刘琛概率问题是中考中的热点问题,与概率有关的题目形式多样,但其中最主要的是考查利用列表法或树状图法求随即事件的概率.而利用列表法或树状图法求随即事件的概率,关键要注意以下三点:(1)注意各种情况出现的可能性务必相同;(2)其中某一事件发生的概率=各种情况出现的次数某一事件发生的次数;(3)在考察各种情况出现的次数和某一事件发生的次数时不能重复也不能遗漏.(4)用列表法或树状图法求得概率是理论概率,而实验估计值是频率,它通常受到实验次数的影响而产生波动,因此两者不一定一致,实验次数较多时,频率稳定于概率,但并不完全等于概率.例1 田忌赛马是一个为人熟知的故事,传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛一次,赢得两局者为胜,看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强.(1). 如果齐王将马按上中下的顺序出阵比赛,那么田忌的马如何出阵,田忌才能取胜? (2). 如果齐王将马按上中下的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)分析:正确理解题意,将齐王和田忌的马正确排列,而后恰当列表. 解:(1)由于田忌的上、中等马分别比齐王的中、下等马强,当齐王的马按上、中、下顺序出阵时,田忌的马按下、上、中的顺序出阵,田忌才能取胜.(2).当田忌的马随机出阵时,双方马的对阵情况如下表: 齐王的马 上中下 上中下 上中下 上中下 上中下 上中下 田忌的马 上中下上下中中上下中下上下上中下中上双方马的对阵中,只有一种对阵情况田忌能赢,所以田忌获胜的概率P=61. 例2 “石头、剪刀、布”是广为流传的游戏,游戏时甲、乙双方每次出“石头”、“剪刀”、“布”三种手势中一种,规定“石头”胜“剪刀”、“剪刀”胜“布”、“布”胜“石头”,同样手势不分胜负,假定甲、乙两人每次都是等可能地出这三种手势,用画树状图或列表的方法分别求出一次游戏中两人同种手势的概率和甲获胜的概率.(提示:为书写方便,解答时可以用S 表示“石头”,用J 表示“剪刀”,用B 表示“布”)解析:解法一:一次游戏、甲、乙两人随机出手势的所有可能的结果如下图:所有可能出的结果:(S ,S )(S ,J )(S ,B )(J ,S )(J ,J )(J ,B )(B ,S )(B ,J )(B ,B )从上面的树状图可以看出,一次游戏可能出现的结果共有9种,而且每种结果出现的可能性相同.所以,P (出同种手势)=93=31 P (甲获胜)=93=31解法二:一次游戏,甲、乙两人随机出手势的所有可能的结果如下表:以下同解法一 评注:(1)利用列表法、树状图法求概率必须是等可能事件.(2)对各种可能出现的情况不能遗漏或重复某种可能.例3.有两个可以自由转动的均匀转盘A 、B ,都被分成了3等份,并在每份内均标有数字,如图所示,规则如下:①分别转动转盘A 、B ;②两个转盘停止后,将两个指针所指份内的数字相乘(若指针停止在等分线上,那么重转一次,直到指针指向某一份为止).(1).用列表法(或树状图)分别求出数字之积为3的倍数和数字之积为5的倍数的概率;(2).小亮和小芸想用这两个转盘做游戏,他们规定:数字之积为3的倍数时,小亮得2分;数字之积为5的倍数时,小芸得3分,这个游戏对双方公平吗?请说明理由;认为不公平的,试修改得分规定,使游戏对双方公平. 解析:(1)每次游戏可能出现的所有结果列表如下:AB表格中共有9种等可能的结果,其中数字之积为3的倍数的有五种,数字之积为5的倍数的有三种,所以P (3的倍数)=95;P (5的倍数)93. (2)这个游戏对双方不公平∵小亮平均每次得分为2×95=910(分), 小芸平均每次得分为3×93=99=1(分).∵910≠1,∴游戏对双方不公平. 修改得分规定为:若数字之积为3的倍数时,小亮得3分;若数字之积为5的倍数时,小芸得5分即可.。
