下载文档原格式
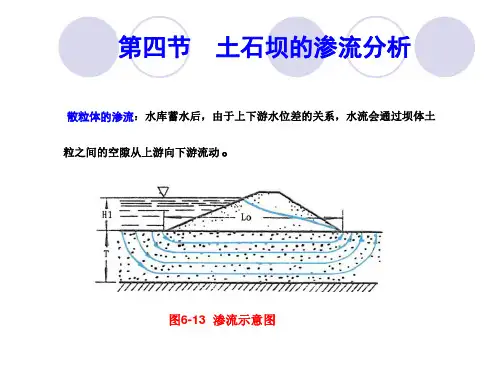
第三节 土石坝的渗流分析一、渗流分析的目的1) 确定浸润线的位置； 2) 确定坝体和坝基的渗流量； 3) 确定渗流逸出区的渗透坡降。
二、渗流分析方法常用的渗流分析方法：流体力学方法、水力学方法、流网法和试验法。
三、水力学方法水力学方法基本假定: 均质, 层流, 稳定渐变流。
1）渗流计算的基本公式图4－19表示一不透水地基上的矩形土体，土体渗透系数为k ，应用达西定律和假定，全断面内的平均流速v 等于：dxdykv -= （4-8） 设单宽渗流量为q ，则：dx dykyvy q -== （4-9）将上式分离变量后，从上游面（x=0，y=H 1）至下游面（x=L ，y=H 2）积分，得：L kqH H 22221=- 即： LH H k q 2)(2221-= （4-10）若将式（5-9）积分限改为：x 由0至x ，y 由H 1至y ，则得浸润线方程：xy H k q 2)(221-=即： x kqH y 221-= （4-11） 2）水力学法渗流计算用水力学法进行土坝渗流分析时，关键是掌握两点：一是分段，根据筑坝材料、坝体结构及渗流特征，把复杂的土坝形状通过分段，划分为几段简单的形状。
二是连续，渗流经上游面渗入、下游面渗出，通过坝体各段渗流量相等。
以此建立各段渗流之间的联系。
一、不透水地基上土坝的渗流计算 （一）均质土坝的渗流计算1．下游有水而无排水设备或有贴坡排水的情况如图4－20所示，可将土石坝剖面分为三段，即：上游三角形段AMF 、中间段AFB″B′以及下游三角形B″B′N。
根据流体力学原理和电模拟试验结果，可将上游三角形段AMF 用宽度为△L 的矩形来代替，这一矩形EAFO 和三角形AMF 渗过同样的流量q ，消耗同样的水头。
△L 值可用下式计算： 11121H m m L +=∆ （4-12）式中：m 1为上游边坡系数，如为变坡可采用平均值。
于是可将上游三角形和中间段合成一段EO B″B′,根据式(4-10），可求出通过坝身段的渗流量为：L H a H k q '+-=2])([220211 （4-13）式中：a 0 为浸润线逸出点距离下游水面的高度；H 2 为下游水深；L '为EO B″B′的底宽，见图5-20。
第三节土石坝的渗流分析土石坝是一种常见的水工结构，用于拦截水流，形成水库储存水资源。
而土石坝在水库的稳定性和安全性方面的最关键问题之一就是渗流问题。
土石坝的渗流分析是为了确定渗流路径和渗流量，从而评估土石坝的稳定性。
土石坝渗流分析的基本理论是达西定律和渗流理论。
根据这两个理论，土石坝的渗流规律可以用渗流方程描述：Q=K×A×i其中，Q是坝体中的渗流量，K是渗透系数，A是渗透面积，i是渗透坡度。
渗透系数是描述土体渗透性质的重要参数，可以通过实验或采样测试得到。
渗透面积是指单位时间内的水流面积，可以通过计算得到。
渗透坡度是指单位长度内的水头差，可以通过坝体的水头测量得到。
土石坝的渗流分析可分为两种情况：一种是均匀渗流情况，另一种是非均匀渗流情况。
对于均匀渗流情况，可以通过渗透方程计算渗流量。
首先需要确定渗透系数，可以采用实验数据或经验公式计算。
然后确定渗透面积和渗透坡度，可以通过坝体的几何和水头测量来计算。
最后代入渗透方程计算出渗流量。
对于非均匀渗流情况，渗流路径复杂，需要进行更详细的分析。
可以采用有限元或有限差分等数值方法进行渗流分析。
首先需要建立坝体的几何模型，包括土石的分层结构、渗透性质等。
然后根据渗透方程和边界条件进行数值计算，得到各点的水头和渗流量分布。
通过分析水头和渗流量的分布，可以评估渗流路径和渗流量，为土石坝的稳定性和安全性评估提供依据。
总之，土石坝的渗流分析是土石坝设计和安全评估的重要内容。
通过理论分析和数值计算，可以得到土石坝的渗流路径和渗流量，评估土石坝的稳定性和安全性，为工程设计和运行提供科学依据。
同时，渗流分析还可以指导渗流控制和排水措施的设计，提高土石坝的渗流性能。
