初中三年级数学测试题 旋转(含答案)

第六单元平移、旋转和轴对称知识点1：平移和旋转1.平移：物体或图形沿着直线运动的现象叫平移。

2.平移的特征：平移时物体的形状、大小和本身的方向都不改变，只是位置发生了改变。

3.旋转：物体或图形绕着一个固定中心转动的现象叫旋转。

4.旋转的特征：旋转时物体的形状，大小都不改变，只是本身的方向和位置发生了改变。

例1：下面的哪些运动是平移？哪些是旋转？是平移的画“√”，是旋转的画“○”。

例2：哪些小鱼通过平移可以和①号鱼重合?在它们的序号上画“√”例3：在括号里填上“平移”或“旋转”。

(1)(2)(3)例4：填一填，画一画。

（1）向（）平移了（）格。

（2）向（）平移了（）格。

（3）向（）平移了（）格。

（4）向右平移了6格，请在图中画出平移后的图形。

（5）向下平移了8格，请在图中画出平移后的图形。

例5：移一移,画一画,填一填。

(1)把Ο先向南平移4格,再向东平移4格。

(2)把∆先向西平移3格,再向北平移3格。

(3)平移后Ο在原来位置的（）方向,平移后∆在原来位置的（）方向。

例6：根据下面图形的变化规律在后面的空格里画出相关图形。

【练习题】1.看图判断下面物体的运动方式,是平移的画“□”,是旋转的画“○”。

2.下面的三幅图，哪幅图是通过图A平移得到的？哪幅图是通过图A旋转得到的？3.在（）里填上“平移”或“旋转”。

4.假如你是一名出租车的调度员，你的任务就是答应顾客要求，调度车辆到达顾客指定的地点。

现在要接顾客（）（选“A”或“B”），汽车要先向（）平移（）格，再向（）平移（）格，就能接到他。

5.把图①向右平移7格，图②向上平移5格。

6.下面的图形中，（）不能通过1号图旋转得到A．B．C．D．知识点2：轴对称1.轴对称图形：把一个图形沿着某一条直线对折，对折后能完全重合，这样的图形就是轴对称图形。

折痕所在的直线是图形的对称轴。

2.轴对称图形的特征:对折后，对称轴两边能完全重合。

例1：是轴对称图形的在下面的（）里画“√”，不是的画“×”。

三年级上册数学一课一练-3.2旋转一、单选题1.下面物体的运动是（）A. 平移B. 旋转2.开冰箱的门是( )现象。

A. 旋转B. 平移C. 旋转与平移D. 不确定3.下列物体的运动，（）是旋转．A. B. C.4.小明在正方形卡片上画了这样的图案(如右图)。

下面的卡片中转动后与小明的卡片图案相同的是( )。

A. B. C. D.5.把数字逆时针旋转90 得到( )。

A. B. C.6.把一个图形顺时针旋转（），又回到了原来的位置。

A. 90°B. 180°C. 360°7.找规律，在里应填的图形是（）A. B. C. D.二、判断题8.将三角形绕点o旋转90°后是。

9.钟表上的时针转动是属于旋转现象。

10.每个旋转的图形都有一个旋转中心或一个旋转轴。

11.钟表上时针在平移运动。

12.火车拐弯是旋转现象。

三、填空题13.与表针旋转方向相同的是________旋转，与表针旋转方向相反的是________旋转。

14.图形一通过________的变换可以得到图二。

15.原地转圈是________现象。

（用“平移”或者“旋转”作答）16.如图，△ABC为等边三角形，D为△ABC•内一点， △ABD•经过旋转后到达△ACP的位置，则，（1）旋转中心是________；（2）•旋转角度是________（3）△ADP•是________三角形.17.图形可以通过________得到图形。

18.一个20°的角，将它的一条边旋转________°可得到一个直角。

四、解答题19.请画出三角形AOB绕O点顺时针旋转90°后的图形．20.按照图中的规律画一画五、综合题21.如图所示，表盘上的时间是8：05。

（1）当分针从“1”绕点O顺时针旋转60°后是________时________分。

（2）当分针从“1”绕点O逆时针旋转90°后是________时________分。

平移和旋转一、单选题1.平移是沿着（）移动A. 直线B. 曲线C. 某个点2.下面哪些图案不能通过平移得到？（）A. B. C.3.分针围绕钟面中心顺时针旋转3圈后，时针围绕钟面中心顺时针旋转了（）A. 60°B. 90°C. 180°D. 360°4.如图：在三角形ABC中∠ACB=90°, ∠A=40°,以C为旋转中心，将三角形ABC旋转到三角形A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边C′A′交AB于D，则旋转角等于（）A. 70°B. 80°C. 60°二、判断题5.杂技演员连续后空翻是旋转现象。

( )6.滑梯是平移现象，风扇是旋转现象。

7.旋转中，对应点划过的痕迹是一条圆弧。

8.判断对错.找出下面图形的变化规律，然后根据这个规律在最后一个图的空格里画上相关的图形.三、填空题9.不倒翁的摆动是________现象。

10.写出分针从12旋转到下面各个位置所经过的时间________分________分________分11.小船向________平移了________格；小鱼向________平移了________格．12.分针和时针的转速比是________。

四、解答题13.把平移前后两幅图中的平行线涂上相同的颜色。

14.下面哪幅图是由图①旋转得到的？圈出来五、综合题15.左边的图形是如何变成右边的图形的？（1）红色三角形：________（2）蓝色三角形：________（3）黄色三角形：________（4）绿色三角形：________六、应用题16.将图先向右平移6格，再向上平移4格，并画出平移后的图形．参考答案一、单选题1.【答案】A【解析】【解答】平移是沿着直线移动【分析】考查了平移的相关知识2.【答案】B【解析】【解答】解：A、一个小三角形平移后得到整个图形；B、曲线所指的方向变化了，不是平移得到的；C、一个五边形平移后得到整个图形.故答案为：B【分析】平移后的图形的形状、大小、方向都不变，位置发生了变化，由此根据平移的特征判断哪些图形是通过平移得到的即可.3.【答案】B【解析】4.【答案】B【解析】【解答】解：图中BC绕C点旋转后得到B′C，CB=CB′，又因为∠A′B′C是∠ABC旋转后的角，因此两角相等都是50度，经过计算得到∠B′CB=80°，故∠ACD=80°.故答案为：B【分析】旋转后的图形的大小不变，各个角的度数也不变，这样∠B′就是50度，三角形BB′C是等腰三角形，所以能计算出∠B′CB的度数，然后就能确定旋转角的大小.二、判断题5.【答案】错误【解析】【解答】杂技演员连续后空翻是平移现象，原题说法错误.故答案为：错误.【分析】杂技演员后空翻是旋转现象，杂技演员连续后空翻是平移现象，据此判断.6.【答案】正确【解析】【解答】解：根据平移、旋转的意义可得滑梯是平移现象，风扇是旋转现象，可见原题说法正确. 故答案为：正确.【分析】平移是水平或竖直或其他方向的平行移动；在平面内将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，根据平移和旋转的定义进行分析即可解答.7.【答案】正确【解析】【解答】解：旋转中，对应点划过的痕迹是一条圆弧，原题说法正确.故答案为：正确【分析】旋转中，对应的点划过的痕迹是一条圆弧，圆弧的圆心角就是旋转的度数.8.【答案】错误【解析】【解答】正确解答：如下图所示。

三年级数学上册第六单元平移、旋转轴对称专项训练——连线题一、连线题
1．第一行的图形分别沿虚线对折后，会变成第二行的哪个图形？连一连。

2．下面的图形，分别从哪张纸上剪下来？连一连。

3．下面的图形各是从哪张纸上剪下来的？连一连。

4．下面各图沿虚线剪下，打开后分别是什么图形？把对应的两个图形用线连起来。

5．把能组成一个整体的两个图案连起来。

6．右边的图案分别是从左边的哪张纸上剪下来的？连一连。

7．连一连,使上下两个图形拼成轴对称图形．
8．下面的图形各是从哪张纸上剪下的？连一连。

9．下面哪些图形通过平移可以互相重合？请连一连。

10．巧手连一连。

11．下面哪些图形可以通过平移互相重合？连一连。

12．观察这些生活现象，连一连。

13．下面哪些图形可以通过平移相互重合？连一连。

14．连一连。

升旗时国旗的运动火车的运动在算盘上拨珠平移电梯的运动风扇叶片的运动旋转时针的运动
光盘在电脑里的运动把握汽车的方向盘15．下面的哪些图形可以通过平移互相重合？连一连。

16．看一看，连一连。

17．连一连．
三年级数学上册第六单元平移、旋转轴对称专项训练——连线题
参考答案
1．
2．
3．
4．
5．
6．
7．8．9．10．11．12．
13．连线如下：14．
15．
16．17．。

小学三年级数学（下)《旋转和平移》练习题一、下面物体的运动是平移的在里画“△”,是旋转的是画“○”。

二、判断。

1、光盘在播放时的运动是旋转现象。

（）2、拧开水龙头的过程是平移现象。

（）3、打开抽屉的过程是平移现象。

（）4、钟面上时针和分针的运动是平移现象。

（）5、国旗的上升与下降是平移现象。

（）三、选择。

1、抽奖游戏中的旋转盘是（）现象。

A、平移B、旋转C、对称2、下面的图案是通过平移得到的图案是（）、3、下面现象中。

既有平移现象。

又在旋转现象的是（）。

A、正在工作的风扇叶片B、在笔直路上行驶的汽车B、运行中的观光电梯D、传输带的物品4、下面各组图形中经过平移可以重合的的是（）四、填空。

1、风扇扇叶的转动是（）现象。

推箱子是（）现象、2、根据图中的物体运动现象。

填“平移”或“旋转”。

3、物体沿直线上、下、左、右、运动,这样的现象叫做（）。

4、下面是平移的在手里打“√”,在旋转的在括号里画“○”。

滚铁环（）升国旗（）开冰箱门（）打开水龙头（）使用中的电风扇（）拉抽屉（）用钥匙开锁（）乘坐电梯（）推开窗户（）坐滑梯（）滚油桶（）开窗帘（）5、物体沿一个固定点作弧线运动,这样的现象叫做（）。

6、看图填一填。

（1）指针绕O点旋转顺时针旋转90°,指着数字是（）（2）指针绕O点顺时针旋转180°,指着的数字是（）（3）指针绕（）点（）旋转90°,指着的数字是10.（4）指针綫（）点（）旋转（）°指着的数字是9.五、连一连。

1、下面哪些图形的是通过平移可以互相重合？连一连。

2、下面右边哪些图开是由左边图形旋转得到的？在（）里画“√”。

六、画一画附参考答案一、辨析平移、旋转。

○,△○,○,△○,△,○,○,△二、判断、√,×,√,×,√,三、选择。

B。

A。

B。

B四、填空。

1、旋转,平移。

2、平移3、平移。

旋转,平移4、○.√,○○,○。

√,○。

√,○,√。

三年级数学平移和旋转试题1.实践操作，你能根据轴对称图形的意义画出另一半吗？【答案】如图所示：【解析】在平面内，如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这样的图形叫做轴对称图形。

另一半应该与画出的一半完全相同。

【考点】作轴对称图形。

总结：沿着中间的折痕对折以后可以完全重合就是轴对称图形。

2.在轴对称图形的下面打“√”，不是的打“×”。

【答案】【解析】一个图形沿某条直线对折，对折后的两部分能完全重合。

这样的图形称作轴对称图形。

看每个物体能否找到那个折痕，然后进行判断。

如图：【考点】生活中常见的对称现象，简单的轴对称图形。

总结：判断是不是轴对称图形，主要是找到可以对折的那条直线。

3.下面的图形是从哪张纸剪下来的？连一连。

【答案】【解析】上图都是由一张纸对称后剪出的，都是沿着折痕对折可以完全重合的图形。

剪纸对折以后应该是和图形的一半恰好是相吻合的。

即所给图形的一半恰好能够嵌入下方所给的剪纸中。

【考点】轴对称图形的剪裁方法。

总结：可以在脑海中想象也可以画出每个图形的一半是什么样的。

4.在平移现象后面画“-”，在旋转现象后面画“○”。

（1）西南商贸城正在安检机的行李包。

（）（2）飞机螺旋桨的运动。

（）（3）电梯上下移动。

（）（4）正沿这笔直旗杆上升的国旗。

（）（5）打开教室门。

（）【答案】-，○-，-，○【解析】根据平移的意义，平移是将一个图形从一个位置变换到另一个位置，拉抽屉是平移现象；根据旋转的意义，旋转是一个图形绕着一个定点旋转一定的角度，拧螺丝是旋转现象。

（1）西南商贸城正在安检机的行李包，它的运动是平移。

（2）飞机螺旋桨的运动，它的运动是旋转。

（3）电梯上下移动，它的运动是平移。

（4）国旗沿笔直旗杆上升是自下而上沿旗杆运动的是平移。

（5）打开教室门，是门围绕竖杆做圆弧运动是旋转。

【考点】平移、旋转。

总结：旋转变换和平移都不改变图形的形状和大小，只是位置的变化。

5.下面的图形中哪两个图形经过平移、旋转后可完全重合。

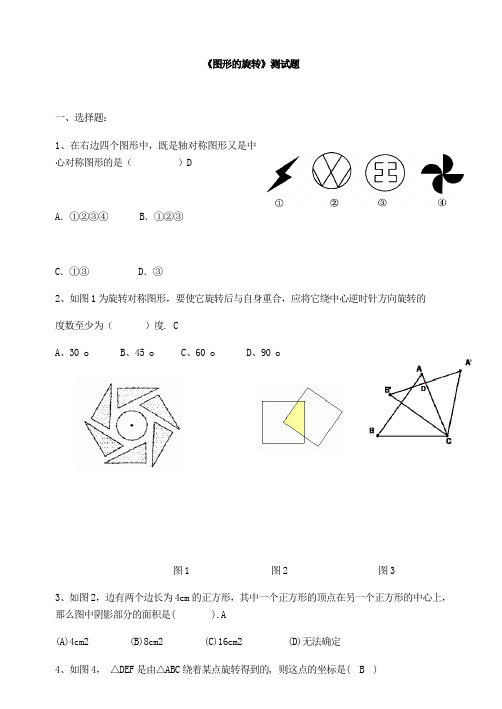
《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（）DA．①②③④ B．①②③C．①③ D．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（）度. CA、30 oB、45 oC、60 oD、90 o图1 图2 图33、如图2，边有两个边长为4cm的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4，△DEF是由△ABC绕着某点旋转得到的, 则这点的坐标是( B )图5 图4 A. (1,1) B. (0,1) C. (−1,1) D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______.80(或120(.三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图6 BA CO图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点A 旋转1800，点C 落在C1处，则C C1的长为（ ）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K是正方形ABCD内一点，以AK为一边作正方形AKLM，使L，M，D在AK的同旁，连结BK和DM，试用旋转的思想说明线段BK与DM的关系．,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

三年级数学平移旋转和对称试题1.电梯的升降是现象，钟面上时针和分针的运动是现象，拉开抽屉时，抽屉做运动．【答案】平移，旋转，平移．【解析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心，所以，它并不一定是绕某个轴的，根据平移与旋转定义判断即可．解答：解：电梯的升降是平移现象，钟面上时针和分针的运动是旋转现象，拉开抽屉时，抽屉做平移运动；故答案为：平移，旋转，平移．点评：本题是考查图形的平移与旋转的意义，关键是看方向是否改变．2.推拉窗户的运动是；风车的运动是．【答案】平移，旋转．【解析】（1）平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；（2）旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心，所以，它并不一定是绕某个轴的；依此根据平移与旋转定义判断即可．解：推拉窗户的运动是平移；风车的运动是旋转；故答案为：平移，旋转．【点评】此题是对平移与旋转理解及在实际当中的运用．3.下列图形中，不是轴对称图形的是（）A．B．C．D．【答案】D【解析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可．解：根据轴对称图形的意义可知：下列图形中，不是轴对称图形的是，其它三个选项中的图形都是轴对称图形；故选：D．【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合．4.周一升国旗时，国旗的上升是现象；拧水龙头是现象．【答案】平移，旋转．【解析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心．所以，它并不一定是绕某个轴的；然后根据平移与旋转定义判断即可．解：周一升国旗时，国旗的上升是平移现象；拧水龙头是旋转现象；故答案为：平移，旋转．【点评】本题是考查图形的平移与旋转．平移与旋转关键是看图形的方向是否改变，平移不改变方向，旋转改变方向．5.在横线里填上“平移”或“旋转”．（1）自行车车轮的转动是现象，人骑车前行是现象；（2）风扇叶片的运动是现象；（3）钟面上分针不停地走动是现象；（4）升国旗时，国旗的升降运动是现象；（5）拉开抽屉是现象，拧水龙头是现象．【答案】旋转，平移；旋转；旋转；平移；平移，旋转．【解析】平移是物体运动时，物体上任意两点间，从一点到另一点的方向与距离都不变的运动；旋转是物体运动时，每一个点离同一个点（可以在物体外）的距离不变的运动，称为绕这个点的转动，这个点称为物体的转动中心．所以，它并不一定是绕某个轴的；由此根据平移与旋转定义判断即可．解：（1）自行车车轮的转动是旋转现象，人骑车前行是平移现象；（2）风扇叶片的运动是旋转现象；（3）钟面上分针不停地走动是旋转现象；（4）升国旗时，国旗的升降运动是平移现象；（5）拉开抽屉是平移现象，拧水龙头是旋转现象．故答案为：旋转，平移；旋转；旋转；平移；平移，旋转．【点评】此题是对平移与旋转理解及在实际当中的运用．6.下列现象属于平移现象的是（）A．风扇转动B．写字C．晃动呼啦圈D．转动风车【答案】B【解析】根据平移不改变图形的形状、大小和方向，结合图形对选项进行一一分析，选出正确答案．解：A．图形的方向发生变化，不符合平移的性质，不属于平移得到，故本选项错误；B．图形的形状和大小没有变化，符合平移的性质，属于平移得到，故本选项正确；C．图形的方向发生变化，不符合平移的性质，不属于平移得到，故本选项错误；D．图形的方向发生变化，不符合平移的性质，不属于平移得到，故本选项错误．故选：B．【点评】本题考查了图形的平移，图形的平移只改变图形的位置，而不改变图形的形状和大小，学生易混淆图形的平移与旋转或翻转，以致选错．7.“里，一，五”都是轴对称的汉字．（判断对错）【答案】错误【解析】根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；依次进行判断即可．解：根据轴对称图形的意义可知：“里，一”都是轴对称的汉字，而“五”不是轴对称图形；故答案为：错误．【点评】此题考查了轴对称图形的意义，判断轴对称图形的关键是寻找对称轴，看图形对折后两部分是否完全重合．8.动手画一画、比一比在方格中画出一个轴对称图形。

MB' A'C A B 图5 图4 《图形的旋转》测试题一、选择题：1、在右边四个图形中，既是轴对称图形又是中心对称图形的是（ ）DA ．①②③④B ．①②③C ．①③D ．③2、如图1为旋转对称图形，要使它旋转后与自身重合，应将它绕中心逆时针方向旋转的度数至少为（ ）度. CA 、30 oB 、45 oC 、60 oD 、90 o图1 图2 图33、如图2，边有两个边长为4cm 的正方形，其中一个正方形的顶点在另一个正方形的中心上，那么图中阴影部分的面积是( ).A(A)4cm2 (B)8cm2 (C)16cm2 (D)无法确定4、如图4， △DEF 是由△ABC 绕着某点旋转得到的, 则这点的坐标是( B )A. (1,1)B. (0,1)C. (−1,1)D. (2,0)二、填空题5、点a 4（，）与3b （，）关于原点对称，则a b += .-76、如图3，把三角形△ABC 绕着点C 顺时针旋转350，得到△A ＇B ＇C ，A ＇B ＇交AC 于点D ，若∠A ＇DC=900，则∠A 的度数是__________。

5507、如图5， △ABC 中, (ACB = 90(, (B = 30(, BC = 6, 三角板绕C 逆时针旋转, 当点A的对应点A' 落在AB 边上时即停止转动, 则BM 的长为 3 .8、如图6，△ABC 中, 已知∠C=90°, ∠B=50°, 点D 在边BC 上, BD=2CD. 把△ABC 绕着点D逆时针旋转m （0(<m<180(）度后, 如果点B 恰好落在初始Rt △ABC 的边上, 那么m = _______. 80(或.O A B C D E F x y2 3图6 A C BD三、解答题9、作图题（1）如图7，画出△ABC 绕点O 顺时针旋转60°所得到的图形．图7 图8（2）如图8,在直角坐标系中,点P 的坐标为(3,4),将OP 绕原点O 逆时针旋转90°得到线段OP ′,(1)在图中画出线段OP ′;(2)P ′的坐标为 ______. (-4,3)1、如图，在△ABC 中，∠B=900，∠C=300，AB=1，将△ABC 绕顶点 A 旋转1800，点C 落在C1处，则C C1的长为（ ）A ．24B ．4C ．32D ．522、如图，△ABC 中，∠ACB=1200，将它绕着点C 旋转300 后得到△DCE ，则∠ACE=∠A+∠E=3、如图，在Rt △ABC 中，∠ACB=90°，∠A=35°，以直角顶点C•为旋转中心，将△ABC 旋转到△A ′B ′C 的位置，其中A ′、B ′分别是A 、B 的对应点，且点B 在斜边A ′B ′上，直角边CA ′交AB 于D ，求∠BDC 的度数．E DC BA B A C O ABC B C4，如图，正方形ABCD 中，E 在BC 上，F 在AB 上且∠FDE=45°，•△DEC 按顺时针方向转动一个角度后成为△DGA ．（1）图中哪一个点是旋转中心？（2）旋转了多少度？（3）指出图中的对应点，对应线段和对应角；（4）求∠GDF 的度数．5、已知如图，正方形ABCD 中，E 为CD 边上一点，F 为BC 边上一点，CE=CF:(1)EBC FDC ∠∠与相等吗？（2）△DCF 能与△BCE 重合吗？（3）试判断BE 与DF 的位置关系并说明理由,6．如图所示，四边形ABCD 中，∠BAD=∠C=90°，AB=AD ，AE ⊥BC 于E ，△BEA 旋转后能与△DFA 重合．（1）旋转中心是哪一点？（2）旋转了多少度？（3）若AE=5cm ，求四边形ABCD 的面积．7，如图，K 是正方形ABCD 内一点，以AK 为一边作正方形AKLM ，使L ，M ，D 在AK 的同旁，连结BK 和DM ，试用旋转的思想说明线段BK 与DM 的关系． C FEDB A,8，.如图所示，等边△ABC中，D是AB边上的动点(不与A、B重合)，以CD为一边，向上作等边△EDC。

第六单元：平移、旋转和轴对称第2课时：旋转与旋转现象班级：姓名: 等级:【基础训练】一、选择题1．下列现象中，（）是平移。

A．B．C．2．下列现象中，不属于旋转变换的是（）。

A．钟摆的运动B．拧紧螺丝C．电梯的升降运动D．方向盘的转动3．下列运动现象属于旋转的是（）。

A．滑冰B．拍球C．国旗沿旗杆上升D．分针的走动4．下面（）是旋转现象。

A．B．C．5．下列五种运动中，属于平移运动的是（）。

①温度计中液柱的上升或下降②自行车轮子的运动③时钟的秒针的运动④高层建筑内的电梯的运动⑤小球从高处做自由落体运动A．①②③B．②③④C．③④⑤D．①④⑤二、填空题6．书本的打开与合上是（______）现象。

小明拉开抽屉，抽屉的运动是（______）现象。

（填“平移”或“旋转”）7．开关推拉窗的运动是（________），拧水龙头的运动是（________）。

（填“平移”或“旋转”）8．选择正确的序号填空：①平移②旋转汽车行驶中，车轮的运动是（______）现象，车身的运动是（______）现象。

用钥匙开门时，拧钥匙开门是（______）现象。

9．下列现象是平移的画“√”，是旋转的画“○”（______）（______）（______）（______）（______）10．上课铃响了，同学们推开教室门走进教室，坐到位子上从书包里拿出课本开始上课。

推开教室门是（________）现象，从书包里拿出课本是（________）现象。

三、判断题11．平移和旋转都不改变物体的大小。

（______）12．乘车时，从整体看是平移现象，车子轮子的转动是旋转现象。

（______）【拓展运用】四、解答题13．下面的图案分别是由哪个图形旋转而成的？请圈出来。

参考答案1．B2．C3．D4．B5．D6．旋转平移7．平移旋转8．②①②9．√○√√○10．旋转平移11．√12．√13．。

三年级上册数学单元测试-第六单元平移、旋转和轴对称（培优卷）一、选择题（满分16分）1．下列属于旋转现象的是（）。

A．汽车方向盘的运动B．拉开抽屉C．电梯的运动D．升国旗2．下面是丽丽书包里的一些数学用品，其中（）不一定是轴对称图形。

A．三角板B．正方形书签C．直尺D．量角器3．下面交通标志中是轴对称图形的是（）。

A．B．C．4．如图的图案是从（）卡纸上剪下来的。

A．B．C．5．在下面的图形中，有（）个是轴对称图形。

A．1个B．2个C．3个D．4个6．下面是平移的是（）。

A．升国旗B．钟面上指针的运动C．吊扇的扇叶在空中运动7．钟面上指针的运动是（），电梯的运动是（）。

①旋转②对称③平移A．①②B．②③C．①③8．下列各种图形中，是轴对称图形的是（）。

A．B．C．D．二、填空题（满分16分）9．如图的哪个图案是通过平移左面的图案得到的？请画“√”。

10．电风扇扇叶的运动是（______）现象，升降机的运动是（______）现象。

11．升国旗时，国旗的上升是（________）现象，滑轮的转动是（________）现象。

（填“平移”或“旋转”）12．在括号里填上“平移”或“旋转”。

（1）电梯下降的运动可以看作（________）；（2）汽车方向盘的运动可以看作（________）。

13．火箭升空，是________现象．（用“平移”或者“旋转”作答）14．下列运动是平移的画“—”，是旋转的画“○”。

（_________）（_________）15．经过平移或旋转的图形，（________）和（________）完全相同。

16．图形的变换方式有：（_____）、（_____）、（_____）．三、判断题（满分8分）17．一个图形经过旋转变换后，它的形状发生了改变。

（______）18．下面的英文字母，都是轴对称图形。

（________）C T Z19．如图的花边是用平移对称的方法设计的．_____20．拧水龙头是旋转现象．荡秋千的运动是平移．（________）四、连线题（满分24分）21．(6分)连一连。

三年级上册数学试题-第六单元平移、旋转和轴对称测试卷-苏教版（含答案）一.选择题(共5题，共10分)1.某宾馆在楼梯上铺地毯，如图这块地毯的长度是（）。

A.M+NB.2M+2NC.M+2ND.2M+N2.下面物体的运动是（）。

A.平移B.旋转3.观察汽车商标，其中是轴对称图形的个数为（）。

A.2B.3C.44.下面这些图形，不是对称图形的为（）。

5.下面是平移现象的是（）。

A.电梯的升降B.拧水龙头C.电风扇的转动D.汽车车轮的转动二.判断题(共5题，共10分)1.观察一个图形的平移过程，只需观察该图形上任意一点的平移过程。

（）2.汽车行驶中车轮的运动是平移。

（）3.晶字可以看成日字平移得到的。

（）4.和都是轴对称图形。

（）5.对称图形一定有对称轴。

（）三.填空题(共5题，共8分)1.选一选：格子中的三角形先向右平移8个格，再向上平移3个格后得到的是（）号图形。

2.看镜子写数字。

（）3.平移不改变图形的（）和（），只改变图形的（）。

4.得到这些图形要用到（）。

5.图形平移有二个关键要素，一是平移的________，二是平移的________。

四.计算题(共1题，共6分)1.要在一块长30m，宽20m的长方形草坪上修一条宽1m的曲折小路（如下图）。

请用你所学过的知识求出草地的面积。

五.作图题(共3题，共16分)1.画一画，请画出平移后的图形。

2.这是一个对称图形的一半，请你想一想，这个对称图形原来可能是怎样的？画一画.你有几种不同的画法？3.下面哪些图案可以通过将纸对折剪出来？六.解答题(共5题，共32分)1.移一移，说一说。

①向（）平移了（）格。

②向（）平移了（）格。

③向（）平移了（）格。

2.如图，三角形ABC是三角形ABC平移后得到的，问三角形是怎么平移的？写出平移前后互相平行的线。

3.如图所示：A.图形①平移到图形②的位置，可以先向（）平移（）格，再向（）平移（）格。

B.画出中间图形的另一半，使它成为轴对称图形。

人教版九年级数学上册第二十三章《旋转》测试题（含答案）一．选择题1．下面生活中的实例，不是旋转的是（）A．传送带传送货物B．螺旋桨的运动C．风车风轮的运动D．自行车车轮的运动2．下列图形绕某点旋转90°后，不能与原来图形重合的是（）A．B．C．D．3．已知点A的坐标为（2，3），O为坐标原点，连接OA，将线段OA绕点A按顺时针方向旋转90°得AB，则点B的坐标为（）A．（5，1）B．（﹣3，2）C．（﹣1，5）D．（3，﹣2）4．下列说法中错误的是（）A．成中心对称的两个图形全等B．成中心对称的两个图形中，对称点的连线被对称轴平分C．中心对称图形的对称中心是对称点连线的中心D．中心对称图形绕对称中心旋转180°后，都能与自身重合5．下列英语单词中，是中心对称图形的是（）A．SOS B．CEO C．MBA D．SAR6．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．7．在平面直角坐标系中，点M（3，﹣5）关于原点对称的点的坐标是（）A．（﹣3，﹣5）B．（3，5）C．（5，﹣3）D．（﹣3，5）8．第24届冬季奥林匹克运动会，将于2022年02月04日~2022年02月20日在中华人民共和国北京市和张家口市联合举行．在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）A．B．C．D．9．将图绕中心按顺时针方向旋转60°后可得到的图形是（）A．B．C．D．10．如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝15，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为（）A．48B．50C．55D．60二．填空题11．与电子显示的四位数6925不相等，但为全等图形的四位数是．12．若数字串“000”和数字串“101”既是轴对称图形，又是中心对称图形，那么数字串“110”是图形（填写“轴对称”、“中心对称”）．13．如图，在△ABC中，AB＝4，AC＝3，∠BAC＝30°，将△ABC绕点A逆时针旋转60°得到△AB1C1，连接BC1，则BC1的长为．14．如图，是4×4正方形网格，其中已有4个小方格涂成了黑色，现在要从其余12个白色小方格中选出一个也涂成黑色，使整个黑色部分图形构成轴对称图形，这样的白色小方格有个．15．如图，△ABC与△DEF关于O点成中心对称．则AB DE，BC∥，AC＝．16．在平面直角坐标系中，点（﹣3，4）关于原点对称的点的坐标是．17．时钟从上午9时到中午12时，时针沿顺时针方向旋转了度．18．时钟的时针在不停地转动，从上午6时到上午9时，时针旋转的旋转角为度，从上午9时到下午5时时针旋转的旋转角为度．19．如图，把这个“十字星”形图绕其中心点O旋转，当至少旋转度后，所得图形与原图形重合．20．如图，在平面直角坐标系中，点P1的坐标为（，），将线段OP1绕点O按顺时针方向旋转45°，再将其长度伸长为OP1的2倍，得到线段OP2；又将线段OP2绕点O按顺时针方向旋转45°，长度伸长为OP2的2倍，得到线段OP3；如此下去，得到线段OP4，OP5，…，OP n（n为正整数），则点P2020的坐标是．三．解答题21．在14×9的方格纸中，每个小正方形的边长都为1，△ABC与△A′B′C′的位置如图所示；（1）请说明△ABC与△A′B′C′的位置关系；（2）若点C的坐标为（0，0），则点B′的坐标为；（3）求线段CC′的长．22．如图所示的图形是一个轴对称图形，且每个角都是直角，小明用n个这样的图形，按照如图（2）所示的方法玩拼图游戏，两两相扣，相互间不留空隙．（1）用含a、b的式子表示c；（2）当n＝2时，求小明拼出来的图形总长度；（用含a、b的式子表示）（3）当a＝4，b＝3时，小明用n个这样的图形拼出来的图形总长度为28，求n的值．23．（1）计算：+﹣2﹣1；（2）一串有趣的图案按一定规律排列．请仔细观察，按此规律画出的第10个图案是；在前16个图案中有个；第2008个图案是．24．在△ABC中，∠B+∠ACB＝30°，AB＝4，△ABC逆时针旋转一定角度后与△ADE重合，且点C恰好成为AD中点，如图（1）指出旋转中心，并求出旋转角的度数．（2）求出∠BAE的度数和AE的长．25．在平面内，如果一个图形绕一个定点旋转一定的角度后能与自身重合，那么就称这个图形是旋转对称图形，转动的这个角称为这个图形的一个旋转角．例如：正方形绕着它的对角线的交点旋转90°后能与自身重合（如图），所以正方形是旋转对称图形，它有一个旋转角为90度．（1）判断下列命题的真假（在相应的括号内填上“真”或“假”）．①等腰梯形是旋转对称图形，它有一个旋转角为180度．（）②矩形是旋转对称图形，它有一个旋转角为180°．（）（2）填空：下列图形中，是旋转对称图形，且有一个旋转角为120°的是（写出所有正确结论的序号）：①正三角形；②正方形；③正六边形；④正八边形．（3）写出两个多边形，它们都是旋转对称图形，都有一个旋转角为72°，并且分别满足下列条件：①是轴对称图形，但不是中心对称图形：；②既是轴对称图形，又是中心对称图形：．26．在平面直角坐标系中，O为原点，点A（4，0），点B（0，3），把△ABO绕点B逆时针旋转，得△A′BO′，点A、O旋转后的对应点为A′、O′，记旋转角为a．（1）如图1，若a＝90°，求AA′的长；（2）如图2，若a＝120°，求点O′的坐标．参考答案一．选择题1．解：传送带传送货物的过程中没有发生旋转．故选：A．2．解：A、绕它的中心旋转90°能与原图形重合，故本选项不合题意；B、绕它的中心旋转90°能与原图形重合，故本选项不合题意；C、绕它的中心旋转90°能与原图形重合，故本选项不合题意；D、绕它的中心旋转120°才能与原图形重合，故本选项符合题意．故选：D．3．解：如图，过A作y轴的平行线，过B作x轴的平行线，交点为C，由∠C＝∠ADO，∠BAC＝∠AOD，AB＝OA，可得△ABC≌△OAD，∴AC＝OD＝2，BC＝AD＝3，∴CD＝5，点B离y轴的距离为：3﹣2＝1，∴点B的坐标为（﹣1，5），故选：C．4．解：在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形与另一个图形重合，那么就说明这两个图形的形状关于这个点成中心对称，中心对称图形的对称中心是对称点连线的交点，根据中心对称图形的定义和性质可知A、C、D正确，B错误．故选：B．5．解：是中心对称图形的是A，故选A．6．解：A、是轴对称图形，不是中心对称图形，故本选项不符合题意；B、既是轴对称图形，又是中心对称图形，故本选项符合题意；C、不是轴对称图形，是中心对称图形，故本选项不符合题意；D、不是轴对称图形，是中心对称图形，故本选项不符合题意．故选：B．7．解：点M（3，﹣5）关于原点对称的点的坐标是（﹣3，5），故选：D．8．解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、是轴对称图形，故此选项错误；D、不是轴对称图形，故此选项正确；故选：D．9．解：将图绕中心按顺时针方向旋转60°后得到的图形是．故选：A．10．解：∵将△ABC绕点B顺时针旋转60°，得到△BDE，∴△ABC≌△BDE，∠CBD＝60°，∴BD＝BC＝15，∴△BCD为等边三角形，∴CD＝BC＝BD＝15，∵AB＝＝＝17，∴△ACF与△BDF的周长之和＝AC+AF+CF+BF+DF+BD＝AC+AB+CD+BD＝8+15+15+17＝55，故选：C．二．填空题11．答：5269．12．解：根据对称图形的概念，知110仅是轴对称图形，对称轴为正中水平直线．13．解：∵将△ABC绕点A逆时针旋转60°得到△AB1C1，∴AC＝AC1＝3，∠CAC1＝60°，∴∠BAC1＝90°，∴BC1＝＝＝5，故答案为：5．14．解：如图所示：1，2，3位置即为符合题意的答案．故答案为：3．15．解：∵△ABC与△DEF关于O点成中心对称∴△ABC≌△DEFAB＝DE，AC＝DF又∵BO＝OE，CO＝OF，∠BOC＝∠FOE∴△BOC≌△EOF∴∠BCO＝∠OFEBC∥EF故填：＝，EF，DF16．解：点（﹣3，4）关于原点对称的点的坐标是（3，﹣4）．故答案为：（3，﹣4）．17．解：从上午9时到中午12时，时针就从指向9，旋转到指向12，共顺时针转了3个“大格”，而每个“大格”相应的圆心角为30°，所以，30°×3＝90°，故答案为：90．18．解：从上午6时到上午9时时针转过3个大格，所以，3×30°＝90°，上午9时到下午5时时针转过8个大格，所以，8×30°＝240°．故答案为：90；240．19．解：把这个“十字星”形图绕其中心点O旋转，当至少旋转360°÷4＝90°后，所得图形与原图形重合，故答案为：90．20．解：∵点P1的坐标为（，），将线段OP1绕点O按顺时针方向旋转45°，再将其长度伸长为OP1的2倍，得到线段OP2；∴OP1＝1，OP2＝2，∴OP3＝4，如此下去，得到线段OP4＝23，OP5＝24…，∴OP n＝2n﹣1，由题意可得出线段每旋转8次旋转一周，∵2020÷8＝252…4，∴点P2020的坐标与点P4的坐标在同一直线上，正好在y轴的负半轴上，∴点P2020的坐标是（0，﹣22019）．故答案为：（0，﹣22019）．三．解答题21．解：（1）△ABC与△A′B′C′成中心对称；（2）根据点C的坐标为（0，0），则点B′的坐标为：（7，﹣2）；（3）线段CC′的长为：＝2．22．解：（1）由图（1）可得，c＝；（2）观察图形可知：当2个图（1）拼接时，总长度为：2a﹣2c＝2a﹣2×＝a+b；（3）结合（2）发现：用n个这样的图形拼出来的图形总长度为：a+（n﹣1）b，当a＝4，b＝3时，4+3（n﹣1）＝28，解得：n＝9．∴n的值为9．23．解：（1）原式＝＝2；（2）根据分析，知应分别为，5，．24．解：（1）在△ABC中，∵∠B+∠ACB＝30°，∴∠BAC＝150°，当△ABC逆时针旋转一定角度后与△ADE重合，∴旋转中心为点A，∠BAD等于旋转角，即旋转角为150°；（2）∵△ABC绕点A逆时针旋转150°后与△ADE重合，∴∠DAE＝∠BAC＝150°，AB＝AD＝4，AC＝AE，∴∠BAE＝360°﹣150°﹣150°＝60°，∵点C为AD中点，∴AC＝AD＝2，∴AE＝2．25．解：（1）等腰梯形必须旋转360°才能与自身重合；矩形旋转180°可以与自身重合．①等腰梯形是旋转对称图形，它有一个旋转角为180度．（假）②矩形是旋转对称图形，它有一个旋转角为180°．（真）（2）①只要旋转120°的倍数即可；②只要旋转90°的倍数即可；③只要旋转60°的倍数即可；④只要旋转45°的倍数即可．故是旋转对称图形，且有一个旋转角为120°的是①、③．（3）360°÷72°＝5．①是轴对称图形，但不是中心对称图形：如正五边形，正十五边形；②既是轴对称图形，又是中心对称图形：如正十边形，正二十边形．26．解：（1）∵点A（4，0），点B（0，3），∴OA＝4，OB＝3．在Rt△ABO中，由勾股定理得AB＝5．根据题意，△A′BO′是△ABO绕点B逆时针旋转900得到的，由旋转是性质可得：∠A′BA＝90°，A′B＝AB＝5，∴AA′＝5．（2）如图，根据题意，由旋转是性质可得：∠O′BO＝120°，O′B＝OB＝3过点O′作O′C⊥y轴，垂足为C，则∠O′CB＝90°．在Rt△O′CB中，由∠O′BC＝60°，∠BO′C＝30°．∴BC＝O′B＝．由勾股定理O′C＝，∴OC＝OB+BC＝．∴点O′的坐标为（，）．。

三年级下册数学单元测试-4.旋转、平移和轴对称一、单选题1.下面各图形中，（）一定是轴对称图形．A. 平行四边形B. 直角梯形C. 长方形2.选一选（1）A.B.（2）A.B.（3）A.B.3.下面的小鱼与( )成轴对称。

A. B. C.4.下面各图形中，对称轴最少的是（）。

A. 正方形B. 圆C. 等腰梯形D. 长方形二、判断题5.我们所学的数字都是对称的。

6.旋转就是以一个点或一个轴为中心而做的圆周运动7.直角三角形，梯形和圆都是轴对称图形．8.等腰梯形是轴对称图形。

三、填空题9.经过两次或几次平移后得到的图形，可以看成是原图形经过________次平移得到的，即平移加平移仍是________。

10.下面的图案是对折后的,如果打开会是什么图案呢?________ ________11.升国旗时，国旗所做的运动是________现象；钟表上时针和分针的运动是________现象；汽车在笔直的公路上行驶，汽车车身的运动是________现象，汽车车轮的运动是________现象。

12.观察图形并填空。

①图1绕点“O”逆时针旋转90°到达图________的位置；②图1绕点“O”逆时针旋转180°到达图________的位置；③图1绕点“O”顺时针旋转________°到达图4的位置；④图2绕点“O”顺时针旋转________°到达图4的位置；⑤图2绕点“O”顺时针旋转90°到达图________的位置；⑥图4绕点“O”逆时针旋转90°到达图________的位置。

13.由________组成四、解答题14.如图，三角形A´B´C´是三角形ABC平移后得到的，问三角形是怎么平移的？写出平移前后互相平行的线。

15.折、剪、拼之后，下图能组成一个轴对称图形吗？五、应用题16.指针从B开始，逆时针旋转90°到几点？参考答案一、单选题1.【答案】C【解析】【解答】解：A、根据轴对称图形的意义可知：平行四边形不是轴对称图形；B、根据轴对称图形的意义可知：直角梯形不是轴对称图形；C、长方形是轴对称图形，符合题意；故选：C．【分析】根据轴对称图形的意义：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做轴对称图形；依次进行判断即可．2.【答案】（1）A（2）B（3）A【解析】平移是物体或图形在直线方向上移动，本身没有发生方向上的改变。

最新初中数学图形的平移，对称与旋转的经典测试题含答案解析(3)一、选择题1．把一副三角板如图（1）放置，其中∠ACB＝∠DEC＝90°，∠A＝45°，∠D＝30°，斜边AB＝4，CD＝5．把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图2），此时AB与CD1交于点O，则线段AD1的长度为（）A13B5C．22D．4【答案】A【解析】试题分析：由题意易知：∠CAB=45°，∠ACD=30°．若旋转角度为15°，则∠ACO=30°+15°=45°．∴∠AOC=180°-∠ACO-∠CAO=90°．在等腰Rt△ABC中，AB=4，则AO=OC=2．在Rt△AOD1中，OD1=CD1-OC=3，由勾股定理得：AD113故选A.考点: 1.旋转；2.勾股定理.2．在平行四边形、菱形、矩形、正方形这四种图形中，是轴对称图形的有( )A．1个 B．2个 C．3个 D．4个【答案】C【解析】【分析】根据轴对称图形的概念求解．【详解】解：平行四边形不是轴对称图形，菱形、矩形、正方形都是轴对称图形．故选：C．【点睛】本题考查轴对称图形的概念，解题关键是寻找轴对称图形的对称轴，图形两部分沿对称轴折叠后可重合．3．下列所述图形中，是轴对称图形但不是中心对称图形的是()A．圆B．菱形C．平行四边形D．等腰三角形【答案】D【解析】【分析】根据轴对称图形与中心对称图形的概念进行判断即可.【详解】A、是轴对称图形，也是中心对称图形，故此选项错误；B、是轴对称图形，也是中心对称图形，故此选项错误；C、不是轴对称图形，是中心对称图形，故此选项错误；D、是轴对称图形，不是中心对称图形，故此选项正确，故选D．【点睛】本题考查了中心对称图形与轴对称图形的概念.辨别轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；.辨别中心对称图形的关键是要寻找对称中心，旋转180度后与原图重合．4．下列说法正确的是（）A．平移不改变图形的形状和大小，而旋转则改变图形的形状和大小B．在成中心对称的两个图形中，连结对称点的线段都被对称中心平分C．在平面直角坐标系中，一点向右平移2个单位，纵坐标加2D．在平移和旋转图形中，对应角相等，对应线段相等且平行【答案】B【解析】【分析】分别利用图形的平移以及中心对称图形的性质和旋转的性质分别判断得出即可．【详解】A、平移不改变图形的形状和大小，旋转也不改变图形的形状和大小，故此选项错误；B、在成中心对称的两个图形中，连结对称点的线段都被对称中心平分，此选项正确；C、在平面直角坐标系中，一点向右平移2个单位，横坐标加2，故此选项错误；D、在平移中，对应角相等，对应线段相等且平行，旋转则对应线段有可能不平行，故此选项错误．故选B．5．在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A．B．C．D．【答案】D【解析】【分析】根据平移只改变图形的位置，不改变图形的形状和大小，逐项进行分析即可得.【详解】A 、不能通过平移得到，故不符合题意；B 、不能通过平移得到，故不符合题意；C 、不能通过平移得到，故不符合题意；D 、能够通过平移得到，故符合题意，故选D.【点睛】本题考查了图形的平移，熟知图形的平移只改变图形的位置，而不改变图形的形状和大小是解题的关键.6．如图，在平面直角坐标系中，AOB ∆的顶点B 在第一象限，点A 在y 轴的正半轴上，2AO AB ==，120OAB ∠=o ，将AOB ∠绕点O 逆时针旋转90o ，点B 的对应点'B 的坐标是（ ）A ．3(2,3)2--B ．33(2,2)22---C ．3(3,2)2--D ．(3,3)-【答案】D【解析】【分析】过点'B 作x 轴的垂线，垂足为M ，通过条件求出'B M ，MO 的长即可得到'B 的坐标.【详解】解：过点'B 作x 轴的垂线，垂足为M ，∵2AO AB ==，120OAB ∠=︒，∴'''2A O A B ==，''120OA B ∠=︒，∴'0'6M B A ∠=︒，在直角△''A B M 中，3==22=B'M B'M 'sin B A M B '''A ∠ ， 1==22=A'M A'M 'cos B A M B '''A ∠， ∴'3B M =，'1A M =， ∴OM=2+1=3，∴'B 的坐标为(3,3)-.故选：D.【点睛】本题考查坐标与图形变化-旋转，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题．7．如图，将ABC V 绕点A 逆时针旋转110o ，得到ADE V ，若点D 在线段BC 的延长线上，则ADE ∠的大小为( )A ．55oB ．50oC ．45oD ．35o【答案】D【解析】【分析】根据旋转的性质可得AB AD =，BAD 110∠=o ，ADE ABC ∠∠=，根据等腰三角形的性质可得ABC ADE 35∠∠==o ．【详解】如图，连接CD ，Q 将ABC V 绕点A 逆时针旋转110o ，得到ADE V ，AB AD ∴=，BAD 110∠=o ，ADE ABC ∠∠=，∴∠ABC=∠ADB=（180°-∠BAD ）÷2=35°，∴∠ADE=ABC 35∠=o ，故选D ．【点睛】本题考查了旋转的性质，等腰三角形的性质，熟练运用旋转的性质是解本题的关键．8．如图，在ABC V 中，60,3,5,B AB BC ∠=︒==将ABC V 绕点A 顺时针方向旋转得到,ADE V 当点B 的对应点D 恰好落在BC 边上时，则CD 的长为（ ）A ．3B ．2.5C ．2D ．1【答案】C【解析】【分析】 由旋转得到AD=AB ，由此证明△ADB 是等边三角形，得到BD=AB=3，即可求出CD.【详解】由旋转得AD=AB ，∵60B ∠=︒，∴△ADB 是等边三角形，∴BD=AB=3，∴CD=BC-BD=5-3=2，故选：C.【点睛】此题考查旋转的性质，等边三角形的判定及性质，根据旋转得到AD=AB 是解题的关键，由此得到等边三角形进行求解.9．下列图形中，是轴对称图形但不是中心对称图形的是（ ）A ．B ．C ．D ．【答案】A【解析】A.是轴对称图形不是中心对称图形，正确；B.是轴对称图形也是中心对称图形，错误；C.是中心对称图形不是轴对称图形，错误；D. 是轴对称图形也是中心对称图形，错误， 故选A.【点睛】本题考查轴对称图形与中心对称图形，正确地识别是解题的关键.10．如图，△ABC 中，∠BAC ＝45°，∠ACB ＝30°，将△ABC 绕点A 顺时针旋转得到△AB 1C 1，当点C 1、B 1、C 三点共线时，旋转角为α，连接BB 1，交AC 于点D ．下列结论：①△AC 1C 为等腰三角形；②△AB 1D ∽△BCD ；③α＝75°；④CA ＝CB 1，其中正确的是（ ）A．①③④B．①②④C．②③④D．①②③④【答案】B【解析】【分析】将△ABC绕点A顺时针旋转得到△AB1C1，得到△ABC≌△AB1C1，根据全等三角形的性质得到AC1=AC，于是得到△AC1C为等腰三角形；故①正确；根据等腰三角形的性质得到∠C1=∠ACC1=30°，由三角形的内角和得到∠C1AC=120°，得到∠B1AB=120°，根据等腰三角形的性质得到∠AB1B=30°=∠ACB，于是得到△AB1D∽△BCD；故②正确；由旋转角α=120°，故③错误；根据旋转的性质得到∠C1AB1=∠BAC=45°，推出∠B1AC=∠AB1C，于是得到CA=CB1；故④正确．【详解】解：∵将△ABC绕点A顺时针旋转得到△AB1C1，∴△ABC≌△AB1C1，∴AC1＝AC，∴△AC1C为等腰三角形；故①正确；∴AC1＝AC，∴∠C1＝∠ACC1＝30°，∴∠C1AC＝120°，∴∠B1AB＝120°，∵AB1＝AB，∴∠AB1B＝30°＝∠ACB，∵∠ADB1＝∠BDC，∴△AB1D∽△BCD；故②正确；∵旋转角为α，∴α＝120°，故③错误；∵∠C1AB1＝∠BAC＝45°，∴∠B1AC＝75°，∵∠AB1C1＝∠BAC＝105°，∴∠AB1C＝75°，∴∠B1AC＝∠AB1C，∴CA＝CB1；故④正确．故选：B．【点睛】本题考查了相似三角形的判定和性质，等腰三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．11．等腰三角形、直角三角形、等边三角形、锐角三角形、钝角三角形和等腰直角三角形中，一定是轴对称图形的有（）A．3个 B．4个 C．5个 D．2个【答案】A【解析】等腰三角形、等边三角形、等腰直角三角形都是轴对称图形，是轴对称图形的有3个.故选：A.12．把一副三角板如图甲放置，其中∠ACB=∠DEC=90°，∠A-45°，∠D=30°，斜边AB=6，DC=7，把三角板DCE绕着点C顺时针旋转15°得到△D1CE1（如图乙），此时AB与CD1交于点O，则线段AD1的长度为（）A．32B．5 C．4 D31【答案】B【解析】【分析】【详解】由题意易知：∠CAB=45°，∠ACD=30°，若旋转角度为15°，则∠ACO=30°+15°=45°．∴∠AOC=180°－∠ACO－∠CAO=90°．在等腰Rt△ABC中，AB=6，则AC=BC=32同理可求得：AO=OC=3．在Rt△AOD1中，OA=3，OD1=CD1－OC=4，由勾股定理得：AD1=5．故选B．，若将△ABO绕点O沿顺时针方向旋转90°13．如图，平面直角坐标系中，已知点B(3,2)后得到△A1B1O，则点B的对应点B1的坐标是( )A ．（3，1）B ．（3，2）C ．（1，3）D ．（2，3）【答案】D【解析】【分析】 根据网格结构作出旋转后的图形，然后根据平面直角坐标系写出点B 1的坐标即可．【详解】解：△A 1B 1O 如图所示，点B 1的坐标是（2，3）．故选D ．【点睛】本题考查了坐标与图形变化，熟练掌握网格结构，作出图形是解题的关键．14．如图，在矩形ABCD 中， 3,4,AB BC ==将其折叠使AB 落在对角线AC 上，得到折痕,AE 那么BE 的长度为（ ）A ．1B ．2C ．32D ．85【答案】C【解析】【分析】由勾股定理求出AC 的长度，由折叠的性质，AF=AB=3，则CF=2，设BE=EF=x ，则CE=4x -，利用勾股定理，即可求出x 的值，得到BE 的长度．【详解】解：在矩形ABCD 中，3,4AB BC ==，∴∠B=90°， ∴22345AC =+=， 由折叠的性质，得AF=AB=3，BE=EF ，∴CF=5-3=2，在Rt △CEF 中，设BE=EF=x ，则CE=4x -，由勾股定理，得：2222(4)x x +=-，解得：32x =； ∴32BE =． 故选：C ．【点睛】本题考查了矩形的折叠问题，矩形的性质，折叠的性质，以及勾股定理的应用，解题的关键是熟练掌握所学的性质，利用勾股定理正确求出BE 的长度．15．如图，在ABC ∆中，90,2,4C AC BC ∠=︒==，将ABC ∆绕点A 逆时针旋转90︒，使点C 落在点E 处，点B 落在点D 处，则B E 、两点间的距离为（ ）A 10B ．2C ．3D ．25【答案】B【解析】【分析】 延长BE 和CA 交于点F ，根据旋转的性质可知∠CAE=90︒，证明∠BAE=∠ABC ，即可证得AE ∥BC ，得出2142EF AF AE FB FC BC ====，即可求出BE ． 【详解】延长BE和CA交于点F∵ABC∆绕点A逆时针旋转90︒得到△AED ∴∠CAE=90︒∴∠CAB+∠BAE=90︒又∵∠CAB+∠ABC=90︒∴∠BAE=∠ABC∴AE∥BC∴2142 EF AF AEFB FC BC====∴AF=AC=2，FC=4∴BF=42∴BE=EF=12BF=22故选：B【点睛】本题考查了旋转的性质，平行线的判定和性质．16．如图，点E是正方形ABCD的边DC上一点，把ADE∆绕点A顺时针旋转90︒到ABF∆的位置．若四边形AECF的面积为20，DE=2，则AE的长为（）A．4 B．5C．6 D．26【答案】D【解析】【分析】利用旋转的性质得出四边形AECF的面积等于正方形ABCD的面积，进而可求出正方形的边长，再利用勾股定理得出答案．【详解】Q绕点A顺时针旋转90︒到ABF∆ADE∆的位置．∴四边形AECF的面积等于正方形ABCD的面积等于20，∴==，AD DC25Q，DE=2∴∆中，2226Rt ADE=+=AE AD DE故选：D．【点睛】本题主要考查了旋转的性质以及正方形的性质，正确利用旋转的性质得出对应边关系是解题关键．17．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．【答案】A【解析】【分析】根据轴对称图形与中心对称图形的概念求解．【详解】A、既是轴对称图形，又是中心对称图形，故本选项不符合题意；B、不是轴对称图形，是中心对称图形，故本选项不符合题意；C、是轴对称图形，不是中心对称图形，故本选项不符合题意；D、是轴对称图形,不是中心对称图形，故本选项符合题意．故选：A．【点睛】此题考查中心对称图形与轴对称图形的概念．解题关键在于掌握轴对称图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．18．如图，在△ABC中，AC=BC，∠ACB=90°，点D在BC上，BD=3，DC=1，点P是AB上的动点，则PC+PD的最小值为（）A．4 B．5 C．6 D．7【答案】B【解析】试题解析：过点C作CO⊥AB于O，延长CO到C′，使OC′=OC，连接DC′，交AB于P，连接CP．此时DP+CP=DP+PC′=DC′的值最小．∵DC=1，BC=4，∴BD=3，连接BC′，由对称性可知∠C′BE=∠CBE=45°，∴∠CBC′=90°，∴BC′⊥BC，∠BCC′=∠BC′C=45°，∴BC=BC′=4，根据勾股定理可得DC′=22'+=22BC BD+=5．故选B．3419．下列图形中，是轴对称图形不是中心对称图形的是（）A．B．C．D．【答案】A【解析】【分析】轴对称图形是指平面内，一个图形沿一条直线折叠，直线两旁的部分能够完全重合的图形；而在平面内，把一个图形绕着某个点旋转180°，如果旋转后的图形能与原来的图形重合，那么这个图形叫做中心对称图形，据此进一步判断求出答案即可.【详解】A：是轴对称图形，但不是中心对称图形，符合题意；B：是轴对称图形，也是中心对称图形，不符合题意；C：是中心对称图形，但不是轴对称图形，不符合题意；D：是轴对称图形，也是中心对称图形，不符合题意；故选：A.【点睛】本题主要考查了轴对称图形与中心对称图形的识别，熟练掌握相关概念是解题关键.20．如图，将△ABC绕点A顺时针旋转60°得到△ADE，点C的对应点E恰好落在BA的延长线上，DE与BC交于点F，连接BD．下列结论不一定正确的是（）A．AD=BD B．AC∥BD C．DF=EF D．∠CBD=∠E【答案】C【解析】【分析】由旋转的性质知∠BAD=∠CAE=60°、AB=AD，△ABC≌△ADE，据此得出△ABD是等边三角形、∠C=∠E，证AC∥BD得∠CBD=∠C，从而得出∠CBD=∠E．【详解】由旋转知∠BAD=∠CAE=60°、AB=AD，△ABC≌△ADE，∴∠C=∠E，△ABD是等边三角形，∠CAD=60°，∴∠D=∠CAD=60°、AD=BD，∴AC∥BD，∴∠CBD=∠C，∴∠CBD=∠E，则A、B、D均正确，故选C．【点睛】本题主要考查旋转的性质，解题的关键是熟练掌握旋转的性质、等边三角形的判定与性质及平行线的判定与性质．。

一、单选题B’分别是A 、B 的对应点，且点B 在斜边A‘B'上，直角边C'A'交AB 于D ,则旋转角等于（）二、判断题5 .杂技演员连续后空翻是旋转现象。

（ ）6 .滑梯是平移现象，风扇是旋转现象。

7 .旋转中，对应点划过的痕迹是一条圆弧。

平移和旋转A. 60°B. 90°C. 180°D. 360°A. 70°B. 80°C. 60°1.平移是沿着（ ）移动A.直线B.曲线2.下面哪些图案不能通过平移得到？（3.分针围绕钟面中心顺时针旋转3圈后， 时针围绕钟面中心顺时针旋转了（ ）4.如图：在三角形ABC 中N ACB=90°, N A=40°,以C 为旋转中心，将三角形ABC 旋转到三角形A'B'C 的位置，其中A’、8.判断对错.找出下面图形的变化规律，然后根据这个规律在最后一个图的空格里画上相关的图形三、填空题9.不倒翁的摆动是 ______ 现象。

12.分针和时针的转速比是 ______四、解答题13.把平移前后两幅图中的平行线涂上相同的颜色。

五、综合题15.左边的图形是如何变成右边的图形的？（1）红色三角形：_____（2）蓝色三角形：_____（3）黄色三角形：_____（4）绿色三角形：_____六、应用题16.将图先向右平移6格，再向上平移4格，并画出平移后的图形．参考答案一、单选题1.【答案】A【解析】【解答】平移是沿着直线移动【分析】考查了平移的相关知识2.【答案】B【解析】【解答】解：A、一个小三角形平移后得到整个图形；B、曲线所指的方向变化了，不是平移得到的；C、一个五边形平移后得到整个图形.故答案为：B【分析】平移后的图形的形状、大小、方向都不变，位置发生了变化，由此根据平移的特征判断哪些图形是通过平移得到的即可.3.【答案】B【解析】4.【答案】B【解析】【解答】解：图中BC绕C点旋转后得到B'C，CB=CB'，又因为N A'B'C是N ABC旋转后的角，因此两角相等都是50度，经过计算得到N B'CB=80°，故N ACD=80°.故答案为：B【分析】旋转后的图形的大小不变，各个角的度数也不变，这样N B’就是50度，三角形BB’C是等腰三角形，所以能计算出N B′CB的度数，然后就能确定旋转角的大小.二、判断题5.【答案】错误【解析】【解答】杂技演员连续后空翻是平移现象，原题说法错误.故答案为：错误.【分析】杂技演员后空翻是旋转现象，杂技演员连续后空翻是平移现象，据此判断.6.【答案】正确【解析】【解答】解：根据平移、旋转的意义可得滑梯是平移现象，风扇是旋转现象，可见原题说法正确. 故答案为：正确.【分析】平移是水平或竖直或其他方向的平行移动；在平面内将一个图形绕一点按某个方向转动一个角度，这样的运动叫做图形的旋转，根据平移和旋转的定义进行分析即可解.答7.【答案】正确【解析】【解答】解：旋转中，对应点划过的痕迹是一条圆弧，原题说法正确.故答案为：正确【分析】旋转中，对应的点划过的痕迹是一条圆弧，圆弧的圆心角就是旋转的度数.8.【答案】错误【解析】【解答】正确解答：如下图所示。

三年级数学平移和旋转试题1.将图所示的图案通过平移后可以得到的图案是（）A．B．C．D．【答案】A【解析】【考点】作平移后的图形．分析：根据平移的特征分析各图特点，只有符合“图形的形状、大小和方向都不改变”即为答案．解答：根据平移不改变图形的形状、大小和方向，将题图所示的图案通过平移后可以得到的图案是A，其它三项皆改变了方向，故错误．2.如图点A、B、C、D、O都在方格纸的格点上，△COD是由△AOB绕点O按逆时针方向旋转而成，则旋转的角度为（）A．30° B．45° C．90° D．135°【答案】C【解析】【考点】旋转．分析：由△COD是由△AOB绕点O按逆时针方向旋转而得，可知旋转的角度是∠BOD的大小，然后由图形即可求得答案．解答：因为△COD是由△AOB绕点O按逆时针方向旋转而得，所以OB=OD，因为旋转的角度是∠BOD的大小，且∠BOD=90°，所以旋转的角度为90°3.如图四边形ABCD是正方形，E是边CD上一点，若△AFB经过逆时针旋转后，与△AED重合，则旋转角可能为（）A．90°B．60°C．45°D．30°【答案】A【解析】【考点】作旋转一定角度后的图形．分析：根据正方形的性质可得∠BAD=90°，再根据旋转的性质，旋转角等于对应边的夹角解答．解答：解因为四边形ABCD是正方形，所以∠BAD=90°，且旋转角=∠BAD=90°4.在算盘上拨珠子是（）A．旋转 B．平移 C．既不是平移，也不是旋转【答案】B【解析】【考点】平移．分析：将一个图形上的所有点都按照某个方向作相同距离的移动，这样的图形运动叫作图形的平移运动；把一个图形绕着某一点O转动一个角度的图形变换叫做旋转；据此解答即可．解答：在算盘上拨珠子是平移。

5.①号三角形绕A点按时针方向旋转了度．【答案】顺，90【解析】【考点】旋转分析：根据图形旋转的特征，一个图形绕某点顺时针（或逆时针）旋转一定的度数，某点的位置不动，其余各点（边）均绕某点按相同的方向旋转相同的度数．解答：①号三角形绕A点按顺时针方向旋转了90度．6.钟表分针的运动可看做一种旋转现象，一只标准时钟的分针匀速旋转，经过15分钟旋转了度．【答案】90【解析】【考点】旋转.分析：根据钟表面的知识，钟表上分针走过一个小格转过的度数是6°，走过15分钟，乘以15，计算即可得解．解答：因为钟表上分针走过一个小格转过的度数是6°，所以经过14分钟旋转了6°×15=90°7.在横线上填上“平移”或“旋转“⑴火车在行使的运动是．⑵风车运动的现象是．⑶运动员举重是．⑷电风扇的运动是．【答案】⑴平移；⑵旋转；⑶平移；⑷旋转【解析】【考点】平移；旋转．分析：掌握好平移的特点，和旋转的特点来解答。