ADF教程：如何计算单重态到三重态的激发(非相对论、禁阻跃迁)

单重态和三重态是指在分子体系中，由同一组电子构成的两种不同的激发态。

这两种激发态的自由能能量差计算在理论化学中是非常重要的，因为它可以用来解释和预测分子体系的性质和行为。

在本文中，我们将探讨单重态和三重态的自由能能量差的计算方法，并讨论其在化学研究中的应用。

1. 单重态和三重态的定义单重态和三重态是分子体系中激发态的两种基本类型。

在单重态中，分子中的所有电子都处于自旋相反的态，总自旋为零。

而在三重态中，分子中至少有一个电子处于与其余电子自旋相反的态，总自旋不为零。

这两种激发态的自由能能量差可以通过一系列计算方法来确定。

2. 自由能能量差的计算方法自由能能量差的计算通常可以利用量子化学计算软件来进行，其中最常用的方法包括密度泛函理论（DFT）、含时密度泛函理论（TDDFT）、多体微扰理论（MBPT）等。

这些方法可以通过求解分子的薛定谔方程或是利用近似方法来计算分子在不同激发态下的能量。

3. 应用领域单重态和三重态的自由能能量差的计算在许多化学研究领域都有重要的应用。

在有机光电子材料的设计中，通过计算单重态和三重态的能量差可以预测材料的光学性质和稳定性；在催化剂设计中，自由能能量差可以用来解释反应中间体的稳定性和反应性能等。

4. 研究进展近年来，随着计算机技术和量子化学方法的不断进步，对于单重态和三重态自由能能量差的计算方法也在不断地得到改进和完善。

开发了一些新的密度泛准理论方法，如双杂化密度泛准理论（DH-DFT）和自洽场双杂化密度泛准理论（SC-DH-DFT），在计算复杂体系的单重态和三重态能量差时取得了一定的成功。

5. 结论在化学研究中，单重态和三重态的自由能能量差计算对于理解和预测分子体系的性质具有重要意义。

通过合理选择计算方法和不断创新，我们可以更准确地计算出这两种激发态的能量差，为材料设计、催化剂设计等领域的研究提供有力的支持。

希望未来能够有更多的研究取得突破，为该领域的发展做出贡献。

在现代理论化学研究中，单重态和三重态的自由能能量差的计算在许多领域都有着广泛的应用。

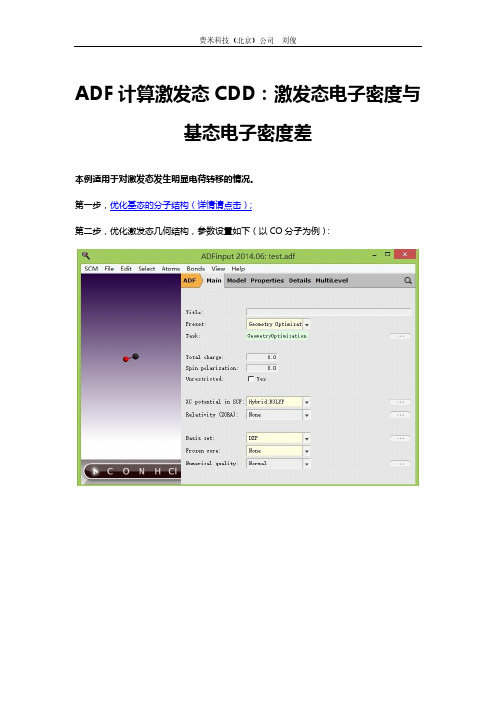
ADF计算激发态CDD：激发态电子密度与基态电子密度差本例适用于对激发态发生明显电荷转移的情况。

第一步，优化基态的分子结构（详情请点击）;第二步，优化激发态几何结构，参数设置如下（以CO分子为例）：注意：LDA、GGA低估了交换作用，因此会产生一种不符合事实的后果——对于能量很低的激发态，也出现了电荷的转移。

一个比较粗暴的解决方式就是替换为杂化泛函，例如B3LYP。

激发态几何优化取消对称性的原因是：我们并不清楚激发态分子结构对称性是不是会降低（当然对于这个例子里面，CO无论怎么变，都是C∞点群对称，是不必要的，但如果这样的话，就需要先知道需要优化的激发态的不可约表示符号，例如是A1不可约表示的第二个态的话，就需要在第3图中将1A替换为2A1），因此将其设置为C1群（没有对称性），这样是合理的。

保存并运行任务。

第三步，结果分析：在ADFinput窗口，SCM-View：将右下角的数值调整（该值为等值面的数值，不同的数值，则窗口显示该值的等值面），例如此例改为0.003这就是该几何结构下，该激发态（激发态几何结构优化那一步指定的那个激发态）与基态的电子密度之差的空间分布。

补充内容：如何要得到总的激发态电子密度？1，Field — Calculate之后最下方下方选择如图所示注意右下角红色圆圈里面的C-1，这是计算出来的“基态密度+激发态基态密度差=激发态密度”的数据编号。

2，显示该密度（C-1这一项）：Add- ISOSurface Double（+/-），最下方，选择如下：即显示激发态电子密度的等值面。

注意倒数第二行编号为C-1，因此，最后一行选择Other — 1 — C-1，即显示激发态的电子密度空间分布。

ADF中文教程：相对论中Scalar与Spin-Orbit的区别在ADF模块的Main面板设置中，有一项Relativity的设置，有三个选项：None、Scalar、Spin-Orbit。

None，非相对论。

哈密顿量也就是我们在教科书上见到的Kohn-Sham 方程的形式。

Scalar，标量相对论。

在物理定性理解上，可以认为是只考虑了相对论对哈密顿量中的动能项有影响。

形式与非相对论仍然是相似的。

在ADF 的Main菜单设置了Scalar，那么计算激发态的时候，就要用Spin－Orbit（Perterbative），也就是说，激发态里面要考虑旋轨耦合，只能使用微扰的方式。

Spin-Orbit，旋轨耦合。

此时波函数不再是一个函数，而是一个矢量，或者说是一个向量，向量中每个元素是一个波函数。

从物理定性上理解，可以认为考虑了相对论对哈密顿量中的动能项有影响，同时也考虑了电子的自旋角动量和轨道角动量之间的耦合（也就是所谓的旋轨耦合、SOC，这个耦合大部分情况下都很小）。

那么计算激发态的时候，就要用Spin－Orbit（SCF），而不能使用Spin－Orbit （Perterbative）。

这种耦合，对于磷光现象而言，是至关重要的，如果没有这种耦合，磷光现象就不会存在于世上——因为三重态与单重态之间的跃迁偶极矩将永远为0，属于禁阻跃迁；自旋角动量-轨道角动量的耦合，使得跃迁偶极矩能够不为0，从而让三重态-单重态之间的跃迁不再是禁阻跃迁(但此时，单／三重态不再是严格的单／三重态)，也就有了磷光现象。

这种耦合，也是所谓“零场劈裂”的必要条件。

对于Scalar来说，得到的是与非相对论一样的形式，有所谓单重态、三重态的概念，单重态电子总自旋为0，三重态电子总自旋为1（即1/2+1/2，两个电子未配对）。

而对于Spin-Orbit来说，得到的电子态的描述，既不是单重态也不是三重态，而是一个“混合”状态。

原先的三重态，也真正变成了三个能量略有差别的三个态，旋轨耦合越大，这个能量差别越大，也就是零场劈裂越显著，反之亦然。

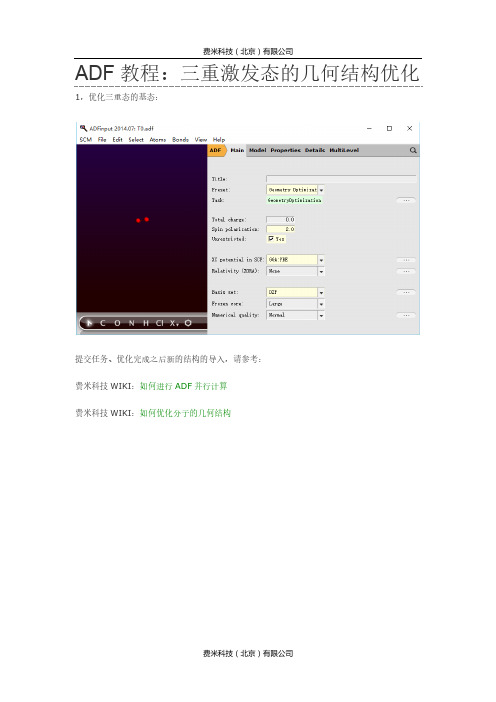
ADF教程：三重激发态的几何结构优化1，优化三重态的基态：提交任务、优化完成之后新的结构的导入，请参考：费米科技WIKI：如何进行ADF并行计算费米科技WIKI：如何优化分子的几何结构2，基于优化之后的分子结构，计算三重激发态：计算完成之后，检查该T1激发态是否合理：查看*.out文件中电子激发的信息对应的轨道，可以在SCM-level中分别查看3，优化所需的三重激发态，例如T1。

注意，软件本身并不能区分能量最低的三重态是实际的基态还是激发态，因此统一地将第一步优化得到的三重态的基态作为T0，此处如果优化T1，也就是三重态中，能量次低的态。

T2、T3，以此类推。

注意：如果优化T2，T3……，则将此处设置为2A、3A……即可。

此处spin type不需要修改，这是目前版本的图形界面的一个bug，保留原样即可，不必改为Triplet。

4，计算结束，收敛正常（得到5个T，尤其是第二个T最重要）：查看激发能的变化情况：最后一个能量，就是优化完成的激发能。

优化经历了6步。

最后用第6步的结构，重新计算了激发能。

SCM-Spectra，显示的就是最后这个几何结构对应的激发能。

要注意，T1的总能量应该是该结构的三重态基态能量加上激发能，也就是：logfile最后显示的Bonding Energy：因此T1的总能量就是：-7.87621845 eV+3.15671 eV = -4.71950845 eV至此完成。

如果要考虑旋轨耦合，请参考：费米科技WIKI：如何计算自旋-轨道耦合矩阵元<S0|SOC|T1>等等费米科技WIKI：如何计算单重态到三重态的激发（非相对论、禁阻跃迁）费米科技WIKI：如何计算单重态到三重态的激发（相对论、许可跃迁）费米科技WIKI：三重态的劈裂。

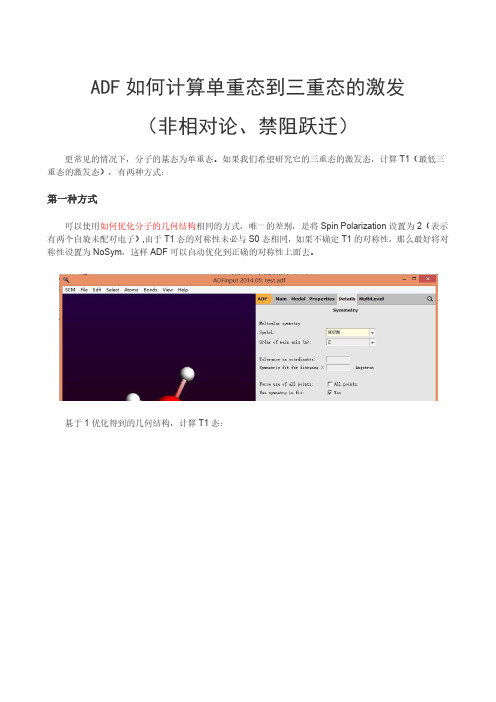
ADF如何计算单重态到三重态的激发
（非相对论、禁阻跃迁）
更常见的情况下，分子的基态为单重态。

如果我们希望研究它的三重态的激发态，计算T1（最低三重态的激发态），有两种方式：
第一种方式
可以使用如何优化分子的几何结构相同的方式，唯一的差别，是将Spin Polarization设置为2（表示有两个自旋未配对电子）,由于T1态的对称性未必与S0态相同，如果不确定T1的对称性，那么最好将对称性设置为NoSym，这样ADF可以自动优化到正确的对称性上面去。

基于1优化得到的几何结构，计算T1态：
此时不必将Symmetry设置为NoSym。

由于T1态的对称性未必与S0态相同，如果不确定T1的对称性，那么最好将对称性设置为NoSym，这样ADF可以自动优化到正确的对称性上面去。

计算完成后，查看三重激发态的激发能（相对该结构对应的S0态能量的差值）：
注意：此处可以看到oscillator strengths f都为0，也即是说，这种跃迁属于禁阻跃迁，跃迁几率为0。

如果考虑相对论的自旋-轨道耦合效应，则有所不同。

详见如何计算单重态到三重态的激发（非相对论、禁阻跃迁）。

第二种方式
首先进行激发态几何结构优化，这较为复杂：首先需要将对称性取消，原因与第一种方式相同，那么需要设置参数如下：
上图1A表示不可约表示A中的第一个激发态，因为对称性设置为NoSym之后，不可约表示只剩下一个，名为A。

优化完成之后，就得到优化后的T1态的结果，在out文件中可以查看到详细信息。

同样地，振子强度f全部为0，属于禁阻跃迁。

如何计算自旋-轨道耦合矩阵前言：自旋-轨道耦合对于磷光很重要，因为如果二者耦合如果严格为0，那么单重态和三重态之间的跃迁就会成为禁阻跃迁，就不会有磷光发生。

有时候我们需要关心某个特定几何结构下（例如S0态与T1态势能面交叉点处），S0态与T1态之间自旋轨道耦合。

用算符来表示即：<S0|SOC|T1>，也就是自旋-轨道耦合算符，左边乘以S0态、右边乘以T1态，然后在全空间积分得到的一个实数（包括实部和虚部）。

这个实数有时候我们把它称作矩阵元，这是因为可能有很多个态，比如S0、T1、S1、S2、S3、T2、T3……，这些所有态之间，都可以有这样一个积分得到的实数。

如果把这些态，按序号排列好，分别叫做State n（N=1,2,3……N），那么就可以对应为一个N*N的矩阵，i行j列，即为<State i|SOC|State j>。

这个矩阵有一个特点，也就是i行j列与j行i列是共轭关系：二者实部相同，虚部反号，因此二者的模相等。

我们可能更关心这个实数的模，即实数的实部与虚部的平方和。

因此我们通过计算，然后找到该矩阵元的实部和虚部，之后求取平方和即可。

步骤：此处以CH 4举例（C1群分子输出结果更简单）第一步，优化分子结构（详情请点击）;第二步，进行自旋-轨道耦合矩阵元的计算。

这一步计算的物理意义：首先以Scalar相对论（无自旋轨道耦合的相对论方法）将较低的单重激发态和三重激发态计算出来，然后将自旋-轨道耦合视为微扰，得到自旋-轨道耦合矩阵元，然后也得到考虑微扰之后的各个激发态的激发能（此时，三重态可能会发生劈裂，即三个态能量不等——这就是由自旋-轨道耦合引起的）。

因此，计算参数设置如下：在Details — User input输入：PRINT SOMATRIXGSCORR保存任务并运行。

第三步，查看结果：首先在*.out文件中找到我们需要的态，例如T1与S0。

首先找到S0态所属的不可约表示（如果没有对称性，点群为C1，那么就只有一个不可约表示，名为A），在此例中，S0态属于不可约表示A1：然后找到T1所属的不可约表示。

如何计算单重态到三重态的激发
（相对论、许可跃迁）-ADF
一般情况下，单重态到三重态的激发，属于禁阻跃迁，只有考虑电子的自旋角动量与轨道角动量的耦合作用时，跃迁几率才能得到非0的值。

而此时，实际上就不存在单重态、三重态的概念，只能是近似为单重态、三重态。

如下以H2O为例：
第一步：优化几何结构，可以采用如何计算单重态到三重态的激发（非相对论、禁阻跃迁）相同的方式，一般可以忽略自旋轨道耦合。

也可以将Relativity设置为Scalar，部分地考虑相对论效应（此时自旋、轨道角动量仍然没有耦合，仍然存在标准的单重态、三重态的概念）。

第二步：计算“三重态激发态”，有两种可选的方式：
基态使用Scalar相对论计算、激发态通过微扰的方法考虑自旋-轨道耦合，参数设置如下：
基态计算考虑自旋-轨道耦合、激发态精确地考虑自旋-轨道耦合，参数设置如下：
这两种方式，后者精确度更高，但前者可以计算自旋轨道耦合矩阵元。

后者计算得到的跃迁几率非常小（例如0.0000001以下）的激发态，并且三个激发态能量很接近，这就是对应的T1态劈裂开的3个激发态，具体可以参考三重态的劈裂。

前者得到的三个态能量完全一样，不能处理三重态的劈裂问题。

在一般温度下，大多数分子处在基态的最低振动能级。

处于基态的分子吸收能量(电能、热能、化学能或光能等)后被激发为激发态。

激发态是很不稳定的，它将很快地释放出能量又重新跃迁回基态。

若分子返回基态时以发射电磁辐射(即光)的形式释放能量，就称为“发光”。

如果物质的分子吸收了光能而被激发，跃迁回基态所发射的电磁辐射，称为荧光和磷光。

现从分子结构理论来讨论荧光和磷光的产生机理。

每个分子中都具有一系列严格分立相隔的能级，称为电子能极，而每个电子能级中又包含有一系列的振动能级和转动能级。

分子中电子的运动状态除了电子所处的能级外，还包含有电子的多重态，用M=2S+1表示，S为各电子自旋量子数的代数和，其数值为0或1 。

根据Pauli不相容原理，分子中同一轨道所占据的两个电子必须具有相反的自旋方向，即自旋配对。

若分子中所有电子都是自旋配对的，则S=0,M=1,该分子便处于单重态(或叫单重线)，用符号S表示。

大多数有机化合物分子的基态都处于单重态。

基态分子吸收能量后，若电子在跃迁过程中，不发生自旋方向的变化，这时仍然是M=1，分子处于激发的单重态；如果电子在跃迁过程中伴随着自旋方向的变化，这时分子中便具有两个自旋不配对的电子，即S=1,M=3，分子处于激发的三重态，用符号T表示。

处于分立轨道上的非成对电子，自旋平行要比自旋配对更稳定些(洪特规则)，因此在同一激发态中，三重态能级总是比单重态能级略低。

处于激发态的分子是很不稳定的，它可能通过辐射跃迁和非辐射跃迁的形式去活化(去激发)释放出多余的能量而返回基态。

辐射跃迁主要涉及到荧光，延迟荧光或磷光的发射；无辐射跃迁是指以热的形式释放多余的能量，包括振动弛豫、内部转移、系间跨越及外部转移等过程。

(3) 荧光发射(Fluorescence emission,FE)——处于激发单重态的电子经振动弛豫及内部转移后到达第一激发单重态(S1)的最低振动能级(V=0)后，以辐射的形式跃迁回基态(S0)的各振动能级，这个过程为荧光发射，发射的荧光波长为。

ADF教程：如何计算临界点电子密度、密度梯度、能量密度、多种能量密度变化率，以及AIM电荷等ADF中包含AIM功能，可以给出电子密度的拓扑结构（电子密度、密度梯度、能量密度、多种能量密度变化率，以及AIM电荷等）。

参数设置结果查看在SCM Logo > Output：RhoT O P O L O G Y O F T H E E L E C T R O N D E N S I T Y (Rho)Module written by Juan I. Rodriguez-Hernandez,ESFM-Instituto Politecnico Nacional-Mexico.Any questions/comments to: juan@esfm.ipn.mx and/or SCM technical support. This subroutine was vectorized, its efficientcy is reported inJuan I. Rodriguez et. al., J. Comput. Chem. 34, 681(2013).Additional CP properties added by L. Joubert and V. Tognetti,University of Rouen, France.THIS IS THE GEOMETRY IN THE CP SEARCH (ANGSTROM):Atom X Y Z180.0000000.000000 -0.68950521 -0.7838370.000000 -1.243761310.7838370.000000 -1.243761TOTAL NUMBER OF CRITICAL POINTS: 5NUMBER OF (3,-1) CRITICAL POINTS: 2NUMBER OF (3,+1) CRITICAL POINTS: 0NUMBER OF (3,+3) CRITICAL POINTS: 0NUMBER OF (3,-3) CRITICAL POINTS: 3Poincare-Hopf satisfied--------------------------------------------------------CP # 1(RANK,SIGNATURE): (3,-3)CP COORDINATES: 0.0000000.000000 -0.689505VALUES OF SOME FUNCTIONS AT CPs (a.u.):Rho = 0.3095877E+03--------------------------------------------------------CP # 2(RANK,SIGNATURE): (3,-3)CP COORDINATES: -0.7838370.000000 -1.243761 VALUES OF SOME FUNCTIONS AT CPs (a.u.):Rho = 0.4734920E+00--------------------------------------------------------CP # 3(RANK,SIGNATURE): (3,-3)CP COORDINATES: 0.7838370.000000 -1.243761 VALUES OF SOME FUNCTIONS AT CPs (a.u.):Rho = 0.4734911E+00--------------------------------------------------------CP # 4(RANK,SIGNATURE): (3,-1)CP COORDINATES: -0.5973420.000000 -1.114696 EIGENVALUES OF HESSIAN MATRIX:-0.1478617E+01 -0.1437285E+01 0.1434451E+01 EIGENVECTORS (ORTHONORMAL) OF HESSIAN MATRIX (COLUMNS):-0.5721015E+00 -0.5095143E-14 0.8201828E+00 0.3376828E-14 0.1000000E+01 0.8567641E-14 0.8201828E+00 -0.7671177E-14 0.5721015E+00HESSIAN MATRIX:0.4810031E+00 0.2033756E-13 0.1366892E+01 -0.1437285E+01 0.1403294E-13-0.5251693E+00 VALUES OF SOME FUNCTIONS AT CPs (a.u.):Rho = 0.3287395E+00|GRAD(Rho)| = 0.1794904E-13GRAD(Rho)x = 0.1114231E-13GRAD(Rho)y = -0.1034380E-13GRAD(Rho)z = 0.9540589E-14Laplacian = -0.1481451E+01(-1/4)Del**2(Rho)) = 0.3703627E+00Diamond = 0.6309743E+01Metallicity = -0.7283594E+01Ellipticity = 0.2875720E-01 INHOMOGENEITY PARAMETERS AT CPs (a.u.)Delta_u = 0.1450178E+01Delta_s = 0.1033036E+01Delta_t = 0.1337742E+01Inhom_s = 0.9680208E+00Inhom_ex = 0.1072315E+01ENERGY COMPONENTS AT CPs (a.u.)Gb(Abramov) = 0.2026868E+00Vb(Abramov) = -0.7757363E+00Hb(Abramov) = -0.5730495E+00Ex_ueg = -0.1675666E+00Ec_ueg = -0.2078983E-01Delta_ex = 0.1457280E+00Delta_ec = 0.5769869E-01Delta_et = -0.1362540E+01Pxc = 0.8060030E+01Qxc = 0.2525673E+01--------------------------------------------------------CP # 5(RANK,SIGNATURE): (3,-1)CP COORDINATES: 0.5973420.000000 -1.114696 EIGENVALUES OF HESSIAN MATRIX:-0.1478617E+01 -0.1437285E+01 0.1434451E+01 EIGENVECTORS (ORTHONORMAL) OF HESSIAN MATRIX (COLUMNS):0.5721015E+00 0.0000000E+00 -0.8201828E+000.0000000E+00 0.1000000E+01 0.0000000E+000.8201828E+00 0.0000000E+00 0.5721015E+00 HESSIAN MATRIX:0.4810031E+00 -0.7312307E-18 -0.1366892E+01 -0.1437285E+01 0.5045501E-18-0.5251693E+00 VALUES OF SOME FUNCTIONS AT CPs (a.u.):Rho = 0.3287395E+00|GRAD(Rho)| = 0.2851652E-15GRAD(Rho)x = 0.1274209E-15GRAD(Rho)y = -0.3719081E-18GRAD(Rho)z = -0.2551136E-15Laplacian = -0.1481451E+01(-1/4)Del**2(Rho)) = 0.3703627E+00Diamond = 0.6309743E+01Metallicity = -0.7283594E+01Ellipticity = 0.2875720E-01 INHOMOGENEITY PARAMETERS AT CPs (a.u.)Delta_u = 0.1450178E+01Delta_s = 0.1033036E+01Delta_t = 0.1337742E+01Inhom_s = 0.9680208E+00Inhom_ex = 0.1072315E+01ENERGY COMPONENTS AT CPs (a.u.)Gb(Abramov) = 0.2026868E+00Vb(Abramov) = -0.7757363E+00Hb(Abramov) = -0.5730495E+00Ex_ueg = -0.1675666E+00Ec_ueg = -0.2078983E-01Delta_ex = 0.1457280E+00Delta_ec = 0.5769869E-01Delta_et = -0.1362540E+01Pxc = 0.8060030E+01Qxc = 0.2525673E+01----------------------------------------------------------------BOND PATHS (BP) AND PROPERTIES ALONG THEM ARE WRITTEN TO TAPE21----------------------------------------------------------------#BP #CP Atom Atom Distance BP Lenth BP Steps-----------------------------------------------------------14120.9600000.9600811625130.9600000.96008315-----------------------------------------------------------其中：1CP COORDINATES，临界点的坐标2VALUES OF SOME FUNCTIONS AT CP(a.u.):Rho，临界点的电子密度|GRAD(Rho)|，临界点电子密度的梯度的模GRAD(Rho)x，临界点电子密度的梯度的x方向分量Laplacian，临界点的电子密度拉普拉斯值(-1/4)Del**2(Rho))：临界点电子密度二阶导乘以-(1/4)Metallicity：Jenkins' metallicity。