2015年第三中学中考模拟题附答案

2015年河南省平顶山市中考数学三模试卷一、选择题（每小题3分，共24分）1．（3分）﹣的相反数是（）A．3 B．C．﹣3 D．﹣2．（3分）甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是S甲2=0.65，S乙2=0.55，S丙2=0.50，S丁2=0.45，则射箭成绩最稳定的是（）A．甲B．乙C．丙D．丁3．（3分）不等式﹣3x＜6的解集为（）A．x＜﹣2 B．x＞﹣2 C．x＜2 D．x＞24．（3分）如图是正方形的展开图，原正方体相对两个面上的数字之和的最小值是（）A．4 B．5 C．6 D．75．（3分）直线y=2x+3与坐标轴围成的面积是（）A．B．3 C．D．66．（3分）如图，平行四边形ABCD中，EF垂直平分AC，与边AD、BC分别相交于点E、F．则四边形AECF一定是（）A．正方形B．矩形C．菱形D．不能确定7．（3分）如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于点E，连接AD，则下列结论正确的个数是（）①AD⊥BC；②∠EDA=∠B；③OA=AC；④DE是⊙O的切线．A．1个 B．2个 C．3个 D．4个8．（3分）如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（）A．B．C．D．二、填空题（每小题3分，共21分）9．（3分）计算：﹣（）﹣1×（1﹣）0=．10．（3分）若x1=﹣3是关于x的方程x2+kx﹣3=0的一个根，x2是另一个根，则x1+x2=．11．（3分）如图，点E是平行四边形ABCD的边CD的中点，AD、BE的延长线相交于点F，DF=3，DE=2，则平行四边形ABCD的周长为．12．（3分）现有点数为2，3，4，5的四张扑克牌背面朝上，洗匀后，从中任意抽出两张牌，这两张牌上的数字之和能被3整除的概率是．13．（3分）如图，点A在双曲线y=上，AB⊥x轴于B，AC⊥y轴于C，且△的面积为2，则k=．14．（3分）如图，在数轴上，A1、P两点表示的数分别为1、2，A1、A2关于O 对称，A2、A3关于点P对称，A3、A4关于点O对称，A4、A5关于点P对称…依次规律，则点A15表示的数是．15．（3分）如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，P是BC边上的动点．设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是．三、解答题（本大题共8个小题，满分75分）16．（8分）解分式方程：﹣=．17．（9分）某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）． 已知A 、B 两组捐款人数的比为1：5．捐款人数分组统计表： 组别 捐款额x/元 人数A1≤x ＜10 a B 10≤x ＜20 100C 20≤x ＜30D 30≤x ＜40 Ex ≥40请结合以上信息解答下列问题．（1）a= ，本次调查样本的容量是 ；）先求出C 组的人数，再补全“捐款人数分组统计图1”；）若任意抽出1名学生进行调查，恰好是捐款数不少于30元的概率是多少？（1）求证：AE ∥CD ；（2）若AC=3，求出DE 的长．19．（9分）我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里，向南直行到B 出测得距钓鱼岛Z的距离100海里，此时测得直行方向与钓鱼岛Z方向夹角为α，如图所示．求渔政巡逻艇行驶路程AB是多少海里？（sinα=，cosα=，tanα=）．20．（10分）如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．（1）求证：△AED≌△CEB′；（2）若P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，则请你证明PH•AP=PG•CP．21．（10分）为迎接第四届世界太阳城大会，德州市把主要路段路灯更换为太阳能路灯．已知太阳能路灯售价为5000元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过100个，按原价付款；若一次购买100个以上，且购买的个数每增加一个，其价格减少10元，但太阳能路灯的售价不得低于3500元/个．乙店一律按原价的80%销售．现购买太阳能路灯x个，如果全部在甲商家购买，则所需金额为y1元；如果全部在乙商家购买，则所需金额为y2元．（1）分别求出y1、y2与x之间的函数关系式；（2）若市政府投资140万元，最多能购买多少个太阳能路灯？22．（10分）如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF，CF．（1）如图 ，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；（2）如图 ，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；（3）在（2）的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由．23．（10分）如图，抛物线y=ax2+bx+c（a≠0）的图象过点M（﹣2，），顶点坐标为N（﹣1，），且与x轴交于A、B两点，与y轴交于C点．（1）求抛物线的解析式；（2）点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标；（3）在直线AC上是否存在一点Q，使△QBM的周长最小？若存在，求出Q点坐标；若不存在，请说明理由．2015年河南省平顶山市中考数学三模试卷参考答案与试题解析一、选择题（每小题3分，共24分）1．（3分）﹣的相反数是（）A．3 B．C．﹣3 D．﹣【分析】根据只有符号不同的两个数互为相反数，0的相反数是0即可求解．【解答】解：﹣的相反数是．故选：B．2．（3分）甲、乙、丙、丁四人进行射箭测试，每人10次射箭成绩的平均数都是8.9环，方差分别是S甲2=0.65，S乙2=0.55，S丙2=0.50，S丁2=0.45，则射箭成绩最稳定的是（）A．甲B．乙C．丙D．丁【分析】根据方差的意义先比较出甲、乙、丙、丁四人谁的方差最小，则谁的成绩最稳定．【解答】解：∵=0.65，=0.55，=0.50，=0.45，丁的方差最小，∴射箭成绩最稳定的是：丁．故选：D．3．（3分）不等式﹣3x＜6的解集为（）A．x＜﹣2 B．x＞﹣2 C．x＜2 D．x＞2【分析】根据不等式的性质在不等式的两边同时除以﹣3即可求出x的取值范围．【解答】解：不等式的性质再不等式的两边同时除以﹣3得，x＞﹣2．故选：B．4．（3分）如图是正方形的展开图，原正方体相对两个面上的数字之和的最小值是（）A．4 B．5 C．6 D．7【分析】根据相对的面相隔一个面得到相对的2个数，相加后比较即可．【解答】解：易得2和5是相对的两个面；3和6是相对两个面；1和4是相对的2个面，∵2+5=7，3+6=9，1+4=5，∴原正方体相对两个面上的数字和最小的是5．故选：B．5．（3分）直线y=2x+3与坐标轴围成的面积是（）A．B．3 C．D．6【分析】设直线与x轴、y轴分别交于A、B两点，可求得A、B两点的坐标，可求得△AOB的面积．【解答】解：如图，设直线与x轴、y轴分别交于A、B两点，在y=2x+3中，令y=0，可得2x+3=0，解得x=﹣，令x=0，可得y=3，∴A（，0），B（0，3），∴OA=，OB=3，∴S=OA•OB=××3=，△AOB故选：C．6．（3分）如图，平行四边形ABCD中，EF垂直平分AC，与边AD、BC分别相交于点E、F．则四边形AECF一定是（）A．正方形B．矩形C．菱形D．不能确定【分析】先根据垂直平分线的性质得∴AE=EC，AF=FC，所以∠1=∠2，∠3=∠4；再结合平行线的性质得出∠1=∠4=∠3，即AF=AE，利用四条边相等的四边形是菱形即可证明．【解答】解：∵EF垂直平分AC，∴AO=OC，∴∠1=∠2，∠3=∠4，又∵四边形ABCD是平行四边形，∴AD∥BC，∴∠1=∠4=∠3，∴AF=AE，∴AE=EC=CF=FA，∴四边形AECF是菱形，故选：C．7．（3分）如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于点E，连接AD，则下列结论正确的个数是（）①AD⊥BC；②∠EDA=∠B；③OA=AC；④DE是⊙O的切线．A．1个 B．2个 C．3个 D．4个【分析】根据圆周角定理和切线的判定，采用排除法，逐条分析判断．【解答】解：∵AB是直径，∴∠ADB=90°，∴AD⊥BC，故①正确；连接DO，∵点D是BC的中点，∴CD=BD，∴△ACD≌△ABD（SAS），∴AC=AB，∠C=∠B，∵OD=OB，∴∠B=∠ODB，∴∠ODB=∠C，OD∥AC，∴∠ODE=∠CED，∴ED是圆O的切线，故④正确；由弦切角定理知，∠EDA=∠B，故②正确；∵点O是AB的中点，故③正确，故选：D．8．（3分）如图，在平面直角坐标系中，边长为1的正方形ABCD中，AD边的中点处有一动点P，动点P沿P→D→C→B→A→P运动一周，则P点的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是（）A．B．C．D．【分析】将动点P的运动过程划分为PD、DC、CB、BA、AP共5个阶段，分别进行分析，最后得出结论．【解答】解：动点P运动过程中：①当0≤s≤时，动点P在线段PD上运动，此时y=2保持不变；②当＜s≤时，动点P在线段DC上运动，此时y由2到1逐渐减少；③当＜s≤时，动点P在线段CB上运动，此时y=1保持不变；④当＜s≤时，动点P在线段BA上运动，此时y由1到2逐渐增大；⑤当＜s≤4时，动点P在线段AP上运动，此时y=2保持不变．结合函数图象，只有D选项符合要求．故选：D．二、填空题（每小题3分，共21分）9．（3分）计算：﹣（）﹣1×（1﹣）0=0．【分析】原式第一项利用算术平方根定义计算，第二项利用负整数指数幂法则及零指数幂法则计算即可得到结果．【解答】解：原式=5﹣5×1=5﹣5=0，故答案为：010．（3分）若x1=﹣3是关于x的方程x2+kx﹣3=0的一个根，x2是另一个根，则x1+x2=﹣2．【分析】根据根与系数的关系得到1•x2=﹣3，再解一次方程求出x2，进而求出x1+x2的值．【解答】解：∵x1=﹣3是关于x的方程x2+kx﹣3=0的一个根，x2是另一个根，∴x1x2=﹣3，∴x2=1，∴x1+x2=﹣3+1=﹣2，故答案为﹣2．11．（3分）如图，点E是平行四边形ABCD的边CD的中点，AD、BE的延长线相交于点F，DF=3，DE=2，则平行四边形ABCD的周长为14．【分析】由平行四边形的性质得出AB=CD，AD=BC，AD∥BC，证出∠CBE=∠F，由AAS证明△BCE≌△FDE，得出BC=DF=3，即可求出平行四边形ABCD的周长．【解答】解：∵四边形ABCD是平行四边形，∴AB=CD，AD=BC，AD∥BC，∴∠CBE=∠F，∵E是CD的中点，∴CE=DE=2，CD=2DE=4，在△BCE和△FDE中，，∴△BCE≌△FDE（AAS），∴BC=DF=3，∴平行四边形ABCD的周长=2（BC+CD）=2（3+4）=14；故答案为：14．12．（3分）现有点数为2，3，4，5的四张扑克牌背面朝上，洗匀后，从中任意抽出两张牌，这两张牌上的数字之和能被3整除的概率是．【分析】先画出树状图展示所有12种等可能的结果数，再找出这两张牌上的数字之和能被3整除的结果数，然后根据概率公式求解．【解答】解：画树状图为：共有12种等可能的结果数，其中这两张牌上的数字之和能被3整除的结果数有4种，所以这两张牌上的数字之和能被3整除的概率==．故答案为．13．（3分）如图，点A在双曲线y=上，AB⊥x轴于B，AC⊥y轴于C，且△ABC 的面积为2，则k=﹣4．【分析】根据反比例函数系数k的几何意义：在反比例函数的图象上任意一点象坐标轴作垂线，这一点和垂足以及坐标原点所构成的三角形的面积是|k|，即可求解．【解答】解：∵AC⊥y轴于C点，AB⊥x轴于B点，∠BOC=90°，∴四边形OBAC是矩形，=S矩形OBAC．∴S△CBA∴S=2S△ABC=4，矩形OBAC=4，∴|k|=S矩形OBAC∵双曲线在第二象限，∴k=﹣4，故答案为：﹣4．14．（3分）如图，在数轴上，A1、P两点表示的数分别为1、2，A1、A2关于O 对称，A2、A3关于点P对称，A3、A4关于点O对称，A4、A5关于点P对称…依次规律，则点A15表示的数是29．【分析】根据对称性质，由题意确定出点A15表示的数即可．【解答】解：根据对称的性质得：A2表示的数为﹣1，A3表示的数为5，A4表示的数为﹣5，A5表示的数为9，A6表示的数为﹣9，A7表示的数为13，A8表示的数为﹣13，A9表示的数为17，A10表示的数为﹣17，A11表示的数为21，A12表示的数为﹣21，A13表示的数为25，则A14表示的数为﹣25．则A15表示的数是29．故答案为：29．15．（3分）如图，在Rt△ABC中，∠ABC=90°，AB=3，BC=4，P是BC边上的动点．设BP=x，若能在AC边上找到一点Q，使∠BQP=90°，则x的取值范围是3≤x≤4．【分析】先根据勾股定理计算出AC=5，由于∠BQP=90°，根据圆周角定理得到点Q在以PB为直径的圆⊙M上，而点Q在AC上，则有AC与⊙M相切于点Q，连结MQ，如图，根据切线的性质得MQ⊥AC，MQ=BM=x，然后证明Rt△CMQ ∽Rt△CAB，再利用相似比得到x：3=（4﹣x）：5，最后解方程即可．【解答】解：∵∠ABC=90°，AB=3，BC=4，∴AC==5，∵∠BQP=90°，∴点Q在以PB为直径的圆⊙M上，∵点Q在AC上，∴AC与⊙M相切于点Q，连结MQ，如图，则MQ⊥AC，MQ=BM=x，∵∠QCM=∠BCA，∴Rt△CMQ∽Rt△CAB，∴QM：AB=CM：AC，即x：3=（4﹣x）：5，∴x=3．当P与C重合时，BP=4，∴BP=x的取值范围是：3≤x≤4，故答案为：3≤x≤4．三、解答题（本大题共8个小题，满分75分）16．（8分）解分式方程：﹣=．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：x2+x﹣x+1=x+3，解得：x=2或x=﹣1，经检验x=﹣1是增根，分式方程的解为x=2．9分）某校学生会干部对校学生会倡导的“助残”自愿捐款活动进行抽样调查，得到一组学生捐款情况的数据，对学校部分捐款人数进行调查和分组统计后，将数据整理成如图所示的统计图（图中信息不完整）．已知A、B两组捐款人数的1：5．捐款人数分组统计表：组捐款额x/元人数别A1≤x＜10aB10≤x＜20100C20≤x＜30D30≤x＜40E x≥40请结合以上信息解答下列问题．（1）a=20，本次调查样本的容量是500；（2）先求出C组的人数，再补全“捐款人数分组统计图1”；（3）若任意抽出1名学生进行调查，恰好是捐款数不少于30元的概率是多少？【分析】（1）根据A、B两组捐款的人数的比列式求解即可得到a的值，求出A、B两组捐款人数所占的百分比的和与A、B两组捐款的人数的和，列式计算即可求出样本容量；（2）用样本容量乘以C组人数所占的百分比，计算即可得解，然后再补全统计图；（3）先求出D、E两组的人数的和，再根据概率公式列式计算即可，或直接求出D、E两组捐款人数所占的百分比的和即可．【解答】解：（1）∵A、B两组捐款人数的比为1：5，B组捐款人数为100人，∴A组捐款人数为：100÷5=20，A、B两组捐款人数所占的百分比的和为：1﹣40%﹣28%﹣8%=1﹣76%=24%，A、B两组捐款的人数的和为：20+100=120，120÷24%=500，故答案为：20，500；…（2分）（2）500×40%=200，C组的人数为200，…（4分）补图见图．…（5分）（3）∵D、E两组的人数和为：500×（28%+8%）=180，…（7分）∴捐款数不少于30元的概率是：=0.36．[或：28%+8%=36%=0.36．]…（9分）18．（9分）已知，如图，AB⊥CD，BE是⊙O的直径，（1）求证：AE∥CD；（2）若AC=3，求出DE的长．【分析】（1）直接利用圆周角定理结合垂直于同一直线的两条直线互相平行得出即可；（2）利用平行弦之间所夹的弧相等进而得出答案．【解答】（1）证明：∵BE是⊙O的直径，∴∠BAE=90°，即AE⊥AB又∵AB⊥CD，∴AE∥CD；（2）解：∵AE∥CD，∴=，∴AC=DE=3．19．（9分）我渔政巡逻艇在A处测得距钓鱼岛Z的距离140海里，向南直行到B 出测得距钓鱼岛Z的距离100海里，此时测得直行方向与钓鱼岛Z方向夹角为α，如图所示．求渔政巡逻艇行驶路程AB是多少海里？（si nα=，cosα=，tanα=）．【分析】作ZC⊥AB于点C，在直角△BCZ中利用三角函数求得BC和CZ，然后在直角△ACZ中利用勾股定理求得AC的长，则AB即可求解．【解答】解：作ZC⊥AB于点C．∵在直角△BCZ中，sina==，cosa=，∴CZ=BZ=50（海里），BC=BZ=50（海里）．在直角△ACZ中，AC===110．∴AB=AC﹣BC=110﹣50=60（海里）．答：渔政巡逻艇行驶路程AB是60海里．20．（10分）如图，将矩形纸片ABCD沿对角线AC折叠，使点B落到点B′的位置，AB′与CD交于点E．（1）求证：△AED≌△CEB′；（2）若P为线段AC上的任意一点，PG⊥AE于G，PH⊥EC于H，则请你证明PH•AP=PG•CP．【分析】（1）由折叠的性质知，CB′=BC=AD，∠B=∠B′=∠D=90°，∠B′EC=DEA，则由AAS得到△AED≌△CEB′；（2）PG⊥AE于G，PH⊥EC于H，则∠PGA=∠PHC=90°，根据折叠的性质和矩形的性质易证∠PAG=∠PCH，则△PGA∽△PHC，所以PH•AP=PG•CP．【解答】解：（1）△AED≌△CEB′证明：∵四边形ABCD为矩形，∴B′C=BC=AD，∠B′=∠B=∠D=90°，又∵∠B′EC=∠DEA，∴△AED≌△CEB′；（2）∵四边形ABCD为矩形，∴CD∥AB∴∠DCA=∠BAC根据折叠的性质∠EAC=∠BAC∴∠PAG=∠PCH，∵PG⊥AE于G，PH⊥EC于H，∴∠PGA=∠PHC=90°，∴△PGA∽△PHC，∴∴PH•AP=PG•CP．21．（10分）为迎接第四届世界太阳城大会，德州市把主要路段路灯更换为太阳能路灯．已知太阳能路灯售价为5000元/个，目前两个商家有此产品．甲商家用如下方法促销：若购买路灯不超过100个，按原价付款；若一次购买100个以上，且购买的个数每增加一个，其价格减少10元，但太阳能路灯的售价不得低于3500元/个．乙店一律按原价的80%销售．现购买太阳能路灯x个，如果全部在甲商家购买，则所需金额为y1元；如果全部在乙商家购买，则所需金额为y2元．（1）分别求出y1、y2与x之间的函数关系式；（2）若市政府投资140万元，最多能购买多少个太阳能路灯？【分析】（1）对甲，由于购买个数不同，售价也不同，因此需按购买个数分成三段由等量关系“所需金额=售价×购买个数”列出函数关系式；对乙，按等量关系“所需金额=售价×购买个数”列出函数关系式．（2）分别计算投资额在甲乙商家各能购买的太阳能路灯的数量，比较得出最大值．【解答】解：（1）由题意可知，当0＜x≤100时，购买一个需5000元，故y1=5000x；当x＞100时，∵购买个数每增加一个，其价格减少10元，但售价不得低于3500元/个，∴x≤+100=250个．即100＜x≤250时，购买一个需5000﹣10（x﹣100）元，故y1=﹣10x2+6000x；当x＞250时，购买一个需3500元，故y1=3500x；∴y1=，y2=5000×80%x=4000x．（2）在甲商家，当0＜x≤100时，y1=5000x≤500000＜1400000；当100＜x≤250时，y1=6000x﹣10x2=﹣10（x﹣300）2+900000＜1400000；∴由3500x=1400000，得x=400；在乙商家，由4000x=1400000，得x=350个．故选择甲商家，最多能购买400个路灯．22．（10分）如图，正方形ABCD的边长是3，点P是直线BC上一点，连接PA，将线段PA绕点P逆时针旋转90°得到线段PE，在直线BA上取点F，使BF=BP，且点F与点E在BC同侧，连接EF，CF．（1）如图 ，当点P在CB延长线上时，求证：四边形PCFE是平行四边形；（2）如图 ，当点P在线段BC上时，四边形PCFE是否还是平行四边形，说明理由；（3）在（2）的条件下，四边形PCFE的面积是否有最大值？若有，请求出面积的最大值及此时BP长；若没有，请说明理由．【分析】（1）由正方形的性质可以得出AB=BC，∠ABP=∠ABC=∠90°，可以得出△PBA≌△FBC，由其性质就可以得出结论；（2）由正方形的性质可以得出AB=BC，∠FBC=∠ABC=∠90°，可以得出△PBA≌△FBC，由其性质就可以得出结论；（3）设BP=x，则PC=3﹣x 平行四边形PEFC的面积为S，由平行四边形的面积公式就可以求出其解析式，再根据二次函数的性质就可以求出其最大值．【解答】解：（1）∵四边形ABCD是正方形，∴AB=BC，∠ABC=∠PBA=90°∵在△PBA和△FBC中，，∴△PBA≌△FBC（SAS），∴PA=FC，∠PAB=∠FCB．∵PA=PE，∴PE=FC．∵∠PAB+∠APB=90°，∴∠FCB+∠APB=90°．∵∠EPA=90°，∴∠APB+∠EPA+∠FCP=180°，即∠EPC+∠PCF=180°，∴EP∥FC，∴四边形EPCF是平行四边形；（2）结论：四边形EPCF是平行四边形，∵四边形ABCD是正方形，∴AB=BC，∠ABC=∠CBF=90°∵在△PBA和△FBC中，，∴△PBA≌△FBC（SAS），∴PA=FC，∠PAB=∠FCB．∵PA=PE，∴PE=FC．∵∠FCB+∠BFC=90°，∠EPB+∠APB=90°，∴∠BPE=∠FCB，∴EP∥FC，∴四边形EPCF是平行四边形；（3）有最大值．设BP=x，则PC=3﹣x 平行四边形PEFC的面积为S，S=PC•BF=PC•PB=（3﹣x）x=﹣（x﹣）2+．∵a=﹣1＜0，∴抛物线的开口向下，∴当x=时，S最大=，∴当BP=时，四边形PCFE的面积最大，最大值为．23．（10分）如图，抛物线y=ax2+bx+c（a≠0）的图象过点M（﹣2，），顶点坐标为N（﹣1，），且与x轴交于A、B两点，与y轴交于C点．（1）求抛物线的解析式；（2）点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标；（3）在直线AC上是否存在一点Q，使△QBM的周长最小？若存在，求出Q点坐标；若不存在，请说明理由．【分析】（1）先由抛物线的顶点坐标为N（﹣1，），可设其解析式为y=a（x+1）2+，再将M（﹣2，）代入，得=a（﹣2+1）2+，解方程求出a的值即可得到抛物线的解析式；（2）先求出抛物线y=﹣x2﹣x+与x轴交点A、B，与y轴交点C的坐标，再根据勾股定理得到BC==2．设P（﹣1，m），当△PBC为等腰三角形时分三种情况进行讨论：①CP=CB；②BP=BC；③PB=PC；（3）先由勾股定理的逆定理得出BC⊥AC，连结BC并延长至B′，使B′C=BC，连结B′M，交直线AC于点Q，由轴对称的性质可知此时△QBM的周长最小，由B （﹣3，0），C（0，），根据中点坐标公式求出B′（3，2），再运用待定系数法求出直线MB′的解析式为y=x+，直线AC的解析式为y=﹣x+，然后解方程组，即可求出Q点的坐标．【解答】解：（1）由抛物线顶点坐标为N（﹣1，），可设其解析式为y=a（x+1）2+，将M（﹣2，）代入，得=a（﹣2+1）2+，解得a=﹣，故所求抛物线的解析式为y=﹣x2﹣x+；（2）∵y=﹣x2﹣x+，∴x=0时，y=，∴C（0，）．y=0时，﹣x2﹣x+=0，解得x=1或x=﹣3，∴A（1，0），B（﹣3，0），∴BC==2．设P（﹣1，m），当CP=CB时，有CP==2，解得m=±；当BP=BC时，有BP==2，解得m=±2；当PB=PC时，=，解得m=0，综上，当△PBC为等腰三角形时，点P的坐标为（﹣1，+），（﹣1，﹣），（﹣1，2），（﹣1，﹣2），（﹣1，0）；（3）由（2）知BC=2，AC=2，AB=4，所以BC2+AC2=AB2，即BC⊥AC．连结BC并延长至B′，使B′C=BC，连结B′M，交直线AC于点Q，∵B、B′关于直线AC对称，∴QB=QB′，∴QB+QM=QB′+QM=MB′，所以此时△QBM的周长最小．由B（﹣3，0），C（0，），易得B′（3，2）．设直线MB′的解析式为y=kx+n，将M（﹣2，），B′（3，2）代入，得，解得，即直线MB′的解析式为y=x+．同理可求得直线AC的解析式为y=﹣x+．由，解得，即Q（﹣，）．所以在直线AC上存在一点Q（﹣，），使△QBM的周长最小．。

二O 一五年模拟考试初三数学试卷（考试时间：120分钟，满分150分）第一部分 选择题（共18分）一、选择题（本大题共6小题，每小题3分，满分18分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，选择正确选项的字母代号涂在答题卡相应的位置上） 1．3-的相反数是 ( ▲ )A ．－13B ．13C ．－3D ．32．下列计算正确的是 （ ▲ ）A ．()33362b a ab = B ．1-=---b a b a C ． 41)2(2-=-- D ．3)3(2=-3．连续四次抛掷一枚硬币都是正面朝上，则“第五次抛掷正面朝上”是（ ▲ ） A ．必然事件 B ．不可能事件 C ．随机事件 D ．概率为1的事件 4．如图所示是几何体的主视图与左视图，那么它的俯视图是（ ▲ ）5．双曲线xky -=1与直线x y 2=没有交点，则k 的取值范围为（ ▲ ） A ．0<k B ．1<k C ．10<<k D ．1>k6．已知：如图，在平面直角坐标系中，有菱形OABC ，点A 的坐标为(10，0)，对角线OB 、AC 相交于点D ，双曲线y ＝kx(x>0)经过点D ，交BC 的延长线于点E ，且OB ·AC ＝160，有下列四个结论： ①双曲线的解析式为y ＝x32(x>0)；②点C 的坐标是(6，8)；③sin ∠COA＝45；④AC ＋OB ＝其中正确的结论有 ( ▲ ) A ．1个B ．2个C ．3个D ．4个第二部分 非选择题（共132分）二、填空题（本大题共10小题，每小题3分，满分30分．请把答案直接填写在答题卡相应第6题图A B C D 主视图 左视图位置上） 7．函数x y 23+=中自变量x 的取值范围是 ▲ ．8．分解因式：2282b a -＝ ▲ ．9．数据201、203、198、199、200、205的平均数为 ▲ ．10．截至2015年4月30日，余额宝规模已达到1853亿元，这个数据用科学记数法可表示为 ▲ ．11．如图, AB 是⊙O 的直径, CD 是弦,若BC=1, AC=3, 则sin ∠ADC 的值为 ▲ ．BA12．如图，AD 为△ABC 的中线，G 为△ABC 的重心，若BGC S ∆ =2，则ABD S ∆= ▲ ． 13．圆锥的母线长为6cm ，底面圆半径为4cm ，则这个圆锥的侧面积为 ▲ ．14．一山坡的的坡比为3:4，一人沿山坡向上走了20米，那么这人垂直高度上升了 ▲ 米．15．定义一个新的运算：2()2()a b a b a b b a b a-+≤⎧⎪⊕=+⎨>⎪-⎩则运算2x ⊕的最小值为 ▲ ．16．一次综合实践活动中，小明同学拿到一只含45°角的三角板和一只含30°角的三角板，如图放置恰好有一边重合，则ODC S ∆：OAB S ∆的值为 ▲ ．三、解答题（本大题共10小题，满分102分，请在答题卡指定区域内作答，解答时应写出必要的文字说明、证明过程或演算步骤）C第12题图第16题图 DBCAO第11题图17．（本题满分6分）计算：3560cos 2)331(00----18．（1）（本题满分6分）已知 是方程组 的解，写出a 、b 的关系式．（2）（本题满分6分）解方程1x 1x －＋－1x 42－＝1 19．（本题满分10分）学生小明、小华为了解本校八年级学生每周上网的时间，各自进行了抽样调查．小明调查了八年级信息技术兴趣小组中40名学生每周上网的时间，算得这些学生平均每周上网时间为2.5小时；小华从全体320名八年级学生名单中随机抽取了40名学生，调查了他们每周上网的时间，算得这些学生平均每周上网时间为1.2小时．小明与小华整理各自样本数据，如下表所示．请根据上述信息，回答下列问题： （1）你认为哪位学生抽取的样本具有代表性？估计该校全体八年级学生平均每周上网时间为多少小时；（2）根据具有代表性的样本，把上图中的频数分布直方图补画完整；（3）在具有代表性的样本中，中位数所在的时间段是______________________小时/周； （4）专家建议每周上网２小时以上(含２小时)的同学应适当减少上网的时间，根据具有代表性的样本估计，该校全体八年级学生中有多少名同学应适当减少上网的时间？20．（本题满分8分）在一个口袋中有4个完全相同的小球，把它们分别标号1、2、3、4．小明先随机地摸出一个小球，小强再随机地摸出一个小球．记小明摸出球的标号为x ，小强摸（每组可含最低值，不含最高值）小时/周 ⎩⎨⎧-=-=23y x ⎩⎨⎧=-=+21by cx cy ax出的球标号为y ．小明和小强在此基础上共同协商一个游戏规则：当x ＞y 时小明获胜，否则小强获胜．（1）若小明摸出的球不放回，求小明获胜的概率； （2）若小明摸出的球放回后小强再随机摸球，问他们制定的游戏规则公平吗？请说明理由．21．（本题满分10分）已知方程092=++bx ax 有一个根为121-=x ，且关于x 的方程ax2＋bx ＋9＝34x +214有两个相等的实数根，求a 、b 的值． 22．（本题满分10分）如图，在正方形ABCD 中，M 是AD 上异于D 的点，N 是CD 的中点，且∠AMB ＝∠NMB ，则AM 2=，求AB 的长．23．（本题满分12分）如图，在△ABC 中，I 是内心，O 是AB 边上一点，⊙O 经过B 点且与AI 相切于I 点．（1）求证：AB ＝AC ；（2）若BC ＝16，⊙O 的半径是5，求AI 的长．24．（本题满分10分）操作：有2张边长都是2的正方形纸片A 和B ，请你将纸片A 的一边的一个端点放在纸片B 的对称轴L 上，另一个端点与纸片B 的一个顶点重合后压平．求纸片D B C AM NA与纸片B重合部分的面积．25．（本题满分12分）如图，正方形OABC的顶点O在坐标原点，且OA边和AB边所在直线的解析式分别为y＝34x和y＝－43x＋253．（1）求正方形OABC的边长；（2）现有动点P、Q分别从C、A同时出发，点P沿线段CB向终点B运动，速度为每秒1个单位，点Q沿折线A→O→C向终点C运动，速度为每秒k个单位，设运动时间为2秒．当k为何值时，将△CPQ沿它的一边翻折，使得翻折前后的两个三角形组成的四边形为菱形？（3）若正方形以每秒53个单位的速度沿射线AO下滑，直至顶点C落在x轴上时停止下滑．设正方形在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围．26．（本题满分14分）已知抛物线y=ax2+x+c（a≠0）经过A（1，0），B（2，0）两点，与y轴相交于点C．（1）求该抛物线的解析式；（2）点E 是该抛物线上一动点，且位于第一象限，当点E 到直线BC 的距离最大时，求点E 的坐标；（3）在（2）的条件下，在x 轴上有一点P ，且∠EAO +∠EPO =∠α，当tan α=2时，求点P 的坐标．O yx数学试题参考答案一、选择题1．D 2．C 3．C 4 ．A 5．D 6．C 二、填空题 7．23-≥x 8．)2)(2(2b a b a -+ 9．201 10．1.853×1110 11．10103 12．3 13．π2414．12 15．2- 16．333+ 三、解答题 17．35-18．（1）149=+b a（2）1=x 是增根，无解 19．（1）小华，1.2小时；（3）0～1；（4）64人 20．解：（1）由题意知（x ，y ）共有（1，2），（1，3），（1，4），（2，1），（2，3），（2，4），（3，1），（3，2），（3，4），（4，1），（4，2），（4，3）12种，其中x ＞y 有6种 ∴小明获胜的概率P （x ＞y ）＝612＝12（2）由题意知（x ，y ）除①中情形外，还有（1，1），（2，2），（3，3），（4，4）共16种，其中x ＞y 有6种∴x ＞y 的概率P （x ＞y ）＝ 616＝38＜12∴游戏规则不公平21． a ＝548，b ＝2 22． 过B 作MN 的垂线，运用勾股定理。

绝密★启用前试卷类型：A2015年度中考模拟试卷一答案一、听力测试（共15小题，计15分）1-15 CBCAA CBAAA BAACB二、单项选择（共20小题，计20分）16-35 CBCDA CDCBA BCDBD ABCBC三、阅读理解（共20题，计30分）36-55 CABDB ABBDC BDBDA BCDCD四、听力填表（共5小题，计5分）56. planning your vacation 57. joining a club 58. Tuesday afternoon59. a new family 60. practice/improve English五、动词填空（共10空，计10分）61.attracted 62.was placed 63.is 64.to play 65.didn’t go66.to learn 67.to improve 68.has got 69.trying 70.working六、综合填空（共10空，计10分）71. understand 72. meeting 73. expect 74. arrive 75. language76. found 77. example 78. prefer 79. each 80. before七、阅读表达（共5题，计10分）81.Yes you could 82. Text messaging ,Using a computer keyboard and playing video games 83.但是科学家们发现发送短信可能会引起手方面的疾病84.随着手机的发展，手机正变得越来越小. 85. Be careful not to send too many text messages, or you’ll get some problems with your hands.八、书面表达（共1题，计20分）Dongying is now making its effort to become a national civilized city. As students, what should we do?We must respect our teachers and be polite to others. We should also help those who are in need and be friendly to the people around us. Besides, we must obey the traffic rules. When crossing the streets, weshould walk on the zebr a crossing. And we mustn’t go across the street when the traffic lights are red.What’s more, we should protect our environment. For example, We mustn’t step on the grass and climb trees.Litter mustn’t be thrown everywhere.Dongying is our hometown. Let’s try our best to make it a civilized city and more and more beautiful.2015年度中考模拟试卷二答案一、听力测试（共15小题，计15分）1-15 ACBAC CBAAB CCBBC二、单项选择（共20小题，计20分）16-35 BDADC DDACB CABAA BADCD三、阅读理解（共20题，计30分）36-55. D A C B D BCDAB CCBDC DCBDB四、听力填表（共5小题，计5分）56. Nine /9 57. easy 58. four/4 59. sad and angry60. not so perfect / grow up / stop complaining / move forward in life or: He is not so perfect /He isgrowing up / He stops complaining / He moves forward in his life五、动词填空（共10空，计10分）61.keeping 62. to join 63. were 64. be used 65. to take66. said 67. should remember 68. being 69 .were 70. have lost六、综合填空（共10空，计10分）71. both 72. top 73. been/become 74. dangerous 75. die76. afraid 77.alone/again 78. while 79. warm 80. dead/dying七、阅读表达（共5题，计10分）81. You should say ―Thank you!‖ 82. When we have told a lie and feel sorry, we will have to use the sameword. 83.请人做事而不说―请‖没有礼貌。

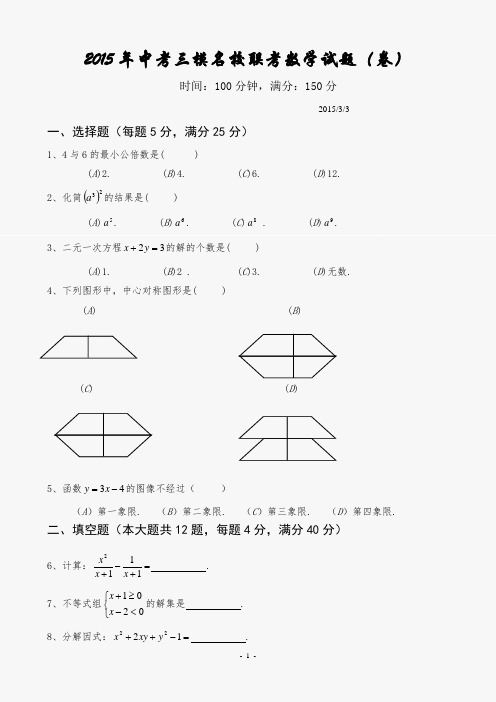
2015年中考三模名校联考数学试题（卷）时间：100分钟，满分：150分2015/3/3一、选择题（每题5分，满分25分）1、4与6的最小公倍数是( )(A)2. (B)4. (C)6. (D)12.2、化简()23a的结果是( )(A)5a. (B)6a. (C)8a . (D)9a.3、二元一次方程3x的解的个数是( )+y2=(A)1. (B)2 . (C)3. (D)无数.4、下列图形中，中心对称图形是( )(A) (B)(C) (D)5、函数4y的图像不经过（）=x3-（A）第一象限. （B）第二象限. （C）第三象限. （D）第四象限. 二、填空题（本大题共12题，每题4分，满分40分）A 1NM C BAB 121l 3l 2 l 1 6、计算：=+-+1112x x x .7、不等式组⎩⎨⎧<-≥+0201x x 的解集是 .8、分解因式：=-++1222y xy x .9、任意掷出一枚质地均匀的骰子后，骰子朝上面的点数为素数的概率是 . 10、抛物线342--=x x y 的顶点坐标为 .11、如果关于x 的方程032=+-k kx x 有两个相等的实数根，那么k 的值为 . 12、如果反比例函数xky =的图像经过点()1,2与()n ,1-，那么n 的值为 . 13、如图1，直线l 1、l 2被直线l 3所截，如果l 1‖l 2，∠1=︒48，那么∠2= 度.（图1） （图2） （图3）14、如图2，⊙O 的半径为5，点P 是弧AB 的中点，OP 交AB 于点H ，如果1=PH ，那么弦AB 的长是 .15、如图3，在ABC ∆中，∠ACB =︒90,AC =4,BC =3,将ABC ∆绕点C 顺时针旋转至C B A 11∆的位置，其中B 1C ⊥AB ,B 1C 、A 1B 1交AB 于M 、N 两点，则线段MN 的长为 .三、解答题（本大题共7题，满分85分）O BAPH不认识展馆人数认识法国馆捷克馆 中国馆 283540 16.（本题11分）计算：()12211260sin 8-︒+++.17.（本题11分）小明在寒假中对他所住的小区学生作了有关上海世博会各国展馆的认识度调查，他随机对他所住小区的40名初中学生调查了对中国馆、捷克馆与法国馆认识情况如下图，接着他又到居委会了解他所住的小区学生数情况如下表.（1）从统计图中可知他所住的小区初中学生中对____________馆的认识度最高； （2）请你估计他所住的小区初中学生中有_____________人认识捷克馆；（3）小明用下面的算式()1602002404035++⨯，计算得到结果为525，并由此估计出他所住的小区共有525名学生认识法国馆.你认为这样的估计正确吗？答：___________；为什么？答：_______________________________________________________.初中学生展馆认识情况统计图学生人数情况表D CB A 学 段 小 学 初 中高 中 人 数240 20016018.（本题11分）如图5，在梯形ABCD 中，AD‖BC , ∠B = 90,AC =AD . (1)若∠BAC ∶∠BCA =3∶2,求∠D 的度数； (2)若AD =5,tan ∠D =2，求梯形ABCD 的面积.（图5）19.（本题11分）动车组的出现使上海到杭州的旅程时间较一般的火车缩短了许多，而计划中上海到杭州磁浮列车的平均速度又将比动车组提高120千米/小时，这样从上海南站到杭州站225千米的旅程时间又将缩短30分钟，问计划中上海到杭州磁浮列车的平均速度将达到NMDCBAO多少千米/小时？20.（本题13分）如图6，在梯形ABCD 中，AD‖BC ，对角线AC 与BD 交于点O ，M 、N 分别为OB 、OC 的中点，又∠ACB =∠DBC . (1)求证：AB =CD ； (2)若AD =21BC .求证：四边形ADNM 为矩形. （图6）yONMP BA xyOx21. （本题13分）已知点P 是函数x y 21=（x >0）图像上一点，PA ⊥x 轴于点A ，交函数xy 1=（x >0）图像于点M , PB ⊥y 轴于点B ，交函数xy 1=（x >0）图像于点N .（点M 、N 不重合）（1）当点P 的横坐标为2时，求△PMN 的面积； （2）证明：MN‖AB ；（如图7）（3）试问：△OMN 能否为直角三角形？若能，请求出此时点P 的坐标；若不能，请说明理由.（图7） （备用图）PONM P ONM F EDCBA22、（本题15分）如图，一把“T 型”尺（图8），其中MN ⊥OP ，将这把“T 型”尺放置于矩形ABCD 中（其中AB =4,AD =5），使边OP 始终经过点A ，且保持OA =AB ，“T 型”尺在绕点A 转动的过程中，直线MN 交边BC 、CD 于E 、F 两点.(图9) （1）试问线段BE 与OE 的长度关系如何？并说明理由； （2）当△CEF 是等腰直角三角形时,求线段BE 的长；（3）设BE =x ,CF =y ，试求y 关于x 的函数解析式，并写出函数定义域.(图8) （图9）参考答案与评分标准一、选择题1、D ；2、B ；3、D ；4、C ；5、B ； 二、填空题6、1-x ；7、x ≤-1<2；8、()()11-+++y x y x ；9、21； 10、()7,2-； 11、0，12； 12、2-； 13、132； 14、6； 15、0.8. 三、解答题16、解：原式1212382++⎪⎪⎭⎫ ⎝⎛+=（2+2+1=5分）124322-++=（3分）4123-=（2分）17、解：（1）中国；（3分） （2）140.（3分） （3）不正确；（1分）对初中学生随机抽样的结果并不能表示小学生与高中生的结果，缺乏代表性.——（3分）18、解：（1）在ABC ∆中，︒=∠90B ， 则︒=∠+∠90BCA BAC ，—（1分）又∠BAC ∶∠BCA =3∶2， ∴∠BCA =︒︒=⨯369052.—————（1分）∵AD‖BC ，∴︒=∠=∠36BCA CAD .————————————（1分）又∵AC =AD ，∴()︒︒=∠-=∠=∠7218021DAC ACD D .————（2分） （2）作AD CH ⊥，垂足为H ，——————————————————（1分） 在CDH Rt ∆中，tan ∠D =2，令k CH k DH 2,==，———————（1分） 则在ACH Rt ∆中，222CH AH AC +=,————————————（1分）即()()222255x x +-=， 解得：2=x .——（1分）则35,42=-====x AH BC x CH ， ∴()1645321=⨯+⨯=ABCD S 梯形.（1分） 19、解：设磁浮列车的平均速度为x 千米/小时，—————————————（1分） 则21225120225=--x x ，（5分） 整理得：0540001202=--x x ，—（1分）解得180,30021-==x x .（1分）经检验，两根均为原方程的根，但1802-=x ，不合题意，舍去.——（1分） 答：计划中上海到杭州磁浮列车的平均速度将达到300千米/小时.————（1分） 20、证明：（1）∵∠ACB =∠DBC ，∴OC OB =，（2分）∵AD‖BC ，∴OBOCOD OA =，即OD OA =（2分） ∴BD AC =,（1分）∴梯形ABCD 为等腰梯形，即AB =CD .（1分）（2）∵AD =21BC ，AD‖BC ，∴21==BC AD OC OA ,又N 为OC 的中点，—（2分） ∵OA ON =，—（1分）同理OD OM =，又OD OA =.—（2分）∴四边形ADNM 为矩形.———————————————————（1分）21、解：（1）∵点P 是函数x y 21=（x >0）图像上一个点，当点P 的横坐标为2， ∴点P 为（2，1），——————————————————————（1分）由题意可得：M 为（2，21），N 为（1，1），———————————（2分）∴4121121=⨯⨯=∆PMN S .———————————————————（1分）（2）令点P 为()a a ,2，（a >0）———————————————————（1分）则()()⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛a a N a a M a B a A ,1,21,2,,0,0,2，∴211221,212=--===aa a a PN PM a a PB PA ，（1分）即PNPMPB PA =——（1分）∴MN‖AB .——（1分） （3）由（2）得， 222222414,1aa OM a a ON +=+=，2222245552112a a a a a a MN +-=⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=，易知︒≠∠90MON .∴当︒=∠90ONM 时， 有22222245551414aa a a a a +-++=+， 解得22,221==a a (舍去)，即点P 为()2,22.——————（2分） 同理当︒=∠90OMN 时，点P 为⎪⎪⎭⎫⎝⎛42,22.——————————（2分）综上所述，当点P 为()2,22与⎪⎪⎭⎫⎝⎛42,22时，能使△OMN 为直角三角形.22、解：（1）线段BE 与OE 的长度相等. —————————————————（1分）联结AE ，在△ABE 与△AOE 中，- 11 - L O F E DC B A K H ∵OA =AB ，AE =AE ，︒=∠=∠90AOE ABE ，——————————（2分）∴△ABE ≌△AOE . —————————————————————（1分）∴BE =OE .（2）延长AO 交 BC 于点T ，———————————————————（1分） 由△CEF 是等腰直角三角形，易知△OET 与△ABT 均为等腰直角三角形.————————————（1分） 于是在△ABT 中，AB =4，则AT =24，—————————————（2分） ∴BE =OE =OT =424-.————————————————————（1分）（3）在BC 上取点H ，使BH = BA =4，过点H 作AB 的平行线，交EF 、AD 于点K 、L ，（如图）————————————————（1分）易知四边形ABHL 为正方形由（1）可知KL =KO令HK =a ,则在△HEK 中，EH =4–a , EK =a x -+4,∴()()22244a x a x -+=+-， 化简得：xx a +=48.—————————————————————（1分） 又HL ‖AB ， ∴x x EH EC a y --==45，即2216840xx x y --=.————————————（1分） ∴函数关系式为2216840xx x y --=，定义域为0<2≤x .—————（1+1=2分）。

2015年中考第三次模拟考（试卷）数 学考生须知：本试卷分试题卷和答题卷两部分，满分120分，考试时间100分钟。

答题时，应该在答题卷上写明校名，姓名和准考证号。

所有答案都必须做在答题卷标定的位置上，务必注意试题序号和答题序号相对应。

考试结束后，上交答题卷。

一．仔细选一选（本题有10个小题，每小题3分，共30分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内。

注意可以用多种不同的方法来选取正确答案。

1． 下列计算正确的是（ ） A ． 2×3=6B ．+=C ． 5﹣2=3D ． ÷=2.在△ABC 中，∠C=90°，tanA=125，则sinA=（ ) A.1312 B.135 C.513 D.5123.已知A 样本的数据如下：72，73，76，76，77，78，78，78，B 样本的数据恰好是A 样本数据每个都加2，则A ，B 两个样本的下列统计量对应相同的是（ ）A ． 平均数B ． 标准差C ．中位数D ． 众数4.用四个相同的小立方体搭几何体，要求每个几何体的主视图、左视图、俯视图中至少有两．．．．5．已知α是一元二次方程x 2﹣x ﹣1=0较大的根，则下面对α的估计正确的是（ ） A ． 0＜α＜1 B ． 1＜α＜1.5 C ． 1.5＜α＜2 D ． 2＜α＜3 6.在一个圆中，给出下列命题，其中真命题是（ ） A ．垂直于弦的直线平分弦，并且平分弦所对的弧 B ．平分弦的直径垂直于弦，并且平分弦所对的两条弧 C ．弦所对的两弧中点的连线，垂直于弦，并且经过圆心D ．平分弧的直线，平分这条弧所对的弦 7.==∙-+-w ,1w )a 319a 62则若（（ ） A.a+3(a ≠-3) B.-a+3(a ≠3) C.a-3(a ≠3) D.-a-3(a ≠-3)∙A DEPB C8.把一枚均匀的骰子连续抛掷两次，则两次朝上面的点数之积为3的倍数的概率是（）A．95B．3615C．114D．319.一名模型赛车手遥控一辆赛车，先前进1m，然后，原地逆时针方向旋转角a(0°<α<180°)。

包钢三中 2015 年中考数学第三次模拟试卷一、选择题(每题 3 分，共 36 分）1. 下列实数是无理数的是（ ） C.10.如图，已知正方形 ABCD 的边长为 4，E 是 BC 边上的一个动点，AE⊥EF，EF22 A. 7B.1 3A16D.交 DC 于 F，设 BE=x，FC=y，则当点 E 从点 B 运动到点 C 时，y 关于 x 的函数 图象是（ ） （第 10 题图）3D）x 1 2. 函数 y  的自变量 x 的取值范围是（ x3BE（第 4 题图）C AA. x≠—3 B. x≥－1 且 x≠—3 C. x≥－1 D. x＞－1 3. 一个多边形的内角和是外角和的 2 倍，则此多边形的对角线有( )条 A.8 B. 9 C.10 D.11 4.如图，△ABC 中，∠C=45°,点 D 在 AB 上，点 E 在 BC 上，AD=DB=DE,AE=1. 则 AC 的长为( ) A. 1 B. 2 C. 3 D.B2C）D11.在同一坐标系内，一次函数 y=ax+b 与二次函数 y=ax +8x+b 的图象可能是（2y B C＇ A o y A o B Cy C x A25.如图,直线 y=2x+4 与 x、y 轴分别交于 A、B 两点，以 OB 为边在 y 轴右侧 作等边三角形 OBC， 将点 C 向左平移， 使其对应点 C＇ 恰好落在直线 AB 上, 则点 C＇的坐标为（ ） A.(-1,1) B.(-1,2) C.(-2,1) D.(-BCD3 ,1) 2（第 5 题图）12.定义 a, b, c 为函数 y= ax  bx  c 的特征数，若给出特征数 2m,1  m,1  m ，则函数6.如图,A 点的坐标为(-4，0),直线 y= 3 x+n 与坐标轴交于点 B、C，连接 AC,如果∠ACD=90°,则 n 的值为( A. －2 B. － )xy= ax  bx  c 的下列结论： ①当 m=﹣3 时，函数图象的顶点横坐标是21 . 3➁当 m＞0 时，函数图象截 X 轴所得的线段长度大于 ➂当 m＜0 时，函数在 x＞y4 2 3C. －4 3 3D. －4 5 3D（第 6 题图）3 . 21 时，y 随 x 的增大而减小。

2015年中考数学模拟测试卷(三)时间120分钟 满分120分 2015.4.11一、选择题（每小题3分共36分）1．对于任意实数x ，代数式53212+-x x 的值是一个（ ▲ ）A ． 非负数B ． 正数C ．负数D ． 整数2．如图，C 、D 是线段AB 上两点，若CB ＝4cm ，DB=7cm ，且D 是AC 的中点，则AC 的长等于（ ）A ．3cmB ．6cmC ．10cmD ．14cm3．某地，今年1月1日至4日每天的最高气温与最低气温如下表：其中温差最大的是（ ） A ．1月1日B ．1月2日C ．1月3日D ．1月4日4．在同一时刻，身高1.6米的小强在阳光下的影长为0.8米，一棵大树的影长为4.8米，则树的高度为（ ） A ．4.8米B ．6.4米C ．9.6米D ．10米5．下列运算正确的是A ．a 3•a 2=a 6B ．2a （3a ﹣1）=6a 3﹣1C ．（3a 2）2=6a 4D ．2a+3a=5a6．下列运算正确的是（ ） A.x 4·x 3=x 12 B.（x 3）4＝x 7 C.x 4÷x 3=x(x ≠0) D.x 4+x 4=x 87．关于函数y= 3x ＋1，下列结论正确的是A ．图象必经过点(－2，5)B ．y 随x 的增大而减小C ．当x ＞—12时，y ＞0 D ．图象经过第一、二、三象限 8．若a为有理数，则说法正确是( )[A ．－a 一定是负数B ．| a |一定是正数C ．| a |一定不是负数D ．－a 2一定是负数9．将y=2x 2的函数图象向左平移2个单位长度后，得到的函数解析式是（ ） A. y=2x 2+2 B. y=2（x+2）2 C. y=（x －2）2 D. y=2x 2－2 10．不等式组⎩⎨⎧><-01x x 的解集在数轴可表示为（ ▲ ）11．下列计算正确的是 （ ）A ．133-=-B ．236a a a ⋅=C ．22(1)1x x +=+D ．=12．某品牌商品，按标价九折出售，仍可获得20%的利润.若该商品标价为28元，则商品的进价为：A. 21元B. 19.8元C. 22.4元D. 25.2元二、填空题（每小题3分共24分）13．观察下面一列数，根据规律写出横线上的数。

2015年中考地理第三次模拟考试试题附参考答案第Ⅰ卷（选择题共60分）每小题给出的四个选项中，只有一个正确答案。

每小题2分，共60分。

由湖南地图出版社与湖北省测绘学会共同编制的竖版《世界知识地图》是对传统横版《世界地图》的一种突破，这意味着使用了400多年的横版地图不再“一统天下”，在地图制图领域具有划时代的意义。

换个角度看世界，根据右图，回答1～5题。

1．图中甲点经纬度位置是A．0°，105°W B．0°，105°EC．0°，75°W D．0°，75°E2．图中丙为A．北冰洋 B．印度洋C．大西洋 D．太平洋3．甲点位于上海的A．东南方向 B．东北方向C．西北方向 D．西南方向4．图中乙为A．亚洲 B．北美洲 C．非洲 D．南美洲5．换个角度看世界，是哪位科学家观察世界地图之后引发了思考并提出“大陆漂移学说”A．麦哲伦 B．哥白尼C．哥伦布 D．魏格纳6．右图是某区域等高线图，下列说法正确的是A．a、b两地之间的相对高度是100米B．王镇地处山脊部位C．刘家位于王镇的西北方向D．图示区域属于丘陵地形7．2015年4月25日14时11分，尼泊尔（北纬28.2度，东经84.7度）发生8.1级地震，地震已造成8200余人遇难。

据此结合右图，判断关于尼泊尔多地震原因解释正确的是A．位于亚欧板块与太平洋板块交界处B．位于阿尔卑斯－喜马拉雅地震带上C．位于环太平洋地震带上D．位于非洲板块与亚欧板块交界处读右图，完成8～9题。

8．造成甲、丙两地降水差异的主要因素是A ．海陆位置B ．纬度位置C ．地形因素D ．人类活动9．据图中信息判断，下列叙述正确的是 A ．甲地为沙漠景观 B ．乙山顶终年积雪 C ．丙地全年高温多雨 D ．该山地位于北半球10. 2014年5月4—11日李克强总理访问了尼日利亚等非洲四国，他坦诚表达了中国愿意携手非洲共同发展的意愿。

哈尔滨三中2015年第⼀次模拟考试数学试题和答案（理）哈尔滨三中2015年第⼀次模拟考试数学试卷（理⼯类）第I 卷（选择题, 共60分）⼀、选择题(本⼤题共12⼩题，每⼩题5分，共60分，在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的．) 1. 集合?>+-=031x x xP ，{}24x y x Q -==，则=Q PA ．]2,1(B ．]2,1[C ．(,3)(1,)-∞-+∞ D ．)2,1[2. 等差数列{}n a 的前n 项和为n S ，且3S =6，1a =4，则公差d 等于A ．1B ．35C ．2-D ．33. 在ABC ?中，3=AB ，1=AC ， 30=∠B ，则ABC ?的⾯积为23，=∠C A ．30 B ．45 C ．60 D ．75 4. 下列函数在),0(+∞上为减函数的是A ．1--=x yB ．xe y = C ．)1ln(+=x y D ．)2(+-=x x y 5. ⽅程2l og2=+x x 的解所在的区间为A ．)1,5.0(B ．)5.1,1(C ．)2,5.1(D ．)5.2,2( 6. 将函数()()?+=x x f 2si n 的图象向左平移8π个单位，所得到的函数图象关于y 轴对称，则?的⼀个可能取值为 A ．43π B ．4πC ．0D ．4π- 7. 给出下列关于互不相同的直线m 、l 、n 和平⾯α、β的四个命题：①若α?m ，A l =α，点m A ?，则l 与m 不共⾯；②若m 、l 是异⾯直线，α//l ，α//m ，且l n ⊥，m n ⊥，则α⊥n ；③若α//l ，β//m ，βα//，则m l //；④若α?l ，α?m ，A m l = ，β//l ，β//m ，则βα//，其中为真命题的是侧视图俯视图A ．①③④B ．②③④C ．①②④D ．①②③8. 变量x 、y 满⾜条件??->≤≤+-1101x y y x ，则22)2(y x +-的最⼩值为A ．223 B ．5 C ．2D ．5 9. 如图，AO B ?为等腰直⾓三⾓形，1=OA ，OC 为斜边AB 的⾼，点P 在射线OC 上，则?的最⼩值为A ．1-B ．81-C ．41-D ．21-10. 如图，四棱锥ABCD P -中，90=∠=∠BAD ABC ，AD BC 2=，PAB ?和PAD ?都是等边三⾓形，则异⾯直线CD与PB 所成⾓的⼤⼩为A ． 90B ．75 C ．60 D ．4511. 已知抛物线C ：x y 82=的焦点为F ，准线为l ，P 是l 上⼀点，Q 是直线PF 与C 的⼀个交点，若QF PF 3=，则QF = A ．25 B ． 38C ． 3D ． 6 12. 设函数)(x f 在R 上存在导数)(x f '，R x ∈?，有2)()(x x f x f =+-，在),0(+∞上x x f <')(，若m m f m f 48)()4(-≥--，则实数m 的取值范围为A ． ]2,2[-B ． ),2[+∞C ． ),0[+∞D ．(,2][2,)-∞-+∞第Ⅱ卷（⾮选择题, 共90分）⼆、填空题（本⼤题共4⼩题，每⼩题5分，共20分，将答案填在答题卡相应的位置上．）13. 正项等⽐数列{}n a 中，42=a ，164=a ，则数列{}n a 的前9项和等于．14. 某⼏何体的三视图如图所⽰，则它的表⾯积为．15. 已知1F ，2F 是椭圆和双曲线的公共焦点，P 是它们的⼀个公共点，且21π=∠PF F ，椭圆的离⼼率为1e ，双曲线的离⼼率2e ，则=+222131e e ． AOCBPBDCPA16．定义：如果函数)(x f y =在定义域内给定区间],[b a 上存在0x )(0b x a <<，满⾜ab a f b f x f --=)()()(0，则称函数)(x f y =是],[b a 上的“平均值函数”，0x 是它的⼀个均值点，例如2x y =是]1,1[-上的平均值函数，0就是它的均值点．现有函数mx x x f +=3)(是]1,1[-上的平均值函数，则实数m 的取值范围是．三、解答题（本⼤题共6⼩题，共70分，解答应写出⽂字说明，证明过程或演算步骤．） 17.（本⼩题满分12分）设ABC ?是锐⾓三⾓形，三个内⾓A ，B ，C 所对的边分别记为a ，b ，c ，并且)3si n()3si n()si n )(si n si n (si n B B B A B A +-=+-ππ.（Ⅰ）求⾓A 的值；（Ⅱ）若12=?，72=a ，求b ，c （其中c b <）． 18.（本⼩题满分12分）已知数列}{n a 满⾜)(3)1)(1(11++-=--n n n n a a a a ，21=a ，令11-=n n a b . （Ⅰ）证明：数列}{n b 是等差数列；（Ⅱ）求数列}{n a 的通项公式． 19.（本⼩题满分12分）ABC ?为等腰直⾓三⾓形，4==BC AC ， 90=∠ACB ，D 、E 分别是边AC 和AB 的中点，现将ADE ?沿DE 折起，使⾯AD E ⊥⾯DEBC ，H 、F 分别是边AD 和BE 的中点，平⾯BCH 与AE 、AF 分别交于I 、G 两点．（Ⅰ）求证：IH //BC ；（Ⅱ）求⼆⾯⾓C GI A --的余弦值；（Ⅲ）求AG 的长．20.（本⼩题满分12分）AHICDBFGE如图，抛物线1C ：px y 22=与椭圆2C ：1121622=+y x 在第⼀象限的交点为B ，O 为坐标原点，A 为椭圆的右顶点，OAB的⾯积为368. （Ⅰ）求抛物线1C 的⽅程；（Ⅱ）过A 点作直线l 交1C 于C 、D 两点，射线OC 、OD 分别交2C 于E 、F 两点，记OEF ?和OCD ?的⾯积分别为1S 和2S ，问是否存在直线l ，使得77:3:21=S S ？若存在，求出直线l21.（本⼩题满分12分）设函数bx x x a x f +++=)1ln()1()(2)1(->x ，曲线)(x f y =过点)1,1(2+--e e e ，且在点)0,0(处的切线⽅程为0=y .（Ⅰ）求a ，b 的值；（Ⅱ）证明：当0≥x 时，2)(x x f ≥；（Ⅲ）若当0≥x 时，2)(mx x f ≥恒成⽴，求实数m 的取值范围．请考⽣在第22、23、24三题中任选⼀题作答，如果多做，则按所做的第⼀题记分.22.（本⼩题满分10分）选修4-1：⼏何证明选讲如图，四边形ABC D 是⊙O 的内接四边形，延长BA 和CD 相交于点P ，1=PB PA ， 21=PC PD . （Ⅰ）求BCAD的值；（Ⅱ）若BD 为⊙O 的直径，且1=PA ，求BC 的长．23.（本⼩题满分10分）选修4-4：坐标系与参数⽅程已知在平⾯直⾓坐标系xOy 中，直线l 的参数⽅程是+==242222t y t x （t 是参数），以原点O 为极点，x 轴正半轴为极轴建⽴极坐标系，曲线C 的极坐标⽅程)4cos(2πθρ+=.P（Ⅰ）判断直线l 与曲线C 的位置关系；（Ⅱ）设M 为曲线C 上任意⼀点，求y x +的取值范围． 24.（本⼩题满分10分）选修4-5：不等式选讲已知函数212)(--+=x x x f . （Ⅰ）解不等式0)(≥x f ；（Ⅱ）若存在实数x ，使得a x x f +≤)(，求实数a 的取值范围．哈尔滨三中2015年第⼀次模拟考试数学试卷（理⼯类）答案及评分标准⼀、选择题：⼆、填空题：13. 1022 14. 8(2π++ 15. 4 16. 3(3,]4-- 三、解答题： 17.解：(Ⅰ)B B B B B A 22sin )sin 21cos 23()sin 21cos 23(sin +-?+= 43)sin (cos 4322=+=B B ， 23sin =∴A ，3π=∴A ． ………………………… 6分 (Ⅱ) 12cos ==?A b ，24=∴bc ，⼜bc c b A bc c b a 3)(cos 22222-+=-+=，10=+∴c b ，c b < ，4=∴b ，6=c ．………………………… 12分18.解：(Ⅰ)[])1()1(3)1)(1(11---=--++n n n n a a a a ，3111111=---∴+n n a a ，即311=-+n n b b ，{}n b ∴是等差数列．………6分 (Ⅱ)11=b ，3231+=∴n b n ，………………………… 10分231+=-n a n ，25++=∴n n a n ．………………………… 12分19. (Ⅰ)因为D 、E 分别是边AC 和AB 的中点，所以BC ED //，因为?BC 平⾯BC H ，?ED 平⾯BC H ，所以//ED 平⾯BC H因为?ED 平⾯BC H ，?ED 平⾯AED ，平⾯BC H ?平⾯HI AED = 所以HI ED //⼜因为BC ED //，所以IH //BC . …………………………………… 4分(Ⅱ))0,0,0(D ，)0,0,2(E ，2,0,0(A )0,1,3(F ，)0,2,0(E ，)1,0,0(H )2,0,2(-=EA ，)0,1,1(=EF )1,2,0(-=CH ，)0,0,1(2 1==，设平⾯AGI 的⼀个法向量为),,(1111z y x n =，则=?=?0011n EB n ，=+=+-01111y x z x ，令11=z ，解得11=x ，11-=y ，则)1,1,1(1-=n 设平⾯C HI 的⼀个法向量为),,(2222z y x n =，则=?=?0022n n CH ，==+-02221x z y ，令22-=z ，解得11-=y ，则)2,1,0(2--=n 15155321,cos 21=->=1515…………………………… 8分（Ⅲ）法（⼀）)2,1,3(-=AF ，设)2,,3(λλλλ-==AF AG)12,,3()2,,3()1,0,0(---=---=-=λλλλλλ则02=?n ，解得32=λ， 3142)2(13323222=-++==AF AG ………………… 12分 AB法（⼆）取CD 中点J ，连接AJ 交CH 于点K ，连接HJ ，HKJ ?与CKA ?相似，得2=KJAK，易证GK HI //，所以314232==AF AG …………… 12分 20. 解: (Ⅰ)因为O A B ?的⾯积为368,所以364=B y ，……………2分代⼊椭圆⽅程得)364,34(B ，抛物线的⽅程是：x y 82= ……………4分 (Ⅱ) 存在直线l : 0411=-±y x 符合条件解：显然直线l 不垂直于y 轴，故直线l 的⽅程可设为4x my =+，与x y 82=联⽴得03282=--my y .设),(),,(2211y x D y x C ,则32,82121-=?=+y y m y y12211sin 21sin 2E F OC OD COD OC OD y y S S OE OF y y OE OF EOF ∠∴===∠F E y y 32= .……………6分由直线OC 的斜率为1118y x y =,故直线OC 的⽅程为x y y 18=，与1121622=+y x 联⽴得 1)1211664(212=+?y y E ，同理1)1211664(222=+?y y F ，所以2E y ?1)1211664)(1211664(22212=+?+?y y y F………8分可得2E y ?223625612148F y m=+ 要使37712=S S ，只需22232(12148)77362563m +??=………10分即21214849121m +=? 解得11±=m ，所以存在直线l : 0411=-±y x 符合条件………………………… 12分 21.解：(Ⅰ)b x a x x a x f +++++=')1()1ln()1(2)(，0)0(=+='b a f ，22(1)(1)(1)f e ae b e a e e -=+-=-+21e e =-+ 1=∴a ，1-=b ． ………………………………4分(Ⅱ)x x x x f -++=)1ln()1()(2，设22)1ln()1()(x x x x x g --++=，)0(≥x ，x x x x g -++=')1ln()1(2)((())2ln(1)10g x x ''=++>，∴)(x g '在[)+∞,0上单调递增，∴0)0()(='≥'g x g ，∴)(x g 在[)+∞,0上单调递增，∴0)0()(=≥g x g ．∴2)(x x f ≥．………………………………8分（Ⅲ）设22)1ln()1()(mx x x x x h --++=，mx x x x x h 2)1ln()1(2)(-+++='，(Ⅱ) 中知)1()1l n()1(22+=+≥++x x x x x x ，∴x x x ≥++)1ln()1(，∴mx x x h 23)(-≥'，①当023≥-m 即23≤m 时，0)(≥'x h ，)(x h ∴在[)+∞,0单调递增，0)0()(=≥∴h x h ，成⽴．②当03<-m 即23>m 时，x m x x x h )21()1l n()1(2)(--++='， m x x h 23)1ln(2)(-++=''，令0)(=''x h ，得012320>-=-m ex ，当[)0,0x x ∈时，0)0()(='<'h x h ，)(x h ∴在[)0,0x 上单调递减0)0()(=<∴h x h ，不成⽴．综上，23≤m ．………………………………12分22. (Ⅰ)由PAD ∠=PCB ∠，A A ∠=∠，得PAD ?与PCB ?相似，设,PA x PD y ==则有24x y y y x=?=，所以24AD x BC y ==………………………………5分 (Ⅱ)90C ∠=，4,PA PC ===10分23.解：(Ⅰ)直线l 的普通⽅程为0x y -+=曲线C 的直⾓坐标系下的⽅程为22(()122x y -++=圆⼼,22-到直线0x y -+=的距离为51d ==> 所以直线l 与曲线C 的位置关系为相离. ……………5分(Ⅱ)设cos ,sin )22M θθ+-+，则cos sin )4x y πθθθ?+=+=+∈?.……………10分24. (Ⅰ)①当12x ≤-时，1223x x x --+≥?≤-，所以3x ≤- ②当102x -<<时，12123x x x ++≥?≥，所以为φ③当0x ≥时，121x x +≥?≥，所以1x ≥综合①②③不等式的解集为(][),31,-∞-?+∞……………5分(Ⅱ)即12122122ax x a x x +-≤+?+-≤+ 由绝对值的⼏何意义，只需11322aa -≤+?≥-…………………10分。

2015年湖北省武汉市吴家山三中中考化学模拟试卷（一）一．选择题：（本题包括20小题，每小题3分，共60分．每题只有一个正确选项）1．（3分）下列变化属于化学变化的是（）A．铁锅生锈B．湿衣服晾干C．蜡烛熔化D．玻璃破碎2．（3分）下列说法正确的是（）A．氢气在空气中燃烧，其变化的最小粒子是氢分子和氧分子B．水是一种氧化物，含有氧元素，因此含有氧元素的化合物都是氧化物C．空气的主要成分是氮气和氧气，因此组成空气的成分都属于单质D．铁、水和氯化钠分别是由原子、分子和离子构成3．（3分）化学与日常生活有着密切联系．下列说法错误的是（）A．人体缺铁会引起贫血，因此应补充铁粉B．垃圾分类回收既可以充分利用资源又可以减少环境污染C．肥皂水区分硬水和软水时，泡沫少的是硬水，泡沫多的是软水D．发生火灾时，要视不同的可燃物选择不同的灭火方法和灭火剂4．（3分）工业上制备氢气的微观过程如图所示．下列说法错误的是（）A．图中“”表示氢分子B．该反应中“”与“”的质量比为8：9C．生成物中有四种不同的分子D．该反应的化学方程式是CH4+H2O CO+3H25．（3分）实验室常用二氧化锰和浓盐酸反应制取氯气，反应的化学方程式为：MnO2+4HCl （浓）MnCl2+2X+Cl2↑其中X的化学式为（）A．H2O B．H2O2C．HClO D．O26．（3分）如图是氢氧化钠溶液与稀硫酸反应时，溶液的pH变化曲线图。

下列说法正确的是（）A．该实验是将稀硫酸滴入氢氧化钠溶液中B．曲线上A点的溶液里溶质有H2SO4、Na2SO4和NaOHC．取曲线上M点的溶液，向其中滴入无色酚酞试液，溶液变红色D．曲线上B点的溶液里溶质有两种7．（3分）用如图实验装置制取干燥的气体正确的是（）a b c①大理石与盐酸浓硫酸CO2②锌粒与稀硫酸浓硫酸H2③双氧水与二氧化锰浓硫酸O2④二氧化锰与氯酸钾浓硫酸O2A．①②③B．①③C．①④D．①③④8．（3分）向一定质量AgNO3和Cu（NO3）2的混合溶液中加入Zn粉，溶液质量与加入Zn粉的质量关系如图所示．关于该实验有如下说法：①取a点溶液，滴加稀盐酸，无白色沉淀②c点溶液中溶质为Zn（NO3）2③若取b～c段的固体，滴加稀盐酸，无气泡产生④取d点的固体，其组成有2种物质其中说法错误的有（）A．0个B．1个C．2个D．3个二、非选择题，共60分）9．（5分）如图A是铁元素在周期表里的部分信息，图B是某元素一种粒子的结构示意图．请你回答下列问题：（1）图A中铁的原子序数是．（2）图B中，若X﹣10＝1，则该粒子的符号是；若X＝8，则该元素与铁元素形成化合物的化学式可能是．（3）铁与稀盐酸反应的化学方程式是．10．（4分）如图是甲、乙、丙三种物质的溶解度曲线．请根据图中给出的信息回答下列问题．（1）M点表示．（2）在t2℃时，甲、乙、丙三种物质的饱和溶液里溶质的质量分数的大小关系是（用“＞”、“＜”或“＝”表示）．（3）若甲中含有少量的乙，欲提纯甲的操作是．（4）下列说法正确的是A．将甲、乙的饱和溶液分别从t1℃升温到t2℃，溶质的质量分数：甲＞乙B．t2℃时，向50g30%甲的饱和溶液中加50g水，充分搅拌，溶液的浓度为15%C．t2℃时，将甲、乙、丙分别溶于等质量的水制成饱和溶液，需物质的质量最多的是甲D．t2℃时，某甲溶液降温至t1℃时，一定有甲物质结晶析出．11．（5分）有一包白色固体粉末，可能含有硝酸钡、氯化钠、氢氧化钠、硫酸钠、硫酸铜中的一种或几种，对该固体进行如下实验：请回答下列问题：（1）原白色固体粉末中一定含有，可能含有．（2）无色溶液B中一定含有的溶质有．（3）写出步骤②中发生反应的化学方程式．12．（7分）某学校化学兴趣小组的学生利用下面的装置（部分固定装置已略去）制备氮化钙，并探究其化学式．开始实验并记录数据如下：硬玻璃管质量m0/g硬玻璃管质量与钙的质量m1/g硬玻璃管质量与产物的质量m2/g 114.8120.8122.2根据实验和数据，回答下面的问题：（1）设氮化钙的化学式为Ca x N2，则金属钙和氮气反应的化学方程式可表示为：xCa+N2Ca x N2该反应属于反应（填“化合”、“分解”、“置换”或“复分解”）．（2）参加反应的金属钙和氮气的质量分别为、．（3）在实验过程中末端导管必须插入试管A的水中，目的是．（4）在实验开始时，打开活塞K，先通入氮气一会儿，再点燃酒精灯，这样操作的作用是．反应结束后的操作是，拆除装置，取出产物．（5）请根据实验的有关数据列式计算氮化钙化学式（Ca x N2）中x的值，相关计算式为．13．（5分）实验室里用加热高锰酸钾固体粉末来制取氧气．某化学兴趣小组的同学称取3.95g 高锰酸钾装于试管里，按要求组装好装置，并进行加热和收集氧气，直到导管口没有气泡冒出，移出导管，停止加热，待冷却后，将试管里的剩余固体倒入烧杯里，加97.54g 水充分溶解后，过滤得到滤液和1.09g的滤渣．试计算：（1）制得氧气的质量．（2）所得滤液中溶质的质量分数．2015年湖北省武汉市吴家山三中中考化学模拟试卷（一）参考答案一．选择题：（本题包括20小题，每小题3分，共60分．每题只有一个正确选项）1．A；2．D；3．A；4．C；5．A；6．D；7．B；8．C；二、非选择题，共60分）9．26；Na+；Fe2O3（合理即可）；Fe+2HCl═FeCl2+H2↑；10．t1℃时，甲和丙的溶解度相等；甲＞乙＞丙；降温结晶；B；11．CuSO4、Ba（NO3）2、NaOH；Na2SO4；NaOH、NaNO3；Cu（OH）2+2HCl═CuCl2+2H2O；12．化合；6g；1.4g；防止空气中的氧气通过末端导管进入实验装置与钙反应；排尽装置内空气，防止空气内氧气与钙反应；停止加热，继续通氮气至装置冷却；X＝3；13．；。