云南省曲靖市会泽县第一中学2019-2020学年高二上学期第一次段考数学(理)word版

会泽一中2020年春季学期半月考试卷1高二数学（理科）一、 选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1.已知集合{11}A x x =-≤≤，2{20}B x x x =-≤，则A B =I （ ） A.[1,0]- B. [1,2]- C. [0,1] D. (,1][2,)-∞+∞U2.已知向量,a b r r 均为单位向量，若它们的夹角为060，则3a b +r r 等于（ ）A 7B 1013．43.若二项式22()n x x-展开式的二项式系数之和为8，则该展开式每一项的系数之和为（ ） A ．-1 B ．1 C ．27 D ．-27 4. “21sin =A ”是“︒=30A ”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件5.已知两条不重合的直线,m n 和两个不重合的平面,αβ，若m α⊥，n β⊂，则下列四个命题：①若//αβ，则m n ⊥；②若m n ⊥，则//αβ；③若//m n ，则αβ⊥；④若αβ⊥，则//m n其中正确命题的个数是（ ）A ．0B ．1 C.2 D ．36.执行右图程序框图，输出的结果s 的值为（ ） A ．32-B ．0 C. 32D 37.已知圆22()1x a y -+=与直线y x =相切于第三象限，则a 的值是（ ）A 2B ．2- C. 2± D ．2-8.若变量,x y 满足条件106010x y x y x --≤⎧⎪+-≤⎨⎪-≥⎩，则xy 的取值范围是（ ）A ．[0,5]B ．35[5,]4 C. 35[0,]4D ．[0,9] 9.在ABC ∆中，060A =，1b =，3ABC S ∆=，则sin cC=（ ）A ．8381B ．2393 C. 2633 D ．2710. 函数2()sin ln(1)f x x x =⋅+的部分图像可能是（ ）Oyx O yx O yx.Oyx .ABCD11.下列4个命题111:(0,),()()23x xp x ∃∈+∞< 21123:(0,1),log log p x x x ∃∈> 3121p :(0,),()log 2x x x∀∈+∞> 41311:(0,),()log 32x p x x ∀∈<真命题是（ ） A.13,p p B.14,p p C.23,p p D.24,p p12．设数列n n na 2sin 22sin 21sin 2+++=Λ，则对任意正整数n m ,)(n m >都成立的是（ ） A ．2||mn a a m n >- B ．2||nm a a m n ->- C ．n m n a a 21||<-D ．n m n a a 21||>-二、填空题（本大题共4个小题，每小题5分，共20分） 13.命题“任意的01,23≤+-∈x x R x ”的否定是 ．14.由数字2，0，1，7组成没有重复数字的四位偶数的个数为 ．15.右图是一个几何体的三视图，其中正视图和侧视图均是高为2，底边长为22的等腰三角形，俯视图是边长为2的正方形，则该几何体的外接球的体积是 ．16.已知函数22cos[(1)sin[(1)]44()45x x f x x x ππ--+-=++（40x -≤≤），则()f x 的最大值为 ．三、解答题（本大题共6个小题，17题10分，其余12分，共70分） 17.（本小题满分10分）在一段时间内，分5次测得某种商品的价格x (万元)和需求量y (t)之间的一组数据如下表： 价格x 1.4 1.6 1.8 2 2.2 需求量y1210753已知6.16,62121==∑∑==i i i i i x y x ，(1)求出y 对x 的线性回归方程；(2)如果价格定为1.9万元，预测需求量大约是多少？(精确到0.01 t)．(附：在线性回归方程a x b yˆˆˆ+=中，∑∑==--=ni ini ii xn xy x n yx b 1221ˆ，x b y aˆˆ-=．) 18.（本小题满分12分）())62sin(cos 22π-+=x x x f 已知函数（1）求函数()x f 的单调增区间；最大值，以及取得最大值时x 的取值集合；（2）已知ABC ∆中，角A 、B 、C 的对边分别为c b a ,,，若()2,23=+=c b A f ，求实数a 的取值范围.19. （本小题满分12分）如图，在几何体ABCDEF 中，底面ABCD 为矩形，//EF CD ，CD EA ⊥，22CD EF ==，3ED =．M 为棱FC 上一点，平面ADM 与棱FB 交于点N ．（1）求证：ED CD ⊥； （2）求证：//AD MN ；（3）若AD ED ⊥，试问平面BCF 是否可能与平面ADMN 垂直？若能，求出FMFC的值；若不能，说明理由．20. （本小题满分12分）某地遭遇跨年霾，很多学校调整元旦放假时间，幼儿园、中小学等教育机构纷纷停课.学生和家长对停课这一举措褒贬不一，有为了健康赞成的，有怕耽误学习不赞成的，某调查机构为了了解公众对该举措的态度，随机调查采访了50人，将调查情况整理汇总成下表： 年龄（岁） [15,25)[25,35)[35,45)[45,55)[55,65)[65,75]频数 5 10 15 10 5 5 赞成人数 469634（1）请在图中完成被调查人员年龄的频率分布直方图；（2）若从年龄在[25,35)，[65,75]两组采访对象中各随机选取2人进行深度跟踪调查，选中4人中不赞成这项举措的人数为X ，求随机变量X 的分布列和数学期望.21. （本小题满分12分）管理部门推出了针对电商的商品和服务的评价体系.现从评价系统中选出200次成功的交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次.(1)完成如下列联表，计算是否可以在犯错误概率不超过0.1%的前提下，认为商品好评与服务好评有关？(2)将频率视为概率，某人在该购物平台上进行的5次购物中，设对商品和服务全好评的次数为随机变量X ：求X 的数学期望和方差.2()0.150.100.050.0250.0100.0050.0012.072 2.7063.841 5.024 6.6357.87910.828P K k k≥（22()()()()()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++）22.（本小题满分12分）等差数列{}n a 中，已知35a =，且521,,a a a 为递增的等比数列. （1）求数列{}n a 的通项公式；（2）若数列{}n b 的通项公式1212,212,2n n na n kb n k +-=-⎧⎪=⎨⎪=⎩（*k N ∈），求数列{}n b 的前n 项和n S .高二 数学（理科）参考答案一、选择题1-5: CCABC 6-10:CBDBB 11、12：DC 二、填空题13. 存在01,20300>+-∈x x R x 14. 10 15. 16.2三、解答题17．(本题满分10分）(1)因为x ＝15×9＝1.8，y ＝15×37＝7.4，∑5i ＝1x i y i ＝62，∑5i ＝1x 2i ＝16.6， 所以b ＝∑5i ＝1x i y i －5x y∑5i ＝1x 2i －5x2＝62－5×1.8×7.416.6－5×1.82＝－11.5，a ＝y －b x ＝7.4＋11.5×1.8＝28.1，故y 对x 的线性回归方程为y ＝28.1－11.5x . (2)y ＝28.1－11.5×1.9＝6.25(t)．所以，如果价格定为1.9万元，则需求量大约是6.25 t. 18.（本小题共12分）解：（1）1)62sin(12sin 232cos 21)62sin(cos 2)(2++=++=-+=ππx x x x x x f 226222πππππ+≤+≤-k x k ，可得f(x)递增区间为)](6,3[z k k k ∈+-ππππ函数f(x)最大值为2，当且仅当1)62sin(=+πx ，即2262πππ+=+k x ，即)(6Z k k x ∈+=ππ取到∴}6|{ππ+=∈k x x x(2)由231)62sin()(=++=πA A f ，化简得21)62sin(=+πA πππ6562A),0(=+∴∈A Θ 3A π=∴在△ABC 中，根据余弦定理，得a 2=b 2+c 2-bc=(b+1)2-3bc 由b+c=2，知bc≤1,即a 2≥1 ∴当b=c=1时，取等号 又由b+c>a 得a<2 所以a∈[1,2)19．(本小题满分12分)（解：（1）因为 ABCD 为矩形，所以 CD AD ⊥．又因为 CD EA ⊥， 所以 CD ⊥平面EAD ．所以 ED CD ⊥． 4分 （2）因为 ABCD 为矩形， 所以 //AD BC ，所以 //AD 平面FBC ． 又因为 平面ADMN I 平面FBC MN =，所以 //AD MN ． 8分 （3）平面ADMN 与平面BCF 可以垂直．证明如下：连接 DF ．因为 AD ED ⊥，AD CD ⊥ ，所以 AD ⊥平面CDEF ． 所以 AD DM ⊥．因为 //AD MN ，所以DM MN ⊥． 因为 平面ADMN I 平面BCF MN =， 若使 平面ADMN ⊥平面BCF ，则 DM ⊥平面BCF ，所以 DM FC ⊥． 在梯形CDEF 中，因为//EF CD ， ED CD ⊥，22CD EF ==，3ED 所以 2DF DC ==．所以 若使DM FC ⊥能成立，则M 为FC 的中点． 所以12FM FC =． 12分 20.(本小题满分12分)（1）补全频率分布直方图如图年示： （2）X 的所有可能的取值为0，1，2，3，2264225109015(0)45075C C P X C C ==•==，2111264644222251051020434(1)45075C C C C C P X C C C C •==•+•==， 1112246444222251051013222(2)45075C C C C C P X C C C C ==•+•==， 124422510244(3)45075C C P X C C ==•==()0123 1.275757575E X =⨯+⨯+⨯+⨯=所以X 的数学期望为() 1.2E X =. 21.(本小题满分12分)(1) 由题意可得关于商品和服务评价的22⨯列联表： 22200(80104070)11.11110.8281505012080K ⨯⨯-⨯=≈>⨯⨯⨯，可以在犯错误概率不超过0.1%的前提下，认为商品好评与服务好评有关. (6分)(2) 每次购物时，对商品和服务都好评的概率为25，且X 的由于2~(5,)5X B ，则()2525=⨯=X E ； ()56521525=⎪⎭⎫ ⎝⎛-⨯⨯=X D . (12分)22.(本小题满分12分)解：（1）设数列{}n a 的公差为d ，由题意2333(2)(2)()a d a d a d -+=-，即220d d -=，解之得2d =或0d =（舍去），所以3(3)21n a a n d n =+-=-，即21n a n =-，*n N ∈为所求（2）当2n k =，*k N ∈时，121321242n n k k S b b b b b b b b b -=+++=+++++++L L L 01112(222)k k a a a -=+++++++L L2(121)1221212k k k k k +--=+=+--22214nn =+-； 当21n k =-，*k N ∈时，12n k +=11122122211(1)23212244n n n n n n n n n S S b ++--++++-=-=+--=+综上，2212221,24232,214nn n n n k S n n n k -⎧+-=⎪⎪=⎨+-⎪+=-⎪⎩，（*k N ∈。

云南省曲靖市会泽县第一中学高二数学理期末试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 若，都是实数，则“”是“”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件参考答案：A略2. 曲线在点处的切线与坐标轴围成的三角形面积为（）A．B．C．D．参考答案：A【考点】62：导数的几何意义．【分析】（1）首先利用导数的几何意义，求出曲线在P（x0，y0）处的切线斜率，进而得到切线方程；（2）利用切线方程与坐标轴直线方程求出交点坐标（3）利用面积公式求出面积．【解答】解：若y=x3+x，则y′|x=1=2，即曲线在点处的切线方程是，它与坐标轴的交点是（，0），（0，﹣），围成的三角形面积为，故选A．3. 等比数列中，，，则等于（ )A. B. C. D.参考答案：A略4. “m=3”是“椭圆焦距为2”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分又不必要条件参考答案：A【考点】椭圆的简单性质．【分析】根据椭圆的标准方程与基本概念，可得当m=3时椭圆的焦点在x轴上，焦距为2；反之，当椭圆焦距为2时，由椭圆的焦点位置可能在x轴或y轴上，得到m=3或5．由此结合充要条件的定义，可得答案．【解答】解：先看充分性，当m=3时，椭圆方程为，可得c===1，∴椭圆的焦距为2c=2．即椭圆焦距为2，充分性成立；再看必要性，当椭圆焦距为2时，若椭圆的焦点在x轴上，则c===1，解得m=3；若椭圆的焦点在y轴上，则c===1，解得m=5．∴m的值为3或5，可得必要性不成立．因此“m=3”是“椭圆焦距为2”的充分不必要条件．故选：A5. 已知点,且,则实数的值是A. 或B. 或C. 或D. 或参考答案：D6. 双曲线的渐近线的方程和离心率分别为( )A. B.C. D.参考答案：D7. 下列结论正确的是( )①函数关系是一种确定性关系；②相关关系是一种非确定性关系③回归分析是对具有函数关系的两个变量进行统计分析的一种方法④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法。

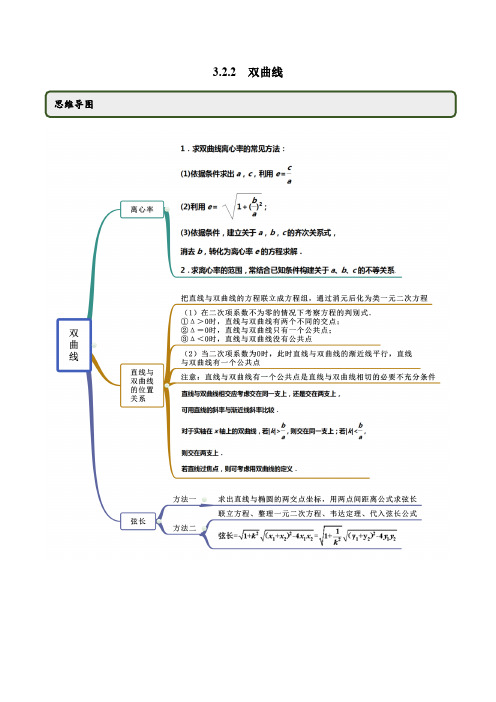
3.2.2 双曲线考点一双曲线的离心率【例1】（2020·云南省下关第一中学高二月考）若实数数列：1，a，81成等比数列，则圆锥曲线221yxa+=的离心率是（）A B C D．13或10【答案】A【解析】由1，a，81成等比数列有：281a=，所以9a=±，当9a=时，方程为2219yx+=，表示焦点在y轴的椭圆，其中13a=，1c==，故离心率113cea==；当9a=-时，方程为2219yx-=，表示焦点在x轴的双曲线，其中21a=，2c==，故离心率22cea==,故选择A.【一隅三反】1．（2020·江苏南京）在平面直角坐标系xOy 中，若点P (0)到双曲线C ：22219x y a -=的一条渐近线的距离为6，则双曲线C 的离心率为（ ）A ．2B ．4C D【答案】A【解析】双曲线C ：22219x y a -=的一条渐近线为30x ay -=6=，解得a =2c e a ===.故选：A. 2．（2020·贵州省思南中学高二期末（理））已知1F 、2F 为双曲线C ：22221x y a b-=(0,0)a b >>的左、右焦点，点P 为双曲线C 右支上一点，212||||PF F F =，1230PF F ∠=，则双曲线C 的离心率为（ ）A B 1C D 1【答案】C【解析】根据题意作图如下：设1222F F PF c ==.∵1230PF F ∠=∴1PF =∵由双曲线焦半径公式知1P PF ex a =+=，22P PF ex a c =-=∴22a c =-∴12c e a ===故选C. 3．（2020·全国）已知1F ，2F 为双曲线22122:1x y C a b-=的焦点，P 为222x y c +=与双由线1C 的交点，且有121tan 4PF F ∠=，则该双曲线的离心率为（ ）A B ．2C D【答案】C【解析】由题意知1290F PF ∠=︒， 在12Rt F PF 中，121tan 4PF F ∠=，可设2PF m =，则14PF m =，由勾股定理得，122F F c ==，又由122PF PF a -=得23a m =，所以3c e a ==. 故选：C4．（2020·沙坪坝.重庆八中高二月考）若双曲线22221x y a b-=（0a >，0b >）的一条渐近线经过点(1,2)-，则该双曲线的离心率为（ ）A B C D ．2【答案】C 【解析】双曲线22221(0,0)x y a b a b-=>>的一条渐近线经过点(1,2)-，∴点(1,2)-在直线by x a=-上， ∴2ba=．则该双曲线的离心率为e ==故选：C ．考点二 直线与双曲线的位置关系【例2】已知双曲线x 2－y 24＝1，问当直线l 的斜率k 为何值时，过点P (1,1)的直线l 与双曲线只有一个公共点．【答案】见解析【解析】①当直线l 的斜率不存在时，直线l ：x ＝1与双曲线相切，符合题意． ②当直线l 的斜率存在时，设直线l 的方程为y ＝k (x －1)＋1， 代入双曲线方程，得(4－k 2)x 2－(2k －2k 2)x －k 2＋2k －5＝0.当4－k 2＝0，即k ＝±2时，直线l 与双曲线的渐近线平行，直线l 与双曲线只有一个公共点．当4－k 2≠0时，令Δ＝0，得k ＝52.综上可知，当k ＝52或k ＝±2或直线l 的斜率不存在时，过点P 的直线l 与双曲线都只有一个公共点．【一隅三反】1．（2018·福建高二期末（理））若直线y kx 2=+与双曲线22x y 6-=的右支交于不同的两点，则k 的取值范围是( )A ．⎛ ⎝⎭B ．⎛ ⎝⎭C ．⎛⎫ ⎪⎝⎭D ．1⎛⎫- ⎪ ⎪⎝⎭【答案】D【解析】把y ＝kx ＋2代入x 2－y 2＝6，得x 2－(kx ＋2)2＝6，化简得(1－k 2)x 2－4kx －10＝0，由题意知2121210000k x x x x ⎧-≠⎪∆>⎪⎪+>⎨⎪⋅>⎪⎪⎩，，，即()22221640104011001k k k k k ⎧+->⎪⎪⎪>⎨-⎪-⎪>⎪-⎩，，，解得3-＜k ＜－1. 答案：D.2．（2020·天水市第一中学高二月考（理））直线l ：1y kx =+与双曲线C ：222x y -=的右支交于不同的两点，则斜率k 的取值范围是（） A．( B ．(11)-， C．(1)- D．(1)(1-⋃ 【答案】C【解析】由2221x y y kx ⎧-=⎨=+⎩ 可得，()221230k x kx ---= ，因为直线:1l y kx =+与双曲线22:2C x y -=交于不同的两点，所以， ()222241210201301k k k k k ⎧+->⎪⎪⎪>⎨-⎪-⎪>⎪-⎩解得12k -<<- ，所以斜率k的取值范围是12⎛⎫-- ⎪ ⎪⎝⎭，故选C. 3．（2020·四川资阳）直线l ：kx －y －2k ＝0与双曲线x 2－y 2＝2仅有一个公共点，则实数k 的值为 A ．－1或1 B ．－1 C ．1 D ．1，－1，0【答案】A【解析】因为直线l ：kx －y －2k ＝0过定点(2,0),而直线l ：kx －y －2k ＝0与双曲线x 2－y 2＝2仅有一个公共点，所以直线l ：kx －y －2k ＝0与双曲线渐近线平行，即实数k 的值为－1或1，选A .4．（2020·宁波市北仑中学高一期中）过双曲线2x 2－y 2＝2的右焦点作直线l 交双曲线于A ，B 两点，若|AB |＝4，则这样的直线l 的条数为( ) A ．1 B ．2 C ．3 D ．4 【答案】C【解析】设11(,)A x y ，22(,)B x y当直线l 与x 轴垂直时，AB 4=，满足题意当直线l 与x 轴不垂直时，设直线l：(y k x =-，联立直线与双曲线方程得：(2222y k x x y ⎧=⎪⎨-=⎪⎩，整理得：2222(2)320k xx k -+--=，所以2122322k x x k +=-，12x x +=，又AB =4=，解得：2k =±， 综上：满足这样的直线l 的条数为3条考点三 弦长【例3】（2019·全国高三课时练习）过双曲线22136x y -=的右焦点F 2，倾斜角为30°的直线交双曲线于A ，B 两点，O 为坐标原点，F 1为左焦点． (1)求|AB |；(2)求△AOB 的面积． 【答案】（1（2【解析】(1)由双曲线的方程得a b ==3c ==，F 1(－3，0)，F 2(3，0)．直线AB的方程为3)y x =-． 设A (x 1，y 1)，B (x 2，y 2)，由223)3136y x x y ⎧=-⎪⎪⎨⎪-=⎪⎩消去y 得5x 2＋6x －27＝0. ∴1265x x +=-，12275x x ⋅=-. ∴AB ===(2)直线AB30y--=.∴原点O到直线AB的距离为32d==.∴113||222 AOBS AB d=⋅==【一隅三反】1．（2020·全国）已知直线y＝kx＋1与双曲线2214yx-=交于A，B两点，且|AB|＝，则实数k的值为() A．±7B．±3或±413C．D．±3【答案】B【解析】由直线与双曲线交于,A B两点，得2k≠±，将1y kx=+代入2214yx-=得22(4)250k x kx---=，则2244(4)50k k∆=+-⨯>，即25k<.设11(,)A x y，22(,)B x y，则12224kx xk+=-，12254x xk=--.∴AB==∴k=3k=±.故选B.2．（2018·全国高二课时练习）求双曲线2214yx-=被直线1y x=+截得的弦长.【解析】由22141yxy x⎧-=⎪⎨⎪=+⎩，得()224140x x-+-=，即23250x x--=．（*）设方程（*）的解为1x，2x，则有122 3x x+=，125 3x x=-，故12d x=-===．3．（2020·邢台市第八中学高二期末）已知双曲线C：22221(0,0)x ya ba b-=>>是双曲线的一个顶点．(1)求双曲线的方程；(2)经过双曲线右焦点F2作倾斜角为30°的直线，直线与双曲线交于不同的两点A，B，求AB.【答案】(1)22136x y-=；(2)5【解析】(1)因为双曲线C：22221(0,0) x ya ba b-=>>是双曲线的一个顶点，所以caa⎧=⎪⎨⎪=⎩解得3,c b==22136x y-=(2)双曲线22136x y-=的右焦点为2(3,0)F所以经过双曲线右焦点F2且倾斜角为30°的直线的方程为3)y x=-．联立)2213633x yy x⎧-=⎪⎪⎨⎪=-⎪⎩得256270x x+-=.设()()1122,,,A x yB x y，则1212627,55x x x x+=-=-.所以5AB==.4．（2020·宾县第二中学高二期末（文））已知曲线22:1C x y-=及直线:1l y kx=-．（1）若l与C左支交于两个不同的交点，求实数k的取值范围；（2）若l与C交于A B、两点，O是坐标原点，且AOB∆，求实数k的值．【答案】（1）()1-；（2）0k =或2k =±【解析】（1）由2211x y y kx ⎧-=⎨=-⎩消去y ，得()221220k x kx -+-=．∵l 与C 左支交于两个不同的交点∴()222104810k k k ⎧-≠⎪⎨∆=+->⎪⎩且121222220,011k x x x x k k +=-=--- ∴k的取值范围为()1-（2）设()()1122,,A x y B x y 、，由（1）得12122222,11k x x x x k k+=-=---． 又l 过点()0,1D -，∴1212OAB S x x ∆=-= ∴()(2212x x -=，即22228811k k k⎛⎫-+= ⎪--⎝⎭． ∴0k =或k =考点四 点差法【例4】（1）（2020·黑龙江南岗）已知双曲线C ：()222210,0x y a b a b-=>>，斜率为2的直线与双曲线C 相交于点A 、B ，且弦AB 中点坐标为()1,1，则双曲线C 的离心率为（ ） A ．2BCD ．3（2）（2020·河南南阳.高二其他（文））直线l 经过()4,2P 且与双曲线2212x y -=交于M ，N 两点，如果点P 是线段MN 的中点，那么直线l 的方程为（ ） A ．20x y --= B ．60x y +-= C ．2320x y --=D ．不存在（3）（2019·黑龙江大庆四中高二月考（理））已知双曲线2212x y -=与不过原点O 且不平行于坐标轴的直线l 相交于,M N 两点，线段MN 的中点为P ，设直线l 的斜率为1k ，直线OP 的斜率为2k ，则12k k = A ．12B ．12-C ．2D ．2-【答案】（1）B （2）A （3）A【解析】（1）设11(,)A x y 、22(,)B x y ，则2211221x y a b -=，2222221x y a b -=，所以2222121222x x y y a b--=，所以2121221212y y x x b x x a y x -+=⨯-+， 又弦AB 中点坐标为()1,1，所以122x x +=，122y y +=，又12122y y x x --=，所以22222b a =⨯，即222b a =，所以双曲线的离心率c e a ====== 故选：B.（2）当斜率不存在时，显然不符合题意； 当斜率存在时，设()11,M x y ，()22,N x y ，因为点P 是线段MN 的中点，所以128x x +=，124y y +=，代入双曲线方程得221122221212x y x y ⎧-=⎪⎪⎨⎪-=⎪⎩，两式相减得()222212122x x y y -=-，则()1212121212y y x x k x x y y -+===-+，又直线过点P ，所以直线方程为2y x =-，联立22122x y y x ⎧-=⎪⎨⎪=-⎩，得到28100x x -+=，经检验>0∆，方程有解，所以直线2y x =-满足题意.故选：A（3）设直线l 的方程为1y k x b =+，代入双曲线方程2212x y -=得到2221112102k x bk x b ⎛⎫----= ⎪⎝⎭，得到11221212k bx x k +=-设()()111212,,,M x k x b N x k x b ++，则()11212,22k x x x x N b ⎛⎫+++ ⎪⎝⎭则21121212b k k x x k =+=+，故1212k k ⋅=，故选A ．【一隅三反】1．（2020·青海西宁）已知倾斜角为π4的直线与双曲线C ：22221x y a b -=（0a >，0b >）相交于A ，B 两点，(4,2)M 是弦AB 的中点，则双曲线的离心率为（ ）ABC ．32D．2【答案】D【解析】因为倾斜角为π4的直线与双曲线C ：22221x y a b-=（0a >，0b >）相交于A ，B 两点，所以直线的斜率tan14πk ==， 设()()1122,,,A x y B x y ，则2211221x y a b-=① 2222221x y a b-=② 由①-②得()()()()1212121222x x x x y y y y a b -+-+=则2121221212y y b x x k x x a y y -+==⋅-+ 因为(4,2)M 是弦AB 的中点，12128,4x x y y ∴+=+=因为直线的斜率为122814b a ∴=⋅即222211,22b b a a == 所以2222112c a b a ⎛⎫=+=+⎪⎝⎭232e ∴=，则e =， 故选：D2．（2020·湖北武汉）已知,A B 分别为双曲线22:13y x Γ-=实轴的左右两个端点，过双曲线Γ的左焦点F作直线PQ 交双曲线于,P Q 两点（点,P Q 异于,A B ），则直线,AP BQ 的斜率之比:AP BQ k k =（ ） A ．13- B ．3- C ．23-D ．32-【答案】B【解析】由已知得双曲线:1a Γ=，b =2c =．故(2,0)F -，(1,0)A -，(1,0)B ．设直线:2PQ x my =-，且1(P x ，1)y ，2(Q x ，2)y ．由22213x my y x =-⎧⎪⎨-=⎪⎩消去x 整理得22(31)1290m y my --+=，∴121222129,3131m y y y y m m +==--，两式相比得121234y y m y y +=⨯①， 121212112211221(3)3:1(1)AP BQ y x y my my y y k k x y y my my y y ---∴=⨯==+--②， 将①代入②得：上式12121121223()33(3)4333()4y y y y y y y y y y +--===--+-． 故:3AP BQ k k =-． 故选：B ．3．（2019·会泽县第一中学校高二月考（理））点(81)P ，平分双曲线2244x y -= 的一条弦，则这条弦所在直线的方程是__________． 【答案】2150x y --=【解析】设弦的两端点分别为1122Ax y B x y （，），（，），AB 的中点是121281162P x x y y ∴+=+=（，），，， 把1122A x y B x y （，），（，）代入双曲线2244x y ，-= 得22112222 4444x y x y ⎧-⎨-⎩＝＝ ， ∴121212121212401680x x x x y y y y x x y y +---+=∴---=（）（）（）（），（）（），12122y y k x x -∴==-，∴这条弦所在的直线方程是2150x y ．--= 故答案为2150x y ．--=．。

云南省曲靖市2019-2020学年中考第一次质量检测数学试题一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB．添加一个条件，不能使四边形DBCE成为矩形的是（）A．AB=BE B．BE⊥DC C．∠ADB=90°D．CE⊥DE2．如图，AB∥CD，那么（）A．∠BAD与∠B互补B．∠1=∠2 C．∠BAD与∠D互补 D．∠BCD与∠D互补3．甲、乙两人同时分别从A，B两地沿同一条公路骑自行车到C地．已知A，C两地间的距离为110千米，B，C两地间的距离为100千米．甲骑自行车的平均速度比乙快2千米/时．结果两人同时到达C地．求两人的平均速度，为解决此问题，设乙骑自行车的平均速度为x千米/时．由题意列出方程．其中正确的是（）A．1101002x x=+B．1101002x x=+C．1101002x x=-D．1101002x x=-4．下列说法中，正确的个数共有（）（1）一个三角形只有一个外接圆；（2）圆既是轴对称图形，又是中心对称图形；（3）在同圆中，相等的圆心角所对的弧相等；（4）三角形的内心到该三角形三个顶点距离相等；A．1个B．2个C．3个D．4个5．方程5x＋2y＝－9与下列方程构成的方程组的解为212xy=-⎧⎪⎨=⎪⎩的是()A．x＋2y＝1 B．3x＋2y＝－8 C．5x＋4y＝－3 D．3x－4y＝－86．如图由四个相同的小立方体组成的立体图像，它的主视图是（）．A．B．C．D．7．如图，一次函数y1＝x与二次函数y2＝ax2＋bx＋c图象相交于P、Q两点，则函数y＝ax2＋（b－1）x ＋c的图象可能是（）A． B．C．D．8．下列计算错误的是（）A．4x3•2x2=8x5B．a4﹣a3=aC．（﹣x2）5=﹣x10D．（a﹣b）2=a2﹣2ab+b29．如图，已知直线l1：y=﹣2x+4与直线l2：y=kx+b（k≠0）在第一象限交于点M．若直线l2与x轴的交点为A（﹣2，0），则k的取值范围是（）A．﹣2＜k＜2 B．﹣2＜k＜0 C．0＜k＜4 D．0＜k＜210．实数4的倒数是（）A．4 B．14C．﹣4 D．﹣1411．如图，在平面直角坐标系中，线段AB的端点坐标为A（-2,4），B（4,2），直线y=kx-2与线段AB有交点，则K 的值不可能是（ ）A ．-5B ．-2C ．3D ．512．以x 为自变量的二次函数y=x 2﹣2(b ﹣2)x+b 2﹣1的图象不经过第三象限，则实数b 的取值范围是（ ）A ．b≥1.25B ．b≥1或b≤﹣1C ．b≥2D ．1≤b≤2二、填空题：（本大题共6个小题，每小题4分，共24分．）13．如图，在平面直角坐标系中，⊙P 的圆心在x 轴上，且经过点A （m ，﹣3）和点B （﹣1，n ），点C 是第一象限圆上的任意一点，且∠ACB=45°，则⊙P 的圆心的坐标是_____．14．2018年1月4日在萍乡市第十五届人民代表大会第三次会议报告指出，去年我市城镇居民人均可支配收入33080元，33080用科学记数法可表示为__．15．如图，菱形OABC 的顶点O 是原点，顶点B 在y 轴上，菱形的两条对角线的长分别是6和4，反比例函数()y x 0xk =<的图象经过点C ，则k 的值为 ．16．我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题：“一百馒头一百僧，大僧三个更无争，小僧三人分一个，大小和尚各几丁？”意思是：有100个和尚分100个馒头，如果大和尚一人分3个，小和尚3人分1个，正好分完，试问大、小和尚各几人？设大、小和尚各有，人，则可以列方程组__________.17．在直径为的圆柱形油槽内装入一些油后，截面如图所示如果油面宽，那么油的最大深度是_________．18．因式分解：a 3b ﹣ab 3=_____．三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（6分）如图，大楼底右侧有一障碍物，在障碍物的旁边有一幢小楼DE ，在小楼的顶端D 处测得障碍物边缘点C 的俯角为30°，测得大楼顶端A 的仰角为45°（点B ，C ，E 在同一水平直线上）．已知AB ＝80m ，DE ＝10m ，求障碍物B ，C 两点间的距离．（结果保留根号）20．（6分）如图，已知AB AD =，AC AE =，BAD CAE ∠=∠．求证：BC DE =．21．（6分）“赏中华诗词，寻文化基因，品生活之美”，某校举办了首届“中国诗词大会”，经选拔后有50名学生参加决赛，这50名学生同时默写50首古诗词，若每正确默写出一首古诗词得2分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：请结合图表完成下列各题：（1）①表中a 的值为 ，中位数在第 组；②频数分布直方图补充完整；（2）若测试成绩不低于80分为优秀，则本次测试的优秀率是多少？（3）第5组10名同学中，有4名男同学，现将这10名同学平均分成两组进行对抗练习，且4名男同学每组分两人，求小明与小强两名男同学能分在同一组的概率． 组别成绩x 分 频数（人数） 第1组 50≤x ＜60 6第2组60≤x ＜70 8 第3组70≤x ＜80 14 第4组80≤x ＜90 a 第5组 90≤x ＜100 1022．（8分）在矩形纸片ABCD 中，AB=6，BC=8，现将纸片折叠，使点D 与点B 重合，折痕为EF ，连接DF ．（1）说明△BEF 是等腰三角形；（2）求折痕EF 的长．23．（8分）在平面直角坐标系中，一次函数y ax b =+（a≠0）的图象与反比例函数(0)k y k x=≠的图象交于第二、第四象限内的A 、B 两点，与y 轴交于点C ，过点A 作AH ⊥y 轴，垂足为点H ，OH=3，tan ∠AOH=43，点B 的坐标为（m ，-2）.求该反比例函数和一次函数的解析式；求△AHO 的周长.24．（10分）如图，小巷左石两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC 为0.7米，梯子顶端到地面的距离AC 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A′D 为1.5米，求小巷有多宽．25．（10分）如图，△ABC 三个顶点的坐标分别为A （1，1），B （4，2），C （3，4）. 请画出△ABC 向左平移5个单位长度后得到的△A B C ；请画出△ABC 关于原点对称的△A B C ； 在轴上求作一点P ，使△PAB 的周长最小，请画出△PAB ，并直接写出P 的坐标.26．（12分）已知二次函数2y x bx c =-++的图象如图6所示，它与x 轴的一个交点坐标为(10)-，，与y 轴的交点坐标为（0，3）．求出此二次函数的解析式；根据图象，写出函数值y 为正数时，自变量x 的取值范围．27．（12分）计算：﹣14﹣2×（﹣3）2+327-÷（﹣13）如图，小林将矩形纸片ABCD 沿折痕EF 翻折，使点C 、D 分别落在点M 、N 的位置，发现∠EFM=2∠BFM ，求∠EFC 的度数．参考答案一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1．B【解析】【分析】先证明四边形DBCE为平行四边形，再根据矩形的判定进行解答．【详解】∵四边形ABCD为平行四边形，∴AD∥BC，AD=BC，又∵AD=DE，∴DE∥BC，且DE=BC，∴四边形BCED为平行四边形，A、∵AB=BE，DE=AD，∴BD⊥AE，∴▱DBCE为矩形，故本选项错误；B、∵对角线互相垂直的平行四边形为菱形，不一定为矩形，故本选项正确；C、∵∠ADB=90°，∴∠EDB=90°，∴▱DBCE为矩形，故本选项错误；D、∵CE⊥DE，∴∠CED=90°，∴▱DBCE为矩形，故本选项错误,故选B．【点睛】本题考查了平行四边形的性质与判定，矩形的判定等，熟练掌握相关的判定定理与性质定理是解题的关键. 2．C【解析】【分析】分清截线和被截线，根据平行线的性质进行解答即可．【详解】解：∵AB∥CD，∴∠BAD与∠D互补，即C选项符合题意；当AD∥BC时，∠BAD与∠B互补，∠1=∠2，∠BCD与∠D互补，故选项A、B、D都不合题意，故选：C．【点睛】本题考查了平行线的性质，熟记性质并准确识图是解题的关键．3．A【解析】设乙骑自行车的平均速度为x千米/时，则甲骑自行车的平均速度为（x+2）千米/时，根据题意可得等量关系：甲骑110千米所用时间=乙骑100千米所用时间，根据等量关系可列出方程即可．解：设乙骑自行车的平均速度为x千米/时，由题意得：1102 x =100x，故选A．4．C【解析】【分析】根据外接圆的性质，圆的对称性，三角形的内心以及圆周角定理即可解出．【详解】（1）一个三角形只有一个外接圆，正确；（2）圆既是轴对称图形，又是中心对称图形，正确；（3）在同圆中，相等的圆心角所对的弧相等，正确；（4）三角形的内心是三个内角平分线的交点，到三边的距离相等，错误；故选：C．【点睛】此题考查了外接圆的性质，三角形的内心及轴对称和中心对称的概念，要求学生对这些概念熟练掌握．5．D【解析】试题分析：将x与y的值代入各项检验即可得到结果．解：方程5x+2y=﹣9与下列方程构成的方程组的解为的是3x﹣4y=﹣1．故选D．点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．6．D【解析】从正面看，共2列，左边是1个正方形，右边是2个正方形，且下齐．故选D.7．A【解析】【分析】由一次函数y 1=x 与二次函数y 2=ax 2+bx+c 图象相交于P 、Q 两点，得出方程ax 2+（b-1）x+c=0有两个不相等的根，进而得出函数y=ax 2+（b-1）x+c 与x 轴有两个交点，根据方程根与系数的关系得出函数y=ax 2+（b-1）x+c 的对称轴x=-12b a-＞0，即可进行判断． 【详解】点P 在抛物线上，设点P （x ，ax 2+bx+c ），又因点P 在直线y=x 上，∴x=ax 2+bx+c ，∴ax 2+（b-1）x+c=0；由图象可知一次函数y=x 与二次函数y=ax 2+bx+c 交于第一象限的P 、Q 两点，∴方程ax 2+（b-1）x+c=0有两个正实数根．∴函数y=ax 2+（b-1）x+c 与x 轴有两个交点， 又∵-2b a＞0，a ＞0 ∴-12b a -=-2b a +12a ＞0 ∴函数y=ax 2+（b-1）x+c 的对称轴x=-12b a-＞0， ∴A 符合条件，故选A ．8．B【解析】【分析】根据单项式与单项式相乘，把他们的系数，相同字母分别相乘，对于只在一个单项式里含有的字母，则连同它的指数作为积的一个因式；合并同类项的法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变；幂的乘方法则：底数不变，指数相乘；完全平方公式：（a±b ）1=a 1±1ab+b 1．可巧记为：“首平方，末平方，首末两倍中间放”可得答案．【详解】A 选项：4x 3•1x 1=8x 5，故原题计算正确；B 选项：a 4和a 3不是同类项，不能合并，故原题计算错误；C 选项：（-x 1）5=-x 10，故原题计算正确；D 选项：（a-b ）1=a 1-1ab+b 1，故原题计算正确；故选：B ．【点睛】考查了整式的乘法，关键是掌握整式的乘法各计算法则．9．D【解析】【分析】【详解】解：∵直线l1与x轴的交点为A（﹣1，0），∴﹣1k+b=0，∴242y xy kx k=-+⎧⎨=+⎩，解得：42282kxkkyk-⎧=⎪⎪+⎨⎪=⎪+⎩．∵直线l1：y=﹣1x+4与直线l1：y=kx+b（k≠0）的交点在第一象限，∴42282kkkk-⎧>⎪⎪+⎨⎪>⎪+⎩，解得0＜k＜1．故选D．【点睛】两条直线相交或平行问题；一次函数图象上点的坐标特征．10．B【解析】【分析】根据互为倒数的两个数的乘积是1，求出实数4的倒数是多少即可．【详解】解：实数4的倒数是：1÷4=14．故选：B．【点睛】此题主要考查了一个数的倒数的求法，要熟练掌握，解答此题的关键是要明确：互为倒数的两个数的乘积是1．11．B【解析】【分析】当直线y=kx-2与线段AB的交点为A点时，把A（-2，4）代入y=kx-2，求出k=-3，根据一次函数的有关性质得到当k≤-3时直线y=kx-2与线段AB有交点；当直线y=kx-2与线段AB的交点为B点时，把B（4，2）代入y=kx-2，求出k=1，根据一次函数的有关性质得到当k≥1时直线y=kx-2与线段AB有交点，从而能得到正确选项．【详解】把A（-2，4）代入y=kx-2得，4=-2k-2，解得k=-3，∴当直线y=kx-2与线段AB有交点，且过第二、四象限时，k满足的条件为k≤-3；把B（4，2）代入y=kx-2得，4k-2=2，解得k=1，∴当直线y=kx-2与线段AB有交点，且过第一、三象限时，k满足的条件为k≥1．即k≤-3或k≥1．所以直线y=kx-2与线段AB有交点，则k的值不可能是-2．故选B．【点睛】本题考查了一次函数y=kx+b（k≠0）的性质：当k＞0时，图象必过第一、三象限，k越大直线越靠近y 轴；当k＜0时，图象必过第二、四象限，k越小直线越靠近y轴．12．A【解析】∵二次函数y＝x2－2(b－2)x＋b2－1的图象不经过第三象限，a＝1>0，∴Δ≤0或抛物线与x轴的交点的横坐标均大于等于0.当Δ≤0时，[－2(b－2)]2－4(b2－1)≤0，解得b≥.当抛物线与x轴的交点的横坐标均大于等于0时，设抛物线与x轴的交点的横坐标分别为x1，x2，则x1＋x2＝2(b－2)>0，Δ＝[－2(b－2)]2－4(b2－1)>0，无解，∴此种情况不存在．∴b≥.二、填空题：（本大题共6个小题，每小题4分，共24分．）13．（2，0）【解析】【分析】作辅助线，构建三角形全等，先根据同弧所对的圆心角是圆周角的二倍得：∠APB=90°，再证明△BPE≌△PAF，根据PE=AF=3，列式可得结论．【详解】连接PB、PA，过B作BE⊥x轴于E，过A作AF⊥x轴于F，∵A（m，﹣3）和点B（﹣1，n），∴OE=1，AF=3，∵∠ACB=45°，∴∠APB=90°，∴∠BPE+∠APF=90°，∵∠BPE+∠EBP=90°，∴∠APF=∠EBP，∵∠BEP=∠AFP=90°，PA=PB，∴△BPE≌△PAF，∴PE=AF=3，设P（a，0），∴a+1=3，a=2，∴P（2，0），故答案为（2，0）．【点睛】本题考查了圆周角定理和坐标与图形性质，三角形全等的性质和判定，作辅助线构建三角形全等是关键．14．3.308×1．【解析】【分析】正确用科学计数法表示即可.【详解】解：33080=3.308×1【点睛】科学记数法的表示形式为10na 的形式, 其中1<|a|<10,n为整数.确定n的值时, 要看把原数变成a时, 小数点移动了多少位, n的绝对值与小数点移动的位数相同. 当原数绝对值大于10时, n是正数; 当原数的绝对值小于1时,n是负数.15．－6【解析】【分析】分析：∵菱形的两条对角线的长分别是6和4，∴A （﹣3，2）.∵点A 在反比例函数()y x 0x k =<的图象上， ∴23k =-，解得k=－6. 【详解】请在此输入详解！16．【解析】【分析】根据100个和尚分100个馒头，正好分完．大和尚一人分3个，小和尚3人分一个得到等量关系为：大和尚的人数+小和尚的人数=100，大和尚分得的馒头数+小和尚分得的馒头数=100，依此列出方程组即可．【详解】设大和尚x 人，小和尚y 人，由题意可得． 故答案为．【点睛】本题考查了由实际问题抽象出二元一次方程组，关键以和尚数和馒头数作为等量关系列出方程组． 17．2m【解析】【分析】本题是已知圆的直径，弦长求油的最大深度其实就是弧AB 的中点到弦AB 的距离，可以转化为求弦心距的问题，利用垂径定理来解决．【详解】解：过点O 作OM ⊥AB 交AB 与M ，交弧AB 于点E ．连接OA ．在Rt △OAM 中：OA=5m ，AM=AB=4m ．根据勾股定理可得OM=3m ，则油的最大深度ME 为5-3=2m ．【点睛】圆中的有关半径，弦长，弦心距之间的计算一般是通过垂径定理转化为解直角三角形的问题． 18．ab （a+b ）（a ﹣b ）【解析】【分析】先提取公因式ab ，然后再利用平方差公式分解即可．【详解】a 3b ﹣ab 3=ab （a 2﹣b 2）=ab （a+b ）（a ﹣b ），故答案为ab （a+b ）（a ﹣b ）.【点睛】本题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．分解因式的步骤一般为：一提（公因式），二套（公式），三彻底.三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．19．（70﹣103）m ．【解析】【分析】过点D 作DF ⊥AB 于点F ，过点C 作CH ⊥DF 于点H.通过解Rt ADF V 得到DF 的长度；通过解Rt CDE△得到CE 的长度，则BC BE CE =-．【详解】如图，过点D 作DF ⊥AB 于点F ，过点C 作CH ⊥DF 于点H.则DE=BF=CH=10m ，在Rt ADF V 中,∵AF=80m−10m=70m,45ADF ∠=o ，∴DF=AF=70m.在Rt CDE △中,∵DE=10m,30DCE ∠=o ，∴)tan30DE CE m ===o ，∴(70.BC BE CE m =-=-答：障碍物B ，C两点间的距离为(70.m -20．证明见解析．【解析】【分析】根据等式的基本性质可得BAC DAE ∠=∠，然后利用SAS 即可证出ABC ADE ∆≅∆，从而证出结论．【详解】证明：BAD CAE ∠=∠Q ，BAD DAC CAE DAC ∴∠+∠=∠+∠，即BAC DAE ∠=∠，在ABC ∆和ADE ∆中，AB AD BAC DAE AC AE =⎧⎪∠=∠⎨⎪=⎩，()ABC ADE SAS ∴∆≅∆，BC DE ∴=．【点睛】此题考查的是全等三角形的判定及性质，掌握利用SAS 判定两个三角形全等和全等三角形的对应边相等是解决此题的关键．21．（1）①12，3. ②详见解析.（2）13. 【解析】分析：（1）①根据题意和表中的数据可以求得a 的值；②由表格中的数据可以将频数分布表补充完整； （2）根据表格中的数据和测试成绩不低于80分为优秀，可以求得优秀率；（3）根据题意可以求得所有的可能性，从而可以得到小明与小强两名男同学能分在同一组的概率． 详解：（1）①a=50﹣（6+8+14+10）=12，中位数为第25、26个数的平均数，而第25、26个数均落在第3组内，所以中位数落在第3组，故答案为12，3；②如图，（2）121050×100%=44%，答：本次测试的优秀率是44%；（3）设小明和小强分别为A、B，另外两名学生为：C、D，则所有的可能性为：（AB﹣CD）、（AC﹣BD）、（AD﹣BC）.所以小明和小强分在一起的概率为：13．点睛：本题考查列举法求概率、频数分布表、频数分布直方图、中位数，解题的关键是明确题意，找出所求问题需要的条件，可以将所有的可能性都写出来，求出相应的概率．22．（1）见解析；（2）15 2.【解析】【分析】（1）根据折叠得出∠DEF=∠BEF，根据矩形的性质得出AD∥BC，求出∠DEF=∠BFE，求出∠BEF=∠BFE即可；（2）过E作EM⊥BC于M，则四边形ABME是矩形，根据矩形的性质得出EM=AB=6，AE=BM，根据折叠得出DE=BE，根据勾股定理求出DE、在Rt△EMF中，由勾股定理求出即可．【详解】（1）∵现将纸片折叠，使点D与点B重合，折痕为EF，∴∠DEF=∠BEF．∵四边形ABCD是矩形，∴AD∥BC，∴∠DEF=∠BFE，∴∠BEF=∠BFE，∴BE=BF，即△BEF是等腰三角形；（2）过E作EM⊥BC于M，则四边形ABME是矩形，所以EM=AB=6，AE=BM．∵现将纸片折叠，使点D与点B重合，折痕为EF，∴DE=BE，DO=BO，BD⊥EF．∵四边形ABCD是矩形，BC=8，∴AD=BC=8，∠BAD=90°．在Rt△ABE中，AE2+AB2=BE2，即（8﹣BE）2+62=BE2，解得：BE=254=DE=BF，AE=8﹣DE=8﹣254=74=BM ，∴FM=254﹣74=92． 在Rt △EMF 中，由勾股定理得：EF=22962（）+=152． 故答案为152．【点睛】本题考查了折叠的性质和矩形性质、勾股定理等知识点，能熟记折叠的性质是解答此题的关键． 23．（1）一次函数为112y x =-+，反比例函数为12y x =-；（2）△AHO 的周长为12 【解析】分析：（1）根据正切函数可得AH=4，根据反比例函数的特点k=xy 为定值，列出方程，求出k 的值，便可求出反比例函数的解析式；根据k 的值求出B 两点的坐标，用待定系数法便可求出一次函数的解析式． （2）由（1）知AH 的长，根据勾股定理，可得AO 的长，根据三角形的周长，可得答案.详解：（1）∵tan ∠AOH=AH OH =43 ∴AH=43OH=4 ∴A （-4，3），代入k y x =，得 k=-4×3=-12∴反比例函数为12y x =-∴122m -=-∴m=6∴B （6，-2）∴4362a b a b -+=⎧⎨+=-⎩ ∴a =12-，b=1 ∴一次函数为112y x =-+ （2）2222345OA AH OH =+=+=△AHO的周长为：3+4+5=12点睛：此题考查的是反比例函数图象上点的坐标特点及用待定系数法求一次函数及反比例函数的解析式．24．2.7米．【解析】【分析】先根据勾股定理求出AB的长，同理可得出BD的长，进而可得出结论．【详解】在Rt△ACB中，∵∠ACB＝90°，BC＝0.7米，AC＝2.2米，∴AB2＝0.72+2.22＝6.1．在Rt△A′BD中，∵∠A′DB＝90°，A′D＝1.5米，BD2+A′D2＝A′B′2，∴BD2+1.52＝6.1，∴BD2＝2．∵BD＞0，∴BD＝2米．∴CD＝BC+BD＝0.7+2＝2.7米．答：小巷的宽度CD为2.7米．【点睛】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．25．（1）图形见解析；（2）图形见解析；（3）图形见解析，点P的坐标为：（2，0）【解析】【分析】(1)按题目的要求平移就可以了关于原点对称的点的坐标变化是:横、纵坐标都变为相反数，找到对应点后按顺序连接即可(3)AB的长是不变的，要使△PAB的周长最小，即要求PA+PB最小，转为了已知直线与直线一侧的两点，在直线上找一个点，使这点到已知两点的线段之和最小，方法是作A、B两点中的某点关于该直线的对称点，然后连接对称点与另一点．【详解】（1）△A 1B 1C 1如图所示；（2）△A 2B 2C 2如图所示；（3）△PAB 如图所示，点P 的坐标为：（2，0）【点睛】1、图形的平移；2、中心对称；3、轴对称的应用26．（1）2x 2x 3y -++=；（2）1x 3-<<.【解析】【分析】（1）将（-1，0）和（0，3）两点代入二次函数y=-x 2+bx+c ，求得b 和c ；从而得出抛物线的解析式； （2）令y=0，解得x 1，x 2，得出此二次函数的图象与x 轴的另一个交点的坐标，进而求出当函数值y>0时，自变量x 的取值范围．【详解】解：（1）由二次函数2y x bx c =-++的图象经过()1,0-和()0,3两点， 得103b c c --+=⎧⎨=⎩， 解这个方程组，得23b c =⎧⎨=⎩， 抛物线的解析式为2x 2x 3y -++=，（2）令y 0=，得2x 2x 30-++=．解这个方程，得1x 3=，2x 1=-．∴此二次函数的图象与x 轴的另一个交点的坐标为()3,0．当1x 3-<<时，y 0>．【点睛】本题考查的知识点是二次函数的三种形式及待定系数法求二次函数解析式及抛物线与坐标轴的交点，解题的关键是熟练的掌握二次函数的三种形式及待定系数法求二次函数解析式及抛物线与坐标轴的交点. 27．（1）﹣10；（2）∠EFC=72°．【解析】【分析】(1)原式利用乘方的意义，立方根定义，乘除法则及家减法法则计算即可;(2)根据折叠的性质得到一对角相等,再由已知角的关系求出结果即可.【详解】（1）原式=﹣1﹣18+9=﹣10；（2）由折叠得：∠EFM=∠EFC ，∵∠EFM=2∠BFM ，∴设∠EFM=∠EFC=x ，则有∠BFM=12x ， ∵∠MFB+∠MFE+∠EFC=180°，∴x+x+12x=180°， 解得：x=72°，则∠EFC=72°．【点睛】本题考查了实数的性质及平行线的性质，解题的关键是熟练掌握实数的运算法则及平行线的性质.。

会泽一中2019年春季学期半月考试卷2高二数学（理科）一、 选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）1. 已知集合A={})1(log |2-=x y x ，B={}2|<x x ，则A∩B=（ ） A.{}20|<<x x B.{}21|<<x x C.{}21|<≤x x D.R2. 椭圆24x +212y =1的焦点坐标为（ ）A.）（0,2± B.）（0,22± C.）（22,0± D.）（32,0± 3. 已知实数y x ,满足⎪⎩⎪⎨⎧≥≤+≤-1521x y x y x ，则函数y x z 3+=的最大值为（ ）A.10B.8C.5D.14. 已知双曲线的离心率为2，焦点是（-4,0），（4,0），则双曲线的方程是（ ）A.141222=-y x B.161022=-y x C.112422=-y x D.110622=-y x 5. 在各项都为正数的等比数列{}n a 中，首项31=a ，前三项和为21，则543a a a ++=（ ） A.33 B.72 C.84 D.189 6. 设向量)3,1(),1,1(+=-=x b x a ，则“2=x ”是“b a //”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 7. 某几何体的三视图如图所示，则它的表面积为（ ） A ．1+52+2π B ．1+252+2π C ．()2+1+5π D ．2+52+2π 8. 有四个关于三角函数的命题：1p ：∃x ∈R, 2sin 2x +2cos 2x =12 2p : ∃x 、y ∈R, sin(x-y)=sinx-siny3p : ∀x ∈[]0,π 4p : sinx=cosy ⇒x+y=2π其中假命题的是（ ）A.1p ，4pB.2p ，4pC.1p ，3pD.2p ，4p9. 已知n m ，为两条不同的直线，βα，为两个不同的平面，则下列命题中正确的是（ ） A.βαβα⊥⇒⊂⊥m m , B.n m n m ⊥⇒⊂⊂⊥βαβα,, C.αα⊥⇒⊥m n m n ,// D.βαββαα////,//,,⇒⊂⊂n m n m10. 已知向量,32==，且与+夹角的余弦值为31，则=⋅（ ）A.-2B.32-C.9462--或 D.4 11. 已知定义在R 上的函数)(x f 满足)()(x f x f =-，且当0<x 时，13)(+=xx f ，若342=a ，524=b ，3125=c ，则有（ ）A.)()()(c f b f a f <<B.)()()(a f c f b f <<C.()()()c f a f b f <<D.)()()(b f a f c f <<12. 已知直线l 与双曲线C 交于A ，B 两点(A ，B 在同一支上),21,F F 为双曲线的两个焦点,则21,F F 在（ ）A ．以A ，B 为焦点的椭圆上或线段AB 的垂直平分线上 B ．以A ，B 为焦点的双曲线上或线段AB 的垂直平分线上C ．以AB 为直径的圆上或线段AB 的垂直平分线上D ．以上说法均不正确二、填空题（本大题共4个小题，每小题5分，共20分）13. 在621⎪⎭⎫⎝⎛+x x 的展开式中常数项是________________．（用数字作答）14．已知抛物线C 的顶点坐标为原点，焦点在x 轴上，直线y=x 与抛物线C 交于A ，B 两点，若(2,2)P 为AB 的中点，则抛物线C 的方程为________________．15．等比数列{}n a 的公比0q >， 已知2a =1，216n n n a a a +++=，则{n a }的前4项和4S =_____________．16．已知数列{}n a 中,11=a ,2n n a n a =-,112+=+n n a a ,则+++321a a a ……100a += . 三、解答题（本大题共6个小题，17题10分，其余12分，共70分） 17.（本小题满分10分）在ΔABC 中，角A 、B 、C 的对边分别为c b a ,,，且满足A c C a cos 4sin 3=，3=⋅AC AB （1）求ΔABC 的面积S ； （2）若1=c ，求a 的值.18.（本小题满分12分）如图，在三棱锥P ABC -中，△P AB 是等边三角形，∠P AC =∠PBC = 90º． （1）证明：AB ⊥ PC ；（2）若4PC =，且平面PAC ⊥平面PBC ，求三棱锥P ABC -体积．19.（本小题满分12分）某工厂有工人1000名，其中250名工人参加过短期培训（称为A 类工人），另外750名工人参加过长期培训（称为B 类工人）.现用分层抽样方法（按A 类，B 类分二层）从该工厂的工人中共抽查100名工人，调查他们的生产能力（生产能力指一天加工的零件数）．（1）A 类工人中和B 类工人各抽查多少工人？（2）从A 类工人中抽查结果和从B 类工人中的抽查结果分别如下表1和表2．表1： 生产能力分组 [)100,110[)110,120[)120,130[)130,140[)140,150人数 48x53表2： 生产能力分组[)110,120[)120,130[)130,140[)140,150人数6y3618（i ）先确定,x y ，再在答题卡上完成下列频率分布直方图．就生产能力而言，A 类工人中个体间的差异程度与B 类工人中个体间的差异程度哪个更小？（不用计算，可通过观察直方图直接回答结论）（ii ）分别估计A 类工人和B 类工人生产能力的平均数，并估计该工厂工人和生产能力的平均数（同一组中的数据用该区间的中点值作代表，精确到0.1）．20.（本小题满分12分）为了响应教育部颁布的《关于推进中小学生研学旅行的意见》,某校计划开设八门研学旅行课程，并对全校学生的选课意向进行调查(调查要求全员参与，每个学生必须从八门课程中选出唯一一门课程).本次调查结果整理成条形图如下.上图中，已知课程,,,,A B C D E 为人文类课程，课程,,F G H 为自然科学类课程.为进一步研究学生选课意向，结合上面图表，采取分层抽样方法从全校抽取1%的学生作为研究样本组(以下简称“组M ”).(1)在“组M”中，选择人文类课程和自然科学类课程的人数各有多少？(2)为参加某地举办的自然科学营活动，从“组M”所有选择自然科学类课程的同学中随机抽取4名同学前往，其中选择课程F或课程H的同学参加本次活动，费用为每人1500元，选择课程G 的同学参加，费用为每人2000元.(ⅰ)设随机变量X表示选出的4名同学中选择课程G的人数，求随机变量X的分布列；(ⅱ)设随机变量Y表示选出的4名同学参加自然科学营的费用总和，求随机变量Y的数学期望.21.（本小题满分12分）已知动点M到点(1,0)N和直线l：1x=-的距离相等.（1）求动点M的轨迹E的方程；（2）已知不与l垂直的直线'l与曲线E有唯一公共点A，且与直线l的交点为P，以AP 为直径作圆C.求证：N在圆C上.22.(本小题满分12分)椭圆C的中心为直角坐标系xOy的原点，焦点在x轴上，它的一个项点到两个焦点的距离分别是7和1．（1）求椭圆C的方程；（2）若P为椭圆C的动点，M为过P且垂直于x轴的直线上的点，OPeOM=，（e为椭圆C的离心率），求点M的轨迹方程，并说明轨迹是什么曲线．高二 数学（理科）参考答案一、选择题1-5: BCACC 6-10:AAACA 11、12：DB12.【解析】：当直线l 垂直于实轴时，则易知21,F F 在AB 的垂直平分线上；当直线l 不垂直于实轴时，不妨设双曲线焦点在x 轴，21,F F 分别为双曲线的左、右焦点，且A 、B 都在右支上，由双曲线定义：12||2AF AF a -=，122BF BF a -=，则2211AF BF AF BF -=-AB <，由双曲线定义可知，21,F F 在以A 、B 为焦点的双曲线上，故选B 二、填空题13. 15 14. 24y x = 15. 15216.1306 一、解答题17．(本题满分12分）解：（1）∵3asinC=4ccosA ，∴3sinAsinC=4sinCcosA ，sinC≠0，∴tanA=，可得sinA=，cosA=． ∵•=3，∴bccosA=3，∴bc=5．∴S=bcsinA==2．（2）由（I ）可得：b=5．∴a 2=1+52﹣2×5×1×=20， 解得a=2．18.（本小题共12分）解：（1）因为△PAB 是等边三角形，90PAC PBC ∠=∠=︒，所以Rt PBC Rt PAC ∆∆≌，可得AC=BC ．如图，取AB 中点D ，连结PD ，CD ，则PD ⊥AB ，CD ⊥AB ， 所以AB ⊥平面PDC ，所以AB ⊥PC ．（2）作BE ⊥PC ，垂足为E ，连结AE ．因为Rt PBC Rt PAC ∆∆≌，所以AE ⊥PC ，AE=BE ．由已知，平面PAC ⊥平面PBC ，故90AEB ∠=︒．因为Rt AEB Rt PEB ∆∆≌，所以,,AEB PEB CEB ∆∆∆都是等腰直角三角形．由已知PC=4，得AE=BE=2，AEB ∆的面积2S =．因为PC ⊥⊥平面AEB ，所以三角锥P ABC -的体积1833V S PC =⨯⨯=．19．(本小题满分12分)解：（1）A 类工人中和B 类工人中分别抽查25名和75名．（2）（ⅰ）由485325x ++++=，得5x =；6361875y +++=，得15y =； 频率分布直方图如下从直方图可以判断：B 类工人中个体间的差异程度更小． （ii ）485531051151251351451232525252525A x =⨯+⨯+⨯+⨯+⨯=， 6153618115125135145133.875757575B x =⨯+⨯+⨯+⨯=， 2575123133.8131.1100100x =⨯+⨯=． A 类工人生产能力的平均数，B 类工人生产能力的平均数以及全厂工人生产能力的平均数的估计值分别为123，133.8和131.1.20.(本小题满分12分) 解：(1)选择人文类课程的人数为(100+200+400+200+300)⨯1%=12(人)；选择自然科学类课程的人数为(300+200+300)⨯1%=8(人). (2) (ⅰ) 依题意，随机变量X 可取0，1，2.4062483(0)14C C p X C ===；3162484(1)7C C p X C ===；2262483(2).14C C p X C === 故随机变量X 的分布列为(ⅱ)法1：依题意，随机变量Y =2000X +1500(4)X -=6000+500X ， 所以随机变量Y 的数学期望为E (Y )=6000+500E (X )=6000+500(34301214714⨯+⨯+⨯) =6500.(ⅱ)法2：依题意，随机变量Y 可取6000，6500，7000. 所以随机变量Y 的分布列为所以随机变量Y 的数学期望为 E (Y )=34360006500700014714⨯+⨯+⨯ =6500.21. (本小题满分12分) （1）设动点(,)M x y ，由抛物线定义可知点M 的轨迹E 是以(1,0)N 为焦点，直线l ：1x =-为准线的抛物线， 所以轨迹E 的方程为24y x =. (5分）（2）由题意可设直线':l x my n =+，由2,4x my n y x =+⎧⎪⎨=⎪⎩可得2440y my n --= （）， 因为直线'l 与曲线E 有唯一公共点A ， 所以216160m n ∆=+=，即2n m =-. 所以（）可化简为22440y my m -+=， 所以2(,2)A m m ， 令1x =-得1(1,)nP m+--， 因为2n m =-，所以()022221,22,122=--+-=⎪⎭⎫ ⎝⎛+--⋅-=⋅n m m n m m所以NA NP ⊥，所以点N 在以P A 为直径的圆C 上. （12分）22.(本小题满分12分)解：（1）设椭圆长半轴长及分别为a ，c ，由已知得17a c a c -=⎧⎨+=⎩ 解得a=4，c=3，所以椭圆C 的方程为221.167x y +=（6分） （2）设M （x ，y ），P(x ，1y )，其中[]4,4.x ∈-由已知得222122.x y e x y +=+而34e =，故 2222116()9().x y x y +=+ ① 由点P 在椭圆C 上得 2211127,16x y -=代入①式并化简得29112,y =所以点M 的轨迹方程为44),y x =-≤≤轨迹是两条平行于x 轴的线段．（12分）。

云南省曲靖会泽县第一中学2018-2019学年高二数学下学期第一次质检考试试题 理一．选择题：（12⨯5分=60分）1．命题“若220a b +=,则00a b ==且”的逆否命题是………………………………（ ） A.若220a b +≠,则00a b ≠≠且 B.若220a b +≠,则00a b ≠≠或 C.若00a b ≠≠且，则220a b +≠ D.若00a b ≠≠或，则220a b +≠ 2. 下列命题中，是假命题的是 ……………………………………………=……….（ ）2.x ,log 0A R x ∃∈= .x ,cos 1B R x ∃∈= 2.,0C x R x ∀∈> .,20x D x R ∀∈>3. 命题“对任意的2,220x R x x ∈++>”的否定是…………………………………( )A. 不存在2000,220x R x x ∈++≤B. 存在2000,220x R x x ∈++≤C. 存在2000,220x R x x ∈++> D. 对任意的2,220x R x x ∈++≤ 4．双曲的线2213x y -=渐近线方程为…………………………………………………( ) A ．33y x =±B ．3y x =±C ．13y x =± D ．3y x =± 5. 设，则是的…………………………………………………………（ ）A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件6. 已知椭圆221(0)259x y a b +=>>的两个焦点分别为1F ,2F , P 是椭圆上一点,且1260F PF ∠=o ,则21PF F ∆的面积等于………………………………………………（ ）A. 6333 C. 6 D. 37. 假设每天从甲地去乙地的旅客人数X 是服从正态分布N(800,502)的随机变量，则一天中从甲地去乙地的旅客人数不超过900的概率P 0=………………………………….（ ） (参考数据:若X ～N(μ,σ2),有P(μ-σ<X ≤μ+σ)=0.6826,P(μ-2σ<X ≤μ+2σ)=0.9544,P(μ-3σ<X ≤μ+3σ)=0.9974．)A ．0.9772B ．0.954C ．0.9774D ．0.97738．已知斜率为2的直线l 与双曲线C ： 22221x y a b-=（0a >， 0b >）交于A ， B 两点，若点()3,1P 是AB 的中点，则双曲线C 的离心率等于……………………………（ ） 252159．将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有……………………………………………………………………………（ ） A.270种 B ．180种 C ．90种 D ．30种10. 已知椭圆2221(02)4x y b b+=<<的左，右焦点分别12,F F ，过1F 的直线l 交椭圆于,A B 两点，若22BF AF +的最大值为5，则b 的值为…………………………………………( )A ．1B 2C 3．1211. 若对于任意实数x ，有3322103)2()2()2(-+-+-+=x a x a x a a x ，则2a 的值为（ ）A ．12B ．9C ．6D ．312．已知直线()0y kx k =≠与椭圆2222:1x y E a b+=（0a b >>）交于A , B 两点,椭圆E 右焦点为F ,直线AF 与E 的另外一个交点为C ，若BF AC ⊥,若4BF CF = ,则E 的离心 率为………………………………………………………………………………………（ ）A.125323二．填空题：（4⨯5分=20分）13．若方程22121x y m m +=++表示双曲线，则实数m 的取值范围是__________． 14. 椭圆2215x y m +=的焦距为2，则m 的值等于 ．15．已知命题01,:0200≤++∈∃x ax R x p 若命题p 是假命题，则实数a 的取值范围是__________16．已知点(1,0)A -，点B 是圆F ：22(1)8x y -+=（F 为圆心）上一动点，线段AB 的垂直平分线交BF 于点P ，则动点P 的轨迹方程为 ．三．解答题：（共70分）17．（12分）经过点(2,1)P 的直线l 与双曲线2212y x -=相交于A 、B 两点 （1）若点P 是A 、B 的中点，求直线l 的方程； （2）若直线l 的斜率为1，求弦AB 的长.18.（12分）已知p ： 3x a -<（a 为常数）； q ()1lg 6x x +-有意义． （1）若1a =，求使“p q ∧”为真命题的实数x 的取值范围； （2）若p 是q 成立的充分不必要条件，求实数a 的取值范围.19.（12分）已知点(4,0),(2,0)A B -，动点P 满足2PA PB =． （1）若点P 为曲线C ，求此曲线的方程；（2）已知直线l 在两坐标轴上的截距相等，且与(1)中的曲线C 只有一个公共点,求直线l 的方程．20．（12分）通过对某城市一天内单次租用共享自行车的时间50分钟到100钟的n 人进行统计，按照租车时间[)50,60， [)60,70， [)70,80， [)80,90， [)90,100分组做出频率分布直方图，并作出租用时间和茎叶图（图中仅列出了时间在[)50,60， [)90,100的数据）．（1）求n 的频率分布直方图中的,x y ；（2）从租用时间在80分钟以上（含80分钟）的人数中随机抽取4人，设随机变量X 表示所抽取的4人租用时间在[)80,90内的人数，求随机变量X 的分布列及数学期望．21．（12分）已知椭圆2222:1(0)x y C a b a b +=>>，其焦点为F 1，F 2，离心率为22，若点P ⎝ ⎛⎭⎪⎫22，32满足122PF PF a +=|(1)求椭圆C 的方程；(2)若直线:(,)l y kx m k m R =+∈与椭圆C 交于A ，B 两点，O 为坐标原点，△AOB 的重心G 满足：F 1G →·F 2G →＝－59，求实数m 的取值范围．22．（10分）（1）求经过点(32,4)P ，(3,6)Q -两点的椭圆的标准方程；（2）求与椭圆2213510x y+=有公共焦点，且离心率5e3=的双曲线的标准方程.数学试题（理工类）参考答案题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 DCBABBADCCCB13. (2,1)-- 14.4或6 15.14a > 16. 2212x y += 17. （Ⅰ）470x y --= ……………………………………………………………………（6分）（Ⅱ）42……………………………………………………（12分）18.p ： 3x a -<等价于： 33x a -<-<即33a x a -<<+；…………………2分q ：代数式()1lg 6x x ++-有意义等价于： 10{60x x +≥->，即16x -≤<..............4分（1）1a =时， p 即为24x -<<若“p q ∧”为真命题，则24{16x x -<<-≤<，得： 14x -≤< 故1a =时，使“p q ∧”为真命题的实数x 的取值范围是[1-， 4) ...................8分（2）记集合{|33}A x a x a =-<<+， {|16}B x x =-≤< 若p 是q 成立的充分不必要条件，则A B ⊂，因此： 31{ 36a a -≥-+≤， ∴ 23a ≤≤，故实数a 的取值范围是[]2,3 (12)分 19.设，点，，动点P 满足．，得：，曲线C 方程为…6分设直线l 的横截距为a ，则直线l 的纵截距也为a ， 当时，直线l 过，设直线方程为．把代入曲线C 的方程，得：，，直线l 与曲线C 有两个公共点，已知矛盾；当时，直线方程为，把代入曲线C 的方程，得：，直线l 与曲线C 只有一个公共点，，解得，直线l 的方程为或．..... 12分.20.(1)由题意可知，样本容量8250,0.0040.016105010n y ====⨯⨯,0.1000.0040.0100.0160.0400.030x =----=. ............4分(2)由题意可知，租用时间在[)80,90内的人数为5，租用时间在[]90,100内的人数为2，共7人.抽取的4人中租用时间在[)80,90内的人数2=X ，3，4 .............6分，，.X 2 3 4P27故. ............................12分21. (1)由e ＝22，可设椭圆C 的方程为x 2a 2＋2y 2a 2＝1， 点P ⎝ ⎛⎭⎪⎫22，32满足|PF 1|＋|PF 2|＝2a ，等价于点P 在椭圆上，∴12a 2＋32a 2＝1，∴a 2＝2，所以椭圆C 的方程为x 22＋y 2＝1………………….5分(2)设A (x 1，y 1)，B (x 2，y 2)，联立得方程组⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2＋2y 2－2＝0， 消去y 并整理得(1＋2k 2)x 2＋4kmx ＋2m 2－2＝0，则⎩⎪⎨⎪⎧Δ>01＋2k 2>m 2x 1＋x 2＝－4km 1＋2k 2x 1x 2＝2m 2－21＋2k2①……………………………………………………….7分设△AOB 的重心为G (x ，y )，由F 1G →·F 2G →＝－59，可得x 2＋y 2＝49.②由重心公式可得G ⎝ ⎛⎭⎪⎫x 1＋x 23，y 1＋y 23，代入②式，整理可得(x 1＋x 2)2＋(y 1＋y 2)2＝4(x 1＋x 2)2＋[k (x 1＋x 2)＋2m ]2＝4，③ 将①式代入③式并整理，得m 2＝（1＋2k 2）21＋4k 2.......................10分 则m 2＝（1＋2k 2）21＋4k 2＝1＋4k 41＋4k 2＝1＋44k 2＋1k 4.又由Δ>0可知k ≠0，令t ＝1k 2>0，∴t 2＋4t >0，∴m 2>1，∴m ∈(－∞，－1)∪(1，＋∞)……………………...12分22. (1)2213632x y +=……………………5分 （2）221916x y -=…………………………….10分。

数学试题（理工类）一．选择题：（12⨯5分=60分） 1．命题“若220a b +=,则00a b ==且”的逆否命题是………………………………（ ）A.若220a b +≠,则00a b ≠≠且B.若220a b +≠,则00a b ≠≠或C.若00a b ≠≠且，则220a b +≠D.若00a b ≠≠或，则220a b +≠ 2. 下列命题中，是假命题的是 ……………………………………………=……….（ ）2.x ,log 0A R x ∃∈= .x ,cos 1B R x ∃∈= 2.,0C x R x ∀∈>.,20x D x R ∀∈>3. 命题“对任意的2,220x R x x ∈++>”的否定是…………………………………( )A. 不存在2000,220x R x x ∈++≤B. 存在2000,220x R x x ∈++≤ C. 存在2000,220x R x x ∈++>D. 对任意的2,220x R x x ∈++≤4．双曲的线2213x y -=渐近线方程为…………………………………………………( )A ．y =±B ．y =C ．13y x =± D ．3y x =±5. 设，则是的…………………………………………………………（ ）A.充分但不必要条件B.必要但不充分条件C.充要条件D.既不充分也不必要条件6. 已知椭圆221(0)259x y a b +=>>的两个焦点分别为1F ,2F , P 是椭圆上一点,且1260F PF ∠=,则21PF F ∆的面积等于………………………………………………（ ）A. 6 D. 37. 假设每天从甲地去乙地的旅客人数X 是服从正态分布N(800,502)的随机变量，则一天中从甲地去乙地的旅客人数不超过900的概率P 0=………………………………….（ ）(参考数据:若X ～N(μ,σ2),有P(μ-σ<X ≤μ+σ)=0.6826,P(μ-2σ<X ≤μ+2σ)=0.9544,P(μ-3σ<X ≤μ+3σ)=0.9974．)A ．0.9772B ．0.954C ．0.9774D ．0.97738．已知斜率为2的直线l 与双曲线C ： 22221x y a b-=（0a >， 0b >）交于A ，B 两点，若点()3,1P 是AB 的中点，则双曲线C 的离心率等于……………………………（ ）2 D.39．将5名实习教师分配到高一年级的3个班实习，每班至少1名，最多2名，则不同的分配方案有……………………………………………………………………………（ ） A.270种 B ．180种 C ．90种 D ．30种10. 已知椭圆2221(02)4x y b b+=<<的左，右焦点分别12,F F ，过1F 的直线l 交椭圆于,A B 两点，若22BF AF +的最大值为5，则b 的值为…………………………………………( )A ．1BC ．1211. 若对于任意实数x ，有3322103)2()2()2(-+-+-+=x a x a x a a x ，则2a 的值为（ ）A ．12B ．9C ．6D ．312．已知直线()0y kx k =≠与椭圆2222:1x y E a b+=（0a b >>）交于A , B 两点,椭圆E 右焦点为F ,直线AF 与E 的另外一个交点为C ，若BF AC ⊥,若4BF CF = ,则E 的离心 率为………………………………………………………………………………………（ ）A. 12B. 3C. 2D. 3二．填空题：（4⨯5分=20分）13．若方程22121x y m m +=++表示双曲线，则实数m 的取值范围是__________． 14. 椭圆2215x y m +=的焦距为2，则m 的值等于 ．15．已知命题01,:0200≤++∈∃x ax R x p 若命题p 是假命题，则实数a 的取值范围是__________16．已知点(1,0)A -，点B 是圆F ：22(1)8x y -+=（F 为圆心）上一动点，线段AB 的垂直平分线交BF 于点P ，则动点P 的轨迹方程为 ． 三．解答题：（共70分）17．（12分）经过点(2,1)P 的直线l 与双曲线2212y x -=相交于A 、B 两点 （1）若点P 是A 、B 的中点，求直线l 的方程； （2）若直线l 的斜率为1，求弦AB 的长.18.（12分）已知p ： 3x a -<（a 为常数）； q ()lg 6x -有意义．（1）若1a =，求使“p q ∧”为真命题的实数x 的取值范围； （2）若p 是q 成立的充分不必要条件，求实数a 的取值范围.19.（12分）已知点(4,0),(2,0)A B -，动点P 满足2PA PB =． （1）若点P 为曲线C ，求此曲线的方程；（2）已知直线l 在两坐标轴上的截距相等，且与(1)中的曲线C 只有一个公共点,求直线l 的方程． 20．（12分）通过对某城市一天内单次租用共享自行车的时间50分钟到100钟的n 人进行统计，按照租车时间[)50,60， [)60,70， [)70,80， [)80,90， [)90,100分组做出频率分布直方图，并作出租用时间和茎叶图（图中仅列出了时间在[)50,60， [)90,100的数据）．（1）求n 的频率分布直方图中的,x y ；（2）从租用时间在80分钟以上（含80分钟）的人数中随机抽取4人，设随机变量X 表示所抽取的4人租用时间在[)80,90内的人数，求随机变量X 的分布列及数学期望．21．（12分）已知椭圆2222:1(0)x y C a b a b +=>>，其焦点为F 1，F 2，离心率为22，若点P ⎝ ⎛⎭⎪⎫22，32满足122PF PF a +=|(1)求椭圆C 的方程；(2)若直线:(,)l y kx m k m R =+∈与椭圆C 交于A ，B 两点，O 为坐标原点，△AOB 的重心G 满足：F 1G →·F 2G →＝－59，求实数m 的取值范围．22．（10分）（1）求经过点4)P ，(3,Q -两点的椭圆的标准方程；（2）求与椭圆2213510x y +=有公共焦点，且离心率5e 3=的双曲线的标准方程.数学试题（理工类）参考答案13. (2,1)-- 14.4或6 15.14a > 16. 212x y += 17. （Ⅰ）470x y --= ……………………………………………………………………（6分）（Ⅱ）12分）18.p ： 3x a -<等价于： 33x a -<-<即33a x a -<<+；…………………2分q ()lg 6x -有意义等价于： 10{60x x +≥->，即16x -≤< (4)分（1）1a =时， p 即为24x -<<若“p q ∧”为真命题，则24{16x x -<<-≤<，得： 14x -≤< 故1a =时，使“p q ∧”为真命题的实数x 的取值范围是[1-， 4) ...................8分（2）记集合{|33}A x a x a =-<<+， {|16}B x x =-≤< 若p 是q 成立的充分不必要条件，则A B ⊂，因此： 31{ 36a a -≥-+≤， ∴ 23a ≤≤，故实数a 的取值范围是[]2,3 (12)分19. 设，点，，动点P 满足．，得：，曲线C 方程为…6分设直线l 的横截距为a ，则直线l 的纵截距也为a ，当时，直线l 过，设直线方程为．把代入曲线C 的方程，得：，，直线l 与曲线C 有两个公共点，已知矛盾；当时，直线方程为，把代入曲线C 的方程，得：，直线l 与曲线C 只有一个公共点，，解得，直线l 的方程为或．..... 12分.20.(1)由题意可知，样本容量8250,0.0040.016105010n y ====⨯⨯,0.1000.0040.0100.0160.0400.030x =----=. ............4分(2)由题意可知，租用时间在[)80,90内的人数为5，租用时间在[]90,100内的人数为2，共7人.抽取的4人中租用时间在[)80,90内的人数2=X ，3，4 .............6分，，. (12)分21. (1)由e ＝22，可设椭圆C 的方程为x 2a 2＋2y 2a 2＝1，点P ⎝ ⎛⎭⎪⎫22，32满足|PF 1|＋|PF 2|＝2a ，等价于点P 在椭圆上，∴12a 2＋32a 2＝1，∴a 2＝2，所以椭圆C 的方程为x 22＋y 2＝1………………….5分 (2)设A (x 1，y 1)，B (x 2，y 2)，联立得方程组⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2＋2y 2－2＝0， 消去y 并整理得(1＋2k 2)x 2＋4kmx ＋2m 2－2＝0，则⎩⎪⎨⎪⎧Δ>01＋2k 2>m 2x 1＋x 2＝－4km1＋2k2x 1x 2＝2m 2－21＋2k2① (7)分设△AOB 的重心为G (x ，y )，由F 1G →·F 2G →＝－59，可得x 2＋y 2＝49.② 由重心公式可得G ⎝ ⎛⎭⎪⎫x 1＋x 23，y 1＋y 23，代入②式， 整理可得(x 1＋x 2)2＋(y 1＋y 2)2＝4(x 1＋x 2)2＋[k (x 1＋x 2)＋2m ]2＝4，③ 将①式代入③式并整理，得m 2＝（1＋2k 2）21＋4k 2 (10)分则m2＝（1＋2k2）21＋4k2＝1＋4k41＋4k2＝1＋44k2＋1k4.又由Δ>0可知k≠0，令t＝1k2>0，∴t2＋4t>0，∴m2>1，∴m∈(－∞，－1)∪(1，＋∞)……………………...12分22.(1)2213632x y+=……………………5分（2）221916x y-=…………………………….10分。

2019学年云南曲靖一中高二上期中数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________题号一二三总分得分一、选择题1. 将二进制数转化为四进制数，正确的是（）A . ____________________B . ______________C .______________ D .2. 已知平面向量，且，则（）A . 10___________B . ______________C . 5______________D .3. 同时掷两枚质地均匀的骰子，所得点数之和为6的概率等于（）A . ____________________B . ______________C . ______________D .4. 的内角的对边分别是，已知，则（）A . ____________________B . ______________C . 2____________________D . 35. 某广告的广告费用与销售额的统计数据如下表根据上表可得回归方程中的为9 . 4，据此模型预报广告费用为6万元是销售额为（）A . 63 . 6万元____________________B . 65 . 6万元______________C . 67 . 7万元______________ D . 72 . 0万元6. 已知，则（）A . ____________________B . ________C .____________________ D .7. 在中，角所对应的边分别为，则“　”是“　”的（）A . 充分必要条件B . 充分非必要条件C . 必要非充分条件 ___________D . 非充分非必要条件8. 如果下边程序执行后输出的结果是132，那么在程序后面的“条件”应为（）A . ___________B .C . _________D .9. 已知等差数列的前项和为，公差为，若，则的值为（）A . ____________________B . ______________C . 10____________________D . 2010. 2016年2月，为保障春节期间的食品安全，某市质量监督局对超市进行食品检查，如图所示是某品牌食品中微量元素含量数据的茎叶图（其中），已知该组数据的平均数为11 . 5，则的最小值为（）A . 9____________________B . ______________C . 8____________________D .411. 设不等式组，表示的平面区域为，在区域内随机取一个点，则此点到坐标原点的距离大于2的概率是（）A . _________B . ______________C . _________D .12. 椭圆：上的一点关于原点的对称点为，为它的右焦点，若，则三角形的面积是（）A . 2___________B . 4______________C . 1___________D .二、填空题13. 若命题，则________________________ .14. 若实数满足不等式，则的取值范围是________________________ .15. 下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术” . 执行该程序框图，若输入的分别为14,20，则输出的________________________ .16. 如图，椭圆的左右焦点分别为，过的直线交椭圆于两点，且，若，则椭圆的心率________________________ .三、解答题17. 已知命题（其中） . （1）若，命题“　且”为真，求实数的取值范围；（2）已知是的充分条件，求实数的取值范围 .18. 已知函数，其中，在中，分别是角的对边，且（1）求角；（2）若，求的面积 .19. 某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布如图所示 .（1）请先求出频率分布表中①、②位置相应的数据，再画出频率分布直方图；（2）该高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？（3）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受考官的面试，求第4组至少有一名学生被考官面试的概率？20. 已知函数（1）求函数的最小正周期和单调减区间；（2）将函数图像向右平移个单位长度后得到函数的图象，求函数在区间上的最小值 .21. 设椭圆中心在坐标原点，焦点在轴上，一个顶点坐标为，离心率为.（1）求这个椭圆的方程；（2）若这个椭圆左焦点为，右焦点为，过且斜率为1的直线交椭圆于两点，求的面积 .22. 已知数列的前项和为，且 .（1）求数列的通项公式；（2）设，数列的前项和为，若对恒成立，求实数的取值范围 .参考答案及解析第1题【答案】第2题【答案】第3题【答案】第4题【答案】第5题【答案】第6题【答案】第7题【答案】第8题【答案】第9题【答案】第10题【答案】第11题【答案】第12题【答案】第13题【答案】第14题【答案】第15题【答案】第16题【答案】第17题【答案】第18题【答案】第19题【答案】第20题【答案】第21题【答案】第22题【答案】。

云南省会泽县一中2019-2020学年高二上学期12月月考数学（理）试卷一、选择题（本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．） 1. 设集合{|13}A x x =-<<，1{|39}3x B x =<<，则A B =( ) A. (1,2) B. (1,2)- C. (1,3) D. (1,3)- 2. 运行如右图所示的程序框图，则输出的S 值为( )A.99212-B. 99212+C. 1010212-D. 1010221+3. 已知向量21=-（，）a ，01=（，）b ，则|2|=a +b ( )A.C. 2D. 4 4. 已知函数5log ,0()2,0xx x f x x >⎧=⎨⎩≤，则1(())25f f =( ) A. 4 B. 14 C. 4- D. 14- 5. 已知实数{},1,2,3,4,5,6x y ∈，且7x y +=，则2xy ≥的概率为( )A. 13B. 23C. 12D. 566. 已知tan 2α=，α为第一象限角，则sin 2cos αα+=( )B.45+C.45+D.257. 如右图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的体积为( )A. 18B. 14C. 12D. 98. 将函数()sin(2)(||)2f x x πϕϕ=+<的图象向右平移12π个单位后的图象关于y 对称，则函数()f x 在[0,]2π上的最小值为()B.12 C. 12-D. 9. 已知变量X 服从正态分布(24)N ，，下列概率与(X 0)P ≤相等的是( ) A.(X 2)P ≥ B.(X 4)P ≥ C.(0X 4)P ≤≤D. 1(X 4)P -≥10. 5名学生和2名老师排成一排照相，2名老师不在两边且不相邻的概率为( ) A.17B.47C.27D.5711. 在ABC ∆中，D 是BC 中点，已知90BAD C ∠+∠=︒,则ABC ∆的形状为( )A.等腰三角形B. 直角三角形C.等腰直角三角形D.等腰三角形或直角三角形 12．小王忘记了自己的银行卡密码，只记得：6位数字的密码中含有两个5，两个2和两个0.他连输三次密码，三次都输错的概率为( ) A ．3029 B ．4544 C ．1514 D ．109 二、填空题（本大题共4个小题，每小题5分，共20分）13. 已知实数,x y 满足⎪⎩⎪⎨⎧≥≥≤+≤0021y x y x ，则2+x y 的最大值为___________.14. 6(2-x 的展开式中常数项为___________. 15. 将2名教师，4名学生分成2个小组，分别安排到甲、乙两地参加社会实践活动，每个小组由1名教师和2名学生组成，不同的安排方案共有___________.16. 某个部件由三个电子元件按下图方式连接而成，元件1或元件2正常工作，且元件3正常工作，则部件正常工作。

云南省曲靖市会泽县第一中学2020-2021学年高二上学期开学考试数学理科试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．已知集合{}1,2,3,4,5,6,7U =，{}3,4,5A =，{}2,3,6,7B =，则U B C A ⋂=（ ） A ．{}2,6,7 B ．{}1,6,7C ．{}3,6,7D ．{}4,6,72．tan255°= A ．－2B ．－C ．2D ．3．若变量x y ，满足约束条件1{11x y y x x +≥-≤≤，则2z x y =-的最小值为（ ）A ．1-B ．0C ．1D ．24．在等差数列{}n a 中,1352,10a a a =+=，则7a =（ ） A ．5B ．8C ．10D ．145．函数()2ln f x x =的图象与函数()245g x x x =-+的图象的交点个数为( ) A ．3B ．2C ．1D ．06．某几何体的三视图如图所示，则该几何体的体积为（ ）A ．116πB ．73π C ．136πD ．83π 7．设n S 为等比数列{}n a 的前n 项和，2580a a +=，则52S S =( ) A ．11B ．5C ．8-D ．11-8．已知函数()()32()sin 4(,),lg log 105f x ax b x a b R f =++∈=，则(lg(lg 2))f =（ ） A ．5-B ．1-C ．1D ．39．在平面直角坐标系xOy 内，经过点(2,3)P 的直线分别与x 轴、y 轴的正半轴交于,A B 两点，则OAB ∆面积最小值为( ) A ．4B ．8C ．12D ．1610．如图，点P 在平行四边形OACD 内部（含边界）运动，点B 为OD 的中点，若OP xOA yOB =+，则x y +的范围是（ ）A ．[0，4]B ．[0，3]C ．[0，2]D ．[0，1]11．已知()()2332A B ---，，，，直线l 方程为10mx y m +--=，且与线段AB 相交，求直线l 的斜率k 的取值范围为（ ） A ．34k ≥或4k ≤- B ．34k ≥或14k ≤- C ．344k -≤≤ D ．344k ≤≤ 12．已知函数23,1,()2, 1.x x x f x x x x ⎧-+≤⎪=⎨+>⎪⎩设a R ∈，若关于x 的不等式()||2x f x a ≥+在R 上恒成立，则a 的取值范围是 A ．47[,2]16-B ．4739[,]1616-C．[- D．39[]16-二、填空题13．已知向量(2,3),(3,)a b m =-=，且a b ⊥，则m =_______. 14．函数()23s 4f x in x =-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是__________． 15．设直线2y x a =+与圆C ：x 2+y 2-2ay -2=0相交于A ，B两点，若AB =C 的面积为________16．已知四面体P ABC -，90PAC PBC ACB ∠=∠=∠=︒，4PC =，PB PA ==P ABC -的体积为_______ .三、解答题17．已知函数()()22f x sin x cos x x cos x x R =--∈ （I ）求2f 3π⎛⎫⎪⎝⎭的值 （II ）求()f x 的最小正周期及单调递增区间.18．如图,在MBC ∆中,MA 是BC 边上的高,3,4MA AC ==,将MBC ∆沿MA 进行翻折,使得90BAC ∠=︒如图，再过点B 作BD ∥AC ,连接,,AD CD MD 且AD =30CAD ∠=︒.(1)求证:CD ⊥平面MAD ； (2)求三棱锥C MAD -的体积.19．ABC 的内角A ，B ，C 的对边分别为a ，b ，c .已知2cos (cos cos )C a B b A c +=.（1）求角C ；（2）若c =ABC S ∆=ABC ∆的周长. 20．如图，在底面为平行四边形的四棱锥P ABCD -中，过点A 的三条棱PA 、AB 、AD 两两垂直且相等，E ，F 分别是AC ，PB 的中点．（Ⅰ）证明：EF//平面PCD ；（Ⅱ）求EF 与平面PAC 所成角的大小． 21．已知圆()222:0O x y rr +=>与直线34150x y -+=相切（1）若直线:25l y x =-+与圆O 交于,M N 两点，求;MN （2）已知()()9,0,1,0A B --，设P 为圆O 上任意一点，证明：PA PB为定值22．设等差数列{}n a 的公差为d ，d 为整数，前n 项和为n S ，等比数列{}n b 的公比为q ，已知11a b =，22b =，d q =，10100S =，*n N ∈ （1）求数列{}n a 与{}n b 的通项公式； （2）设nn na cb =，求数列{}nc 的前n 项和为n T .参考答案1．A 【分析】先计算U C A ，然后进行交集运算即可. 【详解】{1,2,6,7}U C A =，{2,6,7}U B C A ⋂=.故选：A 【点睛】本题考查集合的基本运算，属于基础题. 2．D 【分析】本题首先应用诱导公式，将问题转化成锐角三角函数的计算，进一步应用两角和的正切公式计算求解．题目较易，注重了基础知识、基本计算能力的考查． 【详解】详解：0tan 255tan(18075)tan 75tan(4530)=+==+=001tan 45tan 3021tan 45tan 30++==+- 【点睛】三角函数的诱导公式、两角和与差的三角函数、特殊角的三角函数值、运算求解能力． 3．A 【解析】试题分析：由题意得，画出约束条件所表示的可行域，如图所示，目标函数2z x y =-的最优解为点A ，联立1{1x y y x +=-=，解得(0,1)A ，所以2z x y =-的最小值为min 1z =-．考点：线性规划． 4．B 【解析】试题分析：设等差数列{}n a 的公差为d ，由题设知，12610a d +=，所以，110216a d -== 所以，716268a a d =+=+= 故选B.考点：等差数列通项公式. 5．B 【解析】由已知g (x )＝(x －2)2＋1，所以其顶点为(2,1)，又f (2)＝2ln 2∈(1,2)，可知点(2,1)位于函数f (x )＝2ln x 图象的下方，故函数f (x )＝2ln x 的图象与函数g (x )＝x 2－4x ＋5的图象有2个交点． 6．C 【分析】先由三视图确定几何体形状，再由简单几何体的体积公式计算即可. 【详解】由三视图可知，该几何体由半个圆锥与一个圆柱体拼接而成，所以该几何体的体积2211131211326V πππ=⨯⨯+⨯⨯⨯=.故选C 【点睛】本题主要考查由几何体的三视图求简单组合体的体积问题，只需先由三视图确定几何体的形状，再根据体积公式即可求解，属于常考题型. 7．D试题分析：设公比为，由2580a a +=，得，解得，所以．故选D ．考点：等比数列的前项和. 8．D 【分析】令3()sin g x ax b x =+，则()()4f x g x =+，易证()g x 为奇函数，由()()2lg log 105f =求出2(lg(log 10))1g =，再利用奇函数的性质即可求得(lg(lg 2))f . 【详解】令3()sin g x ax b x =+，则()()4f x g x =+，由3()sin()()g x ax b x g x -=-+-=-知函数()g x 为奇函数，因为()()22lg log 105(lg(log 10))4f g ==+，所以2(lg(log 10))1g =，所以()()22(lg(lg 2))lg lg 24(lg(log 10))4(lg(log 10))43f g g g =+=-+=-+=. 故选：D 【点睛】本题考查函数奇偶性的应用，对数换底公式的推论，属于中档题. 9．C 【分析】设出直线方程，代入定点得到231a b+=,再利用均值不等式得到三角形面积的最小值. 【详解】解:由题意设直线方程为1(0,0)x y a b a b +=>> ,231a b∴+= .由基本不等式知23a b +≥ 即24ab ≥ (当且仅当23a b= ,即4,6a b == 时等号成立). 又11241222S a b =⋅≥⨯=【点睛】本题考查了直线截距式方程，利用均值不等式求最大最小值是常考题型. 10．B 【分析】向量OP 用向量OA 、OD 表示，由点P 在平行四边形OACD 内部（含边界）运动求出x 、y 的范围，作出可行域，数形结合求目标函数z x y =+的范围. 【详解】点B 为OD 的中点则2yOP xOA yOB xOA OD =+=+， 因为点P 在平行四边形OACD 内部（含边界）运动，所以01012x y≤≤⎧⎪⎨≤≤⎪⎩，作出可行域如图所示：目标函数z x y =+可转化为直线l ：y x z =-+，z 为直线的纵截距， 当直线l 过点(0,0)O 时z 取最小值0，当直线l 过点(1,2)A 时取最大值3. 所以x y +的范围是[0，3]. 故选：B 【点睛】本题考查线性规划问题，平面向量基本定理，属于中档题. 11．A 【分析】由题意画出图形，求出P A 、PB 的斜率，数形结合即可得解.直线l ：(1)10m x y -+-=过定点(1,1)P ，如图：312134,21314PA PB k k ----==-==---， 若直线l 与AB 有交点，则斜率k 的取值范围为34k ≥或4k ≤-. 故选：A 【点睛】本题考查直线的普通方程与斜率，直线过定点问题，属于基础题. 12．A 【解析】不等式()2x f x a ≥+为()()2xf x a f x -≤+≤(*)， 当1x ≤时，(*)式即为22332x x x a x x -+-≤+≤-+，2233322x x a x x -+-≤≤-+， 又22147473()241616x x x -+-=---≤-（14x =时取等号）， 223339393()241616x x x -+=-+≥（34x =时取等号），所以47391616a -≤≤， 当1x >时，(*)式为222x x a x x x --≤+≤+，32222x x a x x--≤≤+，又3232()22x x x x --=-+≤-3x =时取等号），222x x +≥=（当2x =时取等号），所以2a -≤≤， 综上47216a -≤≤．故选A ． 【考点】不等式、恒成立问题 【名师点睛】首先满足()2x f x a ≥+转化为()()22x xf x a f x --≤≤-去解决，由于涉及分段函数问题要遵循分段处理原则，分别对x 的两种不同情况进行讨论，针对每种情况根据x 的范围，利用极端原理，求出对应的a 的范围.13．2 【解析】由题意可得2330,m -⨯+=解得2m =.【名师点睛】（1）向量平行：1221x y x y ⇒=∥a b ，,,∥λλ≠⇒∃∈=0R a b b a b ,111BA AC OA OB OC λλλλ=⇔=+++. （2）向量垂直：121200⊥⇔⋅=⇔+=x x y y a b a b .（3）向量的运算：221212(,),||,||||cos ,x x y y ±=±±=⋅=⋅a b a a a b a b a b .14．1 【详解】化简三角函数的解析式，可得()22311cos cos 44f x x x x x =--=-+=2(cos 12x --+， 由[0,]2x π∈，可得cos [0,1]x ∈，当cos 2x =时，函数()f x 取得最大值1．15．4π【解析】因为圆心坐标与半径分别为(0,),=C a r ，所以圆心到直线的距离d ==2232a +=+，解之得22a =，所以圆的面积2(22)4πππ==+=S r ，应填答案4π．16 【分析】取AB 中点为O ，连接CO ，做PD 垂直于CO 的延长线于点D ，求出AC 、BC 、AD ，然后证明PD ⊥平面ABC ，求出PD 进而求得四面体P ABC -的体积.【详解】根据题意，取AB 中点为O ，连接CO ，做PD 垂直于CO 的延长线于点D ，如图所示：由题意可得2AC ==， 2BC ==，AB =因为AC BC =，且O 为AB 中点，所以CO AB ⊥，CO =PO AB ⊥, 又PO CO O =，PO ⊂平面PDC ，CO ⊂平面PDC ，所以AB ⊥平面PDC ， 由PD ⊂平面PDC 得PD AB ⊥，因为AB CD O =，且AB 平面ABC ，CD ⊂平面ABC ，所以PD ⊥平面ABC ，设PD =x ，则OD =在直角PDC △中，222PD DC PC +=, 即2216x +=，解得x =所以11=(22)323P ABC V -⨯⨯⨯⨯=.【点睛】 本题考查棱锥的体积，属于中档题.17．（I ）2；（II ）()f x 的最小正周期是π，2+k +k k 63Z ππππ⎡⎤∈⎢⎥⎣⎦，. 【分析】（Ⅰ）直接利用三角函数关系式的恒等变换，把函数的关系式变形成正弦型函数，进一步求出函数的值．（Ⅱ）直接利用函数的关系式，求出函数的周期和单调区间．【详解】（Ⅰ）f （x ）＝sin 2x ﹣cos 2x -x cos x ，＝﹣cos2x x ，＝﹣226sin x π⎛⎫+⎪⎝⎭， 则f （23π）＝﹣2sin （436ππ+）＝2， （Ⅱ）因为()2sin(2)6f x x π=-+． 所以()f x 的最小正周期是π．由正弦函数的性质得3222,262k x k k Z πππππ+≤+≤+∈， 解得2,63k x k k Z ππππ+≤≤+∈， 所以，()f x 的单调递增区间是2[,]63k k k ππ+π+π∈Z ，． 【点睛】本题主要考查了三角函数的化简，以及函数的性质，是高考中的常考知识点，属于基础题，强调基础的重要性；三角函数解答题中，涉及到周期，单调性，单调区间以及最值等考点时，都属于考查三角函数的性质，首先应把它化为三角函数的基本形式即，然后利用三角函数的性质求解．18．（1）见解析（2）【分析】（1）根据计算得CD ⊥AD ，再根据线面垂直判定与性质定理得结论，（2）根据等体积法以及三棱锥体积公式得结果.【详解】(1)证明:在△ADC 中,AC=4,AD=2,∠CAD=30°,利用余弦定理可得CD=2,所以∠ADC=90°,即CD ⊥AD. 因为MA ⊥AB,MA ⊥AC,AB∩AC=A,故MA ⊥平面ABDC.因为CD ⊂平面ABDC,所以CD ⊥MA.又AD∩MA=A,所以CD ⊥平面MAD.(2)解:C MAD M CAD V V --=因为△ACD 的面积122S =⨯=,故三棱锥133C MADM CAD V V --==⨯=【点睛】本题考查线面垂直判定与性质定理以及等体积法，考查基本分析求解能力，属中档题.19．（1）3C π=（2）5+【详解】试题分析：（1）根据正弦定理把2cos (cos cos )C a B b A c +=化成2cos (sin cos sin cos )sin C A B B A C +=，利用和角公式可得1cos ,2C =从而求得角C ；（2）根据三角形的面积和角C 的值求得6ab =，由余弦定理求得边a 得到ABC ∆的周长. 试题解析：（1）由已知可得2cos (sin cos sin cos )sin C A B B A C +=12cos sin()sin cos 23π∴+=⇒=⇒=C A B C C C（2）11sin 622∆=⇒=⇒=ABC S ab C ab ab 又2222cos +-=a b ab C c2213a b ∴+=，2()255∴+=⇒+=a b a bABC ∆∴的周长为5+考点：正余弦定理解三角形.20．（Ⅰ）见解析； （Ⅱ）见解析.【分析】（Ⅰ）连接BD ，则E 是BD 的中点，F 是PB 的中点得EF//PD ．线面平行转化为线线平行． （Ⅱ）首先找出EF 与平面PAC 所成的角，由题意可得EF 与平面PAC 所成的角的大小等于EPD ∠．根据条件得1sin 2ED EPD PD ∠==，所以30EPD ∠=︒．【详解】（Ⅰ）证明：如图，连接BD ，则E 是BD 的中点又F 是PB 的中点，∴ EF//PD，∵ EF 不在平面PCD 内，∴ EF//平面PCD ．（Ⅱ）连接PE ，∵ ABCD 是正方形，∴BD AC ⊥又PA ⊥平面ABC ，∴PA BD ⊥．∴BD ⊥平面PAC ，故EPD ∠是PD 与平面PAC 所成的角，∵EF//PD，∴EF 与平面PAC 所成的角的大小等于EPD ∠∵PA=AB=AD，90PAD BAD ∠=∠=︒，∴Rt PAD ≌Rt BAD ，因此PD=BD在Rt PED 中，1sin 2ED EPD PD ∠==，30EPD ∠=︒ ∴EF 与平面PAC 所成角的大小是30．【点睛】本题主要考查了证明线面垂直（通常转化成证明线线垂直）．求直线与平面成的夹角通常直接找直线与平面成的角或者建立空间直角坐标系利用向量法．21．（1）4；（2）详见解析.【分析】（1）利用直线与圆相切d r =，结合点到直线距离公式求出半径，从而得到圆的方程；根据直线被圆截得弦长的求解方法可求得结果；（2）设()00,P x y ，则22009x y +=，利用两点间距离公式表示出PA PB ，化简可得结果.【详解】 （1）由题意知，圆心O 到直线34150x y -+=的距离：3d == 圆O 与直线相切 3r d ∴== ∴圆O 方程为：229x y +=圆心O 到直线:25l y x =-+的距离：d '==4MN ∴==，（2）证明：设()00,P x y ，则22009x y +=3PAPB ∴====即PA PB 为定值3【点睛】本题考查直线与圆的综合应用问题，涉及到直线与圆位置关系的应用、直线被圆截得弦长的求解、两点间距离公式的应用、定值问题的求解.解决定值问题的关键是能够用变量表示出所求量，通过化简、消元整理出结果.22．（1）n a ＝2n ﹣1，12n n b -=（2）12362n n n T -+=- 【分析】（1）利用已知条件求出数列的首项与公差与公比，然后求解通项公式．（2）化简数列的通项公式，利用错位相减法求解数列的和即可．【详解】解：（1）有题意可得：1110451002a d a d +=⎧⎨=⎩， 解得1929a d =⎧⎪⎨=⎪⎩（舍去）或112a d =⎧⎨=⎩， 所以n a ＝2n ﹣1，12n n b -=．（2）∵n n n a c b =，1212n n n c --=， ∴2313572112222n n n T --=+++++①， 2345113579212222222n n n T -=++++++②， ①﹣②可得221111212323222222n n n nn n T --+=++++-=-， 故12362n n n T -+=-． 【点睛】用错位相减法求和应注意的问题(1)要善于识别题目类型，特别是等比数列公比为负数的情形；(2)在写出“S n ”与“qS n ”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“S n －qS n ”的表达式；(3)在应用错位相减法求和时，若等比数列的公比为参数，应分公比等于1和不等于1两种情况求解.。