圆柱和圆锥的侧面展开图练习题

(2019年1月最新最细）2019全国中考真题解析考点汇编☆圆柱、圆锥的侧面展开图一、选择题1. （2019江苏无锡，4，3分）已知圆柱的底面半径为2cm ，高为5cm ，则圆柱的侧面积是（ ）A ．20cm 2B ．20πcm 2C ．10πcm 2D ．5πcm 2考点：圆柱的计算。

分析：圆柱的侧面积=底面周长×圆柱的高，据此即可求解． 解答：解：圆柱的底面周长是：2×2π=4πcm ，则圆柱的侧面积是：4π×5=20πcm 2． 故选B ．点评：本题主要考查了圆柱侧面积的计算方法．2. （2019内蒙古呼和浩特，3，3）已知圆柱的底面半径为1，母线长为2，则圆柱的侧面积为（ ）A 、2B 、4C 、2πD 、4π 考点：圆柱的计算． 专题：计算题．分析：圆柱侧面积=底面周长×高． 解答：解：圆柱沿一条母线剪开，所得到的侧面展开图是一个矩形，它的长是底面圆的周长，即2π，宽为母线长为2cm ，所以它的面积为4πcm 2．故选D ．点评：本题考查了圆柱的计算，掌握特殊立体图形的侧面展开图的特点，是解决此类问题的关键．3. （2019四川广安，6，3分）如图所示，圆柱的底面周长为6cm ，AC 是底面圆的直径，高BC ＝ 6cm ，点P 是母线BC 上一点且PC ＝23BC ．一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是（ ）A ．（64π+）cm B ．5cm C ． D ．7cm考点：圆柱的表面展开图，勾股定理 专题：圆柱的表面展开图、勾股定理分析：画出该圆柱的侧面展开图如图所示，则蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离为线段AP 的长．在Rt △ACP 中，AC ＝()632cm =，PC ＝23BC ＝4cm ，所以()5AP cm ==．解答：B点评：解决这类问题要善于将空间图形转化为平面图形，采用“化曲为直”的方法，利用圆柱体的表面展开图，把求最短距离问题转化为求两点之间的线段的长度问题．4. （2019新疆乌鲁木齐，7，4）露露从纸上剪下一个圆形和一个扇形的纸片（如图），用它们恰好能围成一个圆锥模型，若圆的半径为1．扇形的圆心角等于120°，则此扇形的半径为（ ）A 、3B 、6错误！未找到引用源。

九年级上人教新课标圆柱和圆锥的侧面展开图习题Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#第七章第二十一节圆柱和圆锥的侧面展开图习题精选例1 （1）若圆锥的底面半径是3cm，母线长是5cm，则它的侧面展开图的面积是 .（2）若圆锥的母线长为5cm，高为3cm，则其侧面展开图中扇形的圆心角是_______度.分析首先弄清圆的侧面展开图是扇形，（1）中可直接用求得，（2）中先求底面圆半径，扇形弧长，再由弧长公式求圆内角为288°.例2 （1）如果圆柱底面半径为4cm，它的侧面积为，那么圆柱的母线长为（）.（A）16cm （B）16 cm（C）8cm （D）8 cm（2）如果圆柱底面直径为6cm，母线长为10cm，那么圆柱的侧面积为（）（A）30（B）60（C）90（D）120分析圆柱侧面展开图是矩形，（1）可直接用公式求出母线长为8cm，故选（C），（2）中，由直径求出半径是关键，应选（B）.例3 一个圆锥的高是10㎝，侧面展开图是半圆，求圆锥的侧面积.分析：如图，欲求圆锥的侧面积，即求母线长l，底面半径r.由圆锥的形成过程可知，圆锥的高、母线和底面半径构成直角三角形即，且关键找出l与r的关系，又其侧面展开图是半圆，可得关系，即 .解：设圆锥底面半径r，扇形弧长为C，母线长为l，由题意得又得①在中，②由①、②得：∴所求圆锥的侧面积为例4 圆锥的轴截面是等腰，EG是AB上一点，且，那么在锥面上A、M两点间的最短距离是多少分析：设圆锥的侧面展开图是扇形 A点落在点，则所求、M之间的最短距离就是侧面展开图中线段 M的长度.解：如图，扇形的圆心角，在中，过作于N，则中，习题精选一、选择题1．一个圆柱的侧面展开图是正方形，那么它的侧面积和底面积的比是（）（A）1 （B）（C）（D）42．在△ABC中，把△ABC绕直线AC旋转一周得到一个圆锥，其表面积为；把△ABC绕直线AB一周得到另一个圆锥，其表面积为，则（）（A）（B）（C）（D）3．已知一个扇形的半径为60厘米，圆心角为150°，若用它做成一个圆锥的侧面，则这个圆锥的底面半径为（）（A）12.5厘米（B）25厘米（C）50厘米（D）75厘米4．一个圆锥的侧面积是底面积的2倍，这个圆锥的侧面展开图扇形的圆心角是（）（A）60°（B）90°（C）120°（D）180°二、填空题5．用边长分别为和的矩形卷成圆柱，则圆柱的底面面积是_________。

圆柱与圆锥【考点要求】1、认知圆柱与圆锥，掌握它们的各部分特征2、理解并掌握圆柱的侧面积和表面积的计算方法，并会正确计算3、理解并掌握圆柱与圆锥的体积的计算方法，会运用公式计算体积、容积，解决有关的简单的实际问题。

【基础知识回顾】考点一、圆柱的各部分名称，展开图一、圆柱的各部分名称，展开图1、底面、侧面、高：（1）圆柱的两个圆面叫做底面，圆柱的两个底面都是圆，并且大小一样；（2）周围的面叫做侧面，圆柱的侧面是曲面；（3）两个底面之间的距离叫做高，圆柱的高有无数条；拿一张长反省的硬纸，贴在木棒上，快速转动，转动起来的形状就是个一个圆柱。

2、圆柱的侧面展开图：圆柱的侧面展开图是一个长方形，长方形的长相当于圆柱的底面周长，长方形的宽相当于圆柱的高。

【练习一】1、点的运动可以形成（），线的运动可以形成一个（），面的运动可以形成（）。

长方形绕一条边旋转一周可以形成（）2、圆柱由（）个面组成，分别是（）（）（）组成，上下底面都是（），侧面的展开是一个（）。

3、圆柱的侧面展开是一个长方形，长方形的长等于圆柱的（），长方形的宽等于圆柱的（）4、如右图，以长方形的长为轴，旋转一周，得到的立体图形是（），那么，得到的这个立体图形的高是（）厘米，底面周长是（）厘米。

3厘米6厘米5、判断（1）长方体中最多有4个面可能是正方形（）（2）一个圆柱，如果底面直径和高相等，则圆柱的侧面展开是正方形（）（3）如果一个物体上、下底面是面积相等的两个圆，那么这个物体一定是圆柱（）。

考点二、圆柱的表面积π+2πrh=2πr（r+h）二、圆柱的表面积=2个圆的面积+1个侧面积=2r21、圆柱的侧面积=底面周长×高=πdh=2πrh因为圆柱的侧面展开是一个长方形，长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高，所以长方形的面积就是圆柱的侧面积=底面周长×高π×22、圆柱的2个底面积：S=r2π+2πrh=2πr（r+h）3、圆柱的表面积：2个底面积+1个侧面积=2r2注意：有时题目计算表面积时，并不是三个面的面积都要计算，要结合具体题目具体分析，比如，通风管就只用计算侧面积即可，无盖的水桶就只用计算侧面积和1个底面积4、圆柱的截断与拼接：（1）把一个圆柱截成两个圆柱，增加的表面积是两个底面积；（2）把两个同样粗细的圆柱拼成一个圆柱，减少的表面积是两个底面积。

直棱柱、圆锥的侧面展开图1. 下列图形中，是圆锥侧面展开图的是( )2. 下面的图形中，是三棱柱的侧面展开图的是( )3. 经过圆锥顶点的截面的形状可能是( )4. 如图是某个几何体的展开图，该几何体是( )A．圆柱 B．圆锥 C．四棱柱 D．三棱柱5. 小亮为今年参加中考的好友小杰制作了一个正方体礼品盒（如图），六个面上各有一个字，连起来就是“预祝中考成功”，其中“预”的对面是“中”，“成”的对面是“功”，则它的平面展开图可能是( )6. 如图是一个长方体包装盒,则它的平面展开图是( )7. 如图，一个圆锥的侧面展开图是半径为1的半圆，则该圆锥的底面半径是( )A.1B.34C.12D.138. 若圆锥的侧面展开图为半圆，则该圆锥的母线l 与底面半径r 的关系是( )A ．l ＝2rB ．l ＝3rC ．l ＝rD ．l ＝329. 用一圆心角为120°，半径为6 cm 的扇形做成一个圆锥的侧面，这个圆锥的底面的半径是( )A ．1cmB ．2cmC ．3cmD ．4cm10. 将一个圆心角是90°的扇形围成圆锥的侧面，则该圆锥的侧面积S 侧和底面积S 底的关系为( )A ．S 侧＝S 底B ．S 侧＝2S 底C ．S 侧＝3S 底D ．S 侧＝4S 底11. 若一个圆锥的底面积是侧面积的13，则该圆锥侧面展开图的圆心角度数是_______度.12. 如果圆锥的母线长为5cm ，底面半径为3cm ，那么圆锥的全面积为____ cm 2. 13. 若一个圆锥的主视图是腰长为5，底边长为6的等腰三角形，则该圆锥的侧面积是___________．14. 如图，扇形OED 的半径为3，边长为3的菱形OABC 的顶点A ，C ，B 分别在OD ，OE ，DE ︵上，若把扇形OED 围成一个圆锥，则此圆锥的高为_________．15. 在学校组织的实践活动中，小新同学用纸板制作了一个圆锥模型，它的底面半径为1，高为22，则这个圆锥的侧面积是_________．16. 如图，在Rt△ABC中，∠BAC＝90°，AB＝3，BC＝5，若把Rt△ABC绕直线AC旋转一周，则所得圆锥的侧面积等于_________．17. 如图，用圆心角为120°，半径为6cm的扇形纸片卷成一个圆锥形无底纸帽，则这个纸帽的高是_________ cm．18. 如图，如果从半径为5 cm 的圆形纸片上剪去15圆周的一个扇形，将留下的扇形围成一个圆锥(接缝处不重叠)，那么这个圆锥的高是______cm.19. 已知一个扇形的半径为60厘米，圆心角为150°.用它围成一个圆锥的侧面，那么圆锥的底面半径为_______厘米．20. 如图所示，沿虚线折成正方体，对面数字之和为2的数有 对.21. 如图，已知圆锥的母线AB=6，底面半径r=2，求圆锥的侧面展开图的扇形圆心角.22. 要在如图①所示的一个机器零件(尺寸如图②所示，单位：mm)的表面涂上防锈漆，请你帮助计算一下这个零件的表面积．(参考公式：S圆柱侧＝2πrh，SS圆＝πr2，其中r为底面圆半径，h为高，l为母线长，π取3.14) 圆锥侧＝πrl，23. 如图所示的是一个食品包装盒的平面展开图.(1)请写出这个包装盒的多面体形状的名称；(2)请根据图中所标的尺寸，计算这个多面体的侧面积和全面积(侧面积与两个底面积之和).24. 如图，在半径为50cm的圆形铁片上剪一块扇形铁片，用它制作成一个底面直径为80cm，母线长为50cm的圆锥形烟囱帽，求剪下来的扇形的圆心角的度数．25. 如图，有一直径为2m的圆形纸片，要从中去一个最大的圆心角是90°的扇形ABC.(1)求被剪掉的阴影部分的面积；(2)用所留的扇形纸片围成一个圆锥，该圆锥的底面圆的半径是多少？26. 圆锥形烟囱帽的底面直径是100cm，母线长为60cm，求它的侧面展开图中扇形的圆心角及面积．27. 如图，在⊙O中，AB＝43，AC是⊙O的直径，AC⊥BD于点F，∠A＝30°.(1)求图中阴影部分的面积；(2)若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．28. 如图，有一圆锥形粮堆，其轴截面示意图是边长为6 m的正△ABC，粮堆母线AC的中点P处有一老鼠正在偷吃粮食，此时小猫正在B处，它要沿圆锥侧面到达P处捕捉老鼠，则小猫所经过的最短路径是多少？答案：1---10 BABDC ACABD11. 12012. 24π13. 15π 14. 35215. 3π16. 15π17. 4218. 319. 2520. 321. 解：设圆心角为n°，则有2πr=180n π·AB ∴4π=180n π×6，∴n=120，扇形的圆心角α=120° 22. 解：36424mm 223. (1)这个多面体是直六棱柱(2)S 侧=6ab S 全面积b 224. 解：母线l ＝50，底面半径r ＝40，∴圆心角度数θ＝r l·360°＝288° 25. 解：(1)14πm 2 (2)14m 26. 解：设其展开图中扇形的半径为R ，弧长为l ，圆心角为α，则R ＝60cm ，l ＝100πcm.由弧长公式l ＝n πR 180，得n ＝180×100π60π＝300，即α＝n °＝300°，S 扇形＝12×60×100π＝3000π(cm 2) 27. 解：(1)163π (2)4328. 解：设圆锥的底面半径为r ，母线长为l ，展开后所得扇形的圆心角的度数为n °，则底面圆的周长为2πr ，侧面展开图的弧长为n πl 180，∴2πr ＝n πl 180.由题意知，轴截面△ABC 为等边三角形，∵AB ＝BC ，即l ＝2r ＝6.∴r＝3，∴2π×3＝n π×6180，∴n ＝180，即其侧面展开图为半圆，如图，则△ABP 为直角三角形，BP 为最短线路．在Rt △ABP 中，BP ＝AB 2＋AP 2＝62＋32＝35(m)，即小猫所经过的最短路程是35m。

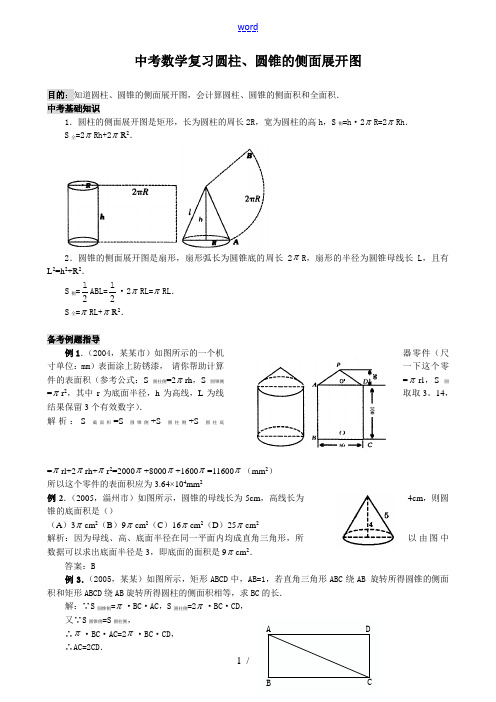
中考数学复习圆柱、圆锥的侧面展开图目的：知道圆柱、圆锥的侧面展开图，会计算圆柱、圆锥的侧面积和全面积．中考基础知识1．圆柱的侧面展开图是矩形，长为圆柱的周长2R，宽为圆柱的高h，S侧=h·2πR=2πRh．S全=2πRh+2πR2．2．圆锥的侧面展开图是扇形，扇形弧长为圆锥底的周长2πR，扇形的半径为圆锥母线长L，且有L2=h2+R2．S侧=21ABL=21·2πRL=πRL．S全=πRL+πR2．备考例题指导例1．（2004，某某市）如图所示的一个机器零件（尺寸单位：mm）表面涂上防锈漆，•请你帮助计算一下这个零件的表面积（参考公式：S圆柱侧=2πrh，S圆锥侧=πrl，S圆=πr2，其中r为底面半径，h为高线，L为线取取3。

14，结果保留3个有效数字）．解析：S截面积=S圆锥侧+S圆柱侧+S圆柱底=πrl+2πrh+πr2=2000π+8000π+1600π=11600π（mm2）所以这个零件的表面积应为3.64×104mm2例2．（2005，淄州市）如图所示，圆锥的母线长为5cm，高线长为4cm，则圆锥的底面积是（）（A）3πcm2（B）9πcm2（C）16πcm2（D）25πcm2解析：因为母线、高、底面半径在同一平面内均成直角三角形，所以由图中数据可以求出底面半径是3，即底面的面积是9πcm2．答案：B例3．（2005，某某）如图所示，矩形ABCD中，AB=1，若直角三角形ABC绕AB•旋转所得圆锥的侧面积和矩形ABCD绕AB旋转所得圆柱的侧面积相等，求BC的长．解：∵S圆锥侧=π·BC·AC，S圆柱侧=2π·BC·CD，又∵S圆锥侧=S圆柱侧，∴π·BC·AC=2π·BC·CD，∴AC=2CD．DA∵ABCD 是矩形，∴CD=AB=1，∴AC=2CD=2， 在Rt △ABC 中，BC=22AC AB -=3∴BC=3．备考巩固练习1．（1）（2005，某某）如图1，圆锥底面圆的直径为6cm ，高为4cm ，•则它的全面积为_______cm 2（结果保留π）（1） (2) (3)（2）（2005，某某）如图2，已知圆锥的母线长OA=8，底面圆的半径r=2，若一只小虫从A•点出发，••绕圆锥的侧面爬行一周后又回到A•点，••则小虫爬行的最短路线的长是______（结果保留根式） （3）（2005，某某）农村常需要塔建截面为半圆形的全封闭蔬菜塑料暖房（•如图3所示），则需塑料布y（m 2）与半径R （m ）的函数关系式是（不考虑塑料埋在土里的部分）________． 2．选择题（1）（2005，某某）如图4，将图中的阴影部分剪下来，围成一个几何体的侧面，•使AB 、DC 重合，则所围成的几何体图形是（ ）(4) (5)（2）（2005，某某）在图5的几何体中，上下底面都是平行四边形，各个侧面都是梯形，那么图中和下底面平行的直线有：（ ）（A ）1条 （B ）2条 （C ）4条 （D ）8条（3）（2005，某某）已知圆柱的侧面积为10π，则它的轴截面面积为（ ） A ．5 B ．10 C ．12 D ．20（4）（2005，某某）若圆锥的轴截面是一个边长为2cm 的等边三角形，则这个圆锥的侧面积是（ ） （A ）2πcm 2 （B ）2c m 2 （C ）4πc m 2 （D ）4cm 2（5）（2005，某某）一个底面半径为5cm 母线长为16cm 线的圆锥，它的侧面展开图的面积是（ ） （A ）80πcm 2 （B ）40πc m 2 （C ）80c m 2 （D ）40c m 23．圆锥母线长为6cm ，底面直径为10cm ，求这个圆锥的侧面积．4．已知，矩形ABCD（如图），AB=2cm，AD=6cm，求分别以AB、AD所在的直线为轴旋转后所得圆柱的侧面积．5．一个圆柱的侧面积等于两底面积之和，试确定它的高h与底面半径R•之间的关系．答案：1．（1）24π（2）（3）y=30πR+πR22．（1）D （2）C （3）B （4）A （5）A 3．30πcm24．12πcm2，12πcm25．h=R。

小学六年级下册圆柱与圆锥展开图练习（含答案）小学六年级下册圆柱与圆锥的展开图练习一．解答题（共19小题）1．（2011?龙湾区）请你制作一个无盖圆柱形水桶，有以下几种型号的铁皮可搭配选择．（1）你选择的材料是_________号和_________号．（2）你选择的材料制成水桶的容积是几升．2．把一张长方形铁皮按下图剪开正好能制成一个底面半径2分米的铁皮油桶．这张铁皮的面积至少多少平方分米？3．（2006?渝中区）如图阴影部分正好能做成一个圆柱形的小油桶，求这个圆柱形小油桶的体积．（接着处忽略不计）4．一个圆柱体的侧面是一个正方形，直径是，正方形面积是_________（保留两位小数）5．一个圆柱体底面周长4cm，高2cm，画出它的侧面展开图．6．一个圆柱，底面直径和高都是2厘米．请你画出它的表面展开图．（作图时取整厘米数）7．如图是一块长方形铁皮，用它做一个圆柱形的水桶，现在要配上一块正方形铁皮，至少需要多大面积的正方形的铁皮？（单位：分米）8．一个圆柱底面直径是10厘米，高是20厘米，把圆柱的侧面沿着它的一条高剪开，再打开，然后按1：10的比例尺画出它的侧面展开图．并标明数据．9．一个圆柱的侧面展开是一个边长厘米的正方形，这个圆柱的底面半径是_________厘米．10．有一个硬纸做成的礼品盒，用彩带扎住（如图），打结处用去的彩带长18厘米．（1）共需要彩带多少厘米？（2）做这样一个礼品盒至少要多少硬纸？（3）这个礼品盒的体积是多少？11．画出一个底面半径1厘米、高5厘米的圆柱的表面展开图．12．画一个底面直径是2厘米、高3厘米的圆柱体的表面展开图（每个方格边长1厘米．）13．利用图中的纸板可以做一个最大的圆柱体，这个圆柱的侧面积是多少平方分米？14．观察填空．a．b．（1）请在上图的括号中填上各面（或量）名称，在横线上填上图形的名称．（2）图a外表的_________面是曲面，相等的两个面是_________形；图b外表的_________面也是曲面，将它展开可得到一个_________形，这种立体图形有_________条高，_________个底面．15．把图①“底面”、“底面的周长”、“高”分别填入图②的圆柱侧面展开图中的合适位置．_________16．已知：一节烟筒的一端所在的平面与轴垂直，这端的半径为r．另一端所在的平面与轴斜交．烟筒的最短母线长为h1，最长母线长为h2．求这节烟筒的面积．17．把下面圆柱的侧面沿高展开，得到的长方形长和宽各是几厘米？两个底面分别是多大的圆？在方格纸上画出这个圆柱的展开图．（每个方格边长1厘米）18．已知圆柱的底面直径是6cm，侧面展开是一个正方形，求圆柱的高．19．如图所示，有一卷紧紧缠绕一起的塑料薄膜，薄膜直径为20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为厘米，求薄膜展开后的面积是多少平方厘米．小学六年级下册圆柱与圆锥的展开图练习参考答案与试题解析一．解答题（共19小题）1．（2011?龙湾区）请你制作一个无盖圆柱形水桶，有以下几种型号的铁皮可搭配选择．（1）你选择的材料是②号和③号．（2）你选择的材料制成水桶的容积是几升．考点：圆柱的展开图；立体图形的容积．专题：压轴题．分析：（1）制作圆柱形水桶，说明要选一个长方形和一个圆形铁皮，而且所选的长方形的一条边和圆的周长相等即可达到要求，关键算出圆的周长；（2）由上面提供的数据直接运用圆柱的体积计算公式列式解决问题．解答：解：（1）材料②的周长×4=（分米），材料②的周长2××3=（分米），所以要选材料②、③；故答案为：②，③；（2）制作成水桶的底面直径是4分米，高是5分米；水桶的容积：×（4÷2）2×5，=×22×5，=×4×5，=（立方分米），立方分米=升，答：水桶的容积为升．点评：此题主要考查圆柱的展开图以及利用圆柱的体积计算公式解答问题．2．把一张长方形铁皮按下图剪开正好能制成一个底面半径2分米的铁皮油桶．这张铁皮的面积至少多少平方分米？考点：长方形、正方形的面积；圆柱的展开图；圆、圆环的周长．专题：压轴题．分析：要求这张铁皮的面积至少是多少平方分米，也就是求这个长方形的面积，这个长方形的宽是这两个圆的直径和，也就是4个半径，即宽=4×半径，长=底面周长+2×半径，根据长方形的面积=长×宽，计算出答案．解答：解：长方形的宽：2×2×2=8（分米）；长方形的长：×2×2+2×2=+4=（分米）；长方形的面积：×8=（平方分米）；答：这张铁皮的面积至少平方分米．点评：解答本道题的关键是首先分清求这张铁皮的面积也就是求大长方形的面积，进一步利用圆柱的侧面展开与长方形的长和宽的关系解决问题．3．（2006?渝中区）如图阴影部分正好能做成一个圆柱形的小油桶，求这个圆柱形小油桶的体积．（接着处忽略不计）考点：图形的拆拼（切拼）；圆柱的展开图．专题：压轴题；立体图形的认识与计算．分析：如图，设圆的直径是d，则圆的周长=πd，两个圆的直径加上底面周长是分米，据此可求出圆的直径，进而求出半径，小油桶的高等于底面直径，根据圆柱的体积公式V=πr2h即可求出这个小油桶的体积．解答：解：设底面直径是d分米2d+==d=÷d=2，×（）2×2=×1×2=（立方分米），答：这个圆柱形小油桶的体积是立方分米；故答案为：立方分米点评：本题是考查图形的切拼问题、圆柱的展开图、圆柱体积的计算等．解答此题的关键是根据两个圆的直径加上底面周长是分米求出圆的直径．4．一个圆柱体的侧面是一个正方形，直径是，正方形面积是平方分米（保留两位小数）考点：圆柱的展开图；长方形、正方形的面积．专题：立体图形的认识与计算．分析：由圆柱的侧面展开图的特点可知：圆柱的侧面展开后是一个长方形，长方形的长等于圆柱的底面周长，宽等于圆柱的高，又因题干中是一个正方形，则圆柱的底面周长等于高，求出圆柱的底面周长，利用长方形的面积公式即可求解，解答：解：（×π）×（×π），=×，≈（平方分米）；答：正方形的面积是平方分米．故答案为：平方分米．点评：解答此题的主要依据是：圆柱的侧面展开图的特点．5．一个圆柱体底面周长4cm，高2cm，画出它的侧面展开图．考点：圆柱的展开图．专题：作图题；立体图形的认识与计算．分析：根据题意知道，沿圆柱的高展开，得到一个长方形，长方形的长是圆柱的底面周长，长方形的宽是圆柱的高，由此画出长方形即可．解答：解：长方形的长4厘米，长方形的宽是2厘米；侧面展开图如下：点评：本题主要考查了圆柱的侧面展开图与圆柱的关系：沿圆柱的高展开得到一个长方形，长方形的长是圆柱的底面周长，长方形的宽是圆柱的高．6．一个圆柱，底面直径和高都是2厘米．请你画出它的表面展开图．（作图时取整厘米数）考点：圆柱的展开图．分析：沿圆柱的高展开，得到一个长方形，长方形的长是圆柱的底面周长，长方形的宽是圆柱的高，由此根据圆的周长公式C=πd，求出圆柱的底面周长，即长方形的长，进而画出长方形即可．解答：解：长方形的长是：×2≈6（厘米），点评：解答此题的关键是，知道圆柱的展开图与圆柱的关系，并求出展开图相应的边长，即可做出图．7．如图是一块长方形铁皮，用它做一个圆柱形的水桶，现在要配上一块正方形铁皮，至少需要多大面积的正方形的铁皮？（单位：分米）考点：圆柱的展开图．专题：立体图形的认识与计算．分析：由题意可知：需要的正方形的铁皮的最大内接圆的直径应等于正方形的边长，这个圆的底面周长已知，则可以求出底面直径，也就等于知道了正方形的边长，再利用正方形的面积公式问题即可得解．解答：解：正方形的边长是：÷=3（分米），面积是：3×3=9（平方分米）．答：至少需要9平方分米的正方形的铁皮．点评：解答此题的关键是根据正方形的铁皮的最大内接圆的直径等于正方形的边长求得正方形的边长．8．一个圆柱底面直径是10厘米，高是20厘米，把圆柱的侧面沿着它的一条高剪开，再打开，然后按1：10的比例尺画出它的侧面展开图．并标明数据．考点：圆柱的展开图．专题：作图题．分析：圆柱的侧面沿着一条高展开会得到一个长方形，它的长等于圆柱的底面周长，它的宽等于圆柱的高；据此可以求出圆柱的侧面展开后长方形的长，然后根据：图上距离=实际距离×比例尺，分别求出长方形图上的长和宽，然后画出即可．解答：解：×10=（厘米），图上的长：×=（厘米）；图上的宽：20×=2（厘米）；画图如下：点评：此题考查了圆柱的侧面展开图，应明确：圆柱的侧面沿着一条高展开会得到一个长方形，它的长等于圆柱的底面周长，它的宽等于圆柱的高；用到的知识点：图上距离、实际距离和比例尺三者之间的关系．9．一个圆柱的侧面展开是一个边长厘米的正方形，这个圆柱的底面半径是5厘米．考点：圆柱的展开图．分析：圆柱的侧面展开后是一个正方形，那么圆柱的底面周长和高都等于正方形的边长；根据r=c÷π÷2，即可列式计算出圆柱的底面半径．解答：解：底面半径：÷÷2，=10÷2，=5（厘米）；答：这个圆柱的底面半径是5厘米．故答案为：5．点评：此题主要考查了圆柱的侧面展开图与圆柱的关系．10．有一个硬纸做成的礼品盒，用彩带扎住（如图），打结处用去的彩带长18厘米．（1）共需要彩带多少厘米？（2）做这样一个礼品盒至少要多少硬纸？（3）这个礼品盒的体积是多少？考点：圆柱的展开图．分析：①彩带的长为4条直径加上4条高和打结处用去的彩带长；②需要的硬纸是指圆柱的表面积，求出两个底面积和侧面积相加即可；③已知底面直径和高，利用圆柱的体积计算公式代入计算即可．解答：答：①彩带长：20×4+50×4+18=80+200+18=298（厘米），答：共需要彩带298厘米．②表面积：×20×50+×（20÷2）2×2，=3140+628，=3768（平方厘米）．答：做这样一个礼品盒至少要3768平方厘米硬纸．③体积：×（20÷2）2×50=15700（立方厘米）．答：这个礼品盒的体积是15700立方厘米．点评：此题综合考查圆柱的体积与表面积的计算方法，计算找准公式，灵活解答．11．画出一个底面半径1厘米、高5厘米的圆柱的表面展开图．考点：圆柱的展开图．专题：立体图形的认识与计算．分析：沿圆柱的高展开，得到一个长方形，长方形的长是圆柱的底面周长，长方形的宽是圆柱的高，由此根据圆的周长公式C=2πr，求出圆柱的底面周长，即长方形的长，进而画出长方形即可；圆柱的上下两个底面是半径为1厘米的圆，画出即可．解答：解：长方形的长是：2××1=（厘米），底面半径1厘米、高5厘米的圆柱的表面展开图为：点评：解答此题的关键是，知道圆柱的展开图与圆柱的关系，并求出展开图相应的边长，即可做出图．12．画一个底面直径是2厘米、高3厘米的圆柱体的表面展开图（每个方格边长1厘米．）考点：圆柱的展开图．专题：作图题．分析：由圆柱的侧面展开图的特点可知：圆柱的侧面展开后是一个长方形，长方形的长等于圆柱的底面周长，宽等于圆柱的高，圆柱的底面直径和高已知，求出底面周长，于是可以画出其表面展开图．解答：解：如图所示，即为所要求画的圆柱的表面展开图：×2=厘米，2÷2=1厘米，点评：解答此题的关键是明白：圆柱的侧面展开后是一个长方形，这个长方形的长就是圆柱的底面周长，宽就是圆柱的高．13．利用图中的纸板可以做一个最大的圆柱体，这个圆柱的侧面积是多少平方分米？考点：关于圆柱的应用题；圆柱的展开图．专题：立体图形的认识与计算．分析：因为圆柱的侧面积=底面周长×高，于是先计算出底面周长，再乘高即可得解．解答：解：×（8÷2），=×4，=（分米）；×8=（平方分米）；答：这个圆柱的侧面积是平方分米．点评：解答此题时，不能把长方形的长当成圆柱的底面周长．14．观察填空．a．b．（1）请在上图的括号中填上各面（或量）名称，在横线上填上图形的名称．（2）图a外表的侧面面是曲面，相等的两个面是圆形；图b外表的侧面面也是曲面，将它展开可得到一个扇形，这种立体图形有一条高，一个底面．考点：圆柱的特征；圆锥的特征；圆柱的展开图．专题：立体图形的认识与计算．分析：圆柱体的上下底面是完全相同的两个圆，侧面是一个曲面，侧面展开是一个长方形；圆锥的侧面是一个曲面，侧面展开是一个扇形，底面是圆，顶点到底面圆心的距离叫做圆锥的高．解答：解：（1）（2）图a外表的侧面面是曲面，相等的两个面是圆形；图b外表的侧面面也是曲面，将它展开可得到一个扇形，这种立体图形有一条高，一个底面．故答案为：侧面，圆，侧面，扇，一，一．点评：此题主要考查圆柱体和圆锥体的特征以及各部分的名称．15．把图①“底面”、“底面的周长”、“高”分别填入图②的圆柱侧面展开图中的合适位置．，考点：圆柱的展开图．专题：立体图形的认识与计算．分析：根据圆柱的特征，它的上、下是完全相同的两个圆，侧面是一个曲面，圆柱侧面沿高展开是一个正方形或长方形；当圆柱体的底面周长和高相等时，侧面展开是正方形，据此解答即可．解答：解：据分析填写如下：点评：此题主要考查圆柱的特征和它的侧面展开图的形状，以及展开图的长、宽与圆柱的底面周长和高的关系．16．已知：一节烟筒的一端所在的平面与轴垂直，这端的半径为r．另一端所在的平面与轴斜交．烟筒的最短母线长为h1，最长母线长为h2．求这节烟筒的面积．考点：圆柱的展开图．专题：立体图形的认识与计算．分析：设想取一节与这烟筒相同的烟筒，二者可以拼成一个圆柱的侧面．这侧面的底半径为r，高为h1+h2，由此根据圆柱的侧面积公式求出它的面积，再除以2即可．解答：解：设想取一节与这烟筒相同的烟筒，二者可以拼成一个圆柱的侧面．这侧面的底半径为r，高为h1+h2；所以这节烟筒的面积是：2πr（h1+h2）÷2=πr（h1+h2），答：这节烟筒的面积是πr（h1+h2）．点评：本题主要是利用假设的方法，构建一个新的圆柱体，再利用圆柱的侧面积公式解决问题．17．把下面圆柱的侧面沿高展开，得到的长方形长和宽各是几厘米？两个底面分别是多大的圆？在方格纸上画出这个圆柱的展开图．（每个方格边长1厘米）考点：圆柱的展开图．专题：作图题．分析：应明确圆柱由三部分组成：圆柱的侧面、圆柱的上、下两个底面；由题意可知：该圆柱的底面直径是2厘米，高为2厘米，根据“圆柱的侧面展开后是一个长方形，长方形的长等于圆柱的底面周长，长方形的宽等于圆柱的高”可知：先根据圆的周长=πd求出圆柱侧面展开后的长，宽为圆柱的高；圆柱的上下两个底面为直径为2厘米的圆，画出即可．解答：解：长方形的长：×2=（厘米），宽为2厘米；两个直径为2厘米的圆；画图如下：点评：此题主要考查圆柱体的侧面沿高展开得到的长方形的长、宽与圆柱体的底面周长、高的关系．18．已知圆柱的底面直径是6cm，侧面展开是一个正方形，求圆柱的高．考点：圆柱的展开图．专题：立体图形的认识与计算．分析：因为圆柱的侧面展开图是一个正方形，说明圆柱的底面周长等于圆柱的高，由此根据圆的周长公式C=πd，求出圆柱的底面周长，即圆柱的高．解答：解：×6=（厘米），答：圆柱的高是厘米．点评：此题主要考查了圆柱的侧面展开图与圆柱的关系，如果圆柱的侧面展开图是一个正方形，说明圆柱的底面周长等于圆柱的高．19．如图所示，有一卷紧紧缠绕一起的塑料薄膜，薄膜直径为20厘米，中间有一直径为8厘米的卷轴，已知薄膜的厚度为厘米，求薄膜展开后的面积是多少平方厘米．考点：圆柱的展开图；长方形、正方形的面积．分析：根据题意可以求出塑料薄膜横截面的环形面积，又知道塑料薄膜的长，所以可以求出塑料薄膜的体积来；塑料薄膜展开后是面很大，高非常小（即薄膜的厚度）的长方体，长方体的体积和高已知，代入公式即可求出底面积．解答：解：由题意知：S环=π（R2﹣r2），=×〔﹣〕，=×（100﹣16），=×84，=（平方厘米），V=S环×80，=×80，=（立方厘米），薄膜展开后的面积：÷，=527520（平方厘米）；答：薄膜展开后的面积是527520平方厘米．点评：此题考查了环形圆柱的体积和圆柱的侧面展开图．。

六年级下圆柱与圆锥单元测试（含答案)2 学校:___________姓名：___________班级：___________考号：___________一、选择题1．圆锥的底面半径缩小到原来的，高（），体积不变。

A．扩大到原来的2倍B．扩大到原来的4倍C．缩小到原来的【答案】B2．圆锥的侧面展开图是一个（）.A．三角形B．长方形或正方形C．圆形D．扇形【答案】D3．求圆柱形木桶内盛多少升水，就是求水桶的（）A．侧面积B．表面积C．体积D．容积【答案】D4．圆柱的高不变，底面半径扩大2倍，它的体积扩大（）。

A．4倍B．8倍C．16倍D．12倍【答案】A，则圆柱的侧面识（）。

5．圆柱的底面直径扩大为原来的2倍，高缩小到原来的12C．不变A．扩大为原来的2倍B．缩小到原来的12【答案】C6．把一个圆柱体的侧面展开得到一个边长4分米的正方形，这个圆柱体的侧面积是（）平方分米．A．16 B．50.24 C．100.48【答案】A7．下列圆柱的表面积示意图中，各长度标注正确的是（）。

A．B．C．D．【答案】B8．用24个铁圆锥，可以熔铸成（）个等底等高的铁圆柱．A．12 B．8 C．6 D．4【答案】B9．一个圆柱与一个圆锥的底面积和体积分别相等，已知圆柱的高是12cm，圆锥的高是（）。

A．36cm B．24cm C．8cm D．4cm【答案】A10．一个圆柱的底面半径扩大4倍，高不变，它的体积扩大（）A．4倍B．8倍C．16倍【答案】C11．一根圆柱形的木料长2米，截成相等的3段，表面积增加24平方厘米，原来的木料的体积是（）立方厘米。

A．480 B．1600 C．12 D．1200【答案】D12．圆锥的高有（）条。

A．1 B．2 C．无数【答案】A二、填空题13．把一块石头，浸没在一个底面积是60平方厘米的圆柱形容器里，容器的水面上升了1.5厘米，这块石头的体积是_____立方厘米．【答案】9014．圆柱上、下两个底面都是（____）形,它们的面积（____）。

六年级下册数学试题--圆柱与圆锥-53-人教新课标一、单选题（共2题；共4分）1.下面四幅图中，不可能是圆柱侧面展开图的是（）。

A. B.C. D.【答案】 D【考点】圆柱的展开图【解析】【解答】圆柱侧面展开图不可能是梯形。

故答案为：D。

【分析】圆柱侧面展开图是长方形、正方形、平行四边形等。

因为圆柱展开图的长为圆柱底面周长，宽为圆柱的高，圆柱的底面周长相等即展开图上下两条边相等。

2.一个空罐（如图）可盛9碗水或8杯水。

如果将3碗水和4杯水倒入空罐中，水面应到达位置（）。

A. PB. QC. RD. S【答案】A【考点】圆柱的体积（容积）【解析】【解答】解：3÷9=，3碗水倒入罐子占2格；4÷8=，4杯水倒入罐子占3格；共占7格，所以水面应到达P处。

故答案为：A。

【分析】先计算出3碗水占罐子的几分之几，然后确定3碗水占几格。

用同样的方法计算出4杯水占几格，然后判断出3碗水和4杯水共占几格即可确定水面应到达的位置。

二、判断题（共1题；共2分）3.把一个圆柱形木块削成一个最大的圆锥，圆锥的体积是削去部分体积的。

【答案】错误【考点】圆柱与圆锥体积的关系【解析】【解答】圆柱与圆锥等底等高时有：圆锥的体积=×圆柱的体积，÷（1-）=÷=所以圆锥的体积是削去部分体积的。

故答案为：错误。

【分析】等底等高的圆柱和圆锥的体积关系：圆锥的体积=×圆柱的体积，削去体积=圆柱的体积-圆锥的体积=×圆柱的体积，即可得出答案。

三、填空题（共3题；共4分）4.一根7m长的圆柱形木棒截成三段后，表面积增加了68dm2，这根圆柱形木棒的体积是________dm3。

【答案】119【考点】圆柱的侧面积、表面积，圆柱的体积（容积）【解析】【解答】圆柱底面积=68÷4=17（dm2）,圆柱的体积=17×7=119（dm3）。

故答案为：119。

【分析】将一个圆柱沿圆柱的高截成3段，圆柱的表面积增加了4个底面积，根据“圆柱的底面积=增加的表面积÷4”即可得出圆柱的底面积，再根据圆柱的体积=底面积×高，即可得出圆柱的体积。