2019届湖南省六校(湖南师大附中、岳阳一中等)高三下学期联考地理试题(解析版)

绝密★启用前湖南省2019届高三毕业班调研联考文科综合能力测试地理试卷★祝考试顺利★注意事项：1、考试范围：高考范围。

2．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B铅笔将答题卡上试卷类型A后的方框涂黑。

3．选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5．选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑．答案写在答题纸上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

6．保持卡面清洁，不折叠，不破损。

7．考试结束后，请将本试题卷、答题卡、草稿纸一并上交。

第Ⅰ卷本卷为选择题，共35小题，每小题4分，共140分。

在每小题给出第四个选项中，只有一项是符合题目要求的。

“绿腰带项目”是德国慕尼黑政府在郊区实施的休闲创意农业项目。

绿腰带项目实施的目的是保持农业用地的同时，最大限度地减少化肥和农药的使用量，种植与当地生态环境相符的农作物，为城市居民提供优质的农产品和适宜的休闲场所。

据此完成1-3题。

1．发展绿腰带项目的前提是当地拥有A．发达便利的交通线B．都市居民的消费需求C．充足的剩余劳动力D．掌握现代科技的农民2．与一般郊区相比，绿腰带农产品的突出优势在于A．种类B．成本C．新鲜度D．品质3．绿腰带项目对慕尼黑郊区的影响是A．完善了服务功能B．扩展了地域范围C．推动城市化进程D．改变土地利用类型人口变动与城市和经济发展密切相关,控制人口总量和增速，是国家对特大城市的要求。

下图示意上海市1996年至2015年小学生人数和常住人口变化图。

读图回答4-5题。

4．据图推断，上海市将小学学制由6年改为5年的时间是A．1999年B．2001年C．2004年D．2007年5．关于上海常住人口及其变化的说法，正确的是A．2012年常住人口要比1997年要少B．常住人口最多的是2007年C．近5年常住人口的变化与产业结构调整和政策有很大关系D．近5年常住人口的变化与上海房价和生活费用太高无关印加文明是在南美洲西部、中安第斯山区发展起来的著名的印第安古代文明。

2019年湖南省娄底市高考数学二模试卷（文科）注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知全集U＝{1，2，3，4，5}，A＝{2，3，4}，B＝{3，5}，则下列结论正确的是（）A．B⊆A B．∁U A＝{1，5} C．A∪B＝{3} D．A∩B＝{2，4，5} 2．（5分）已知i为虚数单位，z（1+i）＝3﹣i，则在复平面上复数z对应的点位于（）A．第四象限B．第三象限C．第二象限D．第一象限3．（5分）某店主为装饰店面打算做一个两色灯牌，从黄、白、蓝、红4种颜色中任意挑选2种颜色，则所选颜色中含有白色的概率是（）A．B．C．D．4．（5分）下列判断正确的是（）A．“α＞45°”是“tanα＞1”的充分不必要条件B．命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”C．命题“∀x∈R，2x＞0”的否定是“∃x0∈R，2x0≤0”D．若命题“p∧q”为假命题，则命题p，q都是假命题5．（5分）已知公差d≠0的等差数列{a n}满足a1＝1，且a2，a4﹣2，a6成等比数列，若正整数m，n满足m﹣n＝10，则a m﹣a n＝（）A．10 B．20 C．30 D．5或406．（5分）秦九韶是我国南宋时期的数学家，他在所著《数书九章》中提出的求多项式值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图，是利用秦九韶算法求一个多项式的值，若输入n，x的值分别为3，，则输出v的值为（）A．17 B．11.5 C．10 D．77．（5分）已知实数x，y满足则z＝2x+y的最小值为（）A．0 B．﹣5 C．2 D．18．（5分）函数f（x）＝的部分图象大致是（）A．B．C．D．9．（5分）将函数f（x）＝sin2x+cos2x的图象向右平移，再把所有点的横坐标伸长到原来的2倍（纵坐标长度不变）得到函数g（x）的图象，则下列说法正确的是（）A．函数g（x）的最大值为+1B．函数g（x）的最小正周期为πC．函数g（x）在区间[，]上单调递增D．函数g（x）的图象关于直线x＝对称10．（5分）已知直线y＝kx﹣1与抛物线x2＝8y相切，则双曲线：x2﹣k2y2＝1的离心率等于（）A．B．C．D．11．（5分）如图，平面四边形ABCD中，E，F是AD，BD中点，AB＝AD＝CD＝2，BD＝2，∠BDC＝90°，将△ABD沿对角线BD折起至△A′D，使平面A′BD⊥平面BCD，则四面体A′BCD中，下列结论不正确的是（）A．EF∥平面A′BCB．异面直线CD与A′B所成的角为90°C．异面直线EF与A′C所成的角为60°D．直线A′C与平面BCD所成的角为30°12．（5分）已知函数f（x）＝lnx﹣+a在x∈[1，e]上有两个零点，则a的取值范围是（）A．[，﹣1）B．[，1）C．[，﹣1] D．[﹣1，e）二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）已知平面向量与的夹角为45°，＝（﹣1，1），||＝1，则|﹣2|＝．14．（5分）已知点A（2，0），B（0，4），O为坐标原点，则△AOB外接圆的标准方程是．15．（5分）已知数列{a n}的前n项和S n＝2a n﹣1（n∈N*），设b n＝1+log2a n，则数列{}的前n项和T n＝．16．（5分）已知四棱锥S﹣ABCD的三视图如图所示，若该四棱锥的各个顶点都在球O的球面上，则球O的表面积等于．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题，共60分．17．（12分）在△ABC中，内角A，B，C所对的边分别为a，b，c，且sin A sin B cos B+sin2B cos A＝2sin C cos B．（1）求tan B的值；（2）若b＝2，△ABC的面积为，求a+c的值18．（12分）如图，ABCD是边长为2的菱形，∠DAB＝60°，EB⊥平面ABCD，FD⊥平面ABCD，EB＝2FD＝4．（1）求证：EF⊥AC；（2）求几何体EFABCD的体积．19．（12分）有一个同学家开了一个小卖部，他为了研究气温对热饮饮料销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的散点图和对比表：（1）从散点图可以发现，各点散布在从左上角到右下角的区域里．因此，气温与当天热饮销售杯数之间成负相关，即气温越高，当天卖出去的热饮杯数越少．统计中常用相关系数r来衡量两个变量之间线性关系的强弱．统计学认为，对于变量x、y，如果r∈[﹣1，﹣0.75]，那么负相关很强；如果r∈[0.75，1]，那么正相关很强；如果r∈（﹣0.75，﹣0.30]∪[0.30，0.75），那么相关性一般；如果r∈[﹣0.25，0.25]，那么相关性较弱．请根据已知数据，判断气温与当天热饮销售杯数相关性的强弱．（2）（ⅰ）请根据已知数据求出气温与当天热饮销售杯数的线性回归方程；（ⅱ）记[x]为不超过x的最大整数，如[1.5]＝1，[﹣4.9]＝﹣5．对于（ⅰ）中求出的线性回归方程y＝x+，将y＝[]x+[]视为气温与当天热饮销售杯数的函数关系．已知气温x与当天热饮每杯的销售利润f（x）的关系是f（x）＝2[]+3（x∈[﹣7，38））（单位：元），请问当气温x为多少时，当天的热饮销售利润总额最大？【参考公式】＝，＝．r＝，【参考数据】（x i﹣）2＝1340，（y i﹣）2≈111，（x i﹣）（y i﹣）＝﹣3953，＝15，＝100，362＝1296，372＝1369．20．（12分）如图，椭圆C：+＝1的右焦点为F，过点F的直线l与椭圆交于A，B两点，直线n：x＝4与x轴相交于点E，点M在直线n上，且满足BM∥x轴．（1）当直线l与x轴垂直时，求直线AM的方程；（2）证明：直线AM经过线段EF的中点．21．（12分）已知函数f（x）＝e x，g（x）＝ax2+x+1（a＞0）．（1）设F（x）＝，讨论函数F（x）的单调性；（2）若0＜a≤，证明：f（x）＞g（x）在（0，+∞）上恒成立．（二）选考题：共10分．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系中，以原点O为极点，x轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的长度单位．已知直线l的参数方程为（t为参数），曲线C的极坐标方程为ρ＝4sin（θ+）．（1）求直线l的普通方程与曲线C的直角坐标方程；（2）若直线l与曲线C交于M，N两点，求△MON的面积．[选修4-5：不等式选讲]23．已知函数f（x）＝|x+1|+2|x﹣a|．（1）设a＝1，求不等式f（x）≤7的解集；（2）已知a＞﹣1，且f（x）的最小值等于3，求实数a的值．2019年湖南省娄底市高考数学二模试卷（文科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）已知全集U＝{1，2，3，4，5}，A＝{2，3，4}，B＝{3，5}，则下列结论正确的是（）A．B⊆A B．∁U A＝{1，5} C．A∪B＝{3} D．A∩B＝{2，4，5} 【分析】由题知集合A与集合B互相没有包含关系，A∩B＝{3}，A∪B＝{2，3，4，5}，∁U A＝{1，5}．【解答】解：全集U＝{1，2，3，4，5}，A＝{2，3，4}，B＝{3，5}，∴由题知集合A与集合B互相没有包含关系，A∩B＝{3}，A∪B＝{2，3，4，5}，∁U A＝{1，5}．故选：B．【点评】本题考查交集、并集、补集的求法，考查交集、并集、补集定义、不等式性质等基础知识，是基础题．2．（5分）已知i为虚数单位，z（1+i）＝3﹣i，则在复平面上复数z对应的点位于（）A．第四象限B．第三象限C．第二象限D．第一象限【分析】把已知等式变形，再由复数代数形式的乘除运算化简得答案．【解答】解：由z（1+i）＝3﹣i，得z＝，在复平面上复数z对应的点的坐标为（1，﹣2），位于第四象限，故选：A．【点评】本题考查复数代数形式的乘除运算，考查复数的代数表示法及其几何意义，是基础题．3．（5分）某店主为装饰店面打算做一个两色灯牌，从黄、白、蓝、红4种颜色中任意挑选2种颜色，则所选颜色中含有白色的概率是（）A．B．C．D．【分析】从黄、白、蓝、红4种颜色中任意选2种颜色，利用列举法能求出所选颜色中含有白色的概率．【解答】解：从黄、白、蓝、红4种颜色中任意选2种颜色的所有基本事件有：黄白，黄蓝，黄红，白蓝，白红，蓝红，共6种．其中包含白色的有3种，∴所选颜色中含有白色的概率为p＝＝．故选：B．【点评】本题考查概率的求法，考查古典概型、列举法等基础知识，考查运算求解能力，是基础题．4．（5分）下列判断正确的是（）A．“α＞45°”是“tanα＞1”的充分不必要条件B．命题“若x2＝1，则x＝1”的否命题为“若x2＝1，则x≠1”C．命题“∀x∈R，2x＞0”的否定是“∃x0∈R，2x0≤0”D．若命题“p∧q”为假命题，则命题p，q都是假命题【分析】利用充要条件判断A的正误；四种命题的真假判断B的正误，命题的否定判断C的正误；复合命题的真假判断D的正误．【解答】解：由否命题的概念知B错；关于A选项，前者应是后者的既不充分也不必要条件；关于D选项，p与q至少有一个为假命题；C选项，满足命题的否定形式，所以C正确．故选：C．【点评】本题考查命题的真假的判断与应用，是基本知识的考查．5．（5分）已知公差d≠0的等差数列{a n}满足a1＝1，且a2，a4﹣2，a6成等比数列，若正整数m，n满足m﹣n＝10，则a m﹣a n＝（）A．10 B．20 C．30 D．5或40【分析】由已知利用等差数列的通项公式结合等比数列的性质列式求解d，再由等差数列的通项公式求解．【解答】解：由题知，∵{a n}为等差数列，∴（3d﹣1）2＝（1+d）（1+5d），∵d≠0，解得d＝3，从而a m﹣a n＝（m﹣n）d＝30，故选：C．【点评】本题考查等差数列的通项公式，考查等比数列的性质，是基础题．6．（5分）秦九韶是我国南宋时期的数学家，他在所著《数书九章》中提出的求多项式值的秦九韶算法，至今仍是比较先进的算法．如图所示的程序框图，是利用秦九韶算法求一个多项式的值，若输入n，x的值分别为3，，则输出v的值为（）A．17 B．11.5 C．10 D．7【分析】根据已知中的程序框图可得，该程序的功能是计算并输出变量v的值，模拟程序的运行过程，可得答案．【解答】解：由程序框图，可得：n＝3，x＝，v＝2v＝4，n＝2v＝7，n＝1v＝11.5．n＝0此时，满足判断框内的条件，退出循环，输出v的值为11.5．故选：B．【点评】本题考查的知识点是程序框图，当程序的运行次数不多或有规律时，可采用模拟运行的办法解答，属于基础题．7．（5分）已知实数x，y满足则z＝2x+y的最小值为（）A．0 B．﹣5 C．2 D．1【分析】画出约束条件的可行域，求出最优解，然后求解即可．【解答】解：由题中给出的三个约束条件，可得可行域为如图所示阴影部分，易知在（0，1）处目标函数取到最小值，最小值为1，故选：D．【点评】本题考查线性规划的简单应用，求出目标函数的最优解的解题的关键．8．（5分）函数f（x）＝的部分图象大致是（）A．B．C．D．【分析】判断函数为减函数排除C，D，再由f（π）＜0得答案．【解答】解：由题知，f（x）的定义域为（﹣∞，0）∪（0，+∞），且f（﹣x）＝﹣f （x），∴f（x）是奇函数，排除C和D，将x＝π代入f（x），得f（π）＜0，故选：A．【点评】本题考查函数的图象及图象变换，考查函数奇偶性的性质及其应用，是基础题．9．（5分）将函数f（x）＝sin2x+cos2x的图象向右平移，再把所有点的横坐标伸长到原来的2倍（纵坐标长度不变）得到函数g（x）的图象，则下列说法正确的是（）A．函数g（x）的最大值为+1B．函数g（x）的最小正周期为πC．函数g（x）在区间[，]上单调递增D．函数g（x）的图象关于直线x＝对称【分析】利用两角和的正弦函数公式化简函数解析式，根函数y＝A sin（ωx+φ）的图象变换可求g（x）＝2sin（x﹣），利用正弦函数的图象和性质即可得解．【解答】解：∵f（x）＝sin2x+cos2x，∴化简得f（x）＝2sin（2x+），∵将函数f（x）＝sin2x+cos2x的图象向右平移，再把所有点的横坐标伸长到原来的2倍（纵坐标长度不变）得到函数g（x）的图象，∴g（x）＝2sin（x﹣），由三角函数性质知：g（x）的最大值为2，最小正周期为2π，对称轴为x＝+kπ，k∈Z，单调增区间为：[﹣+2kπ，+2kπ），k∈Z．故选：C．【点评】本题主要考查了两角和的正弦函数公式，函数y＝A sin（ωx+φ）的图象变换规律，正弦函数的图象和性质的综合应用，考查了数形结合思想，属于基础题．10．（5分）已知直线y＝kx﹣1与抛物线x2＝8y相切，则双曲线：x2﹣k2y2＝1的离心率等于（）A．B．C．D．【分析】联立直线与抛物线方程，利用直线与抛物线相切，求出k，然后求解双曲线的离心率即可．【解答】解：由得x2﹣8kx+8＝0，因为直线与曲线相切，所以△＝64k2﹣32＝0，k2＝，所以双曲线：x2﹣y2＝1的离心率等于＝，故选：C．【点评】本题考查抛物线与直线的位置关系的综合应用，考查转化思想以及计算能力．11．（5分）如图，平面四边形ABCD中，E，F是AD，BD中点，AB＝AD＝CD＝2，BD＝2，∠BDC＝90°，将△ABD沿对角线BD折起至△A′D，使平面A′BD⊥平面BCD，则四面体A′BCD中，下列结论不正确的是（）A．EF∥平面A′BCB．异面直线CD与A′B所成的角为90°C．异面直线EF与A′C所成的角为60°D．直线A′C与平面BCD所成的角为30°【分析】运用线面平行的判定定理可判断A；由面面垂直的性质定理，结合异面直线所成角可判断B；由异面直线所成角和勾股定理的逆定理可判断C；由线面角的求法，可判断D．【解答】解：A：因为E，F分别为A′D和BD两边中点，所以EF∥A′B，即EF∥平面A′BC，EF⊄平面A′BC，A正确；B：因为平面A′BD⊥平面BCD，交线为BD，且CD⊥BD，所以CD⊥平面A′BD，即CD⊥A′B，故B正确；C：取CD边中点M，连接EM，FM，则EM∥A′C，所以∠FEM为异面直线EF与A′C所成角，又EF＝1，EM＝A'C＝，FM＝BC＝，即∠FEM＝90°，故C错误；D：连接A'F，可得A'F⊥BD，由面面垂直的性质定理可得A'F⊥平面BCD，连接CF，可得∠A'CF为A'C与平面BCD所成角，由sin∠A'CF＝＝＝，则直线A′C与平面BCD所成的角为30°，故D正确．故选：C．【点评】本题考查异面直线所成角的求法，线面角的求法和线面平行的判断，考查转化思想和运算能力，属于基础题．12．（5分）已知函数f（x）＝lnx﹣+a在x∈[1，e]上有两个零点，则a的取值范围是（）A．[，﹣1）B．[，1）C．[，﹣1] D．[﹣1，e）【分析】求出函数的导数f′（x）＝+＝，x∈[1，e]．通过当a≥﹣1时，当a ≤﹣e时，当﹣e＜a＜﹣1时，判断导函数的符号，得到函数的单调性然后转化求解a的范围即可．【解答】解：∵f′（x）＝+＝，x∈[1，e]．当a≥﹣1时，f′（x）≥0，f（x）在[1，e]上单调递增，不合题意．当a≤﹣e时，f′（x）≤0，f（x）在[1，e]上单调递减，也不合题意．当﹣e＜a＜﹣1时，则x∈[1，﹣a）时，f′（x）＜0，f（x）在[1，﹣a）上单调递减，x∈（﹣a，e]时，f′（x）＞0，f（x）在（﹣a，e]上单调递增，又f（1）＝0，所以f（x）在x∈[1，e]上有两个零点，只需f（e）＝1﹣+a≥0即可，解得≤a＜﹣1．综上，a的取值范围是：[，﹣1）．故选：A．【点评】本题考查函数的导数的应用，导函数的符号以及函数的单调性的判断，考查分类讨论思想的应用．二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）已知平面向量与的夹角为45°，＝（﹣1，1），||＝1，则|﹣2|＝．【分析】利用已知条件，通过向量的数量积的运算法则化简求解即可．【解答】解：平面向量与的夹角为45°，＝（﹣1，1），||＝1，则|﹣2|＝＝＝故答案为：．【点评】本题考查向量的模以及向量的数量积的运算法则的应用，考查计算能力．14．（5分）已知点A（2，0），B（0，4），O为坐标原点，则△AOB外接圆的标准方程是（x﹣1）2+（y﹣2）2＝5．【分析】由题知OA⊥OB，可得圆心为AB的中点，半径为|AB|，从而写出它的标准方程．【解答】解：由题知OA ⊥OB ，故△ABO 外接圆的圆心为AB 的中点（1，2），半径为|AB |＝，所以△ABO 外接圆的标准方程为（x ﹣1）2+（y ﹣2）2＝5．故答案为：：（x ﹣1）2+（y ﹣2）2＝5．【点评】本题主要考查求圆的标准方程的方法，关键是确定圆心和半径，属于中档题．15．（5分）已知数列{a n }的前n 项和S n ＝2a n ﹣1（n ∈N *），设b n ＝1+log 2a n ，则数列{}的前n 项和T n ＝ ． 【分析】令n ＝1，a 1＝1；n ≥2时，a n ＝S n ﹣S n ﹣1，推出a n ＝2a n ﹣1，然后求解通项公式，化简数列{}的通项公式，求解数列的和即可．【解答】解：令n ＝1，a 1＝1；n ≥2时，a n ＝S n ﹣S n ﹣1＝2a n ﹣2a n ﹣1，整理得：a n ＝2a n ﹣1，所以a n ＝2n ﹣1，b n ＝1+log 22n ﹣1＝n ，T n ＝++…+＝＝1﹣＝．故答案为：． 【点评】本题考查数列的递推关系式的应用，数列求和，考查计算能力．16．（5分）已知四棱锥S ﹣ABCD 的三视图如图所示，若该四棱锥的各个顶点都在球O 的球面上，则球O 的表面积等于 π ．【分析】画出几何体的直观图，利用三视图的数据，判断几何体的外接球的球心的位置，转化求解球的半径，即可得到球的表面积．【解答】解：由该四棱锥的三视图知，该四棱锥直观图如图，平面SAB⊥平面ABCD，r1为△SAB外接圆半径，r2为矩形ABCD外接圆半径，L＝AB．可得R2＝，计算得，R2＝+5﹣4＝，所以S＝4πR2＝π．故答案为：．【点评】本题考查三视图求解几何体的外接球的表面积，考查转化思想以及计算能力．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题，共60分．17．（12分）在△ABC中，内角A，B，C所对的边分别为a，b，c，且sin A sin B cos B+sin2B cos A＝2sin C cos B．（1）求tan B的值；（2）若b＝2，△ABC的面积为，求a+c的值【分析】（1）利用三角函数恒等变换的应用化简已知等式，结合sin C≠0，可求tan B的值．（2）利用同角三角函数基本关系式可求sin B，cos B的值，利用三角形的面积公式可求ac的值，进而根据余弦定理可求a+c的值．【解答】（本题满分为12分）解：（1）∵原等式化简得sin B（sin A cos B+cos A sin B）＝2sin C cos B，∴sin B sin（A+B）＝2sin C cos B，∴sin B sin C＝2sin C cos B，…（3分）∵0＜C＜π，sin C≠0，∴tan B＝2，…（5分）（2）∵tan B＝2，且0＜B＜π，∴B为锐角，且＝2，∴sin B＝，cos B＝，∵S＝ac sin B＝，∴ac＝3，…（9分）∴由余弦定理得：a+c＝2．…（12分）【点评】本题主要考查了三角函数恒等变换的应用，三角形的面积公式，余弦定理在解三角形中的综合应用，考查了计算能力和转化思想，属于中档题．18．（12分）如图，ABCD是边长为2的菱形，∠DAB＝60°，EB⊥平面ABCD，FD⊥平面ABCD，EB＝2FD＝4．（1）求证：EF⊥AC；（2）求几何体EFABCD的体积．【分析】（1）连接DB，由面面垂直的性质可得EB∥FD，设DB∩AC＝O，由ABCD为菱形，得到AC⊥DB，结合线面垂直的判定可得AC⊥平面EFDB，从而得到AC⊥EF；（2）由已知可得EFDB为直角梯形，求出其面积，再由AC⊥平面EFDB，代入棱锥体积公式求解．【解答】（1）证明：连接DB，∵DF⊥平面ABCD，EB⊥平面ABCD，∴EB∥FD，则E，F，D，B四点共面，且AC⊥EB，设DB∩AC＝O，∵ABCD为菱形，∴AC⊥DB．又DB∩EB＝B，∴AC⊥平面EFDB，∵EF⊂平面EFDB，∴AC⊥EF；（2）解：∵EB∥FD，EB⊥BD，∴EFDB为直角梯形，在菱形ABCD中，∠DAB＝60°，AB＝2，BD＝2，AO＝CO＝，∴梯形EFDB 的面积S ＝＝6，∵AC ⊥平面EFDB ，∴V EFABCD ＝V C ﹣EFDB +V A ﹣EFDB ＝S ×AO +S ×CO ＝4．【点评】本题考查空间中直线与直线、直线与平面位置关系的判定与应用，考查空间想象能力与思维能力，训练了多面体体积的求法，是中档题．19．（12分）有一个同学家开了一个小卖部，他为了研究气温对热饮饮料销售的影响，经过统计，得到一个卖出的热饮杯数与当天气温的散点图和对比表：（1）从散点图可以发现，各点散布在从左上角到右下角的区域里．因此，气温与当天热饮销售杯数之间成负相关，即气温越高，当天卖出去的热饮杯数越少．统计中常用相关系数r 来衡量两个变量之间线性关系的强弱．统计学认为，对于变量x 、y ，如果r ∈[﹣1，﹣0.75]，那么负相关很强；如果r ∈[0.75，1]，那么正相关很强；如果r ∈（﹣0.75，﹣0.30]∪[0.30，0.75），那么相关性一般；如果r ∈[﹣0.25，0.25]，那么相关性较弱．请根据已知数据，判断气温与当天热饮销售杯数相关性的强弱．（2）（ⅰ）请根据已知数据求出气温与当天热饮销售杯数的线性回归方程；（ⅱ）记[x ]为不超过x 的最大整数，如[1.5]＝1，[﹣4.9]＝﹣5．对于（ⅰ）中求出的线性回归方程y ＝x +，将y ＝[]x +[]视为气温与当天热饮销售杯数的函数关系．已知气温x 与当天热饮每杯的销售利润f （x ）的关系是f （x ）＝2[]+3（x ∈[﹣7，38））（单位：元），请问当气温x 为多少时，当天的热饮销售利润总额最大？【参考公式】＝，＝．r ＝，【参考数据】（x i﹣）2＝1340，（y i﹣）2≈111，（x i﹣）（y i﹣）＝﹣3953，＝15，＝100，362＝1296，372＝1369．【分析】（1）计算相关系数r的值，即可判断气温与当天热饮销售杯数的相关性；（2）（ⅰ）计算回归系数、，写出线性回归方程；（ⅱ）由题意知气温x与y的关系式，写出函数g（x）的解析式，即它的最大值即可．【解答】解：（1）因为相关系数r＝＝，…（2分）且﹣≈﹣0.96．所以气温与当天热饮销售杯数的负相关很强…（4分）（2）（ⅰ）因为回归系数＝＝＝﹣2.95，＝100+2.95×15＝144.25，所以气温与当天热饮销售杯数的线性回归方程为y＝﹣2.95x+144.25；…（7分）（ⅱ）由题意可知气温x与当天热饮销售杯数y的关系为y＝﹣3x+144，设气温为x时，则当天销售的热饮利润总额为g（x）＝（﹣3x+144）（2[]﹣3），其中（x∈[﹣7，38）），即g（x）＝；…（10分）易知g（﹣7）＝495，g（8）＝600，g（23）＝525；故当气温x＝8时，当天的热饮销售利润总额最大，且最大为600元…（12分）【点评】本题考查了线性回归方程与分段函数应用问题，也考查了相关系数的应用问题，是中档题．20．（12分）如图，椭圆C：+＝1的右焦点为F，过点F的直线l与椭圆交于A，B两点，直线n：x＝4与x轴相交于点E，点M在直线n上，且满足BM∥x轴．（1）当直线l与x轴垂直时，求直线AM的方程；（2）证明：直线AM经过线段EF的中点．【分析】（1）由题意求出点A，M的坐标，即可求出直线AM的方程，（2）设直线l的方程为x＝my+1，与椭圆联立，根据韦达定理和向量的运算即可证明A，N，M三点共线，可得直线AM经过线段EF的中点【解答】解：（1）由c＝＝1，∴F（1，0），∵直线l与x轴垂直，∴x＝1，由得或∴A（1，），M（4，﹣）∴直线AM的方程为y＝﹣x+．证明（2）设直线l的方程为x＝my+1，由得3（my+1）2+4y2＝12，即（3m2+4）y2+6my﹣9＝0，设A（x1，y1），B（x2，y2），则y1+y2＝，y1y2＝﹣，∵EF的中点N（，0），点M（4，y2），∴＝（x1﹣，y1）═（my1﹣，y1），＝（，y2），∴•＝my1y2﹣（y1+y2）＝﹣﹣×＝0．∴A，N，M三点共线，∴直线AM经过线段EF的中点．【点评】本题主要考查了椭圆的标准方程．涉及了直线与椭圆的关系，考查了运算能力和转化能力，属于中档题21．（12分）已知函数f（x）＝e x，g（x）＝ax2+x+1（a＞0）．（1）设F（x）＝，讨论函数F（x）的单调性；（2）若0＜a≤，证明：f（x）＞g（x）在（0，+∞）上恒成立．【分析】（1）F（x）＝＝，F′（x）＝＝．对a分类讨论即可得出单调性．（2）由0＜a≤，可得ax2+x+1≤x2+x+1．设h（x）＝e x﹣x2﹣x﹣1，利用导数研究其单调性即可证明结论在（0，+∞）上恒成立．【解答】解：（1）F（x）＝＝，F′（x）＝＝．（1分）①若a＝，F′（x）＝≤0，∴F（x）在R上单调递减．（2分）②若a ＞，则＞0，当x ＜0，或x ＞时，F ′（x ）＜0，当0＜x ＜时，F ′（x ）＞0，∴F （x ）在（﹣∞，0）或（，+∞）上单调递减，在（0，）上单调递增．③若0＜a ＜，则＜0，当x ＜，或x ＞0时，F ′（x ）＜0，当＜x ＜0时，F ′（x ）＞0．∴F （x ）在（﹣∞，），（0，+∞）上单调递减，在（，0）上单调递增．（6分）（2）证明：∵0＜a ≤，∴ax 2+x +1≤x 2+x +1．（7分）设h （x ）＝e x ﹣x 2﹣x ﹣1，则h ′（x ）＝e x ﹣x ﹣1．设p （x ）＝h ′（x ）＝e x ﹣x ﹣1，则p ′（x ）＝e x ﹣1，在（0，+∞）上，p ′（x ）≥0恒成立．∴h ′（x ）在（0，+∞）上单调递增．（9分）又∵h ′（0）＝0，∴x ∈（0，+∞）时，h ′（x ）＞0，所以h （x ）在（0，+∞）上单调递增，∴h （x ）＞h （0）＝0，∴e x ﹣x 2﹣x ﹣1＞0，e x ＞x 2+x +1，所以e x ＞x 2+x +1≥ax 2+x +1，所以f （x ）＞g （x ）在（0，+∞）上恒成立．（12分）【点评】本题考查了利用导数研究函数的单调性极值与最值、方程与不等式的解法、等价转化方法、分类讨论方法，考查了推理能力与计算能力，属于难题．（二）选考题：共10分．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系中，以原点O 为极点，x 轴的正半轴为极轴建立极坐标系，两种坐标系中取相同的长度单位．已知直线l 的参数方程为（t 为参数），曲线C 的极坐标方程为ρ＝4sin （θ+）．（1）求直线l 的普通方程与曲线C 的直角坐标方程；（2）若直线l与曲线C交于M，N两点，求△MON的面积．【分析】（1）消去参数t可得直线l的普通方程，两边同乘ρ后利用两角和的正弦公式以及互化公式可得曲线C的直角坐标方程；（2）由点到直线l的距离求得三角形的高，再根据面积公式可得．【解答】解（1）由消去参数t得x+y＝4，直线l的普通方程为x+y﹣4＝0．（2分）由ρ＝4sin（θ+）＝2sinθ+2cosθ得，ρ2＝2ρsin θ+2ρcos θ，即x2+y2＝2y+2x，∴曲线C的直角坐标方程是圆：（x﹣）2+（y﹣1）2＝4．（5分）（2）∵原点O到直线l的距离d＝＝2．（7分）直线l过圆C的圆心（，1），∴|MN|＝2r＝4，所以△MON的面积S＝|MN|×d＝4．（10分）【点评】本题搞差了简单曲线的极坐标方程，属中档题．[选修4-5：不等式选讲]23．已知函数f（x）＝|x+1|+2|x﹣a|．（1）设a＝1，求不等式f（x）≤7的解集；（2）已知a＞﹣1，且f（x）的最小值等于3，求实数a的值．【分析】（1）利用分段讨论的方法求解不等式；（2）先确定函数的解析式，然后根据函数的单调性求出最小值，建立方程求解．【解答】解：（1）a＝1时，f（x）＝|x+1|+2|x﹣1|．（1分）当x＜﹣1时，f（x）≤7即为﹣3x+1≤7，解得﹣2≤x＜﹣1．当﹣1≤x≤1时，﹣x+3≤7，解得﹣1≤x≤1．当x＞1时，3x﹣1≤7，解得1＜x≤．（4分）综上，f（x）≤7的解集为（5分）（2）∵a＞﹣1，∴f（x）＝（7分）由y＝f（x）的图象知f（x）min＝f（a）＝a+1＝3，∴a＝2．故实数a的值为2．【点评】本题考查含有两个绝对值不等式的解法以及分段函数的最值问题，属于中档题目．。

湖南师大附中2019届高考模拟卷(三)文科综合能力测试地理部分注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

第Ⅰ卷本卷共35小題，每小题4分，共计140分。

每小题给出的四个选项中，只有一项是符合题目要求的。

南方的大米，分早稻和晚稻，一般早稻的生长期为90～120天，晩稻为150～170天。

近年来，东北水稻种植面积増长迅速，单位面积产量增长较快。

东北大米主要种植在极其肥沃的黑土地上，生长周期一般5个月左右，相较南方大米，东北大米颗粒饱满，色泽清白透明，口感绵软，以五常大米最为著名，下图为“五常市位置图”。

读图完成1～3题。

1.东北大米一般比南方大米品质更佳的主要原因是①生长周期长，有利于营养物质积累②土壤肥沃，有机质含量高③冬季气温低，病虫害少，农药施用量少④悠久的种植历史和先进技术⑤品牌推广好，认知度高A.①②③B.①②④C.①②③④D.①②③④⑤2.近年来，东北水稻种植面积迅速增长的主要原因是①东北水热充足，水稻种植条件优越②水稻种植技术发展，克服不利自然条件③东北人口増长迅速，稻米消费需求増长快④东北大米品质好，市场需求大A.①②B.②④C.①③D.③④3. 五常大米供不应求，为增大市场供应，下列措施最佳的是A.大量使用化肥，提高单产量B.购置南方大米，进行精加工C.增加科技投入，提高单产量D.开垦荒地，扩大水稻种植面积下图为“我国某河段河谷横面示意图＂，T1，T4为不同时期形成的阶地(一种阶梯状地貌)，该阶地原为洪水位下的河床或河漫滩，后经地壳运动演变形成。

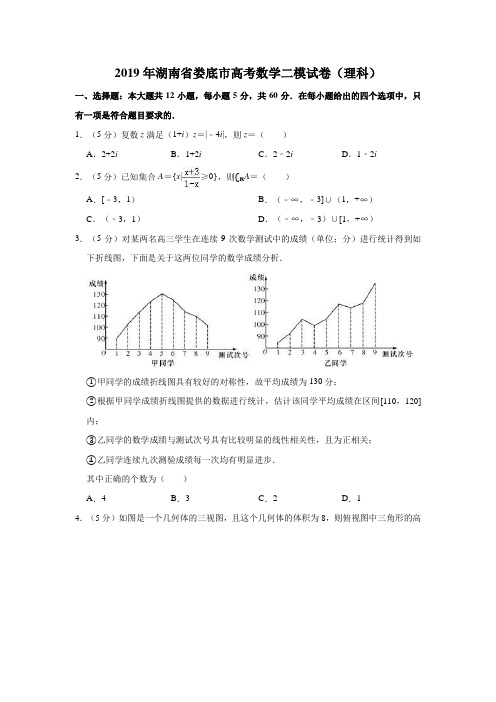
2019年湖南省娄底市高考数学二模试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）复数z满足（1+i）z＝|﹣4i|，则z＝（）A．2+2i B．1+2i C．2﹣2i D．1﹣2i2．（5分）已知集合A＝{x|≥0}，则∁R A＝（）A．[﹣3，1）B．（﹣∞，﹣3]∪（1，+∞）C．（﹣3，1）D．（﹣∞，﹣3）∪[1，+∞）3．（5分）对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到如下折线图，下面是关于这两位同学的数学成绩分析．①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分；②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关；④乙同学连续九次测验成绩每一次均有明显进步．其中正确的个数为（）A．4B．3C．2D．14．（5分）如图是一个几何体的三视图，且这个几何体的体积为8，则俯视图中三角形的高x等于（）A．1B．2C．3D．45．（5分）已知f（x）是奇函数，当x＞0时，f（x）＝﹣，则函数在x＝﹣1处的切线方程是（）A．2x﹣y+1＝0B．x﹣2y+2＝0C．2x﹣y﹣1＝0D．x+2y﹣2＝06．（5分）如图，在矩形OABC中的曲线分别是y＝sin x，y＝cos x的一部分，A（，0），C（0，1），在矩形OABC内随机取一点，若此点取自阴影部分的概率为P1，取自非阴影部分的概率为P2，则（）A．P1＜P2B．P1＞P2C．P1＝P2D．大小关系不能确定7．（5分）已知△ABC中，AB＝2，AC＝3，∠A＝60°，AD⊥BC于D，＝λ+μ，则＝（）A．3B．6C．2D．38．（5分）已知双曲线C：﹣＝1（a＞0，b＞0），以点P（b，0）为圆心，a为半径作圆P，圆P与双曲线C的一条渐近线交于M，N两点，若∠MPN＝90°，则C的离心率为（）A．B．C．D．9．（5分）若m，n均为非负整数，在做m+n的加法时各位均不进位（例如：2019+100＝2119，则称（m ，n ）为“简单的”有序对，而m +n 称为有序对（m ，n ）的值，那么值为2019的“简单的”有序对的个数是（ ） A ．100B ．96C ．60D ．3010．（5分）若x 1是方程xe x ＝1的解，x 2是方程xlnx ＝1的解，则x 1x 2等于（ ）A ．1B ．﹣1C ．eD ．11．（5分）已知函数f （x ）＝sin （ωx +φ）（ω＞0，φ∈[，π]）的部分图象如图所示，且f （x ）上[0，2π]上恰有一个最大值和一个最小值，则ω的取值范围是（ ）A ．[，）B ．[，）C ．（，]D ．（，]12．（5分）已知函数f （x ）＝e x ﹣ax ﹣1在区间（﹣1，1）内存在极值点，且f （x ）＜0恰好有唯一整数解，则a 的取值范围是（其中e 为自然对数的底数，e ＝2.71828…）（ ） A ．[，e ）B ．[，1）∪（e ﹣1，]C ．（e ﹣1，e ）D ．[，）∪（e ﹣1，e ）二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）已知二项式（ax ﹣）6的展开式中的常数项为﹣160，则a ＝ ．14．（5分）若实数x ，y 满足不等式组则目标函数z ＝3x ﹣y 的最大值为 ．15．（5分）在《九章算术》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马．如图，若四棱锥P ﹣ABCD 为阳马，侧棱PA ⊥底面ABCD ，且PA ＝3，BC ＝AB ＝4，设该阳马的外接球半径为R，内切球半径为r，则＝．16．（5分）在△ABC中，a，b，c分别为角A，B，C所对的边，若c＝2b，△ABC的面积为1，则a的最小值为．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题，共60分．17．（12分）已知数列{a n}中，a1＝1，S n是数列{a n}的前n项和，且对任意的r、t∈N*，都有＝（）2．（Ⅰ）判断{a n}是否为等差数列，并证明你的结论；（Ⅱ）若数列{b n}满足＝2n﹣1（n∈N*），设T n是数列{b n}的前n项和，证明：T n＜6．18．（12分）在Rt△ABC中，∠ABC＝90°，tan∠ACB＝．已知E，F分别是BC，AC 的中点．将△CEF沿EF折起，使C到C′的位置且二面角C′﹣EF﹣B的大小是60°．连接C′B，C′A，如图：（Ⅰ）求证：平面C′FA⊥平面ABC′；（Ⅱ）求平面AFC′与平面BEC′所成二面角的大小．19．（12分）已知平面上一动点P到定点F（，0）的距离与它到直线x＝的距离之比为，记动点P的轨迹为曲线C．（Ⅰ）求曲线C的方程；（Ⅱ）设直线l：y＝kx+m与曲线C交于M，N两点，O为坐标原点，若k OM•k ON＝，求△MON面积的最大值．20．（12分）随着食品安全问题逐渐引起人们的重视，有机、健康的高端绿色蔬菜越来越受到消费者的欢迎，同时生产﹣运输﹣销售一体化的直销供应模式，不仅减少了成本，而且减去了蔬菜的二次污染等问题．（Ⅰ）在有机蔬菜的种植过程中，有机肥料使用是必不可少的．根据统计某种有机蔬菜的产量与有机肥料的用量有关系，每个有机蔬菜大棚产量的增加量y （百斤）与使用堆沤肥料x （千克）之间对应数据如表：依据表中的数据，用最小二乘法求出y 关于x 的线性回归方程；并根据所求线性回归方程＝x +，估计如果每个有机蔬菜大棚使用堆沤肥料10千克，则每个有机蔬菜大棚产量增加量y 是多少百斤？（Ⅱ）某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装，以每份10元的价格销售到生鲜超市．“乐购”生鲜超市以每份15元的价格卖给顾客，如果当天前8小时卖不完，则超市通过促销以每份5元的价格卖给顾客（根据经验，当天能够把剩余的有机蔬菜都低价处理完毕，且处理完毕后，当天不再进货）．该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量（单位：份），制成如下表格（注：x ，y ∈N *，且x +y ＝30）：若以100天记录的频率作为每日前8小时销售量发生的概率，该生鲜超市当天销售有机蔬菜利润的期望值为决策依据，当购进17份比购进18份的利润的期望值大时，求x 的取值范围．附：回归方程系数公式＝．21．（12分）已知f （x ﹣1）＝2ln （x ﹣1）﹣+k （x ＞1）． （Ⅰ）判断当﹣1≤k ≤0时f （x ）的单调性；（Ⅱ）若x1，x2（x1≠x2）为f（x）两个极值点，求证：x[f（x1）+f（x2）]≥（x+1）[f （x）+2﹣2x]．三、（二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2＝．（Ⅰ）求直线l的普通方程和曲线C的直角坐标方程；（Ⅱ）设P为曲线C上的点，PQ⊥l，垂足为Q，若|PQ|的最小值为2，求m的值．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣2a|﹣|x﹣a|，a∈R．（Ⅰ）若f（1）＞1，求a的取值范围；（Ⅱ）若a＜0，对∀x，y∈（﹣∞，a]，都有不等式f（x）≤|（y+2020|+|y﹣a|恒成立，求a的取值范围．2019年湖南省娄底市高考数学二模试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）复数z满足（1+i）z＝|﹣4i|，则z＝（）A．2+2i B．1+2i C．2﹣2i D．1﹣2i【分析】把已知等式变形，再由复数代数形式的乘除运算得答案．【解答】解：由（1+i）z＝|﹣4i|＝4，得z＝＝＝2﹣2i．故选：C．【点评】本题考查复数代数形式的乘除运算，考查复数模的求法，是基础题．2．（5分）已知集合A＝{x|≥0}，则∁R A＝（）A．[﹣3，1）B．（﹣∞，﹣3]∪（1，+∞）C．（﹣3，1）D．（﹣∞，﹣3）∪[1，+∞）【分析】先求出集合A，由此能求出∁R A．【解答】解：∵集合A＝{x|≥0}＝{x|（x+3）（x﹣1）≤0且x≠1}＝{x|﹣3≤x＜1}，∴∁R A＝{x|x＜﹣3或x≥1}＝（﹣∞，﹣3）∪[1，+∞）．故选：D．【点评】本题考查补集的求法，考查补集定义、不等式性质等基础知识，是基础题．3．（5分）对某两名高三学生在连续9次数学测试中的成绩（单位：分）进行统计得到如下折线图，下面是关于这两位同学的数学成绩分析．①甲同学的成绩折线图具有较好的对称性，故平均成绩为130分；②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关；④乙同学连续九次测验成绩每一次均有明显进步．其中正确的个数为（）A．4B．3C．2D．1【分析】利用图形，判断折线图平均分以及线性相关性，成绩的比较，说明正误即可．【解答】解：①甲同学的成绩折线图具有较好的对称性，最高130分，平均成绩为低于130分，①错误；②根据甲同学成绩折线图提供的数据进行统计，估计该同学平均成绩在区间[110，120]内，②正确；③乙同学的数学成绩与测试次号具有比较明显的线性相关性，且为正相关，③正确；④乙同学在这连续九次测验中第四次、第七次成绩较上一次成绩有退步，故④不正确．故选：C．【点评】本题考查折线图的应用，线性相关以及平均分的求解，考查转化思想以及计算能力．4．（5分）如图是一个几何体的三视图，且这个几何体的体积为8，则俯视图中三角形的高x等于（）A．1B．2C．3D．4【分析】画出几何体的直观图，利用几何体的体积，转化求解即可．【解答】解：该几何体为四棱锥，体积为V＝•x＝8，∴x＝4．故选：D．【点评】本题考查三视图求解几何体的体积，考查空间想象能力以及计算能力．5．（5分）已知f（x）是奇函数，当x＞0时，f（x）＝﹣，则函数在x＝﹣1处的切线方程是（）A．2x﹣y+1＝0B．x﹣2y+2＝0C．2x﹣y﹣1＝0D．x+2y﹣2＝0【分析】求出函数的解析式，求出函数的导数，求出切点坐标，然后求解切线方程．【解答】解：当x＜0时，﹣x＞0，∴f（﹣x）＝﹣，∴f（x）＝（x＜0），k＝f′（﹣1）＝2，切点为（﹣1，﹣1），∴切线方程为y+1＝2（x+1）．∴切线方程为2x﹣y+1＝0．故选：A．【点评】本题考查函数的导数的应用，切线方程的求法，考查计算能力．6．（5分）如图，在矩形OABC中的曲线分别是y＝sin x，y＝cos x的一部分，A（，0），C（0，1），在矩形OABC内随机取一点，若此点取自阴影部分的概率为P1，取自非阴影部分的概率为P2，则（）A．P1＜P2B．P1＞P2C．P1＝P2D．大小关系不能确定【分析】先用定积分求得阴影部分一半的面积，再根据几何概型概率公式可求得．【解答】解：根据题意，阴影部分的面积的一半为：（cos x﹣sin x）dx＝，于是此点取自阴影部分的概率为P1＝2×＝＞＝．又P2＝1﹣P1＜，故P1＞P2．．故选：B．【点评】本题考查了几何概型，属中档题．7．（5分）已知△ABC中，AB＝2，AC＝3，∠A＝60°，AD⊥BC于D，＝λ+μ，则＝（）A．3B．6C．2D．3【分析】利用已知条件．通过向量的垂直，列出方程推出即可．【解答】解：＝﹣，∵⊥，∴（λ+μ）•（﹣+）＝0，∴﹣λ2+μ2+（λ﹣μ）•＝0，可得﹣4λ+9μ+3（λ﹣μ）＝0，∴λ＝6μ，∴＝6．故选：B．【点评】本题考查向量的数量积判断向量的垂直的条件的应用，考查转化思想以及计算能力．8．（5分）已知双曲线C：﹣＝1（a＞0，b＞0），以点P（b，0）为圆心，a为半径作圆P，圆P与双曲线C的一条渐近线交于M，N两点，若∠MPN＝90°，则C的离心率为（）A．B．C．D．【分析】求出双曲线的一条渐近线方程，利用圆P与双曲线C的一条渐近线交于M，N 两点，若∠MPN＝90°，列出方程，求解离心率即可．【解答】解：不妨设双曲线C的一条渐近线bx﹣ay＝0与圆P交于M，N，因为∠MPN ＝90°，所以圆心P到bx﹣ay＝0的距离为：＝a，即2c2﹣2a2＝ac，e＝＞1，解得e＝．故选：A．【点评】本题考查双曲线的简单性质的应用，考查转化思想以及计算能力．9．（5分）若m，n均为非负整数，在做m+n的加法时各位均不进位（例如：2019+100＝2119，则称（m，n）为“简单的”有序对，而m+n称为有序对（m，n）的值，那么值为2019的“简单的”有序对的个数是（）A．100B．96C．60D．30【分析】值为2019的“简单的”有序对的个数是3×1×2×10＝60【解答】解：值为2019的“简单的”有序对的个数是3×1×2×10＝60．故选：C．【点评】本题考查了排列，组合及简单计数问题，属中档题．10．（5分）若x1是方程xe x＝1的解，x2是方程xlnx＝1的解，则x1x2等于（）A．1B．﹣1C．e D．【分析】将方程方程xe x＝1的解、方程xlnx＝1的解转化为函数y＝e x、函数y＝ln x与函数y＝的图象的公共点A，B的横坐标来求解．【解答】解：考虑到x1，x2是函数y＝e x、函数y＝ln x与函数y＝的图象的公共点A，B的横坐标，而A，B两点关于y＝x对称，因此x1x2＝1．故选：A．【点评】本题考查函数的与方程的综合问题，正确转化是解题的关键，属于中档题目．11．（5分）已知函数f（x）＝sin（ωx+φ）（ω＞0，φ∈[，π]）的部分图象如图所示，且f（x）上[0，2π]上恰有一个最大值和一个最小值，则ω的取值范围是（）A．[，）B．[，）C．（，]D．（，]【分析】根据条件先求出φ的值，结合f（x）上[0，2π]上恰有一个最大值和一个最小值，求出满足条件的表达式进行求解即可．【解答】解：由题意知，f（x）＝sin（ωx+φ），∵f（0）＝，φ∈[，π]）∴φ＝，∵x∈[0，2π]，∴≤ωx+≤2πω+，∵f（x）上[0，2π]上恰有一个最大值和一个最小值，∴≤2πω+＜，∴≤ω＜．故选：B．【点评】本题主要考查三角函数的图象和性质，求出φ的值，结合一个周期性函数最大值和最小值对应的范围是解决本题的关键．12．（5分）已知函数f（x）＝e x﹣ax﹣1在区间（﹣1，1）内存在极值点，且f（x）＜0恰好有唯一整数解，则a的取值范围是（其中e为自然对数的底数，e＝2.71828…）（）A．[，e）B．[，1）∪（e﹣1，]C．（e﹣1，e）D．[，）∪（e﹣1，e）【分析】推导出f′（x）＝e x﹣a＝0在（﹣1，1）上有解，从而＜a＜e，e x＜ax+1有唯一整数解．设g（x）＝e x，h（x）＝ax+1，当1＜a＜e时，唯一整数解为1，应满足当＜a＜1时，唯一整数解为﹣1，应满足由此能求出a的取值范围．【解答】解：由题意得，f′（x）＝e x﹣a＝0在（﹣1，1）上有解，∵f′（x）在（﹣1，1）上单调递增，∴＜a＜e，又∵f（x）＜0恰好有唯一整数解，即e x＜ax+1有唯一整数解．设g（x）＝e x，h（x）＝ax+1，结合题意可知：①若1＜a＜e，则唯一整数解为1，故应满足∴e﹣1＜a≤，故e﹣1＜a＜e；②若＜a＜1，则唯一整数解为﹣1，故应满足∴≤a＜，故≤a＜．由①②得a的取值范围为[，）∪（e﹣1，e）．故选：D．【点评】本题考查实数的取值范围的求法，考查利用导数研究函数极值点问题、利用导数研究函数的单调性与极值、最值问题等基础知识，考查分类讨论思想、化归与转化思想，考查运算求解能力，是难题．二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）已知二项式（ax﹣）6的展开式中的常数项为﹣160，则a＝2．【分析】在二项展开式的通项公式中，令x的幂指数等于0，求出r的值，即可求得常数项，再根据常数项等于﹣160求得实数a的值．【解答】解：∵二项式（ax﹣）6的展开式中的通项公式为T r+1＝•（﹣1）r•a6﹣r•x6﹣2r，令6﹣2r＝0，求得r＝3，可得常数项为﹣•a3＝﹣160，∴a＝2，故答案为：2．【点评】本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题．14．（5分）若实数x，y满足不等式组则目标函数z＝3x﹣y的最大值为12．【分析】画出约束条件的可行域，求出最优解，即可求解目标函数的最大值．【解答】解：作出实数x，y满足不等式组可行域如图，由，解得A（4，0）目标函数y＝3x﹣z，当y＝3x﹣z过点（4，0）时，z有最大值，且最大值为12．故答案为：12．【点评】本题考查线性规划的简单应用，是基本知识的考查．15．（5分）在《九章算术》中，将底面为矩形且有一条侧棱与底面垂直的四棱锥称之为阳马．如图，若四棱锥P﹣ABCD为阳马，侧棱PA⊥底面ABCD，且PA＝3，BC＝AB＝4，设该阳马的外接球半径为R，内切球半径为r，则＝．【分析】该阳马补形所得到的长方体的对角线为外接球的直径，由此能求出R＝，内切球O1在侧面PAD内的正视图是△PAD的内切圆，从而内切球半径为r＝1，由此能求出．【解答】解：∵四棱锥P﹣ABCD为阳马，侧棱PA⊥底面ABCD，且PA＝3，BC＝AB＝4，设该阳马的外接球半径为R，∴该阳马补形所得到的长方体的对角线为外接球的直径，∴（2R）2＝AB2+AD2+AP2＝16+16+9＝41，∴R＝，∵侧棱PA⊥底面ABCD，且底面为正方形，∴内切球O1在侧面PAD内的正视图是△PAD的内切圆，∴内切球半径为r＝1，故＝．故答案为：．【点评】本题考查阳马的外接球半径和内切球半径之比的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．16．（5分）在△ABC中，a，b，c分别为角A，B，C所对的边，若c＝2b，△ABC的面积为1，则a的最小值为．【分析】直接利用正弦定理、余弦定理和三角形面积的应用和三角函数关系式的恒等变换和导数的应用求出结果．【解答】解：设A＝θ，则：a2＝b2+c2﹣2bc cosθ，＝b2+4b2﹣4b2cosθ，由于＝b2sinθ＝1，所以：．则：，设y＝，所以：＝，当4﹣5cosθ＝0时，y的最小值为3，故a的最小值为，故答案为：．【点评】本题考查的知识要点：三角函数关系式的恒等变换，导数的应用，正弦定理余弦定理和三角形面积的应用，主要考察学生的运算能力和转换能力，属于基础题型．三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤．第17-21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．（一）必考题，共60分．17．（12分）已知数列{a n}中，a1＝1，S n是数列{a n}的前n项和，且对任意的r、t∈N*，都有＝（）2．（Ⅰ）判断{a n}是否为等差数列，并证明你的结论；（Ⅱ）若数列{b n}满足＝2n﹣1（n∈N*），设T n是数列{b n}的前n项和，证明：T n＜6．【分析】（Ⅰ）在＝（）2中取r＝n，t＝1求得S n＝n2．然后求出当n≥2时的通项公式，已知n＝1时成立后得到数列{a n}的通项公式，即可得到结论；（Ⅱ）求得＝2n﹣1，可得b n＝（2n﹣1）•（）n﹣1，由数列的错位相减法求和，结合等比数列的求和公式和不等式的性质，即可得证．【解答】解：（Ⅰ）由对任意的r、t∈N*，都有＝（）2．得＝n2，而a1＝1＝S1，∴S n＝n2．＝n2﹣（n﹣1）2＝2n﹣1，当n≥2时，a n＝S n﹣S n﹣1当n＝1时该式成立，∴a n＝2n﹣1，即a n+1﹣a n＝2，可得数列{a n}为公差为，首项为1的等差数列；（Ⅱ）证明：＝2n﹣1，可得b n＝（2n﹣1）•（）n﹣1，即有T n＝1•（）0+3•（）1+…+（2n﹣1）•（）n﹣1，T n＝1•（）+3•（）2+…+（2n﹣1）•（）n，两式相减可得T n＝1+2[（）+（）2+…+（）n﹣1]﹣（2n﹣1）•（）n＝1+2•﹣（2n﹣1）•（）n，化简可得T n＝6﹣（2n+3）•（）n﹣1，由n为自然数，可得（2n+3）•（）n﹣1＞0，则T n＜6．【点评】本题考查数列的通项公式的求法，注意运用数列的递推式，考查等差数列的通项公式和等比数列的求和公式，以及数列的错位相减法，考查化简运算能力，属于中档题．18．（12分）在Rt△ABC中，∠ABC＝90°，tan∠ACB＝．已知E，F分别是BC，AC 的中点．将△CEF沿EF折起，使C到C′的位置且二面角C′﹣EF﹣B的大小是60°．连接C′B，C′A，如图：（Ⅰ）求证：平面C′FA⊥平面ABC′；（Ⅱ）求平面AFC′与平面BEC′所成二面角的大小．【分析】（Ⅰ）法一：由AF＝C′F．设AC′的中点为G，连接FG．设BC′的中点为H，连接GH，EH．从而∠BEC′即为二面角C′﹣EF﹣B的平面角．∠BEC′＝60°，推导出EH⊥BC′．EF⊥C′E，EF⊥BE，从而EF⊥平面BEC′．由EF∥AB，得AB ⊥平面BEC′，从而AB⊥EH，即EH⊥AB．进而EH⊥平面ABC′．推导出四边形EHGF 为平行四边形．从而FG∥EH，FG⊥平面ABC′，由此能证明平面AFC′⊥平面ABC′．法二：以B为原点，在平面BEC′中过B作BE的垂线为x轴，BE为y轴，BA为z轴，建立空间直角坐标系，利用向量法能证明平面AFC′⊥平面ABC′．（Ⅱ）以B为原点，在平面BEC′中过B作BE的垂线为x轴，BE为y轴，BA为z轴，建立空间直角坐标系，利用向量法能求出平面AFC′与平面BEC′所成二面角大小．【解答】证明：（Ⅰ）证法一：∵F是AC的中点，∴AF＝C′F．设AC′的中点为G，连接FG．设BC′的中点为H，连接GH，EH．由题意得C′E⊥EF，BE⊥EF，∴∠BEC′即为二面角C′﹣EF﹣B的平面角．∴∠BEC′＝60°，∵E为BC的中点．∴BE＝EC′，∴△BEC′为等边三角形，∴EH⊥BC′．∵EF⊥C′E，EF⊥BE，C′E∩BE＝E，∴EF⊥平面BEC′．∵EF∥AB，∴AB⊥平面BEC′，∴AB⊥EH，即EH⊥AB．∵BC′∩AB＝B，∴EH⊥平面ABC′．∵G，H分别为AC′，BC′的中点．∴GH FE，∴四边形EHGF为平行四边形．∴FG∥EH，FG⊥平面ABC′，又FG⊂平面AFC′．∴平面AFC′⊥平面ABC′．（6分）法二：如图，以B为原点，在平面BEC′中过B作BE的垂线为x轴，BE为y轴，BA 为z轴，建立空间直角坐标系，设AB＝2．则A（0，0，2），B（0，0，0），F（0，2，1），E（0，2，0），C′（，1，0）．设平面ABC′的法向量为＝（x，y，z），＝（0，0，2），＝（），∴，令x＝1，则＝（1，﹣，0），设平面AFC′的法向量为＝（x，y，z），＝（0，2，﹣1），＝（，1，﹣2），∴，取y＝1，得＝（，1，2）．∵•＝0，∴平面AFC′⊥平面ABC′．（6分）解：（Ⅱ）如图，以B为原点，在平面BEC′中过B作BE的垂线为x轴，BE为y轴，BA为z轴，建立空间直角坐标系，设AB＝2，则A（0，0，2），B（0，0，0），F（0，2，1），E（0，2，0），C′（，1，0）．平面BEC′的法向量＝（0，0，1），（8分）设平面AFC′的法向量为＝（x，y，z），＝（），＝（0，2，﹣1），∴，取y＝1，得＝（）．（9分）∴cos＜＞＝＝，（10分）由图形观察可知，平面AFC′与平面BEC′所成的二面角的平面角为锐角．∴平面AFC′与平面BEC′所成二面角大小为45°．（12分）【点评】本题考查面面垂直的证明，考查二面角的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，是中档题．19．（12分）已知平面上一动点P到定点F（，0）的距离与它到直线x＝的距离之比为，记动点P的轨迹为曲线C．（Ⅰ）求曲线C的方程；（Ⅱ）设直线l：y＝kx+m与曲线C交于M，N两点，O为坐标原点，若k OM•k ON＝，求△MON面积的最大值．【分析】（Ⅰ）设P（x，y），由题意列式，化简得曲线C的方程；（Ⅱ）设M（x1，y1），N（x2，y2），联立直线方程与椭圆方程，化为关于x的一元二次方程，由弦长公式求弦长，再由点到直线的距离公式求原点O到直线l的距离，写出三角形面积公式，再由换元法结合二次函数求最值．【解答】解：（Ⅰ）设P（x，y），则，化简得，∴曲线C的方程为；（Ⅱ）设M（x1，y1），N（x2，y2），联立，得（1+4k2）x2+8kmx+4m2﹣4＝0，依题意，△＝（8km）2﹣4（4k2+1）（4m2﹣4）＞0，化简得：m2＜4k2+1，①，．+m2，若k OM•k ON＝，则，即4y1y2＝5x1x2，∴．即（4k2﹣5）（m2﹣1）﹣8k2m2+m2（4k2+1）＝0，化简得：，②|MN|＝＝．∵原点O到直线l的距离d＝，∴，设4k2+1＝t，由①②得，0≤m2＜，＜k2≤，∴＜t ≤6，≤＜，＝．∴当时，即k＝时，△MON 面积最大为1．【点评】本题考查轨迹方程的求法，考查直线与椭圆位置关系的应用，训练了利用二次函数求最值，考查计算能力，是中档题．20．（12分）随着食品安全问题逐渐引起人们的重视，有机、健康的高端绿色蔬菜越来越受到消费者的欢迎，同时生产﹣运输﹣销售一体化的直销供应模式，不仅减少了成本，而且减去了蔬菜的二次污染等问题．（Ⅰ）在有机蔬菜的种植过程中，有机肥料使用是必不可少的．根据统计某种有机蔬菜的产量与有机肥料的用量有关系，每个有机蔬菜大棚产量的增加量y （百斤）与使用堆沤肥料x （千克）之间对应数据如表：依据表中的数据，用最小二乘法求出y 关于x 的线性回归方程；并根据所求线性回归方程＝x +，估计如果每个有机蔬菜大棚使用堆沤肥料10千克，则每个有机蔬菜大棚产量增加量y 是多少百斤？（Ⅱ）某大棚蔬菜种植基地将采摘的有机蔬菜以每份三斤称重并保鲜分装，以每份10元的价格销售到生鲜超市．“乐购”生鲜超市以每份15元的价格卖给顾客，如果当天前8小时卖不完，则超市通过促销以每份5元的价格卖给顾客（根据经验，当天能够把剩余的有机蔬菜都低价处理完毕，且处理完毕后，当天不再进货）．该生鲜超市统计了100天有机蔬菜在每天的前8小时内的销售量（单位：份），制成如下表格（注：x ，y ∈N *，且x +y ＝30）：若以100天记录的频率作为每日前8小时销售量发生的概率，该生鲜超市当天销售有机蔬菜利润的期望值为决策依据，当购进17份比购进18份的利润的期望值大时，求x 的取值范围．附：回归方程系数公式＝．【分析】（Ⅰ）根据公式计算可得；（Ⅱ）求出概率可得分布列可数学期望．【解答】解：（Ⅰ）＝＝5，＝＝4.2，x i＝22+42+52+62+82＝145，＝＝0.3，＝﹣＝4﹣0.3×5＝2.5，所以y关于x的线性回归方程为：y＝0.3x+2.54，当x＝10时，y＝0.3×10+2.5＝5.5百斤，所以如果每个有机蔬菜大概使用肥料10千克，估计每个有机蔬菜大概产量的增加量是5.5百斤．（Ⅱ）若该超市一天购进17份这种有机蔬菜，Y1表示当天的利润（单位：元），那么Y1的分布列为Y1的数学期望E（Y1）＝65×+75×+85×＝，若该超市一天购进18份这种有机蔬菜，Y2表示当天的利润（单位：元），那么Y2的分布列为：Y2的数学期望E（Y2）＝60×＝，又购进17份比购进18份的利润的期望值大，故，求得x＞24，故求得x的取值范围是[24，30），【点评】本题考查了离散型随机变量的期望和方差，属中档题．21．（12分）已知f（x﹣1）＝2ln（x﹣1）﹣+k（x＞1）．（Ⅰ）判断当﹣1≤k≤0时f（x）的单调性；（Ⅱ）若x1，x2（x1≠x2）为f（x）两个极值点，求证：x[f（x1）+f（x2）]≥（x+1）[f （x）+2﹣2x]．【分析】（Ⅰ）求函数的导数，结合函数单调性和导数的关系进行判断即可．（Ⅱ）根据极值的定义得到f′（x）＝0有两个不相等的正实数根x1，x2，利用根与系数之间的关系进行转化证明即可．【解答】解：（Ⅰ）因为f（x﹣1）＝2ln（x﹣1）+（x＞1），所以f（x）＝2lnx+，（x＞0）．f′（x）＝+＝，当﹣1≤k≤0时，△＝（4+k）2﹣16＝k（k+8）≤0，2x2+（4+k）x+2＞0恒成立．于是，f（x）在定义域上为单调增函数．（Ⅱ）证明：∵f′（x）＝+＝，由题设知，f′（x）＝0有两个不相等的正实数根x1，x2，则，即，得k＜﹣8而f（x1）+f（x2）＝2lnx1++2lnx2+＝2ln（x1x2）+k（+）＝2ln（x1x2）+k•＝k，又＝k，故欲证原不等式等价于证明不等式：≥[f（x）﹣2（x﹣1）]也就是要证明：对任意x＞0，有lnx≤x﹣1令g（x）＝lnx﹣x+1（x＞0），由于g（1）＝0，并且g′（x）＝﹣1，当x＞1时，g′（x）＜0，则g（x）在（1，+∞）上为减函数；当0＜x＜1时，g′（x）＞0，则g（x）在（0，1）上为增函数．则g（x）在（0，+∞）上有最大值g（1）＝0，即g（x）≤0，故原不等式成立．【点评】本题主要考查导数的综合应用，结合函数的单调性极值和导数之间的关系进行转化是解决本题的关键．考查学生的运算能力．三、（二）选考题：共10分．请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分．[选修4-4：坐标系与参数方程]22．（10分）在平面直角坐标系xOy中，直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2＝．（Ⅰ）求直线l的普通方程和曲线C的直角坐标方程；（Ⅱ）设P为曲线C上的点，PQ⊥l，垂足为Q，若|PQ|的最小值为2，求m的值．【分析】（Ⅰ）消去参数t可得直线l的普通方程，（Ⅱ）利用曲线C的参数方程设点P，根据点到直线距离公式求出|PQ|，再根据三角函数性质求出最小值，利用已知列方程可解得m．【解答】解（Ⅰ）因为曲线C的极坐标方程为ρ2＝，即ρ2+ρ2sin2θ＝4，将ρ2＝x2+y2，ρsinθ＝y代入上式并化简得+＝1，所以曲线C的直角坐标方程为+＝1，直线l的普通方程为x﹣﹣m＝0．（Ⅱ）设P（2cosθ，sinθ），由点到直线的距离公式得|PQ|＝＝，由题意知m≠0，当m＞0时，|PQ|min＝＝2，得m＝2，当m＜0时，||PQ|min＝，得m＝﹣2﹣2；所以m＝2+2或m＝﹣2﹣2．【点评】本题考查了简单曲线的极坐标方程，属中档题．[选修4-5：不等式选讲]23．已知函数f（x）＝|x﹣2a|﹣|x﹣a|，a∈R．（Ⅰ）若f（1）＞1，求a的取值范围；（Ⅱ）若a＜0，对∀x，y∈（﹣∞，a]，都有不等式f（x）≤|（y+2020|+|y﹣a|恒成立，求a的取值范围．【分析】（Ⅰ）由题意不等式化为|1﹣2a|﹣|1﹣a|＞1，利用分类讨论法去掉绝对值求出不等式的解集即可；（Ⅱ）由题意把问题转化为[f（x）]max≤[|y+2020|+|y﹣a|]min，分别求出[f（x）]max和[|y+2020|+|y﹣a|]min，列出不等式求解集即可．【解答】解：（Ⅰ）由题意知，f（1）＝|1﹣2a|﹣|1﹣a|＞1，…（1分）若a≤，则不等式化为1﹣2a﹣1+a＞1，解得a＜﹣1；…（2分）若＜a＜1，则不等式化为2a﹣1﹣（1﹣a）＞1，解得a＞1，即不等式无解；…（3分）若a≥1，则不等式化为2a﹣1+1﹣a＞1，解得a＞1，…（4分）综上所述，a的取值范围是（﹣∞，﹣1）∪（1，+∞）…（5分）（Ⅱ）由题意知，要使得不等式f（x）≤|（y+2020|+|y﹣a|恒成立，只需[f（x）]max≤[|y+2020|+|y﹣a|]min，…（6分）当x∈（﹣∞，a]时，|x﹣2a|﹣|x﹣a|≤﹣a，[f（x）]max＝﹣a，…（7分）因为|y+2020|+|y﹣a|≥|a+2020|，所以当（y+2020）（y﹣a）≤0时，[|y+2020|+|y﹣a|]min＝|a+2020|，…（9分）即﹣a≤|a+2020|，解得a≥﹣1010，结合a＜0，所以a的取值范围是[﹣1010，0）…（10分）【点评】本题考查了含有绝对值的不等式恒成立应用问题，也考查了分类讨论思想和转化问题，是中档题．。

湖南省2019届高三六校联考试题文科综合能力测试注意事项：1．答卷前，考生务必用黑色字迹的钢笔或签字笔在答题卡上填写自己的准考证号、姓名、试室号和座位号。

用2B型铅笔把答题卡上试室号、座位号对应的信息点涂黑。

2．选择题每小题选出答案后，用2B型铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其他答案，答案不能答在试卷上。

3．非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内的相应位置上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用铅笔和涂改液。

不按以上要求作答的答案无效。

4．考生必须保持答题卡整洁。

考试结束后，将试卷和答题卡一并交回。

第Ⅰ卷本卷共35小题，每小题4分，共计140分。

每小题给出的四个选项中，只有一项是符合题目要求的。

城市道路绿化隔离带具有隔离汽车行驶，美化环境的作用。

下图为一地理爱好者拍摄的某城市机动车道与非机动车道绿化隔离带照片，每年该市的园林工作人员都要对道路绿化隔离带中的一些树冠庞大的乔灌木进行侧向剪枝，同时用石灰水全部涂白。

据此完成下列各题。

1. 园林工作人员对绿化带中树冠庞大的乔灌木进行侧向剪枝的主要目的是A. 调节树木与道路之间矛盾B. 调整树势，促进树木良好生长C. 改善树冠的通风透光条件D. 美化树形，提高树木观赏效果2. 当地园林丁作人员开始剪枝的季节最好选择在A. 冬末春初B. 春末夏初C. 夏末秋初D. 秋末冬初【答案】1. A 2. D【解析】【分析】本题考查城市绿化.【1题详解】通常，城市绿化隔离带的宽度多在1.5~3米之间，通过人工剪枝来控制庞大树冠枝条的密度、宽度(或直径)和高度，解除树冠过大对交通视线的可能阻挡，保证行亼和车辆通行，减少行车安全事故。

故选A。

【2题详解】根据该地涂白的树木为落叶阔叶林可知，在冬季到来前，树木已接近停止生长，剪枝可以减少树木的水分流失，减少树木的蒸发量为树节省营养，顺利度过严寒。

【解析】湖南省重点⾼中2019届⾼三11⽉⼤联考地理试卷Word版含解析湖南省重点⾼中2019届⾼三11⽉⼤联考地理试卷本试卷分第I 卷（选择题）和第E 卷（⾮选择题）两部分，共 6 页。

满分100 分。

考试⽤时90 分钟。

考试结束后，将本试卷和答题卡⼀并交回。

注意事项：1. 答题前，考⽣务必⽤0. 5 毫⽶⿊⾊签字笔将⾃⼰的姓名、应号、考⽣号、县区和科类填写到答题卡和试卷规定的位直上。

2. 第I卷每⼩题选出答案后，⽤2B 铅笔把答题卡上对应题⽬的答案标号涂⿊；如需改动，⽤橡⽪擦⼲净后，再选涂其他答案标号。

写在本试卷上⽆效。

3. 第II 卷必须⽤0. 5 毫⽶⿊⾊签字笔作答，答案必须写在答题卡各题⽬指定区域内相应的位直；如需改动，先知i掉原来的答案，然后再写上新的答案；不能使⽤涂改淡、胶带纸、修正带。

不按以上要求作答的答案⽆效。

第I卷⼀、选择题：本题共25 ⼩题，每⼩题2 分，共50 分。

在每⼩题给出的四个选项中，只有⼀项是符合题⽬要求的。

冬半年林⽊向阳⾯昼夜温差剧变伎树⼲内外温度不同，收缩不同，导致树⽪破裂的现象，称为冻裂。

为保护树⽊，树⼲上常常刷上⽩漆。

图⽰为我国东北林区某区域等⾼线地形图。

据此完成l-2 题。

1. 图中坡向的树最应刷上⽩漆予以重点保护A. ①B. ② c. ③ D ④2. 与②处相⽐，④处树⽊长势更好，其主要原因是⼈地势低，坡度⼩B. 蒸发量⼩，⼟壤湿润c. 光照条件好，⽓温⾼D. 降⽔量⼤，地下⽔位浅图⽰意L 、P 两国经纬度位直。

完成3 -4 题。

3. 读图可知A. 甲位于⼄的东北⽅向C. P 国⾯积较L 国⼤B. L 国主要位于西半球、低纬度D. b 点对⾯点为（23。

26 'N , 165。

W )4. 图中ab 、cd 、a' b ＇、b'c＇线段等长，ad 、be 线段等长，则各线段⽐例尺⼤⼩是A. ab = cd = adC. ad = bcB. ab= cdD. b'c' < ad< bc湖陆风包括湖风（出湖风）和陆风（进湖风），是在较⼤湖泊和陆地之｜可形成的以24 ⼩时为周期的地⽅性风。

湖南省2019届高三六校联考试题文科综合能力测试注意事项：l．本试卷分第J卷（选择题）和第1I卷（非选择题）两部分，时量150分钟，满分300分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第1卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷本卷共35小题，每小题4分，共计140分。

每小题给出的四个选项中，只有一项是符合题目要求的。

城市道路绿化隔离带具有隔离汽车行驶，美化环境的作用。

下图为一地理爱好者拍摄的某城市机动车道与非机动车道绿化隔离带照片，每年该市的园林工作人员都要对道路绿化隔离带中的一些树冠庞大的乔灌木进行侧向剪枝，同时用石灰水全部涂白。

据此完成下列各题。

1. 园林工作人员对绿化带中树冠庞大的乔灌木进行侧向剪枝的主要目的是A. 调节树木与道路之间矛盾B. 调整树势，促进树木良好生长C. 改善树冠的通风透光条件D. 美化树形，提高树木观赏效果2. 当地园林丁作人员开始剪枝的季节最好选择在A. 冬末春初B. 春末夏初C. 夏末秋初D. 秋末冬初首都地区环线高速公路，俗称“北京大七环”，于2018年8月全线贯通。

“北京大七环”立交桥较多，其中通州一大兴段就建有15座立交桥，且立交桥设计坡度较小。

《北京人口蓝皮书：北京人口发展研究报告(2018)》显示：2017年底，北京市外来人口、户籍人口实现了双下降，20年来首次实现负增长，人口分布中心化趋势有所缓解，其中常住人口主要流向京津冀都市圈内的中小城市。

据此完成下列各题。

3. 关于“大七环”给京津冀带来影响，说法正确的是A. 交通网密度增加．加大北京市巾区的交通压力。

B. 提升北京城市等级，完善北京城市服务功能C. 促进区域城市分工与合作，改善区域投资环境D. 促进北京城市用地规模向周边区域拓展4. 关于北京市外来人口首次出现负增长的原因．推测错误的是A. 近年来产业结构不断调整B. 交通拥堵状况日益严重C. 不断优化城市功能布局D. 政策引导分散城市职能5. 关于北京立交桥设计的说法正确的是①立体交通利于提高运输能力②立交所增加了交通用地缩短了路程③路面坡度小利于冬季行路安全④路面坡度小遗应复杂地质条件A. ①②B. ①③C. ②③D. ③④南美白对虾适应能力强，一般在沿海地区养殖。

2019届高三年级第二次模拟考试文科综合地理试卷第Ⅰ卷 选择题本卷共35小题，每小题4分，共计140分。

每小题给出的四个选项中，只有一项是符合题目要求的。

细绒棉也称陆地棉，喜温、好光，对土壤肥力要求较高，原产中美洲墨西哥等地，19世纪末传入我国。

下图为墨西哥棉花产地示意图。

读图，完成下面小题。

1. 下列关于墨西哥的叙述正确的是（ ）。

A. 以平原为主，地势较平坦B. 位于板块内部，多断块山C. 地壳运动较活跃，多火山地震D. 因沿海地形平坦，城市分布广泛2. 下列关于甲地棉花种植说法正确的是（ ）。

A. 土壤多碱性肥力较高B. 改变当地的气候类型C. 主要是面向国内市场D. 带动相关产业的发展【答案】1. C 2. D【解析】【1题详解】本题主要考查区域特征的分析。

墨西哥以高原为主，A 错误；墨西哥位于板块的交界处，地壳运动活跃，多火山地震，B 错误、C 正确；由图可知，墨西哥主要位于热带，气候湿热，因此城市主要分布在地势较高的高原，气候凉爽适合人类居住，D错误。

故答案选C项。

【2题详解】甲地为热带或者亚热带的气候区，发育的土地多为酸性土壤，A错误；农业发展不会改变当地的气候类型，B错误；甲地的棉花主要面向的额为国际市场，C错误；棉花种植能够带动相关产业的发展，D 正确。

故答案选D项。

贵州构皮滩库区多滑坡，某科学研究小组为了研究土质滑坡发育概率与坡度间的关系，于某年11月对构皮滩库区的113个土质滑坡（潜在滑坡）发育的原始坡度进行统计，并绘制了该区域滑坡累计概率分布图。

读图，完成下面小题。

3. 滑坡的形成（）。

A. 概率与坡度大小呈正相关B. 与人类活动无关C. 与植被覆盖率有关D. 与地层岩性无关4. 某日早晨，科考队员从营地出发前往构皮滩库区土质滑坡区的过程中，发现太阳从左侧照射过来，据此推测，科考队员此时行进的方向是（）。

A. 西南B. 西北C. 东南D. 东北【答案】3. C 4. A【解析】【3题详解】读图分析可知，该图为累计概率分布图，不能反映与坡度大小的关系，A错误；滑坡的形成既有自然原因也有人为原因，B错误；坡面上植被覆盖率越高，水土流失越轻，C正确；滑坡的形成与岩石的岩性有关，D错误。