鸡兔同笼的问题动画版

第11讲鸡兔同笼问题一典型问题◇◇兴趣篇◇◇1. 一只鸡有1个头2条腿，一只兔子有1个头4条腿。

如果笼子里的鸡和兔子共有10个头和26条腿，你知道鸡和兔子各有几只吗？答案：鸡7只，兔子3只【分析】假设全为鸡，一共有10×2条腿，少26-10×2条腿。

兔：（26-10×2）÷（4-2）=3（只）鸡：10-3=7（只）2. 停车场上的自行车和三轮车一共有24辆，其中每辆自行车有2个轮子，每辆三轮车有3个轮子，所有自行车和三轮车一共有56个轮子。

请问：有多少辆自行车？有多少辆三轮车？答案：自行车16辆，三轮车8辆【分析】假设全是三轮车，有24×3个轮子，多出了24×3-56个轮子。

一共有自行车：（24×3-56）÷（3-1）=16（辆）三轮车有：24-16=8（辆）3. 晨星小学有30间宿舍，其中大宿舍每间住6人，小宿舍每间住4人。

如果这些宿舍一共可以住168人，那么有几间大宿舍？答案：24间【分析】假设全为小宿舍，一共能住4×30个人，少了168-4×30人大宿舍一共有（168-4×30）÷（6-4）=24（间）4. 理想小学150名教师参加新年联欢会，其中有一个趣味游戏，要求男教师2人一组，女教师3人一组。

结果共分了62组，恰好分完。

请问：女教师有多少人，男教师有多少人？答案：女教师78人，男教师72人【分析】假设每组全为男老师，一共有62×2人，少了150-6×2人女老师共有（150-62×2）÷（3-2）=26（组），26×3=78（人）男老师有：（62-26）×2=72（人）5. 阿奇的存钱罐里有5角和1元的硬币共25枚，总钱数为19元。

这两种硬币各有多少枚？答案：1元硬币13枚，5角硬币12枚【分析】假设阿奇的硬币全为1元，一共有25×10角，实际为19角，少了25×10-190角∴5角硬币一共（250×10-190）÷（10-5）=12（枚），1元硬币有25-12=13枚。

鸡兔同笼问题1、鸡和兔共有8只,脚共28只,鸡和兔各几只?8×2=16（只）28-16=12（只）4-2=2（只）12÷2=6（只）8-6=2（只）答：鸡有6只，兔有2只。

解题思路：⑴把这8只动物都看做鸡，一只鸡有两只腿，8只动物一共应该有16只腿，可是现在一共有28只腿，少了12只。

为什么会少12只，是因为把兔子算成了鸡，如果有一只兔子那就少了2只腿。

那几只兔子才能少12只腿，就看12里面有几个2，就是有几只兔子。

⑵或者把这8只动物都看做兔，一只兔有四只腿，8只动物一共应该有32，可是现在一共有28只腿，多了4只。

为什么会多4只，因为把鸡算成了兔子，如果有一只鸡看成了兔子，就多算了两只腿。

多少只鸡才能多算4只腿呢，就看4 里面有几个2，就是有几只鸡。

8-2=6（只）兔子有6只。

（3）或者让鸡和兔都抬起一只腿，现在腿数就少了8只，28-8=20（只），再让它们都抬起一只腿，腿数又少了8只，20-8=12（只）。

现在地上就剩下兔子的腿，每只兔子两只腿。

剩下的这12只腿里有几个2，就是有几只兔。

做这样的题时候，尽量假设成腿少的动物。

2、小强是个汽车迷，他来到展厅，一看有大、小两种车，用14辆，数数车轮，大汽车6个轮子，小汽车4个轮子，14辆车数在一起一共64个轮子，请问：有几辆大汽车，几辆小汽车？14×4=56（个）64-56=8（个）6-4=2（个）8÷2=4（辆）14-4=10（辆）答：大汽车4辆，小汽车10辆。

解题思路：⑴把这14辆车都看成小汽车，应该有56个轮子。

可是现在一共有64个轮子，少了8个轮子。

为什么会少8个轮子，是因为把大汽车算成了小汽车，如果一辆大汽车算成小汽车就少算2个轮子。

那几辆大汽车才能少算8个轮子，就看8里面有几个2，就是有4辆大汽车，小汽车就有10辆。

⑵把这14辆车都看成大汽车，应该有84个轮子。

可是现在一共有64个轮子，多了20个轮子。

第八讲较复杂的鸡兔同笼问题（一）“鸡兔同笼”是一类有名的中国古算题.最早出现在《孙子算经》中.许多小学算术应用题都可以转化成这类问题，或者用解它的典型解法--“假设法”来求解.因此很有必要学会它的解法和思路.例1 有若干只鸡和兔子，它们共有88个头，244只脚，鸡和兔各有多少只？解：我们设想，每只鸡都是“金鸡独立”，一只脚站着；而每只兔子都用两条后腿，像人一样用两只脚站着.现在，地面上出现脚的总数的一半，·也就是244÷2=122（只）.在122这个数里，鸡的头数算了一次，兔子的头数相当于算了两次.因此从122减去总头数88，剩下的就是兔子头数122-88=34，有34只兔子.当然鸡就有54只.答：有兔子34只，鸡54只.上面的计算，可以归结为下面算式：总脚数÷2-总头数=兔子数.上面的解法是《孙子算经》中记载的.做一次除法和一次减法，马上能求出兔子数，多简单！能够这样算，主要利用了兔和鸡的脚数分别是4和2，4又是2的2倍.可是，当其他问题转化成这类问题时，“脚数”就不一定是4和2，上面的计算方法就行不通.因此，我们对这类问题给出一种一般解法.还说例1.如果设想88只都是兔子，那么就有4×88只脚，比244只脚多了88×4-244=108（只）.每只鸡比兔子少（4-2）只脚，所以共有鸡（88×4-244）÷（4-2）= 54（只）.说明我们设想的88只“兔子”中，有54只不是兔子.而是鸡.因此可以列出公式：鸡数=（兔脚数×总头数-总脚数）÷（兔脚数-鸡脚数）当然，我们也可以设想88只都是“鸡”，那么共有脚2×88=176（只），比244只脚少了244-176=68（只）.每只鸡比每只兔子少（4-2）只脚，68÷2=34（只）.说明设想中的“鸡”，有34只是兔子，也可以列出公式：兔数=（总脚数-鸡脚数×总头数）÷（兔脚数-鸡脚数）.上面两个公式不必都用，用其中一个算出兔数或鸡数，再用总头数去减，就知道另一个数.假设全是鸡，或者全是兔，通常用这样的思路求解，有人称为“假设法”.鸡兔同笼中的总头数是“两数之和”，如果把条件换成“两数之差”，又应该怎样去解呢？例7 买一些4分和8分的邮票，共花6元8角.已知8分的邮票比4分的邮票多40张，那么两种邮票各买了多少张？解一：如果拿出40张8分的邮票，余下的邮票中8分与4分的张数就一样多.（680-8×40）÷（8+4）=30（张），这就知道，余下的邮票中，8分和4分的各有30张.因此8分邮票有40+30=70（张）.答：买了8分的邮票70张，4分的邮票30张.也可以用任意假设一个数的办法.解二：譬如，假设有20张4分，根据条件“8分比4分多40张”，那么应有60张8分.以“分”作为计算单位，此时邮票总值是4×20+8×60=560.比680少，因此还要增加邮票.为了保持“差”是40，每增加1张4分，就要增加1张8分，每种要增加的张数是：（680-4×20-8×60）÷（4+8）=10（张）.因此4分有20+10=30（张），8分有60+10=70（张）.例8 一项工程，如果全是晴天，15天可以完成.倘若下雨，雨天一天工程要多少天才能完成？解：类似于例3，我们设工程的全部工作量是150份，晴天每天完成10份，雨天每天完成8份.用上一例题解一的方法，晴天有（150-8×3）÷（10+8）= 7（天）.雨天是7+3=10天，总共7+10=17（天）.答：这项工程17天完成.请注意，如果把“雨天比晴天多3天”去掉，而换成已知工程是17天完成，由此又回到上一节的问题.差是3，与和是17，知道其一，就能推算出另一个.这说明了例7、例8与上一节基本问题之间的关系.总脚数是“两数之和”，如果把条件换成“两数之差”，又应该怎样去解呢？例9 鸡与兔共100只，鸡的脚数比兔的脚数少28.问鸡与兔各几只？解一：假如再补上28只鸡脚，也就是再有鸡28÷2=14（只），鸡与兔脚数就相等，兔的脚是鸡的脚4÷2=2（倍），于是鸡的只数是兔的只数的2倍.兔的只数是：（100+28÷2）÷（2+1）=38（只）.鸡是：100-38=62（只）.答：鸡62只，兔38只.当然也可以去掉兔28÷4=7（只）.兔的只数是（100-28÷4）÷（2+1）+7=38（只）.也可以用任意假设一个数的办法.解二：假设有50只鸡，就有兔100-50=50（只）.此时脚数之差是：4×50-2×50=100，比28多了72.就说明假设的兔数多了（鸡数少了）.为了保持总数是100，一只兔换成一只鸡，少了4只兔脚，多了2只鸡脚，相差为6只（千万注意，不是2）.因此要减少的兔数是：（100-28）÷（4+2）=12（只）.兔只数是：50-12=38（只）.另外，还存在下面这样的问题：总头数换成“两数之差”，总脚数也换成“两数之差”.例10 古诗中，五言绝句是四句诗，每句都是五个字；七言绝句是四句诗，每句都是七个字.有一诗选集，其中五言绝句比七言绝句多13首，总字数却反而少了20个字.问两种诗各多少首.解一：如果去掉13首五言绝句，两种诗首数就相等，此时字数相差13×5×4+20=280（字）.每首字数相差：7×4-5×4=8（字）.因此，七言绝句有：28÷（28-20）=35（首）.五言绝句有：35+13=48（首）.答：五言绝句48首，七言绝句35首.解二：假设五言绝句是23首，那么根据相差13首，七言绝句是10首.字数分别是20×23=460（字），28×10=280（字），五言绝句的字数，反而多了：460-280=180（字）.与题目中“少20字”相差：180+20=200（字）.说明假设诗的首数少了.为了保持相差13首，增加一首五言绝句，也要增一首七言绝句，而字数相差增加8.因此五言绝句的首数要比假设增加200÷8=25（首）.五言绝句有23+25=48（首）.七言绝句有10+25=35（首）.在写出“鸡兔同笼”公式的时候，我们假设都是兔，或者都是鸡，对于例7、例9和例10三个问题，当然也可以这样假设.现在来具体做一下，把列出的计算式子与“鸡兔同笼”公式对照一下，就会发现非常有趣的事.例7，假设都是8分邮票，4分邮票张数是（680-8×40）÷（8+4）=30（张）.例9，假设都是兔，鸡的只数是（100×4-28）÷（4+2）=62（只）.例10，假设都是五言绝句，七言绝句的首数是（20×13+20）÷（28-20）=35（首）.首先，请读者先弄明白上面三个算式的由来，然后与“鸡兔同笼”公式比较，这三个算式只是有一处“-”成了“+”.其奥妙何在呢？当你进入初中，有了负数的概念，并会列二元一次方程组，就会明白，从数学上说，这一讲前两节列举的所有例子都是同一件事.例11有一辆货车运输2000只玻璃瓶，运费按到达时完好的瓶子数目计算，每只2角，如有破损，破损瓶子不给运费，还要每只赔偿1元.结果得到运费379.6元，问这次搬运中玻璃瓶破损了几只？解：如果没有破损，运费应是400元.但破损一只要减少1+0.2=1.2（元）.因此破损只数是（400-379.6）÷（1+0.2）=17（只）.答：这次搬运中破损了17只玻璃瓶.请你想一想，这是“鸡兔同笼”同一类型的问题吗？例12 有两次自然测验，第一次24道题，答对1题得5分，答错（包含不答）1题倒扣1分；第二次15道题，答对1题8分，答错或不答1题倒扣2分，小明两次测验共答对30道题，但第一次测验得分比第二次测验得分多10分，问小明两次测验各得多少分？解一：如果小明第一次测验24题全对，得5×24=120（分）.那么第二次只做对30-24=6（题）得分是：8×6-2×（15-6）=30（分）. 两次相差：120-30=90（分）.比题目中条件相差10分，多了80分.说明假设的第一次答对题数多了，要减少.第一次答对减少一题，少得5+1=6（分），而第二次答对增加一题不但不倒扣2分，还可得8分，因此增加8+2=10分.两者两差数就可减少6+10=16（分）.（90-10）÷（6+10）=5（题）.因此，第一次答对题数要比假设（全对）减少5题，也就是第一次答对19题，第二次答对：30-19=11（题）.第一次得分：5×19-1×（24- 9）=90.第二次得分：8×11-2×（15-11）=80.答：第一次得90分，第二次得80分.解二：答对30题，也就是两次共答错24+15-30=9（题）.第一次答错一题，要从满分中扣去5+1=6（分），第二次答错一题，要从满分中扣去8+2=10（分）.答错题互换一下，两次得分要相差6+10=16（分）.如果答错9题都是第一次，要从满分中扣去6×9.但两次满分都是120分.比题目中条件“第一次得分多10分”，要少了6×9+10.因此，第二次答错题数是：（6×9+10）÷（6+10）=4（题）·第一次答错 9-4=5（题）.第一次得分 5×（24-5）-1×5=90（分）.第二次得分 8×（15-4）-2×4=80（分）.习题二1.买语文书30本，数学书24本共花83.4元.每本语文书比每本数学书贵0.44元.每本语文书和数学书的价格各是多少？2.甲茶叶每千克132元，乙茶叶每千克96元，共买这两种茶叶12千克.甲茶叶所花的钱比乙茶叶所花钱少354元.问每种茶叶各买多少千克？3.一辆卡车运矿石，晴天每天可运16次，雨天每天只能运11次.一连运了若干天，有晴天，也有雨天.其中雨天比晴天多3天，但运的次数却比晴天运的次数少27次.问一连运了多少天？4.某次数学测验共20道题，做对一题得5分，做错一题倒扣1分，不做得0分.小华得了76分.问小华做对了几道题？5.甲、乙二人射击，若命中，甲得4分，乙得5分；若不中，甲失2分，乙失3分.每人各射10发，共命中14发.结算分数时，甲比乙多10分.问甲、乙各中几发？6.甲、乙两地相距12千米.小张从甲地到乙地，在停留半小时后，又从乙地返回甲地，小王从乙地到甲地，在甲地停留40分钟后，又从甲地返回乙地.已知两人同时分别从甲、乙两地出发，经过4小时后，他们在返回的途中相遇.如果小张速度比小王速度每小时多走1.5千米，求两人的速度.【例 1】 动物园里养了一些梅花鹿和鸵鸟，共有脚208只，鸵鸟比梅花鹿多20只，梅花鹿和鸵鸟各有多少只？【解析】 假设梅花鹿和鸵鸟的只数相同，则从总脚数中减去鸵鸟多的20只的脚数得：208202168-⨯=(只)．这168只脚是梅花鹿的脚数和鸵鸟的脚数(注意此时梅花鹿和鸵鸟的只数相同)脚数的和，一只梅花鹿和一只鸵鸟的脚数和是：246+=(只)，所以梅花鹿的只数是：168628÷=(只)，从而鸵鸟的只数是：282048+=(只) （本题也可给学生讲成“捆绑法”，一鸡一兔一组，这个怎么分组时有倍数关系得到的）【巩固】 一个养殖园内，鸡比兔多36只，共有脚792只，鸡兔各几只？【解析】 已知鸡比兔多36只，如果把多的36只鸡拿走，剩下的鸡兔只数就相等了，拿走的36只鸡有23672⨯=（只）脚，可知现在剩下79272720-=（只）脚，一只鸡与一只兔有6只脚，那么兔有7206120+=（只）．÷=（只），鸡有12036156【巩固】鸡兔同笼，鸡、兔共有107只，兔的脚数比鸡的脚数多56只，问鸡、兔各多少只？【解析】这道例题和前面的例题有所不同，前面的题是已知头数之和和脚数之和求各有几只，而这道题是已知头数之和和脚数之差，这样就比前面的例题增加了一点难度．我们用两种方法来解这道题．（方法一）考虑如果补上鸡脚少的56只的话，那么就要增加56228÷=（只）鸡．这样一来，鸡、兔共有10728135+=（只），这时鸡脚、兔脚一样多．已知一只鸡的脚数是一只兔的一半，而现在鸡脚、兔脚相同，可知鸡的只数是兔的2倍，根据和倍问题有：兔有：135(21)45÷+=（只）鸡有：135452862-=（只）--=（只）或者1074562（方法二）不妨假设107只都是兔，没有鸡，那么就有兔脚：1074428⨯=（只），而鸡的脚数为零．这样兔脚比鸡脚多428只，而实际上只多56只，这说明假设的兔脚比鸡脚多的数比实际上多：-=（只）．现在以鸡换兔，每换一只，兔脚减少4只，鸡脚增加2只，即兔脚与鸡脚的42856372总数差就会减少426+=（只）．鸡的只数：372662÷=（只）兔的只数：1076245-=（只）【巩固】鸡、兔共100只，鸡脚比兔脚多20只.问：鸡、兔各多少只?【解析】假设100只都是鸡，没有兔，那么就有鸡脚200只，而兔的脚数为零.这样鸡脚比兔脚多200只，而实际上只多20只，这说明假设的鸡脚比兔脚多的数比实际上多20020180-=(只).现在以兔换鸡，每换一只，鸡脚减少2只，兔脚增加4只，即鸡脚比兔脚多的脚数中就会减少426+=(只)，而180630-=(只).÷=，因此有兔子30只，鸡1003070【巩固】鸡、兔共60只，鸡脚比兔脚多60只．问：鸡、兔各多少只？【解析】假设60只都是鸡，没有兔，那么就有鸡脚120只，而兔的脚数为零．这样鸡脚比兔脚多120只，而实际上只多60只，这说明假设的鸡脚比兔脚多的数比实际上多1206060-=(只)．现在以兔换鸡，每换一只，鸡脚减少2只，兔脚增加4只，即鸡脚比兔脚多的脚数中就会减少426+=(只)，而60610-=(只)．÷=，因此有兔子10只，鸡601050【巩固】鸡、兔同笼，鸡比兔多26只，足数共274只，问鸡、兔各几只？【解析】这道例题是已知鸡、兔的脚数和，鸡比兔多的只数，求鸡、兔各几只．我们假设鸡与兔只数一样多，那么现在它们的足数一共有：274226222+=（只），-⨯=（只），每一对鸡、兔共有足：246鸡兔共有对数（也就是兔子的只数）：222637+=（只）．÷=（对），则鸡有 372663【巩固】鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只？【解析】解一:假如再补上28只鸡脚,也就是再有鸡28÷2=14(只),鸡与兔脚数就相等,兔的脚是鸡的脚4÷2=2(倍),于是鸡的只数是兔的只数的2倍.兔的只数是(100+28÷2)÷(2+1)=38(只).鸡是100-38=62(只).当然也可以去掉兔28÷4=7(只).兔的只数是(100-28÷4)÷(2+1)+7=38(只).也可以用任意假设一个数的办法.解二:假设有50只鸡,就有兔100-50=50(只).此时脚数之差是4×50-2×50=100, 比28多了72.就说明假设的兔数多了(鸡数少了).为了保持总数是100,一只兔换成一只鸡,少了4只兔脚,多了2只鸡脚,相差为6只(千万注意,不是2).因此要减少的兔数是 (100-28)÷(4+2)=12(只). 兔只数是50-12=38(只).【巩固】小建和小雷做仰卧起坐，小建先做了3分钟，然后两人各做了5分钟，一共做仰卧起坐136次．已知每分钟小建比小雷平均多做4次，那么小建比小雷多做了多少次？【解析】假设小建每分钟做仰卧起坐的次数与小雷一样多，这样两人做仰卧起坐的总次数就减少了-÷++=（）（）(次)，进而可以分别求出⨯+=（）(次)，由此可知小雷每分钟做了13632355843532小建每分钟做的次数以及两人分别做仰卧起坐的总次数之差．假设小建每分钟做仰卧起坐的次数与小雷一样多，两人做仰卧起坐的总次数就减少：43532（）(次)⨯+=小雷每分钟做：136323558+=(次)-÷++=（）（）(次)；小建每分钟做：8412小建一共做：123596⨯=(次)⨯+=（）(次)；小雷一共做：8540小建比小雷多做：964056-=(次)【巩固】小同有一个储蓄筒，存放的都是硬币，其中2分币比5分币多22个；按钱数算，5分币却比2分币多4角；另外，还有36个1分币．小同共存了多少钱？【解析】假设去掉22个2分币，那么按钱数算，5分币比2分币多8角4分，一个5分币比一个2分币多3分，所以5分币有845228+=（个），528250136⨯+⨯+⨯=（）（个），2分币有282250÷-=++=（分）．14010036276【巩固】买一些4分和8分的邮票,共花6元8角.已知8分的邮票比4分的邮票多40张,那么两种邮票各买了多少张【解析】解一:如果拿出40张8分的邮票,余下的邮票中8分与4分的张数就一样多.(680-8×40)÷(8+4)=30(张),这就知道,余下的邮票中,8分和4分的各有30张.因此8分邮票有 40+30=70(张).解二:譬如,假设有20张4分,根据条件"8分比4分多40张",那么应有60张8分.以"分"作为计算单位,此时邮票总值是 4×20+8×60=560.比680少,因此还要增加邮票.为了保持"差"是40,每增加1张4分,就要增加1张8分,每种要增加的张数是 (680-4×20-8×60)÷(4+8)=10(张).因此4分有20+10=30(张),8分有60+10=70(张).【巩固】现有大小油桶50个，每个大桶可装油4千克，每个小桶可装油2千克，大桶比小桶共多装油20千克，问大小桶各多少个?【解析】分析与解答一：假设50个油桶都是大桶，则共装油(450)200⨯=千克，而这小桶所装油则为0．这样大桶比小桶多装200千克，比条件所给的差数多了(20080)180-=千克，若在50个大桶中把一部分大桶换成小桶，则每拿一个大桶换成小桶，大桶装的油就减少4千克，而小桶共装的油就增加2千克，那么大桶比小桶多装的数量就减少(42)6+=千克，那么该把多少个大桶换成小桶才符合题意呢?解：(45020)(42)⨯-÷+=÷=(个)(小桶)180630-=(个)(大桶)503020分析与解答二：这道题也可以用另外一种假设；每个大桶比每个小桶多装2千克，如果大小桶同样多，大桶要比小桶共多装20千克，则应该大小桶各20(42)10÷-=个，现在共有50个桶，在-⨯=个桶中，大小桶应装同样多的油，而每个大桶装的油是每个小桶装的剩下的(50102)30÷=倍，那么在这30个桶中，应该有[30(12)]10(42)2-=个小桶；所以÷+=个大桶，(3010)20可求出50个桶中，有大小桶各多少个．÷-=(个)解：20(42)10-⨯÷+=(个)(大桶)(50102)(12)10101020+=(个)(大桶共有)-=(个)(小桶共有)502030【巩固】一批钢材，用小卡车装载要45辆，用大卡车装载只要36辆．已知每辆大卡车比每辆小卡车多装4吨，那么这批钢材有多少吨？【解析】要算出这批钢材有多少吨，需要知道每辆大卡车或小卡车能装多少吨．利用假设法，假设只用36辆小卡车来装载这批钢材，因为每辆大卡车比每辆小卡车多装4吨，所以要剩下436144⨯= (吨)．根据条件，要装完这144吨钢材还需要45369-=(辆)小卡车．这样每辆小卡车能装÷=(吨)．由此可求出这批钢材有720吨．144916。

第七讲鸡兔同笼问题第七讲鸡兔同笼问题一、知识要点和基本方法1．兔同笼的基本问题是：已知鸡、免总头数和总脚数，求鸡、兔各有多少只．（1）解决鸡兔同笼问题的方法通常是用假设法，解题思路是：先假设笼子里装的全是鸡，根据鸡兔的总数就可以算出在假设下共有几只脚，把这样得到的脚数与题中给出的脚数相比较，看看差多少，每差2只脚就说明有1只兔，将所差的脚数除以2，就可以算出共有多少只兔．（2）解决鸡兔同笼问题的基本关系式是：鸡数＝（兔脚数×总头数－总脚数）÷（兔脚数－鸡脚数）．兔数＝（总脚数－鸡脚数×总头数）÷（兔脚数－鸡脚数）．注意，这两个基本关系式不必都用，用其中一个算出免数或鸡数，又知总数，所以另一个也就知道了．2．兔同笼问题的变型有两类：（1）将鸡、兔的总头数和总脚数中的“两数之和”变成“两数之差”，这样得到三种情况：已知鸡、兔头数之差和总脚数，求鸡兔各有多少只；已知鸡、兔脚数之差和总头数，求鸡兔各有多少只；已知鸡、兔头数之差和脚数之差，求鸡兔各有多少只．（2）将基本问题中同笼的是鸡、免两种不同东西，还可以引伸到同笼中不同东西是三种，四种等等．注意：鸡兔同笼问题的两种变型均可转化成基本问题来解决．二、例题精讲例1 在同一个笼子中，有若干只鸡和免，从笼子上看有40个头，从笼子下数有130只脚，那么这个笼子中装有免、鸡各多少只？分析题目中给出了鸡、兔共有40只，如果把兔子的两只前脚用绳子捆起来，看作是一只脚，两只后脚也捆起来，也看成是一只脚，那么兔子就成了2只脚（即把兔子都当成两只脚的鸡）．鸡兔总的脚数是40 ×2=80（只）比题中所说的 130只要少130－80＝50（只）．现在松开一只兔子脚上的绳子，总的脚数就会增加 2，即80+2＝82。

再松开一只兔子脚上的绳子，总的脚数又增加 2，即 82+2＝84，…一直继续下去，直至增加到50．此，兔子数是50 ÷2＝25（只）．实际上，这就是上述基本关系式（2）．解（130－40 × 2）÷（4－2）＝（130－80）÷2＝50 ÷ 2＝25（只）．40－25＝15（只）．答笼子中有兔子25只，有鸡15只．例2蜘蛛有8条腿，蜻蜒有6条腿和2对翅膀，蝉有6条腿和1对翅膀，现在这三种小虫共21只，有140条腿和24对翅膀，求每种小虫各几只？分析此题中出现了3种昆虫，不仅有腿的比较，而且又出现了翅膀，显然比前几道题复杂了．解此题的关键就是将3种昆虫转化为2种昆虫，这样解起来就比较容易了．突破口在于：蝉和蜻蜓都有6条腿。

鸡兔同笼问题？看到这个题目，大概有宝宝会不屑地说：“小学生都会！”可是今天的问题，不是要解出答案，而是你会用多少种解法解出答案？不要小看这个“简单”的问题，早在1500年前，《孙子算经》中就记载了这个有趣的问题.WOW，还是个古董呢~好啦，废话少说，请听题……题目：现有一笼子，里面有鸡和兔子若干只，数一数，共有头14个，腿38条，球鸡和兔子各有多少只？（请用尽量多的方法解答）『方法一：人见人爱的列表法』如果二年级小朋友做这道题，可以用列表法！直观、易理解，还不容易出错~好啦，我们来看一下！鸡 0 3 5 79...兔1411 9 7 5...腿5650464238...根据上面的表格，我们可以看出，鸡为9只，兔子为5只.我们在列表的时候不要按顺序列，否则做题的速度会很慢，比如说列完鸡为0只，兔子为14只，发现腿的数量56条，和实际38条相差较大，那么下一个你可以跳过鸡的数量为2只这种情况，直接列鸡的数量为3只，这样做速度会快一些哦！分析：让每只鸡都一只脚站立着，每只兔都用两只后脚站立着，那么地上的总脚数只是原来的一半，即19只脚.鸡的脚数与头数相同，而兔的脚数是兔的头数的2倍，因此从19里减去头数14，剩下来的就是兔的头数19－14=5只，鸡有14－5=9只.『方法四：最逗的吹哨法』分析：假设鸡和兔接受过特种部队训练，吹一声哨，它们抬起一只脚，还有38-14=24只腿在站着，再吹一声哨，它们又抬起一只脚，这时鸡都一屁股坐地上了，兔子还有两只脚立着.这时还有24-14=10只腿在站着，而这10只腿全部是兔子的，所以兔子有10÷2=5只，鸡有14-5=9只.（惊现跑男中包贝尔的抬脚法有木有！）『方法五：最常用的假设法』分析：假设全部是鸡，则有14×2=28条腿，比实际少38-28=10只，一只鸡变成一只兔子腿增加2条，10÷2=5只，所以需要5只鸡变成兔子，即兔子为5只，鸡为14-5=9只.『方法六：最常用的假设法』分析：假设全部是兔子，则有14×4=56条腿，比实际多56-38=18只，一只兔子变成一只鸡腿减少2条，18÷2=9只，所以需要9只兔子变成鸡，即鸡为9只，兔子为14 - 9=5只.『方法七：最牛的特异功能法』分析：鸡有2条腿，比兔子少2条腿，这不公平，但是鸡有2只翅膀，兔子却没有.假设鸡有特级功能，把两只翅膀变成2条腿，那么鸡也有4条腿，此时腿的总数是14×4＝56条，但实际上只有38条，为什么呢？因为我们把鸡的翅膀当作腿来算，所以鸡的翅膀有56-38＝18只，鸡有18÷2＝9只，兔就是14－9＝5只.『方法八：最牛的特异功能法2 』分析：假设每只鸡兔都具有“特异功能”，鸡飞起来，兔立起来，这时立在地上的脚全是兔的，它的脚数就是38－14×2=10条，因此兔的只数有10÷2=5只，进而知道鸡有14-5＝9只.鸡兔具有“特异功能”，这个方法想得太棒了！『方法九：最牛的特异功能法3 』假设孙悟空变成兔子，说“变”，每只兔子又长出一个头来，然后对妖精说“将它劈开”，变成“一头两脚”的两只“半兔”，半兔与鸡都是两只脚，因而共有28÷2=19只鸡兔，19－14=5只，这就是兔子的数目，当然鸡就有14－5=9只.呵呵，小朋友把兔“劈开”成“半兔”，想得奇吧！『方法十：最古老的砍足法』分析：假如把每只砍掉1只脚、每只兔砍掉2只脚，则每只鸡就变成了“独角鸡”，每只兔就变成了“双脚兔”.这样，鸡和兔的脚的总数就由38只变成了19只；如果笼子里有一只兔子，则脚的总数就比头的总数多1.因此，脚的总数19与总头数14的差，就是兔子的只数，即19－14＝5（只）.所以，鸡的只数就是14－5＝9（只）了. 呵呵，这个方法是古人想出来的，但有点残忍！『方法十一：史上最坑的耍兔法』分析：假如刘老师喊口令：“兔子，耍酷！”此时兔子们都把两只前脚高高抬起，两只后脚着地，呈酷酷的姿态，此时鸡兔都是两只脚着地.在地上脚的总数是14×2＝28只，而原来有38只脚，多出38－28＝10只.为什么会多呢？因为兔子们把它们的2只前脚抬了起来，所以兔的只数是10÷2＝5只，鸡则是14－5＝9只.『方法十二：最万能的方程法』分析：设鸡的数量为x只，则兔子有（14-x）只，有2x+4（14-x）=38，解出x=9，所以有鸡9只，兔子14-9=5只.『方法十三：最万能的方程法』分析：设兔子的数量为x只，则鸡有（14-x）只，有4x+2（14-x）=38.解得x=5，所以兔子有5只，鸡有14-5=9只.鸡兔同笼的13种方法就给大家讲完了，最后我们来总结一下！•十三种方法•1、列表法2、画图法3、金鸡独立法4、吹哨法5、假设法6、假设法7、特异功能法8、特异功能法9、特异功能法10、砍足法11、耍兔法12、方程法13、方程法记忆方法：假设“列表”同学画完图以后，有了3大特异功能，摆了一个金鸡独立的pose，吹了一声哨，耍了一下兔，看足了，于是“方程”去了！。

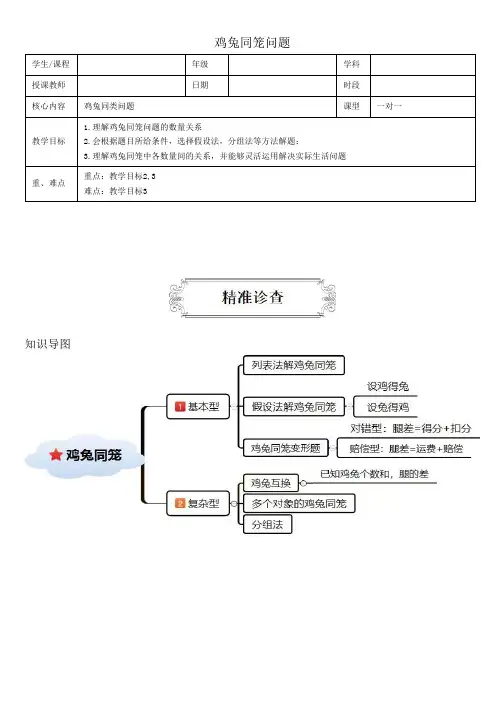
鸡兔同笼问题学生/课程年级学科授课教师日期时段核心内容鸡兔同类问题课型一对一教学目标1.理解鸡兔同笼问题的数量关系2.会根据题目所给条件，选择假设法，分组法等方法解题；3.理解鸡兔同笼中各数量间的关系，并能够灵活运用解决实际生活问题重、难点重点：教学目标2,3 难点：教学目标3知识导图导学一：鸡兔同笼——基本题型知识点讲解 1：列表法解鸡兔同笼当题中数字比较小时，可以用列表法解决鸡兔同笼问题例 1. 笼子里有若干只鸡和兔。

从上面数，有8个头，从下面数，有26只脚。

鸡和兔各有几只？我爱展示1.笼子里有若干只鸡和兔。

从上面数，有8个头，从下面数，有26只脚。

鸡和兔各有几只？知识点讲解 2：假设法解鸡兔同笼（1）使用假设法的前提：已知鸡与兔头的和，腿的和，求鸡和兔的只数。

（2）解题步骤（3）公式解法1：假设全部都是兔：设兔得鸡（兔的脚数×总只数－总脚数）÷鸡与兔的腿差=鸡的只数总只数－鸡的只数=兔的只数解法2：假设全部都是鸡：设鸡得兔（总脚数－鸡的脚数×总只数）÷鸡与兔的腿差=兔的只数总只数－兔的只数=鸡的只数例 1. 笼子里有若干只鸡和兔。

从上面数，有35个头，从下面数，有94只脚。

鸡和兔各有多少只？我爱展示1.鸡兔同笼,共有头100个,足316只,那么鸡有多少只？兔有多少只？知识点讲解 3：鸡兔同笼变形题对错得分题：腿差=得分+扣分赔偿型：腿差=运费+赔偿解题关键：学会找题中的鸡或兔，找头的和，腿的和例 1.乐乐百货商店委托搬运站运送500只花瓶，双方商定每只运费0.24元，但如果发生损坏，那么每打破一只不仅不给运费，而且还要赔偿1.26元，结果搬运站共得运费115.5元。

问：搬运过程中共打破了几只花瓶？例 2. 小红的储钱罐里有面值2元和5元的人民币共65张，总钱数为205元，两种面值的人民币各多少张？例 3.开心辞典智力竞赛中，开心队抢答了10道题，如果以100分开始算分，答对一题加10分，答错一题减10分，最后开心队得了140分，开心队答错了几题？我爱展示1.运输2000只陶瓷碗，运费按到达时完好的数目计算，每只3角，如有破损，破损1个陶瓷碗还要倒赔7角，结果得到运费535元，问这次搬运中陶瓷碗损坏了( )只。

第17讲鸡兔同笼问题二兴趣篇1．★笼子里有一些3腿鸡和6腿兔，共有8个头，30条腿．请问：其中有多少只3腿鸡？答案：6只解答假设全是6腿兔，那么一共有腿6×8=48（条），比实际多了48-30=18（条）．每把1只6腿兔换成1只3腿鸡，腿就会少6-3=3（条），则换了18÷3=6（次）．所以3腿鸡有6×1=6(只)．2-★因生存环境的变化，出现了3条腿的变异青蛙；现在捕到4条腿的正常青蛙和3条腿的变异青蛙共30只，总共115条腿．请问：捕到多少只3条腿的变异青蛙？答案5只解答假设全是正常青蛙，那么一共有腿30×4=120（条），比实际多了120-115=5（条）．每把1只正常青蛙换成1只变异青蛙，腿就会少4-3 =1（条），则换了5÷1=5（次）．所以3条腿的变异青蛙有5×1=5(只)．3．★大卡车一次能运7吨土，小卡车一次能运4吨土，现在有大、小卡车70辆，一次恰好能运土400吨．请问：大卡车有多少辆？答案40辆解答假设全是小卡车，那么一共能装4×70=280(吨)，比实际少了400 -280=120(吨)．每把1辆小卡车换成1辆大卡车，就多装7-4=3（吨），则换了120÷3=40（次）．所以大卡车有40×1=40（辆）． 14．★★一辆卡车运粮食，每次能运5吨，晴天时每天能运8次，雨天时每天只能运3次，这辆卡车10天共运了325吨粮食，在这10天中，晴天和雨天各有几天？答案7个晴天，3个雨天解答方法一：由题意得，晴天每天能运5×8=40（吨），雨天每天能运5×3=15（吨）．假设全是晴天，则一共能运40×10=40O（吨），比实际多了400-325=75（吨）．每把1个晴天换成1个雨天，就会少运40-15 =25（吨），则换了75÷25=3（次）．所以雨天有3天，晴天有10-3=7（天）方法二：因为卡车每次能运5吨粮食，运了325吨粮食需要325÷5=65（次）．假设全是晴天，那么一共能运8×10=80（次），比实际多运了80 - 65—15（次）．每把1个晴天换成1个雨天，就会少运8-3=5（次），则换了15÷5=3（次）．所以雨天有3天，晴天有10-3=7（天）．5．★★有若干只鸡和兔，其中鸡比兔多12只，它们一共有84条腿，问鸡和兔各有多少只？答案鸡22只，兔10只解答方法一：把1只鸡和1只兔分成一组，每组用虚线的方框表示，如下图所示：右边的12只鸡有2×12=24（条）腿，因此所有组内一共有84-24=60（条）腿．又每组里有2+4=6（条）腿，那么一共有60÷6=10（组）．所以兔有10×1= 10（只），鸡有10 +12=22（只）．方法二：假设兔有0只，则鸡就有12只，那么一共有腿O×4+2×12=24（条）．比实际少了84-24=60（条）腿．每增加1只兔，鸡也随着增加了1只，腿数就会增加4+2=6（条）．为了补上少了的60条腿，就需要增加60÷6=10（只）兔．因此兔有0+10=10（只），鸡就有10 +12=22（只）．6．北京大学乒乓球馆内，一共有34人正在进行乒乓球比赛，其中单打比赛的球台比双打比赛的球台多2张．请问：一共有多少张球台正在进行比赛？答案12张解答把1张单打球台和1张双打球台配成一组，全部分组后，单打球台剩下2张.用数字2代表单打球台，数字4代表双打球台，用虚线方框把一组框在一起，如下图所示：由上图可知，组内一共有34-2×2=30(人)．每组有4+2=6（人），则应有30÷6=5（组）．因此，双打球台有5×1=5（张），单打球台有5+2=7（张），则一共有5+7=12（张）球台正在进行比赛．7．★★有若干只鸡和兔，其中鸡和兔的数量一样多，兔的总腿数比鸡的总腿数多3C条，请问：鸡、兔各有多少只？ 8．★★癞蛤蟆和天鹅一块玩游戏，癞蛤蟆比天鹅多12只，癞蛤蟆的总腿数比天鹅的总腿数多68条．那么癞蛤蟆和天鹅各有多少只？答案各15只解答因“鸡和兔的数量一样多”’则将1只鸡和1只兔分为一组，如下图所示：每组兔腿比鸡腿多2条，又兔腿比鸡腿一共多30条，那么一共有30÷2=15（组）。