(推荐)时间测量中随机误差的分布规律

考研心理学统考心理学专业基础综合（心理统计与测量）-试卷25(总分：62.00，做题时间：90分钟)一、单选题(总题数：21，分数：42.00)1.单项选择题（分数：2.00）__________________________________________________________________________________________ 解析：2.关于测验题目区分度的说法正确的是（分数：2.00）A.项目鉴别指数法大于0．2的题目一般可以保留√B.各种方法计算出的区分度可以相互比较C.区分度的大小与样本特点无关D.项目鉴别指数不会受被试分组影响解析：解析：不同方法计算的区分度是不能直接比较的；区分度大小受样本群体的多少以及异质性程度的影响；使用项目鉴别指数作为区分度的指标时，是会受到被试分组大小的影响的。

故本题选A。

3.在确定问卷中的题目是否保留时，符合下列哪种情况的题目最易被保留（分数：2.00）A.难度值越大的题目B.区分度值越大的题目√C.难度越小的题目D.区分度越小的题目解析：解析：在项目分析中，应保留难度值中等、区分度较大的题目。

故本题选B。

4.在真分数理论中，真分数意味着（分数：2.00）A.欲测量的心理品质B.包含随机误差的欲测心理品质C.包含系统误差的欲测心理品质√D.包含随机和系统误差的欲测心理品质解析：解析：经典测验理论或真分数理论假定实测分数中分为真分数和随机误差，而不区分欲测心理品质和系统误差。

故本题选C。

5.用两个平行或等值的测验，间隔适当时距施测于同一组被试得到两组测验分数，求这两组测验分数的相关，其相关系数就是（分数：2.00）A.复本信度√B.重测信度C.评分者信度D.内部一致性信度解析：解析：本题考查了复本信度的概念。

本题选A。

6.使用同一测验间隔适当时距施测于同一组被试得到两组测验分数，所得的相关系数是（分数：2.00）A.复本信度B.重测信度√C.评分者信度D.内部一致性信度解析：解析：本题考查了重测信度的概念。

实验报告：时间测量中随机误差的分布规律张贺PB07210001一、实验题目：时间测量中随机误差的分布规律二、实验目的：用常规仪器（如电子秒表、频率计等）测量时间间隔，通过对时间和频率测量的随机误差分布，学习用统计方法研究物理现象的过程和研究随机误差分布的规律。

三、实验仪器:电子秒表、机械节拍器四、实验原理：1.常用时间测量仪表的简要原理：（1）机械节拍器：由齿轮带动摆做周期性运动，摆动周期可以通过改变摆锤的位置连续调节。

（2）电子节拍器：由石英晶体振荡器、计数器、译码器、电源和分档控制及显示部分组成。

电子节拍器按一定的频率发出有规律的声响和闪光，声、光节拍范围为 1.5～0.28846s，分为39挡，各挡发生和闪光的持续时间约为0.18s。

（3）电子秒表：兼有数种测时功能（秒、分、时、日、月和星期），便于携带和测量的常用电子计时器。

电子秒表机芯由CMOS 集成电路组成，用石英晶体振荡器作时标，一般用六位液晶数字显示，其连续积累时间数为59min59.99s 。

分辨率为0.01s ，平均日差0.5s 。

（4） V AFN 多用数字测试仪：由PMOS 集成元件和100kHz 石英晶体振荡器构成。

可测量计数、振动、累计、速度、加速度、碰撞、频率、转速、角速、脉宽。

时标：由DC10集成电路和100kHz 石英晶体振荡器组成。

电路可直接输出0.01ms ，0.1ms ，1ms ，10ms ，0.1s ，1s 六挡方波脉冲作为时标信号和闸门时间。

石英晶体振荡器的稳定度为1.2×105-s/d ；频率测量范围1Hz~100kHz ；电信号输入幅度为300mV 。

2. 统计分布规律的研究：假设在近似消除了系统误差（或系统误差很小，可忽略不计，或系统误差为一恒定值）的条件下，对某物理量x 进行N 次等精度测量，当测量次数N 趋向无穷大时，各测量值出现的概率密度分布可用正态分布（又称高斯分布）的概率密度函数表示，]2)(exp[21)(22--=σπσx x x f （1）式中x 为测量的算术平均值，σ为测量列的标准差，nxx ni i∑==1（2）1)(12--=∑=n x x ni i σ （3）⎰-=aadx x f a P )()( （4）式中a=σ,2σ,3σ. （1） 统计直方图方法统计直方图是用实验研究某一物理现象统计分布规律的一种直观的方法。

考研心理学统考心理学专业基础综合（心理统计与测量）-试卷5(总分：80.00，做题时间：90分钟)一、单选题(总题数：26，分数：52.00)1.单项选择题（分数：2.00）__________________________________________________________________________________________ 解析：2.稳定地存在于每一次测量中，有规律变化的误差叫做（分数：2.00）A.随机误差B.系统误差√C.被试产生的误差D.主试产生的误差解析：解析：系统误差是稳定地存在于每一次测量中，有规律变化的误差。

它既可以由被试引起，也可以由主试产生。

本题选B。

3.关于测验的信度、效度、项目难度与区分度的下列说法中，不正确的是（分数：2.00）A.增加测验长度，信度会增大B.增加测验长度，效度会增大C.测验项目的难度越大越好√D.测验项目的区分度越大越好解析：解析：本题主要考查了学生对测验信度、效度、难度、区分度这几个指标的掌握情况。

题目较难，因为涉及的知识点比较多，且多为细节。

A、B、D都是正确的，C选项正确的说法是测验项目的难度接近0．5较为理想。

故本题选C。

4.信效度之间关系的说法，正确的是（分数：2.00）A.信度高，效度一定高B.信度高，效度不一定高√C.信度低，效度一定低D.效度高，信度不一定高解析：解析：信度和效度之间的关系是：信度高是效度高的必要而非充分条件。

换言之，信度高，效度未必高，而效度高，则信度必定高。

因此，本题选择B。

5.由与测量目的无关的偶然因素引起的变化无规律的误差叫做（分数：2.00）A.随机误差√B.系统误差C.被试产生的误差D.主试产生的误差解析：解析：测量中的随机误差是指与测量目的无关的偶然因素引起的。

因此，本题选择A。

6.一位研究者使用智力测验对一个孩子进行了三次测量，每次的分数都不同，请问，这里智力分数的不同反映的是（分数：2.00）A.测量的随机误差√B.测量的系统误差C.测量的信度D.测量的效度解析：解析：测量中存在着随机误差，导致每一次测量的分数都会有变化。

实验报告05级 少年班 陈晨 Pb05000827实验题目:单摆的设计和研究实验目的：利用经典的单摆公式，给出的器材和对重力加速度g 的测量精度的要求,进行简单的设计性实验基本方法的训练学会应用误差均分原则选用适当的仪器和测量方法，学习积累放大法的原理及应用。

实验仪器：实验室提供以下器材（及参数）：游标卡尺、米尺、千分尺、电子秒表、支架、细线（尼龙线）、钢球、摆幅测量标尺（提供硬白纸板自制）、天平（公用）。

假设摆长l ≈70.00cm ；摆球直径D ≈2.00cm ；摆动周期T ≈1.700s ；米尺精度Δ米≈0.05cm ；卡尺精度Δ卡≈0.002cm ；千分尺精度Δ千≈0.001cm ；秒表精度Δ秒≈0.01s ；根据统计分析，实验人员开、停秒表总的反映时间近似为Δ人≈0.2s 。

实验原理：单摆结构如图，当摆角充分小（一般θ<5○）摆球直径充分短（相对于摆线）时，单摆的一级近似周期公式为 glT π2= 因此通过测量摆动周期T ，摆长L 可得224T Lg π=实验内容：1、 用误差均分原理设计一单摆装置，测量重力加速度g ，设计要求：（1） 根据误差均分原理，自行设计实验方案，合理选择测量仪器和方法。

（2） 写出详细的推导过程，实验步骤。

（3） 用自制的单摆装置测量重力加速度g ，测量精度要求%1<∆gg。

2、对重力加速度g 的测量结果进行误差分析和数据处理，检验实验结果是否达到设计要求。

实验设计：以下利用误差均分原理设计一套单摆装置，测量重力加速度g ，测量精度要求%1<∆gg。

由于glT π2=，所以224T L g π=取对数 T L g ln 2ln 4ln ln 2-+=π 求微分TdTL dL g dg 2-= 按最大不确定度公式估算，有TTL L g g ∆+∆=∆2 应用均分原理%5.0≤∆L L ，%5.02≤∆TT将摆长L 和摆球直径D 的粗测值cm l 00.70≈，cm D 00.2≈代入，有 cm l 35.0≤∆和cm D 01.0≤∆结合器材精度参数考虑，选用精度足够的米尺测摆线长，游标卡尺测小球直径。

实验报告实验名称 时间测量中随机误差的分布规律实验目的 用常规仪器（如电子秒表、频率计等）测量时间间隔，通过对时间和频率测量的随机误差分布，学习用统计方法研究物理现象的过程和研究随机误差分布的规律。

实验仪器 机械节拍器，电子秒表。

实验原理 1.常用时间测量仪表的简要原理（1）机械节拍器（2）电子节拍器 （3）电子秒表（4）VAFN 多用数字测试仪用电子秒表测量机械节拍器发声的时间间隔,机械节拍器按一定的频率发出有规律的声响，电子秒表用石英晶体振荡器作时标,一般用六位液晶数字显示,其连续积累时间为59min59.99s,分辨率为0.01s,平均日差0.5s 。

2.统计分布规律的研究假设在近似消除了系统误差（或系统误差很小，可忽略不计，或系统误差为一恒定值）的条件下，对某物理量x 进行N 次等精度测量，当测量次数N 趋向无穷时，各测量值出现的概率密度分布可用正态分布（有成高斯分布）的概率密度函数表示，]2)x -(x ex p[-21)(22σπσ=x f （1） 其中 nxx n1i i∑==（2）1-n )x -(xn1i 2i∑==σ （3）⎰=aa-f(x)dx P(a) （4）式中a=σ，2σ，3σ分别对应不同的置信概率。

（1）统计直方图方法用统计直方图表示被研究对象的规律简便易行，直观清晰。

在一组等精度测量所得的N 个结果x 1，x 2，…，x N 中，找出它的最大值x max 与最小值x min ，并求出级差R=x max - x min ，由级差分为K 个小区间，每个小区域的间隔（△x ）的大小就等于Kx -x K R minmax =。

统计测量结果出现在某个小区域内的次数n i 称为频数，Nni 为频率，Nni∑为累计频率，称为频率密度。

以测量值x 值为横坐标，以xN n i∆⋅为纵坐标，便可得到统计直方图。

（2）概率密度分布曲线利用式（1）求出各小区域中点的正态分布的概率密度值f （x ），以f （x ）为纵坐标，x 为横坐标，可得概率密度分布曲线。

时间测量中随机误差的分布规律PB06210273 张成实验名称：时间测量中随机误差的分布规律实验目的：用常规仪器（如电子秒表、频率计等）测量时间间隔，通过对时间和频率的测量的随机误差分布，学习用统计法研究物理现象的过程和研究随机误差的分布规律。

实验原理：1、 常用时间测量仪器的简要原理：① 机械节拍器由齿轮带动摆动作周期性运动。

② 电子节拍器按一定的频率发出有规律的声响和闪光。

③ 电子秒表机芯有CMOS 集成电路组成，用石英晶体振荡器作时标。

④ VAFN 多用数字测试仪由PMOS 集成元件和100KHz 石英晶体振荡器构成，可测量计数、振动、累计、速度、加速度、碰撞、频率、转速、角速脉宽等物理量。

2、 统计分布规律的研究正态分布概率密度函数：()]2exp[21)(22σπσxx x f --=nxx ni i∑==1，()112--=∑=n x x ni iσ ， ⎰-=aadx x f a P )()(① 统计直方图法：计算试验数据的极差min max x x R -=，每小区域的间隔：Kx x K R x minmax -==∆ 频数i n ，相对频数%/)/(N n i ，累计频数%/)/(∑N n i ，频率密度xN n i∆⋅ ② 概率密度分布曲线：以)(x f 为纵坐标，x 为横坐标，可得概率密度分布曲线。

实验内容：用电子秒表测量电子节拍器的周期，共测量150次，每次测量3个周期的时长。

数据处理：s nxx ni i213.415091.6311===∑= s n x xni i0.0981)(12=--=∑=σ 测量结果的不确定度：A 类不确定度（95.0=p ）s nu a 008.0==σ95.0=p ，96.1=t ，s u t a p 016.0008.096.1=⨯=B 类不确定度：s s s B 2.001.02.0＝，，＝，＝估仪估仪估∆=∆∴∆>>∆∆∆12.03=∆=BB u 测量值的合成标准不确定度：s u u U B A 12.022=+=数据中93.3min =x ，44.4max =x ，所以级差51.0min max =-=x x R 。

测量技术基础机械加工车间工作的机械加工工人必须掌握的多种测量技术，量具、量仪以游标卡尺、千分尺、和百分表为主。

对于某一测量对象，一般有多种测量技术可供选择，而某一种测量技术又往往可用于不同的测量对象。

用于同一测量对象，不同测量技术的效果可能大致相同，也可能大不相同。

按照测量的进行方式，测量技术可分为以下两种。

①直接比较测量技术：在测量中，将被测量与已和其值的同一种量相比较。

其测量不确定度主要取决于标准量值的不确定度和比较器的灵敏度和分辨力，它可克服由于测量装置的动态范围不够和频率响应不好所引入的非线性误差。

替代法、换位法等属于这一类。

②非直接比较测量技术：不是将被测量的全值与标准量值相比较的比较测量。

微差法、符合法、补偿法、谐振法、衡消法等属于这一类。

在建立计量标准的测量中，经常采用基本测量技术，即绝对测量技术。

这是通过对有关的基本量的测量来确定被测量值。

其测量不确定度一般是通过实验、分析和计算得出，精度高，但所需装置复杂。

第一讲概述课题：1. 测量技术的概念2. 长度基准与尺寸传递3．量块的基本知识4．形位公差值及有关规定课堂类型：讲授教学目的：1.了解测量技术的基本概念及尺寸传递2.重点掌握量块的使用方法。

教学重点：量块的使用方法。

教具：量块教学方法：例举习题讲解量块的使用，使学生掌握其主要内容教学过程：一、引入新课题由提问学生长度单位的意义引入新课.二、教学内容4.1 概述4.1.1测量技术的概念1.测量是指为确定被测量值而进行的一组操作过程。

其实质是将被测的量L与具有计量单位的标准量E进行比较，从而确定比值q的过程，即q= L/E测量过程包括以下四个要素:（1）测量对象主要指几何量，包括长度、角度、表面形状和位置误差、表面粗糙度以及螺纹、齿轮的各种参数等。

（2）计量单位长度单位为米（m），在机械制造中常用单位为毫米（mm）、微米（μm）;角度单位是弧度（rad），实用中常以度（°）、分（′）、秒（″）为单位。

核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-24时间测量中的随机误差分布规律PB10214023 张浩然一、实验题目：时间测量中的随机误差分布规律二、实验目的：同常规仪器测量时间间隔，通过对时间和频率测量的随机误差分布，学习用统计方法研究物理现象的过程和研究随机误差分布的规律。

三、实验仪器：电子秒表、机械节拍器四、实验原理：1、仪器原理机械节拍器能按一定频率发出有规律的声响，前者利用齿轮带动摆作周期运动，后者利用石英晶体的振荡完成周期运动；电子秒表用石英晶体振荡器作时标测时，精度可达0.01s ； 2、统计分布规律原理在近似消除了系统误差的前提下，对时间t 进行N 次等精度测量，当N 趋于无穷大时，各测量值出现的概率密度分布可用正态分布的概率密度函数表示：222)(21)(σπσx x ex f --=其中n x x ni i∑==1，为测量的算术平均值，1)(12--=∑n x xniσ，为测量列的标准差，有 ⎰-=aa dxx f a P )()(，σσσ3,2,=a利用统计直方图表示测量列的分布规律，简便易行、直观明了。

在本实验中利用f(x)得到概率密度分布曲线，并将其与统计直方图进行比较，在一定误差范围内认为是拟合的，可认为概率密度分布基本符合正态分布，其中的误差是由于环境、仪器、人的判断误差、N 的非无穷大等所决定的。

五、实验步骤：1、检查实验仪器是否能正常工作，秒表归零；2、将机械节拍器上好发条使其摆动，用秒表测量节拍器四个周期所用时间，在核科学技术学院2010 级学号PB10214023 姓名张浩然日期2011-3-24等精度条件下重复测量约200次（本实验中实际测量224次），记录每次的测量结果；3、对数据进行处理（计算平均值、标准差、作出相应图表、误差分析等）；六、数据处理：1.实验数据如下：（单位：s）初步分析得2.由公式（2）（3）计算得: （单位：s）x=平均值 2.415σ=标准差0.1198473.机械节拍器的频数和频率密度分布：令K=16核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-24有 0max min ()/0.04625x x x K ∆=-= （单位：s ） 取max min ()/0.05x x x K ∆=-=（单位：s ）有测量数据的频数和频率密度分布表如下： 小区域/s 小区域中点值/s 频数i n /s 相对频数(/)/%i n N累计频数(/)/%i n N ∑1.95-2.20 1.975 1 0.446428571 0.446428571 2.20-2.05 2.025 1 0.446428571 0.892857143 2.05-2.10 2.075 1 0.446428571 1.339285714 2.10-2.15 2.125 3 1.339285714 2.678571429 2.15-2.20 2.175 2 0.8928571433.571428571 2.20-2.25 2.225 7 3.1256.696428571 2.25-2.30 2.275 177.589285714 14.28571429 2.30-2.35 2.325 31 13.83928571 28.125 2.35-2.40 2.375 28 12.540.6252.40-2.45 2.425 44 19.64285714 60.26785714 2.45-2.50 2.475 26 11.60714286 71.875 2.50-2.55 2.525 35 15.625 87.5 2.55-2.60 2.575 14 6.2593.752.60-2.65 2.625 10 4.464285714 98.21428571 2.65-2.70 2.675 3 1.339285714 99.55357143 2.70-2.752.72510.4464285711004.统计直方图和概率密度分布曲线图像：核科学技术学院 2010 级 学号 PB10214023 姓名 张浩然 日期 2011-3-245.不确定度分析：0.950.015694973s A U t n==对于电子秒表，人的反应时间为0.2s ，远大于0.01s ，则取B ∆=∆估；对于秒表，取C=3。

1、测量的概念测量是借助专门的技术和仪表设备，采用一定的方法取得某一客观事物定量数据资料的实践过程。

2、测量方法的分类（1）根据被测量是否随时间变化，可分为静态测量和动态测量。

（2）根据测量的手段不同，可分为直接测量和间接测量。

（3）根据测量时是否与被测对象接触，可分为接触式测量和非接触式测量。

（4）根据测量的具体手段来分，可分为偏位式测量，零位式测量和微差式测量。

偏位式测量：在测量过程中，被测量作用于仪表内部的比较装置，使该比较装置产生偏移量，直接以仪表的偏移量表示被测量的测量方式称为偏位式测量。

零位式测量：在测量过程中，被测量与仪表内部的标准量相比较，当测量系统达到平衡时，用已知标准量的值决定被测量的值，这种测量方式称为零位式测量。

微差式测量：微差式测量法是综合了偏位式测量法速度快和零位式测量法准确度高的优点的一种测量方法。

3、测量误差的表示方法绝对误差和相对误差相对误差又包括示值（标称）相对误差和引用误差（也叫满度相对误差）4、我国工业模拟仪表有下列常用的7种等级:0.1、0.2、0.5、1.0、1.5、2.5、5.0。

准确度等级对应基本误差：eg：0.1对应±0.1% 5、测量误差的分类粗大误差、系统误差、随机误差、静态误差和动态误差。

静态误差：在被测量不随时间变化时所产生的误差称为静态误差。

动态误差：当被测量随时间迅速变化时，系统的输出量在时间上不能与被测量的变化精确吻合，这种误差称为动态误差。

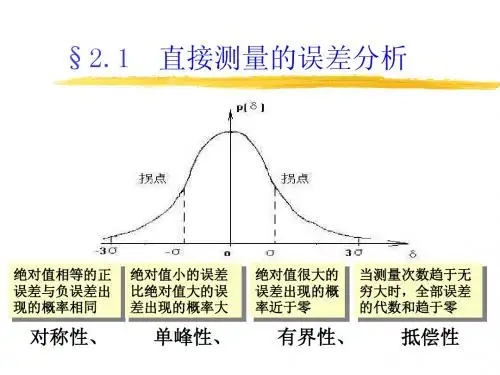
6、随机误差的正态分布曲线的三个规律集中性、对称性、有界性7、不确定度的概念由于测量误差的存在，对被测量值不能肯定的程度，也表明该结果的可信赖程度。

8、测量系统静态误差的合成方法绝对值合成法和方均根合成法9、传感器的定义组合以及每一部分能完成的功能、起到的作用传感器是一种检测装置，能感受规定的被测量，并能将检测感受到的信息，按一定的规律变换成为电信号或其他所需要形式的信息输出。

以满足信息的传输、处理、存储、显示、记录和控制等要求传感器主要包括敏感元件、传感元件和测量转换电路三个部分敏感元件是在传感器中直接感受被测量的元件，即被测量通过传感器的敏感元件转换成与被测量有确定关系、更易于转换的非电量。