第11章热力学基本原理
- 格式:ppt
- 大小:731.50 KB
- 文档页数:59




热力学基本原理热力学是研究能量传递和转化的物理学分支,它包括一系列基本原理和定律,用于描述和解释自然界中的能量变化和行为规律。
本文将介绍热力学的基本原理,包括系统与环境、热力学第一定律、热力学第二定律以及熵的概念。
1. 系统与环境热力学研究的对象是系统和其所处的环境。
系统可以是封闭的、开放的或隔离的,封闭系统与外界没有物质交换;开放系统可以与环境进行物质和能量的交换;隔离系统与环境既没有物质也没有能量的交换。
系统通过界面与环境进行能量交换,这个能量交换可以是热传递或者是物质的传递。
2. 热力学第一定律热力学第一定律,也被称为能量守恒定律,它描述了能量的转化和守恒原理。
根据这个定律,一个系统的内能的增量等于对系统做功和系统热交换的总和。
数学表达式为:ΔU = Q - W其中,ΔU表示系统内能的增量,Q表示系统吸收的热量,W表示对系统做的功。
根据热力学第一定律,我们可以推导出一些重要的热力学量,例如热容、焓和热力学过程中的能量转化等。
3. 热力学第二定律热力学第二定律是描述能量传递方向的定律,它对能量的不可逆性进行了限制。
根据这个定律,自然界的过程总是朝着熵增加的方向进行的。
熵可以理解为一个系统的无序程度,当一个系统的熵增加时,意味着能量的利用效率降低。
热力学第二定律有多种表述方式,其中最为著名的是克劳修斯表述和开尔文表述。
克劳修斯表述指出任何热机都无法实现100%的热量转化为功,总会有一部分热量被浪费。
开尔文表述则指出任何平衡态过程都无法完成自身逆过程,即自发过程不可逆。
4. 熵的概念熵是热力学中一个重要的概念,它用来描述系统的无序程度。
熵增加意味着系统的无序程度增加,能量的利用效率降低。
熵在热力学第二定律中扮演着重要的角色。
熵的数学定义为:ΔS = Q/T其中,ΔS表示系统的熵变,Q表示系统吸收的热量,T表示系统的温度。
根据熵的定义,我们可以推导出其他热力学量,例如焓、自由能和Gibbs自由能等。


第11章 热力学基本原理11.1 一系统由如图所示的状态a 沿abc 到达c ,有350J 热量传入系统,而系统对外做功126J .(1)经adc ,系统对外做功42J ,问系统吸热多少?(2)当系统由状态c 沿曲线ac 回到状态a 时,外界对系统做功为84J ,问系统是吸热还是放热,在这一过程中系统与外界之间的传递的热量为多少?解:(1)当系统由状态a 沿abc 到达c 时,根据热力学第一定律,吸收的热量Q 和对外所做的功A 的关系是Q = ΔE + A ,其中ΔE 是内能的增量.Q 和A 是过程量,也就是与系统经历的过程有关,而ΔE 是状态量,与系统经历的过程无关.当系统沿adc 路径变化时,可得Q 1 = ΔE 1 + A 1, 这两个过程的内能的变化是相同的,即ΔE 1 = ΔE ,将两个热量公式相减可得系统吸收的热量为Q 1 = Q + A 1 - A = 266(J). (2)当系统由状态c 沿曲线ac 回到状态a 时,可得Q 2 = ΔE 2 + A 2, 其中,ΔE 2 = -ΔE ,A 2 = -84(J),可得Q 2 = -(Q – A ) + A 2 = -308(J), 可见:系统放射热量,传递热量的大小为308J .11.2 1mol 氧气由状态1变化到状态2,所经历的过程如图,一次沿1→m →2路径,另一次沿1→2直线路径.试分别求出这两个过程中系统吸收热量Q 、对外界所做的功A 以及内能的变化E 2 -E 1.解:根据理想气体状态方程pV = RT ,可得气体在状态1和2的温度分别为T 1 = p 1V 1/R 和T 2 = p 2V 2. 氧气是双原子气体,自由度i = 5,由于内能是状态量,所以其状态从1到2不论从经过什么路径,内能的变化都是212211()()22i iE R T T p V p V ∆=-=-= 7.5×103(J). 系统状态从1→m 的变化是等压变化,对外所做的功为2121d ()V V A p V p V V ==-⎰= 8.0×103(J).系统状态从m →2的变化是等容变化,对外不做功.因此系统状态沿1→m →2路径变化时,对外做功为8.0×103J ;吸收的热量为Q = ΔE + A = 1.55×104(J).系统状态直接从1→2的变化时所做的功就是直线下的面积,即21211()()2A p p V V =+-= 6.0×103(J).吸收的热量为Q = ΔE + A = 1.35×104(J).11.3 1mol 范氏气体,通过准静态等温过程,体积由V 1膨胀至V 2,求气体在此过程中所做的功?解:1mol 范氏气体的方程为2()()ap v b RT v +-=, 通过准静态等温过程,体积由V 1膨胀至V 2时气体所做的功为图11.12×图11.222112d ()d V V V V RT a A p v v v b v==--⎰⎰21ln()V V a RT v b v =-+212111ln()V b RT a V b V V -=+--.11.4 1mol 氢在压强为1.013×105Pa ,温度为20℃时的体积为V 0,今使其经以下两种过程达同一状态:(1)先保持体积不变,加热使其温度升高到80℃,然后令其作等温膨胀,体积变为原体积的2倍;(2)先使其作等温膨胀至原体积的2倍,然后保持体积不变,升温至80℃.试分别计算以上两过程中吸收的热量,气体所做的功和内能增量.将上述两过程画在同一p-V 图上并说明所得结果.解:氢气是双原子气体,自由度i = 5,由于内能是状态量,所以不论从经过什么路径从初态到终态,内能的增量都是21()2iE R T T ∆=-= 1.2465×103(J). (1)气体先做等容变化时,对外不做功,而做等温变化时,对外所做的功为2211221d d V V V V A p V RT V V==⎰⎰2ln 2RT == 2.0333×103(J), 所吸收的热量为Q 2 = ΔE + A 2 = 3.2798×103(J). (2)气体先做等温变化时,对外所做的功为2211111d d V V V V A p V RT V V==⎰⎰1ln 2RT == 1.6877×103(J), 所吸收的热量为Q 1 = ΔE + A 1 = 2.9242×103(J).如图所示,气体在高温下做等温膨胀时,吸收的热量多些,曲线下的面积也大些.11.5 为了测定气体的γ(γ=C p /C V ),可用下列方法:一定量气体,它的初始温度、体积和压强分别为T 0,V 0和p 0.用一根通电铂丝对它加热,设两次加热电流和时间相同,使气体吸收热量保持一样.第一次保持气体体积V 0不变,而温度和压强变为T 1,p 1;第二次保持压强p 0不变,而温度和体积则变为T 2,V 2,证明:100200()()p p V V V p γ-=-.证:定容摩尔热容为(d )d VV Q C T=,在本题中为C V = ΔQ /(T 1 – T 0);定压摩尔热容为(d )d pp Q C T=,在本题中为C p = ΔQ /(T 2 – T 0).对于等容过程有p 1/T 1 = p 0/T 0,所以T 1 = T 0p 1/p 0;对于等压过程有V 2/T 2 = V 0/T 0,所以T 2 = T 0V 2/V 0. 因此100100200200//p VC T T T p p T C T T T V V T γ--===--100200()()p p V V V p -=-. 证毕.11.7 理想气体的既非等温也非绝热的过程可表示为pV n = 常数,这样的过程叫多方过程,n 叫多方指数.(1)说明n = 0,1,γ和∞各是什么过程. (2)证明:多方过程中理想气体对外做功:11221p V p V A n -=-.(3)证明:多方过程中理想气体的摩尔热容量为:()1V nC C nγ-=-,并就此说明(1)中各过程的值.(1)说明:当n = 0时,p 为常数,因此是等压过程;当n = 1时,根据理想气体状态方程pV = RT ,温度T 为常数,因此是等温过程; 当n = γ时表示绝热过程;当n =∞时,则有p 1/n V = 常数,表示等容过程.(2)证:对于多方过程有pV n = p 1V 1n = p 2V 2n = C (常数), 理想气体对外所做的功为2211d d V V n V V A p V CV V -==⎰⎰11112221()11n n pV p V CV V n n ---=-=--.证毕. (2)[证明]对于一摩尔理想气体有pV = RT ,因此气体对外所做的功可表示为121RT RT A n -=-,气体吸收的热量为Q = ΔE + A = 21211()()21i R T T R T T n-+--,摩尔热容量为2112()212(1)Q i i in C R R T T n n +-==+=---(2)/121Vi i n i nR C n nγ+--=⋅=--.证毕.11.8 一气缸内贮有10mol 的单原子理想气体,在压缩过程中,外力做功209J ,,气体温度升高1℃.试计算气体内能增量和所吸收的热量,在此过程中气体的摩尔热容是多少? 解:单原子分子的自由度为i = 3,一摩尔理想气体内能的增量为2iE R T ∆=∆= 12.465(J),10mol 气体内能的增量为124.65J . 气体对外所做的功为A = - 209J ,所以气体吸收的热量为Q = ΔE + A = -84.35(J). 1摩尔气体所吸收的热量为热容为-8.435J ,所以摩尔热容为C = -8.435(J·mol -1·K -1).11.9 一定量的单原子分子理想气体,从初态A 出发,沿图示直线过程变到另一状态B ,又经过等容、等压过程回到状态A . (1)A →B ,B →C ,C →A ,各过程中系统对外所做的功A ,内能的增量ΔE 以及所吸收的热量Q . (2)整个循环过程中系统对外所做的总功以及从外界吸收的总热量(各过程吸热的代数和).解:单原子分子的自由度i = 3.(1)在A →B 的过程中,系统对外所做的功为AB 直线下的面积,即A AB = (p A + p B )(V B – V A )/2 = 200(J), 内能的增量为()2AB B A i M E R T T μ∆=-()2B B A A ip V p V =-= 750(J). 吸收的热量为Q AB = ΔE AB + A AB = 950(J).B →C 是等容过程,系统对外不做功.内能的增量为()2BC C B i M E R T T μ∆=-()2C C B B ip V p V =-= -600(J). 吸收的热量为Q BC = ΔE BC + A BC = -600(J),就是放出600J 的热量.C →A 是等压过程,系统图11.9对外做的功为A CA = p A (V A – V C ) = -100(J).内能的增量为 ()2CA A C i M E R T T μ∆=-()2A A C C ip V p V =-= -150(J). 吸收的热量为Q CA = ΔE CA + A CA = -250(J),也就是放出250J 的热量.(2)对外做的总功为A = A AB + A BC + A CA = 100(J).吸收的总热量为Q = Q AB + Q BC + Q CA = 100(J).由此可见:当系统循环一周时,内能不变化,从外界所吸收的热量全部转化为对外所做的功.11.10 1mol 单原子分子的理想气体,经历如图所示的的可逆循环,连接ac 两点的曲线Ⅲ的方程为p = p 0V 2/V 02,a 点的温度为T 0.(1)以T 0,R 表示Ⅰ,Ⅱ,Ⅲ过程中气体吸收的热量. (2)求此循环的效率. 解:由题可知:p 0V 0 = RT 0.(1)I 是等容过程,系统不对外做功,内能的变化为I 00()()22b a b i i E R T T p V RT ∆=-=-0000(9)122ip V RT RT =-=. 吸收的热量为Q I = ΔE I = 12RT 0.II 是等容过程,根据III 的方程,当p c = 9p 0时,V c = 3V 0.系统对外所做的功为 A II = p b (V c - V b ) = 9p 02V 0 = 18RT 0. 内能的变化为II ()()22c b c c b b i iE R T T p V p V ∆=-=-00092272i p V RT ==.吸收的热量为Q II = ΔE II + A II = 45RT 0.在过程III 中,系统对外所做的功为20III 20d d aa ccV VV V p A p V V V V ==⎰⎰33002026()33a c p V V RT V =-=-.内能的变化为III 0()()22a c c c i iE R T T RT p V ∆=-=-0000(93)392i RT p V RT =-=-.吸收的热量为Q III = ΔE III + A III = -143RT 0/3.(2)系统对外做的总功为A = A I + A II + A III = 28RT 0/3, 系统从高温热源吸收的热量为Q 1 = Q I + Q II = 57RT 0, 循环效率为1AQ η== 16.37%.11.11 1mol 理想气体在400K 和300K 之间完成卡诺循环.在400K 等温线上,初始体积为1×10-3m 3,最后体积为5×10-3m 3.试计算气体在此循环中所做的功及从高温热源所吸收的热量和向低温热源放出的热量.解:卡诺循环由气体的四个变化过程组成,等温膨胀过程,绝热膨胀过程,等温压缩过程,绝热压缩过程.气体在等温膨胀过程内能不改变,所吸收的热量全部转化为对外所做的功,即22111111d d V V V V Q A p V RT V V ===⎰⎰211ln VRT V == 5.35×103(J).气体在等温压缩过程内能也不改变,所放出的热量是由外界对系统做功转化来的,即90图11.1044332221d d V V V V Q A p V RT V V ===⎰⎰423ln V RT V =,利用两个绝热过程,可以证明V 4/V 3 = V 2/V 1,可得Q 2 = 4.01×103(J).气体在整个循环过程中所做的功为A = Q 1 - Q 2 = 1.34×103(J).11.13 一热机在1000K 和300K 的两热源之间工作,如果 (1)高温热源提高100K , (2)低温热源降低100K ,从理论上说,哪一种方案提高的热效率高一些?为什么? 解:(1)热机效率为η = 1 – T 2/T 1,提高高温热源时,效率为η1 = 1 – T 2/(T 1 + ΔT ), 提高的效率为221111T T T T T ηηη∆=-=-+∆ 2113()110T T T T T ∆==+∆= 2.73%. (2)降低低温热源时,效率为η2 = 1 – (T 2 - ΔT )/T 1, 提高的效率为222211T T T T T ∆ηηη-∆=-=- = ΔT /T = 10%. 可见:降低低温热源更能提高热机效率.对于温度之比T 2/T 1,由于T 2 < T 1,显然,分子减少一个量比分母增加同一量要使比值降得更大,因而效率提得更高.11.14 使用一制冷机将1mol ,105Pa 的空气从20℃等压冷却至18℃,对制冷机必须提供的最小机械功是多少?设该机向40℃的环境放热,将空气看作主要由双原子分子组成. 解:空气对外所做的功为2211d d V V V V A p V p V ==⎰⎰= p (V 2– V 1) = R (T 2– T 1),其中T 2 = 291K ,T 1 = 293K .空气内能的增量为21()2iE R T T ∆=-, 其中i 表示双原子分子的自由度:i = 5.空气吸收的热量为Q = ΔE + A =212()2i R T T +-= -58.17(J). 负号表示空气放出热量.因此,制冷机从空气中吸收的热量为Q 2 = -Q = 58.17(J).空气是低温热源,为了简化计算,取平均温度为T`2 = (T 2 + T 1)/2 = 292(K); 环境是高温热源,温度为T`1 = 313(K).欲求制冷机提供的最小机械功,就要将制冷当作可逆卡诺机, 根据卡诺循环中的公式1122Q T Q T =, 可得该机向高温热源放出的热量为`112`2T Q Q T == 62.35(J),因此制冷机提供的最小机械功为W = Q 1 - Q 2 = 4.18(J).[注意]由于低温热源的温度在变化,所以向高温热源放出的热量的微元为`112`2d d T Q Q T =,其中`222d d d 2i Q Q R T +=-=-,因此``211`2d 2d 2T i Q RT T +=-,积分得制冷机向高温热源放出的热量为`21112ln 2T i Q RT T +=-= 62.35(J), 与低温热源取温度的平均值的计算结果相同(不计小数点后面2位以后的数字).。




热力学基本原理热力学是研究能量转换和物质转化的学科,它是自然科学中非常重要的一部分。
而热力学基本原理则是热力学研究的基础,它包括了热力学系统、能量守恒定律、热传导、热膨胀等多个方面。
一、热力学系统热力学系统是研究对象,它可以是一个具体的物体、一个生物体或者一个空间区域。
根据系统与外界交换能量和物质的情况,热力学系统又可以分为开放系统、封闭系统和孤立系统。
开放系统是与外界交换能量和物质的系统,比如人体就是一个典型的开放系统。
封闭系统是与外界交换能量但不交换物质的系统,而孤立系统则是既不与外界交换能量也不交换物质的系统。
二、能量守恒定律能量守恒定律是自然界中普适的规律,也是热力学基本原理之一。
能量守恒定律表明能量在系统内部的转化和传递过程中,总能量保持不变。
这意味着能量不会从虚无中产生,也不会消失。
在能量转化和传递的过程中,能量可以从一种形式转化为另一种形式,比如热能可以转化为机械能,而机械能也可以转化为热能。
能量守恒定律告诉我们,无论能量转化的方式如何,系统内的总能量始终保持不变。
三、热传导热传导是热力学基本原理中的重要内容之一,它描述了热量如何通过传导的方式从高温区域传递到低温区域。
热传导的过程可以通过物质内部的分子碰撞来实现。
根据热传导的特性,物质可以分为导热体和绝热体。
导热体具有良好的热传导性能,可以迅速传递热量。
而绝热体则是不导热的物质,可以有效隔绝和保护系统内的热量。
四、热膨胀热膨胀指的是物体在受热时由于热量的作用而体积增大的现象。
热膨胀是热力学基本原理中的重要概念,它可以应用于实际生活和工程领域中。
根据热膨胀的原理,我们可以设计和制造出具有特定功能和性能的机械装置。
比如在建筑工程中,我们考虑到房屋在受热后会发生膨胀,因此需要采取相应的措施来避免结构变形或损坏。
总结:热力学基本原理是热力学研究的基础,它涉及到热力学系统、能量守恒定律、热传导和热膨胀等多个方面。
了解和运用热力学基本原理可以帮助我们更好地理解和应用能量转化和物质转化的规律,促进科学技术的发展和进步。
第11章热力学基础教学基本要求1.掌握热力学过程、功、内能、热量、热容量、可逆过程、正循环、逆循环、卡诺循环等概念。
2.掌握热力学第一定律的意义,并能熟练将它运用于理想气体各等值变化过程的分析计算。
3.掌握循环效率的特征,并能计算热循环、致冷循环的效率和致冷系数。
4、理解热力学第二定律的本质,理解实际的宏观过程的不可逆性的意义。
5、理解玻尔兹曼关于熵与热力学概率的关系式。
理解熵增加原理,能进行熵变计算。
教学内容提要热力学是根据实验和观察总结出来的热现象规律。
它从能量的观点出发,研究物质状态变化过程中有关热功转换的关系以及过程进行的方向等,热力学是宏观理论。
引入内能、体积功的概念,给出了状态变化过程中功、热量、内能三者之间的关系;介绍了热循环、致冷循环的特征;阐述了热力学第二定律的意义;介绍了热力学概率和熵的概念以及熵增加原理。
1.基本概念(1)气体分子内能),(T V E E = 理想气体内能RT iM M T E E mol 2)(== (2)准静态过程的功,也等于P -V 图上之间过程曲线下面的面积。
(3)热量的计算 dT C M MdQ m mol=其中m C 为摩尔热容量。
等体摩尔热容量mol V C ,和等压摩尔热容量mol p C ,关系为迈耶公式:R C C mol V mol p +=,, 2.热力学第一定律热力学第一定律是热学范围内的能量守恒定律。
或表明系统从外界吸收的热量,一部分用于增加内能,一部分用于对外做功。
3.热力学第一定律在理想气体等值过程中的应用4.循环循环特征 ,等于P -V 图上循环曲线所包围的面积。
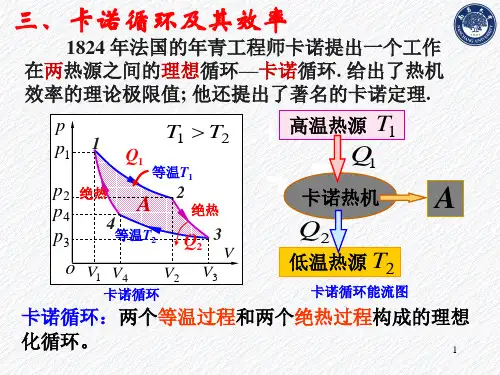
(1)热循环 从高温热源吸热,向低温热源放热,对外做净功,热机效率(2)致冷循环 通过外界做功A ,从低温热源吸热,向高温热源放热,致冷系数2122Q Q Q A Q -='=净ε(3)卡诺循环 由两个等温过程和两个绝热过程组成的准静态循环。
卡诺热机效率 121T T -=η, 卡诺致冷机致冷系数 212T T T -=ε。
第11章蒸汽动力循环一、教案设计教学目标: 使学生熟练掌握水蒸气朗肯循环、回热循环、再热循环和热电循环的组成、热效率计算及提高热效率的方式和途径。
知识点:朗肯循环、回热循环、再热循环和热电循环的组成、热效率计算及提高热效率的方式和途径重点:分析朗肯循环的分析方式,提高循环循环效率的方式和途径。
难点:回热循环、再热循环和热电循环;提装置循环效率的方式和途径。
教学方式:教学+多媒体演示+课堂讨论师生互动设计:提问+启发+讨论☺问:自己观察过身旁的热力系统的状态转变吗?☺问:你以前明白热力系统的状态转变往往伴随着系统与外界间能量的互换吗?☺问:你明白温度计什么原理吗?温度计测温的理论依据你试探过吗?☺问:用过压力计吗?氧气瓶上压力表读数是瓶中的真实压力吗?☺问:能举出几个具体的强气宇、广延量?热力进程、热力循环?☺问:爆炸进程能以为是准静态进程吗?☺问:你能说出进程量与状态量的区别吗?请具体举例。
☺问:你碰到的哪些现象属于不可逆现象?学时分派:4学时+2讨论二、大体知识热机:将热能转换为机械能的设备叫做热力原动机。
热机的工作循环称为动力循环。
动力循环:可分蒸汽动力循环和气动力循环两大类。
第一节 蒸汽动力大体循环一朗肯循环朗肯循环是最简单的蒸汽动力理想循环,热力发电厂的各类较复杂的蒸汽动力循环都是在朗肯循环的基础上予以改良而取得的。
一、装置与流程蒸汽动力装置:锅炉、汽轮机、凝汽器和给水泵等四部份主要设备。
工作原理:p-v 、T-s 和h-s 。
朗肯循环可理想化为:两个定压进程和两个定熵进程。
3’-4-5-1水在蒸汽锅炉中定压加热变成过热水蒸气, 1-2过热水蒸气在汽轮机内定煽膨胀,2-3湿蒸气在凝汽器内定压(也定温)冷却凝结放热, 3-3’凝结水在水泵中的定情紧缩。
二、朗肯循环的能量分析及热效率 取汽轮机为控制体,成立能量方程:3121h h h h --=η三、提高朗肯循环热效率的大体途径 依据:卡诺循环热效率 1.提高平均吸热温度直接方式式提高蒸汽压力和温度。