数学建模：两辆平板车的装货问题

两辆平板车的装货模型摘要：我们建立一个模型来优化这个问题。

该问题目标是包装箱到平板车上的浪费空间最小，我们转化为使得他们占据的平板车上的空间最大的线性规划问题，加上一些约束条件如下：1）每辆平板车的长度都是10.2m ； 2）每辆车的载重是40吨3）对于567,,c c c ，每辆车所占的空间不能超过3.027m 4）每件货物运送到每个平板车上的件数必须为非负值， 5）每种货物又有总量的限制我们列出方程组；通过lingo 求解得出最终的答案；剩余0m ，占据了20.4m ：其中总的分配方略：1类货物装到1车上2件，2车上6件； 2类货物装到1车上3件，2车上2件； 3类货物装到1车上2件，2车上6件； 4类货物装到1车上5件，2车上0件； 5类货物装到1车上0件，2车上0件； 6类货物装到1车上3件，2车上0件； 7类货物装到1车上2件，2车上4件；关键字：优化模型，线性规划问题一 问题重述：有7中规格的包装箱要装到两辆平板车上去，包装箱的宽和高时一样的，但是厚度及重量是不同的。

题目给出了每种包装箱的厚度重量联和数量。

每种平板车有10.2m 长的地方可用来装包装箱，最大载重为40吨。

由于当地货运的限制，对567,,c c c 还有一个特殊的要求，他们在每辆车上所占据的空间不能超过 3.027m ，我们要达到一个目标使得他们浪费的资源最少，既是我们建立的目标函数使得所占据的空间最大。

二 模型假设1） 假设没有其他外界因素的干扰，注：该问题已经是一个理想化的模型了，因此不需要太多的假设二 符号说明：ic ：表示每种货物的总的数量it：第i 种货物的厚度，以米计算。

iw ：第i 种货物的重量，以吨为计算单位。

ijx ：表示第i 种货物转到第j 辆平板车上的数目；三 问题分析：我们首先建立一个目标函数，使得他们占据的平板车上的空间最大，()7121max ii ii t xx ==+∑，然而对于每种箱子都有一定的规格，并且每辆平板车的长度都是10.2m ，所以我们增加以下约束条件；7110.2;ii ji t x=<=∑其中{1,2}j =由于每辆车的载重是40吨：因此我们也增加了约束条件。

数学建模论文题目：两辆铁路平板车的装货问题小组成员：李航纪俊吉刘骏萍两辆铁路平板车的装货问题摘要：本题是一个装货问题，即在有限的空间内装最多的货物，使空间浪费率最小。

包装箱的宽度和高度是一样的，厚度是不同的。

每个装箱策略都会产生不同的浪费。

本文讨论的就是怎么样装箱，使浪费最小。

本文首先建立一个整数规划模型，考虑问题所给的约束条件，使得包装箱装到两辆铁路平板车，并且使得浪费的空间最小。

求解时运用LINGO软件和建立在线性规划求解的单纯基础上的分支界限法求的最优解。

在求得本问题的最优目标后，进一步运用C语言，求得了本问题的所有最优解，一共有30种。

并进一步分析，在实际装货过程中可能遇到的问题，比如在相同的空间利用率的情况下，装货的总重量问题，在30组解中进一步优化，求得最终的结果。

关键字：整数优化 LING最优解装货问题一、问题重述：有7种规格的包装箱要装到两辆铁路平板车上。

包装箱的高和宽是一样的，但厚度（t,以厘米计）及重量（g，以千克计）是不同的。

下表给出来了每种包装箱的厚度，重量以及数量。

每辆平板车有10.2m长的地方可以用来装包装箱（像面包片那样），载重为40t。

由于当地货运的限制，对C5，C6，C7类的包装箱的总数有一个特别的限制：这类箱子所占的空间（厚度）不能超过302.7cm。

试把包装箱装到平板车上去使得浪费的空间最小。

C1 C2 C3 C4 C5 C6 C7厚度（cm） 48.7 52.0 61.3 72.0 48.7 52.0 64.0重量（kg） 2000 3000 1000 500 4000 2000 1000件数（件） 8 7 9 6 6 4 8二、问题分析：七种包装箱的重量和W= 89t，而两辆平板车只能载2*40=80t，因此不能全部装下，究竟在两辆车上装哪些种类的箱子各多少才合适，必须有评价的标准，这标准是遵守题中说明的重量,厚度方面的约束条件，并且体现出尽可能多装。

由题意，只考虑面包重叠那样的装法，把问题简化为：两辆车上装箱总厚度之和尽可能大，解决这一问题，以寻找最合适的方案：所浪费的空间最小，也就是说，是要让使用的空间最大。

大学生数学建模论文---两辆铁路平板车的装货问题题目：两辆铁路平板车的装货问题摘要：在现代物流运输中，铁路平板车被广泛应用于货物运输。

在铁路货运过程中，如何高效地装货是一个重要的问题。

本文通过数学建模的方法，研究了两辆铁路平板车的装货问题。

根据问题的具体要求和约束条件，我们建立了一个优化模型，旨在最大化装货效率和减少装货时间。

我们采用整数规划模型，并使用数值实例进行了求解和验证。

关键词：铁路平板车；装货问题；数学建模；优化模型1. 引言近年来，物流运输行业日益发展，货物运输效率成为一个关键问题。

铁路平板车是一种常用的货物运输工具，它具有运能大、运输距离长、安全可靠等优点。

然而，如何高效地装货是一个需要解决的问题。

2. 问题描述假设有两辆铁路平板车，它们需要装载一批货物。

货物的重量和体积不同，平板车的装载能力也有限制。

问题要求确定如何合理地将货物装载到平板车上，使得装货效率最大化，并且尽量减少装货时间。

3. 模型建立我们首先将问题进行数学抽象，定义相关的变量和参数。

然后根据问题的具体要求和约束条件，建立一个优化模型。

在模型中，我们考虑了货物的重量、体积以及平板车的装载能力等因素，并在保证装货的合理性的前提下，最大化装货效率。

4. 模型求解为了求解优化模型，我们采用整数规划的方法，并使用数学软件进行求解。

通过数值实例的求解和验证，我们得出了合理的装货方案，并评估了装货效率和装货时间等指标。

5. 结论与展望本文研究了两辆铁路平板车的装货问题，通过数学建模的方法，建立了一个优化模型，并采用整数规划进行求解。

通过数值实例的验证，我们证明了模型的合理性和有效性。

然而，由于时间和资源的限制，本文的研究还有一定的局限性。

未来的研究可以进一步考虑更多的因素和约束条件，以提高装货效率和减少装货时间。

两辆铁路平板车的装货问题摘要本文针对包装箱的运输问题，建立了关于使得平板车空间浪费最小的一般数学模型与方法。

即使得空间浪费最小的最优解，属于优化类模型。

利用线性规划原理对问题进行分析求解，建立数学模型。

首先，将7种包装箱的厚度和重量分别设成相应的未知数，方便在题中的代入求解。

由此再进一步的研究。

对于问题，假设出各辆铁路平板车所载的7种包装箱的数目。

并考虑到铁路平板车，对所载包装箱的高度、重量等要求，利用所设未知数和已知的条件限制建立约束条件。

再对铁路平板车得空间浪费最少建立目标函数。

由此，可建立线性规划数学模型，对本文问题进行求解。

利用LINGO编程进行求得最优解,即得到最优设计方案：第一辆平板车载C1种类型的包装箱0件，C2种类型的包装箱5件，C3类型的包装箱2件，C4种类型的包装箱5件，C5种类型的包装箱2件，C6种类型的包装箱1件，C7种类型的包装箱2件；另一辆平板车载C1种类型的包装箱6件，C2种类型的包装箱2件，C3种类型的包装箱6件，C4种类型的包装箱0件，C5种类型的包装箱0件，C6种类型的包装箱0件，C7种类型的包装箱4件；这样的装载能使得两辆平板车的使用高度达到20.4米，空间利用率达到100%。

关键词：最小浪费空间、长度、重量、数量。

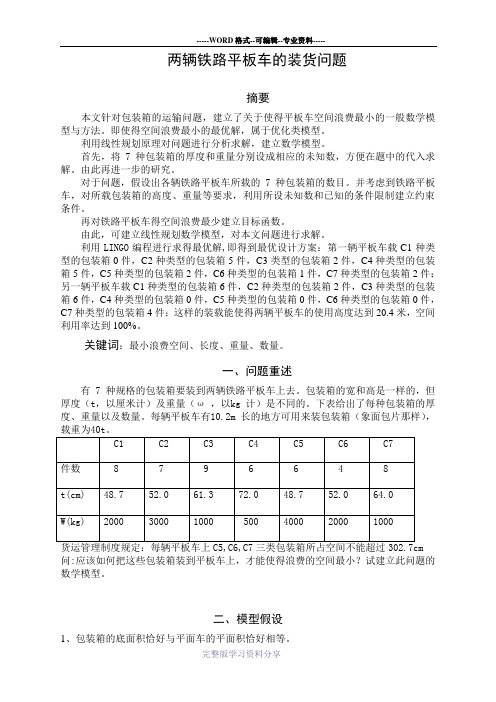
一、问题重述有 7 种规格的包装箱要装到两辆铁路平板车上去。

包装箱的宽和高是一样的，但厚度（t，以厘米计）及重量（ω，以kg 计）是不同的。

下表给出了每种包装箱的厚度、重量以及数量。

每辆平板车有10.2m 长的地方可用来装包装箱（象面包片那样），问:应该如何把这些包装箱装到平板车上，才能使得浪费的空间最小？试建立此问题的数学模型。

二、模型假设2、包装箱之间不存在间隙，即包装箱所铺成的总高度没有影响。

3、将每个包装箱装入平板车都具有可行性。

4、各个货物装在车上的概率相同，相互之间的排放不存在关联性；5、在该平板车装载的过程中不考虑各个货物的厚度及重量的误差性，均为题中所给的准确数值；6、装载的过程中不考虑货物在车上的排列次序及各个货物的重量密度，排除因局部过重而造成的平板车不能行驶的情况；三、符号定义说明i a : 表示第i 类包装箱的厚度 i b ：表示第i 类包装箱的重量 i c ：表示第i 类包装箱i x ：表示在其中一辆车上装第i 类包装箱x 件 i y ：表示在另一辆车上装第i 类包装箱y 件 （i=1,2,3,4,5,6,7）四、问题分析七种包装箱的重量和W= =89t ，而两辆平板车只能载240=80t ，因此不能全部装下，究竟在两辆车上装哪些种类的箱子各多少才合适，必须有评价的标准，这标准是遵守题中说明的重量,厚度方面的约束条件，并且体现出尽可能多装。

两辆铁路平板车的装货问题一、问题重述有七种规格的包装箱要装到两辆铁路平板车上去。

包装箱的宽和高是一样的，但厚度（t，以厘米计）及重量（w，以公斤计）是不同的。

下表给出了每种包装箱的厚度、重量以及数量。

每辆平板车有10.2米长的地方可用来装包装箱（像面包片那样），载重为40吨。

由于当地货运的限制，对C5，C6，C7类的包装箱的总数有一个特别的限制：这类箱子所占的空间（厚度）不能超过302.7cm。

试把包装箱装到平板车上去使得浪费的空间最小。

t（cm） 48.7 52.0 61.3 72.0 48.7 52.0 64.0w（kg） 2000 3000 1000 500 4000 2000 1000件数 8 7 9 6 6 4 8二、模型假设1、假设包装箱之间不存在空隙2、假设包装箱排成一排不存在叠放等形式3、假设外界环境对包装箱不产生磨损等三、符号系统t（i）第i种包装箱的厚度w（i）第i种包装箱的载重x（i）第一辆车第i种包装箱的个数y（i）第二辆车第i种包装箱的个数n（i）第i种包装箱总个数a（i）第i种包装箱装载总个数i=1，2，3，4，5，6四、模型建立一、最小浪费空间计算减少空间浪费存在的限制条件主要包括题目中提到的平板车的长度、载重量限度、包装箱自身的个数以及一些特殊限制。

综合以上提及的限制条件，建立数学模型：Min=2040?1020102040302.7利用Llingo求得把包装箱装到平板车上去浪费的最小空间为0.6cm。

（程序及数据输出见附录1）二、最优解中第七种包装箱的个数必定为0题目中要求总占据空间不超过2040cm，并且C5，C6，C7类所占空间不超过302.7cm，通过计算可知前四类若所有包装箱都装上恰好为最大装载空间1737.3cm。

为了使浪费空间最小，因此前四类和后三类的装载空间都需达到限制范围内的最大值。

下面对后三类包装箱所占空间的最大值。

利用C语言编程求解得最优解为302.1，且在x5=3，x6=3，x7=0的条件下，由此标题得证。

两辆铁路平板车的装货问题公司标准化编码 [QQX96QT-XQQB89Q8-NQQJ6Q8-MQM9N]两辆铁路平板车的装货问题2014摘要：将七种规格的包装箱装到两辆铁路平板车上并要求浪费空间最小的问题，实质上就是整数线性规划问题。

建立整数线性规划模型，并用lingo软件求得目标函数最小值得给出一组最优解。

然而由于LINGO软件的缺陷性，我们发现仍然存在其他多组最优解。

通过对原始数据的分析论证，我们得到一个结论：对任意一组最优解，两辆车的总包装箱种类和数量是确定的（即浪费空间最小的情况下，装载包装箱的厚度和重量一定）。

在此结论的基础上，通过穷举法，并利用Java高级计算机语言进行编程，大大减少了计算量，加快了运算速度，最终求解出24组等价最优解。

关键词：装货问题整数线性规划穷举法 LINGO Java语言1、问题重述有七种规格的包装箱要装到两辆铁路平板车上去。

包装箱的宽和高是一样的，但厚度（t，以cm计）及重量（w，以kg计）是不同的。

表一给出了每种包装箱的厚度、重量以及数量。

每辆平板车有米长的地方可用来装包装箱（像面包片那样），载重为40吨。

由于当地货运的限制，对C5，C6，C7类的包装箱的总数有一个特别的限制：这类箱子所占的空间（厚度）不能超过。

试把包装箱装到平板车上去使得浪费的空间最小。

表一2、问题分析优化问题，一般是指用“最好”的方式，使用或分配有限的资源，即劳动力、原材料、机器、资金等，使得费用最小或者利润最低[]1。

在此问题中，要求浪费的空间最小，且存在车长、载重40t 、货运限制C5，C6，C7类的包装箱的总数≤三个约束条件，并且自变量（包装箱的数量）取整数值才有意义，所以此问题可以通过建立整数线性规划来求解。

其一般形式为：∑==nj jj x c z 1min⎪⎩⎪⎨⎧⋯=⋯==∑=),,2,1(),,2,1(..1n j x m i b x a t s j i nj jij 为非负整数。

两辆铁路平板车的装货问题摘要本题针对铁路平板车装货的问题，有七种规格的包装箱要装到两辆铁路平板车上去。

在厚度、载重、件数等条件的限制下，要求我们把包装箱装到平板车上去使得浪费的空间最小。

针对本问题，初步分析可得：题中所有包装箱共重89t，而两辆平板车只能载重共80t，因此，不可能全安装下。

根据题意可得，浪费的空间最小就是要求尽可能使两辆车上的装箱总厚度尽可能大。

根据题目中关于厚度、载重、件数等限制条件，建立相应的线性规划数学模型，写出相应的目标函数和约束条件。

使用数学软件matlab和lingo得出相应的最优解。

若有数组最优解，最后用Excel 对得到的最优解进行分析，得出最符合题意的答案。

关键词：线性规划最优解lingo matlab一、问题重述有7种规格的包装箱要装到两辆铁路平板车上去。

包装箱的宽和高是一样的，但厚度（t，以厘米计）及重量（w，以公斤计）是不同的。

下表给出了每种包装箱的厚度、重量以及数量。

每辆平板车有10.2米长的地方可用来装包装箱（像面包片那样），载重为40吨。

由于当地货运的限制，对C5,C6,C7类的包装箱的总数有一个特别的限制：这类箱子所占的空间（厚度）不能超过302.7cm。

C1 C2 C3 C4 C5 C6 C7t(cm) 48.7 52.0 61.3 72.0 48.7 52.0 64.0w(kg) 2000 3000 1000 500 4000 2000 1000件数 8 7 9 6 6 4 8问：应该如何把这些包装箱装到平板车上，才能使得浪费的空间最小（尽量使这些包装箱所占的空间最大）？试建立此问题的数学模型。

二、问题分析2.1对题目的分析题目中的所有包装箱的总重量W=2*8+3*7+9*1+0.5*6+4*6+2*4+1*8=89t但是两辆平板车的总载重量只有80t，所以不可能全部装下所有货物。

题目要求试把包装箱装到平板车上去使得浪费的空间最小。

所以不以尽可能装满80t货物为目标函数，而是以使两辆车上的装箱总厚度尽可能大为目标函数建立数学模型。

两辆铁路平板车的装货问题两辆铁路平板车的装货问题摘要本题针对铁路平板车装货的问题，有七种规格的包装箱要装到两辆铁路平板车上去。

在厚度、载重、件数等条件的限制下，要求我们把包装箱装到平板车上去使得浪费的空间最小。

针对本问题，初步分析可得：题中所有包装箱共重89t，而两辆平板车只能载重共80t，因此，不可能全安装下。

根据题意可得，浪费的空间最小就是要求尽可能使两辆车上的装箱总厚度尽可能大。

根据题目中关于厚度、载重、件数等限制条件，建立相应的线性规划数学模型，写出相应的目标函数和约束条件。

使用数学软件matlab和lingo得出相应的最优解。

若有数组最优解，最后用Excel对得到的最优解进行分析，得出最符合题意的答案。

关键词：线性规划最优解lingo matlab７、不考虑方案不同仅仅是AB车车次相互交换的情况；８、不考虑一辆车上同一种包装箱组合方案的不同排列；９、在重量符合要求的情况下，不考虑两车重量差别大小对最优解的影响。

四、符号说明序号符号符号说明1 X1~X7A车中C1~C7类货物装载的数量2 Y1~Y7B车中C1~C7类货物装载的数量3 f 目标函数，即A，B车所装货物的总厚度4 Wa 最优解中A车的实际重量5 Wb 最优解中B车的实际重量6 Ta 最优解中A车的实际厚度7 Tb 最优解中B车的实际厚度8 Lta最优解中A车的C5,C6,C7的实际厚度9 Ltb最优解中B车的C5,C6,C7的实际厚度为了便于问题的求解，我们给出以下符号说明：五、模型的建立与求解经过以上的分析和准备，我们将逐步建立以下数学模型，进一步阐述模型的实际建立过程。

5.1线性规划模型的建立与求解根据题目中的意思，要在符合厚度、质量等的条件下建立相关的数学模型。

我们可以根据题意写出初步的目标函数和约束条件：假设两辆车分别为A 车和B 车，设A 车上的C1、C2、C3、C4、C5、C6、C7种类的箱子分别装x1、x2、x3、x4、x5、x6、x7件，B 车上的C1、C2、C3、C4、C5、C6、C7种类的箱子分别装y1、y2、y3、y4、y5、y6、y7件。

铁路平板车问题最优化论文摘要：为了使平板车装载包装箱所浪费空间达到最小，也就是货物占据空间达到最大，关键字：整数规划，整体最优化,问题重现：有7 种规格的包装箱要装到两辆铁路平板车上去。

包装箱的宽和高是一样的，但厚度（t，以厘米计）及重量（ω，以kg 计）是不同的。

下表给出了每种包装箱的厚度、重量以及数量。

每辆平板车有10.2m 长的地方可用来装包装箱（象面包片那样），载重为40t。

由于当地货运的限制，对c5 ,c6,c7类的包装箱的总数有一个特别的限制：这类箱子所占的空间（厚度）不能超过302.7cm。

试把包装箱上平板车而使浪费的空间最小。

1.问题分析：题中所有包装箱总重为89吨，总厚度达到2749.5cm，而两辆平板车只能承载40吨*2＝80吨，长度为2040cm。

因此所有的包装箱不能全部装在车上。

那么，要在两辆车上装入多少个各种规格的箱子才合适？这需要有一个评价的标准。

这标准就是遵守题中说明的厚度方面的约束条件，并且在这些条件下，能尽可能多装，确定最终的装载方案使得空间利用最大化。

由题意可知，只考虑像面包片重叠那样的装法，把问题简化，为两辆车上装箱总厚度之和尽可能大。

2.模型假设：1) 各个货物装在车上的概率相同，相互之间的排放不存在关联性；2) 在该平板车装载的过程中不考虑各个货物的厚度及重量的误差性，均为题中所给的准确数值；3) 装载的过程中不考虑货物在车上的排列次序及各个货物的重量密度，排除因局部过重而造成的平板车不能行驶的情况；4) 各个货物之间排列时靠在一起，忽略其中的间隙及因搬动等带来的一些空隙；5）铁路平板车只能放置一列包装箱。

3、符号说明：i C .........第1--7种规格的包装物 ti C ........第i C 种规格的包装物的厚度wi C .........第i C 种规格的包装物的重量i x ........在第一辆车上装载i C 种包装箱的个数i y .........在第二辆车上装载i C 种包装物的个数模型分析与建立模型一：整体最优化模型分析：通过运筹学的相关知识可以知道，单个个体都取到最优解，总和起来不一定就能使得总体达到最优结果，模型一即以整体最优为目标建立的。