2019年高考仿真原创押题卷3

2019届高考英语全真模拟密押卷（三）1、The oddness (反常) of life in space never quite goes away. Here are some examples.First consider something as simple as sleep. Its position presents its own challenges. The main question is whether you want your arms inside or outside the sleeping bag. If you leave your arms out, they float free in zero gravity, often giving a sleeping astronaut the look of a funny balled (芭蕾) dancer. “I’m an inside guy,” Mike Hopkins says, who returned from a six-month tour on the International Space S tation. “I like to be wrapped up.”On the station, the ordinary becomes strange. The exercise bike for the American astronauts has no handlebars. It also has no seat. With no gravity, it’s just as easy to pedal violently. You can watch a movie while you pedal by floating a microcomputer anywhere you want. But station residents have to be careful about staying in one place too long. Without gravity to help circulate air, the carbon dioxide you exhale (呼气) has a tendency to form an invisible (隐形的) cloud around you head. You can end up with what astronauts call a carbon-dioxide headache.Leroy Chiao, 54, an American retired astronaut after four flights, describes what happens even before you float out of your seat, “Your inner ear thinks you’re falling. Meanwhi le your eyes are telling you you’re standing straight. That can be annoying—that’s why some people feel sick.” Within a couple days—truly terrible days for some —astronauts, brains learn to ignore the panicky signals from the inner ear, and space sickness disappears.Space travel can be so delightful but at the same time invisibly dangerous. For instance, astronauts lose bone mass. That’s why exercise is considered so vital that National Aeronautics and Space Administration (NASA) puts it right on the workday schedule. The focus on fitness is as much about science and the future as it is about keeping any individual astronauts return home, and, more importantly, how to maintain strength and fitness for the two and a half years or more that it would take to make a round-trip to Mars.1.What is the major challenge to astronauts when they sleep in space?A.Deciding on a proper sleep positionB.Choosing a comfortable sleeping bagC.Seeking a way to fall asleep quicklyD.Finding a right time to go to sleep.2.The astronauts will suffer from a carbon-dioxide headache when _____.A.they circle around on their bikesB.they use microcomputers without a stopC.they exercise in one place for a long timeD.they watch a movie while pedaling3.Some astronauts feel sick on the station during the first few days because _____.A.their senses stop workingB.they have to stand up straightC.they float out of their seats unexpectedlyD.whether they are able to go back to the station4.One of the NASA’s major concerns about astrona uts is _____.A. how much exercise they do on the stationB.how they can remain healthy for long in spaceC.whether they can recover after returning homeD.whether they are able to go back to the station2、 Planning a visit to the U?Here we help with ways to cut your costs.AVOID BIG EVENTS Big sporting events,concerts and exhibitions can increase the cost of accommodation and make it harder to find a room.A standard double room at the Thistle Brighton on the final Friday of the Brighton Comedy Festival(19 Oct.)cost￡169.15 at .A week later,the same room cost ￡118.15.If you can be flexible and want to know dates to avoid—or you’re looking for a big event to pass your time-check out sites such as ,which allow you to search for events in the U by city,date and category.STAY AWAY FROM THE STATION If traveling to your destination by train,you may want to find a good base close to the station,but you could end up paying more for the sake of convenience at the start of your holiday.Don’t be too choosy about the part of town you stay in.Booking two months in advance,the cheapest room at Travelodge’s Central Euston hotel in London for Saturday 22 September was ￡95.95.A room just a tube journey away at its Covent Garden hotel was ￡75.75.And at Farringdon,a double room cost just ￡62.95.LOO AFTER YOURSELF Really central hotels in cities such as London,Edinburgh and Cardiff can cost a fortune,especially at weekends and during big events.As an alternative consider checking into a self-catering flat with its own kitchen.Often these flats are hidden away on the top floors of city centre buildings.A great example is the historic O’Neill Flat onEdinburgh’s Royal Mile,available for￡420 for five days in late September,with room for four adults.GET ON A BIE London’s“Boris Bikes”have attracted the most attention,but other cities also have similar programmes that let you rent a bicycle and explore at your own pace,saving you on public transport or car parking costs.Among the smaller cities with their own programmes are Newcastle(casual members pay around ￡1.50 for two hours) and Cardiff(free for up to 30 minutes,or ￡5 per day).1.The Brighton Comedy Festival is mentioned mainly to show big eventsmay____________________.A.help travelers pass timeB.attract lots of travelers to theUC.allow travelers to make flexible plansD.cause travelers to pay more for accommodation2.“Farringdon” in Paragraph 5 is most probably ____________________.A.a hotel away from the train stationB.the tube line to Covent GardenC.all ideal holiday destinationD.the name of a travel agency3.Cardiff’s program allows a free bike for a maximum period of ____________________.A.half an hourB.one hourC.one hour and a halfD.two hours4.The main purpose of the passage is ____________________.A.to tell visitors how to book in advanceB.to supply visitors with hotel informationC.to show visitors the importance of self-helpD.to offer visitors some money-saving tips3、Ease neck and shoulder pain at the officeIf you work in an office, keeping neck and shoulder pain away may only take two minutes a day.A new study presented at the World Congress of the American College of Sports Medicine in Denver found that office workers doing two minutes of exercise a day reported lower levels of neck and shoulder pain after 10 weeks.The study by Danish researchers involved 198 office workers who had frequent neck and shoulder pain but were otherwise healthy. The workers did either a 2-minute or a 12-minute resistance exercise using elastic tubing. The exercise was a lateral raise, in which the upper arm is raised until it is horizontal and the arms are 10 to 15 inches from the body, says Lars Andersen, the lead researcher.After 10 weeks, the workers who had performed two minutes of daily exercise reported on average a 1.4-point decrease in pain on a 10-point scale. Workers who did 12 minutes of daily exercise had an even lower level of pain, but the difference was not very significant.Though the study may give new encouragement to workers to add even small amounts of exercise into their daily routines, the connection between lower levels of pain and exercise is well-documented, says Lynn Miller, a professor of physical therapy at Andrews University in Berrien Springs, Mich., who was not involved in the study.Even short periods of exercise can help loosen up tight muscles and bring the body back into proper level, Miller says. Office-induced pain also can be reduced by making sure your workspace is set up properly.“For office workers,usually posture is not good," Miller says. Arms are often forward for prolonged periods, and reading a computer screen tends to bring the head into a forward position.1.In which column of a newspaper could we find this passage?A.Entertainment.B.Sports.C.Business.D.Lifestyle.2.According to the passage, where did the researchers come from?A.Germany.B.America.C.Denmark.D.Britain.3.The third paragraph mainly tells us ______.A.the reason why the study was carried outB.the people who carried out the researchC.how the study was carried out in detailD.how to exercise every day4.Which of the following words best describes Lynn Miller’s attitude towards the study result?A.Supportive.B.Negative.C.Shocked.D.Doubtful.4、 Beauty has always been regarded as something praiseworthy. Almost everyone thinks attractive people are happier, have better marriages and have more respectable jobs. Personal advisors give them better advice for finding jobs. Even judges are softer with attractive defendants. But in the executive(主管的) circle,beauty can become a liability.While attractiveness is a positive factor for a man on his way up the executive ladder,it is harmful to a woman.Handsome male executives were considered as having more honesty than plain men, and effort and ability were thought to lead to their success.Attractive female executives were considered to have less honesty than unattractive ones; their success was connected not with ability but with factors such as luck.All unattractive women executives were thought to have more honesty and to be more capable than the attractive female executives. Interestingly, though, the overnight success of the unattractive was attributed more to personal relationships and less to ability than that of the attractive.Why are attractive women not thought to be able? An attractive woman is considered to be more feminine and an attractive man more manly than the less attractive ones. Thus, an attractive woman has an advantage in traditionally female jobs, hut an attractive woman in a traditionally manly position appears to lack the “manly” qualities required.This is true even in politics. kiWhen the only clue is how he or she looks,people treat men and women differently,says Anne Bowman, who recently published a study on the effects of attractiveness on political candidates (候选人). She asked 125 undergraduate students to rank two groups of photographs, one of men and the other of women,in the order of attractiveness. The students were told the photographs were of candidates for political offices. They were asked to rank them again, in the order they would vote for them.The results showed that attractive males completely defeated unattractive men, hut the women who had been ranked the most attractive unchangeably received the fewest votes.1.The word “liability” most probably means_________.A.disadvantageB.advantageC.misfortuneD.trouble2.It can be inferred from the passage that people’s views on beauty are often_______.A.practicalB.supportiveC.old-fashionedD.one-sided3.The author writes this passage to __________.A.give advice to job-seekers who are attractiveB.discuss the disadvantages of being attractiveC.demand equal rights for womenD.state the importance of appearance5、根据短文内容,从短文后的选项中选出能填入空白处的最佳选项,选项中有两项为多余选项。

2019年高考名校仿真模拟联考试题(新课标全国卷)语文(三)本试卷分第Ⅰ卷（阅读题）和第Ⅱ卷（表达题）两部分。

满分150分。

考试用时150分钟。

第Ⅰ卷阅读题一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成1—3题。

①文化自觉是对文化的自我觉醒、自我反思和理性审视，是指生活在一定文化历史圈子中的主体对自己的文化应该有自知之明，同时也要了解和认识其他文化，处理好本土文化与外来文化的关系。

中华文化自觉就是对中国文化的反思、反省和审视。

自中华文化产生以来，中国人民的文化自觉过程就从未停止过。

特别是到了近现代，中国人民对中国文化的反思、反省和审视达到了空前广泛和深刻的程度，涌现出一大批文化名家。

即使他们所持观点迥异，但他们均为中华文化自觉作出了不可忽视的贡献。

他们从不同角度、不同方面对中华传统文化进行了反思、反省，其中不乏真知灼见，对中华文化自觉不无启迪。

但是，中国真正的文化自觉，是在中国共产党的带领下，对中华文化的总体构成和要素，对中华文化的历史、现在和未来作全面、客观的分析和认识，是对中华传统文化积极因素和消极因素的辩证分析和科学认识。

②文化自觉是一个复杂的认识过程和艰苦的探索过程，是在人类文明发展中逐渐提升的。

从中国近代文化自觉的艰难认识和探索历程我们可以比较清楚地认识到这一点。

近代以来，中国闭关自守的大门在西方文化的冲击下逐渐被打开，无数志士仁人开始对中华传统文化进行反思和反省。

在这一过程中，先后产生了关于如何对待中华传统文化与西方文化关系的各种观点和理论，“中体西用”“西体中用”“全盘西化”“儒学复兴”“综合创新”等观点、学说对中国社会的发展都产生了一定影响。

③当代中华文化在经济全球化和世界一体化的进程中、在世界各种文化的冲突和融合中发展，既面临严峻挑战，又迎来巨大机遇。

中华文化自觉的责任意识和担当意识在今天尤显重要。

我们必须坚持文明互鉴、开放包容的方针，既不简单“拿来”，又不盲目排外。

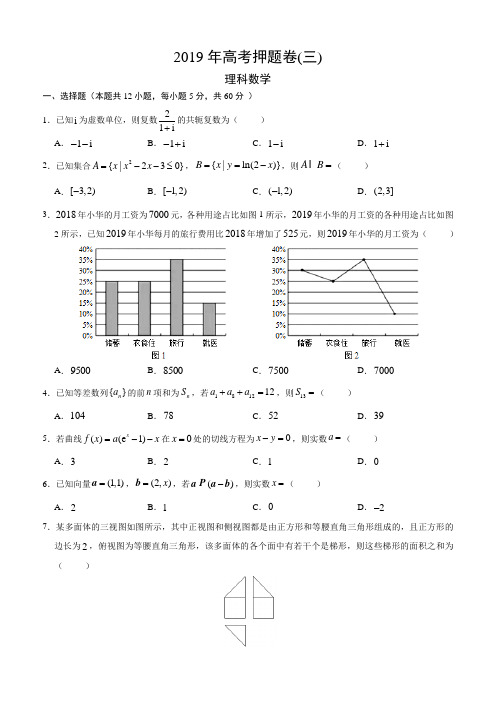
2019年高考押题卷(三)理科数学一、选择题（本题共12小题，每小题5分，共60分 ）1．已知i 为虚数单位，则复数21i +的共轭复数为（ ） A ．1i -- B ．1i -+C ．1i -D ．1i + 2．已知集合2{|230}A x x x =--≤，{|ln(2)}B x y x ==-，则AB =（ ） A ．[3,2)- B ．[l,2)-C ．(l,2)-D ．(2,3] 3．2018年小华的月工资为7000元，各种用途占比如图1所示，2019年小华的月工资的各种用途占比如图2所示，已知2019年小华每月的旅行费用比2018年增加了525元，则2019年小华的月工资为（ ）A ．9500B ．8500C ．7500D ．7000 4．已知等差数列{}n a 的前n 项和为n S ，若181212a a a ++=，则13S =（ ）A ．104B ．78C ．52D ．39 5．若曲线()e ()1x f x a x =--在0x =处的切线方程为0x y -=，则实数a =（ ） A ．3 B ．2 C ．1 D ．06．已知向量(1,1)=a ，(2,)x =b ，若()-aa b ，则实数x =（ ） A ．2 B ．1 C ．0 D ．2- 7．某多面体的三视图如图所示，其中正视图和侧视图都是由正方形和等腰直角三角形组成的，且正方形的边长为2，俯视图为等腰直角三角形，该多面体的各个面中有若干个是梯形，则这些梯形的面积之和为（ ）A ．16B ．14C ．12D ．108．《九章算术》中有如下问题：“今有勾五步，股一十二步，问勾中容圆，径几何？”其大意为：“已知直角三角形的两直角边分别为5步和12步，问其内切圆的直径为多少步？”现向该三角形内随意投一粒豆子，则豆子落在该三角形的内切圆外的概率为（ ）A ．215πB ．2115π-C ．320πD ．3120π- 9．已知抛物线2:2C y px =的焦点为()1,0F ，过点()1,1P 的直线l 与抛物线C 交于A ，B 两点，若P 为线段AB 的中点，则||AB =（ ）A ．2BC ．4D ．5 10．已知函数1()e 2e x x f x x =--，若2(3)(2)0f a f a -+≤，则实数a 的取值范围为（ ） A ．3[1,]2-B ．3(,1][,)2-∞-+∞C ．3[,1]2-D ． 3(,][1,)2-∞-+∞ 11．已知某三棱锥的底面是边长为4的等边三角形，侧棱长都相等，高为2，则该三棱锥的内切球的体积为（ ）A ．481πB ．427πC ．3281πD ．43π 12．在平面直角坐标系xOy 中，过双曲线222:1(0)4x y a a Γ-=>上的一点C 作两条渐近线的平行线，与两条渐近线的交点分别为A ，B ，若平行四边形OACB 的面积为3，则双曲线Γ的离心率e =（） AB ．3 CD 第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）1．已知2()m x y +的展开式的二项式系数的最大值为a ，21()m x y ++的展开式的二项式系数的最大值为b ，其中m 为正整数，若158a b =，则m =________________．2．若实数x ，y 满足约束条件41041x y x y y --≥⎧⎪+≤⎨⎪≥⎩，则ln ln z y x =-的最小值为________________．3．已知数列{}n a 的前n 项和*21()n n S a n =-∈N ，设21log n n b a =+，则数列11{}n n b b +的前n 项和n T =________________．4．若501(2)x a a x -=++23452345a x a x a x a x +++，则2a =____________.5．设x ，y 满足约束条件24010210x y x y x y +-≤⎧⎪--≤⎨⎪++≥⎩，则23y z x +=+的最大值是____________. 6．已知数列{}n a 的前n 项和为n S ，且3122n n S a =-，则3100log a =____________. 7．已知函数1e ,0()21,0x xf x x ax a x -⎧>⎪=⎨⎪++≤⎩（a ∈R ），若方程()20f x -=恰有3个不同的根，则a 的取值范围是____________.三、解答题（本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤）17．（本小题满分12分）在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，已知4A π=，22214b a c -=． （Ⅰ）求tan C 的值；（Ⅱ）若ABC △的面积为52，求b 的值．附加：（本小题满分12分）已知ABC △的内角A B C ,,所对的边分别为a b c ,,，且(1c o s )3c A C +=. （1）求角A 的大小；（2）若a =1b =，求ABC △的面积.18．（本小题满分12分）随着共享单车的成功运营，更多的共享产品逐步走入大家的生活，共享汽车、共享充电宝等各种共享产品层出不穷．在某景区设有共享电动车租车点，共享电动车的收费标准为每小时2元（不足1小时的部分按1小时计算），甲、乙两人各租一辆电动车，若甲、乙不超过1小时还车的概率分别为14，12，超过1小时且不超过2小时还车的概率分别为12，14，且两人租车时间都不会超过3小时． （Ⅰ）求甲、乙两人租车费用相同的概率；（Ⅱ）设甲、乙两人租车费用之和为ξ，求ξ的分布列与数学期望．20．（本小题满分12分）已知椭圆2222:1(0)x y C a b a b +=>>的焦距为2，点在椭圆C 上． （Ⅰ）求椭圆C 的标准方程；（Ⅱ）若直线1l 交椭圆C 于两点A 、B ，且0(1,)M y 是线段AB 的中点，直线2l 是线段AB 的垂直平分线，求证：直线2l 过定点，并求出该定点的坐标．21．（本小题满分12分）设函数()ln x f x ax x=-，a ∈R . （1）若函数()f x 存在单调递减区间，求a 的取值范围；（2）若存在2[e e ]x ∈,，使不等式1()4f x ≥成立，求a 的取值范围.22．（本小题满分10分）选修4-4：坐标系与参数方程已知直线l的参数方程为1(x t y ⎧=⎪⎨=⎪⎩为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为3)4ρθπ=-． （Ⅰ）求直线l 的普通方程及曲线C 的直角坐标方程；（Ⅱ）设直线l 与曲线C 交于A ，B 两点，求||AB 的值．23.（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，圆C 的参数方程为：22cos (2sin x y θθθ=+⎧⎨=⎩为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，射线l 的极坐标方程为θα=(0)ρ>．（1）将圆C 的参数方程化为极坐标方程；（2）设点A的直角坐标为，射线l 与圆C 交于点(B 不同于点)O ，求OAB △面积的最大值．。

2019届全国高考原创仿真卷（三）理综化学试卷本试卷共16页，38题（含选考题）。

全卷满分300分。

考试用时150分钟。

★祝考试顺利★注意事项：1、考试范围：高考范围。

2、答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B铅笔将答题卡上试卷类型A后的方框涂黑。

3、选择题的作答：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4、非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

5、选考题的作答：先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡上对应的答题区域内，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

6、考试结束后，请将本试题卷、答题卡、草稿纸一并上交。

1.纵观古今，化学与生活皆有着密切联系。

下列说法错误的是( )A. 《本草图经》在绿矾项载：“盖此矾色绿，味酸，烧之则赤…”。

因为绿矾能电离出H+，所以有“味酸”.B. 《天工开物》记载：“凡白土曰垩土，为陶家精美器用”。

陶是一种传统硅酸盐材料C. “水声冰下咽，沙路雪中平”描述的是水的三态变化：“冰，水为之，而寒于水”，说明冰转化为水吸热D. 唐未《真元妙道要略)中有云：“以硫黄、雄黄合硝石并蜜烧之；焰起，烧手面及烬屋舍者”，文中描述的是黑火药的制作过程【答案】A【解析】A项，绿矾不能电离出H+，之所以有“味酸”，是由于FeSO4是强酸弱碱盐，易水解而使其水溶液呈酸性，故A项错误；陶瓷是传统硅酸盐材料，属于无极非金属材料，故B 正确；C. “水声冰下咽，沙路雪中平”描述的是水变成冰就没有声音，有三态变化，“冰，水为之，而寒于水”，说明冰转化为水吸热是正确；D.黑火药是由木炭粉(C)、硫磺(S)和硝石(KNO3)按一定比例配制而成的,根据题意可以知道,题中描述的是制备黑火药的过程,所以D 选项是正确的;答案：A。

2019 年高考原创押题预测卷03【新课标Ⅲ卷】语文·参考答案1．B2．C3．D4．C5．D6．①餐饮个性化、品类化发展将会越来越显著。

（2 分）②外卖餐饮零售化和跨界经营将不可避免。

（2 分）③外卖行业将在规范化发展的同时重视并承担更多的社会责任。

（2 分）7．C8.①通过奇特形象的塑造，表现了杂技的精彩刺激，激发读者阅读兴趣；（2 分）②通过对杂技逼真神妙的描绘，表现师父大高技艺的高超；（2 分）③通过制造故事悬念，为后文阿三偷学杂技埋下伏笔。

（2 分）9.①大高对阿三眼睛失明心存愧疚，不愿再因这个绝技而联想到阿三的意外，所以他不再表演这门绝技。

② 阿三因这个绝技而失明，他怕再表演会让阿三伤心，为了不再刺激阿三，他不再表演这门绝技。

③阿三眼睛失明使他意识到这门绝技的危险，为了不再让类似事件发生，他宁可让绝技失传也不再表演。

④火眼金睛在文中暗指大高心明眼亮，看透人性的黑暗，这些让他失望，使他放弃了绝技，回归平静的生活。

（每点2 分，答出三点即可）10．C11．A12．B13．（1）（我）实在无法抑制迫切的愿望，希望从南阳太守的职位上退下来，接受低级的职务。

光武帝爱惜他的才能，没有同意这个请求。

（5 分）（2）近来派遣军队，只用带有皇上印章的书信，有时用皇上的诏命，如有奸邪的人欺诈作伪，就无法发觉。

（5 分）14．A语文第 1 页（共 3 页）15．①倦于尘劳，而能淡泊超然。

诗人劳于俗务，觉得身心疲惫；冬夜闲居，感到悠然自得。

（2 分）②性格豪迈，而能安贫乐道。

诗人饮茶失眠，遣酒争豪，洒脱不羁；坐拥敝袍，不废诗书，情趣高雅。

（2 分）③乐于独处，而能珍视友情。

诗人独自夜读，享受宁静之乐；酬和友人，寄托思念之情。

（2 分）16．（1）钉头磷磷多于在庾之粟粒（2）小楼昨夜又东风恰似一江春水向东流（3）属引凄异林寒涧肃（每空1 分，若有错别字则该空不得分）17．A18．D19．C20．（1）“赶快”改为“立即”（2）“一天”改为“24 小时”（3）“放上”改为“附上”（4）“写上姓名”改为“签字”（5）“拿给”改为“交”21.思维导图一般借助PC 端、移动端等工具，运用手绘或使用软件等方法完成，具有清晰、直观、有色彩、可发散等特点，其用处为：记忆、学习、整理、思考等。

专题03 高考数学仿真押题试卷（三）注意事项：1．答题前，先将自己的姓名、准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷、草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．集合，，则=B A I （ ）A ．)1,(--∞B ．]1,(--∞C ．),1(+∞D ．),1[+∞2．已知复数，则||z z +=（ ） A ．13i 22-- B ．13i 22-+ C ．13i 22+ D ．13i 22- 3．若，(0,)2απ∈，则sin α的值为（ ）A ．624- B ．624+ C ．187 D ．32 4．如图，在矩形区域ABCD 的A ，C 两点处各有一个通信基站，假设其信号覆盖范围分别是扇形区域ADE 和扇形区域CBF （该矩形区域内无其他信号来源，基站工作正常），若在该矩形区域内随机地选一地点，则该地点无信号的概率是（ ）A ．14π-B ．12π- C ．22π-D ．4π 5．已知一几何体的三视图如图所示，则该几何体的体积为（ ）A ．163π+ B ．112π+ C ．1123π+ D ．143π+6．若A ，B 是锐角△ABC 的两个内角，则点P (cos B －sin A ，sin B －cos A )在( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限7．已知函数的部分图象如图所示，则函数图象的一个对称中心可能为（ ）A ．)0,2(-B ．)0,1(C ．)0,10(D ．)0,14(8．函数的大致图象为（ ）A ．B ．C ．D ．9．已知点A ，B ，C ，D 在同一个球的球面上，，2=AC ，若四面体ABCD 的体积为332，球心O 恰好在棱DA 上，则这个球的表面积为（ ） A ．254πB ．4πC ．8πD ．16π10．F 为双曲线22221x y a b-=右焦点，M ，N 为双曲线上的点，四边形OFMN 为平行四边形，且四边形OFMN 的面积为bc ，则双曲线的离心率为（ ） A ．2B ．22C ．2D ．311．已知不等式组表示的平面区域恰好被圆所覆盖，则实数k 的值是（ ） A ．3B ．4C ．5D ．612．已知0x 是方程的实根，则关于实数0x 的判断正确的是（ ）A ．0ln 2x ≥B ．01ex < C ．D ．第Ⅱ卷二、填空题：本大题共4小题，每小题5分． 13．展开式中含3x 项的系数为 ．（用数字表示）14．已知(1,)a λ=r ，(2,1)b =r ，若向量2a b +r r 与(8,6)c =r 共线，则a r 在b r方向上的投影为 ．15．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，，且8=a ，ABC△的面积为34，则c b +的值为 ．16．如图所示，点F 是抛物线x y 82=的焦点，点A ，B 分别在抛物线x y 82=及圆的实线部分上运动，且AB 总是平行于x 轴，则FAB △的周长的取值范围是 ．三、解答题：解答应写出文字说明、证明过程或演算步骤． 17．设n S 为数列}{n a 的前n 项和，且11=a ，，*n ∈N ．（1）证明：数列}1{+nS n为等比数列； （2）求．（2）若参与班级宣传的志愿者中有12名男生，8名女生，从中选出2名志愿者，用X 表示所选志愿者中的女生人数，写出随机变量X 的分布列及其数学期望．20．已知椭圆的长轴长为6，且椭圆C 与圆的公共弦长为3104． （1）求椭圆C 的方程；（2）过点)2,0(P 作斜率为)0(>k k 的直线l 与椭圆C 交于两点A ，B ，试判断在x 轴上是否存在点D ，使得ADB △为以AB 为底边的等腰三角形，若存在，求出点D 的横坐标的取值范围；若不存在，请说明理由．21．已知函数．（1）当0a ≤时，试求)(x f 的单调区间；（2）若)(x f 在)1,0(内有极值，试求a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分． 22．选修4-4：坐标系与参数方程已知曲线C ：，直线（t 为参数，0α<π≤）．（1）求曲线C 的直角坐标方程；（2）设直线l 与曲线C 交于B A ,两点（A 在第一象限），当时，求a 的值．23．选修4-5：不等式选讲 已知函数．（1）求不等式()3f x ≤的解集；（2）若函数)(x f y =的最小值记为m ，设a ，b ∈R ，且有m b a =+22，试证明：．【答案解析】第Ⅰ卷一、选择题 1．【答案】C 【解析】，，，选C ．2．【答案】C【解析】，1z =，．故选C ．3．【答案】A【解析】，，，故选A ． 4．【答案】A【解析】几何概型，由面积比例可以得出答案． 5．【答案】C【解析】由三视图可知：该几何体是由一个三棱锥和一个圆锥的14组成的，故选C ． 6．【答案】B7．【答案】C【解析】由题知23A =，，8ωπ=，再把点()2,23-代入可得34ϕπ=-，，故选C ．8．【答案】D 【解析】由函数不是偶函数，排除A 、C ，当时，sin y x =为单调递增函数，而外层函数e x y =也是增函数，所以在上为增函数．故选D ．11．【答案】D【解析】由于圆心(3,3)在直线上，又由于直线与直线互相垂直其交点为，直线与的交点为(0,6)-．由于可行域恰好被圆所覆盖，及三角形为圆的内接三角形圆的半径为，解得6k =或6k =-（舍去）．故选D ．12．【答案】C 【解析】方程即为，即，令()e xf x x =，，则，函数()f x 在定义域内单调递增，结合函数的单调性有：，故选C ．二、填空题13．【答案】0【解析】5(1)x -展开式中含3x 项的系数为3510C =，含2x 项的系数为3510C -=-，所以展开式中含3x 项的系数为10-10=0．14．【答案】355【解析】由题知1λ=，所以投影为355． 15．【答案】45 【解析】，∴由正弦定理1cos 2A =-，23A π=， 8a =Q ，由余弦定理可得：，又因为ABC △面积1322bc =⨯，16bc =，45b c +=．三、解答题 17．【答案】(1)数列{1}nS n+是首项为2，公比为2的等比数列．(2)．【解析】 (1)因为，所以，即，则，所以，又1121S +=， 故数列{1}nS n+是首项为2，公比为2的等比数列． （2）由（1）知，所以，故．设，则，所以，所以，所以．18．【答案】二面角E AC F --的余弦值为33． 【解析】（1）因为底面ABCD 为菱形，所以AC BD ⊥， 又平面BDEF ⊥底面ABCD ，平面BDEF I 平面，因此AC ⊥平面BDEF ，从而AC EF ⊥．又BD DE ⊥，所以DE ⊥平面ABCD ， 由2AB a =，，，可知，2BD a =，，， 从而，故EF AF ⊥． 又，所以EF ⊥平面AFC ．又EF ⊂平面AEF ，所以平面AEF ⊥平面AFC ．（2）取EF 中点G ，由题可知OG DE ∥，所以OG ⊥平面ABCD ，又在菱形ABCD 中，OA OB ⊥，所以分别以OA u u u r ，OB u u u r ，OG u u u r的方向为x ，y ，z 轴正方向建立空间直角坐标系O xyz -（如图所示），则(0,0,0)O ，(3,0,0)A a ，，，，所以，，．由（1）可知EF ⊥平面AFC ，所以平面AFC 的法向量可取为． 设平面AEC 的法向量为(,,)n x y z =r，则0,0,n AE n AC ⎧⋅=⎪⎨⋅=⎪⎩r u u u r r u u u r ，即，即22,0,y z x ⎧=⎪⎨=⎪⎩，令2z =，得4y =，所以．从而．故所求的二面角E AC F --的余弦值为33． 19．【答案】(1) (2) 【解析】 （1）用分层抽样的方法，每个人被抽中的概率是515010=，所以，参与到班级宣传的志愿者被抽中的有120210⋅=人，参与整理、打包衣物的志愿者被抽中的有130310⋅=人，故“至少有1人是参与班级宣传的志愿者”的概率是．（2）女生志愿者人数0,1,2X =，则，，．∴X 的分布列为X 0 1 2P 3395 4895 1495∴X 的数学期望为．（2）直线l 的解析式为2y kx =+，设11(,)A x y ，22(,)B x y ，AB 的中点为00(,)E x y ．假设存在点(,0)D m ，使得ADB △为以AB 为底边的等腰三角形，则DE AB ⊥．由得，故，所以，．因为DE AB ⊥，所以1DE k k =-，即，所以． 当0k >时，，所以．综上所述，在x 轴上存在满足题目条件的点D ，且点D 的横坐标的取值范围为．（2）若()f x 在(0,1)内有极值，则()f x '在(0,1)x ∈内有解．令，e 0xax -=，e x a x =． 设e ()xg x x=(0,1)x ∈， 所以，当(0,1)x ∈时，()0g x '<恒成立，所以()g x 单调递减． 又因为(1)e g =，又当0x →时，()g x →+∞，即()g x 在(0,1)x ∈上的值域为(e,)+∞，所以当e a >时，有解． 设，则(0,1)x ∈，所以()H x 在(0,1)x ∈单调递减．因为，， 所以在(0,1)x ∈有唯一解0x ．所以有： x 0(0,)x 0x 0(,1)x()H x + 0 - ()f x '- 0 + ()f x ] 极小值 Z所以当e a >时，()f x 在(0,1)内有极值且唯一．当e a ≤时，当(0,1)x ∈时，()0f x '≥恒成立，()f x 单调递增，不成立． 综上，a 的取值范围为(e,)+∞．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分．22．选修4—4：坐标系与参数方程【答案】(1) 244x y =+；(2) ∴6απ=． 【解析】（2）证明：由图可知函数()y f x =的最小值为32，即32m =． 所以2232a b +=，从而，从而．当且仅当时，等号成立， 即216a =，243b =时，有最小值，所以得证。

秘密★启用前2019年全国普通高等学校招生考试终极押题卷（全国新课标Ⅲ）文科数学（考试时间：120分钟 试卷满分：150分）注意事项：1．本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷一、选择题（本题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设，，，则下列结论中正确的是( ){}1,2,3,4,5U ={}1,2,3A ={}2,3,4B =A ．B ．A B ⊆{}2A B = C ． D ．A B U = {}1U A C B = 【答案】D解析：因为1∈A 但1B ，所以A 不对；因为A∩B ＝{2,3}，所以B 不对；因为A ∪B ＝{1,2,3,4}，所以C 不对；∉经检验，D 是正确的，故选D.2.已知为虚数单位,复数,则的实部与虚部之差为( )i 1z i =+1z z -A．1B ．0CD 1-【答案】:D 【解析】：复数，故选D.1z i =+111111,,--1222i z i z i z+=-∴-=--实部，虚部，实部虚部 3.某所学校在一个学期的开支分布的饼图如图1所示，在该学期的水、电、交通开支（单位：万元）如图2所示，则该学期的电费开支占总开支的百分比为（ ）A. B.C.D.【答案】B 【分析】结合图表，通过计算可得：该学期的电费开支占总开支的百分比为 ×20%=11.25%，得解．【详解】由图1，图2可知：该学期的电费开支占总开支的百分比为×20%=11.25%，故选：B ．【点睛】本题考查了识图能力及进行简单的合情推理，属简单题．4. 已知向量,若,则等于( )(1,3),(6,)a b m =-=a b ⊥ 2a b - A ． 80B ． 160C ． 45D ．【答案】C【解析】因为，所以630m -=，解得2m ==，所以，a ，所以a b ⊥，所以2-=a b C ．5. 已知双曲线的右焦点到渐近线的距离等于实轴长，则此双曲线的离心率为（）()2222:10,0x y C ab a b-=>>A BC D 【答案】C【解析】由题意可设双曲线的右焦点，渐进线的方程为，可得，可得C (),0F c by x a =±2d b a ===，可得离心率，故选C．c =ce a ==6.程序框图如下图所示，若上述程序运行的结果，则判断框中应填入（ ）1320A ．B ．12k ≤11k ≤C ．D ．10k ≤9k ≤【答案】D【解析】初始值，；12,1k s ==执行框图如下：；不能满足条件，进入循环；；不能满足条件，进入循环；12,11s k ==132,10s k ==；此时要输出，因此要满足条件，∴．故选D1320,9s k ==7. 若等差数列满足递推关系，则（）{}n a 1n n a a n +=-+5a =A ． B ．9294C ．D ．114134【答案】B【解析】令，得；令，得，两式相加，得，所以，故选B ．4n =544a a +=5n =655a a +=54629a a a ++=594a =8. 已知函数，且，则的最小值为（ ）()sin f x x x =()()124f x f x ⋅=-12xx +A ．B．π3π2C ．D ．2π33π4【答案】C【解析】∵，()1πsin 2sin 2sin 23f x x x x x x ⎛⎫⎛⎫===- ⎪ ⎪ ⎪⎝⎭⎝⎭又，即，()()124f x f x ⋅=-12ππ2sin 2sin 433x x ⎛⎫⎛⎫-⋅-=- ⎪ ⎪⎝⎭⎝⎭∴，∴，12ππ2sin sin 233x x ⎛⎫⎛⎫-⋅-=- ⎪ ⎪⎝⎭⎝⎭12ππsin sin 133x x ⎛⎫⎛⎫-⋅-=- ⎪ ⎪⎝⎭⎝⎭∴且或且．1πsin 13x ⎛⎫-= ⎪⎝⎭2πsin 13x ⎛⎫-=- ⎪⎝⎭2πsin 13x ⎛⎫-= ⎪⎝⎭1πsin 13x ⎛⎫-=- ⎪⎝⎭∴，，或，，．11ππ2π32x k -=+22ππ2π32x k -=-21ππ2π32x k -=+12ππ2π32x k -=-k ∈Z ∴，()()12122π2π3x x k k k +=++∈Z 显然，当时，的最小值为，故选C ．120k k +=12x x +2π39．如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，（单位：cm ），则该几何体的表面积为( )A ．B ．5π52π+C ．D ．4π42π+【答案】B【解析】根据三视图，该几何体为一个圆柱在上半部分的正面截去圆柱所得，它的表面积为14,故选B.2221112111125222ππππππ⨯⨯⨯+⨯⨯++⨯⨯++=+10．过圆上一点作圆的两条切线，切点分别为、，若，则实2216x y +=P ()222:0O x y m m +=>A B 2π3AOB ∠=数（ ）m =A ．2 B ．3C ．4D ．9【答案】A【解析】如图所示，取圆上一点，过作圆的两条切线、，2216x y +=()4,0P P ()222:0O x y m m +=>PA PB 当时，，且，；，则实数．故选A ．2π3AOB ∠=π3AOP ∠=OA AP ⊥4OP =122OA OP ==2m OA ==11.某人5次上班图中所花的时间（单位：分钟）分别为，已知这组数据的平均数为10，方差为2，,,9,10,11x y 则=（ ）x y-A ．B ．12C ．D ．34【答案】:D【解析】：解析：这是一道最新数学素养考题的体现，据题意有，按一般同学的常规思路2220(10)(10)8x y x y +=⎧⎨-+-=⎩解出，导致运算量大而出错，其实由点到直线的距离公式知：代表直线与圆,x y x y -=22x y-⨯20x y +=的交点到直线倍，所以,故选D.22(10)(10)8x y -+-=0x y -=x -22224r ==12在三棱锥中，底面，，，，则此三棱锥的外接球的表面积为D ABC -CD ⊥ABC AC BC ⊥5AB BD ==4BC =A ．B ．30π32πC ．D ．34π36π【答案】:C【解析】：由题意，在三棱锥中，底面，，，，D ABC -CD ⊥ABC AC BC ⊥5AB BD ==4BC =可得，故三棱锥的外接球的半径3AD CD ===D ABC -R =．故选C.24π34π⨯=第Ⅱ卷二、填空题（本题共4小题，每小题5分，共20分）13．若实数满足,则的最大值为______________．,x y02601x y x y x -≤⎧⎪+-≤⎨⎪≥⎩2z x y =-【答案】：2【解析】：作出线性可行域如图，当y=2x 过点A （2,2）时，纵截距最小，此时z 最大，最大值为222 2.⨯-=14. 甲、乙、丙三位同学获得某项竞赛活动的前三名，但具体名次未知，3人作出如下预测：甲说：我不是第三名；乙说：我是第三名；丙说：我不是第一名；若甲、乙、丙三位同学的预测有且只有一个正确，由此判断获得第一名的同学是______________．【答案】：乙【解析】：甲、乙、丙的排名及预测对错如下表：甲对、错乙对、错丙对、错1√2×3√1√3√2√2√1×3√2√3√1×3×1×2√3×2×1×所以满足条件的甲、乙、丙排名依次为第三名，第一名，第二名，故答案为乙。

2019届全国新高三精准仿真试卷（三）语文本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分。

考生作答时，将答案答在答题卡上，在本试卷上答题无效。

★祝考试顺利★注意事项：1、考试范围：高考范围。

2．答题前，考生务必先将自己的姓名、准考证号填写在答题卡上，认真核对条形码上的姓名、准考证号，并将条形码粘贴在答题卡的指定位置上。

3．答题时使用0.5毫米的黑色中性（签字）笔或碳素笔书写，字体工整、笔迹清楚。

4．请按照题号在各题的答题区域(黑色线框)内作答，超出答题区域书写的答案无效。

5．保持卡面清洁，不折叠，不破损。

6、考试结束后，请将本试题卷、答题卡、草稿纸一并上交。

一、现代文阅读（35分）（一）论述类文本阅读（本题共3小题，9分）1、阅读下面的文字，完成1—3题。

（9分）家规与国法崔永东“家规”与“国法”各有自己的领域，对稳定家族秩序和国家秩序发挥着不可替代的作用。

在中国古代社会，家规提倡“孝道”价值观，凸显家族利益至上，注重父慈子孝、兄友弟恭、夫妻和睦；国法提倡“忠道”价值观，凸显国家利益至上，重视忠君爱国、无私奉献。

家规与国法之间在功能上又可以互相支撑，在内容上也可以互相补充。

“家规”重在“修身、齐家”，“国法”重在“治国、平天下”，一个恪守家规的人必然能够遵守国法。

在此层面上，家族利益与国家利益形成了某种“同构”关系。

家有家规，国有国法。

家规连着国法。

家规是治家教子、修养心性、立身处世的重要载体，是中华传统文化的重要组成部分。

它包括“家训”“家戒”等内容，家训的内容旨在要求家人“必须怎么做”，家戒的内容旨在要求家人“不能怎么做”。

以《河东裴氏家训》《河东裴氏家戒》为例：“立志向善，做贤子孙。

贻谋燕翼，勿忘祖恩。

”“勤能补拙，俭以养廉。

丰家裕国，莫此为先。

秃惰奢靡，祸害无边。

”这就阐明了在家修身与在外治国的关联性，揭示了家规通向国法的功能性价值。

单从历史上看，家规与国法存在着很多的共同性，因其均以儒家伦理道德为基础，维护儒家伦理秩序成为其共同的使命。