有限元分析大作业试题
- 格式:pdf
- 大小:462.87 KB
- 文档页数:16
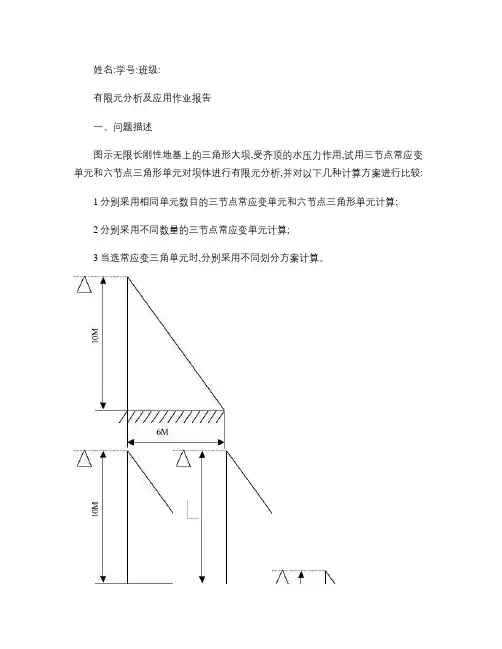
姓名:学号:班级:有限元分析及应用作业报告一、问题描述图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;2分别采用不同数量的三节点常应变单元计算;3当选常应变三角单元时,分别采用不同划分方案计算。
二、几何建模与分析图1-2力学模型由于大坝长度>>横截面尺寸,且横截面沿长度方向保持不变,因此可将大坝看作无限长的实体模型,满足平面应变问题的几何条件;对截面进行受力分析,作用于大坝上的载荷平行于横截面且沿纵向方向均匀分布,两端面不受力,满足平面应变问题的载荷条件。
因此该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图1-2所示,建立几何模型,进行求解。
假设大坝的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3三、第1问的有限元建模本题将分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算。
1设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences为Structural2选择单元类型:三节点常应变单元选择的类型是PLANE42(Quad 4node42,该单元属于是四节点单元类型,在网格划分时可以对节点数目控制使其蜕化为三节点单元;六节点三角形单元选择的类型是PLANE183(Quad 8node183,该单元属于是八节点单元类型,在网格划分时可以对节点数目控制使其蜕化为六节点单元。
因研究的问题为平面应变问题,故对Element behavior(K3设置为plane strain。
3定义材料参数4生成几何模a. 生成特征点b.生成坝体截面5网格化分:划分网格时,拾取所有线段设定input NDIV 为10,选择网格划分方式为Tri+Mapped,最后得到200个单元。


有限元考试试题及答案一、简答题(5道,共计25分)。
1.有限单元位移法求解弹性力学问题的基本步骤有哪些?(5分)答:(1)选择适当的单元类型将弹性体离散化;(2)建立单元体的位移插值函数;(3)推导单元刚度矩阵;(4)将单元刚度矩阵组装成整体刚度矩阵;(5)代入边界条件和求解.2. 在划分网格数相同的情况下,为什么八节点四边形等参数单元精度大于四边形矩形单元?(5分)答:在对于曲线边界的边界单元,其边界为曲边,八节点四边形等参数单元边上三个节点所确定的抛物线来代替原来的曲线,显然拟合效果比四边形矩形单元的直边好。
3。
轴对称单元与平面单元有哪些区别?(5分)答:轴对称单元是三角形或四边形截面的空间的环形单元,平面单元是三角形或四边形平面单元;轴对称单元内任意一点有四个应变分量,平面单元内任意一点非零独立应变分量有三个.4。
有限元空间问题有哪些特征?(5分)答:(1)单元为块体形状。
常用单元:四面体单元、长方体单元、直边六面体单元、曲边六面体单元、轴对称单元。
(2)结点位移3个分量。
(3)基本方程比平面问题多。
3个平衡方程,6个几何方程,6个物理方程。
5.简述四节点四边形等参数单元的平面问题分析过程。
(5)分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。
二、论述题(3道,共计30分)。
1. 简述四节点四边形等参数单元的平面问题分析过程.(10分)答:(1)通过整体坐标系和局部坐标系的映射关系得到四节点四边形等参单元的母单元,并选取单元的唯一模式;(2)通过坐标变换和等参元确定平面四节点四边形等参数单元的几何形状和位移模式;(3)将四节点四边形等参数单元的位移模式代入平面问题的几何方程,得到单元应变分量的计算式,再将单元应变代入平面问题的物理方程,得到平面四节点等参数单元的应力矩阵;(4)用虚功原理求得单元刚度矩阵,最后用高斯积分法计算完成。

一 、20分)(×)1. 节点的位置依赖于形态,而并不依赖于载荷的位置(√)2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元(×)3. 不能把梁单元、壳单元和实体单元混合在一起作成模型(√)4. 四边形的平面单元尽可能作成接近正方形形状的单元(×)5. 平面应变单元也好,平面应力单元也好,如果以单位厚来作模型化处理的话会得到一样的答案(×)6. 用有限元法不可以对运动的物体的结构进行静力分析(√)7. 一般应力变化大的地方单元尺寸要划的小才好(×)8. 所谓全约束只要将位移自由度约束住,而不必约束转动自由度(√)9. 同一载荷作用下的结构,所给材料的弹性模量越大则变形值越小(√)10一维变带宽存储通常比二维等带宽存储更节省存储量。
二、填空(20分)1.平面应力问题与薄板弯曲问题的弹性体几何形状都是 薄板 ,但前者受力特点是: 平行于板面且沿厚度均布载荷作用 ,变形发生在板面内;后者受力特点是: 垂直于板面 的力的作用,板将变成有弯有扭的曲面。
2.平面应力问题与平面应变问题都具有三个独立的应力分量: σx ,σy ,τxy ,三个独立的应变分量:εx ,εy ,γxy ,但对应的弹性体几何形状前者为 薄板 ,后者为 长柱体 。
3.位移模式需反映 刚体位移 ,反映 常变形 ,满足 单元边界上位移连续 。
4.单元刚度矩阵的特点有:对称性 , 奇异性 ,还可按节点分块。
5.轴对称问题单元形状为:三角形或四边形截面的空间环形单元 ,由于轴对称的特性,任意一点变形只发生在子午面上,因此可以作为 二 维问题处理。
6.等参数单元指的是:描述位移和描述坐标采用相同的形函数形式。
等参数单元优点是:可以采用高阶次位移模式,能够模拟复杂几何边界,方便单元刚度矩阵和等效节点载荷的积分运算。
7.有限单元法首先求出的解是 节点位移 ,单元应力可由它求得,其计算公式为{}{}[][]eD B σδ=。



有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。


有限元试题及答案 有限元试题及答案 一 判断题(20分)(×)1. 节点的位置依赖于形态,而并不依赖于载荷的位置(√)2. 对于高压电线的铁塔那样的框架结构的模型化处理使用梁单元 (×)3. 不能把梁单元、壳单元和实体单元混合在一起作成模型 (√)4. 四边形的平面单元尽可能作成接近正方形形状的单元(×)5. 平面应变单元也好,平面应力单元也好,如果以单位厚来作模型化 处理的话会得到一样的答案(×)6. 用有限元法不可以对运动的物体的结构进行静力分析 (√)7. 一般应力变化大的地方单元尺寸要划的小才好(×)8. 所谓全约束只要将位移自由度约束住,而不必约束转动自由度 (√)9. 同一载荷作用下的结构,所给材料的弹性模量越大则变形值越小 (√)10一维变带宽存储通常比二维等带宽存储更节省存储量。
二、填空(20分)1.平面应力问题与薄板弯曲问题的弹性体几何形状都是 薄板 ,但前者受力特点是: 平行于板面且沿厚度均布载荷作用 ,变形发生在板面内;后者受力特点是: 垂直于板面 的力的作用,板将变成有弯有扭的曲面。
2.平面应力问题与平面应变问题都具有三个独立的应力分量: σx ,σy ,τxy ,三个独立的应变分量:εx ,εy ,γxy ,但对应的弹性体几何形状前者为 薄板 ,后者为 长柱体 。
3.位移模式需反映 刚体位移 ,反映 常变形 ,满足 单元边界上位移连续 。
4.单元刚度矩阵的特点有:对称性 , 奇异性 ,还可按节点分块。
5.轴对称问题单元形状为:三角形或四边形截面的空间环形单元 ,由于轴对称的特性,任意一点变形只发生在子午面上,因此可以作为 二 维问题处理。
6.等参数单元指的是:描述位移和描述坐标采用相同的形函数形式。
等参数单元优点是:可以采用高阶次位移模式,能够模拟复杂几何边界,方便单元刚度矩阵和等效节点载荷的积分运算。
7.有限单元法首先求出的解是 节点位移 ,单元应力可由它求得,其计算公式为{}{}[][]eD B σδ=。


有限元分析习题及大作业试题
要求:1)个人独立完成其中的一个习题,并将计算结果编写为计算分析报告上交;
2)计算分析报告应包括以下部分:
A、问题描述及数学建模;
B、有限元建模(单元选择、节点布置及规模、网格划分方
案、载荷及边界条件处理、求解控制)
C、计算结果及结果分析(位移分析、应力分析、正确性分
析评判)
D、多方案计算比较(节点规模增减对精度的影响分析、单
元改变对精度的影响分析、不同网格划分方案对结果的
影响分析等)
E、建议与体会
3)5月20日前必须完成,并递交计算分析报告(报告要求打印)。
试题1:图示为一带圆孔或方孔的单位厚度(1mm )的正方形平板,E=210Gpa ,μ=0.3,在x 方向作用均布压力0.25Mpa ,试用3节点常应变单元和6节点三角形单元(或4节点四边形单元和8节点四边形单元)对平板进行有限元分析,并分别就圆孔或方孔结构对以下几种计算方案的计算结果进行比较:
1) 分别采用相同单元数目的三节点常应变单元和六节点三角形单元
(或4节点四边形单元和8节点四边形单元)计算;
2) 分别采用不同数量的三节点常应变单元计算;
3) 比较圆孔或方孔孔边应力水平;
在y 轴上,圆孔边应力的精确解为:MPa x 75.0-=σ,
在x 轴上,圆孔边应力的精确解为:MPa y 25.0=σ
试题2:确定图示扳手中的应力, E=210Gpa,μ=0.3,假设厚度为10mm。
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==有限元分析试卷篇一:有限元试题有限元分析及应用试卷一.填空题1.平面应力问题与薄板弯曲问题的弹性体几何形状都是薄板;但前者受力特点是:载荷平行于板平面且沿厚度方向均匀分布,而板平面不受任何外力作用;变形发生在板面内;后者受力特点当板受有垂直于板中性面的外力时,板的中性面将发生弯扭变形,板将变成有弯有扭的的曲面。
平面应力问题与平面应变问题都具有三个独立的应力分量、三个独立的应变分量:体几何形状前者为结构形状呈薄板形,后者为结构呈等截面细长形。
3. 位移模式需反映单元的刚体位移,反映单元的常量应变 ,满足单元内部的位移连续性和跨单元的位移连续性。
4. 轴对称问题的单元形状为:截面为四边形或三角形的环形单元,由于轴对称的特性,任意一点的变形只发生在子午面上,因此可作为二维问题处理。
5.一个空间块体单元的节点有个节点位移:。
6. 有限单元法首先求得解是,单元应力可由它求得。
二、问答题1. 简述有限单元法的基本步骤。
答:1.建立求解域,并将之离散化成有限个单元,即将问题分解成节点和单元。
2.假定描述单元物理属性的形函数,即用一个近似的连续函数描述每个单元的解。
3.建立单元刚度矩阵。
4.组装单元,构造总刚矩阵。
5.应用边界条件和初值条件,并施加荷载。
6.求解线性或非线性微分方程得到节点值。
7.分析计算,进行后处理2. 简述有限单元法结构刚度矩阵的特点。
答:(1)对称性(2)奇异性单元处于平衡时,结点力相互不是独立的,满足三个平衡方程(两个方向力平衡,绕一点矩平衡)(3)主元恒正Kij>0,要使u1=1,施加在u1方向的结点力必须与位移u1同向.3. 简述有限单元法中选取单元位移函数(多项式)的一般原则。
答:1)反映单元的刚体位移与常量应变。
2)相邻单元在公共边界上的位移连续,即单元之间不能重叠,也不能脱离。
1如图所示的平面,板厚为0.01m,左端固定,右端作用50kg 的均布载荷,对其进行静力分析。
弹性模量为210GPa,泊松比为0.25.
2简支梁的变形分析
计算分析模型如图1-1 所示, 习题文件名: beam。
NOTE:要求选择不同形状的截面分别进行计算。
梁承受均布载荷:1.0e5 Pa
10m
图1-1梁的计算分析模型
梁截面分别采用以下三种截面(单位:m):
矩形截面:圆截面:工字形截面:
B=0.1, H=0.15 R=0.1 w1=0.1,w2=0.1,w3=0.2,
t1=0.0114,t2=0.0114,t3=0.007
3 超静定桁架的有限元建模与分析
计算分析模型如图5-1 所示, 习题文件名: truss 。
载荷:1.0e8 N
4平板的有限元建模与变形分析
计算分析模型如图7-1 所示, 习题文件名: plane
0.5 m
0.5 m
板承受均布载荷:1.0e5 Pa。
姓名:学号:班级:有限元分析及应用作业报告一、问题描述图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;2分别采用不同数量的三节点常应变单元计算;3当选常应变三角单元时,分别采用不同划分方案计算。
二、几何建模与分析图1-2力学模型由于大坝长度>>横截面尺寸,且横截面沿长度方向保持不变,因此可将大坝看作无限长的实体模型,满足平面应变问题的几何条件;对截面进行受力分析,作用于大坝上的载荷平行于横截面且沿纵向方向均匀分布,两端面不受力,满足平面应变问题的载荷条件。
因此该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图1-2所示,建立几何模型,进行求解。
假设大坝的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3三、第1问的有限元建模本题将分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算。
1设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences为Structural2选择单元类型:三节点常应变单元选择的类型是PLANE42(Quad 4node42,该单元属于是四节点单元类型,在网格划分时可以对节点数目控制使其蜕化为三节点单元;六节点三角形单元选择的类型是PLANE183(Quad 8node183,该单元属于是八节点单元类型,在网格划分时可以对节点数目控制使其蜕化为六节点单元。
因研究的问题为平面应变问题,故对Element behavior(K3设置为plane strain。
3定义材料参数4生成几何模a. 生成特征点b.生成坝体截面5网格化分:划分网格时,拾取所有线段设定input NDIV 为10,选择网格划分方式为Tri+Mapped,最后得到200个单元。
有限元方法及应用试题1、试简要阐述有限元理论分析的基本步骤主要有哪些?答:单元离散(划分、剖分)—单元分析—整体分析有限元分析的主要步骤主要有:A结构的离散化B单元分析。
选择位移函数、根据几何方程建立应变与位移的关系、根据物理方程建立应力与位移的关系、根据虚功原理建立节点力与节点位移的关系(单元刚度方程)C等效节点载荷计算D整体分析,建立整体刚度方程E引入约束,求解整体平衡方程2、有限元网格划分的基本原则是什么?指出图示网格划分中不合理的地方。
题2图答:一般选用三角形或四边形单元,在满足一定精度情况,尽可能少一些单元。
有限元划分网格的基本原则是:1、拓朴正确性原则。
即单元间是靠单元顶点、或单元边、或单元面连接2、几何保形原则。
即网格划分后,单元的集合为原结构近似3、特性一致原则。
即材料相同,厚度相同4、单元形状优良原则。
单元边、角相差尽可能小5、密度可控原则。
即在保证一定精度的前提下,网格尽可能稀疏一些图中:(a)(b)中节点没有有效连接,且b中,单元边长相差很大。
(c )中没有考虑对称性,单元相差太大。
3、分别指出图示平面结构划分为什么单元?有多少个节点?多少个自由度?题3图答:(a )划分为杆单元, 8个节点,12个自由度 (b )划分为平面梁单元,8个节点,15个自由度 (c )平面四节点,四边形单元,8个节点,13个自由度 (d )平面三角形单元,29个节点,38个自由度4、什么是等参数单元?。
如果坐标变换和位移插值采用相同的节点,并且单元的形状变换函数与位移插值的形函数一样,则称这种变换为等参变换,这样的单元称为等参单元。
5、在平面三节点三角形单元中,能否选取如下的位移模式,为什么?(1).⎪⎩⎪⎨⎧++=++=26543221),(),(y x y x v yx y x u αααααα (2). ⎪⎩⎪⎨⎧++=++=2652423221),(),(yxy x y x v yxy x y x u αααααα 答:不能取这样的位移模式,因为在平面三节点三角形单元中,位移模式应该是呈线性的。
有限元分析及应用大作业课程名称: 有限元分析及应用班级:姓名:试题2:图示薄板左边固定,右边受均布压力P=100Kn/m作用,板厚度为0.3cm;试采用如下方案,对其进行有限元分析,并对结果进行比较。
1)三节点常应变单元;(2个和200个单元)2)四节点矩形单元;(1个和50个单元)3)八节点等参单元。
(1个和20个单元)图2-1 薄板结构及受力图一、建模由图2-1可知,此薄板长和宽分别为2m和1.5m,厚度仅为0.3cm,本题所研究问题为平面应力问题。
经计算,平板右边受均匀载荷P=33.33MPa,而左边被固定,所以要完全约束个方向的自由度,如图2-2所示。
取弹性模量E=2.1×11Pa,泊松比μ=0.3。
P=33.33MPa图2-2 数学模型二、第一问三节点常应变单元(2个和200个单元)三节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用2个单元的网格划分后的结果如图2-3,200个单元的网格划分图如图2-6所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-4、7所示,应力云图如图2-5、8所示。
图2-3 2个三角形单元的网格划分图图2-4 2个三角形单元的位移云图图2-5 2个三角形单元的应力云图图2-6 200个三角形单元的网格划分图图2-7 200个三角形单元的位移云图图2-8 200个三角形单元的应力云图三、第二问四节点矩形单元的计算四节点单元类型为PLANE42,设置好单元类型后,实常数设置板厚为0.3M。
采用1个单元的网格划分后的结果如图2-9,50个单元的网格划分图如图2-12所示。
约束的施加方式和载荷分布如图2-2中所示。
约束右边线上节点全部自由度。
计算得到的位移云图分别如图2-10、11所示,应力云图如图2-13、14所示。
图2-9 1个四边形单元的网格划分图图2-10 1个四边形单元的位移云图图2-11 1个四边形单元的应力云图图2-12 50个四边形单元的网格划分图图2-13 50个四边形单元的位移云图图2-14 50个四边形单元的应力云图四、第三问八节点等参单元的计算四节点单元类型为PLANE82,设置好单元类型后,实常数设置板厚为0.3M。
有限元分析习题及大作业试题要求:1)个人按上机指南步骤至少选择习题中3个习题独立完成,并将计算结果上交;也可根据自己科研工作给出计算实例。
2)以小组为单位完成有限元分析计算;3)以小组为单位编写计算分析报告;4)计算分析报告应包括以下部分:A、问题描述及数学建模;B、有限元建模(单元选择、结点布置及规模、网格划分方案、载荷及边界条件处理、求解控制)C、计算结果及结果分析(位移分析、应力分析、正确性分析评判)D、多方案计算比较(结点规模增减对精度的影响分析、单元改变对精度的影响分析、不同网格划分方案对结果的影响分析等)E、建议与体会4)11月5日前必须完成,并递交计算分析报告(报告要求打印)。
习题及上机指南:(试题见上机指南)例题1 坝体的有限元建模与受力分析例题2 平板的有限元建模与变形分析例题1:平板的有限元建模与变形分析计算分析模型如图1-1 所示, 习题文件名: plane图1-1 受均布载荷作用的平板计算分析模型1.1进入ANSYS程序→ANSYSED 6.1 →Interactive →change the working directory into yours →input Initial jobname: plane→Run1.2设置计算类型ANSYS Main Menu: Preferences →select Structural →OK1.3选择单元类型ANSYS Main Menu: Preprocessor →Element T ype→Add/Edit/Delete →Add →select Solid Quad 4node 42 →OK (back to Element T ypes window)→Options… →select K3: Plane stress w/thk →OK→Close (the Element T ype window)1.4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear→Elastic→Isotropic→input EX:2.1e11, PRXY:0.3→OK1.5定义实常数ANSYS Main Menu: Preprocessor →Real Constants… →Add… →select T ype 1→OK→input THK:1 →OK →Close (the Real Constants Window)1.6生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入五个点的坐标:input:1(0,0),2(1,0), 3(1,1),4(0,1),5(0.5,0.5) →OK✓生成平板ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS→连接特征点1,2,5 →Apply →连接特征点2,3,5 →Apply →连接特征点3,4,5 →Apply →连接特征点4,1,5 →OK1.7网格划分ANSYS Main Menu: Preprocessor →Meshing→Mesh T ool →(Size Controls) lines: Set →Pick All(in Picking Menu) →input NDIV:1→OK→(back to the mesh tool window)Mesh: Areas, Shape: Tri, Free →Mesh →Pick All (in Picking Menu) →Close( the Mesh T ool window)1.8模型施加约束✓给模型施加x方向约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→On Lines→拾取模型左部的竖直边:Lab2: UX →OK✓施加y方向约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→On Keypoints→拾取4# 特征点:Lab2: UY →OK1.9 分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK1.10 结果显示ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape…→select Def + Undeformed→OK (back to Plot Results window) →Contour Plot→Nodal Solu →select: DOF solution, UX,UY, Def + Undeformed →OK1.11 退出系统ANSYS Utility Menu: File→Exit →Save Everything→OK例题2:坝体的有限元建模与应力应变分析计算分析模型如图2-1 所示, 习题文件名: dam。
图2-1 坝体的计算分析模型2.1进入ANSYS程序→ANSYSED 6.1 →Interactive →change the working directory into yours →input Initial jobname: dam→Run2.2设置计算类型ANSYS Main Menu: Preferences →select Structural →OK2.3选择单元类型ANSYS Main Menu: Preprocessor →Element T ype→Add/Edit/Delete →Add →select Solid Quad 4node 42 →OK (back to Element T ypes window)→Options… →select K3: Plane Strain →OK→Close (the Element T ype window)2.4定义材料参数ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural→Linear→Elastic→Isotropic→input EX:2.1e11, PRXY:0.3→OK2.5生成几何模型✓生成特征点ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS→依次输入四个点的坐标:input:1(0,0),2(10,0),3(1,5),4(0.45,5)→OK✓生成坝体截面ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS→依次连接四个特征点,1(0,0),2(10,0),3(1,5),4(0.45,5) →OK2.6网格划分ANSYS Main Menu: Preprocessor →Meshing →Mesh T ool→(Size Controls) lines:Set →依次拾取两条横边:OK→input NDIV: 15 →Apply→依次拾取两条纵边:OK →input NDIV: 20 →OK →(back to the mesh tool window)Mesh: Areas, Shape: Quad, Mapped →Mesh →Pick All (in Picking Menu) →Close( the Mesh T ool window)2.7模型施加约束✓分别给下底边和竖直的纵边施加x和y方向的约束ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Displacement→On lines→pick the lines →OK→select Lab2:UX, UY →OK✓给斜边施加x方向的分布载荷ANSYS 命令菜单栏: Parameters→Functions →Define/Edit→1) 在下方的下拉列表框内选择x ,作为设置的变量;2) 在Result窗口中出现{X},写入所施加的载荷函数:1000*{X};3) File>Save(文件扩展名:func) →返回:Parameters→Functions →Read from file:将需要的.func文件打开,任给一个参数名,它表示随之将施加的载荷→OK →ANSYS Main Menu: Solution→Define Loads →Apply→Structural →Pressure →On Lines →拾取斜边;OK →在下拉列表框中,选择:Existing table →OK →选择需要的载荷参数名→OK2.8 分析计算ANSYS Main Menu: Solution →Solve →Current LS→OK(to close the solve Current Load Step window) →OK2.9 结果显示ANSYS Main Menu: General Postproc →Plot Results→Deformed Shape…→select Def + Undeformed→OK (back to Plot Results window)→Contour Plot→Nodal Solu…→select: DOF solution, UX,UY, Def + Undeformed , Stress ,SX,SY,SZ, Def + Undeformed→OK2.10 退出系统ANSYS Utility Menu: File→Exit…→Save Everything→OK大作业试题1:图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(注意ANSYS中用四边形单元退化为三节点三角形单元)2)分别采用不同数量的三节点常应变单元计算;3)当选常应变三角单元时,分别采用不同划分方案计算。