有限元大作业
- 格式:doc
- 大小:95.50 KB
- 文档页数:3

1.题目概况
矩形板尺寸如下图1,板厚为5mm。
材料弹性模量为
松比μ= 0.27 。
施加约束和载荷并讨论:
图
1 计算简图
1.1基本数据
E = 2⨯105N/mm2,泊
序号载荷约束备注42 向下集中载荷F=800N, 作用于cd 边3/4 处(近d) c d 点简支
1.2分析任务/分析工况
讨论板上开孔、切槽等对于应力分布的影响。
(载荷约束组合不变)。
提示:各种圆孔,椭圆孔随大小、形状、数量,分布位置变化引起的应力分布变化;各种形状,大小的切槽及不同位置引起应力分布的变化等,选择二至三种情况讨论,并思考其与机械零部件的构型的相对应关系。
2.模型建立
2.1单元选择及其分析
由于平板长宽分别为300x100,故可取网格单元大小为1。
如图:
2.2模型建立及网格划分
模型按单元为1 划分后的网格大小如图所示:
2.3载荷处理
向下集中载荷F=800N, 作用于cd 边3/4 处(近d) c d 点简支
3.计算分析
3.1位移分布及其分析
(1)位移分布如图:。
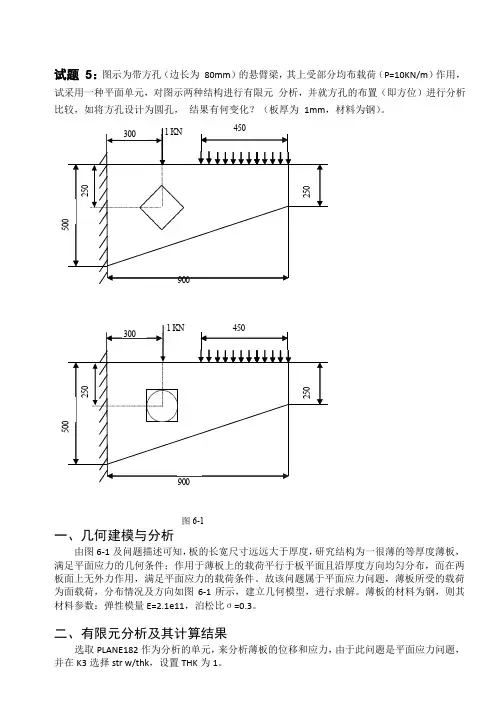
250250试题 5:图示为带方孔(边长为 80mm )的悬臂梁,其上受部分均布载荷(P=10KN/m )作用,试采用一种平面单元,对图示两种结构进行有限元分析,并就方孔的布置(即方位)进行分析比较,如将方孔设计为圆孔,结果有何变化?(板厚为 1mm ,材料为钢)。
3001KN9003001KN图6-1一、几何建模与分析由图6-1及问题描述可知,板的长宽尺寸远远大于厚度,研究结构为一很薄的等厚度薄板,满足平面应力的几何条件;作用于薄板上的载荷平行于板平面且沿厚度方向均匀分布,而在两板面上无外力作用,满足平面应力的载荷条件。
故该问题属于平面应力问题,薄板所受的载荷为面载荷,分布情况及方向如图6-1所示,建立几何模型,进行求解。
薄板的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3。
二、有限元分析及其计算结果选取PLANE182作为分析的单元,来分析薄板的位移和应力,由于此问题是平面应力问题,并在K3选择str w/thk ,设置THK 为1。
1)方孔竖直制,划分方式采用自由方式,划分后网格的模型如图6-2所示。
计算得到的位移和应力分布如图6-3所示。
图6-2 方孔竖直的网格划分图6-3 位移及应力分布云图2)方孔正直制,划分方式采用自由方式,划分后网格的模型如图6-4所示。
计算得到的位移和应力分布如图6-5所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图3)圆孔按图6-1所示模型进行建模。
并用PLANE182单元进行划分网格,网格大小采用全局网格控制,划分方式采用自由方式,划分后网格的模型如图6-6所示。
计算得到的位移和应力分布如图6-7所示。
图6-4 方孔正直的网格划分图6-5 位移及应力分布云图根据以上的模型分析的位移和应力图,可以得出方孔竖直、方孔正直、圆孔的最大最小位移应力的分布如表6-1所示。
三、比较与分析1)方孔竖直与方孔正直的比较,发现方孔正直的位移变形较小,应力相差不大2)圆孔与方孔比较,发现圆孔的位移变性最小,应力也最小,故可以得出圆孔的布置结构对整体布置的效果最好。

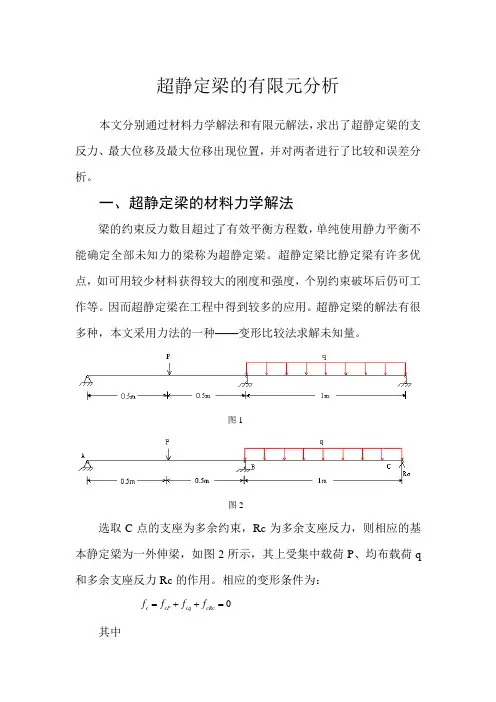
超静定梁的有限元分析本文分别通过材料力学解法和有限元解法,求出了超静定梁的支反力、最大位移及最大位移出现位置,并对两者进行了比较和误差分析。
一、超静定梁的材料力学解法梁的约束反力数目超过了有效平衡方程数,单纯使用静力平衡不能确定全部未知力的梁称为超静定梁。
超静定梁比静定梁有许多优点,如可用较少材料获得较大的刚度和强度,个别约束破坏后仍可工作等。
因而超静定梁在工程中得到较多的应用。
超静定梁的解法有很多种,本文采用力法的一种——变形比较法求解未知量。
图1图2选取C 点的支座为多余约束,Rc 为多余支座反力,则相应的基本静定梁为一外伸梁,如图2所示,其上受集中载荷P 、均布载荷q 和多余支座反力Rc 的作用。
相应的变形条件为:c cP cq cRc f f f f =++=其中316cP B Pl f l EI θ=⨯= 4724cq ql f EI =-323c cRc R l f EI =则316Pl EI 4724ql EI -+323c R l EI=0 将已知数据带入可求得 6.25c R =- 负号表示c R 的方向与假设的方向相反。
再列出平衡方程:0X =∑AX R =0A M =∑ 232022B C ql Pl R l R l ---=0C M =∑ 232022AY B ql PllR R l +--=带入已知条件求得:AX R = 393.75AY R = 812.5B R =用叠加法求最大位移:最大的向下位移在A 与B 两点中间:334410.7910481632C R l Pl ql f EI EI EI -=-++=-⨯最大的向上位移在B 与C 两点中间:3344213490.22525103248512C R l Pl ql f EI EI -=--=⨯二、超静定梁的有限元解法在ANSYS 平台上,求解超静定梁。
建模、单元划分、加载后结果如图3所示。
图3求解后可以通过图形和列表两种方式查看结果。
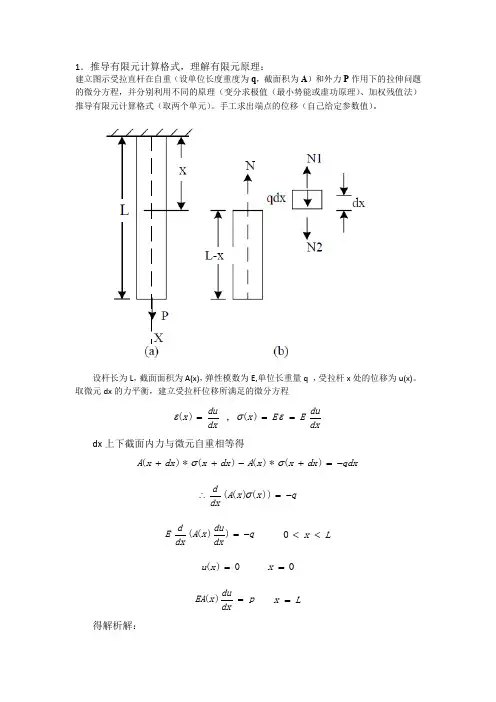
1.推导有限元计算格式,理解有限元原理:建立图示受拉直杆在自重(设单位长度重度为q ,截面积为A )和外力P 作用下的拉伸问题的微分方程,并分别利用不同的原理(变分求极值(最小势能或虚功原理)、加权残值法)推导有限元计算格式(取两个单元)。
手工求出端点的位移(自己给定参数值)。
设杆长为L ,截面面积为A(x),弹性模数为E,单位长重量q ,受拉杆x 处的位移为u(x)。
取微元dx 的力平衡,建立受拉杆位移所满足的微分方程()du x dx ε=,()du x E E dxσε== dx 上下截面内力与微元自重相等得()*()()*()A x dx x dx A x x dx qdx σσ++-+=-(()())dA x x q dxσ∴=- (())d duEA x q dx dx=- 0x L << ()0u x = 0x =()duEA x p dx= x L = 得解析解:2()2q x P u Lx x EA EA=-+将其分为两个单元,节点为1,2,3,得22382qL PL u EA EA=+232qL PL u EA EA=+有限元法:1)位移函数01u α= 2111u u l α-=得1211(1)x x u u u l l =-+ 令11(1)x N l =-21x N l = 11122122u u N u N u N N u⎧⎫⎪⎪⎡⎤=+=⎨⎬⎣⎦⎪⎪⎩⎭{}1u N d ⎡⎤=⎣⎦ 2)应变、应力表达{}{}111211du dN d d dx dx l l ε⎡⎤⎡⎤===-⎢⎥⎣⎦⎣⎦{}1B d ε⎡⎤=⎣⎦ {}1E E B d σε⎡⎤==⎣⎦ {}1S d σ⎡⎤=⎣⎦3)势能表示{}{}(){}{}(){}{}{}{}{}1111''112211''121112210111111111111111121221222T V ll T T T T T U W D dV F u F u qdx u u d B E d Adx F u F u ql EA EA ql l l d d d F d EA EA ql l l εε⎡⎤=-=-+-⎣⎦+⎡⎤=-+-⎣⎦⎡⎤⎡⎤-⎢⎥⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦⎢⎥⎣⎦∏⎰⎰⎰4)单元平衡方程 a)最小势能原理110u ∂=∂∏120u ∂=∂∏111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭b)虚位移原理{}(){}(){}TeTdd F qdx d δδδεσΩ+=Ω⎰⎰{}{}1B d σεδ⎡⎤=⎣⎦ {}1E E B d σεδ⎡⎤==⎣⎦{}(){}{}(){}111111TTT l d F d B E B d Adxδδ⎡⎤=⎣⎦⎰ 由虚位移任意性得,{}{}1111T lF B E B Adxd ⎡⎤=⎣⎦⎰ 积分得111111212112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭ 记为{}{}111k d F ⎡⎤=⎣⎦ 同理222212323112112ql F u AE l u ql F ⎧⎫-⎪⎪⎧⎫⎡⎤-⎪⎪⎪⎪=⎨⎬⎨⎬⎢⎥-⎣⎦⎪⎪⎪⎪⎩⎭+⎪⎪⎩⎭{}{}222k d F ⎡⎤=⎣⎦ {}{}ei i eF R =∑ 12220F F += 23F P =11111112211223222022202EAEAql F l l u ql ql EA EA EA EA u l l l l u ql EAEA P l l ⎡⎤⎧⎫-⎢⎥+⎪⎪⎢⎥⎧⎫⎪⎪⎢⎥⎪⎪⎪⎪⎢-+-⎥=+⎨⎬⎨⎬⎢⎥⎪⎪⎪⎪⎢⎥⎩⎭⎪⎪+⎢⎥⎪⎪--⎢⎥⎩⎭⎣⎦可得:22382qL PLu EA EA=+232qL PL u EA EA=+与解析解结果一致。

有限元分析大作业报告一、引言有限元分析是工程领域中常用的数值模拟方法,通过将连续的物理问题离散为有限个子区域,然后利用数学方法求解,最终得到数值解。
有限元分析的快速发展和广泛应用,为工程领域提供了一种强大的工具。
本报告将介绍在大作业中所进行的有限元分析工作及结果。
二、有限元模型建立本次大作业的研究对象是工程结构的应力分析。
首先,通过对结构进行几何建模,确定了结构的尺寸和形状。
然后,将结构离散为有限个单元,每个单元又可以看作一个小的子区域。
接下来,为了求解结构的应力分布,需要为每个单元确定适当的单元类型和单元属性。
最后,根据结构的边界条件,建立整个有限元模型。
三、材料属性和加载条件在建立有限元模型的过程中,需要为材料和加载条件确定适当的参数。
本次大作业中,通过实验获得了结构材料的弹性模量、泊松比等参数,并将其输入到有限元模型中。
对于加载条件,我们选取了其中一种常见的加载方式,并将其施加到有限元模型中。
四、数值计算和结果分析为了求解结构的应力分布,需要进行数值计算。
在本次大作业中,我们选用了一种常见的有限元求解器进行计算。
通过输入模型的几何形状、材料属性和加载条件,求解器可以根据有限元方法进行计算,并得到结构的应力分布。
最后,我们通过对计算结果进行分析,得出了结论。
五、结果讨论和改进方法根据计算结果,我们可以对结构的应力分布进行分析和讨论。
根据分析结果,我们可以得出结论是否满足设计要求以及结构的强度情况。
同时,根据分析结果,我们还可以提出改进方法,针对结构的特点和问题进行相应的优化设计。
六、结论通过对工程结构进行有限元分析,我们得到了结构的应力分布,并根据分析结果进行了讨论和改进方法的提出。
有限元分析为工程领域提供了一种有效的数值模拟方法,可以帮助工程师进行结构设计和分析工作,提高设计效率和设计质量。
【1】XXX,XXXX。
【2】XXX,XXXX。
以上是本次大作业的有限元分析报告,总结了在建立有限元模型、确定材料属性和加载条件、数值计算和结果分析等方面的工作,并对计算结果进行讨论和改进方法的提出。

有限元大作业一题目要求:图1所示为一悬臂梁,在端部承受载荷,材料弹性模量为E,泊松比为1/3,悬臂梁的厚度(板厚)为t,若该粱被划分为两个单元,单元和节点编号如图所示,试按平面应力问题计算各个节点位移计支反力。
一、单元划分1.计算简图及单元划分如下所示:2.进行节点及单元编号节点i j m单元① 2 3 4② 3 2 13.节点坐标值节点号1 2 3 4坐标值X 2 2 0 0Y 1 0 1 0二、计算单元刚度矩阵1、计算每个单元面积△以及i b ,i c (m j i i ,,=) ①②单元的面积相等,即12121=⨯⨯=∆ 单元①的i b ,i c⎩⎨⎧=--==-=0)(1m j i m j i y x c y y b ⎩⎨⎧=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧-=--=-=-=2)(1j i mj i m y x c y y b 对平面应力问题,其表达式为[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-+-+-+-+∆-=s r s r sr s r s r s r s r s r b b uc c cb u b uc b c u c ub c c u b b u Et Krs 21212121)1(42 然后对单元①求解单元刚度子矩阵2==i r 2==i s []⎥⎦⎤⎢⎣⎡=3/1001329)1(22Et K 2==i r 3==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(23Et K2==i r 4==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(24Et K 3==j r 3==j s []⎥⎦⎤⎢⎣⎡=4003/4329)1(33Et K 3==j r 2==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)1(32Et K 3==j r 4==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(34Et K 4==m r 4==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)1(44Et K 4==m r 2==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)1(42Et K 4==m r 3==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)1(43Et K由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)1(Et K将单元①的单元刚度矩阵补零升阶变为单元刚度矩阵,其在总体刚度矩阵中的位置为:节点号→单元②的i b ,i c⎩⎨⎧=--=-=-=0)(1m j im j i y x c y y b ⎩⎨⎧-=--==-=2)(0i m ji m j x x c y y b ⎩⎨⎧=--==-=2)(1j i mj i m y x c y y b 然后对单元 求解单元刚度子矩阵:3==i r 3==i s []⎥⎦⎤⎢⎣⎡=3/1001329)2(33Et K 3==i r 2==j s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(32Et K 3==i r 1==m s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(31Et K 1 2 3 412[])1(22K[])1(23K[])1(24K3[])1(32K[])1(33K[])1(34K4[])1(42K[])1(43K[])1(44K2==j r 2==j s []⎥⎦⎤⎢⎣⎡=4003/4329)2(22Et K 2==j r 3==i s []⎥⎦⎤⎢⎣⎡=03/23/20329)2(23Et K 2==j r 1==m s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(21Et K 1==m r 1==m s []⎥⎦⎤⎢⎣⎡=3/133/43/43/7329)2(11Et K 1==m r 3==i s []⎥⎦⎤⎢⎣⎡----=3/13/23/21329)2(13Et K 1==m r 2==j s []⎥⎦⎤⎢⎣⎡----=43/23/23/4329)2(12Et K 由子矩阵[]e rs K 合成单元刚度矩阵[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡----------------=3/133/443/23/13/23/43/73/23/43/2143/24003/23/23/403/43/203/13/203/23/103/213/2001329)2(Et K将单元②的单元刚度矩阵补零升阶变为单元贡献矩阵,其在总体刚度矩阵中的位置为:节点号→1 2 3 41 [])2(11K[])2(12K[])2(13K2 [])2(21K[])2(22K[])2(23K3 [])2(31K [])2(32K [])2(33K 4三、计算总体刚度矩阵总体刚度矩阵是由各单元的贡献矩阵迭加而成)2()1(][][][][K K K K e +==∑四、进行节点约束处理根据节点约束情况,在总刚矩阵中可采用划行划列处理约束的方法,由题目易知,节点3和4的已知水平位移和垂直位移都为零,划去其相对应的行和列,则总刚矩阵由8阶变为4阶,矩阵如下:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------2/02/03/13043/203/73/23/443/23/133/43/23/43/43/73292211p p v u v u Et329][Et K =1 2 3 413/133/43/43/743/23/23/4----3/13/23/21----000243/23/23/4----3/13003/73/43/403/13/23/21----33/13/23/21----3/43/403/13003/743/23/23/4----40003/13/23/21----43/23/23/4----3/133/43/43/7化简⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------Et p Et p v u v u 3/1603/160130122072412213424472211 五、求解线性方程组方法:采用LU 分解法 1.求解矩阵[]U 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡------⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------75/10775/640075/6475/353007/767/27/7502447~7/877/87/7607/87/337/207/767/27/7502447~13012207241221342447⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----353/44900075/6475/353007/767/27/7502447~ 得到的[]U 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=353/44900075/6475/353007/767/27/7502447U 2.求解矩阵[]L 各元素⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----13012207241221342447353/44900075/6475/353007/767/27/75024471353/6475/767/20175/27/40017/40001 得到的[]L 矩阵如下:[]⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------=13012207241221342447L3.进行求解⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⇒⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧--=Et p Et p Et p y Et p Et p Ly 79425/850800225/323/1603/1603/160⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧---=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----⇒=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡Et p Et p Et p v u v u y v u v u U 79425/850800225/323/160353/44900075/6475/353007/7675/27/750244722112211 解得Et p v /422.82-= Et p u /497.12-= Et p v /028.91-= Et p u /897.11=于是求得各节点的位移为:⎩⎨⎧-==Etp v Etp u /028.9/897.111 ⎩⎨⎧-=-=Etp v Etp u /422.8/497.122 ⎩⎨⎧==033v u ⎩⎨⎧==044v u 六、求解相应的支反力(运用静力学的平衡方程进行求解)3号节点和4号节点的支反力如下图所示:。

有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences 为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB和lineBC,设定input NDIV 为15;拾取lineAC,设定input NDIV 为20,选择网格划分方式为Tri+Mapped,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。

《有限元分析及应用》大作业——齿根弯曲应力计算报告班级:无可奉告姓名:无可奉告学号:无可奉告指导老师:无可奉告目录目录 (2)1.概述 (3)1.1工程问题描述 (3)1.2问题分析 (3)2.建模过程 (4)2.1几何建模 (4)2.2CAE网格划分与计算 (5)2.3后处理 (8)3.多方案比较与结果分析 (9)3.1多方案比较 (9)3.2结果分析 (11)1.概述1.1工程问题描述我在本次作业中的选题为齿根弯曲应力的计算与校核。
通过对机械设计的学习,我们可以知道,齿轮的失效形式主要是齿面接触疲劳和齿根弯曲断裂,而闭式传动硬齿面齿轮的失效形式以齿根弯曲断裂,这个时候进行齿根弯曲应力的校核才比较有意义,在设计问题的时候应当选取这种类型的算例。
设计计算的另一个主要思路是将有限元计算的结果与传统机械设计的结算结果进行对比,以从多方面验证计算结果的准确性。
综上,我们最终选取了《机械原理》(第三版)P50例3-1中的问题进行校核计算。
已知起重机械用的一对闭式直齿圆柱齿轮,传动,输入转速n1=730r/min,输入功率P1=35kW,每天工作16小时,使用寿命5年,齿轮为非对称布置,轴的刚性较大,原动机为电动机,工作机载荷为中等冲击。
z1=29,z2=129,m=2.5mm,b1=48mm,b2=42mm,大、小齿轮均为20CrMnTi,渗碳淬火,齿面硬度为58~62HRC,齿轮精度为7级,试验算齿轮强度。
齿面为硬齿面,传动方式为闭式传动。
根据设计手册查出的许用接触应力为1363.6Mpa,计算结果为1260Mpa,强度合格。
根据设计手册查出的许用弯曲应力为613.3MPa,计算结果为619Mpa,强度略显不够。
1.2问题分析大小齿轮啮合,小齿轮受载荷情况较为严峻,故分析对象应当为小齿轮。
可以看出,由于齿轮单侧受载荷,传动过程中每个齿上载荷的变化过程是相同的,故问题可被简化为反对称问题,仅需研究单个齿。

《有限元分析》大作业基本要求:1.以小组为单位完成有限元分析计算,并将计算结果上交;2.以小组为单位撰写计算分析报告;3.按下列模板格式完成分析报告;4.计算结果要求提交电子版,报告要求提交电子版和纸质版。
《有限元分析》大作业小组成员:Job name:完成日期:一、问题描述(要求:应结合图对问题进行详细描述,同时应清楚阐述所研究问题的受力状况和约束情况。
图应清楚、明晰,且有必要的尺寸数据。
)二、数学模型(要求:针对问题描述给出相应的数学模型,应包含示意图,示意图中应有必要的尺寸数据;如进行了简化等处理,此处还应给出文字说明。
)三、有限元建模3.1 单元选择(要求:给出单元类型,并结合图对单元类型进行必要阐述,包括节点、自由度、实常数等。
)3.2 实常数(要求:给出实常数的具体数值,如无需定义实常数,需明确指出对于本问题选择的单元类型,无需定义实常数。
)3.3 材料模型(要求:指出选择的材料模型,包括必要的参数数据。
)3.4 网格划分方案(要求:指出网格划分方法,网格控制参数,最终生成的单元总数和节点总数,此外还应附上最终划分好的网格截图。
)3.5 载荷及边界条件处理(要求:指出约束条件和载荷条件。
)四、计算结果及结果分析(要求:此处包括位移分析、应力分析、支反力分析等,应附上相应截图及数据,此外还应对正确性进行分析评判。
)五、多方案计算比较(要求:节点规模增减对计算精度的影响分析、单元改变对计算精度的影响分析、不同网格划分方案对计算结果的影响分析等,至少应选择其一进行分析,此外还应附上相应截图及数据。
)附件1:小组成员工作说明(要求:明确说明小组各个成员在本次大作业中所做的工作,工作内容将作为口试提问的依据之一,同时也作为成绩评定的依据之一。
需注意,附件1的撰写应由小组成员共同完成。
)附件2:详细的计算过程说明(按照上机指导的格式撰写)。
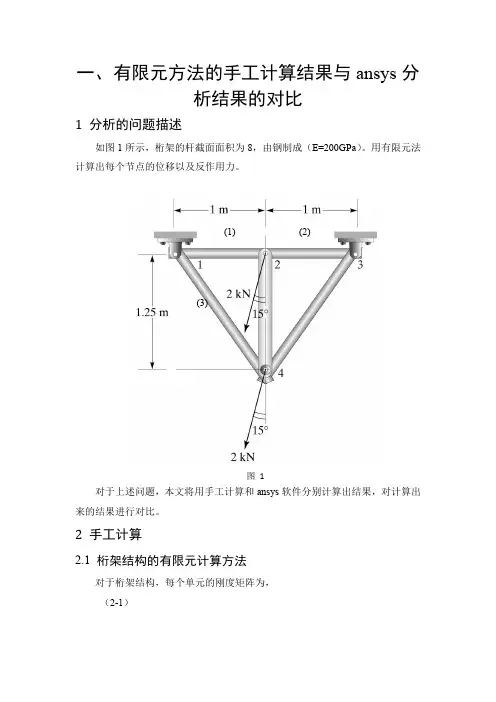
一、有限元方法的手工计算结果与ansys分析结果的对比1分析的问题描述如图1所示,桁架的杆截面面积为8,由钢制成(E=200GPa)。
用有限元法计算出每个节点的位移以及反作用力。
(1)(2)(3)图1对于上述问题,本文将用手工计算和ansys软件分别计算出结果,对计算出来的结果进行对比。
2手工计算2.1桁架结构的有限元计算方法对于桁架结构,每个单元的刚度矩阵为,(2-1)YX图2其中,为桁架单元在整体坐标系中与X轴的夹角;,A为桁架的截面积,E 为弹性模量,L为桁架长度。
在固体力学问题中,有限元公式通常由如下的一般形式,Ku=F(2-2)其中,K为刚度矩阵,u为位移矩阵,F为载荷矩阵。
运用公式(2-3),就能求出反作用力,R=Ku-F(2-3)其中,R为反作用力矩阵。
2.2计算过程计算每个桁架单元的刚度,用公式(2-1)计算每个每个桁架单元的刚度矩阵,将每个单元放入总刚度矩阵,他们的位置分别为:10-100000 00000000 -10100000 00000000 00000000 00000000 00000000 0000000000000000 00000000 0010-1000 0000000000-101000 00000000 00000000 000000003.9-4.90000-3.9 4.9-4.9 6.10000 4.9-6.1 00000000 00000000 00000000 00000000-3.9 4.90000 3.9-4.9 4.9-6.10000-4.9 6.100000000 00000000 00000000 000 1.28000-1.28 00000000 00000000 00000000 000-1.28000 1.2800000000 00000000 00000000 00000000 0000 3.9 4.9-3.9-4.9 0000 4.9 6.1-4.9-6.1 0000-3.9-4.9 3.9 4.9 0000-4.9-6.1 4.9 6.1将个刚度矩阵相加得到总刚度矩阵为,19.9-4.90-16000-3.9 4.9 -4.9 6.100000 4.9-6.1 -160320-16000 00012.8000-12.8 00-16019.9 4.9-3.9-4.9 0000 4.9 6.1-4.9-6.1 -3.9 4.900-3.9-4.97.80 4.9-6.10-12.8-4.9-6.1025应用边界条件施加载荷,将总刚度矩阵带入式(2-2)得:19.9-4.90-16000-3.9 4.9Ux1 -4.9 6.100000 4.9-6.1Uy1 -160320-16000Ux2 00012.8000-12.8Uy200-16019.9 4.9-3.9-4.9Ux3 0000 4.9 6.1-4.9-6.1Uy3 -3.9 4.900-3.9-4.97.80Ux4 4.9-6.10-12.8-4.9-6.1025Uy4带入边界条件解得:将结果带入(2-3)得:=Fx1Fy1Fx2Fy2Fx3Fy3Fx4Fy43用ansys软件求解(单位统一N,mm,Mpa)(1)选择单元(图3)图3(2)附材料属性(图4)图4(3)创建模型(图5)图5(4)施加载荷(图6)图6(5)求解每个节点的位移(图7)图7节点的反力(图8)图8(6)模型变形图(7)位移等值线分布图4结果对比及分析手算结果ansys 计算结果位移(mm)Ux100Uy100Ux2-0.0016-0.0016Uy2-0.0468-0.0468Ux300Uy300Ux4-0.0066-0.0066Uy4-0.0317-0.0317表1手算结果ansys计算结果节点反力(N)Fx1-1027.8-1027.8 Fy11608.31608.3 Fx2 5.60 Fy2-100 Fx32066.72063.1 Fy32257.12255.4 Fx48.80 Fy4-2.70表2由表1和表2可以看出,手工计算的结果与ansys计算的结果基本一致。
一、试题一1、问题描述图示无限长刚性地基上的三角形大坝,受齐顶的水压力,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下集中方案进行比较:1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;2)分别采用不同数量的三节点常应变单元计算;3)当选常应变三角形单元时,分别采用不同划分方案计算。
图 1.12、数学建模及有限元建模2.1数学建模将无限长的三维问题转化为二维问题,取出大坝的一个截面,建立模型如图2.1.1所示,图 2.1.12.2单元选择分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算,分别采用不同数量的三节点常应变单元计算,当选常应变三角形单元时,分别采用不同划分方案计算。
由于是平面应力问题,故Element Behavior K3选择Plane stress。
E=210Gpa,u=0.3。
2.3网格划分按照题意,采用不同数量的三节点常应变单元计算,划分具体的方案见第三部分计算结果。
2.4载荷及边界条件处理边界条件:底端将X,Y方向全约束。
载荷:由于水的压强是随着深度越来越大的P=密度*重力加速度*深度,故对大坝的梯梯形面施加载荷Result = 9800*(10-{Y})3、计算结果及结果分析3.1三节点常应变单元网格划分及结果图 1.3.1.1 图 1.3.1.2图 1.3.1.3 图1.3.1.4 由图可知:DMX=0.143E-4MSMN=49520PASMX=150581PA3.2六节点常应变单元网格划分及结果图1.3.2.1 图 1.3.2.2图 1.3.2.3 图 1.3.2.4由图可知:DMX=0.264E-4MSMN=1893PASMX=306986PA3.3三节点常应变单元网格划分及结果(24个单元)图 1.3.3.1 图 1.3.3.2图 1.3.3.3 图 1.3.3.4由图可知:DMX=0.203E-4MSMN=24617PASMX=199290PA3.4三节点常应变单元网格划分及结果(48个单元)图 1.3.4.1 图 1.3.4.2图 1.3.4.3 图 1.3.4.4由图可知:DMX=0.228E-4MSMN=16409PASMX=243234PA3.5三节点划分方案A图 1.3.5.1 图 1.3.5.2图 1.3.5.3 图 1.3.5.4由图可知:DMX=0.106E-4MSMN=50110PASMX=18194PA3.6三节点划分方案B图 1.3.6.1 图 1.3.6.2图 1.3.6.3 图 1.3.6.44、多方案分析比较4.1相同数目三节点和六节点单元比较DMX(mm) SMN(pa)SMX(pa) 方案数值三节点三角形单元0.143E-4 49520 150581六节点三角形单元0.264E-4 1893 306986表 1.4.1结论:相同的单元划分方案和单元规模,采用不同的阶次的相同形状的单元,分析结果不同。
金属坯料挤压过程有限元分析一、前言:金属挤压是将放在挤压模具内的金属锭坯从一端施加外力,强迫其从特定的模孔中流出,获得所需要的断面形状和尺寸的制品的技术。
冷挤压时由于材料是在冷态下成形,而且变形量一般都很大,挤压过程中作用在模具上的单位压力很大,此时模具有开裂破坏的可能,对压力机也构成威胁,金属坯料在通过模具过程中,坯料与模具之间产生相当大的应力,这就要求模具需要有相当大的强度、硬度、以及耐磨性,因此冷挤压时要进行挤压力的计算。
挤压力的计算是模具设计的重要依据,也是选择挤压设备的依据。
模具角度、接触表面的摩擦系数、坯料变形量都会影响应力变化,在保证加工要求的前提下,应当通过适当方式降低坯料及模具之间的应力。
通过有限元分析,得出应力分布图,分析变形区域、死区,对模具进行优化改进。
二、有限元介绍:ANSYS概述ANSYS软件是融结构、热、流体、电磁、声学于一体的大型通用有限元软件,可广泛地用于核工业、铁道、石油化工、航空航天、机械制造、能源、汽车交通、国防军工、电子、土木工程、生物医学、水利、日用家电等一般工业及科学研究。
该软件提供了不断改进的功能清单,具体包括:结构高度非线性分析、电磁分析、计算流体力学分析、设计优化、接触分析、自适应网格划分及利用ANSYS参数设计语言扩展宏命令功能。
ANSYS软件功能强大,主要特点有:实现多场及多场耦合分析;实现前后处理、求解及多场分析统一数据库的一体化;具有多物理场优化功能;强大的非线性分析功能;多种求解器分别适用于不同的问题及不同的硬件设备;支持异种、异构平台的网络浮动,在异种、异构平台上用户界面统一、数据文件全部兼容;强大的并行计算功能支持分布式并行及共享内存式并行;多种自动网格划分技术;良好的用户开发环境。
ANSYS不仅支持用户直接创建模型,也支持与其他CAD软件进行图形传递,其支持的图形传递有:SAT、Parasolid、STEP。
相应地,可以进行接口的常用CAD 软件有:Unigraphics、Pro/Engineer、I-Deas、Catia、CADDS、SolidEdge、SolidWorks等。
有限元分析技术课程大作业1 工程介绍现需要对某露天大型玻璃平面舞台的钢结构进行分析,该钢结构布置在xy 平面内。
学生序号为079,分格的列数(x向分格)=0×10+7+5=12,分格的行数(y向分格)=9+4=13,共有156个分格。
每个分格x方向尺寸为1m,y方向尺寸为1m。
钢结构的主梁为高160宽100厚14的方钢管;次梁为直径60厚10的圆钢管(单位为毫米),材料均为碳素结构钢Q235;该结构固定支撑点位于左右两端主梁和最中间的次梁的两端。
玻璃采用四点支撑与钢结构连接(采用四点支撑表明垂直作用于玻璃平面的面载荷将传递作用于玻璃所在钢结构分格四周的节点处,表现为点载荷;试对在垂直于玻璃平面方向的22/KN m的面载荷(包括玻璃自重、钢结构自重、活载荷(人员与演出器械载荷)、风载荷等)作用下的舞台进行有限元分析(每分格面载荷对于每一支撑点的载荷可等效于0.5KN的点载荷)。
作业提交的内容:(1)屏幕截图显示该结构的平面布置结构;(2)该结构每个支座的支座反力;(3)该结构节点的最大位移及其所在位置;(4)对该结构中最危险单元(杆件)进行强度校核。
2有限元模型的建立该钢结构中每一分格x方向尺寸为1m,y方向尺寸为1m,x方向分格数量为12,y方向分格数量为13。
该钢结构由主梁和次梁构成,其中主梁为高160mm、宽100mm、厚14mm的方钢管,次梁为直径60mm、厚10mm的圆钢管。
由于在该结构中所有构件均为梁单元,而Ansys程序中提供了多种梁单元,以模拟不同场合的应用,且对于每种梁单元类型都有特定的算法。
在本次建模过程中,考虑到需要对该结构中的危险单元进行强度校核,因此,选择了BEAM188单元类型来建立本钢架结构,进而对其进行有限元分析。
BEAM188为三维线性有限应变梁单元,该单元基于铁木辛哥的梁结构理论,考虑了剪切变形的影响,能够满足本次分析的需求。
以下为基于ANSYS图形界面(Graphic User Interface , GUI)的菜单操作流程(1) 进入ANSYS(设定工作目录和工作文件)程序→ ANSYS → ANSYS Interactive → Working directory(设置工作目录)→Initial Jobname(设置工作文件名):Analysis → Run → OK(2) 设置计算类型ANSYS Main Menu:Preferences → Structural → OK(3) 定义单元类型ANSYS Main Menu:Preprocessor → Element Type → Add/Edit/Delete... → Add → Beam: 3D 2node 188 → OK(返回到Element Types窗口)→ Close(4) 定义材料参数ANSYS Main Menu: Preprocessor → Material Props → Material Models → Structural → Linear → Elastic → Isotropic → input EX: 2.0E5, PRXY: 0.3(定义泊松比及弹性模量) → OK → Close(关闭材料定义窗口)(5)定义梁单元截面ANSYS Main Menu:Preprocessor →Sections→Beam→Common Sections→Beam Tool(6) 构造梁模型生成舞台几何模型ANSYS Main Menu:Preprocessor → Modeling → Create → Keypoints → In Active CS → NPT Keypoint number:1,X,Y,Z Location in active CS:0,0,0 → Apply 通过复制关键点操作,形成14行13列的关键点。
有限元分析及应用作业报告试题10一、问题描述确定图示扳手中的应力, E=210Gpa,μ=0.3, 假设厚度为10mm;并讨论采用何种处理可降低最大应力或改善应力分布。
图1为扳手的基本形状和基本尺寸图二、数学建模与分析由图1及问题描述可知,板手的长宽尺寸远远大于厚度,研究结构为一很薄的等厚度薄板,满足平面应力的几何条件;作用于薄板上的载荷平行于板平面且作用在沿厚度方向均匀分布在办手柄的左边缘线,而在两板面上无外力作用,满足平面应力的载荷条件。
故该问题属于平面应力问题,薄板所受的载荷为面载荷,分布情况及方向如图1所示,建立几何模型,并进行求解。
薄板的材料为钢,则其材料参数:弹性模量E=2.1e11,泊松比σ=0.3三、有限元建模1、单元选择:选取三节点常应变单元来计算分析薄板扳手的位移和应力。
由于此问题为平面应力问题,:三节点常应变单元选择的类型是PLANE42(Quad 4node42),该单元属于是四节点单元类型,在网格划分时可以对节点数目控制使其蜕化为三节点单元。
2、定义材料参数:ANSYS Main Menu: Preprocessor →Material Props →Material Models →Structural →Linear →Elastic →Isotropic →input EX:2.1e11, PRXY:0.3 →OK3、生成几何模型:a.创建关键点点:ANSYS Main Menu: Preprocessor →Modeling →Create →Keypoints →In Active CS →依次输入16个点的坐标→OKb、将这16个关键点有直线依次连起来,成为线性模型4、生成实体模型:ANSYS Main Menu: Preprocessor →Modeling →Create →Areas →Arbitrary →Through KPS →连接特征点→生成两个area→Operate→Subtract→拾取整个扳手区域→OK→生成扳手模型5、结点布置及规模6、网格划分方案ANSYS Main Menu: Preprocessor →Meshing →Mesh Tool →Mesh: Areas, Shape: Tri,Free →Mesh →Pick All (in Picking Menu) →Close( the Mesh Tool window)7、载荷及边界条件处理8、求解控制A、模型施加约束给模型施加x方向约束ANSYS Main Menu: Solution →Define Loads →Apply →Structural →Displacement →On Lines →拾取模型左部的竖直边→OKB、给模型施加载荷ANSYS Main Menu: Solution →Define Loads →Apply →Structural →force→on keypoints→拾取上面左端关键点→700N/mm→okC、分析计算:ANSYS Main Menu: Solution →Solve →Current LS →OK(to close the solve Current Load Step window) →OK6)结果显示:ANSYS Main Menu: General Postproc →Plot Results →Deformed Shape… →select Def + Undeformed →OK (back to Plot Results window) →Contour Plot →Nodal Solu →select: DOF solution →displacement vector sum,von mises stress→OK四、计算结果及结果分析1、三节点常应变单元1)三节点单元的网格划分图2 常应变三节点单元的网格划分平面图图3 常应变三节点单元的网格划分立体图2)三节点单元的约束受载情况图4 常应变三节点单元的约束受载图3)三节点单元的位移分析图5 常应变三节点单元的位移分布图4)三节点单元的应力分析图6 常应变三节点单元的应力分布图2、六节点三角形单元1)六节点三角形单元网格划分图7 六节点三角形单元网格划分图2)六节点三角形单元约束和受载情况分析图8 六节点三角形单元约束受载图3)六节点三角形单元位移分析图9 六节点三角形单元的变形分布图4) 六节点三角形单元的应力分析图9 六节点三角形单元的应力分布图图10 六节点三角形单元的局部应力分布图根据以上位移和应力图,可以得出常应变三节点单元和六节点三角形单元的最小最大位移应力如表1-1所示。
有限元分析大作业报告试题1:一、问题描述及数学建模图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:(1)分别采用相同单元数目的三节点常应变单元和六节点三角形单元计算;(2)分别采用不同数量的三节点常应变单元计算;(3)当选常应变三角单元时,分别采用不同划分方案计算。
该问题属于平面应变问题,大坝所受的载荷为面载荷,分布情况及方向如图所示。
二、采用相同单元数目的三节点常应变单元和六节点三角形单元计算1、有限元建模(1)设置计算类型:两者因几何条件和载荷条件均满足平面应变问题,故均取Preferences为Structural(2)选择单元类型:三节点常应变单元选择的类型是Solid Quad 4 node182;六节点三角形单元选择的类型是Solid Quad 8 node183。
因研究的问题为平面应变问题,故对Element behavior(K3)设置为plane strain。
(3)定义材料参数:弹性模量E=2.1e11,泊松比σ=0.3(4)建几何模型:生成特征点;生成坝体截面(5)网格化分:划分网格时,拾取lineAB 和lineBC ,设定input NDIV 为15;拾取lineAC ,设定input NDIV 为20,选择网格划分方式为Tri+Mapped ,最后得到600个单元。
(6)模型施加约束:约束采用的是对底面BC 全约束。
大坝所受载荷形式为Pressure ,作用在AB 面上,分析时施加在L AB 上,方向水平向右,载荷大小沿L AB 由小到大均匀分布。
以B 为坐标原点,BA 方向为纵轴y ,则沿着y 方向的受力大小可表示为:}{*980098000)10(Y y g gh P -=-==ρρ2、 计算结果及结果分析 (1) 三节点常应变单元三节点常应变单元的位移分布图三节点常应变单元的应力分布图(2)六节点三角形单元六节点三角形单元的变形分布图六节点三角形单元的应力分布图(3)计算数据表单元类型最小位移(mm)最大位移(mm)最小应力(Pa)最大应力(Pa)三节点0 0.0284 5460.7 392364六节点0 0.0292 0.001385 607043 (4)结果分析①最大位移都发生在A点,即大坝顶端,最大应力发生在B点附近,即坝底和水的交界处,且整体应力和位移变化分布趋势相似,符合实际情况;②结果显示三节点和六节点单元分析出来的最大应力值相差较大,原因可能是B点产生了虚假应力,造成了最大应力值的不准确性。
有限元大作业第一篇:有限元大作业有限元应力分析报告大作业机械与运载工程学院车辆四班龙恒 20110402415 2014年8月30日一、问题描述桦木板凳材料参数如图形状参数:长40mm,宽30mm,高45mm(其他详细参数见零件图)通过施加垂直于板凳上表面的均匀载荷600N,分析板凳的应变和应力?二、使用inventor进行建模及应力分析1、通过inventor建立板凳3D模型利用草图拉伸等方法建立与零件图中尺寸一致的三维立体板凳模型2、点选环境下的应力分析开始对板凳进行应力分析3、根据所给条件设置材料等参数、将安全系数设为屈服强度,因为板凳主要受压变形点开“木材(桦木)”根据前面所给参数对其进行参数设置4、固定约束如图板凳的4个脚底面设置为固定约束,使得板凳受载后,脚底面不会沿垂直方向位移,模拟真实情况5、施加载荷在板凳上表面施加大小为600N的垂直均布载荷(这里是模拟一个成人坐上去的重力)6、划分网格通过设置网格的尺寸参数来划分出5种不同网格数量,从而得出5种不同网格数划分得出的应力应变分布图,最后分析划分不同网格数对结果的影响。
(1)网格最大(2)网格较大(3)网格一般大小(4)网格较小(5)网格最小7、求解得出结果得出5组不同网格数所得数据(应力云图,应变云图,所有结果数据)(1)网格数1437根据应力云图可知,红色地方所受的应力最大,最大应力为:15.48Mpa 根据应变云图可知,红色地方的应变最大,最大应变为:0.001434μl(2)网格数8651根据应力云图可知,红色地方所受的应力最大,最大应力为:18.88Mpa 根据应变云图可知,红色地方的应变最大,最大应变为:0.001755μl(3)网格数20484根据应力云图可知,红色地方所受的应力最大,最大应力为:22.62Mpa 根据应变云图可知,红色地方的应变最大,最大应变为:0.002103μl(4)网格数41578根据应力云图可知,红色地方所受的应力最大,最大应力为:23.76Mpa 根据应变云图可知,红色地方的应变最大,最大应变为:0.002206μl(5)网格数68788根据应力云图可知,红色地方所受的应力最大,最大应力为:25.97Mpa 根据应变云图可知,红色地方的应变最大,最大应变为:0.002454μl综合上述5种请况可知随着网格的细分,所得的应变以及应力的结果是收敛的。
有限元
计算分析报告学院:
班级:
姓名:
学号:
试题1:图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:
1.分别采用相同单元数目的三节点常应变单元和六节点三
角形单元计算;
2.采用不同数量的三节点常应变单元计算;
3.当选常应变三角单元时,分别采用不同划分方案计算。
6M
不同划分方案试例
求解过程如下:
一、问题描述及数学建模
无限长刚性地基上的三角形大坝受齐顶水压可看作一个平面问题,简化为平面三角形受力问题。
把无限长地基看成底边收固定支座约束,受力面简化成受均布载荷作用。
有限元建模选用Solid单元的4节点42以及8节
点82单元建模,材料为钢,弹性模量E=210Gpa,泊松比v=。
二、结果分析
1)分别采用相同单元数目的三节点常应变单元和
六节点三角形单元计算
有限元模型
三节点常应变单元(6节点,4单元)
变形图
几何模型图
节点位移图
节点应力图节点应变图。