正态总体参数估计
- 格式:pptx
- 大小:670.71 KB
- 文档页数:43

正态分布的基本特性和参数估计正态分布,也称为高斯分布,是统计学中最为重要的分布之一。
它具有许多独特的特性和应用,被广泛应用于各个领域的数据分析和建模中。
本文将介绍正态分布的基本特性,并探讨参数估计的方法。
一、正态分布的基本特性1. 对称性:正态分布是一种对称分布,其概率密度函数在均值处取得峰值,并向两侧逐渐减小。
这种对称性使得正态分布在实际应用中具有很大的优势,能够较好地描述许多自然现象和随机变量的分布。
2. 峰度和偏度:正态分布的峰度和偏度分别为3和0。
峰度反映了分布的尖锐程度,而偏度则反映了分布的对称性。
正态分布的峰度为3,表示其相对于均匀分布而言具有更为尖锐的峰值。
而偏度为0,表示其对称性较好,左右两侧的分布相似。
3. 68-95-99.7法则:正态分布具有一个重要的特性,即约68%的数据落在均值的一个标准差范围内,约95%的数据落在两个标准差范围内,约99.7%的数据落在三个标准差范围内。
这个法则在实际应用中非常有用,可以帮助我们对数据进行初步的分析和判断。
二、参数估计的方法在实际应用中,我们常常需要根据给定的样本数据来估计正态分布的参数,包括均值和标准差。
以下介绍两种常用的参数估计方法。
1. 极大似然估计:极大似然估计是一种常用的参数估计方法,其基本思想是找到最有可能使得观测到的样本数据出现的参数值。
对于正态分布,我们可以通过最大化似然函数来估计均值和标准差。
具体的计算方法可以使用数值优化算法,如梯度下降法等。
2. 方法 of moments:方法 of moments(矩估计)是另一种常用的参数估计方法,其基本思想是通过样本矩与理论矩的对应关系来估计参数。
对于正态分布,我们可以通过样本均值和样本方差来估计均值和标准差。
具体的计算方法比较简单,只需要求解一组方程即可。
三、正态分布的应用正态分布在实际应用中具有广泛的应用价值。
以下列举几个常见的应用场景。
1. 统计推断:正态分布是统计推断中的重要工具,它可以用来进行假设检验、置信区间估计等。



正态总体参数的区间估计实验结论正态总体参数的区间估计是统计学中一种常用的方法,可以帮助我们估计未知正态总体参数的取值范围。
通过构建置信区间,我们可以在一定的置信水平下对总体参数的取值范围进行估计。
以下是一个关于正态总体参数的区间估计实验结论。
在本实验中,我们以某个地区的成年人男性身高为研究对象,采集了一组样本数据。
通过对样本数据的分析和计算,得出了平均身高和标准差的估计值,并以此构建了置信区间。
首先,我们计算出了样本数据的均值为175cm,并且样本的标准差为5cm。
接下来,我们选择了一个置信水平为95%的置信区间进行计算。
根据正态分布的性质,我们可以使用标准正态分布表来确定置信区间的边界。
通过查表,我们找到了置信水平为95%对应的临界值,记为z。
在本实验中,z的取值为1.96。
然后,我们可以根据样本的均值、标准差和样本容量来计算置信区间的上限和下限。
置信区间的上限计算公式为:上限 = 均值 + z * (标准差/ √样本容量);置信区间的下限计算公式为:下限 = 均值 - z * (标准差/ √样本容量)。
根据实验数据的计算,最终得出了置信区间为(172.04cm,177.96cm)。
这意味着在95%的置信水平下,我们可以合理地推断该地区成年男性的平均身高位于该区间内。
这个实验结论具有以下几个指导意义。
首先,通过正态总体参数的区间估计,我们可以更准确地估计未知总体参数的取值范围,有助于我们了解总体的特征。
其次,通过选择合适的置信水平,我们可以控制估计结果的可靠性和精确度。
在本实验中,我们选择了95%的置信水平,意味着我们有95%的把握让估计结果覆盖真实总体参数。
最后,置信区间的上下限提供了关于总体参数范围的重要信息,可以用来支持决策和制定策略。
总之,正态总体参数的区间估计是一种重要的统计方法,可以为我们提供对未知总体参数取值范围的估计。
通过该方法,我们可以在一定的置信水平下对总体参数进行准确的估计,从而为实际问题的分析和决策提供科学依据。

正态总体参数的区间估计实验结论在统计学中,正态分布是一种非常重要的分布,许多自然现象和实验数据都可以用正态分布来描述。
而在实际应用中,我们常常需要估计正态总体的参数,比如均值和标准差。
在这篇文章中,我将介绍如何利用区间估计的方法来估计正态总体的参数,并给出一个实验结论。
让我们来回顾一下区间估计的基本原理。
区间估计是通过样本数据来估计总体参数的一种方法,其核心思想是利用样本数据给出一个参数的估计区间,该区间包含真实参数的概率较高。
在正态总体参数的区间估计中,我们通常使用样本均值和样本标准差来进行估计。
接下来,我将介绍一个实际的例子来说明正态总体参数的区间估计方法。
假设我们有一批产品的重量数据,我们想要估计这批产品的平均重量。
我们随机抽取了一部分产品进行称重,得到了样本均值和样本标准差。
根据中心极限定理,我们知道样本均值的分布是正态分布的,可以利用这一性质来构建参数的置信区间。
假设我们得到的样本均值为100,样本标准差为5,样本量为30。
我们可以利用正态分布的性质来构建样本均值的置信区间,假设置信水平为95%,那么我们可以计算出置信区间为(98, 102)。
这意味着在95%的置信水平下,真实的总体平均重量落在98到102之间。
通过这个简单的例子,我们可以看到区间估计的重要性和实际应用。
在实际问题中,我们往往无法得知总体参数的真实值,只能通过样本数据来进行估计。
区间估计可以帮助我们对参数的估计进行更准确的评估,同时也可以给出参数估计的不确定性范围。
总的来说,正态总体参数的区间估计是统计学中一种常用的方法,通过构建置信区间来估计总体参数的真实值。
在实际应用中,我们可以根据样本数据来进行参数的估计,同时也可以评估参数估计的置信水平。
通过区间估计的方法,我们可以更准确地了解总体参数的情况,为决策提供更可靠的依据。
希望本文能帮助读者更好地理解正态总体参数的区间估计方法,并在实际问题中应用到实践中。

正态分布估计公式正态分布估计公式是统计分析中一种最为基础的估计方法,用于针对样本数据推测总体的分布情况。
又称为最大似然估计法,适用于样本容量较大、近似正态分布的数据。
本文将详细介绍正态分布估计公式及其在实际应用中的优缺点。
一、正态分布正态分布是概率论中的一种常见分布形式,也被称为高斯分布。
它的密度函数具有如下形式:$$ \mathcal{N}(\mu, \sigma^2) =\frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} $$其中,$\mu$ 表示均值,$\sigma^2$ 表示方差。
正态分布是唯一一个在大量应用中被广泛应用的分布,它具有中心极限定理、最大似然估计等很多重要的数学性质。
二、最大似然估计最大似然估计的原理是在已知样本数据的情况下,估计它们是由什么概率分布所产生。
最大似然的目标是,从所有可能的分布中,选出一个具有最大概率的分布,使得生成当前样本的风险最小化。
在正态分布中,我们要找到一个均值 $\mu$ 和标准差$\sigma$,最大化样本数据的似然函数:$$ L = \prod_{i=1}^n \mathcal{N}(x_i |\mu,\sigma^2 ) = \prod_{i=1}^n \frac{1}{\sqrt{2\pi}\sigma} e^{-\frac{(x_i-\mu)^2}{2\sigma^2}} $$由于连乘十分复杂,我们可以对 $\log{L}$ 取极大值,使得求解最大似然估计可以转化为极大化对数似然。
$$ \log L = -\frac{n}{2}\log(2\pi) - n \log\sigma - \sum_{i=1}^n \frac{(x_i -\mu)^2}{2\sigma^2} $$此时,对 $\mu$ 和 $\sigma^2$ 分别求导,令其等于$0$,就可以求解出最大似然估计值。

双正态总体参数的区间估计双正态总体参数的区间估计是统计学中的一种方法,用于估计由两个正态分布组成的总体的参数。
这种方法适用于当我们需要估计两个总体的平均值或比例时,且这两个总体可以被假定为来自两个不同的正态分布。
下面我们将详细介绍双正态总体参数的区间估计的原理和步骤。
双正态总体参数的区间估计可以分为两种情况:一种是当我们需要估计两个总体的平均值,另一种是当我们需要估计两个总体的比例。
首先,假设我们需要估计两个总体的平均值。
我们可以用样本平均值来估计总体平均值,并通过计算标准误差来构建置信区间。
如果我们假设两个总体的方差相等,则可以使用统计学中的配对t检验方法来进行推断。
具体步骤如下:1.收集样本数据。
从每个总体中随机抽取一定数量的样本,并记录下每个样本的观测值。
2.计算样本平均值。
对于每个总体,计算对应样本的平均值。
3.计算差值。
对于每个配对样本,计算它们的差值。
如果我们关注的是总体平均值的差异,则用两个总体对应样本的平均值之差来作为差值。
4.计算标准差。
计算差值样本的标准差,用来估计差值的标准误差。
5.确定置信水平。
选择一个置信水平,通常为95%。
这意味着我们希望有95%的置信度认为估计的区间包含真实的总体差异。
6.计算临界值。
确定配对t检验的自由度,并使用自由度和置信水平来查找相应的t临界值。
7.构建置信区间。
使用差值平均值±t临界值*标准误差来构建置信区间,这个区间将包含真实的总体差异。
另一种情况是当我们需要估计两个总体的比例。
在这种情况下,我们可以使用两个样本中的比例差异来估计总体的比例差异。
具体步骤如下:1.收集样本数据。
从每个总体中随机抽取一定数量的样本,并记录下每个样本中的成功次数和总次数。
2.计算样本比例。
对于每个总体,计算对应样本的比例,即成功次数除以总次数。
3.计算差异。
对于每个配对样本,计算它们的比例之差。
4.计算标准误差。
计算比例差异样本的标准误差,用来估计比例差异的标准误差。



概率论与数理统计
07
参数估计
问题
如何让与θ的误差体现在估计中?ˆθ•湖中鱼数的真值[ ]对给定的置信水平(置信度)1-α
办法称为未知参数θ的置信度为1-α的置信区间.12
ˆˆ(,)θθ置信下限(X 1, X 2, …, X n )和置信上限(X 1, X 2, …, X n )1ˆθ2
ˆθ12
ˆˆ()1P θθθα<<≥−使含义若1-α=0.95,抽样100次中约有95个包含θ.12
ˆˆ(,)θθ
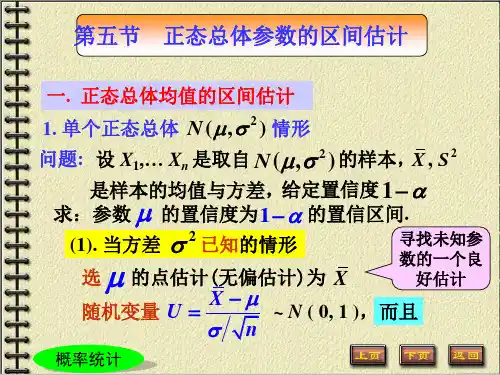
单个正态总体均值的区间估计σ2已知μ的置信度为1-α的置信区间为2~(,)
X N n
σμ/2()1/X P u n
αμασ−<=−/2/2()1P X u X u n n αασσμα−<<+=−/2/2(,);X u X u n n αασσ−+/2()
X u n ασ±2~(0,1)n X N σμ−
➢置信区间长度注➢相同置信水平下,置信区间选取不唯一.
l = 2σn u α/2 /2/2(,)
X u X u n n αασσ−+单个正态总体均值的区间估计
例滚珠直径X ~N (μ, 0.0006),从某天生产的滚珠中随机抽取6个,测得直径为(单位:mm) 1.46 1.51 1.49 1.48 1.52 1.51
求μ 的置信度为95%的置信区间.解/2/2(,)
X u X u n n αασσ−+单个正态总体均值的区间估计
1.495x =,0.05α=,
0.05/20.025 1.96u u ==0.0006(1.495 1.96)6±⨯(1.4754,1.5146)=。
2010年2月吉林师范大学学报(自然科学版)№.1第1期Journal of Jilin N ormal University (Natural Science Edition )Feb.2010收稿日期:2010201205作者简介:陈少云(19692),男,重庆合川人,现为四川建筑职业技术学院副教授.研究方向:高等数学教学.正态总体参数区间估计的MAT LAB 实现陈少云(四川建筑职业技术学院计算机系,四川德阳618000)摘 要:本文介绍了M AT LAB 软件的norm fit ()函数在求解正态总体参数的区间估计中的长处和短处,结合实例编写了M AT LAB 程序求解标准差σ已知时均值μ的置信区间和均值μ已知时标准差σ的置信区间,弥补了norm fit ()函数在该方面的不足.关键词:正态总体;均值;标准差;置信区间中图分类号:O212.2 文献标识码:A 文章编号:1674238732(2010)01200762030 引言总体参数的点估计作为待估参数的近似值给出了明确的数量描述,在统计分析中有多方面的应用.但点估计没有给出这种近似的精确程度和可信程度,使其在实际应用中受到很大的限制,区间估计却可以弥补这一不足.在工程技术中广泛使用的数学软件MAT LAB 提供了现成的函数norm fit ()可以很方便地求出正态总体标准差σ未知时均值μ的置信区间和均值μ未知时标准差σ的置信区间,与数理统计公式和查相关的临界值表计算的结果完全吻合.其函数调用格式为:[muhat ,sigmahat ,muci ,sigmaci ]=norm fit (x ,alpha ).其中muhat ,sigmahat 分别为正态分布的参数μ和σ的估计值,muci ,sigmaci 分别为它们的置信区间,置信度为(1-alpha )×100%,alpha 为显著性水平.例1 商店用机器包装某种商品,每包重量X 服从正态分布,为检查包装的质量,对机器包装的商品抽测8包,其重量为5.08 4.97 5.12 5.05 4.95 4.90 5.00 5.01试估计机器包装的商品重量的均值μ和标准差σ的置信度为0.95的置信区间解 在MAT LAB 的命令窗口输入如下语句>>x =[5.08 4.97 5.12 5.05 4.95 4.90 5.00 5.01];>>[muhat ,sigmahat ,muci ,sigmaci ]=norm fit (x ,0.05)结果显示为muhat =5.0100sigmahat =0.0717muci =4.9500 5.0700sigmaci =0.0474 0.1460结果表明均值μ的估计值为5.0100,其置信度为95%的置信区间为(4.9500,5.0700),这与标准差σ未知时运用数理统计公式和查T 分布临界值表计算的结果一致;标准差σ的估计值为0.0717,其置信度为95%的置信区间为(0.0474,0.1460),这与均值μ未知时运用数理统计公式和查卡方分布临界值表计算的结果一致.但在计算标准差σ已知时均值μ的置信区间和均值μ已知时标准差σ的置信区间方面有较大的误・67・差.下面是结合数理统计知识设计的MAT LAB 程序求解标准差σ已知时均值μ的置信区间和均值μ已知时标准差σ的置信区间的两个例子.1 标准差σ已知时正态总体均值μ的区间估计由数理统计知识,标准差σ已知时正态总体均值的区间估计应采用U 统计量,置信度为1-α的μ置信区间为( x -u α/2σ2/n , x +u α/2σ2/n ).其中u α/2=u (1-α/2).例2 某课程命题初衷,其成绩ζ~N (μ,13152),考毕抽查其中10份试卷的成绩为:74 95 81 43 62 52 86 78 74 67试求该课程平均成绩μ的置信区间.(置信度1-α=0195)解 在MAT LAB 的编辑窗口建立如下的M -文件(并保存为my fun1.m ),以便以后套用. alpha =0.05; %给定的显著性水平sigma =13.5;%已知的标准差x =[74 95 81 43 62 52 86 78 74 67];n =length (x );%计算样本容量mu =mean (x )%计算并显示样本均值u =norminv (1-alpha/2,0,1);%计算置信度为1-alpha/2的正态分布临界值muci =[mu -u 3sqrt (sigma^2/n ),mu +u 3sqrt (sigma^2/n )] %输出置信区间运行后显示结果为mu =71.2000muci =62.8328 79.5672即置信度为0.95时均值μ的置信区间为(62.8328,79.5672).这与运用数理统计公式和查标准正态分布函数数值表计算的结果完全一致.运用norm fit ()函数计算该问题的结果为muhat =71.2000muci =59.9912 82.4088在相同置信度0.95时均值μ的置信区间为(59.9912,82.4088),误差较大.2 均值μ已知时正态总体标准差σ的区间估计根据数理统计知识,均值μ已知时正态总体标准差σ的区间估计采用自由度为n 的卡方统计量,置信度为1-α的σ置信区间为∑n i =1(ζi -μ)2λ1,∑n i =1(ζi -μ)2λ2其中λ1=χ2(1-α/2;n ),λ2=χ2(α/2;n ).例3 设总体ζ~N (μ,σ2),σ为待估参数.样本的一组观察值为(14.6,15.1,14.9,14.8,15.2,15.1),置信度为95%,求μ=14.5时σ的置信区间.解 建立如下M 2文件(并保存为my fun2.m ) alpha =0.05; %给定的显著性水平x =[14.6,15.1,14.9,14.8,15.2,15.1];%样本数据n =length (x );%计算样本容量mu =14.5;%给定的样本均值chi2=sum ((x -mu ).^2);%计算离差的平方和lambda1=chi2inv (1-alpha/2,n );%计算卡方分布的临界值lambda2=chi2inv (alpha/2,n );sigma =[sqrt (chi2/lambda1),sqrt (chi2/lambda2)] %计算方差的置信区间运行后结果显示为sigma =0.3190 1.0900・77・即置信度为95%时所求的置信区间为(0.3190,1.0900),这与运用数理统计公式和查卡方分布临界值表计算的结果完全一致.运用norm fit()函数计算该问题的结果为sigmaci=0.1410 0.5539在相同置信度95%下的置信区间为(0.1410,0.5539),误差极大.综上所述,在计算标准差σ已知时均值μ的置信区间和均值μ已知时标准差σ的置信区间不能再套用MAT LAB所提供的现成函数norm fit(),而必须重新编写程序.笔者在本文中写出的程序较好地解决了这两个问题的MAT LAB实现并且有较强的实用性,有兴趣的读者只需调整显著性水平和更改样本数据便可求出实际问题在给定置信度下的相应置信区间.参 考 文 献[1]金炳陶.概率论与数理统计[M].北京:高等教育出版社,2002.[2]薛定宇,陈阳泉.高等应用数学问题的M AT LAB求解[M].北京:清华大学出版社,2004.I nterval Estimation of N ormal Population P arameter by MAT LABCHEN Shao2yun(C om puter Science Department,S ichuan C ollege of Architectural T echnology,Deyang618000,China)Abstract:This article introduces the advantages and disadvantages of N orm fit()function s olution to interval estimation of normal population parameter in s oftware MAT LAB.With exam ples,the author has written a MAT LAB program to s olve the con fidence interval of:1)the expectationμwhen the standard deviationσis known;and2)the standard deviationσwhen the expectationμis known,which makes up the deficiency of N orm fit()function.K ey w ords:normal population;expectation;standard deviation;con fidence interval(上接第75页)R eferences[1]G.Q.Chen and D.H.W ang,The Cauchy Problem for Euler Equations for com pressible Fluids.Hanbook of M athematical Fluid Dynam oics[J].V ol.I,4212543,N orth2H olland,Amserdam,2002.[2]M.W.Y uen,Analytical Blowup s olutions to the22dimension.is othermal Euler2P ossion equations of gaseous stars II.arX iv:0906.0176v1[3]M.W.Y uen,Analytical Blowup s olutions to the is othermal Euler2P ossion equations of gaseous stars in arX iv:0906.0178v1[4]T.C.S ideris,F ormation of singularitier in Three2dimensional C om pressible Fluids,C omm.M ath.Phys.101(1985),N o.4,4752485[5]P.L.Lions,M athematical T opics in Fluid M echanics.V olume1,2,1998,Ox ford:Clarendon Press,1998.[6]M.W.Y uen,Analytical s olutions to the Navier2stokes equations.arX iv:0811.0377v1[M ath2Ph]3N ov.2008.[7]T.H.Li,S ome special s olutions of the multidimensional Euler equations in,C omm.Pure Appl.Anal.4(4)(2005)7572762.不可压纳维2斯托克斯方程的解析解阎小丽,邓慧琳(河南理工大学数学与信息科学学院,河南焦作454000)摘 要:本文主要构造不可压纳维2斯托克斯方程的解析解.关键词:欧拉方程;纳维2斯托克斯方程;不可压・・87。
正态总体参数的区间估计实验结论引言:在统计学中,参数估计是一项重要的工作,通过样本数据来对总体参数进行估计。
而对于正态总体参数的估计,我们通常使用区间估计的方法来得出结果。
本文将介绍正态总体参数的区间估计实验的结论,并对其意义进行探讨。
实验方法:为了进行正态总体参数的区间估计实验,我们首先需要收集一定数量的样本数据。
然后,根据这些数据的特征,我们可以计算出样本均值和样本标准差。
接下来,我们可以使用统计学中的方法,如t 分布或z分布,来计算出参数的置信区间。
实验结果:经过实验计算,我们得出了正态总体参数的区间估计结果。
以均值为例,我们可以得到一个置信区间,表示在给定置信水平下,总体均值可能位于该区间内。
例如,我们得出了一个95%的置信区间为(μ1, μ2)。
解释和讨论:正态总体参数的区间估计结果是基于样本数据得出的,因此其准确性和可靠性需要进行评估。
在本实验中,我们选择了95%的置信水平,这意味着在重复进行实验的情况下,我们可以有95%的信心认为总体参数位于所得的置信区间内。
区间估计的结果对于统计推断和决策具有重要意义。
在实际应用中,我们可以根据置信区间的上下限来进行决策或评估。
如果待估计的参数值落在置信区间内,我们可以认为该参数是可接受的。
反之,如果参数值超出置信区间,我们可能需要进一步调查或采取相应的行动。
除了均值,我们还可以对正态总体的其他参数进行区间估计,如标准差或方差。
这些参数的区间估计结果也可以为我们提供有关总体特征的重要信息。
总结:正态总体参数的区间估计是统计学中常用的方法之一,可以帮助我们对总体特征进行推断和决策。
本文介绍了正态总体参数区间估计实验的结论,并讨论了其意义和应用。
通过区间估计,我们可以对总体参数进行准确且可靠的估计,为实际问题的解决提供重要依据。
参考文献:[1] 赵建华, 刘曙光. 结果的区间估计[J]. 数学的实践与认识, 2006(06):44-47.[2] 李凯锋. 正态总体参数的区间估计[J]. 统计与决策, 2009, (17):96-97.[3] 陈杰, 窦令媛. 正态总体参数的区间估计及应用[J]. 现代商贸工业,2019(03):93-94.。
双正态总体参数的区间估计双正态总体是指一个总体服从正态分布,且这两个分布的均值和方差都相等。
在双正态总体中,我们常常需要估计总体参数的区间估计,即估计参数的真实值落在哪个区间内。
对于双正态总体的均值μ,我们可以使用Z分数进行区间估计。
假设我们想要在95%的置信水平下估计μ的区间为(a,b),则有:P(μ-a < X < μ+b) = 0.95其中,X是从双正态总体中抽取的样本,a和b是未知的参数。
为了解决这个问题,我们可以利用双正态总体的对称性质,即在均值μ两侧的概率相等。
因此,我们可以使用Z分数的对称性质,得到:P(μ-a < X < μ+b) = 0.975这意味着,在95%的置信水平下,μ的区间为(a,b)的概率为0.975,也就是说,μ的真实值落在这个区间内的概率为0.975。
对于双正态总体的方差σ^2,同样可以使用Z分数进行区间估计。
假设我们想要在95%的置信水平下估计σ^2的区间为(d,e),则有:P(σ2-d < X2 <σ2+e) = 0.95其中,X2是从双正态总体中抽取的样本的方差,d和e 是未知的参数。
同样,我们可以利用双正态总体的对称性质,得到:P(σ2-d < X2 < σ2+e) = 0.975因此,在95%的置信水平下,σ2的区间为(d,e)的概率为0.975,也就是说,σ2的真实值落在这个区间内的概率为0.975。
需要注意的是,对于双正态总体的均值和方差的区间估计,我们需要先确定置信水平和区间长度。
一般来说,置信水平为95%是比较常见的选择,区间长度一般为2倍标准误差。
具体的参数和区间长度需要根据实际情况进行调整。
正态总体参数的bayes估计贝叶斯估计是指从一个随机变量的概率分布或者概率分布中,根据数据样本,假设具有某种先验分布,以求得有关未知参数的极大似然估计,其中固定数据x 与求解估计分布P(θ|x)有关,称作贝叶斯估计。
可以用正态分布的方差的贝叶斯估计,求解正态总体参数的估计。
假设随机变量Xi服从正态N(μ,σ2)分布,Xi的似然函数为:L(μ,σ2)=1/(2πσ2)^n/2 * e^(-1/2σ2(∑i=1...n (Xi-μ)^2))取对数似然函数:lnL(μ,σ2)=ln(1/(2πσ2)^n/2)-1/2σ2(∑i=1...n (Xi-μ)^2)其中μ,σ2是想要求的未知参数,假设在求解时用先验概率,即首先假设μ,σ2遵从,某个先验分布:P(μ,σ2)=P(μ)P(σ2)其中μ,σ2分别遵从均匀分布U(μ0,μ1),Chi-Square分布Χ2(n-1)。
根据贝叶斯定理,有P((μ,σ2)|x)=P(x|(μ,σ2))P(μ,σ2)/P(x)P(x)=∫P(x|(μ,σ2))P(μ)P(σ2 )dμdσ2取log得:lgP((μ,σ2)|x)=lgP(x|(μ,σ2))+lgP(μ)+lgP(σ2)即想要得到最大概率,就需要找出lgP((μ,σ2)|x)的极大值。
利用极大概率估计,可得到优化问题:极大化lgP((μ,σ2)|x)=lgP(x|(μ,σ2))+lgP(μ)+lgP(σ2)即得到最大概率:MLE((μ,σ2))=argmax lgP((μ,σ2)|x)根据极大似然估计的思想,可以推导出MLE((μ,σ2))的估计值:μMLE=∑i=1...nXi/nσMLE=1/n*∑i=1...n(Xi-μMLE)^2即最大似然估计法求得正态总体参数估计值μMLE,σMLE。