下载文档原格式
理论力学第七版答案第一章粒子运动学1.1 基本概念•位矢、速度矢量和加速度矢量的定义和表示方法。
•直角坐标、柱坐标和球坐标系的转换关系。
•速度的瞬时和平均定义。
1.2 运动学基本定理•切线加速度与半径曲线关系。
•速度、加速度与位矢、速度矢量之间的运动学关系。
1.3 平面运动•直线运动：匀速直线运动和变速直线运动的运动学方程。
•曲线运动：实际问题中曲线运动的应用。
第二章力学基本定律2.1 牛顿第一定律•牛顿第一定律的定义和说明。
•惯性系和非惯性系的区别。
2.2 牛顿第二定律•牛顿第二定律的定义和表达式。
•质点和刚体受力的运动学关系。
2.3 牛顿第三定律•牛顿第三定律的定义和说明。
•物体之间相互作用力的特点。
2.4 小结•牛顿定律的应用场景和注意事项。
第三章力的合成与分解3.1 力的合成•力的合成的数学表达式。
•合力的性质和特点。
3.2 力的分解•力的分解的数学表达式。
•杠杆原理和力矩的概念。
3.3 直角坐标系内的力的合成与分解•直角坐标系下力的合成与分解的具体计算方法。
•应用场景和实例。
第四章力的作用点与力矩4.1 力的作用点•力的作用点的概念和性质。
•力的作用点变化对物体运动的影响。
4.2 力矩•力矩的定义和计算公式。
•力矩与力之间的关系。
4.3 平衡条件•平衡条件的定义和判断方法。
•平衡条件的应用。
第五章动力学基本定律5.1 作用力的性质•作用力的性质和判断方法。
•弹力、摩擦力和引力的特点。
5.2 动量定律•动量定律的定义和表达式。
•动量定律与力学问题的应用。
5.3 动能定理•动能定理的定义和表达式。
•动能定理与动力学问题的应用。
5.4 质心运动•质心的概念和运动特点。
•质心运动与动量守恒的关系。
第六章动力学问题6.1 动力学问题的解法思路•动力学问题解决的思路和方法。
•实例分析和解决步骤。
6.2 一维动力学问题•一维动力学问题的求解方法和关键步骤。
•速度-时间图和位移-时间图的应用。
6.3 二维动力学问题•二维动力学问题的求解方法和关键步骤。
课后题答案哈工大.高等教育出版社](https://img.taocdn.com/s1/m/4468d4b7c77da26925c5b0bd.png)
3-4 在图示刚架中，已知q ＝3kN/m ，F 可＝62kN ，M ＝10kN ⋅m ，不计刚架自重。
求固定端A 处的约束反力。
【知识要点】 平面的任意力系的平衡方程及应用，单个物体的平衡问题【解题分析】 本题应注意固定端A 处的受力分析，初学者很容易丢掉约束力偶。
【解答】 以刚架为研究对象，受力如图。
题3－4图∑=-⨯+=045cos 421,00F q F F Ax x ∑=-=045sin ,00F F F Ay y∑=⨯+⨯--⨯⨯-=0445cos 345sin 34421,0)(00F F M q M F M A A 解得 F A x =0, F A y =6kN, M A =m kN ⋅12 3-8 如图所示，行动式起重机不计平衡锤的重为P ＝500kN ，其重心在离右轨1.5m 处。
起重机的起重量为P 1＝250kN ，突臂伸出离右轨10m 。
跑车本身重量略去不计，欲使跑车满载或空载时起重机均不致翻倒，求平衡锤的最小重量P 2以及平衡锤到左轨的最大距离x 。
题3－8图【知识要点】 平面平行力系的平衡方程及应用，单个物体的平衡问题。
【解题分析】 本题仍为翻倒问题，存在两种临界状态。
【解答】 以起重机为研究对象，受力如图。
若满载不翻倒0105.13)3(,0)(12=---+=∑P P F x P F MNA B 由 F NA ≥0,得P 2（x+3）≥3250 (1) 若空载不翻倒 05.43,0)(2∑=-+=P F x P F M NB A由 F NB ≥0得22502≤x P (2) 由式（1）、（2）得kN P P 3.3331000322≥≥即把kN P 3.3332=代入（2）得x ≤6.75m3-11 如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。
已知起重机重P 1＝50kN ，重心在铅直线EC 上，起重载荷P 2＝10kN ，如不计梁重，求支座A 、B 和D 三处的约束反力。
仅供个人学习参考哈工大理论力学（I ）第7版部分习题答案1-2两个老师都有布置的题目2-3?2-6?2-14?2-?20?2-30?6-2?6-4?7-9??7-10?7-17?7-21?8-5?8-8?8-16?8-24?10-4?10-6?11-5?11-15?10-3以下题为老师布置必做题目1-1（i,j ）,1-2(e,k)2-3,2-6,2-14，2-20,2-306-2,6-47-9,7-10,7-17,7-21,7-268-5,8-8(瞬心后留),8-16,8-2410-3,10-410-611-5,11-1512-10,12-15,综4，15，16，1813-11，13-15，13-166-2图6-2示为把工件送入干燥炉内的机构，叉杆OA=1.5m 在铅垂面内转动，杆AB=0.8m ，A 端为铰链，B 端有放置工件的框架。
在机构运动时，工件的速度恒为0.05m/s ，杆AB 始终铅垂。
设运动开始时，角0=?。
求运动过程中角?与时间的关系，以及点B 的轨迹方程。
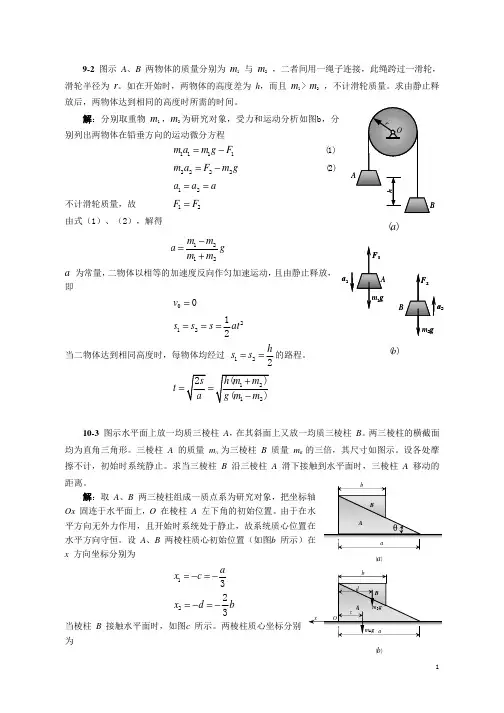
10-3如图所示水平面上放1均质三棱柱A ，在其斜面上又放1均质三棱柱B 。
两三棱柱的横截面均为直角三角形。
三棱柱A 的质量为mA 三棱柱B 质量mB 的3倍，其尺寸如图所示。
设各处摩擦不计，初始时系统静止。
求当三棱柱B 沿三棱柱A 滑下接触到水平面时，三棱柱A 移动的距离。
11-4解取A 、B 两三棱柱组成1质点系为研究对象，把坐标轴Ox 固连于水平面上，O 在棱柱A 左下角的初始位置。
由于在水平方向无外力作用，且开始时系统处于静止，故系统 质心位置在水平方向守恒。
设A 、B 两棱柱质心初始位置（如图b 所示）在x 方向坐标分别为当棱柱B 接触水平面时，如图c 所示。
两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4如图所示，均质杆AB ，长l ，直立在光滑的水平面上。
求它从铅直位无初速地倒下时，端点A 相对图b 所示坐标系的轨迹。
理论力学第七版课后习题答案第一章: 引言习题1-11.问题描述：给定物体的质量m=2kg，加速度a=3m/s^2，求引力F。
2.解答：根据牛顿第二定律F=ma，其中m表示物体的质量，a表示物体的加速度。
代入已知值，可求得F=6N。
习题1-21.问题描述：给定物体的质量m=5kg，引力F=20N，求加速度a。
2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=4m/s^2。
第二章: 运动的描述习题2-11.问题描述：一个物体以恒定速度v=10m/s匀速直线运动，经过t=5s，求物体的位移。
2.解答：位移等于速度乘以时间，即s=vt。
代入已知值，可得s=50m。
习题2-21.问题描述：一个物体以初始速度v0=5m/s匀加速直线运动，加速度a=2m/s^2，经过t=3s，求物体的位移。
2.解答：由于物体是匀加速直线运动，位移可以通过公式s=v0t+0.5at^2计算。
代入已知值，可得s=(53)+(0.52*3^2)=45m。
第三章: 动力学基础习题3-11.问题描述：一个物体质量为m=4kg，受到的力F=10N，求物体的加速度。
2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2.5m/s^2。
习题3-21.问题描述：一个物体质量为m=3kg，受到的力F=6N，求物体的加速度。
2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。
第四章: 动力学基本定理习题4-11.问题描述：一个物体质量为m=8kg，受到的力F=16N，求物体的加速度。
2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。
习题4-21.问题描述：一个物体质量为m=6kg，受到的力F=12N，求物体的加速度。
2.解答：根据牛顿第二定律F=ma，将已知值代入，可求得a=2m/s^2。
以上是理论力学第七版课后习题的答案。
希望能对你的学习有所帮助！。
7-8 纸盘由厚度为a 的纸条卷成，令纸盘的中心不动，而以等速υ拉纸条。
求纸盘的角加速度（以半径r 的函数表示）。
【知识要点】 纸盘转速与边缘速度v 的关系。
【解题分析】 利用纸带的平移速度等于轮边缘的速度求解。
【解答】 令初始状态下纸盘的半径为r 0，则经过时间t 之后纸盘面积为
题7－8图
avt r R =-2
2ππ
上式对时间求导，得 r av dt dr av dt dr r
ππ222-== 由求导，得对t r
v =
ω dt dr r v dt d 2-=ωα＝ 把式（1）代入上式，得
32
2r
v a πα= 7-11 杆AB 在铅垂方向以恒速υ向下运动，并由B 端的小轮带着半径为R 的圆弧杆OC 绕
轴O 转动，如图所示。
设运动开始时，4π
ϕ=，求此后任意瞬时t ，OC 杆的角速度
ω和点C 的速度。
题7－11图
【知识要点】 刚体得定轴转动。
【解题分析】 由点B 的坐标与角ϕ的关系入手。
【解答】 点B 坐标y=2Rcos ϕ
上式时间t 式导得
ϕ
ωϕ
ωϕωsin 2sin 2sin 2v R v R v R y
v C -==-=-== 而 R
OB 2cos =ϕ 其中 vt R OB +=4cos 2π
则 2222221cos 1sin ⎪⎭
⎫ ⎝⎛--=-=R vt R vt ϕϕ
友情提示：部分文档来自网络整理，供您参考！文档可复制、编制，期待您的好评与关注！。
哈工大理论力学（I）第7版部分习题答案
1-2
两个老师都有布置的题目
2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3
以下题为老师布置必做题目
1-1（i,j）, 1-2(e,k)
2-3, 2-6, 2-14，2-20, 2-30 6-2, 6-4
7-9, 7-10, 7-17, 7-21, 7-26
8-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-6
11-5, 11-15
12-10, 12-15, 综4，15，16，18 13-11，13-15，13-16
6-2 图6-2示为把工件送入干燥炉内的机构，叉杆OA=1.5 m在铅垂面内转动，杆AB=0.8 m，A端为铰链，B端有放置工件的框架。
在机构运动时，工件的速度恒为0.05 m/s，杆AB始终铅垂。
设运动开始时，角0=?。
求运动过程中角?与时间的关系，以及点B的轨迹方程。
10-3 如图所示水平面上放 1 均质三棱柱 A ，在其斜面上又放 1 均质三棱柱 B 。
两三棱柱的横截面均为直角三角形。
三棱柱 A 的质量为 mA 三棱柱 B 质量 mB 的 3 倍，其尺寸如图所示。
设各处摩擦不计，初始时系统静止。
求当三棱柱 B 沿三棱柱 A 滑下接触到水平面时，三棱柱 A 移动的距离。
11-4
解取A、B 两三棱柱组成 1 质点系为研究对象，把坐标轴Ox 固连于水平面上，O 在
棱柱A 左下角的初始位置。
由于在水平方向无外力作用，且开始时系统处于静止，故系统
质心位置在水平方向守恒。
设A、B 两棱柱质心初始位置（如图b 所示）在x 方向坐标
分别为
当棱柱B 接触水平面时，如图c所示。
两棱柱质心坐标分别为
系统初始时质心坐标
棱柱B 接触水平面时系统质心坐标
因并注意到得
10-4 如图所示，均质杆AB，长l，直立在光滑的水平面上。
求它从铅直位无
初速地倒下时，端点A相对图b所示坐标系的轨迹。
解取均质杆AB 为研究对象，建立图11-6b 所示坐标系Oxy，原点O
与杆AB 运动初始时的点B 重合，因为杆只受铅垂方向的重力W 和地
面约束反力N F 作用，且系统开始时静止，所以杆AB 的质心沿轴x 坐
标恒为零，即
设任意时刻杆AB 与水平x 轴夹角为θ，则点A坐标
从点A 坐标中消去角度θ，得点A 轨迹方程
10-5 质量为m1 的平台AB，放于水平面上，平台与水平面间的动滑动摩擦因数为f。
质量为m2 的小车D，由绞车拖动，相对于平台的运动规律为，其中b 为已知常数。
不计绞车的质量，求平台的加速度。
解受力和运动分析如图b 所示
式（1）、（4）代入式（3），得
10-6 如图所示，质量为m的滑块A，可以在水平光滑槽中运动，具有刚性系
数为k 的弹簧1 端与滑块相连接，另 1 端固定。
杆AB 长度为l，质量忽略不计，A 端与滑块A 铰接，B 端装有质量m1，在铅直平面内可绕点A 旋转。
设在力偶M 作用下转动角速度ω为常数。
求滑块A 的运动微分方程。
解取滑块A 和小球B组成的系统为研究对象，建立向右坐标x，原点取在
运动开始时滑块A 的质心上，则质心之x 坐标为
系统质心运动定理：
此即滑块A的运动微分方程。
讨论：设，则由上述方程得滑块A 的稳态运动规律（特解）
原题力矩M只起保证ω=常数的作用，实际上M 是随ϕ变化的。
11-15如图所示均质杆AB 长为l，放在铅直平面内，杆的1 端A 靠在光滑铅直墙上，另1端B 放在光滑的水平地板上，并与水平面成0 ϕ角。
此后，令杆由静止状态倒下。
求（1）杆在任意位置时的角加速度和角速度；（2）当杆脱离墙时，此杆与水平面所夹的角。
解（1）取均质杆为研究对象，受力及坐标系Oxy 如图12-17b 所示，杆AB 作平面运
动，质心在点C。
刚体平面运动微分方程为
由于
将其对间t求2 次导数，且注意到
本答案由各班代表负责编排（答案源来自网络），在此感谢为这次编排做出贡献的各位同学。
由于各方面原因，可能个别题目解答不妥甚至有误，或者在编排上有漏洞，希望大家能够指出并共享正确的结果。
——福州大学至诚学院机械系09级
配套 理论力学（I ）第七版 课后习题答案 福州大学至诚学院09机械整理
31
本答案由各班代表负责编排（答案源来自网络），在此感谢为这次编排做出贡献的各位同学。
由于各方面原因，可能个别题目解答不妥甚至有误，或者在编排上有漏洞，希望大家能够指出并共享正确的结果。
——福州大学至诚学院机械系09级。
