当前位置：文档之家 › 理论力学(第七版)课后题答案哈工大

理论力学(第七版)课后题答案哈工大

  • 格式：pdf
  • 大小：9.96 MB
  • 文档页数：210

下载文档原格式

  / 210

合集下载

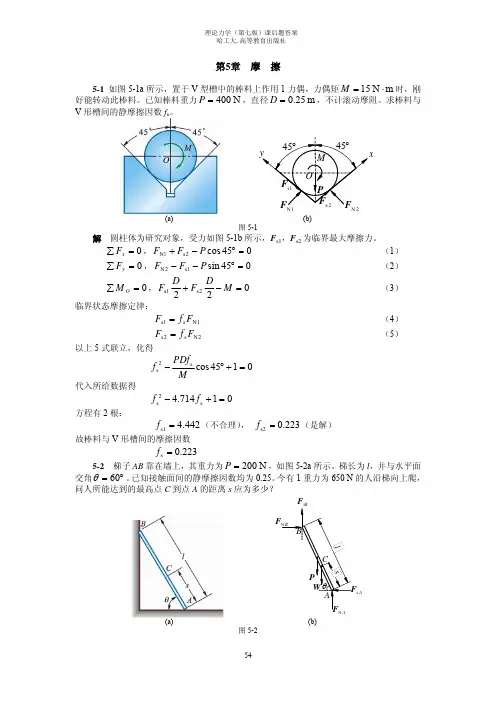
哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

哈尔滨工业大学 第七版 理论力学 第5章 课后习题答案

第5章 摩 擦5-1 如图5-1a 所示，置于V 型槽中的棒料上作用1力偶，力偶矩m N 15⋅=M 时，刚好能转动此棒料。

已知棒料重力N 400=P ，直径m 25.0=D ，不计滚动摩阻。

求棒料与V 形槽间的静摩擦因数f s 。

(a)(b)图5-1解 圆柱体为研究对象，受力如图5-1b 所示，F s1，F s2为临界最大摩擦力。

0=∑x F ，045cos 2s 1N =°−+P F F （1） 0=∑y F ，045sin 1s 2N =°−−P F F （2） 0=∑O M ，0222s 1s =−+M DF D F（3）临界状态摩擦定律：1N s 1s F f F =（4） 2N s 2s F f F =（5）以上5式联立，化得 0145cos s2s =+°−MPDf f 代入所给数据得01714.4s 2s =+−f f 方程有2根：442.4s1=f （不合理）， 223.0s2=f （是解）故棒料与V 形槽间的摩擦因数223.0s =f5-2 梯子AB 靠在墙上，其重力为N 200=P，如图5-2a 所示。

梯长为l ，并与水平面交角°=60θ。

已知接触面间的静摩擦因数均为0.25。

今有1重力为650 N 的人沿梯向上爬，问人所能达到的最高点C 到点A 的距离s 应为多少？AN F As F(a)(b)图5-2解 梯子为研究对象，受力如图5-2b 所示，刚刚要滑动时，A ，B 处都达最大静摩擦力。

人重力N 650=W ，平衡方程： 0=∑x F , 0s N =−A B F F （1） 0=∑y F , 0s N =−−+W P F F B A（2）0=∑A M ，060cos 60sin 60cos 60cos 2s N =°−°−°+°l F l F Ws lPB B （3） 临界补充方程：A s A F f F N s = （4）B s B F f F N s =（5）联立以上5式，解得 N 80012sN =++=f WP F A ，N 200s =A F N 200)(12s N =++=W P f f F sB ，N 50s =B F l PF f W l s B 456.02)3[(N s =−+=5-3 2根相同的匀质杆AB 和BC ，在端点B 用光滑铰链连接，A ，C 端放在不光滑的水平面上，如图5-3a 所示。

哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

哈尔滨工业大学 第7版 理论力学 第4章 课后习题答案

解 （1）方法 1，如图 4-6b 所示，由已知得
Fxy = F cos 60° ， Fz = F cos 30°
F = F cos 60°cos 30°i − F cos 60°sin 30° j − F sin 60°k = 3 i − 1 Fj − 3 Fk 44 2
41
理论力学（第七版）课后题答案 哈工大.高等教育出版社
A
F
β
MA
C
MB
F
10 N
β M θ − 90° C
MB
(a)
(b)
(c)
图 4-11
解 画出 3 个力偶的力偶矩矢如图 4-11b 所示，由力偶矩矢三角形图 4-11c 可见
MC =
M
2 A
+
M
2 B
=
3 0002 + 4 0002 = 5 000 N ⋅ mm
由图 4-11a、图 4-11b 可得
3 = 250 N 13
FRz = 100 − 200 ×
1 = 10.6 N 5
M x = −300 ×
3 × 0.1 − 200 × 1 × 0.3 = −51.8 N ⋅ m
13
5
M y = −100 × 0.20 + 200 ×
2 × 0.1 = −36.6 N ⋅ m 13
M z = 300 ×
z
F45° F3 F3′ B
F2A
E
F1
C
F5
F6
F F4 45°
D
y
K x
M
(a)
(b)
图 4-9
解 (1) 节点 A 为研究对象，受力及坐标如图 4-9b 所示

理论力学(哈工第七版) 课后练习答案 第三部分

理论力学(哈工第七版) 课后练习答案 第三部分
O M
A
ϕ
O
r ϕ
M
W=
2π
∫ 4ϕ dϕ + (m
0
− mB ) g ⋅ 2π r
A B
A mAg
= 8π 2 + (mA − mB ) g ⋅ 2π r = 8π 2 + 1× 9.8 × 2π × 0.5 = 110 (J)
B
mBg
(a)
(b)
7
12-4 图示坦克的履带质量为 m，两个车轮的质量均为 m1。车轮被看成均质圆盘，半径为 R， 两车轮间的距离为 πR。设坦克前进速度为 v，计算此质点系的动能。 解：系统的动能为履带动能和车轮动能之和。将履带分为四部 分，如图b 所示。履带动能：
O
P2 P aB − 1 a A = FN − P 1−P 2 g g
其中， a A = a ， aB = 解得
A
a 2 1 (2 P 1−P 2 )a 2g
B
(a)
FN = P 1+P 2 −
v FN
O
v P 1
A
v aA
v aB B
v P2
(b)
11-1 质量为 m 的点在平面 Oxy 内运动，其运动方程为
得
G1
320
B C
SB
S A = 170 mm S B = 90 mm
(b)
2
10-12 图示滑轮中，两重物 A 和 B 的重量分别为 P1 和 P2。如物体 A 以加速度 a 下降， 不计滑轮质量，求支座 O 的约束力。 解：对整体进行分析，两重物的加速度和支座 O 的约束力如图b 所示。由 动量定理知：
整体受力和运动分析如图b因为0xf所以x方向系统守恒有21cos0brbmvmvv??解得121cosbrmmvvm1所以该系统动能为设此时三棱柱a沿三棱柱b下滑的距离为s则其重力作的功为1sinwmgs??系统动能22b211221sin12cosmmtmmvm由系统动能定理tw即1sinwmgs??上式对时间求导并注意到rdsdtv整理后得22112121sinsincosbbrmmmmvamgvm?????得2b2a212b2b2r2122b21122

哈工大第七版理论力学课后思考题答案

哈工大第七版理论力学课后思考题答案

集美大学诚毅学院机械1093期末复习材料理论力学(思考题答案)思考题i-i猛明下列戏子与丈宇的盘义和区別.(D科二孔,(2)幵一盼⑶力靳等效于力列,*W?答】⑴力乌和町，大小相等帯柯相岡g(2)N和&大小相萄⑶耐刑耳的夫小相等, 方向si^ats同亠1-2试X别片=眄|压和血=凤+骂两个等戎代表的意义。

【岸答】町一耐十用朮示朋是任意方向上箭个为门和A的合力洽力弘的大小和方问由平行四边形抚阳鴉定;打=片一%表示忌足同方向上蘭个力几和月的合.乩含力A的大小为F L和E的大小的和I方向与Fl和F.的方向科同3【解答】均有错•正确图如答1一1图。

1—3图1 - 1C1)〜1-1(0中各物体的受力番是否错谋?如何改正?1-4 刚体上△点受力尸作用.in 18 1-2所示，问罷否在。

点加一个力懐刚体平箕。

为什么?Ul 1 -2(a)也fS P= 0【解答1 不能。

当在E 点械抑力怖时，不能同时保订丿 1，故不能平衡B2JM= o1- 5 如摆】一3所冻结均•科丿JF 作用在E 点，至统能否乎猶?若力F 仍作用在丑点，袒可住 愆改变F 的方向，F 在什么方向上结购能平衡？ 上匕解答】不能， 来/在如簷范围内可以令结构平鸳，如着？ 一 3圖所示.1- 6 将如下间题抽象为力学模型，充分发挥你们的想象、分析和抽躱能力*试画出它心的力 学荒圏及受力<1)用两根细绳將B 光灯吊挂在天花板上»(?)水面匕的一块浮冰*G) 本打开的韦静止于桌面上; <4) 一个人坐在一只足球上*【解答】⑴⑵图1-4<4)u1 -7若将图1-5屮力F作用于三锻拱供较陡C处的请订上，所有物体里虽不计试分别画出左、右两拱茂销匚的受力圈八刃若傭订匚碾于AC•分别画岀汗、右两拱的受力图H3）若洌订C 属于EC,分鬧画出古、右两拱的量力阳°3 1-5mA2_1输亀钱普麦/相同时，电线下垂量片趙小■电线捷易亍拉Wh 为什么？【網答】可儒得J = F B =疵；=好也越小恥越小不和尸庞儿助以电线更易于拉2-2图2 — 1所赤时三种机构，构件自童不计9翅略靡擦，， 平力F,问Aifc 的妁京力是否相同。

哈尔滨工业大学 第七版 理论力学.13

哈尔滨工业大学 第七版 理论力学.13

1 2 T履 = ∑ mi vi = TI + TII + TIII + TIV 2
D II A
(a) 图 13-3
IV
2v
C
ω
v
III
Iv=0
(b)
B
由于 v1 = 0, vIV = 2v ，且由于每部分履带长度均为π R ，因此
mI = mII = mIII = mIV = TI =
m 4
1 2 mI vI = 0 2 1 1 m m 2 TIV = mIV v IV = × (2v) 2 = v 2 2 2 4 2 m m 2 II、III 段可合并看作 1 滚环，其质量为 ，转动惯量为 J = R ，质心速度为 v，角速度 2 2 v 为 ω = ，则 R 1 m 1 mv 2 1 m 2 v 2 m 2 TII + TIII = ⋅ v 2 + Jω 2 = + ⋅ R ⋅ 2 = v 2 2 2 4 2 2 2 R m m T履 = 0 + v 2 + v 2 = mv 2 2 2
理论力学（第七版）课后题答案 哈工大.高等教育出版社
第 13 章 动能定理
13-1 如图 13-1a 所示，圆盘的半径 r = 0.5 m，可绕水平轴 O 转动。在绕过圆盘的绳上 吊有两物块 A、B，质量分别为 mA = 3 kg，mB = 2 kg。绳与盘之间无相对滑动。在圆盘上作 用 1 力偶， 力偶矩按 M = 4ϕ 的规律变化 （M 以 N ⋅ m 计， ϕ 以 rad 计） 。 求由 ϕ = 0到ϕ = 2π 时，力偶 M 与物块 A，B 重力所作的功之总和。
第 2 阶段 ：系统通过搁板继续运动 x2 距离后静止。由动能定理

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案
得
tan θ =
r sin ϕ h − r cos ϕ
sin ω 0 t h − cos ω 0 t r ]
图 7-5
注意到 ϕ = ω 0 t ，得
θ = tan −1 [
（2）
自 B 作直线 BD 垂直相交 CO 于 D，则
tan θ =
r sin ω 0 t BD = DO h − r cos ω 0 t
80
理论力学（第七版）课后题答案 哈工大.高等教育出版社
7-6 如图 7-6 所示，摩擦传动机构的主动轴 I 的转速为 n = 600 r/min 。轴 I 的轮盘与轴Ⅱ的轮 盘接触，接触点按箭头 A 所示的方向移动。距离 d 的变化规律为 d = 100 − 5t ，其中 d 以 mm 计， t 以 s 计。已知 r = 50 mm ， R = 150 mm 。求： （1）以距离 d 表示轴 II 的角加速度； （2）当 d = r 时，轮 B 边缘上 1 点的全加速度。 解 （1）两轮接触点的速度以及切向加速度相同
∠CBO =
π ， x B = 2 R cos ϕ 2 & B = 2 R + vt （↓） x B (0) = 2 R ， x
(2 R) 2 − x B
2
vt vt 1 2 − 2 2 − ( )2 R R 2R 2 v v ， vC = 2 Rω = − ω =− 2 R sin ϕ sin ϕ sin ϕ = =
两边对时间 t 求导：
vt l
& sec 2 ϕ = ， ϕ & = cos 2 ϕ ， ϕ && = − ϕ
当ϕ =
v l
v l
2v & cos ϕ sin ϕ ⋅ ϕ l

理论力学(百度文库)-第七版答案-哈工大

理论力学(百度文库)-第七版答案-哈工大

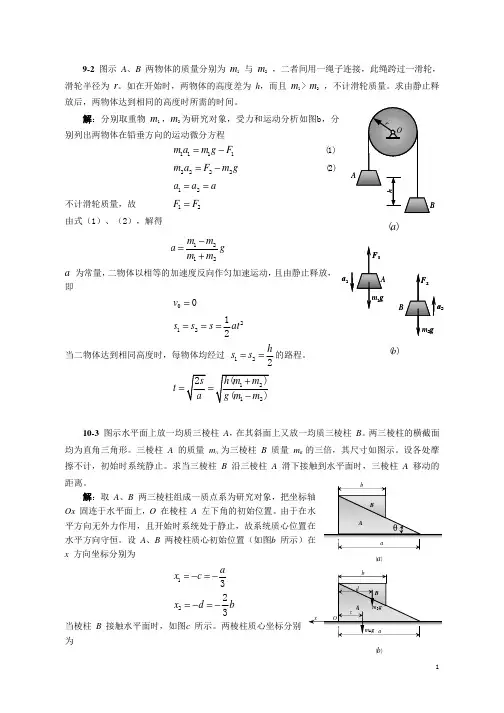
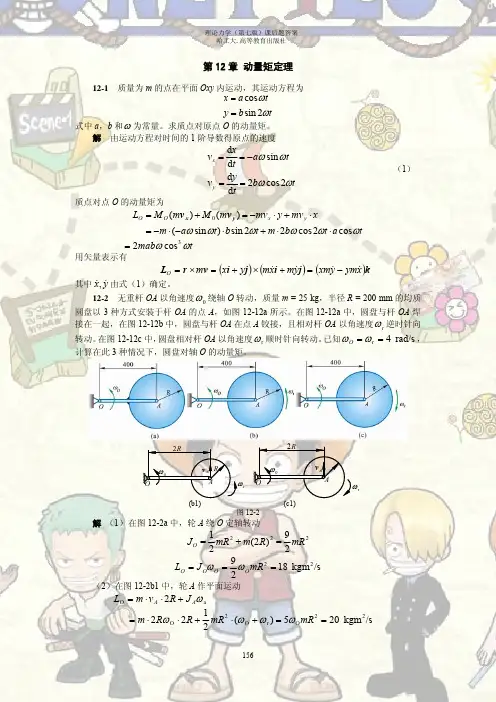
哈工大理论力学（I）第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1（i,j）, 1-2(e,k)2-3, 2-6, 2-14，2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4，15，16，18 13-11，13-15，13-166-2 图6-2示为把工件送入干燥炉内的机构，叉杆OA=1.5 m在铅垂面内转动，杆AB=0.8 m，A端为铰链，B端有放置工件的框架。

在机构运动时，工件的速度恒为0.05 m/s，杆AB始终铅垂。

设运动开始时，角0=?。

求运动过程中角?与时间的关系，以及点B的轨迹方程。

10-3 如图所示水平面上放1 均质三棱柱A，在其斜面上又放1 均质三棱柱B。

两三棱柱的横截面均为直角三角形。

三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍，其尺寸如图所示。

设各处摩擦不计，初始时系统静止。

求当三棱柱B 沿三棱柱A 滑下接触到水平面时，三棱柱A 移动的距离。

11-4解取A、B 两三棱柱组成1 质点系为研究对象，把坐标轴Ox 固连于水平面上，O 在棱柱A 左下角的初始位置。

由于在水平方向无外力作用，且开始时系统处于静止，故系统质心位置在水平方向守恒。

设A、B 两棱柱质心初始位置（如图b 所示）在x 方向坐标分别为当棱柱B 接触水平面时，如图c所示。

两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示，均质杆AB，长l，直立在光滑的水平面上。

求它从铅直位无初速地倒下时，端点A相对图b所示坐标系的轨迹。

哈尔滨工业大学 第七版 理论力学.12

哈尔滨工业大学 第七版 理论力学.12

Lz1 = mv0 (l + r )
(1 )
在任意时刻：
Lz 2 = Jω + M z (mv M ) = Jω + M z (mv 0 ) + M z (mv e )
由图 12-5b 中，可得
Lz 2 = Jω + mv0 [l cos ϕ + r ] + m(l 2 + r 2 + 2lr cos ϕ )ω
12-4 1 半径为 R，质量为 m1 的均质圆盘，可绕通过其中心 O 的铅垂轴无摩擦地旋转， 如图 12-4a 所示。1 质量为 m2 的人在盘上由点 B 按规律 s = 开始时，圆盘和人静止。求圆盘的角速度和角加速度 α 。
1 2 at 沿半径为 r 的圆周行走。 2
R r O
(a) 图 12-4
LO = m ⋅ v A ⋅ 2 R + J Aω a 1 = m ⋅ 2 Rω O ⋅ 2 R + mR 2 ⋅ (ω O + ω r ) = 5ω O mR 2 = 20 kgm 2 /s 2
156
理论力学（第七版）课后题答案 哈工大.高等教育出版社
（3）在图 12-2c1 中，轮 A 绕 O 作圆周曲线平移
接合后，依靠摩擦使轮 2 启动。已知轮 1 和 2 的转动惯量分别为 J1 和 J2。求： （1）当离合 器接合后，两轮共同转动的角速度； （2）若经过 t 秒两轮的转速相同，求离合器应有多大的 摩擦力矩。
Mf
ω
2
(a) 图 12-6
(b)
解 （1）以轮 1 和 2 为一个系统进行研究，因为系统所受外力（包括重力和约束反力） 对转轴之矩均为零，所以系统对转轴的动量矩守恒，即

理论力学(哈工第七版) 课后练习答案 第二部分

理论力学(哈工第七版) 课后练习答案 第二部分

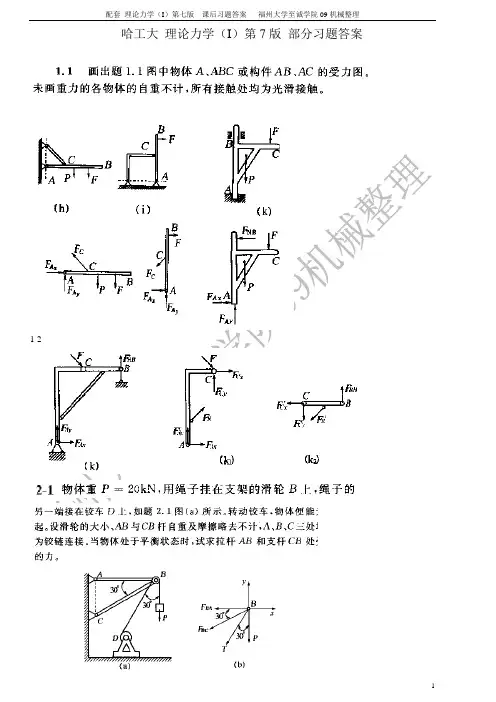
5-1 图示曲线规尺的各杆， 长为OA =AB =200 mm ，CD = DE = AC = AE = 50mm 。

如杆 OA 以等角速度 rad/s 5πω=绕 O 轴转动，并且当运动开始时，杆 OA 水平向右，求尺上点 D 的运动方程和轨迹。

解：如图所示 ∠AOB =ωt ，则点 D 坐标为cos D x OA t ω=⋅sin 2sin D y OA t AC t ωω=⋅−⋅代入已知数据，得到点 D 的运动方程为200cos 5D x t π=× 200sin250sin 55100sin 5D y t t tπππ=×−××=×把以上两式消去 t 得点 D 轨迹方程22221200100x y += 即，D 点轨迹为中心在（0, 0），长半轴为0.2 m ，短半轴为0.1 m 的椭圆。

6-4 机构如图所示，假定杆AB 以匀速v 运动，开始时0ϕ=。

求当4πϕ=时，摇杆OC 的角速度和角加速度。

解：依题意，在0ϕ=时，A 在D 处。

由几何关系得tan vt l ϕ=杆OC 的运动方程为arctanvt lϕ= 角速度222vll v tωϕ==+& 角加速度322222()v lt l v t αϕ==+&&当4πϕ=时，vt l =。

将vt l =代入上二式得 2v lω=222v lα=另解：几何关系 tan vtlϕ=两边对t 求导，可得 2sec v l ϕϕ=& 即 2cos v l ϕϕ=& ；再求导，得 2cos sin v l ϕϕϕϕ=−⋅&&& ，将4πϕ=时，vt l=代入上二式得2vlωϕ==& 222v lαϕ==&&6-5 如图所示，曲柄 CB 以等角速度0ω绕轴 C 转动，其转动方程为0t ϕω=。

滑块 B 带动摇杆 OA 绕轴 O 转动。

哈工大理论力学(I)第七版答案、高等教育出版社出版

哈工大理论力学(I)第七版答案、高等教育出版社出版

哈工大理论力学（I）第7版部分习题答案1-2两个老师都有布置的题目2-3 2-6 2-14 2- 20 2-30 6-2 6-4 7-9 7-10 7-17 7-21 8-5 8-8 8-16 8-24 10-4 10-6 11-5 11-15 10-3以下题为老师布置必做题目1-1（i,j）, 1-2(e,k)2-3, 2-6, 2-14，2-20, 2-30 6-2, 6-47-9, 7-10, 7-17, 7-21, 7-268-5, 8-8(瞬心后留), 8-16, 8-24 10-3, 10-4 10-611-5, 11-1512-10, 12-15, 综4，15，16，18 13-11，13-15，13-166-2 图6-2示为把工件送入干燥炉内的机构，叉杆OA=1.5 m在铅垂面内转动，杆AB=0.8 m，A端为铰链，B端有放置工件的框架。

在机构运动时，工件的速度恒为0.05 m/s，杆AB始终铅垂。

设运动开始时，角0=?。

求运动过程中角?与时间的关系，以及点B的轨迹方程。

10-3 如图所示水平面上放1 均质三棱柱A，在其斜面上又放1 均质三棱柱B。

两三棱柱的横截面均为直角三角形。

三棱柱A 的质量为mA三棱柱B 质量mB的 3 倍，其尺寸如图所示。

设各处摩擦不计，初始时系统静止。

求当三棱柱B 沿三棱柱A 滑下接触到水平面时，三棱柱A 移动的距离。

11-4解取A、B 两三棱柱组成1 质点系为研究对象，把坐标轴Ox 固连于水平面上，O 在棱柱A 左下角的初始位置。

由于在水平方向无外力作用，且开始时系统处于静止，故系统质心位置在水平方向守恒。

设A、B 两棱柱质心初始位置（如图b 所示）在x 方向坐标分别为当棱柱B 接触水平面时，如图c所示。

两棱柱质心坐标分别为系统初始时质心坐标棱柱B 接触水平面时系统质心坐标因并注意到得10-4 如图所示，均质杆AB，长l，直立在光滑的水平面上。

求它从铅直位无初速地倒下时，端点A相对图b所示坐标系的轨迹。

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

哈尔滨工业大学 第七版 理论力学 第7章 课后习题答案

解
设轮缘上任 1 点 M 的全加速度为 a，切向加速度 a t = rα ，法向加速度 a n = ω r ，如图
2
7-11b 所示。
tan θ =
把
α=
dω ， θ = 60° 代入上式，得 dt
at α = 2 an ω
dω tan 60° = dt2
ω
分离变量后，两边积分：
∫ω
得
ω
0
dω
ω
2
=∫
⎤ ⎡ ⎥ ⎢ sin ω t 0 θ = tan −1 ⎢ ⎥ ⎢ h − cos ω 0 t ⎥ ⎥ ⎢ ⎦ ⎣r
故
50 π ⋅ 600 100π r ω1 = rad/s ⋅ = 100 − 5t 30 10 − 0.5t d dω 5 000 π d ⎛ 1 000π ⎞ α2 = 2 = ⎜ ⎟= dt dt ⎝ 100 − 5t ⎠ (100 − 5π )2
故得
h1 =
h4 = 2 mm 6
图 7-7
7-8 如图 7-8 所示，纸盘由厚度为 a 的纸条卷成，令纸盘的中心不动，而以等速 v 拉纸条。求 纸盘的角加速度（以半径 r 的函数表示） 。 解 纸盘作定轴转动，当纸盘转过 2π rad 时半径减小 a。设纸盘转过 dθ 角时半径增加 dr ，则
dθ =
y
B
t aB
α j
O
vA x
ω
(a) 图 7-12
aC
(b)
i 45° A n
C
t aC
解
由图 7-12b 得出
84
理论力学（第七版）课后题答案 哈工大.高等教育出版社
v A = 0.2 j m/s ， v A = ω × Ri ， ω × 0.1i = 0.200 j ， ω = 2k ，

理论力学(第七版)2

理论力学(第七版)2

ω2
30°
θ ω1
(a) 图 8-11
va O
(b)
解 （1）运动分析 ① 活动销子 M 为动点，动系固结于轮 O；牵连运动为绕 O 定轴转动，相对运动为沿 轮上导槽直线，绝对运动为平面曲线。 v a = v e1 + v r1 （1） ② 活动销子 M 为动点，动系固结于杆 OA；牵连运动为绕 O 定轴转动，相对运动为 沿 OA 直线，绝对运动为平面曲线。
91
理论力学（第七版）课后题答案 哈工大.高等教育出版社
v a = v e2 + v r2
速度分析如图 8-11b 所示，由式（1） 、 （2）得 v e1 + v r1 = v e2 + v r2 方向 大小
（2） （3）
⊥ OM OM ⋅ ω 1
√ ？
⊥ OM OM ⋅ ω 2
√ ？
式（3）向 v e2 方向投影，得
ve va = sin(30° − ϕ ) sin 60°
所以
sin(30° − ϕ ) rω sin 60° 3 ϕ = 0° 时， v BC = ； rω （←） 3 ϕ = 30° 时， v BC = 0 v BC = ve =
ϕ = 60° 时， v BC = −
8-9
3 rω （→） 3 π 时点 C 的速度的大小。 4
y va vr
va v r
vr
60° 60°
杆直线运动，牵连运动为绕 O1 定轴转动。速度分析如图 8-7b1 所示。
va
A
ve
ϕ
ve
(a) (a)
60° A
(b) (b) 图 8-8 89
x
A
(c)
ω

哈尔滨工业大学 第七版 理论力学11

哈尔滨工业大学 第七版 理论力学11

上式代入式（4）得
FN = 4mB g − mB
11-10 如图 11-10a 所示，质量为 m 的滑块 A，可以在水平光滑槽中运动，具有刚性系 数为 k 的弹簧 1 端与滑块相连接，另 1 端固定。杆 AB 长度为 l，质量忽略不计，A 端与滑 块 A 铰接，B 端装有质量 m1，在铅直平面内可绕点 A 旋转。设在力偶 M 作用下转动角速度 ω 为常数。求滑块 A 的运动微分方程。
质量为 m2 的小车 D，由绞车拖动，相对于平台的运动规律为 s = 不计绞车的质量，求平台的加速度。
1 2 bt ，其中 b 为已知常数。 2
m2 g
y
S D
A
vr
m1 g FN
B
ω
v
(a) 图 11-8
x
(b)
解
受力和运动分析如图 11-8b 所示
& = bt vr = & s ar = & s& = b a Da = a e + a r = a AB + a r a Da = ar − a AB m2 (a r − a AB ) − m1a AB = F F = f (m1 + m2 ) g
1
(
)
开伞后，他受重力 mg 和阻力 F 作用，如图 11-2 所示。取铅直轴 y 向下为正， 根据动量定理有
mg y
图 11-2
mv 2 − mv1 = I y = (mg − F )t
由题知：当 t=5 s 时，有 v2=4.3 m/s 即
60 × (4.3 − 44.3) = (60 × 9.8 − F ) × 5
棱柱 B 接触水平面时系统质心坐标
a b ⎤ ⎡ m A (l − ) + m B ⎢l − (a − )⎥ 3 3 ⎦ 3(m A + m B )l − a (m A + 3m B ) + m B b ⎣ ′ = xC = m A + mB 3(m A + m B )
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

x
F1 40° F2
O
b
40° F2
a F1
θ
FR
O
F3 y
(a) 图 2-2 (b)
F3 c
(c)
解 （1）解析法 建立如图 2-2b 所示的直角坐标系 Oxy。
∑ Fx = F1 + F2 cos 40° = 2 000 N + 2 500 N ⋅ cos 40° =3 915 N
9
∑ Fy = F3 + F2 sin 40° = 1 500 N + 2 500 N ⋅ sin 40° =3 107 N FR = (∑ Fx ) 2 + (∑ Fy ) 2 =
第1章 静力学公理和物体的受力分析
1-1 画出下列各图中物体 A，ABC 或构件 AB，AC 的受力图。未画重力的各物体的自 重不计，所有接触处均为光滑接触。
FN 1
A
P FN 2
(a)
(a1)
FT A P FN
(b)
A
(b1)
FN1
P
B FN 3
FN 2
(c)
(c1)
FT B
FAy
P1 A P2
FAx
B
A
F Ax
C
FC
(d)
F Ay
(d1)
q
FDy
D
q
FB B
A
F Ax
C
FDx D FC
′ FDx ′ FDy
(d3)
(d2)
FAy FAx A
FCy
q
FAy
B P C
FCx
′ FBx
B
′ FBy
q
B FBy
(e2)
FAx
A
FBx
FCx
C
FCy
P
(e)
(e1)
(e3)
F1
C
FAy
F2
FBy
A
(f)
FAx
∠( FR , Fx ) = arccos(
( 3 915
2
+ 3 107 2
)
N = 4 998 N
∑ Fx 3 915 N ) = arccos( ) = 38°26′ 4 998 N FR
（2）几何法 作力多边形 Oabc，封闭边 Oc 确定了合力 FR 的大小和方向。根据图 2-2c，得
FR = ( F1 + F2 cos 40°) 2 + ( F3 + F2 sin 40°) 2
y FAB 30° B 30° FT P
(a) 图 2-3 (b)
x
FCB
解
取支架、滑轮及重物为研究对象，坐标及受力如图 2-3b 所示。由平衡理论得
∑ Fx = 0, ∑ Fy = 0,
− FAB − FCB cos 30° − FT sin 30° = 0 − FCB − sin 30° − FT cos 30° − P = 0
11
∑ F y = 0, FTA sinθ − W1 = 0
式（1） 、 （2）联立，解得
(2)
FT A =
W1 = sin θ
200 N 1 10 2 + 12
= 2 010 N
10 10 2 + 12
FT C = FT A cosθ = 2 010 N ×
因对称
= 2 000 N
FT B = FT A = 2 010 N
y
F2
ϕ
γ β
F1
(a) 图 2-4
θ
x
P
(b)
解
坐标及受力如图 2-4b 所示，由平衡理论得
∑ Fx = 0, F1 cos(θ + β ) − F2 sin ϕ = 0 F2 sin ϕ = F1 cos(θ + β )
10
(1)
∑ Fy = 0,
式(1)除以式(2)，得
F1 sin(θ + β ) − P + F2 cos ϕ = 0
B
A FA
C
E
C
E FEy
FEx
FC
(l2)’
FC
(l4)’
(l3)’
′ FAD
A
FCy FCx F1 B
C
(m)
(m1)
FAD
D E
H
F2
FAD
A
FE
(m2)
FH
(m3) 7
D
′ FAD
A
FN A
Fk
FOy FOx O
B
FN B
(n)
(n1)
FN1
B ′ FB
D
q
FN 2 FN 3
(n2)
F
B
D
FBx
B
(f1)
4
FCx F1 FAy
C
FCy
C
′ FCx
′ FCy
F2
FBy
A
FAx
B
(f3)
FBx
(f2)
F Ay
C
FB
FAx
A
B
P
(g)
(g1)
′ FCy
FT
F Ay
FAx
A
D
FT
FCx
FB
C B
C
′ FCx
P
(g2)
D
(g3)
F1 ′ FB B FAy A FAx
FCy F2
C
FB
FCx
B
将 FT=P=20 kN 代入上述方程，得 FAB = 54.6 kN （拉） ， FCB = −74.6 kN （压）
如图 2-4a 所示。 火箭的推力 2-4 火箭沿与水平面成 β = 25° 角的方向作匀速直线运动，
F1=100 kN，与运动方向成 θ = 5° 角。如火箭重 P=200 kN，求空气动力 F2 和它与飞行方向 的交角 γ 。
FAx
(a2)
(a3)
FN1
A P1 B P2
FN 3
FN 2
(b)
(b1)
′ FN
FN 1
A
B P2
FN 3
P1
FN
FN 2
(b3)
(b2)
3
FAy
A C D B P1
FAx
FN 2
P2
FN1
(c)
FT D A
(c1)
FAy FAx
FN 2
B
′ FT
P1
P2
FN1
(c2) (c3)
F Ay
q
FB D
F2 = 173 kN
如图 2-5a 所示，刚架的点 B 作用 1 水平力 F，刚架重量不计。求支座 A，D 的约
y F B C x
FA
(a) 图 2-5
A
(b)
D
FD
解 研究对象：刚架。由三力平衡汇交定理，支座 A 的约束力 FA 必通过点 C，方向如 图 2-5b 所示。取坐标系 Cxy ，由平衡理论得
F
FA
A
(o)
B
FC
C
(o1)
F
FE
E
FG
G
FB
A FA
(o2)
B ′ FBห้องสมุดไป่ตู้
D
D
F
F C C (o3)
图 1-2
FD
′ FD
FE FF E (o4)
8
第2章 平面汇交力系与平面力偶系
2-1 铆接薄板在孔心 A，B 和 C 处受 3 个力作用，如图 2-1a 所示。 F1 = 100 N ，沿铅 直方向； F3 = 50 N ，沿水平方向，并通过点 A； F2 = 50 N ，力的作用线也通过点 A，尺 寸如图。求此力系的合力。
(d)
(d1)
FA
A
F
FB
B
(e)
(e1)
1
q
F
FAy A FAx B
FB
(f)
(f1)
F
B
C FC FA
(g)
F Ay
A
(g1)
FC
C FAx
P1 P2 B
A
(h)
(h1)
B
F
C
FC
D
FAx
A
FAy
(i) (i1)
(j)
(j1)
B
FB
F
C
FAy A
(k) 2
P FAx
(k1)
FCA
C A
FAB
（1）轮 B，受力如图 2-7 b 所示。由平衡理论得
F （压） sin θ （2）节点 C，受力如图 2-7c 所示。由图 2-7c 知， F ' BC ⊥ FCD ，由平衡理论得 F ∑ Fx = 0, FBC − FCE cos(90° − 2θ ) = 0 ， FCE = BC sin 2θ ∑ Fy = 0 , FBC =
∑ Fx = 0, ∑ Fy = 0,
式(1)、(2)联立，解得
F − FA × FD − FA ×
2 5 1
=0 =0
（1） （2）
5
FA =
5 F = 1.12 F ， FD = 0.5 F 2
2-6 如图 2-6a 所示， 输电线 ACB 架在两线杆之间， 形成 1 下垂曲线， 下垂距离 CD=f=1 m，两电线杆距离 AB=40 m。电线 ACB 段重 P=400 N，可近似认为沿 AB 连线均匀分布。求 电线中点和两端的拉力。
C
FCy
FCx
90° − θ