计算流体力学与传热学大作业

大作业一、假设0,1x y≤≤的方腔内充满不可压缩流体，左、右、下壁面固定，上壁面以()22161u x x=--运动。

试求腔内的定常解。

（流体的物性取20℃的水。

同时，可以使用20℃的甘油作为对比）二、求解二维圆柱坐标中的Poisson-Nernst-Plack（PNP）方程，PNP方程来描述纳米孔内带电离子在浓度梯度及电场作用下的迁移行为和离子浓度分布。

具体方程如下所示：其中i=+/-，分别代表阴阳离子。

以及连续性方程:其中Φ是局域的电动势，c i表示i种离子的浓度，左侧边界上c+=10,c-=10，右侧边界上c+=1,c-=1。

j i表示离子流，D i为离子的扩散系数2×10-9，z i为离子的带电量,z i=1，T为溶液的温度,T=300。

e是电子电量1.602×10-19，ε0×εr=80，k B为波尔兹曼常数,k B=1.38×10-23。

边界上的电势Φ由高斯定律决定：对于带电的纳米孔壁（图中红色实线所示），有σs=σ（σ为纳米孔的表面电荷密度，数值为0.05）；对于其余区域有σs=0。

离子流j i在边界上的法向分量为零，即，求解φ、浓度c i以及ij的场。

（备注：求解区域为一圆柱形区域，长度为1200，直径为d=10。

建议步骤：可首先猜想浓度场c+和c-，并求解电动势场φ，通过连续性方程修正离子流场ij）大作业要求：1-3人为一组，完成以上任选一题目。

最终截止时间为12月26日。

在最终截止时间之前可以提交1次，若不满意得分可以继续修改。

大作业以报告形式提交，内容至少包括计算域的网格划分、方程的离散化、边界条件的处理、计算收敛的判据、计算的结果、结果的图形化显式、结果分析等。

源代码作为附录附在报告的最后。

计算流体⼒学⼤作业管壳式换热器壳程流动传热数值模拟机械与动⼒⼯程学1．问题描述⼀⼯业⽤换热器，功能是加热壳程介质。

管程流体为上⼀⼯段的⾼温废液。

近似认为废液在管内流动时，管壁温度恒定。

2．软件环境表1 软件环境前处理软件计算软件后处理软件Gambit2.3.6/Pro-e ANSYS-Fluent15.0 Fluent15.0其他软件如截图⼯具，图⽚编辑软件等不逐⼀列举。

3．模型建⽴表2 换热器⼏何参数折流板尺⼨依据GB151选取。

在gambit中建⽴壳程流体的⽔⼒模型，建模时进⾏必要的简化，忽略折流板和壳体之间的间隙，忽略定距管和拉管。

从观察中可以看出管壳式换热器是左右对称的装置，为了减少计算的时间，提⾼⼯作的效率，可以去对称的⼀半进⾏计算，然后由软件处理得到结果。

图1 ⼏何模型4．⽹格划分⽹格总数1649730。

折流板之间的流动区域选⽤⾮结构化⽹格，以便于⽹格划分。

⽹格质量检查复合要求。

图2 ⽹格模型由于本⽂只需得到壳程的⼤致流动情况，不要要精确解，因此为了节约⽹格划分⼯作量，没有划分边界层⽹格。

图3⽹格局部放⼤5．边界条件设置表3 边界条件设置进⼝流速取2m/s，分别取壳程⾛空⽓和⽔两种介质，⽐较壳程流体对传热的影响。

打开能量⽅程；湍流模拟采⽤k-ε⽅程；迭代求解⽅法默认。

6．计算结果当壳程⾛⽔时，出⼝温度为323K，温度升⾼了25℃。

图4壳程⾛⽔时温度分布图5壳程⾛⽔时流速分布图6壳程⾛⽔时折流板处的回流当壳程⾛空⽓时，出⼝温度为378K，温度升⾼了65℃。

与管壁温度⼀致。

图7壳程⾛空⽓时温度分布图8壳程⾛空⽓时流速分布图8壳程⾛空⽓时折流板处的回流从两种流体的对⽐可以看出，由于空⽓和⽔的粘性都很⼩，所以两者的流动状态并没有显著差别，回流区的位置和⼤⼩也基本⼀直。

因此可以说明，当⼊⼝速度⼀致时，在低粘度，不考虑重⼒的前提下，流体的性质对换热器壳程内流速分布的影响可以忽略。

另外从加热效果的⾓度讲，虽然壳程⾛空⽓时出⼝温度⽐较⾼，但空⽓的密度低，⽐热低，因此实际上带⾛的管程热量只有壳程⾛⽔时的千分之⼀。

数值计算大作业一、用数值方法求解尺度为100mm×100mm 的二维矩形物体的稳态导热问题。

物体的导热系数λ为1.0w/m·K。

边界条件分别为： 1、上壁恒热流q=1000w/m2; 2、下壁温度t1=100℃； 3、右侧壁温度t2=0℃; 4、左侧壁与流体对流换热，流体温度tf=0℃，表面传热系数 h 分别为1w/m2·K、10 w/m2·K、100w/m2·K 和1000 w/m2·K;要求：1、写出问题的数学描述；2、写出内部节点和边界节点的差分方程；3、给出求解方法；4、编写计算程序(自选程序语言)；5、画出4个工况下的温度分布图及左、右、下三个边界的热流密度分布图；6、就一个工况下（自选）对不同网格数下的计算结果进行讨论；7、就一个工况下（自选）分别采用高斯迭代、高斯——赛德尔迭代及松弛法（亚松弛和超松弛）求解的收敛性（cpu 时间，迭代次数）进行讨论；8、对4个不同表面传热系数的计算结果进行分析和讨论。

9、自选一种商业软件（fluent 、ansys 等）对问题进行分析，并与自己编程计算结果进行比较验证（一个工况）。

（自选项）1、写出问题的数学描述 设H=0.1m微分方程 22220t tx y∂∂+=∂∂x=0，0<y<H ：()f th t t xλ∂-=-∂ 定解条件 x=H ，0<y<H ：t=t 2 y=0，0<x<H ：t=t1t 1t 2h ；t fq=1000 w/m 2y=H ，0<x<H ：tq yλ∂-=∂ 2、写出内部节点和边界节点的差分方程 内部节点：()()1,,1,,1,,122220m n m n m nm n m n m n t t t t t t x y -+-+-+-++=∆∆左边界： (),1,,1,1,,,022m n m n m n m nm n m n f m n t t t t t t x x h y t t y y y xλλλ-++---∆∆∆-+++∆=∆∆∆右边界： t m,n =t 2上边界： 1,,1,,,1,022m n m n m n m nm n m n t t t t t t y y q x x x x yλλλ-+----∆∆∆+++∆=∆∆∆ 下边界： t m,n =t 13、求解过程利用matlab 编写程序进行求解，先在matlab 中列出各物理量，然后列出内部节点和边界节点的差分方程，用高斯-赛德尔迭代法计算之后用matlab 画图。

传热学数值计算大作业传热学数值计算大作业一选题《传热学》第四版P179页例题 4-3二相关数据及计算方法1．厚2δ=0.06m的无限大平板受对称冷却，故按一半厚度作为模型进行计算2. δ=0.03m，初始温度t0=100℃,流体温度t∞=0℃；λ=40W/(m.K),h=1000W/(m2.K),Bi=h*△x/λ=0.25；3.设定Fo=0.25和Fo=1两种情况通过C语言编程（源程序文件见附件）进行数值分析计算；当Fo=0.25时，Fo<1/(2*(1+Bi)),理论上出现正确的计算结果；当Fo=1时，Fo>1/(2*(1+Bi))，Fo>0.5,理论上温度分布出现振荡，与实际情况不符。

三网格划分将无限大平面的一半划分为6个控制体，共7个节点。

△x=0.03/N=0.03/6=0.005，即空间步长为0.005m四节点离散方程绝热边界节点即i=1时，tij+1=2Fo△ti+1j+(1-2Fo△)tij 内部节点即0tij+1=tij（1-2Fo△Bo△-2Fo△）+2Fo△ti-1j+2Fo△Bo△tf五温度分布线图（origin）六结果分析1 空间步长，时间步长对温度分布的影响空间步长和时间步长决定了Bo和Fo，两者越小计算结果越精确，但同时计算所需的时间就越长。

2 Fo数的大小对计算结果的影响编程时对Fo=1及0.25的情况分别进行了计算，发现当Fo=1时，各点温度随时间发生振荡，某点的温度高反而会使下一时刻的温度变低，违反了热力学第二定律，因此在计算中对Fo的选取有限制。

为了保证各项前的系数均为正值，对于内节点，Fo>0.5；对于对流边界节点，Fo<1/(2*(1+Bi))。

3 备注在Fo=0.25时，为了反映较长时间后温度的分布，取T=600,并选取了其中部分时刻的温度输出进行画图。

图像显示，随着时间的增长，各点温度趋向一致。

而当Fo=1时由于结果会出现振荡，只取T=6观察即可。

课程综合作业课程名称： _________ 计算流体力学 ___________专业班级： _______________ 研究方向：_______________ 学生姓名： ________________ 学号：________________完成日期： _______________________________________计算流体力学课程综合报告1. 简介计算流体动力学（Computational Fluid Dynamics ，简称CFD是通过计算机数值计算和图像显示，对包含有流体流动和热传导等相关物理现象的系统所做的分析。

其基本思想为: 把原来在时间域及空间域上连续的物理量的场，如速度场和压力场，用一系列有限个离散点上的变量值的集合来代替，通过一定的原则和方式建立起关于这些离散点上场变量之间关系的代数方程组，然后求解代数方程组获得场变量的近似值。

CFD可以看作是在流动基本方程（质量守恒方程、动量守恒方程、能量守恒方程）控制下对流动的数值模拟。

通过这种数值模拟，我们可以得到极其复杂问题的流场内各个位置上的基本物理量（速度、压力、温度、浓度等）的分布，以及这些物理量随时间的变化情况，确定旋涡分布特性、空化特性及脱流区等。

还可据此算出相关的其他物理星，如旋转式流体机械的转矩、水力损失和效率等。

此外，与CAD联合，还可进行结构优化设计等。

2. 计算流体动学的特点:①流动问题的控制方程一般是非线性的，自变量多，计算域的几何形状和边界条件复杂，很难求得解析解，而用CFD方法则有可能找出满足工程需要的数值解。

②可利用计算机进行各种数值试验，例如，选择不同流动参数进行物理方程中各项有效性和敏感性试验，从而进行方案比较。

③它不受物理模型和实验模型的限制，省钱省时，有较多的灵活性，能给出详细和完整的资料，很容易模拟特殊尺寸、高温、有毒、易燃等真实条件和实验中只能接近而无法达到的理想条件。

④数值解法是一种离散近似的计算方法，依赖于物理上合理、数学上适用、适合于在计算机上进行计算的离散的有限数学模型，且最终结果不能提供任何形式的解析表达式，只是有限个离散点上的数值解，并有一定的计算误差。

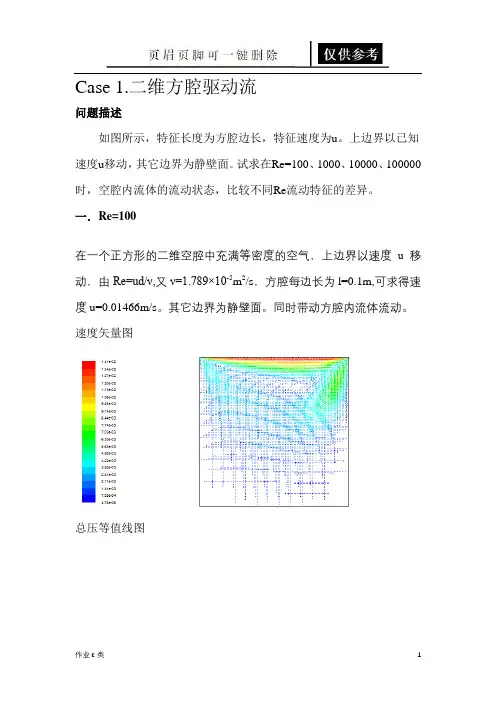
Case 1.二维方腔驱动流问题描述如图所示，特征长度为方腔边长，特征速度为u。

上边界以已知速度u移动，其它边界为静壁面。

试求在Re=100、1000、10000、100000时，空腔内流体的流动状态，比较不同Re流动特征的差异。

一．Re=100在一个正方形的二维空腔中充满等密度的空气，上边界以速度u移动，由Re=ud/ν,又ν=1.789×10-5m2/s，方腔每边长为l=0.1m,可求得速度u=0.01466m/s。

其它边界为静壁面。

同时带动方腔内流体流动。

速度矢量图总压等值线图水平中心线（y=0）上竖直速度分量(v)分布V-x竖直中心线（x=0）上水平速度分量（u）分布U-y不同Re方腔内流函数的分布情况Re=1000Re=10000Re=100000不同Re方腔内总压分布情况Re=1000Re=10000Re=100000方腔驱动流是数值计算中比较简单，具有验证性的一种流动情况，受到很多研究者的关注。

本文通过不同雷诺数观察方腔流动，所得结论如下：（1）当雷诺数较小时，腔中涡旋位置贴近腔体上壁面中部，随着雷诺数Re的增加，涡旋位置逐渐向下方靠近。

（2）随着雷诺数的增加，涡旋的位置逐渐靠近腔体中心。

（3）方腔壁面上的速度大于其他地方的速度。

Case2.圆管的沿程阻力1.问题描述如图，常温下，水充满长度l的一段圆管。

圆管进口存在平均速度u，壁面的当量粗糙高度为0.15mm。

试求在不同雷诺数下，计算该圆管的沿程阻力系数λ，分析比较Re与λ 的关系。

出口截面速度分布如下可见，出口截面流速分布较为明显，呈同心圆分布，内层流速偏大，外层靠近壁面处流速几乎为0，分层更为严重，边界层很薄。

Y=0截面速度分布图可以看出圆管水流湍流入口段及之后的流速发展趋势，而且显示流速变化的规律更为明显。

轴线压降圆管湍流中的压降，除了入口段压强分布因流速急剧上升而下降稍快外，管道后端速度呈充分发展状态，压降呈线性，即△p随L 的增加而降低。

传热学数值计算大作业传热学是研究物体内部和之间热量传递的科学，其应用范围广泛，例如在工程领域中，传热学的数值计算被广泛用于优化热传递过程，提高能源利用效率。

本文将介绍传热学数值计算的大作业，主要内容包括问题陈述、计算方法和结果分析等。

问题陈述：本次大作业的问题是研究一个热管的热传递特性。

具体来说，热管由内外两个半圆形的金属管组成，内管壁与外管壁之间是一种导热的传热介质。

问题要求计算热管内外壁的温度分布，并分析传热过程的效率和优化热管的设计。

计算方法：计算热传递过程需要运用一些热传导定律和传热方程。

首先，根据Fourier 热传导定律，可得到内外壁的温度梯度。

然后，使用热传导方程来描述热传递过程，其中包括热扩散项和传热源项。

在计算热传导时需要注意材料的热导率、导热介质的热传导性质等参数。

在计算中，可以使用一些数值方法来离散化热传导方程，例如有限差分法、有限元法等。

其中，有限差分法是一种常见的数值方法。

通过将热传导方程中的导数用差分表达式替代，可以将偏微分方程转化为代数方程。

然后，可以使用迭代方法求解代数方程，得到温度分布的数值解。

结果分析：通过数值计算，可以得到热管内外壁的温度分布。

根据温度分布，可以分析热传递过程中的热流分布和传热效果。

例如，可以计算内外壁之间的热传导率，评估热管的热传递效率。

同时，可以对热管的设计进行优化。

例如，可以通过改变热导率高低、加大导热介质的厚度等方式，来提高热传递效果。

此外，对于热管的材料选择和导热介质的设计，还可以进行参数敏感性分析。

通过改变各个参数的数值，可以研究其对热传递过程的影响程度。

这有助于优化热管的设计，并提供一些实际应用方面的建议。

总结：传热学的数值计算是研究热传递现象的重要工具，可以帮助我们深入了解传热过程，优化传热装置的设计。

通过本次大作业，我们可以学习和练习传热学数值计算的方法和技巧，提升对传热现象的理解和分析能力。

希望通过这次大作业，能够更好地应用所学知识，解决实际问题。

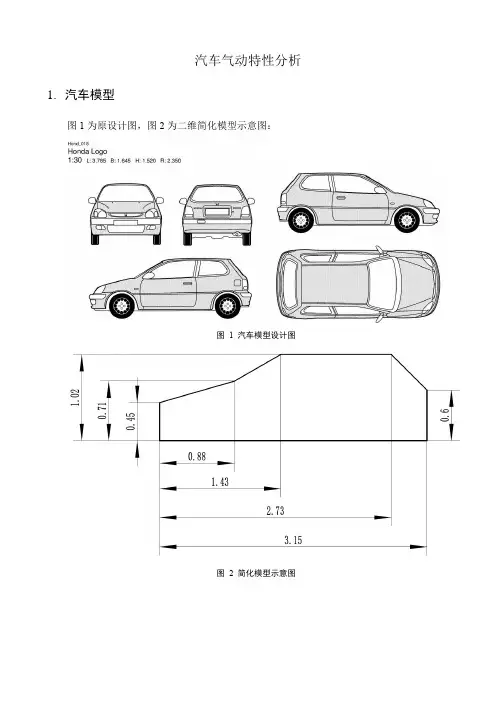
汽车气动特性分析1.汽车模型图1为原设计图，图2为二维简化模型示意图：图 1 汽车模型设计图图 2 简化模型示意图2. 题目要求流体属性：空气静温T=300K 、静压Pa p 510015.1⨯=、气体常数R=8314./29.、比热比4.1=γ，只计算层流。

（1）工况一：汽车在地面行驶，速度分别为：12、120、240km/h ，对应马赫数取为Ma = 0.01、0.1、0.2。

（2）工况二：假设汽车在天空飞行，速度分别为：Ma = 0.2、0.8、2.0。

（3）分别采用基于密度的算法和基于压力的算法。

输出结果：（1）网格生成推荐采用ICEM ，要求在Tecplot 中显示温度场、压力场、马赫数分布、流线图；（2）对比分析当Ma = 0.2时工况1和工况2流场的差别。

（3）对于工况二，Ma = 2.0，基于密度的算例在原网格(大约100*80)基础上加密1倍(200*160)，分析网格对计算结果的影响。

（4）比较采用基于密度的算法和基于压力的算法的收敛情况。

（5）分析汽车的阻力和升力随行驶速度的变化规律。

（6）在完成二维计算的基础上，尝试采用三维模型计算可获得加分(工况1或者工况2，Ma = 0.2)。

3. 输出结果3.1. 工况一网格如图3所示（140*80）：图 3 工况一网格3.1.1.温度场图 4 基于密度0.01马赫图 5 基于密度0.1马赫图 6 基于密度0.2马赫注：初始温度设置为300K 图7 基于压力0.01马赫图8 基于压力0.1马赫图9 基于压力0.2马赫3.1.2.压力场图10 基于密度0.01马赫图11 基于密度0.1马赫图12 基于密度0.2马赫注：初始压强设置为101325Pa 图13 基于压力0.01马赫图14 基于压力0.1马赫图15 基于压力0.2马赫3.1.3.马赫数分布图16 基于密度0.01马赫图17 基于密度0.1马赫图18 基于密度0.2马赫图19 基于压力0.01马赫图20 基于压力0.1马赫图21 基于压力0.2马赫3.1.4.流线图图22 基于密度0.01马赫图23 基于密度0.1马赫图24 基于密度0.2马赫图25 基于压力0.01马赫图26 基于压力0.1马赫图27 基于压力0.2马赫3.2.工况二网格如图28所示（100*80）：图28 工况二网格（计算结果图见下一页）3.2.1.温度场图29 基于密度0.2马赫图30 基于密度0.8马赫图31 基于密度2马赫注：初始温度设置为300K 图32 基于压力0.2马赫图33 基于压力0.8马赫图34 基于压力2马赫3.2.2.压力场图35 基于密度0.2马赫图36 基于密度0.8马赫图37 基于密度 2.0马赫注：初始压强设置为101325Pa 图38 基于压力0.2马赫图39 基于压力0.8马赫图40 基于压力 2.0马赫3.2.3.马赫数分布图41 基于密度0.2马赫图42 基于密度0.8马赫图43 基于密度 2.0马赫图44 基于压力0.2马赫图45 基于压力0.8马赫图46 基于压力 2.0马赫3.2.4.流线图图47 基于密度0.2马赫图48 基于密度0.8马赫图49 基于密度 2.0马赫图50 基于压力0.2马赫图51 基于压力0.8马赫图52 基于压力 2.0马赫3.3.对比分析当Ma = 0.2时工况1和工况2流场的差别3.4.对于工况2，Ma = 2.0，基于密度的算例在原网格(大约100*80)基础上加密1倍(200*160)，分析网格对计算结果的影响网格对比如下：图53 100*80网格图54 200*160网格计算结果如下所示：总结：加密网格后结果的连续性较差。

中科大计算流体力学CFD之大作业一中科大计算流体力学CFD之大作业一中科大计算流体力学(CFD)课程是一门非常实践性的课程，着重于学生对流体流动过程的数值模拟和分析。

在课程结束前的大作业一是一个很好的机会，通过完成一个真实流体力学问题的数值模拟，学生可以将所学的知识应用到实际的问题中，提高对流体流动过程的理解。

我选择的大作业一是模拟一个风扇在房间中的空气流动。

这是一个常见的问题，也是一个比较复杂的数值模拟任务。

通过模拟风扇产生的气流，我们可以了解风扇的性能，以及气流对房间内温度和空气质量的影响。

在开始模拟之前，首先需要确定模拟的几何模型。

我选择了一个具有一个大门和一个窗户的简单房间模型。

这个模型符合实际情况，而且不会太复杂，方便进行数值模拟。

接下来，需要确定模拟中的物理模型和边界条件。

根据风扇产生的气流特性，我采用了湍流模型，并对大门和窗户设置了适当的进出口边界条件。

接下来是最关键的一步，即选择和优化数值模拟的方法。

我使用了基于有限体积法的求解器，在计算网格上进行离散，将房间划分为小的网格单元。

然后，我对求解器的算法和网格进行了优化，以提高计算效率和精度。

通过进行一系列的数值实验，我成功地优化了数值模拟方法，并获得了较为准确的结果。

最后，我对模拟结果进行了分析和讨论。

通过对不同位置和高度的温度和速度分布进行分析，我得出了以下结论：风扇对房间中的温度和空气质量有着显著影响；风扇的位置和角度对气流的分布和速度分布有着重要影响；房间的尺寸和几何形状也会对气流分布产生影响。

通过完成这个大作业一，我不仅提高了CFD方法的理论知识，还掌握了实际应用的技能。

在模拟中，我还学习了如何进行参数优化和结果分析。

最重要的是，我进一步认识到了流体力学的复杂性和重要性。

总之，中科大计算流体力学(CFD)大作业一是一次非常有意义的学习经历。

通过模拟一个风扇在房间中的空气流动，我不仅巩固了所学的知识，还学会了如何应用这些知识解决实际问题。