4-1 齐次性和叠加定理

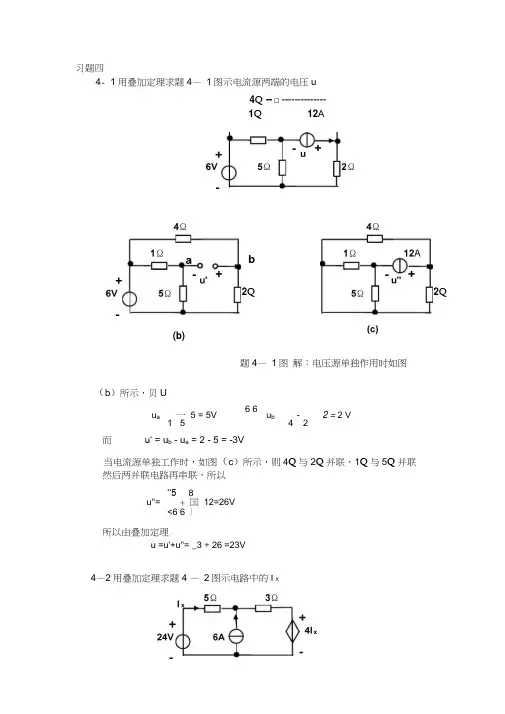
习题四4- 1用叠加定理求题4— 1图示电流源两端的电压u题4— 1图 解：电压源单独作用时如图（b ）所示，贝U6 6u a一 5 = 5Vu b- 2 = 2 V1 54 2而u‘ = u b - u a = 2 - 5 = -3V当电流源单独工作时，如图（c ）所示，则4Q 与2Q 并联，1Q 与5Q 并联然后两并联电路再串联，所以‘‘58u''=+ 国 12=26V <6 6丿所以由叠加定理u =u'+u''= _3 + 26 =23V4—2用叠加定理求题4 — 2图示电路中的I Xb2Q4Q -- □ -------------- 1Q 12A(b)2Q解：电压源单独作用时的电路如图（b）所示，则5 3 I x 41 x = 24 解得I x = 2A电流源单独作用时的电路如图（c）所示，图中虚线为网孔电流，则5I''x 36 I''x 4I“x=0 解得I”x=「1.5A所以I x=I'x T'X=2-1.5=0.5A4 —3图示电路中的独立电压源和独立电流源发出的4 —3用叠加定理求题功率。

4Q(b)+O 2V4Q i'' ii'°2i''(c)i''4Q+2V(b) 3Q41x41(c)x4Q2Ai4Q题4 —3图解：电流源单独作用时的电路如图（b）所示，则i1 =2A i，=0则u；=4i；-2i< 8V电压源单独作用时的电路如图（b）所示，则，，2 ,, ,,i i 0.5A i - -i i = 0.5A4则u，，= 2 _ 2i，，= 1V所以由叠加定理h =i；• i；=2—0.5=1.5A5 = u1 u；，= 8 1 = 9V可得电压源和电流源的功率分别为P2V一2i；一3WP2A=2u；=18W4-4题4—4图示电路中，N R为电阻网络，由两个电流源供电。

第4章 电路的若干定理 (Circuit Theorems )4.1 叠加定理 (Superposition Theorem)4. 2 替代定理 (Substitution Theorem )4.3 戴维南定理和诺顿定理(Thevenin -Norton Theorem )4. 5＊特勒根定理 (Tellegen’s Theorem )4. 6 互易定理 (Reciprocity Theorem )4. 7＊对偶原理 (Dual Principle )4.4 最大功率传输定理(Maximum Power Transfer Theorem )4.1 叠加定理 (Superposition Theorem )一、线性电路的齐次性和叠加性线性电路：由线性元件和独立源构成的电路。

1.齐次性（homogeneity)(又称比例性，proportionality)电路x (t )y (t )+-+-齐次性：若输入x (t ) → 响应y (t ) ，则输入K x (t) → K y (t ) 电路K x (t )K y (t )+-+-2.叠加性（superposition)若输入x 1(t ) → y 1(t )(单独作用） , x 2(t ) → y 2(t ) … x n (t ) → y n (t )则x 1(t ) 、x 2(t ) … x n (t ) 同时作用时响应y (t )= y 1(t )+ y 2(t )+ … +y n (t )注： x 1(t ) … x n (t ) 可以是不同位置上的激励信号电路x 1(t )y (t )+-+-x 2(t )x n (t )++--3.线性=齐次性+叠加性(t) →y1(t)(单独作用）若输入x1x2(t) →y2(t)…x n(t) →y n(t)则:K1x1(t) +K2x2(t) +…+K n x n(t) →K1y1(t)+ K2y2(t)+ … + K n y n(t)注：齐次性是一种特殊的叠加性。

叠加定理与齐次定理的关系及应用姓名：常永娟学号：20075042095院系：物理电子工程学院专业：电子信息工程指导老师：余本海职称：副教授摘要：讨论了线性电路中叠加定理和齐次定理的证明及应用，并讨论了两者之间的关系，即：齐次定理可从叠加定理推出，电路满足叠加定理也一定满足齐次定理，同时说明了应用两个定理时应注意的问题。

关键词：线性电路；叠加定理；齐次定理The relationship between Superposition theorem andHomogeneous theorem and its application Abstract：The proof and applications of Superposition theorem and Homogeneous theorem are discussed respectively in this paper．And the relationship between Superposition theorem and Homogeneous theorem has been proven too，namely：The Homogeneous theorem may promote from the Superposition theorem．The Superposition theorem is satisfied in the electric circuit certainly to be also Homogeneous theorem is satisfied．Account for some problems we should notice when we use the Superposition theorem or the Homogeneous theorem．Key Words：Linear circuit ；the Superposition theorem ；the Homogeneous theorem引言叠加定理与齐次定理在线性电路分析中起着重要作用，它们是分析线性电路的基础，线性电路中很多定理都与叠加定理及齐次定理有关。

简述叠加定理和齐次定理
叠加定理（Superposition principle）是一个物理学原理，它指出在线性系统中，如果系统对于输入的响应满足线性叠加的条件，则多个输入的响应可以通过将每个输入的响应分别计算然后相加得到。

在电路学中，叠加定理可以用来简化复杂的电路分析。

根据叠加定理，可以将多个电源或信号源的作用分解为独立的部分，并分别计算每个部分产生的效应，最后将它们相加得到整个系统的响应。

齐次定理（Homogeneity principle）是线性系统理论中的一个基本原则。

它指出，如果将输入信号的振幅（倍数）进行缩放，系统的输出信号的振幅（倍数）也会以相同的比例进行缩放。

简而言之，齐次定理表明线性系统对于输入信号的幅度具有比例性。

齐次定理的应用非常广泛，特别是在线性差分方程、微分方程和物理系统的研究中。

通过使用齐次定理，可以简化复杂系统的分析和计算，并帮助研究者更好地理解系统的行为和性质。

叠加定理和齐次定理一、叠加定理图 4.1-1 （ a ）所示电路中，有两个激励，即独立电压源和独立电流源，现欲求 R1 支路上的电流。

用网孔电流法求解。

设网孔电流分别为，其方向都为顺时针方向，如图 4.1-1 （ a ）所示。

网孔方程为解方程得，网孔电流为所以， R1 支路电流为其中，可以看成是当时的的值，则可看成是当时的的值。

如图 4.1-1 （ b ）、（ c ）。

令则其中， k1 ， k2 是由电路的结构和元件的参数决定的。

对于线性电路， R1 、 R2 、 R3 都是常数，不会随着电路中激励的数目和大小的改变而改变，所以 k1 ， k2 也不会随激励的改变而改变，即为常数。

i 是激励的一次线性函数。

叠加定理（ superposition theorem ）由线性元件组成的线性电路，当 n 个激励共同作用时，在某条支路上产生的响应，等于各个激励单独作用时产生的响应的代数和。

其中，表示 n 个激励（独立电压源或独立电流源）， r 表示某条支路上产生的响应（电压或电流）。

都是常数，其大小由电路的结构和元件的参数决定。

应用叠加定理时应注意的问题1 ．叠加定理是线性电路的一个重要性质，因此只适用于线性电路，对于非线性电路则不能使用。

2 ．当某个激励单独作用时，其他激励均取 0 。

将独立电压源取 0 ，是把电压源短路，将独立电流源取 0 是把电流源开路。

3 ．受控源虽然带有电源的性质，但不直接起激励作用，因此，在叠加定理中，受控源一般不单独作用，而是把受控源当电路元件处理。

当独立源单独作用时，受控源应保留在电路中。

4 ．叠加定理只适用于计算电压或电流，而不适用于计算功率，因为功率与电压、电流之间的关系不是线性关系。

例 4.1-1 图 4.1-2 （ a ）所示电路，试用叠加定理求 3 Ω电阻上的电压 U 及功率。

解：电路中有两个独立源共同激励。

1 、当 12V 电压源单独激励时，电流源应视为 0 ，即把电流源开路，如图 4.1-2 （ b ）所示。