逻辑联结词(2)
- 格式:ppt
- 大小:651.50 KB
- 文档页数:17

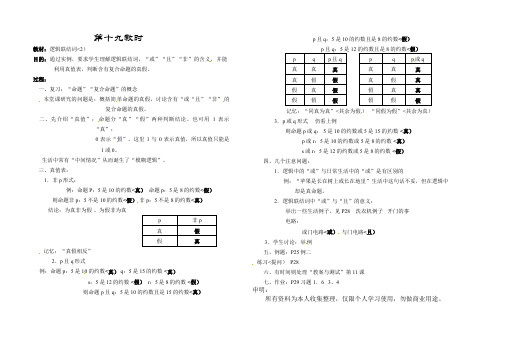
第十九教时教材:逻辑联结词<2)目的:通过实例,要求学生理解逻辑联结词,“或”“且”“非”的含义,并能利用真值表,判断含有复合命题的真假。
过程:一、复习:“命题”“复合命题”的概念本堂课研究的问题是:概括简单命题的真假,讨论含有“或“且”“非”的复合命题的真假。
二、先介绍“真值”:命题分“真”“假”两种判断结论。
也可用1表示“真”;0表示“假”。
这里1与0表示真值,所以真值只能是1或0。
生活中常有“中间情况”从而诞生了“模糊逻辑”。
三、真值表:1.非p形式:例:命题P:5是10的约数<真)命题p:5是8的约数<假)则命题非p:5不是10的约数<假)非p:5不是8的约数<真)结论:为真非为假、为假非为真记忆:“真假相反”2.p且q形式例:命题p:5是10的约数<真) q:5是15的约数<真)s:5是12的约数<假) r:5是8的约数<假)则命题p且q:5是10的约数且是15的约数<真)p且q:5是10的约数且是8的约数<假)12或记忆:“同真为真”<其余为假)“同假为假”<其余为真)3.p或q形式仍看上例则命题p或q: 5是10的约数或5是15的约数<真)p或r:5是10的约数或5是8的约数<真)s或r:5是12的约数或5是8的约数<假)四、几个注意问题:1.逻辑中的“或”与日常生活中的“或”是有区别的例:“苹果是长在树上或长在地里”生活中这句话不妥,但在逻辑中却是真命题。
2.逻辑联结词中“或”与“且”的意义:举出一些生活例子,见 P28 洗衣机例子开门的事电路:或门电路<或)与门电路<且)3.学生讨论:举例五、例题:P25例二练习<提问) P28六、有时间则处理“教案与测试”第11课七、作业:P29 习题1.6 3、4申明:所有资料为本人收集整理,仅限个人学习使用,勿做商业用途。

1.3.1 简单的逻辑联结词(二)班级: 姓名: 编者:陆祖银 高二数学备课组 学习目标 "与“否命题”之间的区别和联系.2.理解“且”“或’’“非"构成的复合命题与集合的“交”“并”“补"之间的关系. 自主探究命题的否定与否命题是两个不同的概念,只有弄清它们之间的区别才小会出错.⑴概念:命题的否定是直接对命题的进行否定;而否命题则是对原命题的________和________分别否定后组成的命题.⑵构成:对于“若p ,则q ”形式的命题,其否定一般为“若____,则____”,也就是不改变条件,只否定结论;而其否命题则为“若________,则________”,既否定命题的条件,又否定命题的结论.2.逻辑联结词“且”“或”“ 非”与集合中“交”“ 并”“ 补”密切相连.例如,交集、并集、补集的定义分别是________________A B = ;________________A B = ;A C u = .3.常见关键词的否定互动探究例题1、写出下列命题的形式否定形式和否命题:(1)面积相等的三角形是全等三角形;(2)若22220m n a b +++=,则实数,,,m n a b 全为零; (3)若0xy =,则0x =或0y =.(4)若0m >,则关于x 的方程20x x m +-=有实根; (5)若x 、y 都是奇数.则x y +是奇数;(6)若0abc =,则a 、b 、c 中至少有一个为0.当堂检测1.命题p :x π=是|sin |y x =的一条对称轴,q :2π是|sin |y x =的最小正周期,下列命题:①p 或q ,②p 且q ,③非p ,④非q ,其中真命题有 ( )A .0个B .1个C .2个D .3个2.下列各组命题中.满足“p q ∨”真,“p q ∧”假, “p ⌝”为真的命题的个数是 ( ) ①p :0φ=; q :0φ∈;②p :在ABC 中,若cos 2cos 2A B =,则A B =; q :sin y x =在第一象限是增函数;③p :a b +≥,)a b ∈R ;q :||x x >的解集为(,0)-∞.A .0B .1C .2D .33.设p :2x >或23x <;q :2x >或1x <-,则p ⌝是q ⌝的________条件. 4.已知p :|23|1x ->;q :2106x x >+-,则p ⌝是q ⌝的________条件.知识拓展命题甲;关于x 的不等式22(1)x a x a +-+≤0的解为φ;命题乙:函数2(2)x y a a =-为增函数;(1)甲、乙至少有一个是真命题;(2)甲、乙中有且只有一个真命题.分别求出符合(1)(2)的实数a 的取值范围.作业18页习题1.3 A 组 第3题和B 组第1题自我评价)A.非常好 B.较好 C.一般 D.较差 E.很差。


逻辑联结词“且”“或”“非”(二) 日期:学习目标:加深对逻辑联结词“或”“且”“非”含义的理解,并能熟练地判定由“或”“且”“非”组成新命题的真假. 重点难点:“或”“且”“非”构成命题的真假判断;利用“或”“且”“非”构成命题的真假判断求解有关字母范围.学习过程:一、自学课本,解决课后练习;二、交流探究:1、判断一个复合命题的真假,一般有三个步骤:①确定复合命题的构成形式及其中简单命题的内容;②判断各简单命题的真假; ③利用真值表判断复合命题的真假.2、在考虑命题“非p ”时,往往需要对一些词语进行否定,常见的一些词语的否定词如下表:1、写出由下列各组命题构成的“p 或q ”、“p 且q ”、“非p ”形式的命题,并判断他们的真假: ⑴p :3是质数,q :3是偶数;⑵p :方程220x x +-=的解是2x =-,q :方程220x x +-=的解是1x =.思考:(2)中,命题“p 或q ”与命题“方程220x x +-=的解是2x =-或1x =”有区别吗?2、判断下列命题的真假:(1)43≥; (2)44≥; (3)45≥.3、已知命题p :关于x 的方程210x mx ++=有两个不相等的负实根;命题q :关于x 的方程()244210x m x +-+=无实根,如果复合命题“p 或q ”为真,“p 且q ”为假,求出满足要求的m 的取值范围.4、以下判断正确的是 ( ) A .若p 是真命题,则“p 且q ”一定是真命题 B .命题“p 且q ”是真命题,则命题p 一定是真命题 C .命题“p 且q ”是假命题时,命题p 一定是假命题 D .命题p 是假命题时,命题“p 且q ”不一定是假命题5、如果命题“p 或q ”与命题“非p ”都是真命题,那么 ( ) A .命题p 不一定是假命题 B .命题q 一定是真命题C .命题q 不一定是真命题D .命p 与命题q 的真值相同6、若p 、q 是两个简单命题,且“p 或q ”的否定是真命题,则必有 ( ) A .p 真q 真 B .p 假q 假 C .p 真q 假 D .p 假q 真7、如果命题“p 或q ”是真命题,“非p ”是假命题,那么 ( ) A .命题p 一定是假命题 B .命题q 一定是假命题C .命题q 一定是真命题D .命题q 是真命题或者假命题 8、分别写出下列命题的逆否命题(含有逻辑联结词“或”,“且”的否定)⑴若00,0===y x xy 或则 ⑵若0,0,022===+y x y x 则四、概括升华:五、温故知新:习题1-4补充:1已知下列三个方程:24430x ax a +-+=,()2210x a x a +-+=,2220x ax a +-= 至少有一个方程有实根,求实数a 的取值范围.1、解:⑴“p 或q ”:3是质数或3是偶数; “p 且q ”:3是质数且3是偶数; “ 非 p ”:3不是质数.因为p 真,q 假,所以“p 或q ”为真,“p 且q ”为假,“非p ”为假. ⑵“p 或q ”:方程220x x +-=的解是2x =-或方程220x x +-=的解是1x =; “p 且q ”:方程220x x +-=的解是2x =-且方程220x x +-=的解是1x =; “ 非 p ”:方程220x x +-=的解不是2x =-. 因为p 假,q 假,所以“p 或q ”为假,“p 且q ”为假,“非p ”为真.有区别.命题“方程220x x +-=的解是2x =-或1x =”中的“或”不是逻辑联结词,因此它不是“p 或q ”形式的命题.2、解:(1)“43≥”的含义是“43>或43=”,其中“43>”是真命题,所以“43≥”真命题.(2)“44≥”的含义是“44>或44=”,其中“44=”是真命题,所以“44≥”真命题. (2)“45≥”的含义是“45>或45=”,其中“45>”与“45=”都是假命题,所以“45≥”是假命题.3、分析:先由“p 或q ”为真,“p 且q ”为假得出p 、q 的真假,然后再求出m 的取值范围.解: 若方程210x mx ++=有两个不相等的负实根,则2121240,0,10,m x x m x x ⎧∆=->⎪+=-<⎨⎪=>⎩ 解得2m >,即p :2m >; 若方程()244210x m x +-+=无实根,则()()221621616430m m m ∆=--=-+<解得13m <<,即q :13m <<.因“p 或q ”为真,所以p 、q 至少有一个为真,又“p 且q ”为假,所以p 、q 至少有一个为假,因此这两个命题应是一真一假.当“p 为真,q 为假”时,2,13,m m m >⎧⎨≤≥⎩或 解得3m ≥;当“p 为假,q 为真”时,2,13,m m ≤⎧⎨<<⎩ 解得12m <≤;综上得3m ≥或12m <≤.4、解:根据真值表,选B .说明 在记忆真值表的时候,要体会它的合理性. 5、分析:p 为假,从而q 为真. 解:选B .6、分析 利用逆否命题与原命题的等价性,结合真值表确定结论. 解:∵“p 或q ”的否定是“非p 且非q ”,这是一个真命题,所以由真值表.非p 、非q都是真命题,那么p 假q 假.选B . 7、分析:利用真值表回推. 答:选D . 说明:解题过程中注意发挥逆向思维的作用.8、解:(1)命题“若00,0===y x xy 或则”的逆否命题为“若0x ≠且0y ≠,则0xy ≠”; (2)命题“若0,0,022===+y x y x 则” 的逆否命题为“若0x ≠或0y ≠,则220x y +≠。

第二课时 1.3简单的逻辑联结词(二)教学要求:通过教学实例,了解逻辑联结词“且”、“或”、“非”的含义,使学生能正确地表述相关数学内容.教学重点:正确理解逻辑联结词“且”、“或”、“非”的含义,并能正确表述这“p q ∧”、“p q ∨”、“p ⌝”这些新命题.教学难点:简洁、准确地表述新命题“p q ∧”、“p q ∨”、“p ⌝”.教学过程:一、复习准备:1. 分别用“p q ∧”、“p q ∨”填空:(1)命题“6是自然数且是偶数”是 的形式;(2)命题“3大于或等于2”是 的形式;(3)命题“正数或0的平方根是实数”是 的形式.2. 下列两个命题间有什么关系?(1)7是35的约数;(2)7不是35的约数.二、讲授新课:1. 教学命题p ⌝:①一般地,对一个命题p 全盘否定,就得到一个新命题,记作p ⌝,读作“非p ”或“p 的否定.②规定:若p 是真命题,则p ⌝必是假命题;若p 是假命题,则p ⌝必是真命题. ③例1:写出下列命题的否定,并判断它们的真假:(1)p :tan y x =是周期函数;(2)p :32<;(3)p :空集是集合A 的子集;(4)p :若220a b +=,则,a b 全为0;(5)p :若,a b 都是偶数,则a b +是偶数.(学生自练→个别回答→学生点评)④练习教材P20页 练习第3题⑤例2:分别指出由下列各组命题构成的“p q ∧”、“p q ∨”、“p ⌝”形式的复合命题的真假:(1)p :9是质数,q :8是12的约数;(2)p :1{1,2}∈,q :{1}{1,2}⊂;(3)p :{0}∅⊂,q :{0}∅=;(4)p :平行线不相交.2. 小结:逻辑联结词的理解及“p q ∧”、“p q ∨”、“p ⌝”这些新命题的正确表述和应用.三、巩固练习:1. 练习:判断下列命题的真假:(1)23≤;(2)22≤;(3)78≥.2. 分别指出由下列命题构成的“p q ∧”、“p q ∨”、“p ⌝”形式的新命题的真假:(1)p :π是无理数,q :π是实数;(2)p :23>,q :8715+≠;(3)p :李强是短跑运动员,q :李强是篮球运动员.3. 作业:教材P20页 习题第1、2、3题。