二次函数的区间最值及应用教师版

二次函数在闭区间上的最值问题一、二次函数知识点回顾（一）二次函数的概念：一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

这里需要强调：和一元二次方程类似，二次项系数0a ≠，而b c ，可以为零．二次函数的定义域是全体实数． （二）二次函数2y a x b x c=++的性质 1. 当0a >时，抛物线开口向上，对称轴为2bx a =-，顶点坐标为2424b ac b aa ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而减小；当2bx a>-时，y 随x 的增大而增大； 当2b x a =-时，y 有最小值244ac b a-．2. 当0a <时，抛物线开口向下，对称轴为2bx a =-，顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭，．当2b x a <-时，y 随x 的增大而增大；当2bx a>-时，y 随x 的增大而减小； 当2b x a =-时，y 有最大值244ac b a-．（三）二次函数基本形式：1、2y ax =的性质：a 的绝对值越大，抛物线的开口越小。

2. 2y ax c =+的性质：上加下减。

3. ()2y a x h =-的性质：左加右减。

4. ()2y a x h k =-+的性质：二、二次函数闭区间上的最值解题思路分析一元二次函数的区间最值问题，核心是函数对称轴与给定区间的相对位置关系的讨论。

一般分为：对称轴在区间的左边，中间，右边三种情况.如设：f x a x b xc a ()()=++≠20，求f x ()在x m n ∈[]，上的最大值与最小值。

方法思路分析：将f x ()配方，得顶点为--⎛⎝ ⎫⎭⎪b aa cb a 2442，、对称轴为x b a =-2 当a >0时，它的图象是开口向上的抛物线，数形结合可得在[m ，n ]上f x ()的最值：（1）当[]-∈b am n 2，时，f x ()的最小值是f b a a c b a f x -⎛⎝ ⎫⎭⎪=-2442，()的最大值是f m f n ()()、中的较大者。

二次函数区间及最值问题解析对于二次函数2(0)y ax bx c a =++>在m x n ≤≤上的最值问题（其中a 、b 、c 、m 和n 均为定值，max y 表示y 的最大值，min y 表示y 的最小值）：（1）若自变量x 为全体实数，如图①，函数在2b x a =-时，取到最小值，无最大值．（2）若2b n a<-，如图②，当x m =，max y y =；当x n =，min y y =．（3）若2b m a>-，如图③，当，x m =min y y =；当x n =，max y y =．（4）若2b m n a -≤≤，22b b n m a a +>--，如图④，当2b x a =-，min y y =；当x n =，max y y =．【题型1二次函数中的定轴定区间求最值】【例1】已知二次函数y ＝﹣x 2+2x +4，关于该函数在﹣2≤x ≤2的取值范围内，下列说法正确的是（）A ．有最大值4，有最小值0B ．有最大值0，有最小值﹣4C ．有最大值4，有最小值﹣4D ．有最大值5，有最小值﹣4【解题思路】根据题目中的函数解析式和二次函数的性质，可以得到该函数的对称轴和开口方向，然后根据﹣2≤x ≤2，即可得到相应的最大值和最小值，从而可以解答本题．【解答过程】解：∵二次函数y ＝﹣x 2+2x +4＝﹣（x ﹣1）2+5，∴该函数的对称轴是直线x ＝1，函数图象开口向下，∴当﹣2≤x ≤2时，x ＝1时取得最大值5，当x ＝﹣2时，取得最小值﹣4，故选：D ．【变式1-1】当﹣1≤x ≤3时，二次函数y ＝x 2﹣3x +m 最大值为5，则m ＝．【解题思路】根据题目中的函数解析式和二次函数的性质，可以求得m 的值，本题得以解决．【解答过程】解：∵二次函数y ＝x 2﹣3x +m ＝（x −32）2+m −94，∴该函数开口向上，对称轴为x =32，∵当﹣1≤x ≤3时，二次函数y ＝x 2﹣3x +m 最大值为5，∴当x ＝﹣1时，该函数取得最大值，此时5＝1+3+m ，解得m ＝1，故答案为：1．【变式1-2】已知二次函数y＝x2﹣4x+3，当自变量满足﹣1≤x≤3时，y的最大值为a，最小值为b，则a﹣b的值为．【解题思路】根据题目中的函数解析式和二次函数的性质，可以得到自变量满足﹣1≤x≤3时，x＝﹣1时取得最大值，x＝2时取得最小值，然后即可得到a、b的值，从而可以求得a﹣b的值，本题得以解决．【解答过程】解：∵二次函数y＝x2﹣4x+3＝（x﹣2）2﹣1，∴该函数图象开口向上，对称轴为直线x＝2，∵当自变量满足﹣1≤x≤3时，y的最大值为a，最小值为b，∴当x＝﹣1时，取得最大值，当x＝2时，函数取得最小值，∴a＝1+4+3＝8，b＝﹣1，∴a﹣b＝8﹣（﹣1）＝8+1＝9，故答案为：9．【变式1-3】若函数y＝x2﹣6x+5，当2≤x≤6时的最大值是M，最小值是m，则M﹣m＝．【解题思路】根据题意画出函数图象，即可由此找到m和M的值，从而求出M﹣m的值．【解答过程】解：原式可化为y＝（x﹣3）2﹣4，可知函数顶点坐标为（3，﹣4），当y＝0时，x2﹣6x+5＝0，即（x﹣1）（x﹣5）＝0，解得x1＝1，x2＝5．如图：m＝﹣4，当x＝6时，y＝36﹣36+5＝5，即M＝5．则M﹣m＝5﹣（﹣4）＝9．故答案为9．【题型2二次函数中的动轴定区间求最值】【例2】已知二次函数y＝mx2+2mx+1（m≠0）在﹣2≤x≤2时有最小值﹣2，则m＝（）A．3B．﹣3或38C．3或−38D．﹣3或−38【解题思路】先求出对称轴为x＝﹣1，分m＞0，m＜0两种情况讨论解答即可求得m的值．【解答过程】解：∵二次函数y＝mx2+2mx+1＝m（x+1）2﹣m+1，∴对称轴为直线x＝﹣1，①m＞0，抛物线开口向上，x＝﹣1时，有最小值y＝﹣m+1＝﹣2，解得：m＝3；②m＜0，抛物线开口向下，∵对称轴为直线x＝﹣1，在﹣2≤x≤2时有最小值﹣2，∴x＝2时，有最小值y＝4m+4m+1＝﹣2，解得：m=−38；故选：C．【变式2-1】已知二次函数y＝ax2﹣4ax﹣1，当x≤1时，y随x的增大而增大，且﹣1≤x≤6时，y的最小值为﹣4，则a的值为（）A．1B．34C．−35D．−14【解题思路】根据二次函数y＝ax2﹣4ax﹣1，可以得到该函数的对称轴，再根据当x≤1时，y随x的增大而增大，可以得到a的正负情况，然后根据﹣1≤x≤6时，y的最小值为﹣4，即可得到a的值．【解答过程】解：∵二次函数y＝ax2﹣4ax﹣1＝a（x﹣2）2﹣4a﹣1，∴该函数的对称轴是直线x＝2，又∵当x≤1时，y随x的增大而增大，∴a＜0，∵当﹣1≤x≤6时，y的最小值为﹣4，∴x＝6时，y＝a×62﹣4a×6﹣1＝﹣4，解得a=−14，故选：D．【变式2-2】已知二次函数y＝2ax2+4ax+6a2+3（其中x是自变量），当x≥2时，y随x的增大而减小，且﹣2≤x ≤1时，y的最小值为15，则a的值为（）A．1或﹣2B．−2或2C．﹣2D．1【解题思路】先求出二次函数的对称轴，再根据二次函数的增减性得出抛物线开口向下a＜0，然后由﹣2≤x≤1时，y的最小值为15，可得x＝1时，y＝15，即可求出a．【解答过程】解：∵二次函数y＝2ax2+4ax+6a2+3（其中x是自变量），∴对称轴是直线x=−42×2=−1，∵当x≥2时，y随x的增大而减小，∵﹣2≤x≤1时，y的最小值为15，∴x＝1时，y＝2a+4a+6a2+3＝15，∴6a2+6a﹣12＝0，∴a2+a﹣2＝0，∴a＝1（不合题意舍去）或a＝﹣2．故选：C．【变式2-3】已知二次函数y=12（m﹣1）x2+（n﹣6）x+1（m≥0，n≥0），当1≤x≤2时，y随x的增大而减小，则mn的最大值为（）A．4B．6C．8D．494【解题思路】由二次函数解析式求出对称轴直线方程，分类讨论抛物线开口向下及开口向上的m，n的取值范围，将mn转化为含一个未知数的整式求最值．【解答过程】解：抛物线y=12（m﹣1）x2+（n﹣6）x+1的对称轴为直线x=6−K1，①当m＞1时，抛物线开口向上，∵1≤x≤2时，y随x的增大而减小，∴6−K1≥2，即2m+n≤8．解得n≤8﹣2m，∴mn≤m（8﹣2m），m（8﹣2m）＝﹣2（m﹣2）2+8，∴mn≤8．②当0≤m＜1时，抛物线开口向下，∵1≤x≤2时，y随x的增大而减小，∴6−K1≤1，即m+n≤7，解得m≤7﹣n，∴mn≤n（7﹣n），n（7﹣n）＝﹣（n−72）2+494,∴mn≤494，∵0≤m＜1，∴此情况不存在．综上所述，mn最大值为8．【题型3二次函数中的定轴动区间求最值】【例3】当a﹣1≤x≤a时，函数y＝x2﹣2x+1的最小值为1，则a的值为．【解题思路】利用二次函数图象上点的坐标特征找出当y＝1时x的值，结合当a﹣1≤x≤a时函数有最小值1，即可得出关于a的一元一次方程，解之即可得出结论．【解答过程】解：当y＝1时，有x2﹣2x+1＝1，解得：x1＝0，x2＝2．∵当a﹣1≤x≤a时，函数有最小值1，∴a﹣1＝2或a＝0，∴a＝3或a＝0，故答案为：0或3．【变式3-1】函数y＝﹣x2+4x﹣3，当﹣1≤x≤m时，此函数的最小值为﹣8，最大值为1，则m的取值范围是（）A．0≤m＜2B．0≤m≤5C．m＞5D．2≤m≤5【解题思路】根据题目中的函数解析式和二次函数的性质，可以求得m的取值范围．【解答过程】解：∵y＝﹣x2+4x﹣3＝﹣（x﹣2）2+1，∴该函数图象开口向下，对称轴是直线x＝2，顶点坐标为（2，1），∴x＝﹣1和x＝5对应的函数值相等，∵当﹣1≤x≤m时，此函数的最小值为﹣8，最大值为1，当x＝﹣1时，y＝﹣8，∴2≤m≤5，故选：D．【变式3-2】若二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），当t≤x≤2时，y有最大值3，最小值﹣1，则t的取值范围应是（）A．﹣6≤t≤2B．t≤﹣2C．﹣6≤t≤﹣2D．﹣2≤t≤2【解题思路】根据二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），可以求得a的值，然后即可得到该函数的解析式，再根据二次函数的性质和当t≤x≤2时，y有最大值3，最小值﹣1，即可得到t的取值范围．【解答过程】解：∵二次函数y＝ax2﹣x+2的图象经过点（2，﹣1），∴﹣1＝a×22﹣2+2，解得a=−14，∴y=−14x2﹣x+2=−14（x+2）2+3，∴该函数的图象开口向下，对称轴是直线x＝﹣2，当x＝﹣2时，该函数取得最大值3，∵当t≤x≤2时，y有最大值3，最小值﹣1，当x＝2时，y＝﹣1，∴﹣6≤t≤﹣2，【变式3-3】已知二次函数y＝（x+1）2﹣4，当a≤x≤b且ab＜0时，y的最小值为2a，最大值为2b，则a+b的值为（）A．23B．−72C．3−2D．0【解题思路】根据a的取值范围分﹣1≤a＜0，﹣b﹣2≤a＜﹣1，a＜﹣b﹣2三种情况讨论，求出满足题目条件的情况即可．【解答过程】解：∵a≤x≤b且ab＜0，∴a，b异号，∴a＜0，b＞0，由二次函数的对称性，b关于对称轴的对称点为﹣b﹣2，若﹣1≤a＜0，则（a+1）2﹣4＝2a，解得=−3（舍），若﹣b﹣2≤a＜﹣1，则﹣4＝2a，a＝﹣2，且（b+1）2﹣3＝2b，解得b=3，∴+=3−2，若a＜﹣b﹣2，则2a＝﹣4，a＝﹣2，2b＝（a+1）2﹣4＝﹣3，∴=−32（舍），故选：C．【题型四解答题中区间求最值】1．如图，在平面直角坐标系xOy中，点A（–3，5），B（0，5）．抛物线y=-x2+bx+c交x轴于C（1，0），D（-3，0）两点，交y轴于点E．(1)求抛物线的解析式及顶点坐标；(2)当-4≤x ≤0时，求y 的最大值与最小值的积；(3)连接AB ，若二次函数y =-x 2+bx +c 的图象向上平移m (m >0)个单位时，与线段AB 有一个公共点，结合函数图象，直接写出m 的取值范围．【答案】(1)223y x x =--+，(1,4)-(2)20-(3)1m =，或25m < 【分析】（1）通过待定系数法求出函数解析式，将解析式化为顶点式求解．（2）根据抛物线开口方向及顶点坐标，结合x 的取值范围求解．（3）结合图象，分别求出抛物线顶点在AB 上，经过点A ，B 时m 的值，进而求解．（1）解：将(1,0)C ，(3,0)D -代入2y x bx c=-++得01093b c b c=-++⎧⎨=--+⎩，解得23=-⎧⎨=⎩b c ，2223(1)4y x x x ∴=--+=-++，∴抛物线顶点坐标为(1,4)-．（2）解： 抛物线开口向下，顶点坐标为(1,4)-，∴函数最大值为4y =，对称轴为直线=1x -，1(4)0(1)--->-- ，4x ∴=-时，16835y =-++=-为函数最小值，∴y 的最大值与最小值的积为4(5)20⨯-=-．（3）解：二次函数2y x bx c =-++的图象向上平移m 个单位后解析式为223y x x m =--++，抛物线顶点坐标为(1,4)m -+，当顶点落在线段AB 上时，45m +=，解得1m =，当抛物线向上移动，经过点(0,5)B 时，53m =+，解得2m =，当抛物线经过点(3,5)A -时，5963m =-+++，解得5m =，∴当1m =，或25m < 时，函数图象与线段AB 有一个公共点．【我思故我在】本题考查二次函数的综合应用，解题的关键是掌握二次函数与方程的关系，掌握二次函数图象的平移规律．2．已知抛物线2y x bx c =++的对称轴为直线1x =，图象与x 轴交于点()1,0-．（1）求抛物线的函数表达式．（2）若把抛物线的图象沿x 轴平移m 个单位，在自变量x 的值满足23x ≤≤的情况下，与其对应的函数值y 的最小值为-2，求m 的值．【我思故我在】本题考查了二次函数的综合运用，主要知识点有通过已知条件求函数解析式，函数的增减性，平移等，注意分类讨论．3．如图，抛物线22y x x c =-++与x 轴正半轴，y 轴正半轴分别交于点,A B ，且,OA OB =点G 为抛物线的顶点．()1求抛物线的解析式及点G 的坐标；()2点,M N 为抛物线上两点(点M 在点N 的左侧)，且到对称轴的距离分别为3个单位长度和5个单位长度，点Q 为抛物线上点,M N 之间(含点,M N )的一个动点，求点Q 的纵坐标Q y 的取值范围．【答案】（1）223y x x =-++，G （1,4）；（2）﹣21≤Q y ≤4.【分析】（1）根据,OA OB =用c 表示出点A 的坐标，把A 的坐标代入函数解析式，得到一个关于c 的一元二次方程，解出c 的值，从而求出函数解析式，求出顶点G 的坐标．（2）根据函数解析式求出函数图像对称轴，根据点M,N 到对称轴的距离，判断出M,N 的横坐标，进一步得出M,N 的纵坐标，求出M,N 点的坐标后可确定Q y 的取值范围．【详解】解：（1）∵抛物线22y x x c =-++与y 轴正半轴分别交于点B ，∴B 点坐标为（c ，0），∵抛物线22y x x c =-++经过点A ，∴﹣c 2+2c+c=0，解得c 1=0（舍去），c 2=3，∴抛物线的解析式为223y x x =-++∵223y x x =-++=﹣（x －1）2+4，∴抛物线顶点G 坐标为（1,4）．（2）抛物线223y x x =-++的对称轴为直线x=1，∵点M,N 到对称轴的距离分别为3个单位长度和5个单位长度，∴点M 的横坐标为﹣2或4，点N 的横坐标为﹣4或6，点M 的纵坐标为﹣5，点N 的纵坐标为﹣21，又∵点M在点N的左侧，∴当M坐标为（﹣2，﹣5）时，点N的坐标为（6，﹣21），则﹣21≤Q y≤4当当M坐标为（4，﹣5）时，点N的坐标为（6，﹣21），则﹣21≤Q y≤﹣5，∴Q y的取值范围为﹣21≤Q y≤4．【我思故我在】本题考查的是二次函数的基本的图像与性质，涉及到的知识点有二次函数与坐标轴交点问题，待定系数法求函数解析式，对称轴性质等，解题关键在于利用数形结合思想正确分析题意，进行计算．4．如图，已知二次函数y＝ax2＋3x＋1的图像经过点A（－1，－3）．2(1)求a的值和图像的顶点坐标．(2)若横坐标为m的点B在该二次函数的图像上．①当点B向右平移4个单位长度后所得点B′也落在该二次函数图像上时，求m的值；②若点B到x轴的距离不大于3，请根据图像直接写出m的取值范围．5．如图，抛物线()230y ax bx a =+-≠与x 轴交于点()1,0A -，点()3,0B ，与y 轴交于点C ．(1)求抛物线的表达式；(2)在对称轴上找一点Q ，使ACQ 的周长最小，求点Q 的坐标；(3)P 是第四象限内抛物线上的动点，求BPC △面积S 的最大值及此时P 点的坐标．⊥轴于点（3）解：过点P作PD x【我思故我在】本题主要考查了二次函数综合，一次函数综合，待定系数法求函数解析式，轴对称最短路径问题等等，正确作出辅助线利用数形结合的思想求解是解题的关键．6．如图，抛物线2y x mx =+与直线y x b =-+交于点A (2，0)和点B ．（1）求m 和b 的值；（2）求点B 的坐标，并结合图象写出不等式2x mx x b +>-+的解集；（3）点M 是直线AB 上的一个动点，将点M 向左平移3个单位长度得到点N ，若线段MN 与抛物线只有一个公共点，直接写出点M 的横坐标M x 的取值范围．【答案】（1）2m =-，2b =；（2）不等式2x mx +>x b -+的解集为1x <-或2x >；（3）点M 的横坐标M x 的取值范围是：12M x -≤<或3M x =．【分析】（1）把A (2，0)分别代入两个解析式，即可求得m 和b 的值；（2）解方程222x x x -=-+求得点B 的坐标为(-1，3)，数形结合即可求解；（3）画出图形，利用数形结合思想求解即可．【详解】解：（1）∵点A (2，0)同时在2y x mx =+与y x b =-+上，∴2022m =+，02b =-+，解得：2m =-，2b =；（2）由（1）得抛物线的解析式为22y x x =-，直线的解析式为2y x =-+，解方程222x x x -=-+，得：1221x x ==-，．∴点B 的横坐标为1-，纵坐标为23y x =-+=，∴点B 的坐标为(-1，3)，观察图形知，当1x <-或2x >时，抛物线在直线的上方，∴不等式2x mx +>x b -+的解集为1x <-或2x >；（3）如图，设A 、B 向左移3个单位得到A 1、B 1，∵点A (2，0)，点B (-1，3)，∴点A 1(-1，0)，点B 1(-4，3)，∴A A 1=BB 1=3，且A A 1∥BB 1，即MN 为A A 1、BB 1相互平行的线段，对于抛物线()22211y x x x =-=--，∴顶点为(1，-1)，如图，当点M 在线段AB 上时，线段MN 与抛物线22y x x =-只有一个公共点，此时12M x -≤<，当线段MN 经过抛物线的顶点(1，-1)时，线段MN 与抛物线22y x x =-也只有一个公共点，此时点M 1的纵坐标为-1，则12M x -=-+，解得3M x =，综上，点M 的横坐标M x 的取值范围是：12M x -≤<或3M x =．．【我思故我在】本题考查了二次函数的图象与性质；能够画出图形，结合函数图象，运用二次函数的性质求解是关键．7．如图，直线y =x −5交x 轴于点A ，交y 轴于点B ，抛物线y =ax 2−4x +c 经过A ，B 两点．(1)求抛物线的解析式；(2)以AB 为边作矩形ABCD ，设点C 的横坐标为m ．①用含m 的代数式表示C ，D 两点的坐标；②当CD 边与抛物线只有一个公共点时，请直接写出m 的取值范围．【答案】(1)抛物线的解析式为y =x 2-4x -5；(2)①点C 的坐标为(m ，-m -5)；点D 的坐标为(m +5，-m )；②-7≤m ≤3且m ≠0．【分析】（1）先求得点A 、B 的坐标，再利用待定系数法求解即可；（2）①利用等腰直角三角形的性质以及坐标与图形的性质可求得点C 的坐标；再利用平移的性质求得点D 的坐标即可；②根据点C 恰好在抛物线上时，是与抛物线只有一个公共点的临界条件，据此求解即可．（1）解：∵直线y =x −5交x 轴于点A ，交y 轴于点B ，∴点A 的坐标为(5，0)，点B 的坐标为(0，-5)，∵抛物线y =ax 2−4x +c 经过A ，B 两点，∴252005a c c -+=⎧⎨=-⎩，解得：15a c =⎧⎨=-⎩，∴抛物线的解析式为y =x 2-4x -5；（2）解：①∵点A 的坐标为(5，0)，点B 的坐标为(0，-5)，∴OA =OB =5，∴△OAB 是等腰直角三角形，则∠OAB =∠OBA =45°，过点C 作CE ⊥y 轴于点E ，∵四边形ABCD 是矩形，点C 的横坐标为m ．∴CB ⊥AB ，则∠CBE =∠OBA =45°，∴CE =BE =-m ，∴点C 的坐标为(m ，-m -5)；∵四边形ABCD 是矩形，∴CD =AB ，CD ∥AB ，∵点A 是点B 向右平移5个单位，向上平移5个单位得到的，∴点D 的坐标为(m +5，-m )；②设BC 的解析式为y =kx -5，把(m ，-m -5)代入y =kx -5，得-m -5=mk -5，解得：k =-1，∴BC 的解析式为y =-x -5，设AD 的解析式为y =-x +n ,把点D 的坐标（m +5,m ）代入y =-x +n ,得-m =-m -5+n ,解得：n =5,∴AD 的解析式为y =-x +5,当点C 恰好在抛物线上时，是与抛物线只有一个公共点的临界条件，联立2545y x y x x =-+⎧⎨=--⎩,解得：x 1=5，x 2=-2，当x =5时，点A 和点D 重合，不符合要求，x <-2即m +5<-2，得m <-7时，线段CD 与抛物线无交点，当点C 恰好在抛物线上时，是与抛物线只有一个公共点的临界条件，联立2545y x y x x =--⎧⎨=--⎩，解得：x 1=0，x 2=3，当x =0时，点C 与点B 重合，不符合要求，当x >3即m>3时，线段CD 与抛物线无交点，故-7≤m ≤3且m ≠0．【我思故我在】本题考查二次函数的图象及性质，直线和抛物线的交点以及解方程组和不等式组等知识，熟练掌握二次函数的图象及性质是解题关键．8．在平面直角坐标系xOy 中，点()1,P m y 在二次函数2y x bx c =++的图象上，点()2,Q m y 在一次函数1y x =-+的图象上．(1)若二次函数图象经过点()0,1，()2,1．①求二次函数的解析式与图象的顶点坐标；②当1m >时，请直接写出1y 与2y 的大小关系；(2)若只有当0m ≥时，满足120y y ⋅≤，请求出此时二次函数的解析式．【答案】(1)①221y x x =-+，顶点坐标为(1,0)②12y y ＞(2)2y x x=-【分析】（1）利用待定系数法即可求解出二次函数的解析式，配成顶点式即可求出二次函数的顶点坐标；求出y 1和y 2，再根据m 的取值范围即可比较；（2）先根据点P (m ,y 1)在2y x bx c =++图象上，点Q (m ,y 2)在一次函数y =−x +1的图象上，得到21y m bm c =++和21y m =-+，即有212()(1)y y m bm c m ⋅=++-+，再根据m 的取值范围可得：当01m ≤≤时，函数20y m bm c =++≤；当1m＞时，函数20y m bm c =++＞，可以判断出可知2y m bm c =++经过点(0,0)，(1,0)，则可求出b 、c ，则问题得解．（1）①∵2y x bx c =++经过点(0,1)、(2,1)，∴有1421c b c =⎧⎨++=⎩，解得12c b =⎧⎨=-⎩，∴二次函数解析式为：221y x x =-+，∵2221(1)y x x x =-+=-，∴顶点坐标为(1,0)，②∵点P (m ,y 1)在221y x x =-+图象上，点Q (m ,y 2)在一次函数y =−x +1的图象上，∴21(1)y m =-，21y m =-+，∴2212(1)(1)(1)(1)(1)y y m m m m m m -=---+=-+-=-，∵m ＞1，∴m -1＞0，∴12(1)0y y m m -=-＞，∴12y y ＞；（2）∵点P (m ,y 1)在2y x bx c =++图象上，点Q (m ,y 2)在一次函数y =−x +1的图象上，∴21y m bm c =++，21y m =-+，∴212()(1)y y m bm c m ⋅=++-+，∵只有当0m ≥时，120y y ⋅≤，当01m ≤≤时，1-m ≥0，∵120y y ⋅≤，∴20m bm c ++ ，即当01m ≤≤时，函数20y m bm c =++ ，当1m＞时，1-m <0，∵120y y ⋅≤，∴20m bm c ++＞，即当1m＞时，函数20y m bm c =++＞，∴2y m bm c =++经过点(0,0)，(1,0)，∴010c b c =⎧⎨++=⎩，解得01c b =⎧⎨=-⎩，∴二次函数的解析式为：2y x x =-．【我思故我在】本题考查了二次函数的性质、待定系数法求解二次函数解析式、求解顶点坐标等知识，判断出可知2y m bm c =++经过点(0,0)，(1,0)是解答本题的关键．9．在平面直角坐标系xOy 中，抛物线2450)(y ax ax a =-+<与x 轴交于A ，B 两点，与y 轴交于点C ，且OB OC =．(1)求这条抛物线的解析式；(2)求抛物线顶点坐标和对称轴方程；(3)若点1,()P x b 与2,()Q x b 在（1）中的抛物线上，且12x x <，将抛物线在PQ 上方的部分沿PQ 翻折180°，抛物线的其他部分保持不变，得到一个新图象，当这个新图象与过（0，-3）且平行于x 轴的直线恰好只有两个公共点时，请直接写出b 的取值范围．【答案】(1)245y x x =-++；(2)顶点坐标为（2，9），对称轴方程为2x =；(3)39b <<或3b =-．【分析】（1）由245y ax ax =-+得出OC ，再由OB OC =得出OB 的值，代入点B 可求出抛物线的解析式；（2）将抛物线化为顶点式即可得出顶点坐标和对称轴方程；（3）讨论PQ 在直线=3y -上方和在直线=3y -上两种情况即可得出b 的取值范围．(1)（1）∵245y ax ax =-+，令0x =，5y =，∴5OC =∴5OB OC ==，即B （5，0），将B （5，0）代入245x y a ax =-+得252050a a -+=，解得1a =-，即二次函数的解析式为245y x x =-++．(2)（2）由2245(2)9y x x x =-++=--+得，顶点坐标为（2，9），对称轴方程为2x =．(3)（3）如图，过（0，-3）且平行于x 轴的直线=3y -，当顶点M （2，9）的对称点在直线=3y -上，此时3b =，∴39b <<，当3b =-时，此时与=3y -的交点为2个，∴39b <<或3b =-．【我思故我在】此题考查了用代入法求二次函数的解析式，二次函数的对称轴及顶点坐标及二次函数的翻折与交点问题，熟练掌握二次函数的图像和性质是解决本题的关键．10．已知一次函数12y x b =+的图象与二次函数()221y a x bx =++（0a ≠，a 、b 为常数）的图象交于A 、B 两点，且A 的坐标为(0,1)．（1）求出a 、b 的值，并写出1y ，2y 的表达式；（2）验证点B 的坐标为(1,3)，并写出当12y y 时，x 的取值范围；（3）设12u y y =+，12v y y =-，若m x n 时，u 随着x 的增大而增大，且v 也随着x 的增大而增大，求m 的最小值和n 的最大值．【答案】（1）1a =，1b =，121y x =+，221y x x =++；（2）见解析；01x ；（3）m 的最小值为 1.5-，n 的最大值为0.5【分析】（1）把A 点的坐标分别代入两个函数的解析式，便可求得a 与b 的值；（2）画出函数图象，根据函数图象作答；（3）求出出个函数的对称轴，根据函数的性质得出“u 随着x 的增大而增大，且v 也随着x 的增大而增大”时x 的取值范围，进而得m 的最小值和n 的最大值．【详解】（1）解：（1）把(0,1)A 代入12y x b =+得1b =，把(0,1)A 代入()221y a x bx =++得，1a =，∴121y x =+，221y x x =++；（2）解方程组2211y x y x x =+⎧⎨=++⎩得01x y =⎧⎨=⎩或13x y =⎧⎨=⎩，∴()1,3B ，作121y x =+，221y x x =++的图象：由函数图象可知，121y x =+不在221y x x =++下方时，01x ，∴当12y y 时，x 的取值范围为01x ；（3）∵2221221132( 1.5)0.25u y y x x x x x x =+=++++=++=+-，∴当 1.5x - 时，u 随x 的增大而增大；()22212(21)1(0.5)0.25v y y x x x x x x =-=+-++=-+=--+，∴当0.5x 时，v 随x 的增大而增大，∴当 1.50.5x - 时，u 随着x 的增大而增大，且v 也随着x 的增大而增大，∵若m x n 时，u 随着x 的增大而增大，且v 也随着x 的增大而增大，∴m 的最小值为 1.5-，n 的最大值为0.5.【我思故我在】本题是二次函数的综合题，主要考查了函数的图象与性质，利用函数图象求不等式的解集，待定系数法，关键是熟练掌握二次函数的性质，灵活运用性质解题．11．如图，二次函数2y x bx c =++的图象与x 轴交于A ，B 两点，与y 轴交于点C ，且关于直线1x =对称，点A 的坐标为()1,0-．（1）求二次函数的表达式；（2）连接BC ，若点P 在y 轴上时，BP 和BC 的夹角为15︒，求线段CP 的长度；（3）当1a x a ≤≤+时，二次函数2y x bx c =++的最小值为2a ，求a 的值．。

二次函数的最值问题一、内容与内容解析1.内容含参二次函数在m x n ≤≤内的最值问题.２.内容解析本节课在讨论了影响0a ＞时二次函数在m x n ≤≤内最值的因素后对0a ＞时含参二次函数在m x n ≤≤内最值问题进行探究.主要的研究方法是从函数图像入手，通过几何画板动态演示，确定分类标准，进行分类讨论,进而对分类标准进行优化，得到解决此类问题的一般方法，并运用此方法解决相关的最值问题.基于以上分析，确定本节课的教学重点是：从函数图像入手，运用分类讨论思想求含参二次函数在m x n ≤≤内最值.二、目标和目标解析1.目标(1)通过复习二次函数图像的特征和性质，能够借助二次函数的图像研究二次函数的最值.(2)通过对二次函数在m x n ≤≤内最值问题初探、对含参二次函数在m x n ≤≤内最值问题的探究，经历直观感知、抽象概括、运算求解、反思与构建等思维过程，体会函数思想，分类讨论等数学思想方法，发展数学感知、数学表征、抽象概括、运算能力等.2.目标解析达成目标(1)的标志是：学生会借助二次函数的图像研究二次函数在m x n ≤≤内的最值，并能由此得到二次函数在m x n ≤≤内最值的影响因素，进一步体会函数思想.达成目标(2)的标志是：借助二次函数的图像求解含参二次函数在m x n ≤≤内最值，进一步体会函数思想和分类讨论的思想.三、教学问题诊断分析学生已学习了二次函数的概念、图像和性质，已经具备了一定的识图能力、分析图形特征的能力、数学说理能力，这为本节课的学习奠定了基础.但对于含参二次函数在m x n ≤≤内的图像及最值问题，由于其抽象程度较高，学生可能会在为什么要进行分类讨论以及如何确定分类标准这两个问题上产生一定的困难.基于以上分析，本节课的教学难点是：如何确定分类标准.四、教学过程设计引言:(展现生活实例，体现研究二次函数在m x n ≤≤内最值的必要性)本节课，我们将结合二次函数的相关知识深入研究二次函数的最值问题.1.复习导入，自主发现问题1如图，(5,),(8,),(1,),( 3.9,)A B C D A y B y C y D y --在二次函数2134y x x =--的图像上，请比较：(1)B y A y ；（2） D y C y ；（3）D y B y ；（4）C y A y .问题2根据问题1的结论填空：（1）二次函数2134y x x =--（58x ≤≤），当x =时，y 取到最大值；当x =时，y 取到最小值.（2）二次函数2134y x x =-- ( 3.91x -≤≤-)，当x =时，y 取到最大值；当x =时，y 取到最小值.（3）二次函数2134y x x =--（ 3.98x -≤≤），当x =时，y 取到最大值；当x =时，y 取到最小值.（4）二次函数2134y x x =--（15x -≤≤），当x =时，y 取到最大值；当x =时，y 取到最小值.师生活动: 教师提出问题，学生尝试用已有知识解决这些问题，并交流问题中蕴含的函数知识和对这些知识的理解.追问1：这些二次函数的图像是完整的抛物线吗？追问2：为什么有的（二次函数的）最值能在顶点处取到，有的却不能呢？追问3：通过对上面问题的研究，你认为二次函数在 内的最值的取得与什么有关？师生活动:通过对前面问题的研究，自主发现影响二次函数在 内的最值的因素：对称轴和m x n ≤≤的相对位置.若对称轴不在m x n ≤≤内时，最值在端点处取得；对称轴在m x n ≤≤内时，最值在顶点和端点处分别取得.遇到这类问题时，我们通常要结合函数图象进行分析.设计意图：引导学生通过观察函数图像，直观地发现对称轴和 的相对位置影响了二次函数的最值.为下一步解决0a ＞时含参二次函数在 内的最值问题做铺垫. 2.问题剖析，合作探究探究1：求二次函数2134y x tx =--（21x -≤≤）的最小值. 师生活动:教师引导学生先观察函数解析式，分析参数t 的变化对二次函数图像的影响，然后借助计算机软件，直观感受对称轴和m x n ≤≤的相对位置如何影响二次函数的最小值.最后全班交流，确定分类标准，学生独立补全解题过程.追问1：观察本题中的函数解析式与前面 有什么区别？ m x n ≤≤2134y x x =--m x n ≤≤m x n ≤≤m x n ≤≤追问2：随着参数t 的变化，二次函数2134y x tx =--图象的开口方向和开口大小会改变吗？对称轴呢？追问3：二次函数2134y x tx =--（21x -≤≤）的最小值是唯一确定的吗？ 师生活动:关注学生是否明确此处为什么要进行分类讨论，体会分类讨论的必要性. 追问4：如何确定分类标准？如何用数学符号表达这种关系呢？师生活动: 师生共同讨论写出分类标准.教师规范格式以后要求学生将过程补齐. 设计意图：探究0a ＞时含参二次函数在 内的最小值问题，让学生体会解决这一类问题的基本方法.培养学生直观感知、抽象概括、数学表征能力，激发自主学习的积极性和探究意识.引导观察，发现分类依据，培养探究意识.探究2：已知关于x 的二次函数y 1＝x 2+bx +c （实数b ，c 为常数）．（1）若二次函数的图象经过点（0，4），对称轴为x ＝1，求此二次函数的表达式；（2）若b 2﹣c ＝0，当b ﹣3≤x ≤b 时，二次函数的最小值为21，求b 的值；（3）记关于x 的二次函数y 2＝2x 2+x +m ，若在（1）的条件下，当0≤x ≤1时，总有y 2≥y 1，求实数m 的最小值．师生活动：要求学生独立解决，写出分析过程，小组内交流讨论，最后全班汇报交流.对于学生展示的分类方法，教师适当引导和纠正，让学生理解如何进行分类讨论（不重复，不遗漏），并对分类方法进行优化.最后共同归纳出求含参二次函数在m x n ≤≤内最值的一般方法：一般先确定对称轴与m x n ≤≤的相对位置关系，分别画出示意图，确定分类标准，再进行分类讨论.设计意图：在探究1的基础上进一步探究 时含参二次函数在 内的最大值问题，重点体会解题过程中分类标准的确定.师生活动：回顾探究1和探究2的过程，体会它们的相同与不同之处.追问1：为什么有时候分3类，有时候分2类就可以了？什么时候分2类，什么时候分3类呢？追问2：你能直接判断它们分别分几类进行讨论吗：师生活动：通过类比探究1和探究2归纳：求二次函数在m x n ≤≤上的最值不仅min 2min min 2min 10242,12,2211,2321111,1,2422(1)13()2111()42x t t t x y t t t x t y t t t x y t t t y t t t t =--=-=---==---==--⎧⎪--⎪⎪=---⎨⎪⎪--⎪⎩解：＞，对称轴：（1）当2＜即＜时：（2）当2≤2≤即1≤≤时：，（3）当2＞即＞-时：＜综上所述：1≤≤＞-m x n≤≤m x n ≤≤0a ＞要看对称轴与m x n ≤≤的相对位置，还要看开口方向.开口向下时，可类比开口向上的数学模型进行讨论.设计意图：讨论0a ＞时含参二次函数在 内最小值的分类问题，体会开口方向对函数最值的影响.3.归纳总结师生共同回顾本节课所学主要内容，并请学生回答以下问题：（1）本节课我们研究了哪些问题？（2）我们是如何分析、解决这些问题的？（3）在研究过程中你遇到的问题是什么？怎么解决的？设计意图：通过小结，理清本节课的研究内容和研究方法.让学生体会提出问题、分析问题、解决问题的方法.4.课外作业(1) 必做题：①求二次函数223y x ax =--+（45x -≤≤）的最值.②已知二次函数221y ax ax =++（12x -≤≤）有最大值4，求实数a 的值.(2) 选做题：求二次函数223y x x =-+（2t x t ≤≤+）上的最值.（3）兴趣作业：通过本节课的学习，你能自己提出一个二次函数最值相关的问题并进行解答吗？试试看，和同伴交流你的想法.设计意图：巩固本节课所学内容，利用前面归纳的结论来解决二次函数最值的相关问题，加深对含参二次函数在 内的最值问题的认识.体会函数思想.提升学生分析问题，解决问题的能力.m x n ≤≤m x n≤≤。

二次函数在给定区间上的最值问题【学前思考】二次函数在闭区间上取得最值时的x ，只能是其图像的顶点的横坐标或给定区间的端点. 因此，影响二次函数在闭区间上的最值主要有三个因素：抛物线的开口方向、对称轴以及给定区间的位置. 在这三大因素中，最容易确定的是抛物线的开口方向（与二次项系数的正负有关），而关于对称轴与给定区间的位置关系的讨论是解决二次函数在给定区间上的最值问题的关键. 本节，我们将以若干实例说明解决此类问题的具体方法.【知识要点＆例题精讲】二次函数在给定区间上的最值问题，常见的有以下三种类型，分别是： Case Ⅰ、给定区间确定，对称轴位置也确定说明：此种类型是较为简单的一种，只要找到二次函数的对称轴，画出其函数图像，再将给定区间标出，那么二次函数的最值一目了然.解法：若二次函数的给定区间是确定的，其对称轴的位置也确定，则要求二次函数在给定区间上的最值，只需先考察其对称轴的横坐标是否在给定区间. （i ）当其对称轴的横坐标在给定区间时，二次函数在给定区间上不具有单调性，此时其一个最值在顶点处取得，另一个最值在离对称轴的横坐标较远的端点处取得；（ii ）当其对称轴的横坐标不在给定区间时，二次函数在给定区间上具有单调性，此时可利用二次函数的单调性确定其最值.例1、二次函数223y x x =-+在闭区间[]1,2-上的最大值是_______.例2、函数2()42f x x x =-+-在区间[]0,3上的最大值是_______，最小值是_______.例3、已知223x x ≤，则函数2()1f x x x =++的最大值是_______，最小值是______.Case Ⅱ、给定区间确定，对称轴位置变化说明：此种类型是非常重要的，是考试必考点，主要是讨论二次函数的对称轴与给定区间的位置关系，一般需要分对称轴在给定区间的左侧、部以及右侧三种情况进行分类讨论，然后根据不同情况求出相应的最值.解法：若二次函数的给定区间是确定的，而其对称轴的位置是变化的，则要求二次函数2y ax bx c =++（0a ≠）在给定区间[],p q 上的最值，需对其对称轴与给定区间的位置关系进行分类讨论. 这里我们以0a >的情形进行分析： （ⅰ）若2b p a-<，即对称轴在给定区间[],p q 的左侧，则函数()f x 在给定区间[],p q 上单调递增，此时max [()]()f x f q =，min [()]()f x f p =； （ⅱ）若2b p q a ≤-≤，即对称轴在给定区间[],p q 的部，则函数()f x 在[,]2b p a-上单调递减，在[,]2b q a -上单调递增，此时min [()]()2b f x f a =-，max [()]()f x f p =或()f q ，至于最大值究竟是()f p 还是()f q ，还需通过考察对称轴与给定区间的中点的位置关系作进一步讨论：若22b p q p a +≤-<，则max [()]()f x f q =；若22p q b q a +≤-≤，则max [()]()f x f p =； （ⅲ）若2b q a->，即对称轴在给定区间[],p q 的右侧，则函数()f x 在给定区间[],p q 上单调递减，此时max [()]()f x f p =，min [()]()f x f q =. 综上可知，当0a >时，max (),22[()](),22b p q f q a f x b p q f p a +⎧-<⎪⎪=⎨+⎪-≥⎪⎩若若； min (),2[()](),22(),2b f p p a b b f x f p q a a b f q q a ⎧-<⎪⎪⎪=-≤-≤⎨⎪⎪->⎪⎩若若若.通过同样的分析可得到：当0a <时，max(),2[()](),22(),2b f p p a b b f x f p q a a b f q q a ⎧-<⎪⎪⎪=-≤-≤⎨⎪⎪->⎪⎩若若若； min (),22[()](),22b p q f q a f x b p q f p a +⎧-<⎪⎪=⎨+⎪-≥⎪⎩若若.例4、已知21x ≤且2a ≥，求函数2()3f x x ax =++的最值.例5、求函数()()f x x x a =--在区间[]1,1-上的最大值.例6、求函数2()21f x x ax =--在区间[]0,2上的最大值和最小值.例7、设函数2()f x x ax b =++（,a b R ∈），当214a b =+时，求函数()f x 在区间[]1,1-上的最小值()g a 的解析式.22222222()1()1422122()[1,1]()(1)11244122()[1,1]()(1)11244a a a f x x axb x ax x x a a f x a a g a f a a a a f x a a g a f a a =++=+++=++=--<->-=-=-++=-+-><--==+++=++函数的图像是开口向上，对称轴为直线的抛物线（i ）若,即此时函数在上单调递增于是（ii ）若,即此时函数在上单调递减于是（iii ）[解析] 2211222()[1,][,1]22()()12224()1,22224a a a a f x a g a f a a a g a a a a a -≤-≤-≤≤---=-=⎧-+>⎪⎪⎪=-≤≤⎨⎪⎪++<-⎪⎩若,即此时函数在上单调递减,在上单调递增于是，综上可知，，例8、已知函数2()1f x x mx =+-，若对于任意的[,1]x m m ∈+，都有()0f x <成立，则实数m 的取值围是_______.Case Ⅲ、给定区间变化，对称轴位置确定说明：此种类型，考试中出现的较少，一般是给定区间里含有参数. 解决此类问题，亦可根据对称轴与给定区间的位置关系，分对称轴在给定区间的左侧、部以及右侧三种情况进行分类讨论，然后根据不同情况求出相应的最值.解法：若二次函数的给定区间是变化的，而其对称轴的位置是确定的，则要求二次函数在给定区间上的最值，需对变化区间是否包含其对称轴的横坐标进行分类讨论，分类标准为：变化区间包含其对称轴的横坐标，变化区间不包含其对称轴的横坐标. 解决方法与知识点2类似，这里不再赘述.例9、已知函数2()(1)1f x x =-+定义在区间[],1t t +（t R ∈）上，求()f x 的最小值.例10、已知函数2()23f x x x =-+，当[],1x t t ∈+（t R ∈）时，求()f x 的最大值.CaseIV 、与二次函数最值问题有关的综合题型利用二次函数在给定区间上取得最值，可以求解、证明或探究以下综合问题：（1）求函数的最值或最值的取值围；（2）求函数的解析式；（3）证明不等式；（4）求参数的取值围；（5）探究参数是否存在；……例11、设函数()221f x x ax a =+--，[]0,2x ∈，a 为常数.（I ）求()f x 的最小值()g a 的解析式；（II ）在（I ）中，是否存在最小的整数m ，使得()0g a m -≤对于任意a R ∈均成立. 若存在，求出m 的值；若不存在，请说明理由.【解析】（I ）函数()22221()1f x x ax a x a a a =+--=+---的图像是开口向上，对称轴为直线x a =-的抛物线（i ）若0a -<，即0a >此时函数()f x 的对称轴x a =-不在区间[]0,2上，()f x 在区间[]0,2上单调递增 于是min ()[()](0)1g a f x f a ===--（ii ）若2a ->，即2a <-此时函数()f x 的对称轴x a =-不在区间[]0,2上，()f x 在区间[]0,2上单调递减 于是min ()[()](2)44133g a f x f a a a ===+--=+（iii ）若02a ≤-≤，即20a -≤≤此时函数()f x 的对称轴x a =-在区间[]0,2上，()f x 在区间[]0,a -上单调递减，在区间[],2a -上单调递增于是2min ()[()]()1g a f x f a a a ==-=---综上可知，21,0()1,2033,2a a g a a a a a a -->⎧⎪=----≤≤⎨⎪+<-⎩（II ）要使()0g a m -≤对于任意的a R ∈均成立，只需max [()]m g a ≥，a R ∀∈ 下求max [()]g a由函数()g a 的图像可见，()g a 在1(,]2-∞-上单调递增，在1[,)2-+∞上单调递减 2max 1113[()]()()()12224g a g ∴=-=-----=- 于是34m ≥- 又m Z ∈故m 的最小值为0例12、已知函数2()2f x x ax b =-+（,a b R ∈），记M 是|()|f x 在区间[0,1]上的最大值.（Ⅰ）当0b =且2M =时，求a 的值； （Ⅱ）若12M ≤，证明01a ≤≤. 【解析】（I ）函数222()2()f x x ax b x a a b =-+=--+的图像是开口向上，对称轴为直线x a =的抛物线 而函数()f x 的图像是将函数()f x 在x 轴上方的图像保持不变、把它在x 轴下方的图像翻折上去得到的（I ）当0b =时，函数222()2()f x x ax x a a =-=--（i ）若0a <此时函数()f x 的对称轴x a =不在区间[0,1]上，()f x 在区间[0,1]上单调递增于是{}{}max [()]max (0),(1)max 0,12122M f x f f a a ===-=-=122122a a ⇒-=-=-或，即12a =-（舍去32a =） （ii ）若1a >此时函数()f x 的对称轴x a =不在区间[0,1]上，()f x 在区间[0,1]上单调递减 于是{}{}max [()]max (0),(1)max 0,12122M f x f f a a ===-=-=122122a a ⇒-=-=-或，即32a =（舍去12a =-） （iii ）若01a ≤≤ 此时函数()f x 的对称轴x a =在区间[0,1]上，()f x 在区间[]0,a 上单调递减，在区间[],1a 上单调递增 于是{}{}2max [()]max (),(1)max ,122M f x f a f a a ===-=当22a =时，[0,1]a =，舍去 当122a -=时，122122a a -=-=-或⇒12a =-或32a =，均舍去 综上可知，12a =-或32a = （II ）(0)(1)12fb f a b =⎧⎨=-+⎩ 1(11(0)(11(0)(12222b f f f f f a +-+--∴===+））） 又12M ≤ 1(0)2f ∴≤，1(1)2f ≤ 11(0)22f ⇒-≤≤，11(1)22f -≤≤ 于是有1(0)(1)1f f -≤-≤ 故111(0)(11101222222f f a -=-≤=+≤+=），即[0,1]a ∈例13、（2015高考）已知函数2()f x x ax b =++（a ，b R ∈），记(,)M a b 是()f x 在区间[]1,1-上的最大值.（1）证明：当2a ≥时，(,)2M a b ≥；（2）当a ，b 满足(,)2M a b ≤时，求a b +的最大值.【分析】本题考查的知识点是二次函数在区间定、对称轴位置变化的情形下的最值问题. 解决此类问题的关键是正确理解“(,)M a b 是()f x 在区间[]1,1-上的最大值”这一条件，并结合函数图像以及三角不等式等知识。

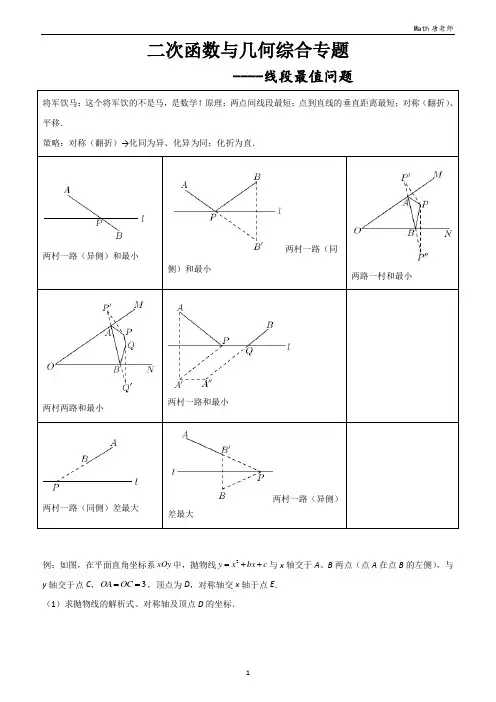
二次函数与几何综合专题----线段最值问题将军饮马：这个将军饮的不是马，是数学！原理：两点间线段最短；点到直线的垂直距离最短；对称（翻折）、平移．策略：对称（翻折）→化同为异、化异为同；化折为直．两村一路（异侧）和最小两村一路（同侧）和最小两路一村和最小两村两路和最小两村一路和最小两村一路（同侧）差最大两村一路（异侧）差最大例：如图，在平面直角坐标系xOy 中，抛物线2y x bx c =++与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，3OA OC ==，顶点为D ，对称轴交x 轴于点E ． （1）求抛物线的解析式、对称轴及顶点D 的坐标．PN y轴交AC于N，求线段PN的最大值及此时点P （2）直线AC下方的抛物线上有一动点P，过点P作//的坐标．于H，求线段PH的最大值及此时点P的坐标．（3）直线AC下方的抛物线上有一动点P，过点P作PH AC（4）直线AC 下方的抛物线上有一动点P ，过点P 作//PN y 轴交AC 于N ，过点P 作PH AC 于H ，求PNH △周长的最大值及此时点P 的坐标．（5）在抛物线对称轴上找一点N ，使得BCN △的周长最小，求BCN △周长的最小值及此时点N 的坐标．⊥交AC于点M，求CM的最小值．（6）在线段OA上找一点N，连接NC，作NM NCMN=，求四边形BNMC周长的最小值及（7）在抛物线对称轴上有两动点N、M（点N在点M上方），且1此时M的坐标．（8）在对称轴上找一点N ，使得NA NC -最大，求点N 的坐标．【答案】（1）223y x x =+-，对称轴为：直线x ＝－1，顶点坐标为：D （－1，－4）；（2）PN 的最大值为94，此时P （－32，154-）；（3）当PN 最大为94时，PH 92P （－32，154-）；（4）当PNH △周9294，此时P （－32，154-）；（5）1032N （－1，－2）；（6）1262-（7）6105（8）10131,M （713-，-）；（9）N 的坐标为：（－1，－6）． 【详解】（1）解：∵3OA OC ==， ∴A （－3，0），C （0，－3），∴()20333b c c ⎧=--+⎪⎨-=⎪⎩，解得：23b c =⎧⎨=-⎩，∴抛物线的解析式为：223y x x =+-，对称轴为：直线x ＝－1，顶点坐标为：D （－1，－4）． （2）解：设P （x ，223x x +-），则N （x ，－x －3），∴PN ＝－x －3－（223x x +-）＝23x x --＝23924x ⎛⎫-++ ⎪⎝⎭，∴当x ＝－32时，PN 的最大值为94，此时P （－32，154-）．（3）解：过点P 作PN ∥y 轴，交AC 于点N ， ∵OA ＝OC ＝3， ∴∠ACO ＝45°， ∵PN ∥y 轴，∴∠PNH ＝45°，即：PNH 是等腰直角三角形，∴PH 2PN ， 设P （x ，223x x +-），则N （x ，－x －3），∴PN ＝－x －3－（223x x +-）＝23x x --＝23924x ⎛⎫-++ ⎪⎝⎭，∴当x ＝－32时，PN 的最大值为94，∴当PN 最大为94时，PH 最大值＝94×22＝928，此时P （－32，154-）．（4）解：∵OA ＝OC ＝3， ∴∠ACO ＝45°， ∵PN ∥y 轴，∴∠PNH ＝45°，即：PNH 是等腰直角三角形， ∴PH ＝NH 2， ∴PNH △周长＝ PH ＋NH ＋PN 22PN 22PN ＋ PN ＝(21)PN ， 设P （x ，223x x +-），则N （x ，－x －3），∴PN ＝－x －3－（223x x +-）＝23x x --＝23924x ⎛⎫-++ ⎪⎝⎭，∴当x ＝－32时，PN 的最大值为94，∴当PN 最大为94时，PNH △周长最大值＝94×)219294，此时P （－32，154-）．（5）解：连接AC 交对称轴于点N ′，∵A、B关于对称轴对称，∴AN′＝BN′∴BCN△的周长＝BC＋CN′＋BN′＝BC＋CN′＋AN′＝BC＋AC，∴此时BCN△的周长最小值＝BCN'的周长＝BC＋AC222213331032++∵直线AC的解析式为：y＝－x－3，∴当x＝－1时，y＝－2，即N（－1，－2）．（6）解：由题意得：点N在以CM为直径的圆上，设CM的中点为E，连接EN，则当圆E与x轴相切时，即：EN⊥x轴时，EN最小，此时CM＝2EN最小，设M（x，－x－3），则E（622x x--，），∴EN＝62x+，CM()222332x x x+--+=∴2×62x +22x 662x =-62x =+， ∴M （662-629）， ∴CM ()()2266262931262-+-+-（7）解：过点N 作作NQ ∥MC 交y 轴于点Q ，连接AQ 交DE 于点N ′，连接BN ′，则Q （－2，0），∵NQ ∥MC ，MN ∥CQ ， ∴四边形MNQC 是平行四边形， ∴CM ＝QN ，∴四边形BNMC 的周长＝BC ＋BN ＋MN ＋CM ＝BC ＋BN ＋1＋QN 101＋BN ＋QN ， ∵B 、A 关于DE 对称， ∴AN ′＝BN ′，∴四边形BNMC 101＋BN ′＋QN ′101＋AN ′＋QN 101＋AQ 101＋222310131+，∵直线AQ 的解析式为：223y x =--，∴N ′（413-，-），∴此时M （713-，-）．（8）解：连接BC ，并延长交ED 于点N ′，连接BN ，∵A 、B 关于DE 对称， ∴AN ＝BN ，∴NA NC -＝NB NC -≤BC ＝N B N C ''-， ∵B （1，0），C （0，－3）， ∴直线BC 的解析式为：33y x =-， 令x ＝－1代入33y x =-得：y ＝－6， ∴N ′（－1，－6），∴NA NC -最大时，N 的坐标为：（－1，－6）．二次函数与几何综合专题---- 胡不归和阿氏圆问题【胡不归最值问题】 求BC +kAC 的最小值．解决思路：构造射线AD 使得sin ∠DAN=k ，即CHk AC，CH=kAC ．将问题转化为求BC+CH 最小值，过B 点作BH ⊥AD 交MN 于点C ，交AD 于H 点，此时BC+CH 取到最小值，即BC+kAC 最小．1．已知抛物线y ＝ax 2+bx +c 与x 轴交于A （﹣1，0），B （5，0）两点，C 为抛物线的顶点，抛物线的对称轴交x 轴于点D ，连结BC ，且tan ∠CBD =43，如图所示． （1）求抛物线的解析式；（2）设P 是抛物线的对称轴上的一个动点．①过点P 作x 轴的平行线交线段BC 于点E ，过点E 作EF ⊥PE 交抛物线于点F ，连结FB 、FC ，求△BCF 的面积的最大值；②连结PB ，求35PC +PB 的最小值．CH=kACsin α=CH AC=kHDαA BCM MCBAαDH2．在平面直角坐标系中，抛物线y＝ax2+bx+3与x轴交于点A（﹣3，0）、B（1，0），交y轴于点N，点M 为抛物线的顶点，对称轴与x轴交于点C．（1）求抛物线的解析式；（2）如图1，连接AM，点E是线段AM上方抛物线上一动点，EF⊥AM于点F，过点E作EH⊥x轴于点H，交AM于点D．点P是y轴上一动点，当EF取最大值时：①求PD+PC的最小值；②如图2，Q点为y轴上一动点，请直接写出DQ+14OQ的最小值．3．如图，抛物线y ＝ax 2﹣2ax +c 的图象经过点C （0，﹣2），顶点D 的坐标为（1，−83），与x 轴交于A 、B 两点．（1）求抛物线的解析式．（2）连接AC ，E 为直线AC 上一点，当△AOC ∽△AEB 时，求点E 的坐标和AE AB的值．（3）在（2）的条件下，点F （0，y ）是y 轴上一动点，当y 为何值时，√55FC +BF 的值最小．并求出这个最小值．（4）点C 关于x 轴的对称点为H ，当√55FC +BF 取最小值时，在抛物线的对称轴上是否存在点Q ，使△QHF 是直角三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由．4．如图1，抛物线y＝x2+（m﹣2）x﹣2m（m＞0）与x轴交于A，B两点（A在B左边），与y轴交于点C．连接AC，BC．且△ABC的面积为8．（1）求m的值；（2）在（1）的条件下，在第一象限内抛物线上有一点T，T的横坐标为t，使∠ATC＝60°．求（t﹣1）2的值．（3）如图2，点P为y轴上一个动点，连接AP，求CP+AP的最小值，并求出此时点P的坐标．【阿氏圆最值问题】计算PA k PB +的最小值时，利用两边成比例且夹角相等构造母子型相似三角形问题：在圆上找一点P 使得PA k PB +的值最小，解决步骤具体如下： ①如图，将系数不为1的线段两端点与圆心相连即OP ，OB ②计算出这两条线段的长度比OPk OB= ③在OB 上取一点C ，使得OC k OP =，即构造△POM ∽△BOP ，则PCk PB=，PC k PB = ④则=PA k PB PA PC AC ++≥，当A 、P 、C 三点共线时可得最小值1．如图，抛物线2y ax bx c =++与x 轴交于(3A 0)，B 两点（点B 在点A 的左侧），与y 轴交于点C ，且33OB OA OC ==，OAC ∠的平分线AD 交y 轴于点D ，过点A 且垂直于AD 的直线l 交y 轴于点E ，点P 是x 轴下方抛物线上的一个动点，过点P 作PF x ⊥轴，垂足为F ，交直线AD 于点H ． （1）求抛物线的解析式；（2）设点P 的横坐标为m ，当FH HP =时，求m 的值； （3）当直线PF 为抛物线的对称轴时，以点H 为圆心，12HC 为半径作H ，点Q 为H 上的一个动点，求14AQ EQ +的最小值．2．如图1，抛物线y＝ax2+bx+c与x轴正半轴交于点A，点B（点A在点B的左侧），与y轴交于点C．若线段AB绕点A逆时针旋转120°，点B刚好与点C重合，点B的坐标为（3，0）．（1）求抛物线的表达式；（2）抛物线的对称轴上是否存在一点P，使△ACP为直角三角形？若存在，请求出点P的坐标，若不存在，请说明理由；（3）如图2，以点B为圆心，以1为半径画圆，若点Q为⊙B上的一个动点，连接AQ，CQ，求AQ+CQ 的最小值．3．如图，已知抛物线y＝﹣x2+2x+3与x轴交于点A，B（点A在点B的右侧），与y轴交于点C．（1）如图①，若点D为抛物线的顶点，以点B为圆心，3为半径作⊙B．点E为⊙B上的动点，连接A，DE，求DE+AE的最小值．（2）如图②，若点H是直线AC与抛物线对称轴的交点，以点H为圆心，1为半径作⊙H，点Q是⊙H 上一动点，连接OQ，AQ，求OQ+AQ的最小值；（3）如图③，点D是抛物线上横坐标为2的点，过点D作DE⊥x轴于点E，点P是以O为圆心，1为半径的⊙O上的动点，连接CD，DP，PE，求PD﹣PE的最大值．4．如图1，抛物线y＝ax2+bx﹣4与x轴交于A、B两点，与y轴交于点C，其中点A的坐标为（﹣1，0），抛物线的对称轴是直线x＝．（1）求抛物线的解析式；（2）若点P是直线BC下方的抛物线上一个动点，是否存在点P使四边形ABPC的面积为16，若存在，求出点P的坐标若不存在，请说明理由；（3）如图2，过点B作BF⊥BC交抛物线的对称轴于点F，以点C为圆心，2为半径作⊙C，点Q为⊙C 上的一个动点，求BQ+FQ的最小值．【课后训练】1．如图，直线y＝x+2与抛物线y＝x2﹣2mx+m2+m交于A、B两点（A在B的左侧），与y轴交于点C，抛物线的顶点为D，抛物线的对称轴与直线AB交于点M．（1）当四边形CODM是菱形时，求点D的坐标；（2）若点P为直线OD上一动点，求△APB的面积；′（3）作点B关于直线MD的对称点B'，以点M为圆心，MD为半径作⊙M，点Q是⊙M上一动点，求QB'+QB的最小值．2．如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B（8，0），点A为抛物线的顶点．（1）求二次函数的表达式；（2）在抛物线的对称轴上是否存在点M，使△ABM是等腰三角形？如果存在，请求出点M的坐标．如果不存在，请说明理由；（3）若点P为⊙O上的动点，且⊙O的半径为，求的最小值．3.抛物线y＝ax2+bx﹣5的图象与x轴交于A、B两点，与y轴交于点C，其中点A坐标为（﹣1，0），一次函数y＝x+k的图象经过点B、C．（1）试求二次函数及一次函数的解析式；（2）如图1，点D（2，0）为x轴上一点，P为抛物线上的动点，过点P、D作直线PD交线段CB于点Q，连接PC、DC，若S△CPD＝3S△CQD，求点P的坐标；（3）如图2，点E为抛物线位于直线BC下方图象上的一个动点，过点E作直线EG⊥x轴于点G，交直线BC于点F，当EF+√22CF的值最大时，求点E的坐标．4.如图①，直线y＝﹣x﹣3分别与x轴、y轴交于点B，C，抛物线y＝ax2+bx+c经过B，C两点，且与x轴的另一交点为A（1，0）．（1）求抛物线的函数解析式；（2）如图①，点P在第三象限内的抛物线上．①连接AC，PB，PC，当四边形ABPC的面积最大时，求点P的坐标；②在①的条件下，G为x轴上一点，当PG+√55AG取得最小值时，求点G的坐标；（3）如图②，Q为x轴下方抛物线上任意一点，D是抛物线的对称轴与x轴的交点，直线AQ，BQ分别交抛物线的对称轴于点M，N．问：DM+DN是否为定值？如果是，请求出这个定值；如果不是，请说明理由．21Math唐老师22。