当前位置：文档之家 › 第一章 数值分析的基本概念(删减版)

第一章 数值分析的基本概念(删减版)

  • 格式：ppt
  • 大小：1.66 MB
  • 文档页数：41

下载文档原格式

  / 41

合集下载

数值分析 知识点总结

数值分析 知识点总结

数值分析知识点总结一、数值分析的基本概念1. 数值分析的对象数值分析的对象是现实生活中的数字数据和信息。

这些数据和信息可以来自各个领域，包括自然科学、社会科学、技术工程等。

例如，物理实验中测得的实验数据、经济管理中的统计信息、天气观测中的气象数据等，都是数值分析的对象。

2. 数值分析的目的数值分析的主要目的是通过对数值数据和信息的定量分析，发现其中的规律，提取有用的信息，做出科学的预测和决策。

例如，通过对某种药物的临床试验数据进行数值分析，可以得出这种药物的疗效和毒性情况，为临床医生的治疗决策提供依据。

3. 数值分析的方法数值分析采用数学和计算机科学的方法对数值数据和信息进行处理和分析。

它涉及的具体方法包括数值计算、插值与逼近、数值微分和积分、常微分方程数值解、数值线性代数等。

二、数值分析的基本内容1. 数值计算数值计算是数值分析的基本方法之一，它包括离散化、数值稳定性、误差分析等内容。

离散化是将连续问题转化为离散问题，这是数值计算的基本工作方式。

数值稳定性研究的是数值方法对误差的敏感程度，是评价数值方法好坏的重要指标。

误差分析则研究数值计算中产生的误差的成因和大小。

2. 插值与逼近插值与逼近是数值分析的重要内容之一，它研究如何通过已知的数值数据估计未知函数的值。

插值是通过已知的离散数据点构造一个连续函数，使得这个函数通过这些数据点；逼近则是通过已知的离散数据点构造一个近似函数，使得这个函数与原函数的差尽量小。

3. 数值微分和积分数值微分和积分是数值分析的又一重要内容，它研究如何通过已知的函数值计算函数的导数和定积分值。

数值微分是通过函数值计算函数的导数值；数值积分则是通过函数值计算函数的定积分值。

这两项工作在科学计算中有着广泛的应用。

4. 常微分方程数值解常微分方程数值解也是数值分析的重要内容之一，它研究如何通过数值方法计算常微分方程的近似解。

常微分方程是自然界和技术工程中经常出现的数学模型，因此其数值解的研究有着广泛的应用价值。

数值分析第一章PPT

数值分析第一章PPT

1.1.2 计算数学与科学计算 现代科学的三个组成部分: 科学理论, 科学实验, 科学计算 科学计算 的核心内容是以现代化的计算机及数学软件 （Matlab, Mathematica, Maple, MathCAD etc. ）为工具，以数学 模型为基础进行模拟研究。
一些边缘学科的相继出现：
计算数学,计算物理学,计算力学,计算化学,计算生物学, 计算地质学,计算经济学,等等

取 0 e
1
x2
dx S4 ,
S4
R4
/* Remainder */
1 1 1 1 由留下部分 称为截断误差 /* Truncation Error */ 4! 9 5! 11 /* included terms */ 1 1 这里 R4 引起.005 0 由截去部分 4! 9 /* excluded terms */ 1 1 1 S4 1 1 0 .333 0 .1 0 .024 0 .743 引起 3 10 42 | 舍入误差 /* Roundoff Error */ | 0.0005 2 0.001
数值分析
第1章
数值分析与科学计算引论
§1.1 数值分析的对象、作用与特点
1.1.1 什么是数值分析 数值分析是计算数学的主要部分,计算数学是数学 科学的一个分支,它研究用计算机求解各种数学问题的 数值计算方法及其理论与软件实现.这门课程又称为(数 值)计算方法、科学与工程计算等。
•
在电子计算机成为数值计算的主要工具的今天， 需要研究适合计算机使用的数值计算方法。使用计 算机解决科学计算问题时大致要经历如下几个过程:
造成这种情况的是不稳定的算法 /* unstable algorithm */ 我们有责任改变。

数值分析课件

数值分析课件

辛普森方法
一种基于矩形法思想的数值积分方法 ，适用于计算定积分。
自适应辛普森方法
一种基于辛普森方法和梯形法的自适 应数值积分方法，能够根据函数性质 自动选择合适的积分策略。
常微分方程的数值求解
01
欧拉方法
一种基于常微分方程初值 问题的数值求解方法，通 过逐步逼近的方式求解近 似解。
02
龙格-库塔方法
定积分是函数在区间上积分和的极限；不定积分是函数在 某个区间上的原函数。
02
应用领域
积分广泛应用于物理、工程、经济等领域，如求曲线下面 积、求解变速直线运动位移等。
03
数值计算方法
使用数值积分方法（如梯形法、辛普森法等）来近似计算 定积分和不定积分的值。这些方法将积分区间划分为若干 个小段，并使用已知的函数值和导数值来近似计算每个小 段的积分值，最后求和得到积分的近似值。
一种基于常微分方程初值 问题的数值求解方法，通 过构造龙格-库塔曲线来 逼近解。
03
阿达姆斯-图灵 方法
一种基于常微分方程初值 问题的数值求解方法，通 过构造阿达姆斯-图灵曲 线来逼近解。
04
自适应步长控制 方法
一种基于欧拉方法和龙格 -库塔方法的自适应步长 控制方法，能够根据误差 自动调整步长。
偏微分方程的数值求解
高斯消元法的步骤
1. 将方程组按照行进行排列，并将每个方程中的未知数 按照列排列。
2. 对于每个方程，选取一个未知数作为主元，并将其余 的未知数用主元表示。
3. 将主元所在的行与其他行进行交换，使得主元位于对 角线上。
4. 将主元所在的列中位于主元下方的元素消为0，从而得 到一个阶梯形矩阵。
线性方程组的解法
数值分析是一种工具，它可以帮助我 们更好地理解和解决实际问题，同时 也可以帮助我们更好地理解和应用数 学理论。

数值分析(第一章)修正版描述

数值分析(第一章)修正版描述

2
例:为使 x 20 的近似值 x 的相对误差不超过 问查开方表时至少要取几位有效数字? * 解:设近似值 x 取n位有效数字可满足题设要求。 对于 x
1 103 2
*
20, 有x1 4
* r
1 1 1 n 1 n e 10 10 由定理,有 2 x1 8
1 1 1 n 3 10 10 令 8 解得 2
e* x* x * ，则称 * 为x* 近似x的一个绝对 差限，简称误差限。 误 . 实际计算中所要求的绝对误差，是指估计一个 尽可能小的绝对误差限。
*
2.相对误差及相对误差限
0) 的一个近似,称 定义 设 x 是准确值 x( *
*
为 x 近似x的一个绝对误差。在不引起混淆时，简称符 * * 号 er ( x )为 er * * * * 因 e e e x x
(1)有效数字
定义 :设x的近似值 x 有如下标准形式
*
x 10 0.x1x2 xn1 xp 9且x1 0, p n 其中m为整数, xi 0,1,2 ，
*
1 mn e x x 10 如果 2
* *
, * 则称 x 为的具有n位有效数字的近似数. 或称 x* 准确到 10m n 位,其中数字 x1 x2 xn ,分别 * x 被称为 的第一,第二,…第n个有效数字.
*
n
* i *
x * * f 'i ( x1 , x2 , i 1 y
n
* i *
x )er ( x )
* n
* i
绝对误差限和相对误差限满足传播不等式：
( y ) f 'i ( x , x ,

数值分析的所有知识点总结

数值分析的所有知识点总结

数值分析的所有知识点总结一、数值分析的基本概念1.1 数值分析的定义和作用数值分析是研究利用计算机对数学问题进行数值计算的一门学科。

它旨在发展和分析数值计算方法，以解决实际问题中出现的数学模型。

数值分析的主要作用在于加快科学研究和工程设计的速度，提高计算精度和可靠性，以及发现新的科学规律和工程技术。

1.2 数值计算的基本步骤数值计算通常包括以下基本步骤：建立数学模型、选择适当的数值方法、编写计算程序、进行计算和分析结果。

其中，建立数学模型是数值计算的基础，它将实际问题抽象为数学公式或方程组的形式；选择适当的数值方法是指根据具体问题的特点，选择合适的数值计算方法进行求解；编写计算程序是指将选择的数值方法用计算机程序的形式实现；进行计算和分析结果是指利用计算机进行数值计算，并分析计算结果的准确性和可靠性。

1.3 数值分析的应用范围数值分析广泛应用于科学、工程、经济、金融等领域。

在科学研究中，数值分析常用于数学建模、实验数据处理、科学计算等方面；在工程领域，数值分析常用于工程设计、结构分析、流体力学、传热传质等方面；在经济金融领域，数值分析常用于风险评估、金融工程、市场预测等方面。

二、数值计算方法2.1 插值法插值法是利用已知的离散数据（如实验数据、观测数据）推导出未知的数据值的一种数值计算方法。

常用的插值方法包括拉格朗日插值、牛顿插值、分段插值等。

2.2 数值微分与数值积分数值微分是指利用离散数据计算函数的导数值的数值计算方法。

常用的数值微分方法包括差商法、中心差商法等。

数值积分是指利用离散数据计算函数的积分值的数值计算方法。

常用的数值积分方法包括复合梯形法、复合辛普森法等。

2.3 数值线性代数数值线性代数是研究线性代数问题的数值计算方法。

它涉及到线性方程组的求解、线性方程组的特征值和特征向量的计算、矩阵的LU分解、矩阵的QR分解等内容。

2.4 非线性方程求解非线性方程求解是研究非线性方程的数值计算方法。

数值分析-第一章ppt课件

数值分析-第一章ppt课件

数及其图形作出判断. 整理版课件
6
由分部积分法可得:
Ine101xndex
n=1,2,4,6, 8,10,15
e 1 x n ex|1 0 e 1 0 1 nn 1 x ex dx
1 nn 1 I (n 1 ,2 , ).
如果取 I0 = 1–e–1 = 0.63212056 (八位有效数字).
x1,2b
b24ac 2a
直接进行计算则得: x1=109, x2=0. 其中的x2=0明பைடு நூலகம்失真, 这也是由于舍入误差造成的.
整理版课件
8
§1 误差的来源
实际 问题
建立数 学模型
确定计 算方法
编程 上机
由抽象简 化产生的 模型误差 及参数的 观测误差
由计算方 法本身产 生的截断 误差或称 方法误差
er(x* )e(x x* )x xx*
同样, 由于精确值 x 经常是未知的, 所以, 需要另
外的近似表达形式. 我们注意如下公式的推导,
当
|
e ( x*) x*
|
较小时,
有
e(x* )e(x* )e(x*x )* (x)
x x*
xx*
[x*[ee((xx**))2]x] *1[e(exx(**x*)]2)
整理版课件
18
乘法相关的误差公式： 设 f (x1, x2)= x1 x2 . e ( x 1 x 2 ) x 2 e ( x 1 ) x 1 e ( x 2 ) e r ( x 1 x 2 ) e r ( x 1 ) e r ( x 2 ) |e ( x 1 x 2 ) | |e ( x 1 ) | |e ( x 2 ) | |e r ( x 1 x 2 ) | |e r ( x 1 ) | |e r ( x 2 ) |

第一章数值分析的基本概念(删减版)资料

第一章数值分析的基本概念(删减版)资料

| y%|| f (x1*, x2*,L , xn* ) f (x%1, x%2,L , x%n ) | ?
算法的数值稳定: 计算过程中舍入误差 不会被严重放大
误差的传播
线性情形用严格估计
n
| y%|| f ( x1* , x2* ,L , xn* ) f ( x%1, x%2 ,L , x%n ) | | ai | i i 1
研究过程 （理论上有解，而无求解公式或计算量过大难以用
手工实现的数学问题）
实际问题
数学模型
数值分析理论 程序设计
重点内容
研究并求解数学问题的数 值（近似）解的方法
上机计算
理论分析 科学实验 科学计算
计算的目的不在于数据，而在于洞察事物。 －－理查德·哈明
The purpose of computing is insight，not numbers. －－Richard Wesley Hamming
单位，则从这一位起，直到最左边的第一位非零数字为止的
所有数字都称为有效数字。并说x“准确”到这一位。
例1.3 (误差限和有效数字)
圆周率 =3.1415926。
x1=3.14; x 2=3.141; x 3=3.142; x 4=3.1414
解 (1)
|x1|
0.x51=100.321,4有130位1 有, 效数x字1=0；.15926102,
数值分析 Numerical Analysis
于佳平 东华大学
Email：jpyu@
教材
《数值分析及其MATLAB实验》
姜健飞 吴笑千 胡良剑编
上课(2--17周)
每周五 8:15-9:45 第二教学楼129室 每个单周五 10:05-11:35 图文3号机房 (图文 信息中心) 请按机号入座！

数值分析第一章

数值分析第一章

截断误差：
Rn(x)
f (n1)()xn1
(n1)!
舍入误差：机器字长有限
R 3 .14 0 1 .05 09 0 .数0 制转0 换、2 机器6 数.
二、误差、有效数字
定义1 绝对误差，简称误差： e*x* x,其x* 中 为准 x的 确 近 .值 似
误差限：*|e*|的一个上 . 界
数值分析
第1章 绪论
§1 数值分析的研究对象与特点
一、什么是数值分析
数值分析是计算数学的一个主要部分,计算数学是数 学科学的一个分支,它研究用计算机求解各种数学问题 的数值计算方法及其理论与软件实现.
实际问题→数学模型→数值计算方法 →程序设计→上机计算求出结果
先看两个例子。 例1 求方程 x2=2sinx，在区间(1,2)内的根。 理论上可知显然找不出根的解析式，即无法求出
而 按 (2.相 1 )， m 对 3 ,误 n3 差绝 .2限对 相误 同 2 *差 ： 1 21限 05. r*0.005 /90..80000/00.0050.980
定理１设近似x*数 表示为
x*10m(a1a2101al 10(l1)) (2.)1
一般 Cp10认为是病 . 态 其他计算问题条 也件 要 ,考 数 考虑虑是否 . 病态
二、算法的数值稳定性
考虑初始数据误差在计算中的传播问题.
例 5计In算 e 10 1xnexdx,n0,1 , ,并估.计误
In 1 n n 1 I ,n 1 ,2 , , I01e1. (A) II0 n 1 0.6nI3n ,1 2,n11,2, . (B)II9n** 10.01n(168,In*4),n9,8, ( ,1I9. 1 2(110e110)0.06)8 定义一3个算法若输 误入 差 ,而数 在据 计有 算过 误差不,则 增称 长此算法是 的,否 数则 值是 稳不 定. 稳

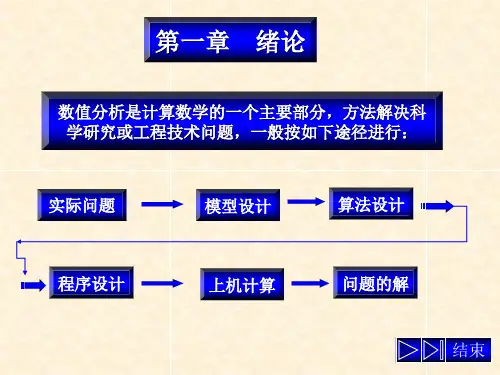
数值分析 (7-1) 第1章 引言

数值分析 (7-1) 第1章 引言

如计算 sin 0.5，取n=3 sin 0.5 0.5 0.53 0.55 0.57 0.479625
3! 5! 7!
结束
据泰勒余项公式，它的误差应为
R (1)9 9
9!
0,
4
R ( / 4)9 3.13 10 7
362880
( 1.2)
可见结果是相当精确的.实际上结果的六位数字都是正确的.
第二法：执行n 次(1.7)式，每次1次乘法，一次加法， 共计n次乘法， n 次加法.
结束
显然第二种方法运算量小，它是我国宋代数学家秦九韶 最先提出的（1247年），被称为“秦九韶算法”.
例4 不用开平方计算 a (a＞0)的值.
一个小于 a ,可以设想它们的平均值应为 a 的更好的 平均值，于是设计一种算法：
问题，今后课程将进一步讨论.
结束
§ 1.2 误差
1.2.1 误差的来源 在运用数学方法解决实际问题的过程中，每一步都可
能带来误差. 1、模型误差 在建立数学模型时，往往要忽视很多次要因 素，把模型“简单化”，“理想化”，这时模型就与真实 背景有了差距，即带入了误差.
2、测量误差 数学模型中的已知参数，多数是通过测量得 到.而测量过程受工具、方法、观察者的主观因素、不可 预料的随机干扰等影响必然带入误差.
我们将采用前三种方式表述各种算法 1.1.2 算法的基本特点
1 算法常表现为一个无穷过程的截断：
结束
例1 计算 sin x的值，
x 0, π 4
根据sin x 的无穷级数
sin x x x3 x5 x7 (1)n x2n1 ( 1.1)
3! 5! 7!
(2n 1)!
这是一个无穷级数，我们只能在适当的地方“截断” ，使计算量不太大，而精度又能满足要求.

数值分析第1章

数值分析第1章

11
若能根据测量工具或计算情况估计出误差绝对值的一个 上界，即
e* = x*−x ≤ ε*,
则 ε * 叫做近似值的误差限 它总是正数. 误差限， 误差限 对于一般情形 x*−x ≤ ε *， 即
x *− ε * ≤ x ≤ x *+ ε*,
也可以表示为
x = x*±ε *.
但要注意的是，误差限的大小并不能完全表示近似值的 误差限的大小并不能完全表示近似值的 好坏. 好坏
（2.2）
17
按这个定义， 如取 x*= 3.14 作为 π的近似值， * x 就有3位有效数字， 取 x* = 3.1416≈ π ， x* 就有5位有效数字.
18
例1 按四舍五入原则写出下列各数具有5位有效数字的 近似数： 187.9325, 0.03785551, 8.000033, 2.7182818.
数值分析
主讲: 陈星玎
北京工商大学 计算机与信息工程学院 应用数学系
1
玎(ding): 玉石碰撞发出的声音. 比如：玎当响(表示很有名 气). 毕业院校：中国科学院计算数学研究所 博士 专业：计算数学 Email: chenxingding@
《数值分析》 数值分析》
李庆扬 王能超 易大义 编 清华大学出版社
x
* 2 2
* (x2 ≠ 0).
25
一般情况下，当自变量有误差时函数值也产生误差， 其误差限可利用函数的泰勒展开式进行估计. 设 f (x)是一元函数， x的近似值为 x* ，以 f (x*)近 似 f (x)，其误差界记作 ε ( f (x*)) ， 利用泰勒展开
f (x) − f (x*) = f ′(x*)(x − x*) + ′ f ′ (ξ ) (x − x*)2 , 2 ξ介 x, x*之 ， 于 间

数值分析第一章

数值分析第一章

(3) 有好的计算复杂性：
节省时间（时间复杂性）和计算机存储空间 （空间复杂性）
(4) 要有数值实验。
通过数值实验证明是有效的.
研究的内容 1 非线性方程与方程组的数值方法；(第2、5章)
2 线性方程组的数值方法；(第3、4章)
3 插值与数值逼近；(第6、7章) 4 数值积分与数值微分；(第8章) 5 微分方程的数值解法. (第9章) 6 特征值与特征向量的计算. (第10章)
f ( x ) tan( x ) 1 2 f ( x ) 1 tan ( x) 2 cos ( x ) x * f ( x*) 1 Cp x* tan( x*) f ( x*) tan( x*)
1 | x x | 10m n , 2

称 x 有n位有效数字.

例：按四舍五入原则将下列各数保留到5位有 效数字：187.9325, 0.03785551, 8.000033. 解：
187.9325 187.93 0.03785551 0.037856 8.000033 8.0000
1 10 ( n1) 2(a1 1)
(a1 1) 10
1 10m n 2

m 1
所以 x 至少具有n位有效数字.
定理１说明有效数字越多，相对误差限越小. 例 要使 20 的近似值的相对误差限小于0.1% 要取几位有效数字？ 解 假设取n位有效数字，由定理1可知
从而 即
x 0.5 x x 0.5,
70 0.5 x 70 0.5, x [69.5,70.5].


或
设某量的准确值为x, x 是x的近似值， 定义： * er 为 x 的相对误差，若 e 为 x 的绝对误差，

数值分析

数值分析

数值分析第一章绪论1.1数值分析研究对象与特点数值分析又叫计算数学。

实际问题→数学模型→数值计算方法→程序设计→上机计算求结果1.2数值计算的误差1.2.1误差来源于分类有限差分方法（Finite Differenc Methods,FDM），是通过有限差分来近似导数或者偏导数，从而求得微分方法的近似解。

在实际中，许多数学问题都很难得到其解析解，所谓解析解就是可以通过给出解的具体函数形式，从解的表达式中就可以算出任何自变量对应值；而数值解是在特定条件下通过近似计算得出来的一个数值。

数值解只能由具体的系数确定：ax2+bx+c=0(a≠0)。

假设f(x)在x0处各阶可导，则根据定理，其在x0+h的泰勒展开式为：f(x0+ℎ)=f(x0)+f′(x0)1!ℎ+f(2)(x0)2!ℎ2+⋯+f(n)(x0)n!ℎn+R n(x)可以推导函数f一階导数的近似值：f(x0+ℎ)=f(x0)+f′(x0)ℎ+R1(x)设定x0=a，可解f′(a)=f(a+ℎ)−f(a)ℎ−R1(x)ℎ，R1(x)是x→a时的高阶无穷小，可以将f的一阶导数近似为f′(a)≈f(a+ℎ)−f(a)ℎ(一阶近似)。

这种由于截断所引起的误差就是截断误差(truncation error)或方法误差或结尾误差。

由“四舍五入”引起的误差称为舍入误差(round-off error）。

步长不可能是无穷小，所以这也会引入一个误差。

1.2.2误差与有效数字定义1：设x为准确值，x*为x的一个近似值，称e*= x*-x为近似值的绝对误差，简称误差。

准确值是不知道的，否则没必要给出近似值，这也就是说，绝对误差是没法算的，所以我们给出绝对误差e*的误差限：|x∗−x|≤ε∗，即x∗−ε∗≤x≤x∗+ε∗；对于10、11和1000、1001，它们的绝对误差都是1，但是它们误差的程度是不同的，所以，我们引入相对误差。

绝对误差:△＝│测量值—真值│相对误差:相对误差＝(绝对误差/真值的绝对值）×100%≈绝对误差/测量值的绝对值）×100%，相对误差用e r∗表示。

数值分析第一章

数值分析第一章

n L2 n Ln / cos 2n
Ln n si n

ˆ (4L L ) / 3 L 2n 2n n
n L error 192 3.1414524 1.4e-004 384 3.1415576 3.5e-005 3.1415926 4.6e-010
通信卫星信号覆盖率
设地球为球体, R为地球半径,H为 卫星高度,覆盖面为球冠面积
(4)尽量减少计算工作量(乘、除法次数)
例 计算 P(x) = 1+2x+3x2+4x3 + 5x4 的值 秦九韶算法 P(x)=1+x(2+x(3+x(4+5x)))
应用: 2进制数转换为10进制数算法
(1 1 1 0 1 1 1 0)2 = 27+26 +25 +0 +23 +22 +2 +0 =((((((1· 2+1)2+1)2+0)2+1)2+1)2+1)2+0 =238
x
dx n x n1e x dx) 1 nI n1
0
19/25
e (x e
1
x 1 0
1
递推公式: In = 1 – nIn-1 (I0 = 1- e-1)
–1 ≈0.63212055882856 I = 1 – e 初值： 0
S0=1-exp(-1);S(1)=1-S0; for n=2:20 |e(S0)|=|S0 –I0|<0.5· 10-14 S(n)=1-n*S(n-1) end error
n=20时，S20= -30.19239488558378 实际计算: Sn=1-nSn-1,S0=0.63212055882856

第一章数值分析

第一章数值分析
x* 0.a1a2 an 10m (a1 0)有n位
有效数字
r
1 10n1 2(a1 1)

e x x* er x x
x* 0.a1a2 an 10m (a1 0)有n位
1 10n1 2a1
绝对误差（限）
相对误差（限）
e
er r ,
16
4 有效数字与绝对误差、相对误差的关系：
(1)若某数x的近似值x*有n位有效数字，则
数值分析
主讲数值分析课题组 Chenning
1
数值分析课程简介
数值分析
数值分析主要包括计算方法和数值方法两 部分。它是研究科学与工程技术中数学问题的 数值解及其理论的一个重要的数学分支，它主 要涉及到代数、微积分、微分方程的数值解等 问题。
数值分析及计算的主要任务，就是研究适合
于在计算机上使用的的数值计算方法及与此相
第八章 非线性方程的数值解法
第九章 常微分方程的数值解法
3
数值分析
第一章 数值计算中的误差分析
本章的主要内容有：
（一） 误差的来源； （二） 绝对误差、相对误差和有效数值; （三） 数值计算中误差的传播； （四） 数值计算中应注意的问题。
4
第一节 误差与数值计算 的误差估计
第二节 选用和设计算法 适应遵循的原则
3.14 3.14 0.0016 1 102.
2 ( 3.1416 3.14 0.0016) 3.142 3.142 0.00041 1 103
2 ( 3.14241 3.142 0.00041)
10
例：问3.142,3.141,22/7分别作为 的近似值各具有几位有效数字？
数值分析
5
误差与数值计算误差估计 一 误差的来源与分类 二 误差与有效数字

数值分析1

数值分析1

数值分析数值分析是数学中一个非常重要的分支，在实际工程中有着广泛的应用。

本文将从数值分析的定义、基本概念、方法和应用等方面对其进行阐述。

一、数值分析的定义和概念数值分析是指利用数学方法和计算机技术对数学模型和实际问题进行数值处理和求解的方法。

它主要涉及数值计算的方法和技术，如数值逼近、数值积分、数值解微分方程等。

在数值分析中，需要了解一些基本概念。

首先是误差概念。

误差是指数值计算过程中由于取样或近似方法等导致的计算结果与真实值之间的差异。

误差可以分为截断误差和舍入误差。

截断误差是取步长过程中的误差，而舍入误差是由于计算机存储和处理数据时产生的误差。

其次是插值和逼近的概念。

插值是指已知一些离散数据点，通过构造一个多项式函数来逼近这些离散数据点，从而得到一个连续的函数曲线。

逼近是插值的推广，它不要求通过所有点，而是利用一些有限的数据点，构造一个逼近函数来近似原函数。

最后是数值积分和数值解微分方程的概念。

数值积分是利用特定的数值积分公式对某个函数的积分进行数值计算。

数值解微分方程是利用差分方法进行数值计算，从而解决实际问题中的微分方程问题。

二、常用的数值分析方法1.插值和逼近插值和逼近是最基本的数值分析方法，也是求解数学问题中经常使用的方法。

插值和逼近方法的核心是构造一个函数来逼近原函数，在方法的过程中，可以使用拉格朗日插值、牛顿插值、埃尔米特插值等方法。

插值和逼近方法的优势是可以通过构造一个泛函，对真实函数进行逼近。

但其缺点是容易受到数量级和选点方式的影响，对于一些特定的问题，也存在舍入误差的影响。

2.数值积分数值积分是将某函数的积分转化为一个数值计算的方法，它可以通过考虑取样点的数量和步长等因素，来计算多项式或复合三点数值积分等方法进行积分求解。

数值积分的优势在于其可以通过对积分上下限和取样点的选择来精确求解某个函数的积分。

但同样的，其也容易受到取步长等误差的影响，而且对于某些奇特的函数，需要选取合理的步长来避免误差的出现。

数值分析课件第1章

数值分析课件第1章

解：
(s ) l (d ) d (l )
110 (0.1) 80 (0.2) 27( m 2 )
r
(
s
)
(s)
s
(s)
ld
27 0.31% 8800
2、函数误差 当自变量有误差时计算函数值也产生误差，可以利用
函数的泰勒展开式进行估计。
工科研究生公共课程数学系列
（f (x)） f (x)（x）.
例1-4 设x0,x的相对误差为，求lnx的误差。
解：
lnx*
-lnx
1 x*
(x*
-
x), 即有
e(lnx) er(x)
进而有(ln(x)) 。
工科研究生公共课程数学系列
机动 上页 下页 首页 结束
1.3 误差定性分析与避免误差危害
一、几种定性分析误差的方法 1、概率分析法：考虑到误差分布的随机性，用概率统计的
二、数值分析的特点
• 面向计算机，要根据计算机的特点提供切实可行的有效算 法。
• 有可靠的理论分析，能任意逼近并达到精度要求，对近似 算法要保证收敛性和数值稳定性，还要对误差进行分析。 这些都是建立在数学理论的基础上，因此不应片面的将数 值分析理解为各种数值方法的简单罗列和堆积。
• 要有好的计算复杂性，时间复杂性好是指节省时间，空间 复杂性好是指节省存上实现。
• 要有数值实验，即任何一个算法除了从理论上要满足上述 三点外，还要通过数值实验证明是行之有效的。
工科研究生公共课程数学系列
机动 上页 下页 首页 结束
三、数值分析的学习方法 初学可能仍会觉得公式多，理论分析复杂。给出如下的 几点学习方法。
• 认识建立算法和对每个算法进行理论分析是基本任务，主 动适应公式多和讲究理论分析的特点。

数值分析第一章

数值分析第一章

n
xi2 ,
i 1
||
x
||
max
1in
|
xi
|
则 || ||1 , |和| ||2 都|是| |向| 量范数.
2 矩阵的范数
❖定义 矩阵的范数是刻画矩阵大小的量, 又叫 矩阵的模.
❖定义 Rnn上的实值函数‖·‖叫矩阵范数, 如果对 Rnn中任意的矩阵 A 和 B, 均满足下列 4 个条件:
复习
§1.3 向量与矩阵的范数
1 向量的范数ຫໍສະໝຸດ ❖定义 向量的范数是刻画向量大小的量, 又
叫向量的模.
❖定义 Rn 上的实值函数 || ·|| 称为向量范数， 如果对任意的 x, y∈Rn, 它均满足下列条件:
(1)正定性: || x ||,且0 x 0;|| x || 0
(2)齐次性:对 k ,有R
(1) A 0, 且 A 0 A 0; (2) k R, kA k A ; (3) A B A B ; (4) AB A B ;
矩阵范数与向量范数的相容性
❖定义 给定向量范数||·||和矩阵范数||·||, 如果对
任意的向量 xRn和任意的矩阵 ARn×n,它们总
满足
Ax A x ,
则称所给的矩阵范数与向量范数是相容的。
❖定理1.3 设在 Rn 中给定一种向量范数, 对任
意的矩阵 ARn×n，下式 (1.2)中定义的函数
是一种矩阵范数,并且它与给定的向量范数是
相容的.
单位球上的 最大像值
A max Ax || x ||1
(1.2)
|| kx ||;| k | || x ||
(3)三角不等式: || x y || || x.|| || y ||

《数值分析》第1章

《数值分析》第1章
T (h) = I + c1 h2 + c2 h4 + L，
b
上两式作用得到：
4T ( h) − T ( 2h) = 3 I + O (h4 )
忽略高阶项得， I ≈ T (h) + (T (h) − T (2h)) . 公式的精度为 O (h4 ) .
1 3
此
其中 c1 , c2 ,L与 h 无关，则有，
19
20
§3 误差来源与误差分析的重要性
误差来源（或分类）
(1) 模型误差：建立数学模型时忽略一些次要 因素而引起的与真实情况的误差.
(2) 测量误差：数学模型中的一些已知参数， 由于受到测量工具或其它主观因素的影 响所带来的误差.
21
(3) 截断误差：数学模型常难以求解，往往要 用近似、易于求解的问题代替，这种简化 引起的误差.
P ( x ) = a0 x n + L + an −1 x + an 已知，对输入
的x，要计算P(x)的值，采取方法
u0 = 0 ⎧ t 1 = 1, ⎪ ⎨ t k = xt k − 1 , k = 2 , L , n ⎪u = u k = 1, L , n k −1 + a n− k tk , ⎩ k
29 30
例 15. 为使 20 的相对误差小于 0.1% ，要取几 位有效数字.
例 16. 用 3. 1416 表示π 的近似值，求其相对误 差？
解：因为 a1 = 3, n = 5 ，所以
er ( x ) ≤
1 1 × 10−5 + 1 = × 10−4 2× 3 6
解： 由 er ≤ 只需
1 × 10− n + 1 且 a1 = 4 ， 为使 er ≤ 0.1% ， 2a1

数值分析PPT课件

数值分析PPT课件

03
数值分析的方法和技巧广泛应用于科学计算、工程、经 济、金融等领域。
主题的重要性
随着计算机技术的不断发展， 数值计算已经成为解决实际问 题的重要手段。
数值分析为各种数学问题提供 了有效的数值计算方法和技巧， 使得许多问题可以通过计算机 得以解决。
掌握数值分析的知识和方法对 于数学建模、科学计算、数据 分析等领域具有重要意义。
意义。
未来数值分析的发展方向
随着计算机技术的不断发展，数值分析 将更加依赖于计算机实现，因此数值算 法的优化和并行化将是未来的重要研究
方向。
随着大数据时代的到来，数值分析将更 加注重对大规模数据的处理和分析，因 此数据科学和数值分析的交叉研究将成
为一个新的研究热点。
随着人工智能和机器学习的发展，数值 分析将更加注重对非线性、非平稳问题 的处理，因此新的数值算法和模型将不
数值积分和微分
矩形法
将积分区间划分为若干个小的矩形区域，求 和得到近似积分值。
辛普森法
梯形法
利用梯形公式近似计算定积分，适用于简单 的被积函数。
利用三个矩形区域和一个梯形区域的面积近 似计算定积分。
02
01
高斯积分法
利用高斯点将积分区间划分为若干个子区间， 通过求和得到近似积分值。
04
03
矩阵的特征值和特征向量
数值分析ppt课件
目录
• 引言 • 数值分析的基本概念 • 数值分析的主要算法 • 数值分析的误差分析 • 数值分析的实例和应用 • 结论
01
引言
主题简介
01
数值分析是数学的一个重要分支，主要研究如何利用数 值计算方法解决各种数学问题。
02
它涉及到线性代数、微积分、微分方程、最优化理论等 多个数学领域。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2. 截断误差与收敛性
截断误差：一个无限的数学极限过程用有限次运算 近似计算产生的误差。 例（无限） 2 n 近似计算（有限）
x
x x e 1 x 2! n!
x
x x e Sn ( x ) 1 x 2! n!
2
n
n1 x x e Sn ( x ) Rn ( x ) e (n 1)! 在0与x之间
Байду номын сангаас
数值算法的特点
有穷性 数值性 近似性
§1.2 误差分析的概念
1. 2. 3. 4. 误差限和有效数字 截断误差与收敛性 舍入误差和数值稳定性 数据误差和病态问题
1. 误差限和有效数字
误差和相对误差(定义1.1)
设x*是某量的准确值，x是x*的近似值 称x = x*-x 为x的误差或绝对误差。 | x*-x |, 称为x的(绝对)误差限或精度， rx = (x*-x)/x*称为x的相对误差 |(x*- x)/ x *| r, 称 r为x的相对误差限。 当 r 很小时， r /| x |。 误差的四则运算见后
应用：大数据搜索、金融、核实验、飞行器、 油田勘探、天气预报 ......
地球外部大气流动模型
飞机外形优化设计问题
数值分析课程的期望
掌握各种解决数学问题的数值方法 对近似解进行评估 在计算机上实现求解 仿真模拟
1. 例1. 1 (易计算问题)
(1) 求解线性方程组AX=b, 其中A为3阶可逆方 阵，X=(x1, x2, x3)T; (2) 求代数方程x2+x6=0在[0,4]上的根x*； (3) 已 知 y=P(x) 为 [x0, x1] 上 的 直 线 ， 满 足 P(x0)=y0, P(x1)=y1, x2(x0, x1), 求P(x2)； b 1 (4) 计算定积分 I a x dx (1<a<b)； (5) 解常微分方程初值问题 y ' x y ( 0) 0
b a
y ( 0) 0
解：例1.2同例1.1“差不多” ？
(1) 计算量非常大，31＊30！＊29次乘法； (2) 无法求得x*的解析形式，只能求近似值； y1 y0 y0 ( x2 x0 ) (3) f(x2) 试试； x1 x0 (4) 无法找到原函数，考虑近似方法； (5) 没有解析解，数值解法求取近似解。
I0=1-1/e I1 I2 … I20 误差很大(见书P8) ，
* * n = nn-1, 20 =(20!) 0 ，不稳定 In 1 nI n 1 ,
算法二：递推公式 In-1=(1In)/n, n= 20 ,,1
I20估计式中点 I19 … I1 I0 误差很小
截断误差（余项公式）
算法的收敛性：该算法总可以通过提高计算 量使得截断误差任意小。即 余项0
3. 舍入误差和数值稳定性
舍入误差: 由于机器字长的限制而产生的误差 机器数(二进制0-1,离散) 规格化浮点式: 阶码m（用二进制数表示）,字长t , 尾数 (1=1) 2m0.12t, m=12s
数值分析 Numerical Analysis
于佳平 东华大学
Email：jpyu@
教材
《数值分析及其MATLAB实验》
姜健飞 吴笑千 胡良剑编
上课(2--17周)
每周五 8:15-9:45 第二教学楼129室
每个单周五 10:05-11:35 图文3号机房 (图文 信息中心) 请按机号入座！
|| f ( x , x ,, x ) f ( x 1, x 2 ,, x n ) | ? | y
* 1 * 2 * n
算法的数值稳定: 计算过程中舍入误差 不会被严重放大
误差的传播
线性情形用严格估计
* * * || f ( x1 1 , x 2 , , x n ) | | ai | i | y , x2 , , xn ) f (x i 1 n
数值计算软件
Fortran
C++
Matlab
三类计算机算法
数值算法主要指与连续数学模型有关的算法， 如数值线性代数、方程求解、数值逼近、数 值微积分、微分方程数值解和最优化计算方 法等；(本课程内容) 非数值算法主要指与离散数学模型有关的算 法，如排序、搜索、分类、图论算法等； 软计算方法是近来发展的不确定性算法的总 称，包括神经网络计算、模糊逻辑、遗传算 法、蚂蚁算法等。
n-1 = n /n, 0 =20 /(20!)，稳定
4. 数据误差和病态问题
3 21 949 49 x x x 36 1 4 2 40 3 360 61 3 1061 3 x x x 1 2 3 4 144 10 720 3 769 3739 21 40 x1 10 x2 3600 x3 3600
计算误差限: 例如：| (a b) || a b | ?
| (ab) || b a a b | ?
例1.5 (数值稳定性)
估计
In x e
0
1
n x 1
dx ,
n=0, 1, …, 20
1 1 In ( n 1)e n1
算法一: 分部积分递推公式 In=1nIn-1, n=1,,20
例1.6 (病态问题)（保留4位有效数字）
1.361 x1 0.7500 x2 0.5250 x3 2.636 0.7500 x1 0.4236 x2 0.3000 x3 1.474 0.5250 x 0.3000 x 0.2136 x 1.039 1 2 3
等价定义：如果近似值x的绝对误差限不超过它某一位的半个 单位，则从这一位起，直到最左边的第一位非零数字为止的
所有数字都称为有效数字。并说x“准确”到这一位。
例1.3 (误差限和有效数字)
圆周率 =3.1415926。 x1=3.14; x 2=3.141; x 3=3.142; x 4=3.1414 解 (1) x1=0.314101 , x1=0.15926102, |x1| 0.5102,有3位有效数字； (2) x2=0.5926103, |x2|0.5102,有3位 有效数字； (3) x3= 0.4073103, |x3|0.5103,有4位 有效数字； (4) x4=0.1926103, |x4|0.5103, 有4位 有效数字。
x1=x2=x3=1 x1=1.2203, x2= -0.3084, x3= 2.2981. 病态问题: 很小的变化数据却导致解产生了很大的 变化。 区别：收敛性和数值稳定性主要源于算法，病态性 主要是模型本身的原因 。
§1.3 数值算法设计的一些要点
设计算法基本原则
计算精度：收敛性、稳定性 计算速度：计算量、收敛速度、多个CPU通信 计算空间：存储量
xi
条件数很大 病态问题
误差的四则运算
(ab)=ab, r(ab)= [a/(ab)]ra[b/(ab)]rb(相近数相减 不稳定) (ab) ba+ab r(ab) ra+rb (a/b) (1/b)a(a/b2)b (分母b 0不稳定) r(a/b) rarb
0
单精度32位(4字节): t=23,s=7, 符号2位, 表示范 围 2.910393.41038 (2-128 2128) 双精度64位(8字节) : t=52,s=10, 符号2位,表示 范围 5.56103091.7910308 (2-1024 21024) 上溢出和下溢出0
利用计算机！但是：
计算机的认识能力是有限的 （例如C语言不 能识别“积分”） 计算机的计算能力也是有限的（例如例2(1), 超级计算机“天河二号”每秒做33.86千万亿 次乘法，也需要591亿年）
解决方案：
可行且高效的算法+计算机
2 数值算法的特点：
计算机算法
对于给定的问题和设备（计算机），一个算法是 用该设备可理解的语言表示的，对解决这个问题 的一种方法的精确刻画。 计算机算法主要包含数值算法、非数值算法和软 计算方法三类。
准确位数和有效数字(定义1.2)
设x =0.a1 a 2an 10m (m为整数) (1.1) 其中a 1~an为0~9中一个数字且a 10。 如果 | x*-x|0.510k (1.2) 即x的误差不超过10-k位的半个单位 则称近似数x准确到第k位小数，并说x有m+k位 有效数字。
§1.1 数值算法的研究对象
研究对象
数学分析、高等代数、概率论与数理统计都是精确 数学，例如极限、导数、积分都是唯一的。 数值分析不同，我们面对的问题是理论上有解的， 但我们没有求解公式；另外一种情况，计算量过大， 我们手工难以实现的。这样的一类问题，实际上都 是无限的，但我们只能取有限项求解，因此得到的 是近似解。 近似解就有个近似程度，这个解就不是唯一的了， 精确度不同，解就不同，距离真解误差越小越好。
Dj
, j 1, 2, 3
, 其中D=|A|,
例1.2 (难计算问题)
(1) 求解线性方程组AX=B, 其中A为30阶可逆方 阵，X=(x1, x2,, x30)T; (2) 求超越方程xex =1在[0,1]上的根x*； (3) 已知y=f(x)为[x0, x1]上的函数，满足f(x0)=y0, f(x1)=y1, x2(x0, x1), 求f(x2)； 1 I (4) 计算定积分 ln x dx (1<a<b)； (5) 解常微分方程初值问题 y ' x y 2
非线性情形用线性近似
f * ( i , y )x i 1 xi
n
f * xi* ) ( i ) r ( y ) * r (x y i 1 xi
n
绝对误差传播主要取决于条件数 | ( f )* |