等效电源定理

解释等效电源定理等效电源定理是电路分析中重要的定理之一，它包括戴维南定理和诺顿定理两个主要部分。

这两个定理都是用来将复杂电路简化成简单电路的方法，从而方便我们进行电路的分析和计算。

1.戴维南定理戴维南定理（Thevenin's Theorem）是将一个有源二端网络等效成一个电源模型的方法。

这个电源模型包括一个理想电压源和一个内阻串联，其中电压源等于网络开路电压，内阻等于网络所有元件的电阻之和。

戴维南定理的作用是将复杂的有源二端网络简化成一个简单的电源模型，方便我们进行电路的分析和计算。

应用戴维南定理时，需要注意以下几点：（1）开路电压的求解要正确，不能漏掉任何元件；（2）内阻的计算要将所有元件的电阻相加，不能漏掉任何元件；（3）等效电源模型与原网络在端口处要满足电压电流关系。

2.诺顿定理诺顿定理（Norton's Theorem）是将一个有源二端网络等效成一个电源模型的方法。

这个电源模型包括一个理想电流源和一个内阻并联，其中电流源等于网络短路电流，内阻等于网络所有元件的电阻之和。

诺顿定理的作用是将复杂的有源二端网络简化成一个简单的电源模型，方便我们进行电路的分析和计算。

应用诺顿定理时，需要注意以下几点：（1）短路电流的求解要正确，不能漏掉任何元件；（2）内阻的计算要将所有元件的电阻相加，不能漏掉任何元件；（3）等效电源模型与原网络在端口处要满足电压电流关系。

等效电源定理在电路分析中有着广泛的应用。

例如，我们可以通过应用等效电源定理将复杂电路简化成简单电路，从而方便我们进行电路的分析和计算。

同时，等效电源定理还可以用于电路的匹配和优化，以帮助我们更好地理解和设计电路。

需要注意的是，戴维南定理和诺顿定理虽然都是用来简化电路的方法，但它们在使用上有一定的区别。

一般来说，当电路中存在电压源时，我们通常使用戴维南定理；当电路中存在电流源时，我们通常使用诺顿定理。

此外，在应用等效电源定理时，还需要注意电路的换路定理解题技巧，从而正确地求解出开路电压和短路电流等参数。

戴维南等效电源定理一、引言戴维南等效电源定理是电路分析中非常重要的一个定理，它可以将任意线性电路转化为一个等效电源和一个负载。

这个定理是在解决电路分析问题时非常有用的工具，可以简化复杂的电路分析问题，提高计算效率。

二、戴维南等效电源定理的定义戴维南等效电源定理是指：在任意线性电路中，可以将整个电路看作是一个等效的单一电源和一个等效负载的组合。

这个单一电源称为戴维南等效电源，而等效负载则称为戴维南等效负载。

三、戴维南等效电源定理的证明1. 首先需要明确一个概念：内阻和外阻。

内阻指的是在网络中两个节点之间存在的阻抗，而外阻则指与网络相连的其他部分所提供的阻抗。

2. 假设我们要将一个复杂的线性网络转化为一个戴维南等效电源和一个等效负载。

我们需要先找到网络中两个节点，并计算出它们之间的内阻。

3. 接下来，我们需要断开这两个节点之间所有与外界相连的支路，并测量出这两个节点的电压。

这个电压就是戴维南等效电源的电动势。

4. 接下来，我们需要将所有与外界相连的支路重新接回来，并测量出整个网络的总电流。

这个电流就是戴维南等效负载的电流。

5. 最后，我们需要计算出戴维南等效电源和等效负载之间的等效阻抗。

这个等效阻抗可以通过测量戴维南等效电源和等效负载之间的开路电压和短路电流来计算得到。

四、戴维南等效电源定理的应用1. 简化复杂线性网络：通过使用戴维南等效电源定理，可以将一个复杂的线性网络转化为一个简单的等效单一电源和一个等效负载，从而简化分析过程。

2. 优化设计：通过使用戴维南等效电源定理，可以找到最大功率传输点，从而优化设计。

3. 计算功率：通过使用戴维南等效电源定理，可以计算出整个线性网络中消耗或输出的功率。

五、总结戴维南等效电源定理是解决线性网络分析问题时非常有用的工具。

它可以将任意线性网络转换为一个单一的等效电源和等效负载，从而简化分析过程。

在实际应用中，戴维南等效电源定理可以用于简化复杂线性网络、优化设计以及计算功率等方面。

等效电源定理
“等效电源定理”是基本的电子学理论，许多电子电路的模拟计算都需要用到这个定理。

在电子学中，等效电源定理是一个重要的定理，它利用电子学模型的特殊性，将元件的微扰变现为电路的消声效应，从而解决电路的复杂性。

简而言之，等效电源定理就是使用电路模型来描述电子斯压模型，以求得等效电源，其中，等效电源可以用来模拟计算各种电子电路。

等效电源定理的基本原理是，将电子元件的连续电流分解为两个部分，一部分流过元件，另一部分流过电路外部。

根据这个原理，就能够计算出元件的输出电压和输出电流。

可以说，等效电源定理是电子设计中的一个重要基础，它能够有效地利用元件的微扰特性，将其变为电路的消声现象，从而解决电路复杂性和模拟计算难度。

等效电源定理有四个基本步骤，分别是：利用欧拉定律计算电路的电压；对电路中的每个元件利用电子斯压模型，把它们的阻抗分解为两个部分；把这两部分阻抗分别代入电压方程，计算出这两部分的电压；最后再将这两个电压相加，就得到了等效电源的电流。

等效电源定理的应用非常广泛，其应用于电子电路的比较、元件的测量和精确控制等方面，都可以发挥出它的实际作用。

例如，可以利用它来分析电子系统中的瞬态现象，以及元件的线性谐振器特性。

此外，等效电源定理还可以用来计算变压器的工作状态，以便清楚地辨别出其特定的模式。

等效电源定理在许多电子学方面都发挥了重要作用，它能够揭示
电子元件的行为，并为系统设计提供准确的参考。

它的广泛应用反映出，它是目前最有效的电子电路模拟计算方法之一。

必须强调的是，熟悉等效电源定理，可以让我们更好地了解电子电路，使用它们来实现更多的应用。

等效电源定理等效电源定理又称为费拉里-德米赛特定理，是一种常用的电源控制和电路设计原理，由意大利物理学家费拉里和德米赛特在19世纪末初提出。

它规定了在某一特定信号或场强的作用下，多个电源的特性相似。

等效电源定理认为，在恒定的电路状态下，任何电路内，只要电源数量一定，由它们提供的动力都是相等的，不管它们是有相互抵消和加强作用，还是它们之间发生无相互作用，总之，只要它们有相同的输入和输出，那么它们之间就可以被当成等效的。

现在，市场上的电路板设计一般采用等效电源定理。

它可以极大地提高电路板设计的效率，消除容易引起电路板设计故障的错误，以及大大减少电路板的故障率，因而使电路板设计工作变得更加高效。

首先，等效电源定理使得电路板设计工作变得容易。

一般而言，电路板设计工作往往需要处理大量复杂的电源问题，而等效电源定理表明，一个电路板只需要一种电源，而不需要考虑其他电源有什么影响，这样做可以显著减少电路板设计所需的时间。

其次，等效电源定理消除了导致电路板设计失败的常见错误。

经常发生的一个错误是，在电路板设计中，用于控制不同类型的电源的电子元件可能会出现“浮动”现象，也就是这些电子元件在不同的电源状态下发出的信号不一致，而等效电源定理提出，只要每个电源的输入和输出相同，它们就可以被当成等效的，这使得电路板设计设计人员可以容易地控制和统一不同电源的信号，从而避免了这种错误。

此外，等效电源定理有助于降低电路板的故障率。

如果不采用等效电源定理，由于存在多种电源，可能会造成电路板设计中的“漏洞”，也就是某一种特定的电源所产生的信号有可能溢出到其它不同类型的电源上，从而产生电路板故障。

而等效电源定理则表明，不管电源有多少种，只要它们具有相同的输入和输出，它们就可以被当成等效的，这样就可以大大降低电路板故障率。

综上所述，等效电源定理具有重要的应用价值，对电路板设计中的电源控制具有重要的意义，使得电路板设计工作变得更加高效，提高了电路板的可靠性和性能。

等效电源定理
等效电源定理，也称作替代电源定理，是一个基本的电路定理，该定理可以用来简化复杂的电路。

它的定义是：“任意电路都可以被等同的（即对象、功率、相位和频率相同）源或组合的源来表示”。

等效电源定理的原理很简单，它把一个复杂的电路用一个等效的电源来表示。

这样，复杂的电路可以用更简单的方式来考虑，而不用一个一个元件分析。

等效电源定理的物理意义是，在一个复杂的电路中，电流和电压的变化是由电源的影响所决定的，因此可以用一个等效的电源来表示原电路。

该定理可以用两种方式来实现：一种是将源放进电路中，另一种是将电路的元件放进源中。

首先，将源放进电路，也就是等效电源定理的一般形式，即用一个等效源来代替原电路中的元件。

当将源放进电路中时，可以假设电路中的元件（如电阻、电容、电感）可以被忽略，只保留源。

此时，等效源可以模拟电路中的元件形成新的电路网络，因此可以简化原电路的分析。

然后，将电路的元件放进源中，也就是等效电源定理的特例，即将电路中的元件表示成一个电源的形式，这种
电源称为等效电源。

当将电路的元件放进源中时，可以假设电路中的源（如电压源、电流源）可以被忽略，只保留元件。

此时，等效电源可以模拟电路中的源形成新的电路网络，因此可以简化原电路的分析。

等效电源定理有助于简化电路的分析，使电路的计算更加简单、快速。

它可以用来求解复杂的电路，包括电路中的源和元件，以及电路中的各种参数，如电压、电流、功率等。

总的来说，等效电源定理是一个重要的电路定理，它可以用来简化复杂的电路，减少电路的计算时间，使电路的分析更加简单易行。

等效电源定理《等效电源定理》是一种有关电学基础理论的定理，它描述了一个电路中各部分之间的能量关系，在电路分析和设计中有很广泛的应用。

据美国科学家大卫沃森于1845年提出，它经过多年的发展和改进，在学术上被公认为是最强有力的电力学定理。

等效电源定理定义了一个电路中各部分之间的能量关系，它表明每一部分都可以用一个等效电源来表示，并用一个等效电流源来表示它们之间的能量转化。

因此，可以将电路中的每一部分抽象为一个等效电源和一个等效电流源，这样就可以更容易地进行电路分析，这对电路设计具有重要意义。

为了消除非等效电源或电流源对电路的影响，需要计算每一部分的电压和电流，然后将计算结果代入等效电源定理，求出等效电源的值。

求解的主要方法有用电路分析法确定等效电源，用拉普拉斯变换确定等效电源，用卡尔曼滤波器确定等效电源等。

等效电源定理在电路设计中有广泛的应用。

它可以用来分析复杂的电路，帮助我们确定元件的电压和电流，以及求解等效电源等。

此外，等效电源定理还可用于有关滤波器、可调电路等电路的分析与设计，它可以更清楚地表示电路的特性，从而为电子工程师们的工作提供了便利，也有利于电子设备的更新和改进。

等效电源定理提供了一种更为简洁的电路分析方法，它能够有效地分析复杂电路中的特性，而不需要考虑电路中每个部分的细节。

此外，它还有助于精确地计算电路中各元件之间的电压、功率、频率等参数，以便于建立起复杂的电路模型，从而实现对电路的更有效的控制。

总之，等效电源定理是一种强大的电力学定理，它为电路分析和设计提供了一种简单的分析方法，具有非常广泛的应用前景。

它将电路中的每一部分抽象为一个等效电源和一个等效电流源，可以用来分析复杂电路，确定元件的电压、电流，求解电路中各元件之间的参数，从而实现对模型电路的更有效的控制。

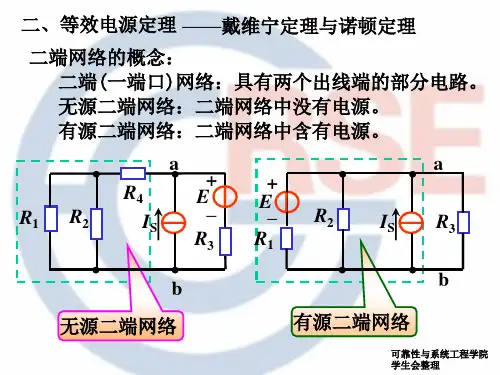
等效电源定理等效电源定理包括电压源等效（戴维南定理），和电流源等效（诺顿定理）两个定理。

其中，电压源等效定理在电路故障诊断中应用较多，其内容是：任何一个线性的有源二端网络对外电路而言，可以用一个电压源来等效代替。

如图（1-08）所示，其中：等效电压源的电动势E（或源电压Vo）的数值，等于该有源二端网络的“开路电压”；等效电压源的内阻Ro等于该有源二端网络“除源”后的等效电阻值。

所谓的“开路电压”是指：将负载RL从电路上断开后，a、b间的电压；所谓“除源”是指：假设将有源二端网络中的电源去除（衡压源短路、衡流源开路）。

电压源等效定理是“模块化电路分析方法”和后面将要探讨的“电器故障诊断层次分析法”的理论基础。

根据这个定理，我们可以将任何线性有源二端网络，或者线性四端传输网络的输出端，等效为一个电压源，按照电压源的特性去分析诊断电路故障，从而大大简化了电路分析或故障诊断的难度。

电压源等效定理中的“电动势”既可以是直流的，也可以是交流的，因此，该定理既适合电源环节的电路故障诊断，也适合于信号通道的故障诊断。

在应用于信号通道时，上述“电动势”就是信号源的电压（交流），称为“源电压”；上述等效“内阻”就是信号源得输出电阻。

电流源等效定理类似于电压源等效定理，其内容是：任何一个线性的有源二端网络对外电路而言，可以用一个电流源来等效代替，如图（1-09）所示。

其中，等效电流源的恒流源Is等于该有源二端网络的“短路电流”；等效电流源的内阻Rs等于该有源二端网络“除源”后的等效电阻值。

由此可见，对于同一个有源二端网络，既可以等效为电压源形式，也可以等效为电流源形式，而且，Rs于Ro是相同的，即：Rs=Ro。

例（1-07）：有一台实验室使用的直流稳压电源，内部电路不详，希望通过实验的方法求得它的源电压Vo和输出电阻Ro，请设计测量方法。

分析：直流稳压电源的输出端，可以看成是线性有源二端网络，由电压源等效定理可知：等效电压源的电动势E（源电压Vo）的数值，等于该有源二端网络的开路电压。

等效电源定理戴维南定理和诺顿定理分别能把含源二端网络等效成为一个实际电压源支路和实际电流源支路，故统称等效电源定理。

1、戴维南定理任一线性含源二端网络，对外电路讲，可以等效为一个电压源和电阻串联的组合，电压源的电压为该网络的开路电压u oc，串联电阻等于该网络中所有独立源为零时的入端等效电阻R o。

2、诺顿定理任一线性含源二端网络，对外电路讲，可以等效为一个电流源和电阻并联的组合，电流源的电流为该网络的短路电流isc，并联电阻等于该网络中所有独立源为零值时的入端等效电阻R o。

图(a)所示为一接有外电路的含源二端网络，根据替代定律，把R L支路分别用流过它的电流i和两端电压u作为电压源等效替代，然后运用叠加定理分别得到u＝u oc－R o i＝i sc－u/R o等效电源电路如图（b）所示。

这两条定律所得到的电压源支路和电流源支路可以互相等效，所以人们多应用戴维南等效电压源定律，然后变化为诺顿等效电流源电路，如图（b）上、下图所示。

戴维南定律对求解电路中某一支路的电压、电流和功率，特别是负载吸收的最大功率最为方便。

求解时含源二端网络必须是线性的，待求支是线性的或非线性、有源或无源均可。

应用这两条定律，一般分三个步骤：(1)断开待求支路或将待求支路短路，分别求得开路电压u oc和短路电流i sc;(2)让全部独立源为零，求入端等效电阻R o。

(3)画出等效电源电路，接上待求支路，求解待求量。

3、用戴维南定律分析含受控源电路根据受控源的性质和等效电源定律的要求，当用戴维南定律和诺顿定律分析受控源电路时，必须掌握：(1)当控制量在端口上时，它要随端口开路或短路变化，必须用变化了的控制量来表示受控源的电压或电流。

(2)当控制量在网络内，则在短路或开路时，必须保证受控源及其控制量同在含源二端网络内。

(3)受控源不能充当激励，具有电阻性。

在求戴维南等效电阻时，独立源为零，受控源和电阻一样要保留，故必须采取：(1)开路短路法：将待求支路开路和短路，分别求得二断网络的开路电压u oc和短路电流i sc，由图所示可知R o＝u o/i o。