山西省2012届高考地理复习 区域地理 第1章 第1节世界地理概况课件 新人教版
- 格式:ppt
- 大小:1.02 MB
- 文档页数:42






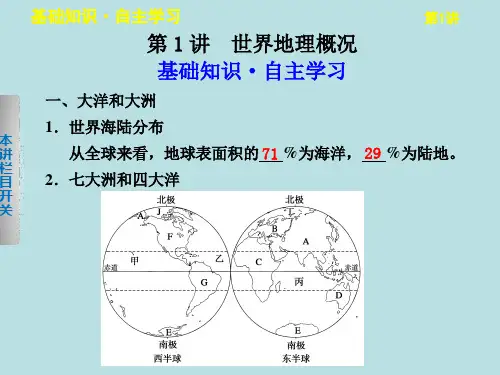



第一章世界地理第一讲世界地理概况(2012·天津高考)读部分地理事物数量的纬度差异示意图,完成1~2题。
1.下列叙述,符合上图所示的动物种群数量分布规律的是( )A.南半球的种群数量多于北半球B.信风带的种群数量多于西风带C.低纬地区的种群数量少于中纬地区D.森林地带的种群数量少于草原地带2.结合图中的信息判断,世界特大城市数量纬度差异的形成,主要由于( )A.气候、土地资源的差异B.生物、土地资源的差异C.矿产、生物资源的差异D.气候、矿产资源的差异解析:1.B 2.A 第1题,从图中可以看出,南半球由于陆地较少,因此动物种群的数量比北半球少,A项错误;信风带的动物种群数量比西风带多,B项正确;低纬地区水热条件好,因此动物种群数量多,C项错;森林地区生产的有机质多,可以供养更多的动物种群,D项错误。
第2题,在北半球的亚热带和温带地区大城市最多,原因是该地区有肥沃的土壤、适宜的气候(水热配合较好)等优越的自然条件。
3.(2011·四川高考)下图为“某大洲地形剖面示意图”。
下列叙述正确的是( )A.该剖面穿过的地形以山地为主B.乙地所在国工业集中分布在该国西部C.该剖面走向为西北——东南向D.乙地所在国农业集中分布在该国北部解析:选C 根据图中信息“加勒比海”“里约热内卢”可判断该大洲为南美洲;结合图中地形区的海拔和地势起伏以及南美洲的地形分布可知,该剖面穿过的地形以高原为主;乙地所在国为巴西,巴西的工业集中分布在该国的东南沿海地区;结合“加勒比海”和“里约热内卢”所处的位置,可判断该剖面的走向为西北—东南向;巴西北部为亚马孙热带雨林地区,不是主要的农业区。
读“沿某大陆80°经线7月气温分布曲线图”。
读图,完成4~5题。
4.有关④地所在国家叙述正确的是( )A.东北部和东南部濒临同一大洋B.气候干旱,以种植玉米为主C.旱涝灾害频繁,对农业影响大D.畜牧业和工矿业发达5.下列叙述正确的是( )A.④地至①地气温逐渐降低B.影响④地至②地气温变化大的主要因素是纬度C.③地是谷地,气温偏低D.③地种植业主要分布在河谷解析:4.C 5.D 第4题,根据陆地的分布可判断该经线为80°E,④地位于印度,受季风气候影响,旱涝灾害频发。