二分图的匹配和图论

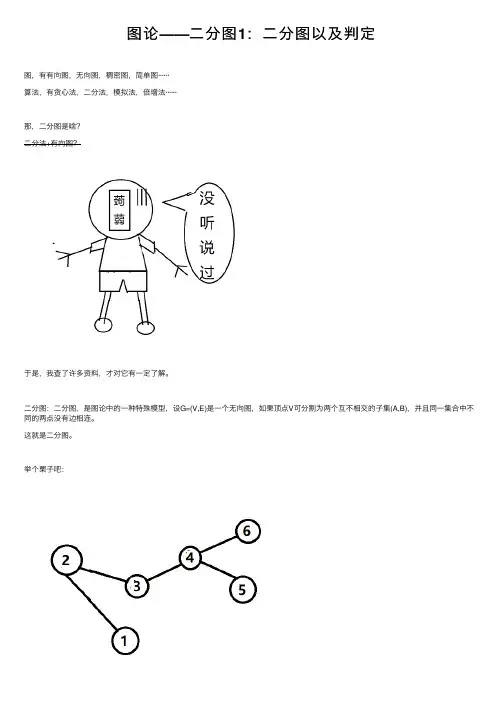
图论——⼆分图1：⼆分图以及判定图，有有向图，⽆向图，稠密图，简单图······算法，有贪⼼法，⼆分法，模拟法，倍增法······那，⼆分图是啥？⼆分法+有向图？于是，我查了许多资料，才对它有⼀定了解。

⼆分图：⼆分图，是图论中的⼀种特殊模型，设G=(V,E)是⼀个⽆向图，如果顶点V可分割为两个互不相交的⼦集(A,B)，并且同⼀集合中不同的两点没有边相连。

这就是⼆分图。

举个栗⼦吧：这是不是⼆分图？反正我第⼀次看觉得不是其实，是的，他是⼆分图，尽管看上去是连着的。

若我们将图中的⼀些边转⼀下，变成：这就是⼀个明显的⼆分图。

集合A与B中的点互不相连。

因此，在⼿动判定⼆分图时学会转边！辣魔，⼆分图要⽤计算机判定怎么实现？数竞⼤佬：简单！！！！染⾊⼤法！！！有没有熟悉的感觉0表⽰还未访问，1表⽰在集合A中，2表⽰在集合B中。

col（color）储存颜⾊。

初始化为0.上代码：其实是模板可以记忆。

1 vector <int> v[N];2void dfs(int x,int y){3 col[x]=y;4for (int i=0; i<v[x].size(); i++) {5if (!col[v[x][i]]) dfs(v[x][i],3-y);6if (col[v[x][i]]==col[x]) FLAG=true; //产⽣了冲突7 }8 }9for (i=1; i<=n; i++) col[i]=0; //初始化10for (i=1; i<=n; i++) if (!col[i]) dfs(i,1); //dfs染⾊11if (FLAG) cout<<"NO"; else cout<<"YES";下⼀章我们将讲到⼆分图的匹配，我们明天见。

图论：⼆分图多重匹配使⽤最⼤流和费⽤流解决⼆分图的多重匹配之前编辑的忘存了好⽓啊。

本来打算学完⼆分图的乱七⼋糟的匹配之后再去接触⽹络流的，提前撞到了之前我们说的⼆分图最⼤匹配和⼆分图最⼤权匹配有⼀个特点，那就是没个点只能与⼀条边相匹配如果规定⼀个点要与L条边相匹配，这样的问题就是⼆分图的多重匹配问题然后根据边是否带权重，⼜可以分为⼆分图最⼤多重匹配和⼆分图最⼤权多重匹配（⼆分图多重最佳完美匹配）⾸先给出⼆分图多重最⼤匹配的做法：在原图上建⽴源点S和汇点T，S向每个X⽅点连⼀条容量为该X⽅点L值的边，每个Y⽅点向T连⼀条容量为该Y⽅点L值的边原来⼆分图中各边在新的⽹络中仍存在，容量为1（若该边可以使⽤多次则容量⼤于1），求该⽹络的最⼤流，就是该⼆分图多重最⼤匹配的值然后给出⼆分图多重最优匹配（⼆分图多重最⼤权匹配）的做法：在原图上建⽴源点S和汇点T，S向每个X⽅点连⼀条容量为该X⽅点L值、费⽤为0的边，每个Y⽅点向T连⼀条容量为该Y⽅点L值、费⽤为0的边原来⼆分图中各边在新的⽹络中仍存在，容量为1（若该边可以使⽤多次则容量⼤于1），费⽤为该边的权值。

求该⽹络的最⼤费⽤最⼤流，就是该⼆分图多重最优匹配的值这道题⾥⾯，⼀共有X⽅点这么多的电影，每个电影需要拍摄多少天就是对应的X⽅点L值，然后每⼀天是⼀个Y⽅点，由于每⼀天只能拍摄⼀部电影，所有Y⽅点的L值均为1下⾯介绍⼀下实现：int n,sum,cnt,ans;int g[maxn],cur[maxn];int str[25][10];struct Edge{int u,v,next,cap,flow;}e[maxm];这⾥⾯的cur数组是g数组的临时数组str⽤来保存每⼀个电影可以在哪⼀天拍摄Edge是⽹络流图⾥⾯的边void addedge(int u,int v,int c){e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;}建图的时候，注意怎么赋值的接下来根据题意建图：for(int i=1;i<=n;i++){for(int j=1;j<=7;j++)scanf("%d",&str[i][j]);scanf("%d%d",&d,&w);sum+=d;addedge(0,i,d); //容量为需要多少天for(int j=1;j<=7;j++)for(int k=0;k<w;k++)if(str[i][j]) addedge(i,20+k*7+j,1);}for(int i=21;i<=370;i++) addedge(i,371,1);ans=maxflow(0,371);0为源点，371为汇点sum最后进⾏⼀个统计，和源点出发的最⼤流量进⾏⽐较，如果相等，说明电影排的开然后是求最⼤流的⼀个板⼦int maxflow(int st,int ed){int flowsum=0;while(bfs(st,ed)){memcpy(cur,g,sizeof(g));flowsum+=dfs(st,ed,INF);//cout<<"#"<<flowsum<<" ";}return flowsum;}具体的DFS和BFS这⾥不作为重点，以后再说下⾯给出完整的实现：1 #include<cstdio>2 #include<cstring>3 #include<algorithm>4using namespace std;5const int INF=1000000000;6const int maxn=1005;7const int maxm=20005;8int n,sum,cnt,ans;9int g[maxn],cur[maxn];10int str[25][10];11struct Edge{int u,v,next,cap,flow;}e[maxm];12void addedge(int u,int v,int c)13 {14 e[++cnt].u=u;e[cnt].v=v;e[cnt].cap=c;15 e[cnt].flow=0;e[cnt].next=g[u];g[u]=cnt;1617 e[++cnt].u=v;e[cnt].v=u;e[cnt].cap=0;18 e[cnt].flow=0;e[cnt].next=g[v];g[v]=cnt;19 }20int q[maxn],vis[maxn],d[maxn];21bool bfs(int st,int ed)22 {23 memset(q,0,sizeof(q));24 memset(vis,0,sizeof(vis));25 memset(d,-1,sizeof(d));26 vis[st]=1;d[st]=0;27int h=0,t=1;28 q[t]=st;29while(h!=t)30 {31 h=h%maxn+1;32int u=q[h];33for(int tmp=g[u];tmp;tmp=e[tmp].next)34 {35if(!vis[e[tmp].v]&&e[tmp].cap>e[tmp].flow)36 {37 vis[e[tmp].v]=1;38 d[e[tmp].v]=d[u]+1;39if(e[tmp].v==ed) return true;40 t=t%maxn+1;41 q[t]=e[tmp].v;42 }43 }44 }45return false;46 }47int getpair(int x)48 {49if(x%2==0)50return x-1;51else return x+1;52 }53int dfs(int x,int ed,int a)54 {55if(x==ed||a==0) return a;56int flow=0,f;57for(int tmp=cur[x];tmp;tmp=e[tmp].next)58 {59if(d[e[tmp].v]==d[x]+1&&(f=dfs(e[tmp].v,ed,min(a,e[tmp].cap-e[tmp].flow)))>0)60 {61 e[tmp].flow+=f;62 e[getpair(tmp)].flow-=f;63 a-=f;64 flow+=f;65if(a==0) break;66 }67 }68return flow;69 }70int maxflow(int st,int ed)71 {72int flowsum=0;73while(bfs(st,ed))74 {75 memcpy(cur,g,sizeof(g));76 flowsum+=dfs(st,ed,INF);77//cout<<"#"<<flowsum<<" ";78 }79return flowsum;8081 }82void init()83 {84 sum=cnt=0;85 memset(g,0,sizeof(g));86 }87int main()88 {89int T,d,w;90 scanf("%d",&T);91while(T--)92 {93 init();94 scanf("%d",&n);95for(int i=1;i<=n;i++)96 {97for(int j=1;j<=7;j++)98 scanf("%d",&str[i][j]);99 scanf("%d%d",&d,&w);100 sum+=d;101 addedge(0,i,d); //容量为需要多少天102for(int j=1;j<=7;j++)103for(int k=0;k<w;k++)104if(str[i][j]) addedge(i,20+k*7+j,1);105 }106for(int i=21;i<=370;i++) addedge(i,371,1);107 ans=maxflow(0,371);108if(ans==sum) printf("Yes\n");109else printf("No\n");110 }111return0;112 }据说这是典型的最⼤流题⽬，然⽽为了强⾏安利⼀波⼆分图的多重匹配，就不说成那个了。

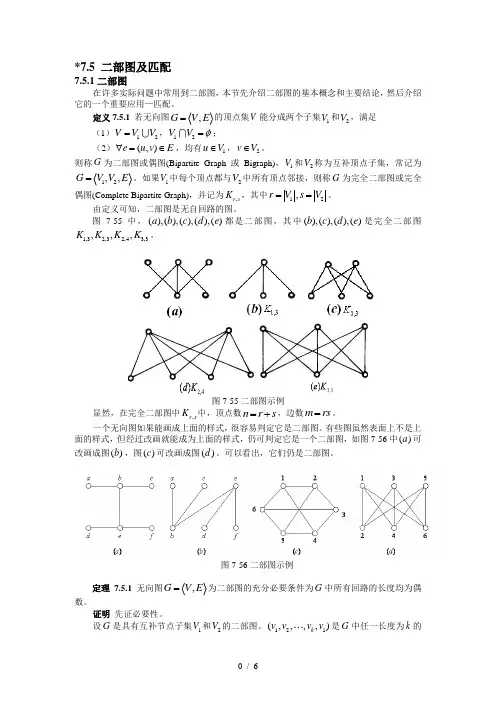
*7.5 二部图及匹配7.5.1二部图在许多实际问题中常用到二部图，本节先介绍二部图的基本概念和主要结论，然后介绍它的一个重要应用—匹配。

定义7.5.1 若无向图,G V E =的顶点集V 能分成两个子集1V 和2V ，满足（1）12V V V =，12V V φ=；（2）(,)e u v E ∀=∈，均有1u V ∈，2v V ∈。

则称G 为二部图或偶图(Bipartite Graph 或Bigraph)，1V 和2V 称为互补顶点子集，常记为12,,G V V E =。

如果1V 中每个顶点都与2V 中所有顶点邻接，则称G 为完全二部图或完全偶图(Complete Bipartite Graph)，并记为,r s K ，其中12,r V s V ==。

由定义可知，二部图是无自回路的图。

图7-55中，(),(),(),(),()a b c d e 都是二部图，其中(),(),(),()b c d e 是完全二部图1,32,32,43,3,,,K K K K 。

图7-55二部图示例显然，在完全二部图中,r s K 中，顶点数n r s =+，边数m rs =。

一个无向图如果能画成上面的样式，很容易判定它是二部图。

有些图虽然表面上不是上面的样式，但经过改画就能成为上面的样式，仍可判定它是一个二部图，如图7-56中()a 可改画成图()b ，图()c 可改画成图()d 。

可以看出，它们仍是二部图。

图7-56二部图示例定理7.5.1 无向图,G E =为二部图的充分必要条件为G 中所有回路的长度均为偶数。

证明 先证必要性。

设G 是具有互补节点子集1V 和2V 的二部图。

121(,,,,)k v v v v 是G 中任一长度为k 的回路，不妨设11v V ∈，则211m v V +∈，22m v V ∈，所以k 必为偶数，不然，不存在边1(,)k v v 。

再证充分性。

设G 是连通图，否则对G 的每个连通分支进行证明。

二分图的最优匹配（KM算法）KM算法用来解决最大权匹配问题：在一个二分图内，左顶点为X，右顶点为Y，现对于每组左右连接XiYj有权wij，求一种匹配使得所有wij的和最大。

基本原理该算法是通过给每个顶点一个标号（叫做顶标）来把求最大权匹配的问题转化为求完备匹配的问题的。

设顶点Xi的顶标为A[ i ]，顶点Yj的顶标为B[ j ]，顶点Xi与Yj之间的边权为w[i,j]。

在算法执行过程中的任一时刻，对于任一条边(i,j)，A[ i ]+B[j]>=w[i,j]始终成立。

KM算法的正确性基于以下定理：若由二分图中所有满足A[ i ]+B[j]=w[i,j]的边(i,j)构成的子图（称做相等子图）有完备匹配，那么这个完备匹配就是二分图的最大权匹配。

首先解释下什么是完备匹配，所谓的完备匹配就是在二部图中，X点集中的所有点都有对应的匹配或者是Y点集中所有的点都有对应的匹配，则称该匹配为完备匹配。

这个定理是显然的。

因为对于二分图的任意一个匹配，如果它包含于相等子图，那么它的边权和等于所有顶点的顶标和；如果它有的边不包含于相等子图，那么它的边权和小于所有顶点的顶标和。

所以相等子图的完备匹配一定是二分图的最大权匹配。

初始时为了使A[ i ]+B[j]>=w[i,j]恒成立，令A[ i ]为所有与顶点Xi关联的边的最大权，B[j]=0。

如果当前的相等子图没有完备匹配，就按下面的方法修改顶标以使扩大相等子图，直到相等子图具有完备匹配为止。

我们求当前相等子图的完备匹配失败了，是因为对于某个X顶点，我们找不到一条从它出发的交错路。

这时我们获得了一棵交错树，它的叶子结点全部是X顶点。

现在我们把交错树中X顶点的顶标全都减小某个值d，Y顶点的顶标全都增加同一个值d，那么我们会发现：1）两端都在交错树中的边(i,j)，A[ i ]+B[j]的值没有变化。

也就是说，它原来属于相等子图，现在仍属于相等子图。

2）两端都不在交错树中的边(i,j)，A[ i ]和B[j]都没有变化。

二分图匹配一、二分图的概念二分图又称作二部图，是图论中的一种特殊模型。

设G=(V,{R})是一个无向图。

如顶点集V可分割为两个互不相交的子集，并且图中每条边依附的两个顶点都分属两个不同的子集。

则称图G为二分图。

二、最大匹配给定一个二分图G，在G的一个子图M中，M的边集{E}中的任意两条边都不依附于同一个顶点，则称M是一个匹配。

选择这样的边数最大的子集称为图的最大匹配问题(maximal matching problem)如果一个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配。

三、匈牙利算法求最大匹配的一种显而易见的算法是：先找出全部匹配，然后保留匹配数最多的。

但是这个算法的复杂度为边数的指数级函数。

因此，需要寻求一种更加高效的算法。

1、增广路的定义(也称增广轨或交错轨)：若P是图G中一条连通两个未匹配顶点的路径，并且属M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广路径。

由增广路的定义可以推出下述三个结论：●P的路径长度必定为奇数，第一条边和最后一条边都不属于M。

●P经过取反操作可以得到一个更大的匹配M’。

●M为G的最大匹配当且仅当不存在相对于M的增广路径。

2、用增广路求最大匹配(称作匈牙利算法，匈牙利数学家Edmonds于1965年提出)。

算法轮廓：(1)置M为空(2)找出一条增广路径P，通过取反操作获得更大的匹配M’代替M(3)重复(2)操作直到找不出增广路径为止程序清单：Function find(k:integer):integer;var st,sf,i,j,t:integer;queue,father:array[1..100] of integer;beginqueue[1] := k; st := 1; sf := 1;fillchar(father,sizeof(father),0);repeatfor i:=1 to n doif (father[i]=0)and(a[queue[st],i]=1) thenbeginif match2[i]<>0 thenbegininc(sf);queue[sf] := match2[i];father[i] := queue[st];end elsebeginj := queue[st];while true dobegint := match1[j];match1[j] := i;match2[i] := j;if t = 0 then break;i := t; j := father[t];end;find := 1;exit;end;end;inc(st);until st>sf;find := 0;end;在主程序中调用下面的程序即可得出最大匹配数。

konig 定理
Konig定理是图论中的一个重要定理，它是由匈牙利数学家Dénes Konig在1936年首次证明的。

这个定理主要应用于二分图（bipartite graph）的研究中，二分图是一种特殊的图，其中所有的顶点都可以被分成两个互不相交的子集，并且每一条边都连接这两个子集中的一个顶点。

Konig定理的表述如下：在一个二分图中，最大匹配数等于最小点覆盖数。

换句话说，一个图中的最大匹配数等于覆盖该图中所有顶点所需的最小边数。

为了更好地理解这个定理，我们可以先了解一下什么是匹配和点覆盖。

在图论中，一个匹配是一个边的集合，其中任意两条边都不共享一个顶点。

最大匹配是指一个匹配中包含的边数最多。

点覆盖是指一个顶点的集合，该集合中的任意顶点都是边的一个端点。

最小点覆盖是指覆盖所有顶点所需的最小顶点数。

根据Konig定理，在二分图中，最大匹配数等于最小点覆盖数。

这个定理的证明过程需要使用到一些图论中的技巧和结论，例如Kőnig-Egerváry定理和Hall定理等。

这个定理的应用非常广泛，它可以用于解决一些组合优化问题，例如最大匹配问题和最小点覆盖问题等。

此外，Konig定理还可以用于证明一些其他图论中的结论，例如Kőnig-Egerváry定理和Hall定理等。

关于二部图与匹配问题的研究关于二部图与匹配问题的研究二部图与匹配问题是图论中的经典研究领域，对于理解和解决实际问题具有重要的意义。

在本文中，我们将介绍二部图的基本概念，以及匹配问题在实际中的应用，并探索相关算法的研究与改进。

一、二部图的基本概念二部图是一种特殊的图结构，其中的顶点可以被分为两个互不相交的集合（通常表示为U和V），集合U中的顶点与集合V中的顶点之间没有边相连。

二部图可以用数学方式表示为G=(U, V, E)，其中U和V表示两个顶点集合，E表示边的集合。

二部图的一个关键性质是，一个边的两个顶点必须分别属于两个不同的集合。

这个概念在实际中有很多应用，比如在婚姻匹配问题中，假设有一组男性和一组女性，我们可以用二部图来表示可能的婚姻关系。

二、匹配问题的定义与应用在二部图G=(U, V, E)中，我们称一个边的集合M为一个匹配，如果M中的边两两之间没有公共顶点。

换句话说，任意两条边都不连接同一个顶点。

匹配问题的目标是找到一个具有最大边数的匹配M，或者找到一个最小边数的匹配。

匹配问题在实际中有很多应用。

例如，在网络中，我们可以将二部图中的两个顶点集合U和V分别表示为发送方和接收方，边表示连接发送方和接收方的通信链路。

这时，匹配问题等价于如何合理分配通信链路，使得网络的容量得到最大利用。

另一个应用是在任务分配问题中。

假设有一组任务和一组工作者，每个任务需要特定的技能，每个工作者也具有特定的技能。

二部图可以用来表示任务与工作者之间的技能匹配情况。

匹配问题就变成了如何将任务分配给工作者，使得每个任务都能被合适的工作者完成。

三、匹配问题的经典算法与改进匹配问题的研究已经有了很长的历史，可以追溯到20世纪40年代。

最初，匈牙利算法是解决匹配问题最常用的算法之一。

该算法基于增广路径的概念，通过不断寻找增广路径并更新匹配，最终得到最大匹配。

然而，匈牙利算法存在一些局限性。

首先，它只能解决二部图中的最大匹配问题，不适用于其他相关问题。