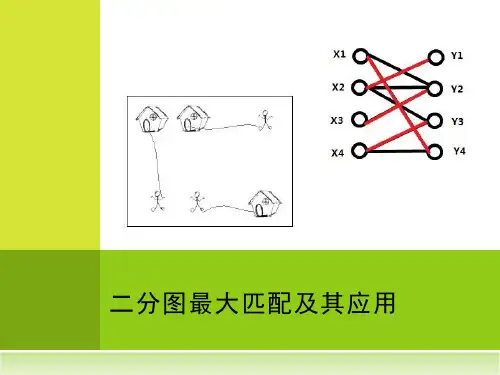
二分图最大匹配算法的应用及Matlab实现+++

匈⽛利算法解决⼆分图最⼤匹配预备知识 匈⽛利算法是由匈⽛利数学家Edmonds于1965年提出，因⽽得名。

匈⽛利算法是基于Hall定理中充分性证明的思想，它是⼆分图匹配最常见的算法，该算法的核⼼就是寻找增⼴路径，它是⼀种⽤增⼴路径求⼆分图最⼤匹配的算法。

⼆分图 ⼆分图⼜称作⼆部图，是图论中的⼀种特殊模型。

设G=(V,E)是⼀个⽆向图，如果顶点V可分割为两个互不相交的⼦集(A，B)，并且图中的每条边（i，j）所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集(i in A，j in B)，则称图G为⼀个⼆分图。

匹配 在图论中，⼀个图是⼀个匹配（或称独⽴边集）是指这个图之中，任意两条边都没有公共的顶点。

这时每个顶点都⾄多连出⼀条边，⽽每⼀条边都将⼀对顶点相匹配。

例如，图3、图4中红⾊的边就是图2的匹配。

图3中1、4、5、7为匹配点，其他顶点为⾮匹配点，1-5、4-7为匹配边，其他边为⾮匹配边。

最⼤匹配 ⼀个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最⼤匹配。

图 4 是⼀个最⼤匹配，它包含 4 条匹配边。

任意图中，极⼤匹配的边数不少于最⼤匹配的边数的⼀半。

完美匹配 如果⼀个图的某个匹配中，所有的顶点都是匹配点，那么它就是⼀个完美匹配。

显然，完美匹配⼀定是最⼤匹配，但并⾮每个图都存在完美匹配。

最⼤匹配数：最⼤匹配的匹配边的数⽬。

最⼩点覆盖数：选取最少的点，使任意⼀条边⾄少有⼀个端点被选择。

最⼤独⽴数：选取最多的点，使任意所选两点均不相连。

最⼩路径覆盖数：对于⼀个DAG（有向⽆环图），选取最少条路径，使得每个顶点属于且仅属于⼀条路径，路径长可以为0（即单个点）定理1：Konig定理——最⼤匹配数 = 最⼩点覆盖数定理2：最⼤匹配数 = 最⼤独⽴数定理3：最⼩路径覆盖数 = 顶点数 - 最⼤匹配数匈⽛利算法例⼦ 为了便于理解，选取了dalao博客⾥找妹⼦的例⼦： 通过数代⼈的努⼒，你终于赶上了剩男剩⼥的⼤潮，假设你是⼀位光荣的新世纪媒⼈，在你的⼿上有N个剩男，M个剩⼥，每个⼈都可能对多名异性有好感（惊讶，-_-||暂时不考虑特殊的性取向） 如果⼀对男⼥互有好感，那么你就可以把这⼀对撮合在⼀起，现在让我们⽆视掉所有的单相思（好忧伤的感觉，快哭了），你拥有的⼤概就是下⾯这样⼀张关系图，每⼀条连线都表⽰互有好感。

二分图的最大匹配、完美匹配和匈牙利算法August 1, 2013 / 算法这篇文章讲无权二分图（unweighted bipartite graph）的最大匹配（maximum matching）和完美匹配（perfect matching），以及用于求解匹配的匈牙利算法（Hungarian Algorithm）；不讲带权二分图的最佳匹配。

二分图：简单来说，如果图中点可以被分为两组，并且使得所有边都跨越组的边界，则这就是一个二分图。

准确地说：把一个图的顶点划分为两个不相交集U和V，使得每一条边都分别连接U、V中的顶点。

如果存在这样的划分，则此图为一个二分图。

二分图的一个等价定义是：不含有「含奇数条边的环」的图。

图 1 是一个二分图。

为了清晰，我们以后都把它画成图 2 的形式。

匹配：在图论中，一个「匹配」（matching）是一个边的集合，其中任意两条边都没有公共顶点。

例如，图3、图 4 中红色的边就是图 2 的匹配。

我们定义匹配点、匹配边、未匹配点、非匹配边，它们的含义非常显然。

例如图 3 中 1、4、5、7 为匹配点，其他顶点为未匹配点；1-5、4-7为匹配边，其他边为非匹配边。

最大匹配：一个图所有匹配中，所含匹配边数最多的匹配，称为这个图的最大匹配。

图 4 是一个最大匹配，它包含 4 条匹配边。

完美匹配：如果一个图的某个匹配中，所有的顶点都是匹配点，那么它就是一个完美匹配。

图 4 是一个完美匹配。

显然，完美匹配一定是最大匹配（完美匹配的任何一个点都已经匹配，添加一条新的匹配边一定会与已有的匹配边冲突）。

但并非每个图都存在完美匹配。

举例来说：如下图所示，如果在某一对男孩和女孩之间存在相连的边，就意味着他们彼此喜欢。

是否可能让所有男孩和女孩两两配对，使得每对儿都互相喜欢呢？图论中，这就是完美匹配问题。

如果换一个说法：最多有多少互相喜欢的男孩/女孩可以配对儿？这就是最大匹配问题。

基本概念讲完了。

matlab otsu算法什么是Otsu算法？Otsu算法，也被称为最大类间方差法，是一种常用于图像处理和计算机视觉中的图像二值化方法。

该算法是由日本学者大津秀一在1979年提出的。

Otsu算法的主要目标是将图像转化为黑白二值图像，以便进行后续的图像分割和特征提取等操作。

其基本原理是在图像中寻找一个最佳的阈值，将图像的像素点分成两个互补的类别，使得两个类别之间的方差最大化。

如何实现Otsu算法？步骤1：计算灰度直方图首先，我们需要计算图像的灰度直方图。

灰度直方图是一种统计图，用于显示图像中各个灰度级别的像素点的分布情况。

在MATLAB中，我们可以使用imhist函数来计算灰度直方图。

步骤2：计算类间方差接下来，我们需要计算图像的类间方差。

类间方差是指图像中不同类别（即黑色和白色）之间的方差。

在Otsu算法中，我们要找到一个最佳的阈值，使得将图像分为两个类别时，类间方差最大化。

计算类间方差的公式为：\[\sigma^2_w(t) = \omega_1(t)\omega_2(t)[\mu_1(t)-\mu_2(t)]^2\]其中，\(\sigma^2_w(t)\)表示在阈值t处的类间方差，\(\omega_1(t)\)和\(\omega_2(t)\)表示在阈值t处两个类别的像素点比例，\(\mu_1(t)\)和\(\mu_2(t)\)表示在阈值t处两个类别的平均灰度值。

步骤3：寻找最佳阈值在这一步中，我们通过遍历不同的阈值，找到一个使类间方差最大化的阈值。

具体的实现方法如下：1. 根据步骤2中的类间方差公式，计算每个阈值下的类间方差值。

2. 找到类间方差最大的阈值，这个阈值即为最佳阈值。

步骤4：二值化图像最后，我们使用最佳阈值来将图像进行二值化处理。

二值化即将图像中的像素点分为只有黑色和白色两种颜色的情况。

根据最佳阈值，大于阈值的像素点被赋值为白色，小于等于阈值的像素点被赋值为黑色。

在MATLAB中，可以使用下列代码执行Otsu算法：matlab读取图像img = imread('image.jpg');将图像转化为灰度图像gray_img = rgb2gray(img);计算灰度直方图histogram = imhist(gray_img);计算类间方差class_variances = zeros(256, 1);for t = 1:256计算每个阈值下的类间方差omega1 = sum(histogram(1:t)) / numel(gray_img);omega2 = sum(histogram(t+1:end)) / numel(gray_img);mu1 = sum((0:t-1)' .* histogram(1:t)) / sum(histogram(1:t));mu2 = sum((t:255)' .* histogram(t+1:end)) /sum(histogram(t+1:end));class_variances(t) = omega1 * omega2 * (mu1 - mu2)^2;end找到最佳阈值[~, threshold] = max(class_variances);二值化图像binary_img = gray_img > threshold;显示二值化图像imshow(binary_img);总结：Otsu算法是一种常用的图像二值化方法，它能够通过寻找最佳的阈值，将图像转化为黑白二值图像。

静止背景下的多目标追踪随着计算机技术以及智能汽车行业的发展，多目标的检测与追踪的实用性与研究价值逐渐提高。

在计算机视觉的三层结构中，目标跟踪属于中间层，是其他高层任务，例如动作识别以及行为分析等的基础。

其主要应用可包括视频监控，检测异常行为人机交互，对复杂场景中目标交互的识别与处理，以及虚拟现实及医学图像。

目标跟踪又包括单目标跟踪和多目标跟踪。

单目标跟踪可以通过目标的表观建模或者运动建模，以处理光照、形变、遮挡等问题，而多目标跟踪问题则更加复杂，除了单目标跟踪回遇到的问题外，还需要目标间的关联匹配。

另外在多目标跟踪任务中经常会碰到 目标的频繁遮挡、轨迹开始终止时刻未知、目标太小、表观相似、目标间交互、低帧率等等问题。

静止背景下的多目标追踪可分为两步来实现，第一步是在视频文件的每帧中检测出移动的目标，第二步是将检测到的目标与跟踪轨迹实时匹配。

在本次实验中，利用混合高斯模型进行背景减除，使用形态学操作消除噪声，通过卡尔曼滤波预测目标位置，最后利用匈牙利算法进行匹配，实现静止背景下的多目标追踪。

1 实验原理1.1 混合高斯模型单高斯模型是利用高维高斯分布概率来进行模式分类：11()exp[(x )(x )]2T x N C μσμ-=--- 其中μ用训练样本均值代替，σ用样本方差代替，X 为d 维的样本向量。

通过高斯概率公式就可以得出类别C 属于正（负）样本的概率。

而混合高斯模型就是数据从多个高斯分布中产生，每个GMM 由k 个单高斯分布线性叠加而成。

相当于对各个高斯分布进行加权，权系数越大，那么这个数据属于这个高斯分布的可能性越大。

(x)(k)*p(x |k)P p =∑利用混合高斯模型(GMM)可以进行背景减除，将前后景分离，得到移动的目标。

对每个像素点建立由k 个单高斯模型线性叠加而成的模型，在这些混合高斯背景模型中，认为像素之间的颜色信息互不相关，对各像素点的处理都是相互独立的。

单个像素点在t 时刻服从混合高斯分布概率密度函数：,,,1(x )(x ,,)kt i t t i t i t i p w ημτ==∑其中k 为分布模式总数，,,(x ,,)t i t i t ημτ为t 时刻第i 个高斯分布，,i t μ为其均值，,i t τ为其协方差矩阵。

⼆分图的最⼤匹配—匈⽛利算法【基本概念】：⼆分图：⼆分图⼆分图⼜称作⼆部图，是图论中的⼀种特殊模型。

设G=(V,E)是⼀个⽆向图，如果顶点V可分割为两个互不相交的⼦集(A,B)，并且图中的每条边（i，j）所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B)，则称图G为⼀个⼆分图。

⽆向图G为⼆分图的充分必要条件是，G⾄少有两个顶点，且其所有回路的长度均为偶数。

最⼤匹配最⼤匹配：给定⼀个⼆分图G，在G的⼀个⼦图M中，M的边集中的任意两条边都不依附于同⼀个顶点，则称M是⼀个匹配. 选择这样的边数最⼤的⼦集称为图的最⼤匹配问题，如果⼀个匹配中，图中的每个顶点都和图中某条边相关联，则称此匹配为完全匹配，也称作完备匹配.最⼩覆盖：最⼩覆盖要求⽤最少的点（Ｘ集合或Ｙ集合的都⾏）让每条边都⾄少和其中⼀个点关联。

可以证明：最少的点（即覆盖数）＝最⼤匹配数最⼩路径覆盖：⽤尽量少的不相交简单路径覆盖有向⽆环图Ｇ的所有结点。

解决此类问题可以建⽴⼀个⼆分图模型。

把所有顶点i拆成两个：Ｘ结点集中的i 和Y结点集中的i',如果有边i->j，则在⼆分图中引⼊边i->j'，设⼆分图最⼤匹配为m,则结果就是n-m。

增⼴路（增⼴轨）：（增⼴轨）：增⼴路若P是图G中⼀条连通两个未匹配顶点的路径，并且属于M的边和不属于M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的⼀条增⼴路径（举例来说，有A、B集合，增⼴路由A中⼀个点通向B中⼀个点，再由B中这个点通向A中⼀个点……交替进⾏）。

增⼴路径的性质：1 有奇数条边。

2 起点在⼆分图的左半边，终点在右半边。

3 路径上的点⼀定是⼀个在左半边，⼀个在右半边，交替出现。

（其实⼆分图的性质就决定了这⼀点，因为⼆分图同⼀边的点之间没有边相连，不要忘记哦。

）4 整条路径上没有重复的点。

5 起点和终点都是⽬前还没有配对的点，⽽其它所有点都是已经配好对的。

用匈牙利算法求二分图的最大匹配二分图的最大匹配有两种求法，第一种是最大流；第二种就是匈牙利算法。

这个算法说白了就是最大流的算法，但是它跟据二分图匹配这个问题的特点，把最大流算法做了简化，提高了效率。

最大流算法的核心问题就是找增广路径（augment path）。

匈牙利算法也不例外，它的基本模式就是：初始时最大匹配M为空while 找得到增广路径do 把增广路径加入到最大匹配中去可见和最大流算法是一样的。

但是这里的增广路径就有它一定的特殊性，下面我来分析一下。

（注：匈牙利算法虽然根本上是最大流算法，但是它不需要建网络模型，所以图中不再需要源点和汇点，仅仅是一个二分图。

每条边也不需要有方向。

）图1是我给出的二分图中的一个匹配：［1，5］和［2，6］。

图2就是在这个匹配的基础上找到的一条增广路径：3->6->2->5->1->4。

我们借由它来描述一下二分图中的增广路径的性质：(1)有奇数条边。

(2)起点在二分图的左半边，终点在右半边。

(3)路径上的点一定是一个在左半边，一个在右半边，交替出现。

（其实二分图的性质就决定了这一点，因为二分图同一边的点之间没有边相连。

）(4)整条路径上没有重复的点。

(5)起点和终点都是目前还没有配对的点，而其它所有点都是已经配好对的。

（如图1、图2所示，［1，5］和［2，6］在图1中是两对已经配好对的点；而起点3和终点4目前还没有与其它点配对。

）(6)路径上的所有第奇数条边都不在原匹配中，所有第偶数条边都出现在原匹配中。

（如图1、图2所示，原有的匹配是［1，5］和［2，6］，这两条配匹的边在图2给出的增广路径中分边是第2和第4条边。

而增广路径的第1、3、5条边都没有出现在图1给出的匹配中。

）(7)最重要的一条，把增广路径上的所有第奇数条边加入到原匹配中去，并把增广路径中的所有第偶数条边从原匹配中删除（这个操作称为增广路径的取反），则新的匹配数就比原匹配数增加了1个。

算法———艺术二分图匹配剖析很多人说，算法是一种艺术。

但是对于初学者的我，对算法认识不是很深刻，但偶尔也能感受到他强大的魅力与活力。

这让我追求算法的脚步不能停止。

下面我通过分析匈牙利算法以及常用建图方式，与大家一起欣赏算法的美。

匈牙利算法匈牙利算法是用来解决最大二分图匹配问题的，所谓二分图即“一组点集可以分为两部分，且每部分内各点互不相连，两部分的点之间可以有边”。

所谓最大二分图匹配即”对于二分图的所有边，寻找一个子集，这个子集满足两个条件，1：任意两条边都不依赖于同一个点。

2：让这个子集里的边在满足条件一的情况下尽量多。

首先可以想到的是，我们可以通过搜索，找出所有的这样的满足上面条件的边集，然后从所有的边集中选出边数最多的那个集合，但是我们可以感觉到这个算法的时间复杂度是边数的指数级函数，因此我们有必要寻找更加高效的方法。

目前比较有效的方法有匈牙利算法和通过添加汇点和源点的网络流算法，对于点的个数都在200 到300 之间的数据，我们是采取匈牙利算法的，因为匈牙利算法实现起来要比网络流简单些。

下面具体说说匈牙利算法：介绍匈牙利之前，先说说“增广轨”。

定义：若P是图G中一条连通两个未匹配顶点的路径，并且属最大匹配边集M的边和不属M的边(即已匹配和待匹配的边)在P上交替出现，则称P为相对于M的一条增广轨定义总是抽象的下面通过图来理解它。

图中的线段（2->3, 3->1, 1->4）便是上面所说的p路径，我们假定边（1,3）是以匹配的边，（2,3）（1,4）是未匹配的边，则边（4,1）边（1,3）和边（3,2）在路径p上交替的出现啦，那么p就是相对于M的一条增广轨，这样我们就可以用边1,4 和边2,3来替换边1,3 那么以匹配的边集数量就可以加1,。

匈牙利算法就是同过不断的寻找增广轨实现的。

很明显如果二分图的两部分点分别为n 和m，那么最大匹配的数目应该小于等于MIN（n,m）; 因此我们可以枚举任第一部分（的二部分也可以）里的每一个点，我们从每个点出发寻找增广轨，最后吧第一部分的点找完以后，就找到了最大匹配的数目，当然我们也可以通过记录找出这些边。

摘要本文从原理和应用效果上对经典的图像分割方法如边缘检测、阈值分割技术和区域增长等进行了分析。

对梯度算法中的Roberts算子、Sobel算子、Prewitt算子、拉普拉斯(Laplacian)算子、LoG(Laplacian-Gauss)算子、坎尼（Canny）算子的分割步骤、分割方式、分割准则相互比较可以看出根据坎尼（Canny）边缘算子的3个准则得出的边缘检测结果最满意。

而阈值分割技术的关键在于阈值的确定，只有阈值确定好了才能有效的划分物体与背景，但这种方法只对于那些灰度分布明显，背景与物体差别大的图像的分割效果才明显。

区域增长的基本思想是将具有相似性质的像素集合起来构成新区域。

与此同时本文还分析了图像分割技术研究的方向。

关键词：图像处理图像分割AbstractThis article analyses the application effect to the classics image segmentation method like the edge examination, territory value division technology, and the region growth and so on.For comparing the Roberts operator, Sobel operator, Prewitt operator, the operator of Laplacian and the operator of LoG(Laplacian-Gauss),Canny operator in gradient algorithm,the step, the way and the standard of the image segmentation,we can find out the three standard of Canny edge operator the edge detection result of reaching most satisfy. And the key point of threshold segmentation lie in fixing the threshold value, it is good to have only threshold value to determine it then can be effective to divide object and background,but this kind of method is good to those gray scales,the big difference image effect between the background and obiect. The basic idea of area is to form the new region from similar nature.And also, this paper analyses the research direction of image segmentation technology at the same time.Key words: image processing image segmentation operator目录（一般目录要求最多是三级目录，不要出现四级目录）第一章绪论 (1)1.1数字图像处理的基本特点 (1)1.1.1数字图像处理的信息大多是二维信息，处理信息量很大（三级标题有问题）1 1.1.2数字图像处理占用的频带较宽 (2)1.1.3数字图像中各个像素是不独立的，其相关性大 (2)1.1.4作合适的假定或附加新的测量 (2)1.1.5数字图像处理后的图像受人的因素影响较大 (2)1.2数字图像处理的优点 (2)1.2.1再现性好 (2)1.2.2处理精度高 (3)1.2.3适用面宽 (3)1.2.4灵活性高 (3)1.3数字图像处理的应用 (4)1.3.1航天和航空技术方面的应用 (4)1.3.2生物医学工程方面的应用 (5)1.3.3通信工程方面的应用 (5)1.3.4工业和工程方面的应用 (5)1.3.5军事公安方面的应用 (5)1.3.6文化艺术方面的应用 (6)1.4数字图像分割技术的发展概况 (6)1.4.1 基于分形的图像分割技术 (6)1.4.2 基于神经网络的图像分割技术 (7)1.5本文的主要流程图 (8)第二章数字图像处理的处理方式 (9)2.1图像变换 (9)2.2图像编码压缩 (9)2.3图像增强和复原 (9)2.4图像分割 (9)2.5图像描述 (10)2.6图像分类（识别） (10)第三章 MATLAB平台及其开发环境 (11)3.1.MATLAB的组成 (11)3.1.1MATLAB主要有以下几个部分 (11)a.数值计算功能 (12)b.符号计算功能 (12)c.数据分析功能 (12)d.动态仿真功能 (12)e.程序借口功能 (13)f.文字处理功能 (13)3.2MATLAB的特点 (13)3.2.1功能强大，可扩展性强 (13)3.2.2界面友好，编程效率高 (14)3.2.3图像功能，灵活且方便 (14)3.3MATLAB在图像处理中的应用 (14)第四章图像分割概念及算法研究 (16)4.1图像分割的基本概念 (16)4.1.1图像分割定义 (16)4.2边缘检测方法（4.1和4.2之间不是并行关系） (17)4.2.1边缘检测概述 (17)4.2.2边缘检测梯度算法 (19)a.梯度边缘检测算法基本步骤及流程图 (19)b.Robert算子 (20)c.Sobel算子 (21)d.Prewitt算子 (21)4.2.3拉普拉斯（Laplacian）算子 (22)4.2.4LoG(Laplacian-Gauss)算子 (24)4.2.5坎尼（Canny）算子 (25)4.3灰度阈值分割 (27)4.3.1阈值分割介绍 (28)a.阈值化分割原则 (28)b.阈值分割算法分类 (29)4.3.2全局阈值 (30)a.极小值点阈值 (31)b.最优阈值 (31)c.迭代阈值分割 (33)4.3.3动态阈值 (34)a.阈值插值 (35)b.水线阈值算法 (35)4.4区域分割 (37)4.4.1区域生长的基本原理、步骤及流程图 (37)4.4.2生长准则和过程 (40)a.灰度差准则 (40)b.灰度分布统计准则 (41)c.区域形状准则 (42)4.4.3分裂合并 (43)第五章总结 (45)5.1对于图像边缘检测的分析 (45)5.2对于图像阈值分割的分析 (45)5.3对于图像区域分割的分析 (46)5.4改进意见（改进可另外做为一章比如说某某算法等的若干改进等，不要放入总结一章中）（总结是对整篇文章的一个概述，应该是写比如得出些什么结论，一些算法间比较等相关问题。