(易错题精选)初中数学因式分解图文答案(1)

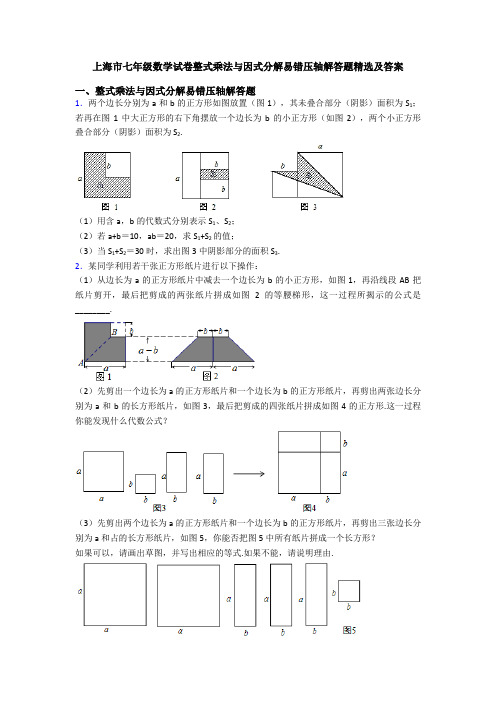
上海市七年级数学试卷整式乘法与因式分解易错压轴解答题精选及答案一、整式乘法与因式分解易错压轴解答题1．两个边长分别为a和b的正方形如图放置（图1），其未叠合部分（阴影）面积为S1；若再在图1中大正方形的右下角摆放一个边长为b的小正方形（如图2），两个小正方形叠合部分（阴影）面积为S2.（1）用含a，b的代数式分别表示S1、S2；（2）若a+b＝10，ab＝20，求S1+S2的值；（3）当S1+S2＝30时，求出图3中阴影部分的面积S3.2．某同学利用若干张正方形纸片进行以下操作：（1）从边长为a的正方形纸片中减去一个边长为b的小正方形，如图1，再沿线段AB把纸片剪开，最后把剪成的两张纸片拼成如图2的等腰梯形，这一过程所揭示的公式是________.（2）先剪出一个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出两张边长分别为a和b的长方形纸片，如图3，最后把剪成的四张纸片拼成如图4的正方形.这一过程你能发现什么代数公式？（3）先剪出两个边长为a的正方形纸片和一个边长为b的正方形纸片，再剪出三张边长分别为a和占的长方形纸片，如图5，你能否把图5中所有纸片拼成一个长方形？如果可以，请画出草图，并写出相应的等式.如果不能，请说明理由.3．[数学实验探索活动]实验材料现有若干块如图①所示的正方形和长方形硬纸片.实验目的：用若干块这样的正方形和长方形硬纸片拼成一个新的长方形，通过不同的方法计算面积，得到相应的等式，从而探求出多项式乘法或分解因式的新途径.例如，选取正方形、长方形硬纸片共6块，拼出一个如图②的长方形，计算它的面积，写出相应的等式有a2+3ab+2b2=（a+2b）（a+b）或（a+2b）（a+b）=a2+3ab+2b2.问题探索：（1）小明想用拼图的方法解释多项式乘法（2a+b）（a+b）=2a2+3ab+b2，那么需要两种正方形纸片________张，长方形纸片________张；（2）选取正方形、长方形硬纸片共8块，可以拼出一个如图③的长方形，计算图③的面积，并写出相应的等式；（3）试借助拼图的方法，把二次三项式2a2+5ab+2b2分解因式，并把所拼的图形画在虚线方框3内.4．如图1，有A型、B型正方形卡片和C型长方形卡片各若干张.（1）用1张A型卡片，1张B型卡片，2张C型卡片拼成一个正方形，如图2，用两种方法计算这个正方形面积，可以得到一个等式，请你写出这个等式________；（2）选取1张A型卡片，10张C型卡片，________张B型卡片，可以拼成一个正方形，这个正方形的边长用含a，b的代数式表示为________；（3）如图3，两个正方形边长分别为m、n，m+n=10，mn=19，求阴影部分的面积. 5．阅读材料：把形如的二次三项式（或其一部分）配成完全平方式的方法叫做配方法，配方法的基本形式是完全平方公式的逆写，即 .例如：是的一种形式的配方，是的另一种形式的配方请根据阅读材料解决下列问题：（1）比照上面的例子，写出的两种不同形式的配方；（2）已知，求的值；（3）已知，求的值.6．如图，长方形ABCD中，AB=x(6<x<9)，AD=y(6<y<9)，放入一个边长为6的正方形AEFG 和两个边长都为3的正方形CHIJ及正方形DKMN，S1， S2， S3分别表示对应阴影部分的面积．（1）MH=________，KG=________，BJ=________(结果用含x或y的代数式表示)（2）若S2=S3，求长方形ABCD的周长．（3）若2S1+3S2=5S3，且AD比AB长1，求长方形ABCD的面积．7．如图，将几个小正方形与小长方形拼成一个边长为(a+b+c)的正方形（1）若用不同的方法计算这个边长为(a+b+c)的正方形面积，就可以得到一个等式，这个等式可以为 ________ .(只要写出一个即可)（2）请利用(1)中的等式解答下列问题:①若三个实数a，b，c满足a+b+c=11，ab+bc+ac=38，求a2+b2+c2的值②若三个实数x，y，z满足2x×4y÷8z= ，x2+4y2+9z2=44，求2xy-3xz-6yz的值8．【阅读与思考】整式乘法与因式分解是方向相反的变形.如何把二次_一项式ax2+bx+c进行因式分解呢?我们已经知道，(a1x+c1)(a2x+c2)=a1a2x2+a1c2x+a2c1x+c1c2=a1a2x2+(a1c2+a2c1)x+c1c2.反过来，就得到：a1a2x2+(a1c2+a2c1)x+c1c2=(a1x+c1)(a2x+c2).我们发现，二次项的系数a分解成a1a2，常数项c分解成c1c2，并且把a1， a2， c1，c2，如图①所示摆放，按对角线交叉相乘再相加，就得到a1c2+a2c1，如果a1c2+a2c1的值正好等于ax2+bx+c的一次项系数b，那么ax2+bx+c就可以分解为(a1x+c1)(a2x+c2)，其中a1， c1位于图的上一行，a2， c2位于下一行.像这种借助画十字交叉图分解系数，从而帮助我们把二次三项式分解因式的方法，通常叫做“十字相乘法”.例如，将式子x2-x-6分解因式的具体步骤为：首先把二次项的系数1分解为两个因数的积，即1=1×1，把常数项-6也分解为两个因数的积，即-6=2×（-3)；然后把1，1，2，-3按图②所示的摆放，按对角线交叉相乘再相加的方法，得到1×(-3)+1×2=-1，恰好等于一次项的系数-1，于是x2-x-6就可以分解为(x+2)(x-3).（1）请同学们认真观察和思考，尝试在图③的虚线方框内填入适当的数，并用“十字相乘法”分解因式：x2+x-6=________.（2）【理解与应用】请你仔细体会上述方法，并尝试对下面两个二次三项式进行分解因式：Ⅰ.2x2+5x-7=________；Ⅱ.6x2-7xy+2y2=________ .（3）【探究与拓展】对于形如ax2+bxy+cy2+dx+ey+f的关于x，y的二元二次多项式也可以用“十字相乘法”来分解.如图④，将a分解成mn乘积作为一列，c分解成pq乘积作为第二列，f分解成jk乘积作为第三列，如果mq+np=b，pk+qj=e，mk+nj=d，即第1，2列、第2，3列和第1，3列都满足十字相乘规则，则原式=(mx+py+j)(nx+qy+k)，请你认真阅读上述材料并尝试挑战下列问题：Ⅰ.分解因式3x2+5xy-2y2+x+9y-4=________ .Ⅱ.若关于x，y的二元二次式x2+7xy-18y2-5x+my-24 可以分解成两个一次因式的积，求m的值.________Ⅲ.己知x，y为整数，且满足x2+3xy+2y2+2x+3y=-1，请写出一组符合题意的x，y的值.________9．若x满足（5-x）（x-2）=2，求（x-5）2+（2-x）2的值；解：设5-x=a，x-2=b，则（5-x）（x-2）=ab=2，a+b=（5-x）+（x-2）=3，所以（x-5）2+（2-x）2=（5-x）2+（x-2）2=a2+b2=（a+b）2-2ab=32-2×2=5，请仿照上面的方法求解下面的问题（1）若x满足（9-x）（x-4）=4，求（9-x）2+（x-4）2的值；（2）已知正方形ABCD的边长为x，E，F分别是AD，DC上的点，且AE=2，CF=4，长方形EMFD的面积是63，分别以MF、DF为边作正方形，求阴影部分的面积．10．如图所示,在边长为a米的正方形草坪上修建两条宽为b米的道路.（1）为了求得剩余草坪的面积，小明同学想出了两种办法，结果分别如下：方法①：________ 方法②：________请你从小明的两种求面积的方法中，直接写出含有字母a，b代数式的等式是：________（2）根据（1）中的等式，解决如下问题：①已知：，求的值；②己知：，求的值.11．认真阅读材料，然后回答问题：我们初中学习了多项式的运算法则，相应的，我们可以计算出多项式的展开式，如：（a+b）1=a+b，（a+b）2=a2+2ab+b2，（a+b）3=（a+b）2（a+b）=a3+3a2b+3ab2+b3，…下面我们依次对（a+b）n展开式的各项系数进一步研究发现，当n取正整数时可以单独列成表中的形式：上面的多项式展开系数表称为“杨辉三角形”；仔细观察“杨辉三角形”，用你发现的规律回答下列问题：（1）多项式（a+b）n的展开式是一个几次几项式？并预测第三项的系数；（2）请你预测一下多项式（a+b）n展开式的各项系数之和．（3）结合上述材料，推断出多项式（a+b）n（n取正整数）的展开式的各项系数之和为S，（结果用含字母n的代数式表示）．12．阅读下面材料:通过整式运算一章的学习，我们发现要验证一个结论的正确性可以有两种方法：例如：要验证结论方法1：几何图形验证：如下图，我们可以将一个边长为（a+b）的正方形上裁去一个边长为(a-b)的小正方形则剩余图形的面积为4ab,验证该结论正确。

（易错题精选）初中数学因式分解经典测试题含答案(1)一、选择题1．下列从左到右的变形，是因式分解的是( )A ．2(a ﹣b)＝2a ﹣2bB ．221(a b)(a b)1-=-+++a bC ．2224(2)x x x -+=-D ．22282(2)(2)x y x y x y -=-+ 【答案】D【解析】【分析】根据因式分解的定义，把一个多项式变形为几个整式的积的形式是分解因式进行分析即可得出.【详解】解：由因式分解的定义可知：A. 2(a ﹣b)＝2a ﹣2b ，不是因式分解，故错误；B. 221(a b)(a b)1-=-+++a b ，不是因式分解，故错误；C. 2224(2)x x x -+=-，左右两边不相等，故错误；D. 22282(2)(2)x y x y x y -=-+是因式分解；故选：D【点睛】本题考查了因式分解的定义，熟知因式分解的定义和分解的规范要求是解题关键.2．已知实数a 、b 满足等式x=a 2+b 2+20，y =a(2b －a )，则x 、y 的大小关系是（ ）． A ．x ≤ yB ．x ≥ yC ．x < yD ．x > y【答案】D【解析】【分析】判断x 、y 的大小关系，把x y -进行整理，判断结果的符号可得x 、y 的大小关系．【详解】解：22222202()x y a b ab a a b a -=++-+=-++20， 2()0a b -≥Q ，20a ≥，200>,0x y ∴->，x y ∴>，故选:D ．【点睛】本题考查了作差法比较大小、配方法的应用；进行计算比较式子的大小；通常是让两个式子相减，若为正数，则被减数大；反之减数大.3．多项式x2y（a-b）-xy（b-a）+y（a-b）提公因式后，另一个因式为（）A．21x x-+B．21x x++C．21x x--D．21x x+-【答案】B【解析】解：x2y(a－b)－xy(b－a)＋y(a－b)= y(a－b)（x2+x+1）．故选B．4．下列分解因式正确的是（）A．x3﹣x=x（x2﹣1）B．x2﹣1=（x+1）（x﹣1）C．x2﹣x+2=x（x﹣1）+2D．x2+2x﹣1=（x﹣1）2【答案】B【解析】试题分析：根据提公因式法分解因式，公式法分解因式对各选项分析判断利用排除法求解．解：A、x3﹣x=x（x2﹣1）=x（x+1）（x﹣1），故本选项错误；B、x2﹣1=（x+1）（x﹣1），故本选项正确；C、x2﹣x+2=x（x﹣1）+2右边不是整式积的形式，故本选项错误；D、应为x2﹣2x+1=（x﹣1）2，故本选项错误．故选B．考点：提公因式法与公式法的综合运用．5．下列分解因式正确的是（）A．x2-x+2=x（x-1）+2 B．x2-x=x（x-1）C．x-1=x（1-1x）D．（x-1）2=x2-2x+1【答案】B【解析】【分析】根据因式分解的定义对各选项分析判断后利用排除法求解．【详解】A、x2-x+2=x（x-1）+2，不是分解因式，故选项错误；B、x2-x=x（x-1），故选项正确；C、x-1=x（1-1x），不是分解因式，故选项错误；D、（x-1）2=x2-2x+1，不是分解因式，故选项错误．故选：B．【点睛】本题考查了因式分解，把一个多项式写成几个整式的积的形式叫做因式分解，也叫做分解因式．掌握提公因式法和公式法是解题的关键．6．下列各式中，由等式的左边到右边的变形是因式分解的是() A．(x＋3)(x－3)＝x2－9 B．x2＋x－5＝(x－2)(x＋3)＋1C．a2b＋ab2＝ab(a＋b) D．x2＋1＝x1 () xx【答案】C【解析】【分析】根据因式分解是把一个多项式转化成几个整式积的形式，可得答案．【详解】A、是整式的乘法，故A错误；B、没有把一个多项式转化成几个整式积的形式，故B错误；C、把一个多项式转化成了几个整式积的形式，故C正确；D、没有把一个多项式转化成几个整式积的形式，故D错误；故选：C．【点睛】本题考查了因式分解，因式分解是把一个多项式转化成几个整式积的形式．7．如图，边长为a，b的矩形的周长为10，面积为6，则a2b+ab2的值为（）A．60 B．16 C．30 D．11【答案】C【解析】【分析】先把所给式子提公因式进行因式分解，整理为与所给周长和面积相关的式子，再代入求值即可．【详解】∵矩形的周长为10，∴a+b=5，∵矩形的面积为6，∴ab=6，∴a2b+ab2=ab（a+b）=30．故选：C．【点睛】本题既考查了对因式分解方法的掌握，又考查了代数式求值的方法，同时还隐含了整体的数学思想和正确运算的能力．8．下列各式能用平方差公式分解因式的是（ ）A ．21a +B ．20.040.09y --C ．22x y +D ．22x y -【答案】D【解析】【分析】判断各个选项是否满足平方差的形式，即：22a b -的形式【详解】A 、C 都是22a b +的形式，不符；B 中，变形为：－(20.04+0.09y )，括号内也是22a b +的形式，不符；D 中，满足22a b -的形式，符合故选：D【点睛】本题考查平方差公式，注意在利用乘法公式时，一定要先将式子变形成符合乘法公式的形式，我们才可利用乘法公式简化计算.9．将多项式x 2+2xy+y 2﹣2x ﹣2y+1分解因式，正确的是（ ）A ．（x+y ）2B ．（x+y ﹣1）2C ．（x+y+1）2D ．（x ﹣y ﹣1）2 【答案】B【解析】【分析】此式是6项式，所以采用分组分解法．【详解】解：x 2+2xy+y 2﹣2x ﹣2y+1=（x 2+2xy+y 2）﹣（2x+2y ）+1=（x+y ）2﹣2（x+y ）+1=（x+y ﹣1）2．故选：B10．下列因式分解正确的是（ ）A ．x 3﹣x ＝x （x 2﹣1）B ．x 2+y 2＝（x+y ）（x ﹣y ）C ．（a+4）（a ﹣4）＝a 2﹣16D ．m 2+4m+4＝（m+2）2【答案】D【解析】【分析】逐项分解因式，即可作出判断．【详解】A 、原式＝x （x 2﹣1）＝x （x+1）（x ﹣1），不符合题意；B 、原式不能分解，不符合题意；C 、原式不是分解因式，不符合题意；D 、原式＝（m+2）2，符合题意，故选：D ．【点睛】此题主要考查了提公因式法，以及公式法在因式分解中的应用，要熟练掌握．11．下面式子从左边到右边的变形中是因式分解的是（ ）A ．()2212x x x x --=--B ．()()22a b a b a b +-=-C ．()()2422x x x -=+-D ．()2222a b a b ab +=++ 【答案】C【解析】【分析】根据把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解进行分析即可．【详解】A 选项：等式右边不是乘积的形式，故不是因式分解，不符合题意.B 选项：等式右边不是乘积的形式，故不是因式分解，不符合题意.C 选项：等式右边是乘积的形式，故是因式分解，符合题意.D 选项：等式右边不是乘积的形式，故不是因式分解，不符合题意.故选：C.【点睛】考查了因式分解的意义，关键是掌握因式分解的定义（把一个多项式化为几个整式的积的形式）．12．下列各式中从左到右的变形，是因式分解的是（ ）A ．（a +3）（a -3）=a 2-9B ．x 2+x -5=（x -2）（x +3）+1C ．a 2b +ab 2=ab （a +b ）D ．x 2+1=x （x +1x） 【答案】C【解析】【分析】根据因式分解是把一个多项式转化成几个整式积的形式，可得答案．【详解】A 、是整式的乘法，故A 错误；B 、没把一个多项式转化成几个整式积的形式，故B 错误；C 、因式分解是把一个多项式转化成几个整式积的形式，故C 正确；D 、因式中含有分式，故D 错误；故选：C ．本题考查了因式分解，因式分解是把一个多项式转化成几个整式积的形式．13．下列各因式分解的结果正确的是（ ）A ．()321a a a a -=-B ．2()b ab b b b a ++=+C ．2212(1)x x x -+=-D ．22()()x y x y x y +=+-【答案】C【解析】【分析】将多项式写成整式乘积的形式即是因式分解，且分解到不能再分解为止，根据定义依次判断即可．【详解】 ()321a a a a -=-=a （a+1）（a-1），故A 错误； 2(1)b ab b b b a ++=++，故B 错误；2212(1)x x x -+=-，故C 正确；22x y +不能分解因式，故D 错误，故选：C ．【点睛】此题考查因式分解的定义，熟记定义并掌握因式分解的方法及分解的要求是解题的关键．14．将下列多项式因式分解,结果中不含有因式(a+1)的是( )A ．a 2-1B ．a 2+aC ．a 2+a-2D ．(a+2)2-2(a+2)+1【答案】C【解析】试题分析：先把四个选项中的各个多项式分解因式，即a 2﹣1=（a+1）（a ﹣1），a 2+a=a （a+1），a 2+a ﹣2=（a+2）（a ﹣1），（a+2）2﹣2（a+2）+1=（a+2﹣1）2=（a+1）2，观察结果可得四个选项中不含有因式a+1的是选项C ；故答案选C ．考点：因式分解.15．把多项式分解因式，正确的结果是（ ）A ．4a 2+4a +1=（2a +1）2B ．a 2﹣4b 2=（a ﹣4b ）（a +b ）C ．a 2﹣2a ﹣1=（a ﹣1）2D ．（a ﹣b ）（a +b ）=a 2﹣b 2【答案】A【解析】直接利用平方差公式和完全平方公式进行分解因式，进而判断得出答案．【详解】A ．4a 2+4a +1=（2a +1）2，正确；B ．a 2﹣4b 2=（a ﹣2b ）（a +2b ），故此选项错误；C ．a 2﹣2a ﹣1在有理数范围内无法运用公式分解因式，故此选项错误；D ．（a ﹣b ）（a +b ）=a 2﹣b 2，是多项式乘法，故此选项错误．故选：A ．【点睛】此题主要考查了公式法分解因式，正确应用乘法公式是解题关键．16．若a b c 、、为ABC ∆三边，且满足222244a c b c a b -=-，则ABC ∆的形状是（ ） A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．以上均有可能 【答案】D【解析】【分析】把已知等式左边分解得到()()()2220a b a b c a b ⎡⎤+--+=⎣⎦，-a b =0或()222c a b -+=0，即a=b 或222c a b =+，然后根据等腰三角形和直角三角形的判定方法判断．【详解】因为a b c 、、为ABC ∆三边，222244a c b c a b -=-所以()()()2220a b a b c a b ⎡⎤+--+=⎣⎦ 所以-a b =0或()222c a b -+=0，即a=b 或222c a b =+所以ABC ∆的形状是等腰三角形、等腰三角形、等腰直角三角形故选：D【点睛】本题考查因式分解的应用：利用因式分解解决求值问题；利用因式分解解决证明问题；利用因式分解简化计算问题．17．已知12,23x y xy -==，则43342x y x y -的值为( )A ．23B ．2C ．83D ．163【答案】C【解析】【分析】利用因式分解以及积的乘方的逆用将43342x y x y -变形为(xy)3(2x-y)，然后代入相关数值进行计算即可．【详解】 ∵12,23x y xy -==，∴43342x y x y -=x 3y 3(2x-y)=(xy)3(2x-y)=23×13=83， 故选C ．【点睛】本题考查了因式分解的应用，代数式求值，涉及了提公因式法，积的乘方的逆用，熟练掌握和灵活运用相关知识是解题的关键．18．若x 2+mxy+y 2是一个完全平方式，则m=（ ）A ．2B ．1C ．±1D ．±2【答案】D【解析】根据完全平方公式：(a +b )2=a 2+2ab +b 2与(a -b )2=a 2-2ab +b 2可知，要使x 2+mxy +y 2符合完全平方公式的形式，该式应为：x 2+2xy +y 2=(x +y )2或x 2-2xy +y 2=(x -y )2. 对照各项系数可知，系数m 的值应为2或-2.故本题应选D.点睛：本题考查完全平方公式的形式，应注意完全平方公式有(a +b )2、(a -b )2两种形式. 考虑本题时要全面，不要漏掉任何一种形式.19．下列由左到右边的变形中，是因式分解的是（ ）A ．（x +2）（x ﹣2）＝x 2﹣4B ．x 2﹣1＝1()x x x-C ．x 2﹣4+3x ＝（x +2）（x ﹣2）+3xD ．x 2﹣4＝（x +2）（x ﹣2）【答案】D【解析】【分析】直接利用因式分解的意义分别判断得出答案．【详解】A 、（x+2）（x-2）=x 2-4，是多项式乘法，故此选项错误；B 、x 2-1=（x+1）（x-1），故此选项错误；C 、x 2-4+3x=（x+4）（x-1），故此选项错误；D 、x 2-4=（x+2）（x-2），正确．故选D ．【点睛】此题主要考查了因式分解的意义，正确把握定义是解题关键．20．下列等式从左到右的变形，属于因式分解的是（ ）A ．()21x x x x -=- B ．()22121x x x x -+=-+ C ．()()21323x x x x -+=+- D ．()a b c ab ac -=-【答案】A【解析】【分析】根据因式分解的意义：把一个多项式转化成几个整式积的形式叫因式分解，可得答案．【详解】解：A 、把一个多项式转化成几个整式积的形式，符合题意；B 、右边不是整式积的形式，不符合题意；C 、是整式的乘法，不是因式分解，不符合题意；D 、是整式的乘法，不是因式分解，不符合题意；故选：A ．【点睛】本题考查了因式分解的意义，掌握因式分解的意义是解题关键．。

初一数学因式分解易错题例1.18x ³y-21xy ³ 错解：原式=)36(2122y x - 分析：提取公因式后，括号里能分解的要继续分解。

正解： 原式=21xy （36x ²-y ²） =21xy （6x+y ）（6x-y ） 例2. 3m ²n （m-2n ）[])2(62n m mn --错解：原式=3mn （m-2n ）（m-2n ）分析：相同的公因式要写成幂的形式。

正解：原式=3mn （m-2n ）（m-2n ）=3mn （m-2n ）² 例3．2x+x+41 错解：原式=)14121(41++x x 分析：系数为2的x 提出公因数41后，系数变为8，并非21；同理，系数为1的x 的系数应变为4。

正解：原式=)148(41++x x =)112(41+x 例4.412++x x 错解：原式=)14141(412++x x =2)121(41+x 分析：系数为1的x 提出公因数41后，系数变为4，并非41。

正解：原式=)144(412++x x =2)12(41+x 例5.6x ()2y x -+3()3x y -错解：原式=3()()[]x x y x y 22+-+- 分析：3()3x y -表示三个()x y -相乘，故括号中2)(x y -与)(x y -之间应用乘号而非加号。

正解：原式=6x ()2x y -+()2x y - =3()2x y -()[]x y x -+2 =3()2x y -()y x + 例6.()8422--+x x错解：原式=()[]242-+x =()22-x 分析：8并非4的平方，且完全平方公式中b 的系数一定为正数。

正解：原式=()22+x －4（x+2） =(x+2)()[]42-+x=（x+2）（x －2）例7.()()223597n m n m --+ 错解：原式=()()[]23597n m n m --+ =()2122n m + 分析：题目中两二次单项式的底数不同，不可直接加减。

适用标准文档初一数学因式分解易错题例1. 18x 3 y-12xy31 2 2错解：原式= (36 )x y2剖析：提取公因式后，括号里能分解的要持续分解。

正解：原式=12xy 〔36x 2 -y 2 〕= 12xy 〔6x+y〕〔6x-y 〕例2. 3m2 n〔m-2n〕 6 m n2(m2n) 错解：原式=3mn〔m-2n〕〔m-2n〕剖析：同样的公因式要写成幂的形式。

正解：原式=3mn〔m-2n〕〔m-2n〕=3mn 〔m-2n〕2例3．2x+x+141 1 1错解：原式= 1)( x x4 2 4剖析：系数为 2 的x 提出公因数变成4。

14后，系数变成8，并不是12；同理，系数为 1 的x 的系数应1正解：原式= (8 4 1)x x41= (1 21)x4例4. 2 xx141 12 1错解：原式= 1)( x x4 4 4= 14(12x 21)剖析：系数为 1 的x 提出公因数1 2 14后，系数变成4，并不是14。

= 14(2x 21)例 2x y +3 y x3 文案大全适用标准文档2错解：原式=3 y x y x 2x剖析：3 3y x 表示三个y x 相乘，故括号中2( y x) 与(y x) 之间应用乘号而非加号。

正解：原式=6x 2y x + y x2=3 2y x 2x y x=3 2y x x y2 x例6. x 2 4 82错解：原式= x 2 42= x 2剖析：8 并不是4 的平方，且完整平方公式中 b 的系数必定为正数。

正解：原式= 2x 2 －4〔x+2〕=(x+2) x 2 4= 〔x+2〕〔x－2〕例7. 2 5 37m 9n m n22错解：原式= 7m 9n 5m 3n2= 2m 12n剖析：题目中两二次单项式的底数不同，不行直接加减。

正解：原式= 7m 9n 5m 3n 7m 9n 5n 3n = 12m 6n 2m 12n=12 〔2m+n〕〔m+6n〕4例8. 1a22错解：原式= a 1= 〔a2 +1〕〔a2 －1〕剖析：分解因式时应注意能否化到最简。

整式的乘法与因式分解易错题精选第1节 整式的乘法一、同底数幂的乘法 易错点：同底数幂的乘法公式理解不准确 1、请分析以下解答是否正确，若不正确，请写出正确的解答．（1）计算：63232x x x x ==⋅⨯（2）计算：5055x x x x ==⋅+2、【变式1】下列计算结果等于a 6的是（ ） A ．a 4+a 2 B ．a 2+a 2+a 2C ．32a a ⋅D ．222a a a ⋅⋅ 参考答案1、（1）错，a 5；（2）错，a 62、D易错点：不会倒着用同底数幂的乘法公式 1、若3=m a ，7=n a ，则1073=+=+=+n m n m a a a ． 上述计算是否有误，若有错，请改正． 2、【变式1】若32+m a 不能写成（ ） A ．32a a m ⋅ B ．3+⋅m m a a C ．32a a m +D ．21++⋅m m a a3、【变式2】若a x =10，b y =10，则210++y x 等于（ ） A ．2ab B ．a+b C ．a+b+2 D ．100ab 参考答案1、错；正确的结果是212、C3、D易错点：不会转换底数为相反数的幂 1、计算：=-⋅-4)()(m n n m 2、计算：=--3))(x y y x （ 3、计算：=-⋅-32)()(p q q p4、若k 为正整数，则122)2()2(2+-+-⋅k k 等于（ ） A ．0 B ．122-k C ．122+-k D ．222-k参考答案 1、(m -n)5 2、-(x -y)4 3、(q -p)5 4、A二、幂的乘方易错点：对幂的乘方计算方法理解出错1、判断下面计算的对错，并把错误的改正过来． 3332b b b =⋅（1）1644x x x =⋅（2）725)(a a =（3）9423)(a a a =⋅（4） 623a a a =⋅（5）224)2(a a -=-（6） 2、【变式1】判断下面计算的对错，并把错误的改正过来． 1313)(++=x x a a （1）623322)()(a a a =⋅（2） 623322)()(a a a =+（3） 53210)10(=（4）632)(a a =-（5） 623])[(a a =-（6） 参考答案1、（16b ）错，；（28x ）错，；（310a ）错，；（4）10a 错，；（55a ）错，；（724a ）错，2、（133+x a ）错，；（212a ）错，；（3）对；（4）610错，；（56a -）错，；（6）对易错点：混淆乘法和乘方1、若k 为正整数，则（ ）A ．B ．C ．D ．参考答案 1、A三、积的乘方易错点：对积的乘方法则理解出错1、将下列计算中错误的找出来，并改正 （1）(ab 2)3=ab 6 （2）(3cd)3=9c 3d 3 （3）(-3a 3)2=-9a 6 （4）(-x 3y)3=-x 6y 3参考答案1、（1）错，a 2b 6；（2）27c 3d 3；（3）9a 6；（4）-x 9y 3易错点：分不清负数的乘方和幂的相反数 1、计算：0.12530×(-829)= 2、计算：=-⋅815)16()41(3、【变式1】计算：=-⋅)16()41(8154、【变式2】计算：=-⋅2120)1314()1413(参考答案 1、-0.125 2、4 3、-44、1314-四、单项式乘以单项式易错点：漏乘只在一个单项式中出现的字母 1、计算：=⋅z xy y x 2223)(2、【变式1】计算：=⋅-4233)2(2n m p mn 参考答案 1、3x 5y 4z 2、-32m 13n 11p易错点：弄错运算顺序 1、计算：=-⋅-2224)3(2y x y x 2、【变式1】=-⋅-223)3()2(a a 3、【变式2】=-+⋅-)2(4)2(23ab ab b a 参考答案 1、-18x 8y 4 2、-72a 73、16a 7b 3-2ab五、单项式乘以多项式 易错点：漏掉常数项1、计算：=+-)13(222xy x xy2、【变式1】计算：=---)22(3322n m n m 参考答案1、2x 3y -6x 2y 3+2xy2、-3m 4n+6m 2n 4+6m 2n易错点：忘记负号 1、计算：=--)(32xy x xy2、【变式1】=--+)3(2222y x y x y x y x 参考答案 1、-x 3y+x 2y 42、3x 2y -3x 3y+x 2y 2六、多项式乘以多项式 易错点：弄错符号和漏乘 1、计算：=--)2)(2(y x y x 2、计算：=-+-))(32(22y x xy x 参考答案1、22252y xy x +-2、2336644xy y x xy x -++- 七、同底数幂的除法易错点：弄错运算顺序1、计算：=÷÷3310a a a2、【变式1】计算：=÷÷-2242)(xy xy y x 参考答案 1、a 4 2、x 6易错点：不会转换相反数的幂 1、计算：=-÷-45)()(x y y x2、【变式1】计算：=-÷-34)()(m n n m3、【变式2】计算：=-÷-35)()(m n n m 参考答案 1、y x - 2、m n - 3、2)(m n --第2节 乘法公式一、平方差公式易错点：对平方差公式的特征理解偏差 1、下列计算正确的是（ ） A ．(a+3b)(a -3b) = a 2-3b 2 B ．(-a+3b)(a -3b) = -a 2-9b 2 C ．(-a -3b)(a -3b) = -a 2+9b 2 D ．(-a -3b)(a+3b) = a 2-9b 2参考答案 1、C二、完全平方公式易错点：混淆积的乘方与完全平方1、已知5)1(2=+x x ，求221xx +的值．2、【变式1】已知7)(2=-y x ，1=xy ，求22y x +的值．3、【变式2】已知5)1(2=-a a ，求221aa +的值．参考答案 1、3 2、9 3、7易错点：开方漏解1、已知25)(2=+b a ，6=ab ，则______=-b a ．2、【变式1】已知25)(2=-b a ，6=ab ，求b a +的值．3、【变式2】已知722=+b a ，1=ab ，则___=+b a ． 参考答案 1、1± 2、7± 3、3±三、添括号和去括号易错点：添括号或去括号时符号出错1、在括号内添上适当的项：（1）a+b-c = a+(______________）（2）a+b-c = a-(______________）（3）a-b-c = a-(______________）（4）a+b+c = a-(______________）（5）a-b-c+d = a-(______________）（6）a-b+c+d = a-(______________）（7）(a+b-c)(a-b+c) =[a+(______________）][a-(______________）]（8）2x+3y-4z+5t = -(______________）= 2x-(______________）= 2x+3y-(___________）2、在下列去括号或添括号中错误的是（）A．a3-(2a-b-c)=a3-2a+b+cB．3a-5b-1+2c=-(-3a)-[5b-(2c-1)]C．-(a+1)-(-b+c)=+(-1+b-a-c)D．a-b+c-d=a-b+(d+c)参考答案1、解：（1）b-c（2）-b+c（3）b+c（4）-b-c（5）b+c-d（6）b-c-d（7）b-c；b-c（8）-2x-3y+4z-5t；-3y+4z-5t；4z-5t2、D第3节因式分解一、提取公因式易错点：第一项有负号1、因式分解：-2a2b-4ab+8a=2、【变式1】因式分解：-2a2b+12ab-8b参考答案1、-2a(ab+2b-4)2、-2b(a2-6a+4)易错点：整体法时不会处理互为相反数的项1、因式分解：2x(a-b)-y(b-a)=2、【变式1】因式分解：2x(a-b)-y(b-a)2=3、【变式2】因式分解：-a(x-y)-b(y-x)+c(x-y)=参考答案1、(a-b)(2x+y)2、(a-b)(2x-ay+by)3、(y-x)(a-b-c)二、平方差公式易错点：因式分解不彻底1、因式分解：a4-16=2、【变式1】因式分解：81-x4=3、【变式2】因式分解：4m2-36=4、【变式3】因式分解：16-36n2=5、【变式4】因式分解：16x4-1=参考答案1、(a2+4)(a+2)(a-2)2、(9+x2)(3+x)(3-x)3、4(m+3)(m-3)4、4(2+3n)(2-3n)5、(4x2+1)(2x+1)(2x-1)三、完全平方公式易错点：没考虑完全平方有两种情况1、若x2+mx+16是一个完全平方式，则常数m=____．2、【变式1】在括号里填________时，能使式子a2-( )+36成为完全平方式．3、【变式2】多项式x2-mx+25可以因式分解成(x+n)2，则m+n=_______．参考答案1、-8或82、a123、5或15易错点：因式分解不彻底1、因式分解：a4-2a2+1=(a2-1)2是否正确？若错误，请改正．2、【变式1】因式分解：16x4-8x2y2+y43、【变式2】因式分解：a4-8a2+16参考答案1、错误，(a+1)2(a-1)22、(2x+y)2(2x-y)23、(a+2)2(a-2)2。

专题15 因式分解 易错题之解答题（20题）Part1 与 提取公因式法 有关的易错题1．（2020·利辛县七年级月考）因式分解3()2()x a b y b a ---；【答案】（a -b ）（3x+2y ）【提示】先把b a -化为：(),a b -- 再利用提公因式的方法分解因式即可．【详解】解：3()2()x a b y b a ---()()32x a b y a b =-+-()()32a b x y =-+【名师点拨】本题考查提公因式法分解因式，注意互为相反数的两个因式之间的变形，掌握以上知识是解题的关键． 2．（2020·陕西西安市·七年级期末）长方形的长为a 厘米，宽为b 厘米，其中a b >，将原长方形的长和宽各增加3厘米，得到的新长方形的面积为1S ；将原长方形的长和宽分别减少2厘米，得到的新长方形的面积为2S ． （1）若a ，b 为正整数，请说明1S 与2S 的差一定是5的倍数；（2）若2120S S -=，求将原长方形的长和宽分别减少7厘米后得到的新长方形的面积．【答案】（1）见解析 （2）502cm【提示】（1）根据题意得到1(3)(3)339S a b ab a b =++=+++，2(2)(2)224S a b ab a b =--=--+，将1S -2S 的结果化为5(1)a b ++即可得到结论；（2）根据2120S S -=得到771ab a b --=，再根据将原长方形的长和宽分别减少7厘米后得到的新长方形的面积为()()777749a b ab a b --=--+，代入求值即可.【详解】解：（1）1(3)(3)339S a b ab a b =++=+++，2(2)(2)224S a b ab a b =--=--+，所以123392245555(1)S S ab a b ab a b a b a b -=+++-++-=++=++，所以1S 与2S 的差一定是5的倍数；（2）因为2120S S -=，所以2(224)(339)0ab a b ab a b --+-+++=，所以7710ab a b ---=，所以771ab a b --=.因为将原长方形的长和宽分别减少7厘米后得到的新长方形的面积为()()77774914950a b ab a b --=--+=+=（平方厘米）.【名师点拨】此题考查了多项式乘法，提公因式法分解因式，列代数式，整式的加减法计算法则，已知式子的值求整式的值，正确理解长方形的长与宽的变化，根据变化的量列整式计算是解题的关键.3．（2020·咸阳市七年级月考）阅读材料：求2342019122222++++++的值．解：设234201820191222222s =+++++++，将等式两边同时乘2，得2S=2345201920202222222+++++++将下式减去上式，得2S -S=202021-，即S=202021-请你仿照此法计算下面各题（1）23410122222++++++（2）234133333n ++++++（其中n 为正整数）【答案】（1）1121-；（2）()11312n +-．【提示】（1）利用例题的方法将原式进行变形进而可以得出答案；（2）仿照例题的思路进行变形即可．【详解】解：（1）设23410122222S =++++++，将等式两边同时乘2，得23410112222222S =++++++将下式减去上式，得11221S S -=-，即1121S =-∴结果为1121-（2）设234133333n S =++++++，将等式两边同时乘3，得23413333333n n S +=++++++将下式减去上式，得1331n S S +-=-，即1213n S +=-， ∴()11132n S +-=， ∴结果为()11312n +- 【名师点拨】本题主要考查了有理数的混合运算，提取公因式法分解因式，正确将式子进行变形是解题的关键．4．（2020·浙江金华市·七年级期末）已知a ﹣b ＝7，ab ＝﹣12．（1）求a 2b ﹣ab 2的值；（2）求a 2+b 2的值；（3）求a +b 的值；【答案】(1)-84 ;(2) 25; (3)1或-1【提示】（1）直接提取公因式ab ，进而分解因式得出答案；（2）直接利用完全平方公式进而求出答案；（3）直接利用（2）中所求，结合完全平方公式求出答案．【详解】(1)∴a−b=7，ab=−12，∴a 2b ﹣ab 2=ab(a−b)=−12×7=−84；(2)∴a−b=7，ab=−12，∴()2a b -=49，∴a 2+b 2−2ab=49，∴a 2+b 2=25；(3)∴a 2+b 2=25，∴()2a b +=25+2ab=25−24=1，∴a+b=±1.【名师点拨】此题考查因式分解-提公因式法、完全平方公式，解题关键在于掌握因式分解的综合运用.5．（2021·湖南株洲市·七年级期末）阅读材料：“整体思想”是中学教学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛，如我们把()a b +看成一个整体，4()2()((421)()3())a b a b a b a b a b =+-+++-++=+．尝试应用：（1）把2()a b -看成一个整体，合并2223()5()7()---+-a b a b a b 的结果是_________．（2）已知221x y -=，求2362021--x y 的值．拓广探索：（3）已知22,25,9-=-=--=a b b c c d ，求()(2)(2)a c b d b c -+---的值．【答案】（1）25()a b -；（2）-2018；（3）6【提示】（1）把2()a b -看做一个整体，合并即可得到结果；（2）原式前两项提取3变形后，将已知等式代入计算即可求出值；（3）原式去括号整理后，将已知等式代入计算即可求出值．【详解】解：（1）25()a b -．（2）∴221x y -=，∴2362021--x y()2322021x y =--32021=-2018=-（3）∴22,25,9-=-=--=a b b c c d ，∴()(2)(2)a c b d b c -+---=a -c+2b -d -2b+c=a -d=a -2b+2b -c+c -d=（a -2b ）+（2b -c ）+（c -d ）=2-5+9=6．【名师点拨】此题考查了代数式求值，熟练掌握运算法则是解本题的关键．6．（2019·浙江杭州市·七年级期末）（1）填空：①3234353-⨯+⨯= ．②43234353-⨯+⨯= ．③54334353-⨯+⨯= ．（2）猜想下列各题的结果并验证下列第②个等式：①20212020201934353-⨯+⨯= ．②2134353n n n ++-⨯+⨯= ．【答案】（1）①6；②18；③54；（2）①201923⨯；②23n ⨯【提示】（1）①对每一项提取公因式3，然后进行计算即可得出答案；②对每一项提取公因式23 ，然后进行计算即可得出答案；③对每一项提取公因式33，然后进行计算即可得出答案；（2）①对每一项提取公因式20193，然后进行计算即可得出答案；②对每一项提取公因式3n ，然后进行计算即可得出答案；【详解】（1）①322343533(3435)326-⨯+⨯=⨯-⨯+=⨯=②432222343533(3435)3218-⨯+⨯=⨯-⨯+=⨯=③543323343533(3435)3254-⨯+⨯=⨯-⨯+=⨯=（2）猜想下列各题的结果并验证下列第②个等式：①20212020201934353-⨯+⨯=2019220193(3435)23⨯-⨯+=⨯．②2134353n n n ++-⨯+⨯=23(3435)23n n ⨯-⨯+=⨯．【名师点拨】本题主要考查提取公因式和规律探索，掌握提取公因式法是解题的关键．7．（2018·上海市七年级期末）因式分解：2222bc a abcd bc ab ac c d++---【答案】ab c ac cd b【提示】先分组分解后提取公因式即可.【详解】2222bc a abcd bc ab ac c d ++---22abc ad b c ab c a d ad abc c b c ab c ad ab c b c ab ab c ac cd b【名师点拨】本题考查的是分解因式，能正确的进行分组是关键.8．（2019·张家港市七年级期末）甲同学分解因式 x 2＋ax ＋m ，其结果为(x ＋2）(x ＋4)，乙同学分解因式x 2＋nx ＋b ，其结果为(x ＋1）(x ＋9)，在此情形下，请你来分解因式 x 2＋ax ＋b ．【答案】(x+3)2【提示】利用整式的乘法求出a,b 的值，再进行因式分解即可.【详解】∴(x ＋2）(x ＋4)= x 2＋6x ＋8，∴a=6,∴(x ＋1）(x ＋9)= x 2＋10x ＋9∴b=9∴x 2＋ax ＋b= x 2＋6x ＋9=(x+3)2.【名师点拨】此题主要考查因式分解，解题的关键是熟知整式的乘法法则.9．（2019·张家港市七年级期末）分解因式(1)－3m 3＋12m(2)2x 2y －8xy ＋8y(3)a 4＋3a 2－4【答案】(1) -3m （m+2）（m -2），(2)2y(x -2)2，(3)(a 2+4) (a+1) (a -1)【提示】（1）提取-3m 后，再根据平方差公式因式分解；（2）先提取2y ，再根据完全平方公式因式分解；（3）先利用十字相乘法因式分解，再用公式法因式分解.【详解】(1)－3m 3＋12m=-3m （m 2-4）=-3m （m+2）（m -2）(2)2x 2y －8xy ＋8y=2y(x 2-4x+4)=2y(x -2)2(3)a 4＋3a 2－4=(a 2-1) (a 2+4)= (a 2+4) (a+1) (a -1)【名师点拨】此题主要考查因式分解，解题的关键是熟知因式分解的方法.10．（2019·安徽安庆市·七年级期末）（1）因式分解：2(2)(2)a b b -+-（2）已知x ≠y ，且210x x -=，210y y -=，则x +y 的值.【答案】（1）(1)(1)(2)a a b +--或(2)(1)(1)b a a -+-;（2）1x y +=【提示】利用因式分解和平方差公式。