proe函数
- 格式:pdf
- 大小:135.99 KB
- 文档页数:10

proe 表格提取函数
在Pro/Engineer (ProE) 中,表格提取函数通常用于从数据库或模型中提取数据,并将其存储在表格中。
这些函数可以帮助您在ProE 的环境中进行数据处理和分析。
以下是ProE 中一些常用的表格提取函数:
1.get_feature_table:该函数用于从指定的零件或组件中提取特征表格。
您可
以通过指定特征类型和特征名称来提取特定特征的表格。
2.get_model_table:该函数用于从整个模型中提取表格。
您可以选择要提取
的表格类型,例如参数、关系、设计表等。
3.get_table:这是一个更通用的函数,用于从数据库或模型中提取任何类型的
表格。
您需要指定要提取的表格的名称和路径。
4.create_table:这个函数用于在ProE 中创建新的表格。
您可以使用它来创
建包含自定义数据或信息的表格,并在模型中使用。
这些函数的使用方法可能会因您的具体需求而有所不同,因此建议查阅ProE 的官方文档或相关教程以获取更详细的信息和示例代码。

Creo(PROE)中关系式的理解一)关系式中可以用下列数学函数式表达:1)、正弦 sin( )2)、余弦 cos( )3)、正切 tan( )4)、反正弦 asin( )5)、反余弦 acos( )6)、反正切 atan( )7)、双曲线正弦 sinh( )8)、双曲线余弦 cosh( )9)、双曲线正切 tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根 sqrt( )11)、以10为底的对数 log( )12)、自然对数 ln( )13)、e的幂 exp( )14)、绝对值 abs( )15)、不小于其值的最小整数(上限值) ceil( )16)、不超过其值的最大整数(下限值) floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或 number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为 10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同 ]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415举例一:以上函数式通常用的四种表达式如下图:以上两种曲线是在proe中的曲线—从方程—指定坐标系(选系统中固有的坐标系)—选笛卡儿坐标,就会出现公式界面,再输入如上公式。

致力于数控技术的网络分享 Sunlight'blogCovering research, news, and knowledge in CNC technology and e-Learning.« FANUC数控系统的使用心得监控功能-Monitoring functions »PROE函数公式Monday, November 26, 2007 7:53:44 AM 发布:sunlight名称:正弦曲线建立环境:Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0名称:螺旋线(Helical curve)建立环境:PRO/E;圆柱坐标(cylindrical)r=ttheta=10+t*(20*360)z=t*3蝴蝶曲线球坐标 PRO/E方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta)y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)*********************************圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)渐开线的方程r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0对数曲线z=0x = 10*ty = log(10*t+0.0001)球面螺旋线(采用球坐标系)rho=4theta=t*180phi=t*360*20名称:双弧外摆线卡迪尔坐标方程: l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360)名称:星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3名稱:心脏线建立環境:pro/e,圓柱坐標a=10r=a*(1+cos(theta))theta=t*360名稱:葉形線建立環境:笛卡儿坐標a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t一抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =0名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t方程: 阿基米德螺旋线x = (a +f sin (t))cos(t)/ay = (a -2f +f sin (t))sin(t)/bpro/e关系式、函数的相关说明资料?关系中使用的函数数学函数下列运算符可用于关系(包括等式和条件语句)中。


Creo(PROE)中关系式的理解一)关系式中可以用下列数学函数式表达:1)、正弦sin( )2)、余弦cos( )3)、正切tan( )4)、反正弦asin( )5)、反余弦acos( )6)、反正切atan( )7)、双曲线正弦sinh( )8)、双曲线余弦cosh( )9)、双曲线正切tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根sqrt( )11)、以10为底的对数log( )12)、自然对数ln( )13)、e的幂exp( )14)、绝对值abs( )15)、不小于其值的最小整数(上限值)ceil( )16)、不超过其值的最大整数(下限值)floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415举例一:以上函数式通常用的四种表达式如下图:以上两种曲线是在proe中的曲线—从方程—指定坐标系(选系统中固有的坐标系)—选笛卡儿坐标,就会出现公式界面,再输入如上公式。
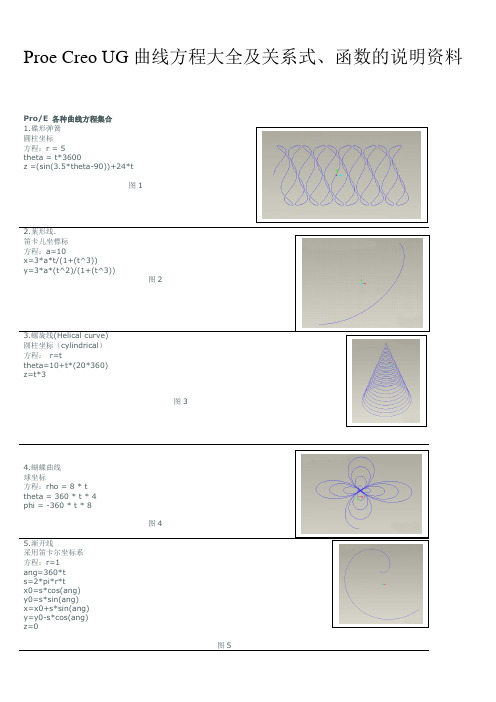
Proe Creo UG曲线方程大全及关系式、函数的说明资料Pro/E 各种曲线方程集合1.碟形弹簧圓柱坐标方程:r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t图12.葉形线.笛卡儿坐標标方程:a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))图23.螺旋线(Helical curve)圆柱坐标(cylindrical)方程:r=ttheta=10+t*(20*360)z=t*3图34.蝴蝶曲线球坐标方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8图45.渐开线采用笛卡尔坐标系方程:r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0图56.螺旋线.笛卡儿坐标方程:x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t图6 7.对数曲线笛卡尔坐标系方程:z=0x = 10*ty = log(10*t+0.0001)图78.球面螺旋线采用球坐标系方程:rho=4theta=t*180phi=t*360*20图8 9.双弧外摆线卡迪尔坐标方程:l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360)Y=3*b*sin(t*360)+l*sin(3*t*360)图910.星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3图10 11.心脏线圓柱坐标方程:a=10r=a*(1+cos(theta))theta=t*360Pro/E 各种曲线方程集合(二)22.外摆线迪卡尔坐标方程:theta=t*720*5b=8a=5x=(a+b)*cos(theta)-b*cos((a/b+1)*theta)y=(a+b)*sin(theta)-b*sin((a/b+1)*theta)z=0图22 23. Lissajous 曲线theta=t*360a=1b=1c=100n=3x=a*sin(n*theta+c)y=b*sin(theta)图23 24.长短幅圆内旋轮线卡笛尔坐标方程:a=5b=7c=2.2theta=360*t*10x=(a-b)*cos(theta)+c*cos((a/b-1)*theta)y=(a-b)*sin(theta)-c*sin((a/b-1)*theta)图24 25.长短幅圆外旋轮线卡笛尔坐标方程:theta=t*360*10a=5b=3c=5x=(a+b)*cos(theta)-c*cos((a/b+1)*theta)y=(a+b)*sin(theta)-c*sin((a/b+1)*theta)图25 26. 三尖瓣线a=10x = a*(2*cos(t*360)+cos(2*t*360))y = a*(2*sin(t*360)-sin(2*t*360))图26 27.概率曲线!方程:笛卡儿坐标x = t*10-5y = exp(0-x^2)图27 28.箕舌线笛卡儿坐标系a = 1x = -5 + t*10y = 8*a^3/(x^2+4*a^2)图28 29.阿基米德螺线柱坐标a=100theta = t*400r = a*theta图29 30.对数螺线柱坐标theta = t*360*2.2a = 0.005r = exp(a*theta)图30 31.蔓叶线笛卡儿坐标系a=10y=t*100-50solvex^3 = y^2*(2*a-x)for x图31 32.tan曲线笛卡儿坐标系x = t*8.5 -4.25y = tan(x*20)图32 33.双曲余弦x = 6*t-3y = (exp(x)+exp(0-x))/2图33 34.双曲正弦x = 6*t-3y = (exp(x)-exp(0-x))/2图34 35.双曲正切x = 6*t-3y = (exp(x)-exp(0-x))/(exp(x)+exp(0-x))图35 36.一峰三驻点曲线x = 3*t-1.5y=(x^2-1)^3+1图36 37.八字曲线x = 2 * cos ( t *(2*180))y = 2 * sin ( t *(5*360))z = 0图37 38.螺旋曲线r=t*(10*180)+1theta=10+t*(20*180)z=t图38 39.圆x = cos ( t *(5*180))y = sin ( t *(5*180))z = 0图39 40.封闭球形环绕曲线rho=2theta=360*tphi=t*360*10图40 41.柱坐标螺旋曲线x = 100*t * cos ( t *(5*180))y = 100*t * sin ( t *(5*180))z = 0Pro/E 各种曲线方程集合(三)42.蛇形曲线x = 2 * cos ( (t+1) *(2*180))y = 2 * sin ( t *(5*360))z = t*(t+1)图42 43.8字形曲线柱坐标theta = t*360r=10+(8*sin(theta))^2图43 44.椭圆曲线笛卡尔坐标系a = 10b = 20theta = t*360x = a*cos(theta)y = b*sin(theta)图44 45.梅花曲线柱坐标theta = t*360r=10+(3*sin(theta*2.5))^2图45 46.另一个花曲线theta = t*360r=10-(3*sin(theta*3))^2z=4*sin(theta*3)^2图46 47.改一下就成为空间感更强的花曲线了;)theta = t*360r=10-(3*sin(theta*3))^2z=(r*sin(theta*3))^2图4748.螺旋上升的椭圆线a = 10b = 20theta = t*360*3x = a*cos(theta)y = b*sin(theta)z=t*12图48 49.甚至这种螺旋花曲线theta = t*360*4r=10+(3*sin(theta*2.5))^2z = t*16图49 50 鼓形线笛卡尔方程r=5+3.3*sin(t*180)+ttheta=t*360*10z=t*10图50 51 长命锁曲线笛卡尔方程:a=1*t*359.5b=q2*t*360c=q3*t*360rr1=w1rr2=w2rr3=w3x=rr1*cos(a)+rr2*cos(b)+rr3*cos(c)y=rr1*sin(a)+rr2*sin(b)+rr3*sin(c)图51 52 簪形线球坐标方程:rho=200*ttheta=900*tphi=t*90*10图52 53.螺旋上升曲线r=t^10theta=t^3*360*6*3+t^3*360*3*3z=t^3*(t+1)图53 54.蘑菇曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*20*20图54 55. 8字曲线a=1b=1x=3*b*cos(t*360)+a*cos(3*t*360)Y=b*sin(t*360)+a*sin(3*t*360)图55 56.梅花曲线theta=t*360r=100+50*cos(5*theta)z=2*cos(5*theta)图56 57.桃形曲线rho=t^3+t*(t+1)theta=t*360phi=t^2*360*10*10图57 58.名稱:碟形弹簧建立環境:pro/e圓柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24图58 59.环形二次曲线笛卡儿方程:x=50*cos(t*360)y=50*sin(t*360)z=10*cos(t*360*8)图59 60 蝶线球坐标:rho=4*sin(t*360)+6*cos(t*360^2)theta=t*360phi=log(1+t*360)*t*360图60 61.正弦周弹簧笛卡尔:ang1=t*360ang2=t*360*20x=ang1*2*pi/360y=sin(ang1)*5+cos(ang2)z=sin(ang2)Pro/E 各种曲线方程集合(四)62.环形螺旋线x=(50+10*sin(t*360*15))*cos(t*360)y=(50+10*sin(t*360*15))*sin(t*360)z=10*cos(t*360*5)图62 63.内接弹簧x=2*cos(t*360*10)+cos(t*180*10)y=2*sin(t*360*10)+sin(t*180*10)z=t*6图63 64.多变内接式弹簧x=3*cos(t*360*8)-1.5*cos(t*480*8)y=3*sin(t*360*8)-1.5*sin(t*480*8)z=t*8图64 65.柱面正弦波线柱坐标:方程r=30theta=t*360z=5*sin(5*theta-90)图65 66. ufo (漩涡线)球坐标:rho=t*20^2theta=t*log(30)*60phi=t*7200图66 67. 手把曲线thta0=t*360thta1=t*360*6r0=400r1=40r=r0+r1*cos(thta1)x=r*cos(thta0)y=r1*sin(thta1)z=0图67 68.篮子圆柱坐标r=5+0.3*sin(t*180)+ttheta=t*360*30z=t*5图68 69. 圆柱齿轮齿廓的渐开线方程:afa=60*tx=10*cos(afa)+pi*10*afa/180*sin(afa)x=10*sin(afa)-pi*10*afa/180*cos(afa)z=0注:afa为压力角,取值范围是0到60,10为基圆半径。
指令位置:单击创建基准曲线的图标,在弹出的边菜单中选择From Equation…(从方程式…)(图eqcurve.1.01)。
创建方程式曲线必需一个坐标系作为参考,所以下一步我们要给它选择一个坐标系,在Pro/Engineer中,有三种使用坐标系的方式来创建方程式曲线,它们是Cartesian(笛卡尔坐标)、Cylindrical(圆柱坐标)和Spherical(球坐标也就是极坐标)(图eqcurv.1.02)三种坐标系对于不同的形式的方程式曲线各有独特的优势,根据曲线的表现选用适当的坐标系方法可以大大简化方程式并且也更直观易懂,在本文的后面我们将详细讨论这三种坐标系的应用方法。
选择了坐标系后就可以进入方程式的编辑环境了(图eqcurve.1.04)。
可以看到在编辑器的前面是一些方程式的编写指导。
在Pro/Engineer的关系式(方程实际是关系式)编写中/*是代表注释。
在注释下面你就可以输入自己的曲线方程式了,一行对应一条关系内幕:系统默认的设置一般方程式的编辑器是Pro/Engineer自带的Pro/Table编辑器,如果想改用系统默认的记事本来编辑,你可以设定config选项:relation_file_editor的值为editor。
2. 方程式的含义和编写在Pro/Engineer中,方程式的编写规则和关系式的是一样的,并且可以使用关系式的所有函数,实际上方程式本身就是关系式。
在所有的坐标系形式中,都有一个共用的可变参数t,这个实际就是用来确定方程式取值域的,同时也是用它来驱动方程式的生成的。
它的变动范围是0~1,如果我们要需要别的范围,可以通过乘以系数和添加前导值来实现,比如我们要求变动范围是0~10,那么我们可以用10*t来表达;而如果我们需要的变动范围是5~10,那么可以用5+5*t来表达。
如果你对数学的参数方程式足够熟悉的话,那么理解曲线的方程式是毫无障碍的。
如果你不熟悉,可以这样来看待方程式:把一个方程式看成是某一个点的坐标值,通过t的变化实际就是产生一系列的点。
pro/e關係式、函數的相關說明資料關係中使用的函數數學函數下列運算符可用於關係(包括等式和條件語句)中。
關係中也可以包括下列數學函數:cos () 余弦tan () 正切sin () 正弦sqrt () 平方根asin () 反正弦acos () 反余弦atan () 反正切sinh () 雙曲線正弦cosh () 雙曲線余弦tanh () 雙曲線正切注釋:所有三角函數都使用單位度。
log() 以10為底的對數ln() 自然對數exp() e的冪abs() 絕對值ceil() 不小於其值的最小整數floor() 不超過其值的最大整數可以給函數ceil和floor加一個可選的自變量,用它指定要圓整的小數位數。
帶有圓整參數的這些函數的語法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中number_of_dec_places是可選值:·可以被表示為一個數或一個使用者自定義參數。
如果該參數值是一個實數,則被截尾成為一個整數。
·它的最大值是8。
如果超過8,則不會舍入要舍入的數(第一個自變量),並使用其初值。
·如果不指定它,則功能同前期版本一樣。
使用不指定小數部分位數的ceil和floor函數,其舉例如下:ceil (10.2) 值為11 floor (10.2) 值為11使用指定小數部分位數的ceil和floor函數,其舉例如下:ceil (10.255, 2) 等於10.26ceil (10.255, 0) 等於11 [ 與ceil (10.255)相同]floor (10.255, 1) 等於10.2floor (10.255, 2) 等於10.26曲線表計算曲線表計算使使用者能用曲線表特征,通過關係來驅動尺寸。
Creo(PROE)中关系式的理解一)关系式中可以用下列数学函数式表达:1)、正弦sin( )2)、余弦cos( )3)、正切tan( )4)、反正弦asin( )5)、反余弦acos( )6)、反正切atan( )7)、双曲线正弦sinh( )8)、双曲线余弦cosh( )9)、双曲线正切tanh( )以上九种三角函数式所使用的单位均为“度”。
10)、平方根sqrt( )11)、以10为底的对数log( )12)、自然对数ln( )13)、e的幂exp( )14)、绝对值abs( )15)、不小于其值的最小整数(上限值)ceil( )16)、不超过其值的最大整数(下限值)floor( )可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数位数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places)floor (parameter_name 或number, number_of_dec_places)其中的parameter_name或number意为参数名称或者一个带小数位的精确数值后面跟随着的number_of_dec_places意为十进位的小数位数,是可选值:A)可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
B)它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
C)如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为10使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同]ceil(10.25531415926,7)等于10.2553142ceil(10.25531415926,8)等于10.25531416floor (10.255, 2) 等于10.25floor (10.255, 0) 等于10.Floor(10.2531415926,7)等于10.2553141Floor(10.2531415926,8)等于10.25531415举例一:以上函数式通常用的四种表达式如下图:以上两种曲线是在proe中的曲线—从方程—指定坐标系(选系统中固有的坐标系)—选笛卡儿坐标,就会出现公式界面,再输入如上公式。
体或曲面在做变截面扫描(Var Sec Swp )时,外型变化除了受到X-vector Trajectory的3D曲线控制之外也可用下列两种方式来控制:1. 使用relation结合trajpar参数来控制截面参数的变化。
Trajpar是Pro/E的内参(轨迹参数),它是从0到1的一个变量(呈线性变化)代表扫出特征的长度百分比。
在扫出的开始时,trajpar的值是0;结束时为1。
使用举例:在草绘的Relation中加入关系式sd#=trajpar+n,此时尺寸sd#受到trajpar+n控制。
在sweep开始时值为n,结束时值为n+1。
截面的高度尺寸呈线性变化。
若截面的高度尺寸受sd#=sin(trajpar*360)+n控制,则呈现sin曲线变化。
2. 使用relation结合基准图形(datum graph)及trajpar参数来控制截面参数的变化。
我们可利用datum graph来控制截面的变化,也可使用datum graph来控制三维实体或曲面的造型变化。
先说明datum graph曲线的使用情况,创建位置为feature>create>datum>graph再给出graph曲线的名称。
绘制时给定坐标系,曲线的x轴方向会随着sweep变化,起点代表sweep开始,终点代表sweep结束。
(说明:在控制方程中根据需要选取曲线的一段或全部)曲线在某点的y值即是变量值。
使用datum graph控制截面的格式如下:SD#=evalgraph(“graph_name” , x_value)式中SD#代表欲变化的参数(SD表示草绘尺寸),graph_name为datum graph的名称,x_value代表扫描的“行程”,evalgraph(Evaluate Graph)是Pro/E系统默认的基准控制曲线计算函数,其功能为当变量x_value变化时计算相应的y值,然后指定给SD#。
X_value的值可以是实数或表达式,如果是表达式可含有trajpar参数(根据用户需求而定)。
注:datum graph必须在sweep特征之前创建,或使用reorder 将之置于sweep特征之前。
名称:正弦曲线建立环境:Pro/E软件、笛卡尔坐标系x=50*ty=10*sin(t*360)z=0名称:螺旋线(Helical curve)建立环境:PRO/E;圆柱坐标(cylindrical)r=ttheta=10+t*(20*360)z=t*3蝴蝶曲线球坐标 PRO/E方程:rho = 8 * ttheta = 360 * t * 4phi = -360 * t * 8Rhodonea 曲线采用笛卡尔坐标系theta=t*360*4x=25+(10-6)*cos(theta)+10*cos((10/6-1)*theta) y=25+(10-6)*sin(theta)-6*sin((10/6-1)*theta)*********************************圆内螺旋线采用柱座标系theta=t*360r=10+10*sin(6*theta)z=2*sin(6*theta)渐开线的方程r=1ang=360*ts=2*pi*r*tx0=s*cos(ang)y0=s*sin(ang)x=x0+s*sin(ang)y=y0-s*cos(ang)z=0对数曲线z=0x = 10*ty = log(10*t+0.0001)球面螺旋线(采用球坐标系)rho=4theta=t*180phi=t*360*20名称:双弧外摆线卡迪尔坐标方程: l=2.5b=2.5x=3*b*cos(t*360)+l*cos(3*t*360) Y=3*b*sin(t*360)+l*sin(3*t*360) 名称:星行线卡迪尔坐标方程:a=5x=a*(cos(t*360))^3y=a*(sin(t*360))^3名称:心脏线建立环境:pro/e,圆柱坐标a=10r=a*(1+cos(theta))theta=t*360名称:叶形线建立环境:笛卡儿坐标a=10x=3*a*t/(1+(t^3))y=3*a*(t^2)/(1+(t^3))笛卡儿坐标下的螺旋线x = 4 * cos ( t *(5*360))y = 4 * sin ( t *(5*360))z = 10*t一抛物线笛卡儿坐标x =(4 * t)y =(3 * t) + (5 * t ^2)z =0名称:碟形弹簧建立环境:pro/e圆柱坐r = 5theta = t*3600z =(sin(3.5*theta-90))+24*t方程: 阿基米德螺旋线x = (a +f sin (t))cos(t)/ay = (a -2f +f sin (t))sin(t)/bpro/e关系式、函数的相关说明资料?关系中使用的函数数学函数下列运算符可用于关系(包括等式和条件语句)中。
关系中也可以包括下列数学函数:cos () 余弦tan () 正切sin () 正弦sqrt () 平方根asin () 反正弦acos () 反余弦atan () 反正切sinh () 双曲线正弦cosh () 双曲线余弦tanh () 双曲线正切注释:所有三角函数都使用单位度。
log() 以10为底的对数ln() 自然对数exp() e的幂abs() 绝对值ceil() 不小于其值的最小整数floor() 不超过其值的最大整数可以给函数ceil和floor加一个可选的自变量,用它指定要圆整的小数字数。
带有圆整参数的这些函数的语法是:ceil(parameter_name或number, number_of_dec_places) floor (parameter_name 或 number, number_of_dec_places) 其中number_of_dec_places是可选值:•可以被表示为一个数或一个使用者自定义参数。
如果该参数值是一个实数,则被截尾成为一个整数。
•它的最大值是8。
如果超过8,则不会舍入要舍入的数(第一个自变量),并使用其初值。
•如果不指定它,则功能同前期版本一样。
使用不指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.2) 值为11floor (10.2) 值为 11使用指定小数部分位数的ceil和floor函数,其举例如下:ceil (10.255, 2) 等于10.26ceil (10.255, 0) 等于11 [ 与ceil (10.255)相同 ]floor (10.255, 1) 等于10.2floor (10.255, 2) 等于10.26曲线表计算曲线表计算使使用者能用曲线表特征,通过关系来驱动尺寸。
尺寸可以是草绘器、零件或组件尺寸。
格式如下:evalgraph("graph_name", x),其中graph_name是曲线表的名称,x是沿曲线表x-轴的值,返回y 值。
对于混合特征,可以指定轨线参数trajpar作为该函数的第二个自变量。
注释:曲线表特征通常是用于计算x-轴上所定义范围内x值对应的y 值。
当超出范围时,y值是通过外推的方法来计算的。
对于小于初始值的x值,系统通过从初始点延长切线的方法计算外推值。
同样,对于大于终点值的x值,系统通过将切线从终点往外延伸计算外推值。
复合曲线轨道函数在关系中可以使用复合曲线的轨道参数trajpar_of_pnt。
下列函数返回一个0.0和1.0之间的值:trajpar_of_pnt("trajname", "pointname")其中trajname是复合曲线名,pointname是基准点名。
轨线是一个沿复合曲线的参数,在它上面垂直于曲线切线的平面通过基准点。
因此,基准点不必位于曲线上;在曲线上距基准点最近的点上计算该参数值。
如果复合曲线被用作多轨道扫瞄的骨架,则trajpar_of_pnt与trajpar 或1.0 - trajpar一致(取决于为混合特征选择的起点)。
关于关系关系(也被称为参数关系)是使用者自定义的符号尺寸和参数之间的等式。
关系捕获特征之间、参数之间或组件组件之间的设计关系,因此,允许使用者来控制对模型修改的影响作用。
关系是捕获设计知识和意图的一种方式。
和参数一样,它们用于驱动模型-改变关系也就改变了模型。
关系可用于控制模型修改的影响作用、定义零件和组件中的尺寸值、为设计条件担当约束(例如,指定与零件的边相关的孔的位置)。
它们用在设计过程中来描述模型或组件的不同部分之间的关系。
关系可以是简单值(例如,d1=4)或复杂的条件分支语句。
关系类型有两种类型的关系:•等式- 使等式左边的一个参数等于右边的表达式。
这种关系用于给尺寸和参数赋值。
例如:简单的赋值:d1 = 4.75复杂的赋值:d5 = d2*(SQRT(d7/3.0+d4))•比较- 比较左边的表达式和右边的表达式。
这种关系通常用于作为一个约束或用于逻辑分支的条件语句中。
例如:作为约束:(d1 + d2) > (d3 + 2.5)在条件语句中;IF (d1 + 2.5) >= d7增加关系可以把关系增加到:•特征的截面(在草绘模式中,如果最初通过选择“草绘器”>“关系”>“增加”来创建截面)。
•特征(在零件或组件模式下)。
•零件(在零件或组件模式下)。
•组件(在组件模式下)。
当第一次选择关系菜单时,预设为查看或改变当前模型(例如,零件模式下的一个零件)中的关系。
要获得对关系的访问,从“部件”或“组件”菜单中选择“关系”,然后从“模型关系”菜单中选择下列命令之一:•组件关系 - 使用组件中的关系。
如果组件包含一个或多个子组件,“组件关系”菜单出现并带有下列命令:—当前 - 缺省时是顶层组件。
—名称 - 键入组件名。
•骨架关系 - 使用组件中骨架模型的关系(只对组件适用)。
•零件关系 - 使用零件中的关系。
•特征关系- 使用特征特有的关系。
如果特征有一个截面,那么使用者就可选择:获得对截面(草绘器)中截面(草绘器)中关系的访问,或者获得对作为一个整体的特征中的关系的访问。
•数组关系 - 使用数组所特有的关系。
注释:—如果试图将截面之外的关系指派给已经由截面关系驱动的参数,则系统再生模型时给出错误信息。
试图将关系指派给已经由截面之外关系驱动的参数时也同样。
删除关系之一并重新生成。
—如果组件试图给已经由零件或子组件关系驱动的尺寸变量指派值时,出现两个错误信息。
删除关系之一并重新生成。
—修改模型的单位元可使关系无效,因为它们没有随该模型缩放。
有关修改单位的详细信息,请参阅“关于公制和非公制度量单位”帮助主题。