数据结构第七章图(2016)
- 格式:ppt
- 大小:2.40 MB
- 文档页数:68


数据结构习题第七章图一、选择题1、一个有n个顶点的无向图最多有( C )条边。
A、nB、n(n-1)C、n(n-1)/2D、2n2、具有4个顶点的无向完全图有( A )条边。
A、6B、12C、16D、203、具有6个顶点的无向图至少有( A )条边才能保证是一个连通图。
A、5B、6C、7D、84、设连通图G的顶点数为n,则G的生成树的边数为( A )。
A、n-1B、nC、2nD、2n-15、已知一个图,若从顶点a出发进行深度和广度优先搜索遍历,则可能得到的顶点序列分别为( D )和(B )(1)A、abecdf B、acfebd C、acebfd D、acfdeb(2)A、abcedf B、abcefd C、abedfc D、acfdeb6、采用邻接表存储的图的深度和广度优先搜索遍历算法类似于二叉树的( B )和( D )。
A、中序遍历B、先序遍历C、后序遍历D、层次遍历7、已知一有向图的邻接表存储结构如下图所示,分别根据图的深度和广度优先搜索遍历算法,从顶点v1出发,得到的顶点序列分别为( C )和( B )。
A、v1,v2,v3,v4,v5B、v1,v3,v2,v4,v5C、v1,v2,v3,v5,v4D、v1,v4,v3,v5,v28、已知一个图如下,在该图的最小生成树中各边上权值之和为( C ),在该图的最小生成树中,从v1到v6的路径为(G )。
A、31B、38C、36D、43E、v1,v3,v6F、v1,v4,v6G、v1,v5,v4,v6H、v1,v4,v3,v69、正确的AOE网必须是(C )A、完全图B、哈密尔顿图C、无环图D、强连通图10、已知一个图如下,则由该图得到的一种拓扑序列为( A )。
A、v1,v4,v6,v2,v5,v3B、v1,v2,v3,v4,v5,v6C、v1,v4,v2,v3,v6,v5D、v1,v2,v4,v6,v3,v511、下面结论中正确的是( B )A、在无向图中,边的条数是顶点度数之和。

第7章 《图》习题参考答案一、单选题(每题1分,共16分)( C )1. 在一个图中,所有顶点的度数之和等于图的边数的倍。
A .1/2 B. 1 C. 2 D. 4 (B )2. 在一个有向图中,所有顶点的入度之和等于所有顶点的出度之和的倍。
A .1/2 B. 1 C. 2 D. 4 ( B )3. 有8个结点的无向图最多有条边。
A .14 B. 28 C. 56 D. 112 ( C )4. 有8个结点的无向连通图最少有条边。
A .5 B. 6 C. 7 D. 8 ( C )5. 有8个结点的有向完全图有条边。
A .14 B. 28 C. 56 D. 112 (B )6. 用邻接表表示图进行广度优先遍历时,通常是采用来实现算法的。
A .栈 B. 队列 C. 树 D. 图 ( A )7. 用邻接表表示图进行深度优先遍历时,通常是采用来实现算法的。
A .栈 B. 队列 C. 树 D. 图( C )8. 已知图的邻接矩阵,根据算法思想,则从顶点0出发按深度优先遍历的结点序列是( D )9. 已知图的邻接矩阵同上题8,根据算法,则从顶点0出发,按深度优先遍历的结点序列是A . 0 2 4 3 1 5 6 B. 0 1 3 5 6 4 2 C. 0 4 2 3 1 6 5 D. 0 1 23465 ( D )10. 已知图的邻接表如下所示,根据算法,则从顶点0出发按深度优先遍历的结点序列是( A )11. 已知图的邻接表如下所示,根据算法,则从顶点0出发按广度优先遍历的结点序列是A .0 2 4 3 1 5 6B. 0 1 3 6 5 4 2C. 0 1 3 4 2 5 6D. 0 3 6 1 5 4 2⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡0100011101100001011010110011001000110010011011110A .0 1 3 2 B. 0 2 3 1 C. 0 3 2 1 D. 0 1 2 3A.0 3 2 1 B. 0 1 2 3C. 0 1 3 2D. 0 3 1 2(A)12. 深度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(D)13. 广度优先遍历类似于二叉树的A.先序遍历 B. 中序遍历 C. 后序遍历 D. 层次遍历(A)14. 任何一个无向连通图的最小生成树A.只有一棵 B. 一棵或多棵 C. 一定有多棵 D. 可能不存在(注,生成树不唯一,但最小生成树唯一,即边权之和或树权最小的情况唯一)二、填空题(每空1分,共20分)1. 图有邻接矩阵、邻接表等存储结构,遍历图有深度优先遍历、广度优先遍历等方法。
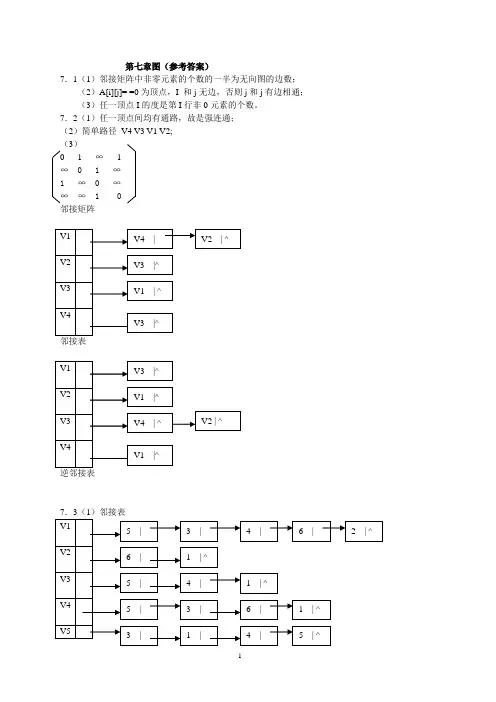
第七章图(参考答案)7.1(1)邻接矩阵中非零元素的个数的一半为无向图的边数;(2)A[i][j]= =0为顶点,I 和j无边,否则j和j有边相通;(3)任一顶点I的度是第I行非0元素的个数。
7.2(1)任一顶点间均有通路,故是强连通;(2)简单路径V4 V3 V1 V2;(3)0 1 ∞ 1∞ 0 1 ∞1 ∞ 0 ∞∞∞ 1 0邻接矩阵邻接表(2)从顶点4开始的DFS序列:V5,V3,V4,V6,V2,V1(3)从顶点4开始的BFS序列:V4,V5,V3,V6,V1,V27.4(1)①adjlisttp g; vtxptr i,j; //全程变量② void dfs(vtxptr x)//从顶点x开始深度优先遍历图g。
在遍历中若发现顶点j,则说明顶点i和j间有路径。
{ visited[x]=1; //置访问标记if (y= =j){ found=1;exit(0);}//有通路,退出else { p=g[x].firstarc;//找x的第一邻接点while (p!=null){ k=p->adjvex;if (!visited[k])dfs(k);p=p->nextarc;//下一邻接点}}③ void connect_DFS (adjlisttp g)//基于图的深度优先遍历策略,本算法判断一邻接表为存储结构的图g种,是否存在顶点i //到顶点j的路径。
设 1<=i ,j<=n,i<>j.{ visited[1..n]=0;found=0;scanf (&i,&j);dfs (i);if (found) printf (” 顶点”,i,”和顶点”,j,”有路径”);else printf (” 顶点”,i,”和顶点”,j,”无路径”);}// void connect_DFS(2)宽度优先遍历全程变量,调用函数与(1)相同,下面仅写宽度优先遍历部分。





第七章 图一、写出如下有向图的邻接矩阵及图中各顶点的入度、出度和度。
【分析】有向图中顶点的度=顶点的入度+顶点的出度。
【参考答案】邻接矩阵:⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡010*******010101000000110 顶点a;入度1,出度2,度3;顶点b;入度2,出度1,度3;顶点c;入度1,出度2,度3;顶点d;入度2,出度1,度3;顶点e;入度1,出度1,度2。
二、设如下有向网以邻接表形式存储,画出其存储结构示意图。
【分析】表结点中应含三个域:邻接到顶点的下标域、权值域和指向下一表结点的指针域。
【参考答案】三、写出对如下无向图从顶点a出发进行广度优先遍历可能得到的所有遍历序列。
【分析】广度优先遍历中应保证先被访问的顶点的邻接点先于后被访问的顶点的邻接点处理。
图中各顶点间并无必然的先后顺序。
各顶点的邻接点间也并无必然的先后顺序。
【参考答案】abcdefgabdcegfacbdfegacdbfgeadbcgefadcbgfe四、设有无向网如下,写出其邻接矩阵,并在此基础上按普里姆算法求最小生成树。
【分析】【参考答案】邻接矩阵:⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞6456252363794567555553955434最小生成树:五、写出对如下有向无环图进行拓扑排序可能得到的所有拓扑序列。
【分析】每次输出一个入度为0的顶点。
【参考答案】abcdefgabcdfegabcfdeg六、设有AOE网如下,试求关键路径。
【分析】【参考答案】关键路径1:v1→v2→v5→v7关键路径2:v1→v3→v6→v7七、设有向网如下,用迪杰斯特拉算法求从顶点a出发到其余各顶点的最短路径。
【分析】【参考答案】ab:3af:5afe:7afec:8afecd:10八、编写算法,由依次输入的顶点数、弧数、各顶点信息和各条弧信息建立有向图的邻接表。