二维方腔环流计算

4.2顶盖驱动流4.2.1物理模型在一个正方形的二维空腔中充满等密度的空气，方腔每边长为0.1m，其顶板以0.1m/s 的速度向右移动，同时带动方腔内流体的流动，流场内的流体为层流。

计算区域示意图如图4-2-1所示。

图4-2-1 计算区域示意图4.2.2在Gambit中建立模型Step1：启动Gambit并选择求解器为Fluent5/6。

Step2：创建面操作：→→打开对话框如图4-2-2所示。

输入长度和宽度10，在Direction中选择XY Centered。

图4-2-2 创建面设置对话框Step3：划分面网格操作：→→打开对话框如图4-2-3所示，Shift+鼠标左键选择正方形面，Internal size=0.5，其它保留默认，点击Apply确认。

划分后的网格如图4-2-4所示。

图4-2-3 网格划分设置对话框图4-2-4 计算区域网格图Step4：设置边界类型操作：→●在Name栏输入边界名称wall-1，将Type栏选为Wall，在Entity栏选取Edges，并选中方腔顶部边线。

●在Name栏输入边界名称wall-2，将Type栏选为Wall，在Entity栏选取Edges，并选中方腔其它三条边线。

Step5：输出网格文件操作：Fil m→export→mesh打开对话框如图4-2-5所示，选中Export 2-D mesh 前面的复选框，输出网格文件。

图4-2-5 网格文件输出对话框4.2.3求解计算Step1：启动Fluent选择2d单精度求解器，点击Run，如图4-2-6所示。

图4-2-6 启动求解器图4-2-7 网格尺寸设置对话框Step2：导入并检查网格1．读入网格文件操作：Fil e→Read→Case...找到文件后，单击OK按键确认。

2．检查网格操作：Grid→Check网格读入后，一定要进行网格检查，注意最小体积不能为负值。

3．网格比例设置操作：Grid→Scale...在Gambit中，生成网格使用的单位是cm，在Grid Was Created In下拉菜单中，选取cm，如图4-2-7所示，然后单击Scale，关闭对话框。

水泥3D打印喷头内浆体流动的MRT-LBM分析吴伟伟;黄筱调;方成刚;李媛媛【摘要】水泥3D打印时,水泥浆体在喷头内的流动性对挤出成型有重要影响.以水泥、水、聚羧酸减水剂、改性棒土和纤维素醚作为原始打印材料,根据流变特性测试,采用Herschel-Bulkley模型作为水泥浆体的流变模型,并利用多松弛时间的格子Boltzmann方法(MRT-LBM)对浆体在喷头中的流动进行了分析,引入矩函数来描述松弛过程中的碰撞步,并利用泊肃叶流的理论解对MRT模型进行了验证.在进行实际仿真时,以雷诺数作为准则进行物理单位和格子单位之间的转换,获得相关的流线图和速度场分布图.结果表明:水泥浆体在螺槽截面的流动呈现环流形状,环流的中心在(0. 5W,0. 7h)位置处;根据速度场的分布,在螺槽横截面的左下角和右下角不存在流体流动,适当增大螺杆速度或螺槽宽度有助于水泥浆体在螺槽内的有效输送.【期刊名称】《南京工业大学学报（自然科学版）》【年(卷),期】2018(040)005【总页数】6页(P79-84)【关键词】水泥3D打印;Herschel-Bulkley流体;多松弛时间的LBM;数值模拟;流线;速度分布【作者】吴伟伟;黄筱调;方成刚;李媛媛【作者单位】南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800;南京工业大学机械与动力工程学院,江苏省工业装备数字制造及控制技术重点实验室,江苏南京 211800【正文语种】中文【中图分类】TH12对浆体在喷头内部的流动进行分析,可以很好揭示其流动规律,流线图可以描述浆体在腔体中的主要流动区域和环流的形成,速度场分布图可以描述各速度分量沿不同方向的分布情况,速度较大的区域更有利于浆体的输送,速度较小的区域往往受黏性系数和机械结构的影响,因此合理的机械结构有助于浆体在喷头内部的流动。

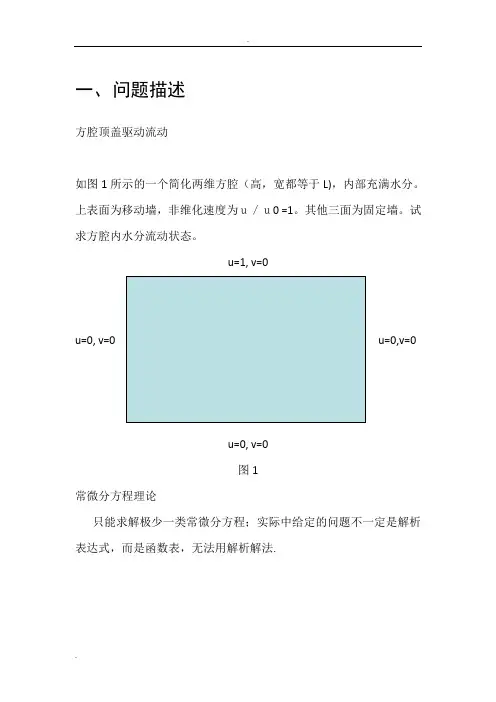
一、问题描述方腔顶盖驱动流动如图1所示的一个简化两维方腔（高，宽都等于L)，内部充满水分。

上表面为移动墙，非维化速度为ｕ／ｕ0 =1。

其他三面为固定墙。

试求方腔内水分流动状态。

u=1, v=0u=0, v=0 u=0,v=0u=0, v=0图1常微分方程理论只能求解极少一类常微分方程；实际中给定的问题不一定是解析表达式，而是函数表，无法用解析解法.二、离散格式数值解法:求解所有的常微分方程 计算解函数 y(x) 在一系列节点a = x 0< x 1<…<x n = b 处的近似值),...,1()(n i x y y i i =≈节点间距为步长，通常采用等距节点，即取 hi = h (常数)。

步进式：根据已知的或已求出的节点上的函数值计算当前节点上的函数值，一步一步向前推进。

因此只需建立由已知的或已求出的节点上的函数值求当前节点函数值的递推公式即可。

欧拉方法1(,) 0,1,...n n n n y y h f x y n +=+=几何意义在假设 y n = y (x n )，即第 n 步计算是精确的前提下，考虑公式或方法本身带来的误差: R n = y (x n +1) y n +1 , 称为局部截断误差.截断误差: 实际上，y (x n ) ? y n ， y n 也有误差，它对y n +1的误差也有影响，见下图。

但这里不考虑此误差的影响，仅考虑方法或公式本身带来的误差，因此称为方法误差或截断误差。

局部截断误差的分析：由于假设y n = y (x n ) ，即y n 准确，因此分析局部截断误差时将y (x n +1) 和 y n +1都用点x n 上的信息来表示，工具：Taylor 展开。

显式欧拉公式一阶向前差商近似一阶导数推导如下：223111232()[()()()()][ (,)] ()()h n n n n n n n n n h n R y x y y x hy x y x O h y hf x y y x O h +++'''=-=+++-+''=+1()()()n n n y x y x y x h+-'≈111()()() ()()(,)n n n n nn n n n n y x y x hy x y x y y x y y h f x y +++'≈+↑≈≈=+隐式欧拉公式xn +1点向后差商近似导数 推导如下：几何意义设已知曲线上一点 P n (x n , y n ),过该点作弦线，斜率为(x n +1 , y n +1 ) 点的方向场f (x ,y )方向,若步长h 充分小，可用弦线和垂线x =x n +1的交点近似曲线与垂线的交点。

流函数- 涡量法的二维方腔流数值模拟基本方程：22v tξγξψξ∂=∇-∇∂-∇=⎧⎨⎩t ———时间步长, s;γ———流体的运动粘度, m2 /s;ξ———涡量, s- 1;ψ———流函数, m2 /s;v ———速度矢量, m/s;差分格式：采用FTCS 格式，对于ξ有：1,,1,1,,1,11,,1,,1,,1,2222()22()()n n n nn nn n nn n ni j i ji j i ji j i j i j i j i ji j i j i j nni ji juvtxyx y ξξξξξξξξξξξξυ++-+-+-+-+----+-+=--++∆∆∆∆∆采用FTCS 格式，对于ξ有：1,,1,,1,,1,,1,2222)()()n nn n n n n n i j i ji j i j i j i j i j i j i j tx y ψψψψψψψψξ++-+---+-+=++∆∆∆边界条件：速度的边界条件：固体壁面处设置无滑移边界条件, 即u=0, v=0; 流函数的边界条件：在固体壁面及平板驱动处的流函数ξ=0; 涡量的边界条件： 平板驱动处：2uxξ=∆ 左右壁面上:;,1,,22()()i j i j i j y ξξξ+-=∆网格划分：采用等距结构化网格划分（40*40）编程计算：本算例采用MATLAB进行编译，其主要优势是语言简单，可以方便地描绘出方腔环流的等值线图等。

主要语句：while norm(c1)>1e-4|norm(c2)>1e-4n=n+1;O1=O;E1=E;t=t+dt;for i=2:Ifor j=2:JO(i,j)=O(i,j)-dt*(u(i,j)*(O(i+1,j)-O(i-1,j))/(2*dx)+v(i,j)*(O(i,j+1)-O(i,j-1))/ (2*dy))+dt/re*((O(i+1,j)-2*O(i,j)+O(i-1,j))/dx^2+(O(i,j+1)-2*O(i,j)+O(i,j-1))/d y^2);endendfor i=2:Ifor j=2:JE(i,j)=E(i,j)+0.25*(E(i+1,j)+E(i-1,j)+E(i,j+1)+E(i,j-1)-4*E(i,j)+dx^2*O(i,j)); endend% 0为涡量，E流函数%计算效果图：分别设置雷诺数为200，500,1000雷诺数Re=200时的流函数图及速度矢量图雷诺数Re=500时的流函数图及速度矢量图雷诺数Re=1000时的流函数图及速度矢量图。

二维流体力学流函数方程解巴巴二维流体力学的流函数方程是用来描述二维流体流动的一种数学方法。

在流体力学中，流函数是一个与速度场相关的标量场，是通过将速度场的分量与流体的密度相乘得到的。

流函数方程可以通过求解一个偏微分方程得到，其解可以给出流体在平面上任意点的速度和流线的分布。

∇²Ψ=0其中，∇²表示拉普拉斯算子，Ψ表示流函数。

这个方程是一个二阶偏微分方程，可以通过数值或解析方法求解。

为了求解流函数方程，需要满足一些边界条件。

常见的边界条件有：1.无物体边界条件：在流体的边界上，流函数Ψ的值可以设定为常数。

这个常数可以根据物理问题的条件来确定。

2.固壁边界条件：如果存在凸起的固体物体，可以设定在固体物体表面上流函数Ψ的梯度为零。

这意味着流体在固体物体表面上流动时，流线是与固体表面垂直的。

3.对称边界条件：当存在对称性时，可以设定在对称线上流函数的梯度为零。

这意味着在对称线上流体的速度分量与对称线垂直。

对于简单的几何形状，可以使用解析方法求解流函数方程。

例如，对于圆柱体的流动，可以使用柱坐标系下的方程来求解。

而对于复杂的几何形状或非线性问题，通常需要使用数值方法来求解流函数方程。

常用的数值方法有有限差分法、有限元法和有限体积法等。

一旦求解了流函数方程，就可以通过流函数求解速度场和流线的分布。

流函数的等值线是与速度场的切线垂直的，在流线上速度矢量的切线方向与流函数梯度的方向相同。

因此，通过流函数可以方便地描绘流体流动的图像。

总之，二维流体力学的流函数方程是求解二维流体流动的一种数学方法。

通过数值或解析方法求解流函数方程，可以得到流体在平面上的速度和流线的分布。

这对于研究和理解流体流动的特性和行为具有重要意义。

MAC算法计算二维方腔顶盖流动李江飞;石兆东;段兴华;李岩芳;张康;逯国强;陈颖超;任亚东【摘要】二维方腔流动是不可压缩黏性的典型流动,可以用来检验各种数值算法计算精度和可靠性,目前尚不能求得它的解析解.基于Matlab编程,采用交错网格MAC算法求解二维方腔流动,计算采用控制容积积分法离散控制方程,对流项和扩散项采用中心差分格式,得到流动达到稳定状态时各物理量的分布.【期刊名称】《宜宾学院学报》【年(卷),期】2015(015)006【总页数】4页(P28-31)【关键词】数值模拟;方腔流动;控制容积积分法;MAC算法;离散【作者】李江飞;石兆东;段兴华;李岩芳;张康;逯国强;陈颖超;任亚东【作者单位】承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德067000;承德石油高等专科学校热能工程系,河北承德 067000;承德石油高等专科学校热能工程系,河北承德 067000【正文语种】中文【中图分类】TB126Li JF,ShiZD,Duan XH,etal.Calculation of Two-dimensionalCavity Flow Based on MAC[J].Journal of Yibin Univer⁃sity,2015,15（6）：28-31.二维不可压缩黏性流体方腔流动顶盖拖动速度为utop，方腔的长度和高度均为H,流体密度为ρ、动力粘度为μ.边界条件：流动速度u、v采用无滑移边界条件，利用动量方程推导压力p的边界条件[1].流动与传热的控制方程如下：其中，p为压力，u、v分别为x、y方向速度分量.用高度H、流体密度ρ和拖动速度utop作为无量纲标尺，将控制方程无量纲化，流场初始状态为静止，Re=1000求流动达到稳定状态时，x方向中垂线（x=H/2）上的无量纲速度U，y 方向中垂线（y=H/2）上的无量纲速度V，绘制出速度分布曲线，并求出中垂线上||U、||V的平均值.1.1 涡量控制方程无量纲化以高度H、流体密度ρ和速度utop作为无量纲标尺，将控制方程无量纲化[2]：将上述无量纲量代入题中流动与传热的控制方程，得出如下的无量纲方程：1.2 边界条件边界条件为：流动速度采用无滑移边界条件，壁面处法向速度恒为0，切向速度也为零.顶盖u=1，v=0；其余u=v=0.采用均分网格，网格数80×80的交错网格来离散方程，将压力和速度放在不同位置，压力放在网格中心，以Pi,j为主节点，背离P点的U、V与P点有相同的编号，速度分量U与P在X方向位置相错半个网格，速度分量V与P在Y方向位置相错半个网格，具体如下[3]：P：X方向：0—81，左边点0，右边点81，边点与内点距离为，其余ΔX；Y方向：0—81，下边点0，上边点81，边点与内点距离，其余ΔY；U：X方向：0—80，左边点0，右边点80，相邻两点距离ΔX；Y方向：0—81，下边点0，上边点81，边点与内点距离，其余ΔY；V：X方向：0—81，左边点0，右边点81，边点与内点距离，其余ΔX；Y方向：0—80，下边点0，上边点80，相邻两点距离ΔY.对于MAC算法而言，采用交错网格，用控制容积积分法离散控制方程，对流项和扩散项采用中心差分格式.时间步长为Δτ，空间步长为ΔX、ΔY.对速度分量U进行离散[4-5]：内点处理：非稳态项：对流项：扩散项：压力项：边界点处理：对于上边界点，扩散项：对于下边界点，扩散项：内点离散后的动量方程为：对速度分量V进行离散：内点处理：非稳态项：对流项：扩散项：压力项：对于左边界点，其扩散项：对于右边界点，其扩散项：离散后的动量方程为：将，代入离散的连续性方程，如下：整理化简可得压力离散方程：其中：aP=aE+aW+aN+aS,aE=aW= aN=与上边界相邻的内点：与下边界相邻的内点：与左边界相邻的内点：与右边界相邻的内点：求解步骤如下[6-8]：①确定网格信息，如空间步长、时间步长：ΔX，ΔY，Δτ；②定义变量，给速度场和压力场赋初始值和边界值；③经过（1）、（2），可得完整的速度场离散结果，据公式求；④根据（3）求解压力泊松方程，采用Gauss-Seidel迭代求解，循环直至满足收敛条件；⑤用该时层满足收敛条件最新的压力场去更新速度场，得到下一时层的，；⑥用下一时层的，返回（4），直到稳态的解，求出速度场和压力场.程序流程如图1所示.U、V、P放置在相同的网格位置时，取中心差分，切断相邻点间关系，计算结果会出现非物理意义的振荡；通过交错网格，引入相邻两点的压差，在物理上保证了相邻点压力的相互影响，避免了振荡的压力解.稳定状态时，计算结果如图2、图3所示.【相关文献】[1] Peng Y F,Shiau Y H,Hwang R R.Transtion in a 2-D lid-driven cavity flow[J].Computer＆Fluids,2003,32（3）：337-352.[2] 陶文铨.数值传热学[M].第二版.西安：西安交通大学出版社，2010.[3] Abdallah S.Numerical solutions for the pressure poisson equation with neumann boundary conditions using a non-staggeredgrid[J].Journalofcomputationalphysics,1987,70（1）：182-192.[4] Hortmann M,PerićM,ScheuererG.Finite volumemultigrid predic⁃tion of laminar natural convection：Bench-mark solutions[J].Inter⁃national Journal for Numerical Methods in Fluids,1990,11（2）：189-207.[5] DemirdžićI,PerićM.Finite volumemethod for prediction of fluid flow in arbitrarily shaped domainswithmoving boundaries[J].Inter⁃national Journal for Numerical Methods in Fluids,1990,10（7）：771-790.[6] Brandt A.Multi-level adaptive technique（MLAT）for fast numeri⁃cal solution to boundary value problems[C].Proceedings of the Third International Conference on NumericalMethods in Fluid Me⁃chanics,Springer Berlin/Heidelberg,1973：82-89.[7] Wang J,Li JF,ChengW X,et parison of finite difference and finite volume method for numerical simulation of the incom⁃pressible viscous driven cavityflow[J].Advanced Materials Re⁃search,2013（732-733）：413-416.[8] Li JF,Long J,Yuan L A,parison of finite difference and finite volumemethod for numerical simulation of driven cavity flow based on MAC[C].Computational and Information Sciences（IC⁃CIS）,2013 Fifth International Conference on,Shiyang,2013：891-894.。

实验名称：方腔环流实验实验日期：2023年3月15日实验地点：流体力学实验室实验人员：张三、李四、王五一、实验目的1. 理解和掌握方腔环流的基本原理。

2. 观察和测量方腔环流的速度分布和压力分布。

3. 分析方腔环流在不同条件下的流动特性。

二、实验原理方腔环流是一种典型的二维流动问题，其基本原理是利用流体力学中的Navier-Stokes方程来描述。

在方腔环流中，流体在腔体内受到重力、压力梯度和边界条件的影响，形成复杂的流动结构。

本实验通过改变方腔的几何形状和边界条件，研究方腔环流的流动特性。

三、实验仪器与材料1. 方腔环流实验装置2. 高精度流量计3. 压力传感器4. 数据采集系统5. 计算机及分析软件四、实验步骤1. 安装实验装置，确保其稳定性。

2. 连接数据采集系统，对流量计和压力传感器进行校准。

3. 设置方腔的几何形状和边界条件，例如方腔的尺寸、入口和出口的流量等。

4. 启动实验装置，开始方腔环流的流动过程。

5. 在流动过程中，实时采集流量计和压力传感器的数据。

6. 实验结束后，关闭实验装置，整理实验数据。

五、实验结果与分析1. 速度分布通过对实验数据的分析，可以得到方腔环流的速度分布图。

从图中可以看出，在方腔中心区域，速度较大，而在靠近边界区域，速度较小。

这是因为中心区域的流体受到的压力梯度较大，导致流体流速加快。

2. 压力分布通过对实验数据的分析，可以得到方腔环流的压力分布图。

从图中可以看出，在方腔中心区域，压力较小，而在靠近边界区域，压力较大。

这是因为中心区域的流体流速较快，导致压力降低。

3. 不同条件下的流动特性（1）改变方腔尺寸当方腔尺寸增大时，中心区域的速度和压力都增大，边界区域的速度和压力都减小。

这是因为方腔尺寸增大，流体在腔体内的流动空间增大，导致流速和压力分布发生变化。

（2）改变入口和出口的流量当入口和出口的流量增大时，中心区域的速度和压力都增大，边界区域的速度和压力都减小。

二维流场速度计算公式文二维流场速度计算公式。

在流体力学中，流场速度是描述流体在空间中运动的重要参数。

对于二维流场，其速度可以通过一些基本的计算公式来进行求解。

本文将介绍二维流场速度计算公式的推导和应用。

一、二维流场速度计算公式的基本假设。

在进行二维流场速度计算时，我们通常会做出一些基本的假设，以简化问题的复杂度。

这些假设包括：1. 流场是二维的，即流体的速度只与平面上的两个坐标变量有关，与垂直于流动方向的坐标轴无关。

2. 流场是定常的，即流体的性质在空间和时间上都是不变的。

3. 流场是不可压缩的，即流体的密度在流动过程中保持不变。

4. 流场是无粘性的，即流体在流动过程中不受粘性力的影响。

在这些假设的基础上，我们可以推导出二维流场速度计算公式。

二、二维流场速度计算公式的推导。

在二维流场中，流体的速度可以用一个二维矢量来表示，即：\[ \vec{V} = (u, v) \]其中，\(u\) 和 \(v\) 分别表示流体在 \(x\) 和 \(y\) 方向上的速度分量。

根据流体力学的基本方程，我们可以得到流场速度的计算公式。

1. 连续性方程。

在二维流场中，流体的连续性方程可以表示为：\[ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 \]这个方程描述了流体在空间中的连续性，即流体在单位时间内通过一个单位面积的流体截面的流量是不变的。

2. 动量方程。

在二维流场中，流体的动量方程可以表示为：\[ \frac{\partial u}{\partial t} + u\frac{\partial u}{\partial x} + v\frac{\partialu}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial x} + \nu\left(\frac{\partial^2 u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2}\right) \]\[ \frac{\partial v}{\partial t} + u\frac{\partial v}{\partial x} + v\frac{\partialv}{\partial y} = -\frac{1}{\rho}\frac{\partial p}{\partial y} + \nu\left(\frac{\partial^2 v}{\partial x^2} + \frac{\partial^2 v}{\partial y^2}\right) \]其中，\(p\) 表示流体的压力，\(\rho\) 表示流体的密度，\(\nu\) 表示流体的动力粘度。

Case 1.二维方腔驱动流问题描述如图所示，特征长度为方腔边长，特征速度为u。

上边界以已知速度u移动，其它边界为静壁面。

试求在Re=100、1000、10000、100000时，空腔内流体的流动状态，比较不同Re流动特征的差异。

一．Re=100在一个正方形的二维空腔中充满等密度的空气，上边界以速度u移动，由Re=ud/ν,又ν=1.789×10-5m2/s，方腔每边长为l=0.1m,可求得速度u=0.01466m/s。

其它边界为静壁面。

同时带动方腔内流体流动。

速度矢量图总压等值线图水平中心线（y=0）上竖直速度分量(v)分布V-x竖直中心线（x=0）上水平速度分量（u）分布U-y不同Re方腔内流函数的分布情况Re=1000Re=10000Re=100000不同Re方腔内总压分布情况Re=1000Re=10000Re=100000方腔驱动流是数值计算中比较简单，具有验证性的一种流动情况，受到很多研究者的关注。

本文通过不同雷诺数观察方腔流动，所得结论如下：（1）当雷诺数较小时，腔中涡旋位置贴近腔体上壁面中部，随着雷诺数Re的增加，涡旋位置逐渐向下方靠近。

（2）随着雷诺数的增加，涡旋的位置逐渐靠近腔体中心。

（3）方腔壁面上的速度大于其他地方的速度。

Case2.圆管的沿程阻力1.问题描述如图，常温下，水充满长度l的一段圆管。

圆管进口存在平均速度u，壁面的当量粗糙高度为0.15mm。

试求在不同雷诺数下，计算该圆管的沿程阻力系数λ，分析比较Re与λ 的关系。

出口截面速度分布如下可见，出口截面流速分布较为明显，呈同心圆分布，内层流速偏大，外层靠近壁面处流速几乎为0，分层更为严重，边界层很薄。

Y=0截面速度分布图可以看出圆管水流湍流入口段及之后的流速发展趋势，而且显示流速变化的规律更为明显。

轴线压降圆管湍流中的压降，除了入口段压强分布因流速急剧上升而下降稍快外，管道后端速度呈充分发展状态，压降呈线性，即△p随L 的增加而降低。

附录F 二维不可压缩黏性流体方腔流动问题的有限体积算法与计算程序二维方腔流动问题是一个不可压缩黏性流动中典型流动。

虽然目前尚不能求得它的解析解，但是它常被用来作为检验各种数值算法计算精度和可靠性的算例。

文献中几乎大多数算法都对它进行过计算。

在本算例中采用有限体积算法三阶迎风型QUICK 离散格式对它进行数值求解。

同时，为了初学者入门和练习方便,这里给出了用C 语言和Fortran77语言编写的计算二维不可压缩黏性方腔流动问题计算程序，供大家学习参考。

F-1利用有限体积算法三阶迎风型QUICK 离散格式求解二维不可压缩黏性流体方腔流动问题1.二维不可压缩黏性流体方腔流动问题二维不可压缩黏性流体方腔流动（cavity flow ）：有一正方形腔室，其量纲为一的宽度为1.0，里面充满静止的不可压缩黏性流体，方腔内初始时刻压力和密度为=1.0=1.0p ρ、它周围壁面（左右壁面和底面）固定不动，上壁面以量纲为一的速度1.0沿着上壁面方向自左向右运动（图F.1）。

2. 基本方程组、初始条件和边界条件设流体是黏性流体。

二维方腔流动问题在数学上可以由二维不可压缩黏性流动N - S 方程组来表示，把它写成通用变量的微分方程组形式，有：()()u v S x y x x φφφρφρφμμ⎛⎫∂∂∂∂∂∂⎛⎫+=++ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭（F.1） 其中u 为变量φ在水平x 方向的流速，v 为φ在垂直y 方向的流速，μ为黏度，S φ为源项。

源项中不仅包含压力梯度项，也包含时间导数项。

初始条件：方腔上壁面以量纲为一的速度1.0沿着上壁面方向自左向右运动。

图F.1二维不可压缩黏性方腔流问题示意图图F.1 二维不可压缩黏性方腔流动问题示意图边界条件：流动速度u v、均可采用无滑移边界条件，压力p采用自由输出边界条件。

3.计算网格划分和控制体单元与节点定义采用交错网格，图F.2和图F.3是计算网格、控制体单元和节点示意图。

驱动方腔（粘性不可压流），方腔示意图如左下：物理背景：如左图所示,装满黏性不可压流体的方腔上底面以速度U 运动,其它壁面固定,其内部流体将作类似湍流的运动.流体运动复杂度将依赖于以下要素:(1)方腔形状 ；(2)U 的大小；(3)流体的黏性,即雷诺数Re 的大小。

本题只讨论理想流体在二维正方形空腔中的流动，如左图，作无量纲化处理后,方腔长度和上底面运动速度均取为1,通过差分数值模拟计算出运动的流函数，涡量函数，画出Re=100和200时的流线图和涡量图。

并标出窝心位置。

采用流函数-涡方法：对于二维不可压缩的理想流体,流速 ),(u v u = 应满足如下方程组:：（1）连续方程：0u =⋅∇（1）(2) N-S 方程：0)(2222=∂∂-∂∂+∂∂=∂∂+∂∂+∂∂x pyu x u u y u v x u u t u ρ （2）0)(2222=∂∂-∂∂+∂∂=∂∂+∂∂+∂∂ypy u x u u y u v x v u t v ρ（3）引入流函数：),,(t y x ψ和),,(t y x Ω：y u ∂∂=ψ，xv ∂∂-=ψ，y u x v ∂∂-∂∂=Ω （4）（4）代入（1）的流函数的方程：）＋－（2222yx ∂∂∂∂=Ωψψ； （5） 把（5）代入)2()3(x y ∂-∂，的涡量方程：)(Re 12222yx y v x u t ∂Ω∂+∂Ω∂=∂Ω∂+∂Ω∂+∂Ω∂ （6） 以上方法称之为流函数－涡方法。

数值方法：将区域分为N ×N 个方格单元，只有（N+1）×（N+1）格网格点要计算，令h=1/N 为空间步长，τ为时间步长。

1：流函数与速度的边界条件：;0.........;0,0,1,1....,........2,1,0,,,x 1,y x 0,,,,,,i ==========≤≤j i N i N i N i N i N i j v u else v u y if N j i jh y ih ψψ，2涡量的边界条件： 固壁上的涡量：N j i hhhH jN j N j j j i N i ..........0,,2;2;2;/22,1,2,1,02,10,,=-=Ω-=Ω-=Ω=Ω-ψψψ计算：1，方腔内的流函数：采用中心五点差分格式对（5）进行离散并简化得：1...........1,;4/)(,21,1,,1,1,-=+++-=-+-+N j i h j i j i j i j i j i j i ψψψψψψ算出j i ,ψ后，对（4）采用中心差分离散可以求得u,v. 2,方腔内得涡量：采用迎风格式对涡量方程（6）进行离散：);22(Re1212/1,1,11,21,11,1,112/1,12/1,1,12/11,2/11,,,hh hv h u n j i n j i n j i n ji n ji n ji n j i n j i n ji n i n ji n ji nji n j i +-++++-++++-++++-+++Ω+Ω-Ω+Ω+Ω-Ω=Ω-Ω+Ω-Ω+Ω-Ωτ程序实现过程如下：clear all clcjishi=cputime; timestep=2000;[x,y]=meshgrid(0:1/100:1); Nx=length(x);Ny=length(y); dh=1/100;dt=0.6*dh; renold=200;fluidfun=zeros(Nx,Ny); vortex=zeros(Nx,Ny); velocityx=zeros(Nx,Ny); velocityy=zeros(Nx,Ny); %%%初始条件 velocityx(:,Ny)=1; vortex(:,Ny)=-2/dh; %fluidfun(Ny,:)=0; %velocityy(Ny,:)=0; for t=1:timestep for i=2:Nx-1 for j=2:Ny-1fluidfun(i,j)=(fluidfun(i+1,j)+fluidfun(i-1,j)+fluidfun(i,j+1)+fluidfun(i,j-1)+dh^2*vortex(i,j))/4;endendfor i=2:Nx-1for j=2:Ny-1velocityx(i,j)=(fluidfun(i,j+1)-fluidfun(i,j-1))/(2*dh);velocityy(i,j)=(fluidfun(i-1,j)-fluidfun(i+1,j))/(2*dh);endendfor i=2:Nx-1for j=2:Ny-1a=renold*(abs(velocityx(i,j))+abs(velocityy(i,j)))/dh+4/dh^2+renold/(dt);b=renold*abs(velocityx(i,j))/dh+1/dh^2;c=renold*abs(velocityy(i,j))/dh+1/dh^2;if (velocityx(i,j)>=0)&&(velocityy(i,j)>=0)vortex(i,j)=((vortex(i+1,j)+vortex(i,j+1))/dh^2+b*vortex(i-1,j)+c*vortex(i,j-1)+renold*vortex(i,j)/ (dt))/a;elseif (velocityx(i,j)>=0)&&(velocityy(i,j)<0)vortex(i,j)=((vortex(i+1,j)+vortex(i,j-1))/dh^2+b*vortex(i-1,j)+c*vortex(i,j+1)+renold*vortex(i,j)/ (dt))/a;elseif (velocityx(i,j)<0)&&(velocityy(i,j)>=0)vortex(i,j)=((vortex(i-1,j)+vortex(i,j+1))/dh^2+b*vortex(i+1,j)+c*vortex(i,j-1)+renold*vortex(i,j)/ (dt))/a;elseif (velocityx(i,j)<0)&&(velocityy(i,j)<0)vortex(i,j)=((vortex(i-1,j)+vortex(i,j-1))/dh^2+b*vortex(i+1,j)+c*vortex(i,j+1)+renold*vortex(i,j)/ (dt))/a;endendendendc1=max(abs(fluidfun));b1=find(c1==max(c1));%%%在第几列d1=find(abs(fluidfun(:,b1))==max(c1));%%%在第几行figurecontour(x,y,fluidfun,10)%text(0,0.2,['re=200时驱动方腔流线图']);hold onplot(d1*0.01,b1*0.01,'ks')title('re=200时驱动方腔流线图');figurecontour(x,y,vortex,10)%text(0,0.2,['re=200时驱动方腔等涡量图']); hold onplot(d1*0.01,b1*0.01,'ks')title('re=200时驱动方腔等涡量图');数值模拟结果：其中，小方块表示中心位置。

流函数- 涡量法的二维方腔流数值模拟基本方程：① 在直角坐标系下，不可压非定常流体所满足的流函数涡量形式的N-S 方程为221Re u v tx y ξξξξψξ∂∂∂⎧++=∇⎪∂∂∂⎨⎪∇=-⎩其中,u v y xψψ∂∂==-∂∂ Re 为雷诺数差分格式：采用FTCS 格式有：1,,1,1,,1,11,,1,,1,,1,,2222122Re ()()n n n nn nn n n n n ni j i ji j i ji j i j i j i j i j i j i j i j nni ji juvtxyx y ξξξξξξξξξξξξ++-+-+-+-⎛⎫----+-+=--++ ⎪ ⎪∆∆∆∆∆⎝⎭1,,1,,1,,1,2222=0()()i j i j i j i j i j i j i j x y ψψψψψψξ+-+--+-+++∆∆,1,11,1,,,,22n n n n i j i j i j i jn i ji j u v yxψψψψ+-+---==-∆∆对于本问题，将方腔四边同时分为n 等分，则有x y h ∆=∆=∆ 故()()1,1,,1,1,1,,,1,1,,,1,124+()2Re n n n n ni j i j i j i j i j n n n n n n n ni ji ji j i j i j i j i j i j th u v h ξξξξξξξξξξξ+-+-++-+-⎡⎤+++-∆∆⎡⎤=--+-+⎢⎥⎣⎦∆⎢⎥⎣⎦21,1,,1,1,1,,,()4n n n n n i j i j i j i j i j n n n i ji ji j h ψψψψξψψψ+-+-+⎡⎤++++⨯∆=+-⎢⎥⎢⎥⎣⎦,1,11,1,,,,22n n n n i j i j i j i jni ji j uv hhψψψψ+-+---==-∆∆② 在直角坐标系下，不可压定常流体所满足的流函数涡量形式的N-S 方程为221Re =0u v x y ξξξψξ∂∂⎧+=∇⎪∂∂⎨⎪∇+⎩其中,u v y xψψ∂∂==-∂∂ Re 为雷诺数差分格式：采用FTCS 格式有：1,1,,1,11,,1,,1,,1,22221+=22Re ()()i j i ji j i j i j i j i j i j i j i j n i ji ju vxyx y ξξξξξξξξξξ+-+-+-+-+⎛⎫---+-++ ⎪ ⎪∆∆∆∆⎝⎭1,,1,,1,,1,2222=0()()i j i j i j i j i j i j i j x y ψψψψψψξ+-+--+-+++∆∆,1,11,1,,,,22i j i j i j i ji j i j u v yxψψψψ+-+---==-∆∆对于本问题，将方腔四边同时分为n 等分，则有x y h ∆=∆=∆，则有即()()1,1,,1,11,,,1,1,,,1,1,Re =+48n n n n i j i j i j i j n n n n n n n n n i j i j i j i j i j i j i j i j i j h u v ξξξξξξξξξξξ+-+-++-+-⎧⎫+++⨯∆⎪⎪⎡⎤+----⎨⎬⎣⎦⎪⎪⎩⎭21,1,,1,1,1,,,()4n n n n n i j i j i j i j i j n n n i ji ji j h ψψψψξψψψ+-+-+⎡⎤++++⨯∆=+-⎢⎥⎢⎥⎣⎦,1,11,1,,,,22n n n n i j i j i j i jni ji j uv hhψψψψ+-+---==-∆∆边界条件：在腔体的两侧和顶边，*22()()s s s s h ψψψξ=-=-∆ （第二式由泰勒级数展开得到）在底边*22()()s s s s h h ψψψξ=-+∆=-∆ （第二式由泰勒级数展开得到）其中s 代表边界，*s 代表与边界相邻的节点。