雷达成像技术保铮版第二章距离高分辨和一维距离像
- 格式:doc
- 大小:548.51 KB
- 文档页数:18

第2章雷达距离估算Lamont V. Blake2.1 引言对于自由空间中特定目标的检测(该目标的检测受热噪声的限制),雷达最大作用距离估算的基本物理机理从雷达出现起就为人所熟知。
本章的术语自由空间指以雷达为球心、半径远远延伸到目标之外的球形空域内仅有雷达和目标。
本章采用的自由空间定义对具体的雷达而言是相当准确的,而通用定义是冗长的,且用处不大。
该定义还暗示,自由空间内可被检测的雷达频率电磁波除了来源于雷达自身的辐射外,仅来自于自然界热或准热噪声源,如2.5节所述。
尽管上述的条件是不可能完全实现的,但是它接近许多雷达的实际环境。
在许多非自由空间和完全非热噪声的背景下,估算问题要复杂得多。
这些在早期分析中没有考虑到的复杂性也是由接收系统电路的信号和噪声关系的改变(信号处理)引起的。
在本章中将给出自由空间方程,讨论基本的信号处理,以及考虑一些十分重要的非自由空间环境下的方程和信号处理。
另外还将考虑一些常见非热噪声的影响。
虽然不可能涉及所有可能的雷达环境,但是本章所叙述的方法将简要地说明那些适合于未考虑到的环境和条件的必然方法的一般性质。
一些要求采用特定分析的专用雷达将在后面章节中叙述。
定义雷达作用距离方程包含许多雷达系统及其环境的参数,其中一些参数的定义是相互依赖的。
正如2.3节所讨论的,某些定义含有人为因素,不同作者使用不同的作用距离方程因子定义是常见的。
当然,若存在被广泛接受的定义,则采用该定义。
但更重要的是,虽然某些定义允许一定的随意性,但是一旦一个距离方程因子采用特定的定义,则一个或更多的其他因子的定义将不再具有随意性。
例如,脉冲雷达的脉冲功率和脉冲宽度的定义各自均具有很大的随意性,但是一旦任何一个定义被确定,那么另一个定义将由限制条件决定,即脉冲功率与脉冲宽度的乘积必须等于脉冲能量。
在本章中将给出一套定义,该定义遵循上述准则,并已被权威组织采纳。
约定由于传播途径因子和其他距离方程因子的变化很大,因此在这些因子的具体值未知的标准条件下,某些约定是估算作用距离所必需的。

高分辨率雷达目标一维距离像的编码识别算法
张文峰;何松华;郭桂蓉
【期刊名称】《国防科技大学学报》
【年(卷),期】1996(018)004
【摘要】文中提出了一种高分辨率雷达目标一维距离像识别算法。
该算法图像处
理方法,先对雷达目标的一维距离像进行编码,经过傅里叶变换提取一组形状特征。
这组特征精确地描维距离像曲经珠走向。
而后,利用人工神经网络技术对一定姿态角变化范围内的这组形状特征进行识别,实验结果表明,可以获得良好的识别效果。
该算法为雷达目标一维距离像识别算法的实时处理提供了一条有效途径。
【总页数】5页(P62-65,87)
【作者】张文峰;何松华;郭桂蓉
【作者单位】ATR实验室;ATR实验室
【正文语种】中文
【中图分类】TN959.17
【相关文献】
1.基于一维距离像的雷达目标识别 [J], 李飞
2.匀加速运动对频率步进雷达目标一维距离像的影响及其运动补偿方法 [J], 崔应留;罗文茂;王德纯
3.基于高分辨率一维距离像雷达目标识别研究 [J], 袁祖霞;高贵明
4.雷达目标一维距离像识别创新课程设计 [J], 梁菁;余萧峰;毛诚晨;熊金涛;万群
5.基于动态时间规整算法的一维距离像雷达目标识别方法 [J], 吴昭;夏鹏;田西兰
因版权原因,仅展示原文概要,查看原文内容请购买。




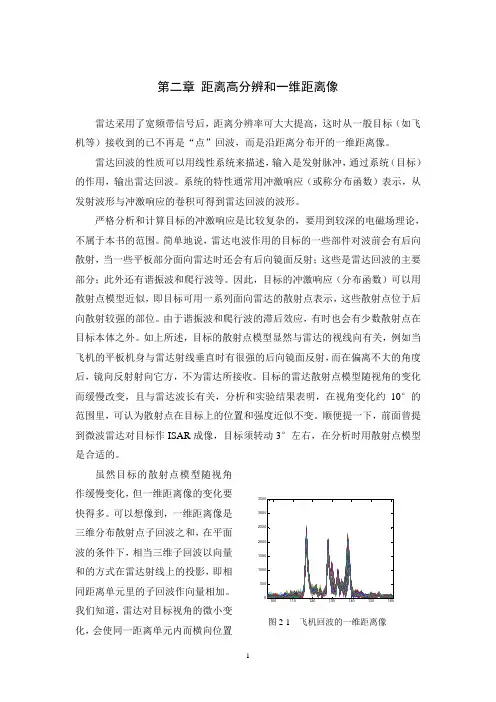
第二章距离高分辨和一维距离像雷达采用了宽频带信号后,距离分辨率可大大提高,这时从一般目标(如飞机等)接收到的已不再是“点”回波,而是沿距离分布开的一维距离像。
雷达回波的性质可以用线性系统来描述,输入是发射脉冲,通过系统(目标)的作用,输出雷达回波。
系统的特性通常用冲激响应(或称分布函数)表示,从发射波形与冲激响应的卷积可得到雷达回波的波形。
严格分析和计算目标的冲激响应是比较复杂的,要用到较深的电磁场理论,不属于本书的范围。
简单地说,雷达电波作用的目标的一些部件对波前会有后向散射,当一些平板部分面向雷达时还会有后向镜面反射;这些是雷达回波的主要部分;此外还有谐振波和爬行波等。
因此,目标的冲激响应(分布函数)可以用散射点模型近似,即目标可用一系列面向雷达的散射点表示,这些散射点位于后向散射较强的部位。
由于谐振波和爬行波的滞后效应,有时也会有少数散射点在目标本体之外。
如上所述,目标的散射点模型显然与雷达的视线向有关,例如当飞机的平板机身与雷达射线垂直时有很强的后向镜面反射,而在偏离不大的角度后,镜向反射射向它方,不为雷达所接收。
目标的雷达散射点模型随视角的变化而缓慢改变,且与雷达波长有关,分析和实验结果表明,在视角变化约10°的范围里,可认为散射点在目标上的位置和强度近似不变。
顺便提一下,前面曾提到微波雷达对目标作ISAR成像,目标须转动3°左右,在分析时用散射点模型是合适的。
虽然目标的散射点模型随视角快得多。
可以想像到,一维距离像是三维分布散射点子回波之和,在平面波的条件下,相当三维子回波以向量和的方式在雷达射线上的投影,即相同距离单元里的子回波作向量相加。
我们知道,雷达对目标视角的微小变化,会使同一距离单元内而横向位置不同散射点的径向距离差改变,从而使两者子回波的相位差可能显著变化。
以波长3厘米为例,若两散射点的横距为10米,当目标转动0.05°时,两者到雷达的径向距离差变化为1厘米,它们子回波的相位差改变240°!由此可见,目标一维距离像中尖峰的位置随视角缓慢变化(由于散射点模型缓变),而尖峰的振幅可能是快变的(当相应距离单元中有多个散射点)。

《成像雷达技术》目录前言第一章概论1.1雷达成像及其发展概况1.2雷达成像的基本原理1.3本书的内容安排第二章距离高分辨和一维距离像2.1宽带信号的逆滤波、匹配滤波和脉冲压缩2.2线性调频信号和解线频调处理2.3散射点模型与一维距离像2.4一维距离像回波的相干积累2.5高距离分辨雷达的检测和测高第三章方位高分辨和合成阵列3.1合成阵列的特点3.2运动平台的合成孔径雷达的横向分辨3.3用波数域分析合成孔径雷达的横向分辨率第四章合成孔径雷达4.1条带模式合成孔径雷达成像的基本原理4.2合成孔径雷达在三维空间里的二维成像4.3场景高程起伏引起的几何失真4.4合成孔径雷达的性能指标4.5合成孔径雷达的电子反对抗第五章合成孔径雷达成像算法5.1距离徙动5.2距离-多普勒(R-D)算法及其改进算法5.3线频调变标(Chirp Scaling 简称CS)算法5.4频率变标(Frequency Scaling 简称FS)算法5.5距离徙动算法(RMA)5.6极坐标格式(PFA)算法第六章基于回波数据的合成孔径雷达运动补偿6.1多普勒参数估计6.2存在运动误差情况下的SAR模型6.3基于多普勒参数估计的运动参数估计6.4垂直航线运动分量的补偿6.5沿航线运动分量的补偿(速度不稳时的运动补偿)6.6PGA自聚焦6.7结合运动补偿的SAR成像及验证第七章逆合成孔径雷达7.1 ISAR成像的转台模型和平动补偿原理7.2平动补偿的包络对齐7.3平动补偿的初相校正7.4目标转动时散射点徙动及其补偿7.5机动目标的ISAR成像7.6用时频分析方法对非平稳运动目标成像第八章干涉合成孔径雷达8.1 InSAR高程测量的基本原理8.2 InSAR高程测量的过程8.3 InSAR观测去相关和预滤波8.4图像配准8.5降噪滤波8.6二维相位解缠绕8.7高程测量误差分析8.8地面动目标检测(GMTI)8.9单脉冲ISAR。

高分辨雷达一维距离像的融合特征识别胡玉兰;赵子铭;片兆宇【摘要】雷达目标识别中,提取目标的有效特征将直接影响识别效果.针对雷达目标高分辨距离像(HRRP)具有平移敏感性,提出了一种基于多特征的融合特征来作为目标特征进行识别.利用PCA将三种平移不变特征融合,采用支持向量机算法来实现识别.仿真实验结果表明,该方法不仅降低了目标特征的存储量,同时也克服了高分辨距离像的平移敏感性,具有较高的识别率和很好的推广性.【期刊名称】《微型机与应用》【年(卷),期】2015(034)004【总页数】4页(P52-54,57)【关键词】一维距离像;主成分分析;支持向量机;幅度谱差分特征;中心距特征;功率谱特征【作者】胡玉兰;赵子铭;片兆宇【作者单位】沈阳理工大学信息科学与工程学院,辽宁沈阳110159;沈阳理工大学信息科学与工程学院,辽宁沈阳110159;沈阳理工大学信息科学与工程学院,辽宁沈阳110159【正文语种】中文【中图分类】TN957.51本文主要针对目标高分辨一维距离像的平移敏感性,提出了一种基于主成分分析方法的多特征融合的目标识别方法。
首先对一维距离像进行预处理,消除一维距离像的噪声干扰并且克服一维距离像的强度敏感性。
在此基础上分别提取具有平移不变性的功率谱特征、中心矩特征及幅度谱差分特征,然后利用PCA方法将以上特征融合作为目标特征,采用支持向量机分类器进行识别分类。
根据实测雷达目标的数据进行多次试验,结果显示,提取的该融合特征与单一特征和串联融合特征相比在减少模板特征向量的个数和测试样本识别的计算量的同时,得到了较高的识别率。
1.1 一维距离像模型当雷达发射信号带宽足够大时,目标尺寸远大于雷达的距离分辨单元,此时雷达回波就是由多个目标散射点子回波组成;同时回波中所呈现的结构反映了目标散射点的分布情况,可用于目标识别[1],如图1所示。
1.2 数据预处理雷达回波信号经过逆离散傅里叶变换就可以得到目标的一维距离像[2-3]。

雷达高分辨距离像分类器的参数自适应学习算法
袁莉;刘宏伟;保铮
【期刊名称】《电子与信息学报》
【年(卷),期】2008(030)001
【摘要】雷达高分辨率距离像具有目标姿态敏感性的特点,在识别时的一种解决方法是对目标不同角域建立不同的统计模型.在给定系统参数条件下,选择目标划分角域个数及每个角域覆盖范围是影响识别器运算量及识别性能的关键.该文给出了一种基于数据的自适应学习上述分类器参数的算法,基于联合高斯分布的数据模型通过迭代算法来确定数据划分边界,并自动确定目标角域个数.与等间隔数据划分方法相比,本文方法在降低识别运算量的同时,可以提高识别性能.基于实测数据的实验结果表明该方法是有效的.
【总页数】5页(P198-202)
【作者】袁莉;刘宏伟;保铮
【作者单位】西安电子科技大学雷达信号处理重点实验室,西安,710071;西安电子科技大学雷达信号处理重点实验室,西安,710071;西安电子科技大学雷达信号处理重点实验室,西安,710071
【正文语种】中文
【中图分类】TN957.51
【相关文献】
1.雷达高分辨距离像的特征提取算法研究 [J], 沈丽民
2.利用稳健字典学习的雷达高分辨距离像目标识别算法 [J], 冯博;陈渤;王鹏辉;刘宏伟;严俊坤
3.基于稳健深层网络的雷达高分辨距离像目标特征提取算法 [J], 冯博;陈渤;王鹏辉;刘宏伟
4.基于多分类器融合的雷达高分辨距离像目标识别与拒判新方法 [J], 张学峰;王鹏辉;冯博;杜兰;刘宏伟
5.基于稳健变分自编码模型的雷达高分辨距离像目标识别算法 [J], 翟颖;陈渤
因版权原因,仅展示原文概要,查看原文内容请购买。

高分辨一维距离像的雷达目标识别方法
樊萍;景占荣
【期刊名称】《火力与指挥控制》
【年(卷),期】2008(033)011
【摘要】提出了一种基于高分辨一维距离像的宽带雷达目标识别方法.首先使用零相位描述对雷达回波进行预处理,实现距离像的绝对对准,解决了平移敏感性问题.然后根据多分辨分析构造出3次Battle-Lemarie小波函数和尺度函数,对预处理后的一维距离像进行小波变换提取目标特征矢量,在显著降低特征存储空间的同时保留了主要散射点.最后对3类不同目标的雷达实测数据进行识别试验,结果表明本算法不但具有较高的正确识别率,而且能够有效降低加性高斯白噪声对识别率的影响.【总页数】4页(P112-115)
【作者】樊萍;景占荣
【作者单位】西北工业大学,陕西,西安,710072;西北工业大学,陕西,西安,710072【正文语种】中文
【中图分类】TN95
【相关文献】
1.基于目标一维距离像的雷达目标识别方法 [J], 张善文;甄蜀春;赵兴录;赵栓堂;陈世亮
2.基于目标一维距离像的雷达目标识别方法 [J], 张善文;甄蜀春;赵兴录;赵栓堂
3.基于一维距离像的雷达目标识别方法研究 [J], 沈明华;曲毅;冯新喜
4.雷达目标一维距离像识别方法研究 [J], 刘江波;王瑞革;金虎
5.基于动态时间规整算法的一维距离像雷达目标识别方法 [J], 吴昭;夏鹏;田西兰因版权原因,仅展示原文概要,查看原文内容请购买。
专利名称:一种基于多次样本的高分辨雷达一维距离像目标识别方法
专利类型:发明专利
发明人:梁菁,毛诚晨,刘怀远,刘晓旭,余萧峰,张健,段珍珍
申请号:CN201610722921.8
申请日:20160825
公开号:CN106338722A
公开日:
20170118
专利内容由知识产权出版社提供
摘要:本发明涉及一种基于多次样本的高分辨雷达一维距离像目标识别方法,其主旨在于针对最小K‑L距离准则在对称性上的缺陷性,引入一种新的距离判决准则,即最小Resistor‑Average(RA)距离准则,用以提高雷达目标识别性能。
具体方案为第一步:多次距离像样本高分辨率雷达一维模板距离像特征提取;第二步:多次距离像样本高分辨率雷达一维测试距离像特征提取;第三步为本申请提案与现有技术不同之处:利用最小RA距离准则进行多次距离像样本高分辨率雷达一维测试距离像目标识别。
申请人:电子科技大学
地址:611731 四川省成都市高新区(西区)西源大道2006号
国籍:CN
代理机构:成都弘毅天承知识产权代理有限公司
代理人:李龙
更多信息请下载全文后查看。
前言雷达成像技术是上个世纪50年代发展起来的,它是雷达发展的一个重要里程碑。
从此,雷达不仅仅是将所观测的对象视为“点”目标,来测定它的位置与运动参数,而是能获得目标和场景的图像。
同时,由于雷达具有全天候、全天时、远距离和宽广观测带,以及易于从固定背景中区分运动目标的能力,雷达成像技术受到广泛重视。
雷达成像技术应用最广的方面是合成孔径雷达(Synthetic Aperture Radar,简称SAR)。
当前,机载和星载SAR的应用已十分广泛,已可得到亚米级的分辨率,场景图像的质量可与同类用途的光学图像相媲美。
利用SAR的高分辨能力,并结合其它雷达技术,SAR还可完成场景的高程测量,以及在场景中显示地面运动目标(GMTI)。
SAR的高分辨,在径向距离上依靠宽带带信号,几百兆赫的频带可将距离分辨单元缩小到亚米级;方向上则依靠雷达平台运动,等效地在空间形成很长的线性阵列,并将各次回波存贮作合成的阵列处理,这正是合成孔径雷达名称的来源。
合成孔径可达几百米或更长,因而可获得高的方位分辨率。
雷达平台相对于固定地面运动形成合成孔径,实现SAR成像。
反过来,若雷达平台固定,而目标运动,则以目标为基准,雷达在发射信号过程中,也等效地反向运动而形成阵列,据此也可对目标成像,通称为逆合成孔径雷达(ISAR)。
ISAR显然可以获取更多的目标信息。
最简单的雷达成像是只利用高距离分辨(HRR)的一维距离像。
当距离分辨率达米级,甚至亚米级时,对飞机、车辆等一般目标,单次回波已是沿距离分布的一维距离像,它相当目标三维像以向量和方式在雷达射线上的投影,其分布与目标相对于雷达的径向结构状况有关。
同时,高距离分辨率有利于分辨距离接近的目标,以及目标回波的直达波和多径信号。
本书将对当前已经广泛应用和具有应用潜力的内容作较为全面的介绍。
本书是《雷达技术丛书》中的一册,主要对象为从事雷达研制工作的技术人员,因此,本书编著时考虑到读者已有《雷达原理》和《雷达系统》方面的基础,对雷达各部件的基本情况也已比较熟悉,与上述内容有关的部分,本书均作了省略。
第二章距离高分辨和一维距离像雷达采用了宽频带信号后,距离分辨率可大大提高,这时从一般目标(如飞机等)接收到的已不再是“点”回波,而是沿距离分布开的一维距离像。
雷达回波的性质可以用线性系统来描述,输入是发射脉冲,通过系统(目标)的作用,输出雷达回波。
系统的特性通常用冲激响应(或称分布函数)表示,从发射波形与冲激响应的卷积可得到雷达回波的波形。
严格分析和计算目标的冲激响应是比较复杂的,要用到较深的电磁场理论,不属于本书的范围。
简单地说,雷达电波作用的目标的一些部件对波前会有后向散射,当一些平板部分面向雷达时还会有后向镜面反射;这些是雷达回波的主要部分;此外还有谐振波和爬行波等。
因此,目标的冲激响应(分布函数)可以用散射点模型近似,即目标可用一系列面向雷达的散射点表示,这些散射点位于后向散射较强的部位。
由于谐振波和爬行波的滞后效应,有时也会有少数散射点在目标本体之外。
如上所述,目标的散射点模型显然与雷达的视线向有关,例如当飞机的平板机身与雷达射线垂直时有很强的后向镜面反射,而在偏离不大的角度后,镜向反射射向它方,不为雷达所接收。
目标的雷达散射点模型随视角的变化而缓慢改变,且与雷达波长有关,分析和实验结果表明,在视角变化约10°的范围里,可认为散射点在目标上的位置和强度近似不变。
顺便提一下,前面曾提到微波雷达对目标作ISAR成像,目标须转动3°左右,在分析时用散射点模型是合适的。
虽然目标的散射点模型随视角快得多。
可以想像到,一维距离像是三维分布散射点子回波之和,在平面波的条件下,相当三维子回波以向量和的方式在雷达射线上的投影,即相同距离单元里的子回波作向量相加。
我们知道,雷达对目标视角的微小变化,会使同一距离单元内而横向位置不同散射点的径向距离差改变,从而使两者子回波的相位差可能显著变化。
以波长3厘米为例,若两散射点的横距为10米,当目标转动0.05°时,两者到雷达的径向距离差变化为1厘米,它们子回波的相位差改变240°!由此可见,目标一维距离像中尖峰的位置随视角缓慢变化(由于散射点模型缓变),而尖峰的振幅可能是快变的(当相应距离单元中有多个散射点)。
图2-1是C 波段雷达实测的飞机一维距离像的例子,图中将视角变化约3°的回波重合画在一起。
一维距离像随视角变化而具有的峰值位置缓变性和峰值幅度快变性可作为目标特性识别的基础。
本章将用上述散射点模型对高分辨的一维距离像进行讨论。
2.1 宽带信号的逆滤波、匹配滤波和脉冲压缩根据散射点模型,设散射点为理想的几何点,若发射信号为()p t ,对不同距离多个散射点目标,其回波可写成: 22()()c i f j R i c r i iR s t A p t e c π-=-∑ (2.1) i A 和()i m R t 分别为第i 个散射点回波的幅度和某时刻的距离;()p •为归一化的回波包络;c f 为载波频率,c 为光速。
若以单频脉冲发射,脉冲越窄,信号频带越宽。
但发射很窄的脉冲,要有很高的峰值功率,实际困难较大,通常都采用大时宽的宽频带信号,接收后通过处理得到窄脉冲。
为此,我们将(2.1)式的回波信号换到频域来讨论如何处理,这时有:2()()()c i f f j R c r i i S f A P f eπ+-=∑ (2.2)对理想的几何点目标当然希望重建成冲激脉冲,如果()P f 在所有频率没有零分量,则冲激脉冲信号可通过逆滤波得到,即21()2()e ()()c i f j R i r c i iR S f F A t P f c πωδ--⎡⎤=-⎢⎥⎣⎦∑ (2.3) 实际()P f 的频带虽然较宽,但总是带限信号,所以一种实用距离成像方法是通过匹配滤波,主要将各频率分量的相位校正成一样,为了提高信噪比再按信号频谱幅度加权,而频谱为零部分是无法恢复的。
匹配滤波后的输出为,1*()2()1*()2()()()()()2epsf ()c i c i r M f r f f j R c f i i f j R i c i i s t F S f P f F A P f P f e R A t cππ-+---⎡⎤=⎣⎦⎡⎤=⎢⎥⎣⎦=-∑∑ (2.4)这里*()P •为()P •的复共轭,而21()psf ()()f t F P f -⎡⎤=⎣⎦(2.5) 在时域上看,滤波相当于信号与滤波器冲激响应的卷积,对一已知波形的信号作匹配滤波,其冲激响应为该波形的共轭倒置。
当波形的时间长度为p T ,则卷积输出信号为p T 2。
实际上,匹配滤波可实现脉冲压缩,输出主瓣的宽度为B 1(B 为信号的频带宽度,为降低副瓣而作加权,主瓣要展宽一些),即距离分辨率为)2(B c ,脉压信号的B 通常较大(1>>BT ),输出主瓣是很窄的,时宽为p T 2的输出中,绝大部分区域为幅度很低的副瓣。
当反射体是静止的离散点时,回波为一系列不同延时和复振幅的已知波形之和,对这样的信号用发射波形作匹配滤波时,由于滤波是线性过程,可分别处理后迭加。
如果目标长度相应的回波距离段为r ∆,其相当的时间段为T ∆(=c r ∆2),考虑到发射信号时宽为p T ,则目标所对应的回波时间长度为p T T +∆,而匹配滤波后的输出信号长度为p T T 2+∆。
虽然如此,具有离散点主瓣的时间段仍只有T ∆,两端的部分只是副瓣区,没有目标位置信息。
应当指出,通过卷积直接作匹配滤波脉压的运算量相对较大,可以在频率域通过共轭相乘再作IFFT 求得。
需要注意的是两离散信号频率域相乘相当它们在时域作圆卷积,为使圆卷积与线性卷积等价,待处理的信号须加零延伸,避免圆卷积时发生混叠。
实际处理中,为了压低副瓣,通常是将匹配函数加窗,然后加零延伸为p T T +∆的时间长度,作傅立叶变换后并作共轭,和接收信号的傅立叶变换相乘后,作傅立叶逆变换,取前T ∆时间段的有效数据段。
为了便于采用快速傅立叶变换,可能对匹配函数要补更多的零,对接收信号也要补零。
脉压处理过程的如图2-2所示,其中虚框部分可事先计算好,以减小运算量。
接收信号图2-2 匹配滤波脉压示意图 距离匹配滤波压缩后,不管是否补零,其距离分辨率为)2(B c ,距离采样率为)2(s F c ,其中s F 为采样频率,1s sT F =为采样周期,距离采样周期要求小于等于距离分辨单元长度。
2.2 线性频调信号和解线频调处理大时宽宽频带信号可以有许多形式,如脉冲编码等,但用得最多的是线性调频(LFM )脉冲信号。
由于线性调频信号的特殊性质,对它的处理不仅可用一般的匹配滤波方式,还可用特殊的解线频调(Dechirping )方式来处理。
解线频调脉压方式是针对线性调频信号提出的,对不同延迟时间信号进行脉冲压缩,在一些特殊场合,它不仅运算简单,而且可以简化设备,已广泛应用于SAR 和ISAR 中作脉冲压缩。
应当指出,解线频调处理和匹配滤波虽然基本原理相同,但两者还是有些差别的,为了能正确利用解线频调方式作脉冲压缩,我们对它作一些详细的说明。
假设发射信号为s t t t T e m p j f t t c (∃,)∃(∃)=⎛⎝ ⎫⎭⎪⎪+rect 2122πγ, (2.6) 其中⎩⎨⎧>≤=212101)rect(u u u ,f c 为中心频率,T p 为脉宽,γ为调频率,∃t t mT =-为快时间,m 为整数,T 脉冲重复周期,mT t m =为慢时间。
解线频调是用一时间固定,而频率、调频率相同的LFM 信号作为参考信号,用它和回波作差频处理。
设参考距离为R ref ,则参考信号为⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=2212ˆ222ˆrect ),ˆ(c R t c R t f j ref ref m ref ref ref c e T c R t t t s γπ (2.7)式中ref T 为参考信号的脉宽,它比T 要大一些(参见图2-3)。
某点目标到雷达的距离为t R ,雷达接收到的该目标信号),ˆ(m r t t s 为⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛-=2212ˆ222ˆrect ),ˆ(c R t c R t f j p t m r i i c e T c R t A t t s γπ (2.8)解线频调的示意图如图2-3,若ref t R R R -=∆,则其差频输出为),ˆ(),ˆ(),ˆ(*m ref m r m if t ts t t s t t s ⋅= 即2244)2ˆ(42ˆrect ),ˆ(∆∆∆---⎪⎪⎭⎫ ⎝⎛-=R c j R f c j R c Rt c j p t m if e e e T c R t A t t s c ref πγπγπ (2.9)若暂将讨论限制在一个周期里(即R ∆为常数),则上式为频率与R ∆成正比的单频脉冲。
如果所需观测的范围为]2,2[r R r R ref ref ∆+∆-,图2-3中画出了范围两侧边缘处的回波。
我们再结合,图2.3是解线频调的差频处理示意图作一些说明,图中纵坐标均为频率,图2.3(a)中除参考信号外,有远、近的两个回波。
参考信号与回波作其共轭相乘,即作差频处理,回波变成单频信号,且其频率与回波和参考信号的距离差成正比,因而也叫解线频调处理。
由图2-3(b)可知cR f i ∆-=2γ。
因此,对解线频调后的信号作傅立叶变换,便可在频域得到对应的各回波的sinc 状的窄脉冲,脉冲宽度为p T 1,而脉冲位置与∆R 成正比(c R ∆-2γ),如图2-3(b)的左侧所示。