下载文档原格式
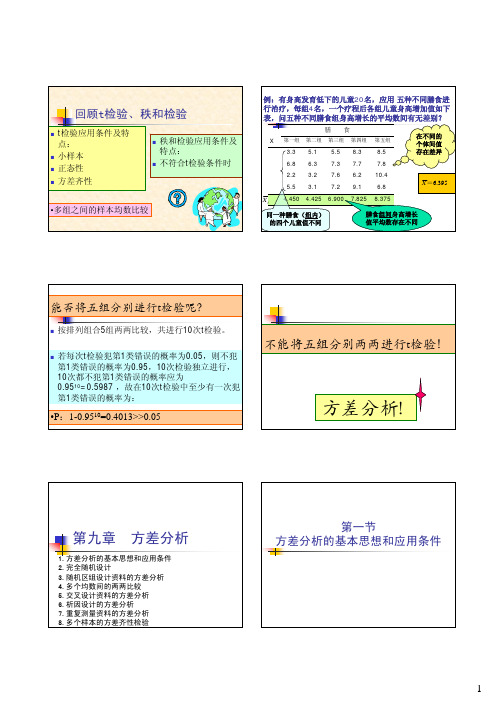
回顾t检验、秩和检验 t检验应用条件及特 点： 小样本 正态性 方差齐性 秩和检验应用条件及 特点： 不符合t检验条件时•多组之间的样本均数比较例：有身高发育低下的儿童20名，应用 五种不同膳食进 行治疗，每组4名，一个疗程后各组儿童身高增加值如下 表，问五种不同膳食组身高增长的平均数间有无差别？膳食 X 第一组 第二组 第三组 第四组 第五组3.3 5.1 5.5 8.3 8.5在不同的 个体间值 存在差异6.8 6.3 7.3 7.7 7.82.2 3.2 7.6 6.2 10.4 5.5 3.1 7.2 9.1 6.8X ＝6.395X i 4.450 4.425 6.900 7.825 8.375同一种膳食（组内） 的四个儿童值不同膳食组间身高增长 值平均数存在不同能否将五组分别进行t检验呢？ 按排列组合5组两两比较，共进行10次t检验。
若每次t检验犯第1类错误的概率为0.05，则不犯 第1类错误的概率为0.95，10次检验独立进行， 10次都不犯第1类错误的概率应为 0.9510=0.5987 ，故在10次t检验中至少有一次犯 第1类错误的概率为：•P：1-0.9510=0.4013>>0.05不能将五组分别两两进行t检验！方差分析!第九章 方差分析1.方差分析的基本思想和应用条件 2.完全随机设计 3.随机区组设计资料的方差分析 4.多个均数间的两两比较 5.交叉设计资料的方差分析 6.析因设计的方差分析 7.重复测量资料的方差分析 8.多个样本的方差齐性检验第一节 方差分析的基本思想和应用条件1第一节 完全随机设计的方差分析1. 方差分析的概念 方差分析（ANOVA）又称变异数分析或F检验，其目的是推断两组或多组资料的总体均数是否相 同，检验两个或多个样本均数的差异是否有统计 学意义。
应用条件： • 各样本相互独立 • 均来自总体方差具有齐性的正态分布方差分析的基本思想 将全部观察值的总变异按影响实验结果的诸 因素分解为若干变异，构造出反映各部分变 异作用的统计量（SS），之后构造假设检验 统计量（F），实现对总体均数的推断。
专题九 方差分析方差分析（ANOV A ），又称F 检验，是一种以分析数据的变异为基础，以F 值为统计量的计量资料的假设检验方法。
用较不同变异来源的均方，借助F 分布做出统计推断。
⑴方差分析的应用条件：①各观察值相互独立，且每一水平下的观察值均服从正态分布。
②各总体方差相等，即具有方差齐性。
⑵对于不满足方差分析应用条件的资料，可采用以下两种方式进行处理：①变量变换，是指满足方差分析的基本假定。
②应用非参数统计分析方法。
⒉完全随机设计的ANOV A各组样本均数各不相等，这种差异可能由两种原因引起：①随机误差；②处理因素。
⑴完全随机设计的变异分解：完全随机设计（成组设计）资料的总变异可以分解为组间变异和组内变异。
①总变异：SS 总，用所有观察值与均数的离均差平方和表示。
SS 总=∑∑-ij2ijx x ）（，υ总=N-1（N 为总例数）②组间变异：SS 组间，用各组均数与总均数的离均差平方和表示。
SS 组间=∑-i2ii x xn ）（，υ组间=k-1（k 为处理组数）③组内变异：SS 组内，用各组内每个测量值xij 与该组均数得离均差平方和表示，仅反映随机误差，又称误差变异。
SS 组内=∑∑-ij2i ij x x ）（，υ组内=N-k⑵三种变异及相关自由度的关系为：SS 总=SS 组间+SS 组内，υ总=υ组间+υ组内均方MS 组间=SS 组间／υ组间；MS 组内= SS 组内／υ组内⑶方差分析的统计量F ：F=MS 组间／MS 组内⑷F 界值表：纵标目为组间自由度υ1，横标目为组内自由度υ2，表中给出了α=0.05和α=0.01时供方差分析用的单侧F 界值，用F α，（υ1，υ2）表示。
若F ≥F α，（υ1，υ2），则P ≤α，按α水准拒绝H 0，接受H 1，差别有统计学意义，可以认为总体均数不等或不全等（处理因素有效应）；反之，则差别无统计学意义，尚不能认为总体均数不等或不全等（尚不能认为处理因素有效应）。
