二次函数压轴题之相三角形似存在性问题(二)

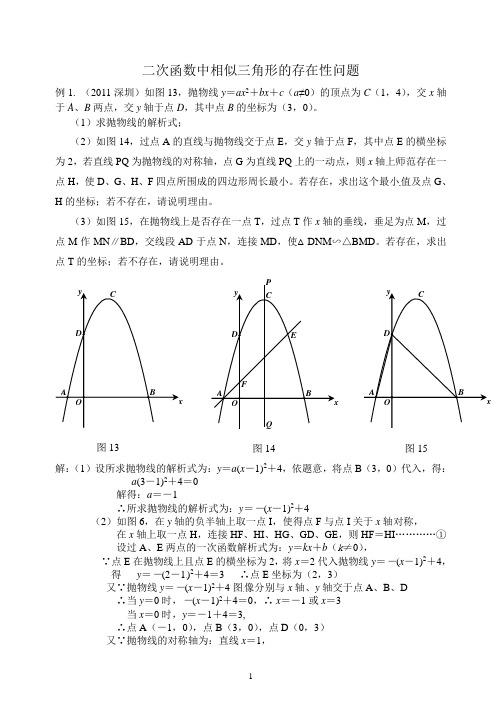
2023年中考数学压轴题专项训练压轴题05二次函数与三角形存在性问题（与等腰、直角、等腰直角三角形、相似三角形）题型一：二次函数与等腰三角形存在性问题例1．（2022•百色）已知抛物线经过A（﹣1，0）、B（0，3）、C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM，交BC于点F．（1）求抛物线的表达式；（2）求证：∠BOF＝∠BDF；（3）是否存在点M，使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长．题型二：二次函数与直角三角形存在性问题例2．（2022•滨州）如图，在平面直角坐标系中，抛物线y＝x2﹣2x﹣3与x轴相交于点A、B（点A在点B 的左侧），与y轴相交于点C，连接AC、BC．（1）求线段AC的长；（2）若点P为该抛物线对称轴上的一个动点，当P A＝PC时，求点P的坐标；（3）若点M为该抛物线上的一个动点，当△BCM为直角三角形时，求点M的坐标．题型三：二次函数与等腰直角三角形存在性问题例3．（2022•枣庄）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点．（1）求抛物线的关系式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出P点坐标；（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE内（包括△OAE的边界），求h的取值范围；（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．题型四：二次函数与相似三角形存在性问题例4．（2023•宜兴市一模）如图，在平面直角坐标系xOy中，二次函数y＝ax2+bx﹣2的图象经过点A（﹣1，0），B（3，0），与y轴交于点C，连接BC、AC．（1）求二次函数的函数表达式；（2）设二次函数的图象的顶点为D，求直线BD的函数表达式以及sin∠CBD的值；（3）若点M在线段AB上（不与A、B重合），点N在线段BC上（不与B、C重合），是否存在△CMN 与△AOC相似，若存在，请直接写出点N的坐标，若不存在，请说明理由．一．解答题（共20小题）1．（2023•绥宁县模拟）如图，一次函数y=12x+2与x轴，y轴分别交于A、C两点，二次函数y＝ax2+bx+c的图象经过A、C两点，与x轴交于另一点B，其对称轴为直线x=−3 2．（1）求该二次函数表达式；（2）在y轴的正半轴上是否存在一点M，使以点M、O、B为顶点的三角形与△AOC相似，若存在，求出点M的坐标，若不存在，请说明理由；（3）在对称轴上是否存在点P，使△P AC为等腰三角形，若存在，求出点P的坐标；若不存在，请说明理由．2．（2023•泗阳县校级一模）如图，二次函数y＝ax2+bx+4与x轴交于点A（4，0）、B（﹣1，0），与y轴交于点C．（1）求函数表达式及顶点坐标；（2）连接AC，点P为线段AC上方抛物线上一点，过点P作PQ⊥x轴于点Q，交AC于点H，当PH ＝2HQ时，求点P的坐标；（3）是否存在点M在抛物线上，点N在抛物线对称轴上，使得△BMN是以BN为斜边的等腰直角三角形，若存在，直接写出点M的横坐标；若不存在，请说明理由．3．（2023•碑林区校级一模）二次函数y＝ax2+bx+2的图象交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．4．（2023•崂山区开学）如图1，已知二次函数y＝ax2+32x+c（a≠0）的图象与y轴交于点A（0，4）．与x轴交于点B，C，点C坐标为（8，0），连接AB、AC．（1）请直接写出二次函数y＝ax2+32x+c（a≠0）的表达式；（2）判断△ABC的形状，并说明理由；（3）如图2，若点N在线段BC上运动（不与点B，C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标；（4）若点N在x轴上运动，当以点A，N，C为顶点的三角形是等腰三角形时，请写出此时点N的坐标．5．（2023•泰山区校级一模）已知二次函数y＝ax2+32x+c（a≠0）的图象与y轴交于点A（0，4），与x轴交于点B、C，点C坐标为（8，0），连接AB、AC．（1）求出二次函数表达式；（2）判断△ABC的形状，并说明理由；（3）若点N在x轴上运动，当以点A、N、C为顶点的三角形是等腰三角形时，求出此时点N的坐标，并说明理由；（4）如图2，若点N在线段BC上运动（不与点B、C重合），过点N作NM∥AC，交AB于点M，当△AMN面积最大时，求此时点N的坐标．6．（2023•灞桥区校级二模）如图，二次函数y=−12x2−x+4的图象与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．（1）求点A、B、C的坐标；（2）若点P在抛物线对称轴上，且在x轴上方，当△PBC为等腰三角形时，求出所有符合条件的点P 的坐标．7．（2023春•仓山区校级期中）如图抛物线y＝﹣x2+bx+c交x轴于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求二次函数的解析式及顶点P的坐标；（2）过定点（1，3）的直线l：y＝kx+b与二次函数的图象相交于M，N两点．①若S△PMN＝2，求k的值；②证明：无论k为何值，△PMN恒为直角三角形．8．（2023春•兴化市月考）已知：二次函数y＝ax2+2ax﹣8a（a为常数，且a＞0）的图象与x轴交于点A、B（点A在点B的左侧），与y轴交于点C，顶点为点D．（1）分别求点A、B的坐标；（2）若△ABC是直角三角形，求该二次函数相应的表达式；（3）当a=12时，一次函数y=12x+b的图象过B点，与二次函数的对称轴交于Q点，N为一次函数图象上一点，过N点作y的平行线交二次函数图象于M点，当D、M、N、Q四点组成的四边形是平行四边形时，求N点的坐标．9．（2023•广水市模拟）二次函数y＝ax2+bx+c交x轴于点A（﹣1，0）和点B（﹣3，0），交y轴于点C（0，﹣3）．（1）求二次函数的解析式；（2）如图1，点E为抛物线的顶点，点T（0，t）为y轴负半轴上的一点，将抛物线绕点T旋转180°，得到新的抛物线，其中B，E旋转后的对应点分别记为B'，E'，当四边形BEB'E'的面积为12时，求t的值；（3）如图2，过点C作CD∥x轴，交抛物线于另一点D．点M是直线CD上的一个动点，过点M作x 轴的垂线，交抛物线于点P．是否存在点M使△PBC为直角三角形，若存在，请直接写出点M的坐标，若不存在，请说明理由．10．（2023•江油市模拟）抛物线y=ax2+114x−6与x轴交于A（t，0），B（8，0）两点，与y轴交于点C，直线y＝kx﹣6经过点B．点P在抛物线上，设点P的横坐标为m．（1）求二次函数与一次函数的解析式；（2）如图1，连接AC，AP，PC，若△APC是以CP为斜边的直角三角形，求点P的坐标；（3）如图2，若点P在直线BC上方的抛物线上，过点P作PQ⊥BC，垂足为Q，求CQ+12PQ的最大值．11．如图，已知一次函数y＝0.5x+2的图象与x轴交于点A，与二次函数y＝ax2+bx+c的图象交于y轴上的一点B，二次函数y＝ax2+bx+c的图象与x轴只有唯一的交点C，且OC＝2．（1）求二次函数的表达式；（2）点M为一次函数下方抛物线上的点，△ABM的面积最大时，求点M的坐标；（3）设一次函数y＝0.5x+2的图象与二次函数的图象的另一交点为D，已知P为x轴上的一个动点，且△PBD为直角三角形，求点P的坐标．12．（2023•儋州一模）如图，在直角坐标系中有Rt△AOB，O为坐标原点，A（0，3），B（﹣1，0），将此三角形绕原点O顺时针旋转90°，得到Rt△COD，二次函数y＝ax2+bx+c的图象刚好经过A，B，C三点．（1）求二次函数的解析式及顶点P的坐标；（2）过定点Q的直线l：y＝kx﹣k+3与二次函数图象相交于M，N两点．①若S△PMN＝2，求k的值；②证明：无论k为何值，△PMN恒为直角三角形；③当直线l绕着定点Q旋转时，△PMN外接圆圆心在一条抛物线上运动，直接写出该抛物线的表达式．13．（2023•保亭县一模）如图，二次函数y＝ax2+bx+5的图象经过点（1，8），且与x轴交于A、B两点，与y轴交于点C，其中点A（﹣1，0），M为抛物线的顶点．（1）求二次函数的解析式；（2）求△MCB的面积；（3）在坐标轴上是否存在点N，使得△BCN为直角三角形？若存在，求出点N的坐标；若不存在，请说明理由．14．（2022秋•蔡甸区期末）如图，一次函数y=12x+1的图象与x轴交于点A，与y轴交于点B，二次函数y=12x2+bx+c的图象与一次函数y=12x+1的图象交于B、C两点，与x轴交于D、E两点，且D点坐标为（1，0）．（1）求抛物线的解析式；（2）在x轴上找一点P，使|PB﹣PC|最大，求出点P的坐标；（3）在x轴上是否存在点P，使得△PBC是以点P为直角顶点的直角三角形？若存在，求出点P的坐标，若不存在，请说明理由．15．（2023•二道区校级一模）已知一次函数y＝x+4的图象与二次函数y＝ax（x﹣2）的图象相交于A（﹣1，b）和B，点P是线段AB上的动点（不与A、B重合），过点P作PC⊥x轴，与二次函数y＝ax（x﹣2）的图象交于点C．（1）求a、b的值；（2）如图1，M为∠APC内一点，且PM＝1，E，F分别为边P A和PC上两个动点，求△MEF周长的最小值；（3）若△P AC是直角三角形，求点C的坐标．16．（2023•靖江市一模）已知二次函数y＝ax2+bx+c（a≠0）的图象与x轴正半轴交于点A，与y轴交于点（0，−32），顶点为C（﹣1，﹣2）．（Ⅰ）求该二次函数的解析式；（Ⅱ）过A、C两点作直线，并将线段AC沿该直线向上平移，记点A、C分别平移到点D、E处．若点F在这个二次函数的图象上，且△DEF是以EF为斜边的等腰直角三角形，求点F的坐标；（Ⅲ）当p+q≥﹣2时，试确定实数p，q的值，使得当p≤x≤q时，p≤y≤q．17．（2023•泰山区一模）二次函数y＝ax2+bx+2的图象交x轴于点A（﹣1，0），点B（4，0）两点，交y 轴于点C．动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）连接BD，当t=32时，求△DNB的面积；（3）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．18．（2023•东营区一模）如图，已知二次函数的图象与x轴交于A（1，0）和B（﹣3，0）两点，与y轴交于点C（0，﹣3），直线y＝﹣2x+m经过点A，且与y轴交于点D，与抛物线交于点E．（1）求抛物线的解析式；（2）如图1，点M在AE下方的抛物线上运动，求△AME的面积最大值；（3）如图2，在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由．19．（2023•铁西区模拟）如图①，已知抛物线y＝mx2﹣3mx﹣4m（m＜0）的图象与x轴交于A、B两点（A 在B的左侧），与y的正半轴交于点C，连结BC，二次函数的对称轴与x轴交于点E，且OC＝2OE．（1）求出抛物线的解析式；（2）如图②Q（t，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，若△MCN与△BQM相似，请求出Q的坐标；（3）如图②Q（t，0）是x的正半轴上一点，过点Q作y轴的平行线，与直线BC交于点M，与抛物线交于点N，连结CN，将△CMN沿CN翻折，M的对应点为M'，是否存在点Q，使得M'恰好落在y轴上？若存在，请求出Q的坐标；若不存在，请说明理由．20．（2023•东胜区模拟）如图，在平面直角坐标系中，二次函数的图象交坐标轴于A（﹣2，0），B（4，0），C（0，8）三点，点P是直线BC上方抛物线上的一个动点．（1）求这个二次函数的解析式；（2）动点P运动到什么位置时，△PBC的面积最大，求此时P点坐标及△PBC面积的最大值；（3）在y轴上是否存在点Q，使以O，B，Q为顶点的三角形与△AOC相似？若存在，请直接写出点Q 的坐标；若不存在，请说明理由．。

二次函数中三角形存在性问题（二）1.相似三角形2.等腰直角三角形例一：1.如图,抛物线经过三点A（1，0）,B（4,0）,C（0，-2）(1)求出抛物线的解析式;(2)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以B,P,M为顶点的三角形与OBC△相似(相似比不为1）？若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.2.如图,抛物线与x轴交于A（1,0）、B（-3,0）两点,与y轴交于点C（0,3）,设抛物线的顶点为D.(1)求该抛物线的解析式与顶点D的坐标.(2)试判断△BCD的形状,并说明理由.(3)探究坐标轴上是否存在点P,使得以P、A、C为顶点的三角形与△BCD相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.y=向左平移1个单位，再向下平移4个单位，得到抛物线3.如图，在平面直角坐标系xOy中，抛物线2x()k-=2，所得抛物线与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，顶点为D。

xy+h（1）求h、k的值。

（2）判断△ACD的形状，并说明理由。

（3）在线段AC上是否存在点M，使△AOM与△ABC相似？若存在，求出点M的坐标；若不存在，说明理由。

4.如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y 轴上，OA=OD=2，OC=OE=4，2OB=OD，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M．点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．（1）求经过B、E、C三点的抛物线的解析式；（2）是否存在点P，使得以P、Q、M为顶点的三角形与△AOD相似？若存在，求出满足条件的点P的坐标；若不存在，请说明理由．5. 在平面直角坐标系中,现将一块等腰直角三角板ABC 放在第二象限,斜靠在两坐标轴上,且点A （0,2）,点C （-1,0）,如图所示:抛物线22-+=ax ax y 经过点B.(1)求点B 的坐标; (2)求抛物线的解析式;(3)在抛物线上是否还存在点P(点B 除外),使△ACP 仍然是以AC 为直角边的等腰直角三角形?若存在,求所有点P 的坐标;若不存在,请说明理由.6.如图，在平面直角坐标系中，点A 、B 在x 轴上，点C 、D 在y 轴上，且OB=OC=3，OA=OD=1，抛物线（1）求这条抛物线的解析式。

二次函数背景下的相似三角形存在性问题
二次函数背景下的相似三角形存在性问题是中考数学常考的题型，在考试中一般出现在压轴题的位置，综合性强，难度略大。

这篇文章主要来讨论下二次函数背景下的相似三角形存在性问题的解题思路方法及应用举例。

【模型解读】
在坐标系中确定点，使得由该点及其他点构成的三角形与其他三角形相似，即为“相似三角形存在性问题”．
【相似判定】
判定1：三边对应成比例的两个三角形是相似三角形；
判定2：两边对应成比例且夹角相等的两个三角形是相似三角形；
判定3：有两组角对应相等的三角形是相似三角形．
以上也是坐标系中相似三角形存在性问题的方法来源，根据题目给的已知条件选择恰当的判定方法，解决问题．
【题型分析】
通常相似的两三角形有一个是已知的，而另一三角形中有1或2个动点，即可分为“单动点”类、“双动点”两类问题．
【思路总结】
根据相似三角形的做题经验，可以发现，判定1基本是不会用的，这里也一样不怎么用，对比判定2、3可以发现，都有角相等！
所以，要证相似的两个三角形必然有相等角，关键点也是先找到一组相等角．
然后再找：
思路1：两相等角的两边对应成比例；
思路2：还存在另一组角相等．
事实上，坐标系中在已知点的情况下，线段长度比角的大小更容易表示，因此选择方法可优先考虑思路1．
一、如何得到相等角？
二、如何构造两边成比例或者得到第二组角？
搞定这两个问题就可以了．
【例题】
【分析】
综上所述，点P的坐标为（3，2）或（3，9）．
【总结】
【练习】
声明：文章图文来源网络，意在分享，仅限交流学习使用，如有分享不当或侵权，请联系删除。

中考数学复习---二次函数中三角形存在性问题压轴题练习（含答案解析）一．相似三角形的存在性1．（2022•陕西）已知抛物线y＝ax2+bx﹣4经过点A（﹣2，0），B（4，0），与y 轴的交点为C．（1）求该抛物线的函数表达式；（2）若点P是该抛物线上一点，且位于其对称轴l的右侧，过点P分别作l，x 轴的垂线，垂足分别为M，N，连接MN．若△PMN和△OBC相似，求点P的坐标．【解答】解：（1）把A（﹣2，0），B（4，0）代入y＝ax2+bx﹣4得：，解得，∴抛物线的函数表达式为y＝x2﹣x﹣4；（2）如图：∵y＝x2﹣x﹣4＝（x﹣1）2﹣，∴抛物线y＝x2﹣x﹣4的对称轴是直线x＝1，在y＝x2﹣x﹣4中，令x＝0得y＝﹣4，∴C（0，﹣4），∴OB＝OC＝4，∴△BOC是等腰直角三角形，∵△PMN和△OBC相似，∴△PMN是等腰直角三角形，∵PM⊥直线x＝1，PN⊥x轴，∴∠MPN＝90°，PM＝PN，设P（m，m2﹣m﹣4），∴|m﹣1|＝|m2﹣m﹣4|，∴m﹣1＝m2﹣m﹣4或m﹣1＝﹣m2+m+4，解得m＝+2或m＝﹣+2或m＝或m＝﹣，∵点P是该抛物线上一点，且位于其对称轴直线x＝1的右侧，∴P的坐标为（+2，+1）或（，1﹣）．2．（2022•绵阳）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B两点，交y轴于点C（0，3），顶点D的横坐标为1．（1）求抛物线的解析式；（2）在y轴的负半轴上是否存在点P使∠APB+∠ACB＝180°，若存在，求出点P的坐标，若不存在，请说明理由；（3）过点C作直线l与y轴垂直，与抛物线的另一个交点为E，连接AD，AE，DE，在直线l下方的抛物线上是否存在一点M，过点M作MF⊥l，垂足为F，使以M，F，E三点为顶点的三角形与△ADE相似？若存在，请求出M点的坐标，若不存在，请说明理由．【解答】解：（1）∵顶点D的横坐标为1，∴抛物线的对称轴为直线x＝1，∵A（﹣1，0），∴B（3，0），∴设抛物线的解析式为：y＝a（x+1）（x﹣3），将C（0，3）代入抛物线的解析式，则﹣3a＝3，解得a＝﹣1，∴抛物线的解析式为：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．（2）存在，P（0，﹣1），理由如下：∵∠APB+∠ACB＝180°，∴∠CAP+∠CBP＝180°，∴点A，C，B，P四点共圆，如图所示，由（1）知，OB＝OC＝3，∴∠OCB＝∠OBC＝45°，∴∠APC＝∠ABC＝45°，∴△AOP是等腰直角三角形，∴OP＝OA＝1，∴P（0，﹣1）．（3）存在，理由如下：由（1）知抛物线的解析式为：y＝﹣x2+2x+3，∴D（1，4），由抛物线的对称性可知，E（2，3），∵A（﹣1，0），∴AD＝2，DE＝，AE＝3．∴AD2＝DE2+AE2，∴△ADE是直角三角形，且∠AED＝90°，DE：AE＝1：3．∵点M在直线l下方的抛物线上，∴设M（t，﹣t2+2t+3），则t＞2或t＜0．∴EF＝|t﹣2|，MF＝3﹣（﹣t2+2t+3）＝t2﹣2t，若△MEF与△ADE相似，则EF：MF＝1：3或MF：EF＝1：3，∴|t﹣2|：（t2﹣2t）＝1：3或（t2﹣2t）：|t﹣2|＝1：3，解得t＝2（舍）或t＝3或﹣3或（舍）或﹣，∴M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．综上，存在点M，使以M，F，E三点为顶点的三角形与△ADE相似，此时点M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．3．（2022•恩施州）在平面直角坐标系中，O为坐标原点，抛物线y＝﹣x2+c与y 轴交于点P（0，4）．（1）直接写出抛物线的解析式．（2）如图，将抛物线y＝﹣x2+c向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．（3）直线BC与抛物线y＝﹣x2+c交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．（4）若将抛物线y＝﹣x2+c进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出抛物线y＝﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标．【解答】解：（1）∵抛物线y＝﹣x2+c与y轴交于点P（0，4），∴c＝4，∴抛物线的解析式为y＝﹣x2+4；（2）△BCQ是直角三角形．理由如下：将抛物线y＝﹣x2+4向左平移1个单位长度，得新抛物线y＝﹣（x+1）2+4，∴平移后的抛物线顶点为Q（﹣1，4），令x＝0，得y＝﹣1+4＝3，∴C（0，3），令y＝0，得﹣（x+1）2+4＝0，解得：x1＝1，x2＝﹣3，∴B（﹣3，0），A（1，0），如图1，连接BQ，CQ，PQ，∵P（0，4），Q（﹣1，4），∴PQ⊥y轴，PQ＝1，∵CP＝4﹣3＝1，∴PQ＝CP，∠CPQ＝90°，∴△CPQ是等腰直角三角形，∴∠PCQ＝45°，∵OB＝OC＝3，∠BOC＝90°，∴△BOC是等腰直角三角形，∴∠BCO＝45°，∴∠BCQ＝180°﹣45°﹣45°＝90°，∴△BCQ是直角三角形．（3）在x轴上存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似．∵△ABC是锐角三角形，∠ABC＝45°，∴以B、N、T三点为顶点的三角形与△ABC相似，必须∠NBT＝∠ABC＝45°，即点T在y轴的右侧，设T（x，0），且x＞0，则BT＝x+3，∵B（﹣3，0），A（1，0），C（0，3），∴∠ABC＝45°，AB＝4，BC＝3，设直线BC的解析式为y＝kx+b，则，解得：，∴直线BC的解析式为y＝x+3，由，解得：，，∴M（﹣，），N（，），∴BN＝×＝，①当△NBT∽△CBA时，则＝，∴＝，解得：x＝，∴T（，0）；②当△NBT∽△ABC时，则＝，∴＝，解得：x＝，∴T（，0）；综上所述，点T的坐标T（，0）或（，0）．（4）抛物线y＝﹣x2+4的顶点为P（0，4），∵直线BC的解析式为y＝x+3，∴直线BC与y轴的夹角为45°，当抛物线沿着垂直直线BC的方向平移到只有1个公共点时，平移距离最小，此时向右和向下平移距离相等，设平移后的抛物线的顶点为P′（t，4﹣t），则平移后的抛物线为y＝﹣（x﹣t）2+4﹣t，由﹣（x﹣t）2+4﹣t＝x+3，整理得：x2+（1﹣2t）x+t2+t﹣1＝0，∵平移后的抛物线与直线BC最多只有一个公共点，∴Δ＝（1﹣2t）2﹣4（t2+t﹣1）＝0，解得：t＝，∴平移后的抛物线的顶点为P′（，），平移的最短距离为．二．直角三角形的存在性4．（2022•广安）如图，在平面直角坐标系中，抛物线y＝ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，﹣4），点C 坐标为（2，0）．（1）求此抛物线的函数解析式．（2）点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．（3）点P为该抛物线对称轴上的动点，使得△P AB为直角三角形，请求出点P 的坐标．【解答】解：（1）∵抛物线y＝ax2+x+m（a≠0）的图象经过点B（0，﹣4），点C（2，0），∴，解得，∴抛物线的解析式为y＝x2+x﹣4；（2）存在．理由：如图1中，设D （t ，t 2+t ﹣4），连接OD ．令y ＝0，则x 2+x ﹣4＝0，解得x ＝﹣4或2，∴A （﹣4，0），C （2，0），∵B （0，﹣4），∴OA ＝OB ＝4，∵S △ABD ＝S △AOD +S △OBD ﹣S △AOB ＝×4×（﹣﹣t +4）+×4×（﹣t ）﹣×4×4＝﹣t 2﹣4t ＝﹣（t +2）2+4，∵﹣1＜0，∴t ＝﹣2时，△ABD 的面积最大，最大值为4，此时D （﹣2，﹣4）； （3）如图2中，设抛物线的对称轴交x 轴于点N ，过点B 作BM ⊥抛物线的对称轴于点M ．则N （﹣1.0）．M （﹣1，﹣4）；∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝∠OBA＝45°，当∠P1AB＝90°时，△ANP1是等腰直角三角形，∴AN＝NP1＝3，∴P1（﹣1，3），当∠ABP2＝90°时，△BMP2是等腰直角三角形，可得P2（﹣1，﹣5），当∠APB＝90°时，设P（﹣1，n），设AB的中点为J，连接PJ，则J（﹣2，﹣2），∴PJ＝AB＝2，∴12+（n+2）2＝（2）2，解得n＝﹣2或﹣﹣2，∴P3（﹣1，﹣2），P4（﹣1，﹣﹣2），综上所述，满足条件的点P的坐标为（﹣1，3）或（﹣1，﹣5）或（﹣1，﹣2）或（﹣1，﹣﹣2）．5．（2022•辽宁）如图，抛物线y＝ax2﹣3x+c与x轴交于A（﹣4，0），B两点，与y轴交于点C（0，4），点D为x轴上方抛物线上的动点，射线OD交直线AC 于点E，将射线OD绕点O逆时针旋转45°得到射线OP，OP交直线AC于点F，连接DF．（1）求抛物线的解析式；（2）当点D在第二象限且＝时，求点D的坐标；（3）当△ODF为直角三角形时，请直接写出点D的坐标．【解答】解：（1）将点A（﹣4，0），C（0，4）代入y＝ax2﹣3x+c，∴，解得，∴y＝﹣x2﹣3x+4；（2）过点D作DG⊥AB交于G，交AC于点H，设直线AC的解析式为y＝kx+b，∴，解得，∴y＝x+4，设D（n，﹣n2﹣3n+4），H（n，n+4），∴DH＝﹣n2﹣4n，∵DH∥OC，∴＝＝，∵OC＝4，∴DH＝3，∴﹣n2﹣4n＝3，解得n＝﹣1或n＝﹣3，∴D（﹣1，6）或（﹣3，4）；（3）设F（t，t+4），当∠FDO＝90°时，过点D作MN⊥y轴交于点N，过点F作FM⊥MN交于点M，∵∠DOF＝45°，∴DF＝DO，∵∠MDF+∠NDO＝90°，∠MDF+∠MFD＝90°，∴∠NDO＝∠MFD，∴△MDF≌△NOD（AAS），∴DM＝ON，MF＝DN，∴DN+ON＝﹣t，DN＝ON+（﹣t﹣4），∴DN＝﹣t﹣2，ON＝2，∴D点纵坐标为2，∴﹣x2﹣3x+4＝2，解得x＝或x＝，∴D点坐标为（，2）或（，2）；当∠DFO＝90°时，过点F作KL⊥x轴交于L点，过点D作DK⊥KL交于点K，∵∠KFD+∠LFO＝90°，∠KFD+∠KDF＝90°，∴∠LFO＝∠KDF，∵DF＝FO，∴△KDF≌△LFO（AAS），∴KD＝FL，KF＝LO，∴KL＝t+4﹣t＝4，∴D点纵坐标为4，∴﹣x2﹣3x+4＝4，解得x＝0或x＝﹣3，∴D（0，4）或（﹣3，4）；综上所述：D点坐标为（，2）或（，2）或（0，4）或（﹣3，4）．三．等腰三角形的存在性6．（2022•百色）已知抛物线经过A（﹣1，0）、B（0，3）、C（3，0）三点，O 为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM，交BC于点F．（1）求抛物线的表达式；（2）求证：∠BOF＝∠BDF；（3）是否存在点M，使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长．【解答】（1）解：设抛物线的表达式为y＝ax2+bx+c，把A（﹣1，0）、B（0，3）、C（3，0）代入得：，解得，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）证明：∵正方形OBDC，∴∠OBC＝∠DBC，BD＝OB，∵BF＝BF，∴△BOF≌△BDF，∴∠BOF＝∠BDF；（3）解：∵抛物线交正方形OBDC的边BD于点E，∴令y＝3，则3＝﹣x2+2x+3，解得：x1＝0，x2＝2，∴E（2，3），①如图，当M在线段BD的延长线上时，∠BDF为锐角，∴∠FDM为钝角，∵△MDF为等腰三角形，∴DF＝DM，∴∠M＝∠DFM，∴∠BDF＝∠M+∠DFM＝2∠M，∵BM∥OC，∴∠M＝∠MOC，由（2）得∠BOF＝∠BDF，∴∠BDF+∠MOC＝3∠M＝90°，∴∠M＝30°，在Rt△BOM中，BM＝，∴ME＝BM﹣BE＝3﹣2；②如图，当M在线段BD上时，∠DMF为钝角，∵△MDF为等腰三角形，∴MF＝DM，∴∠BDF＝∠MFD，∴∠BMO＝∠BDF+∠MFD＝2∠BDF，由（2）得∠BOF＝∠BDF，∴∠BMO＝2∠BOM，∴∠BOM+∠BMO＝3∠BOM＝90°，∴∠BOM＝30°，在Rt△BOM中，BM＝，∴ME＝BE﹣BM＝2﹣，综上所述，ME的值为：3﹣2或2﹣．7．（2022•山西）综合与探究如图，二次函数y＝﹣x2+x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m．过点P作直线PD⊥x轴于点D，作直线BC交PD于点E．（1）求A，B，C三点的坐标，并直接写出直线BC的函数表达式；（2）当△CEP是以PE为底边的等腰三角形时，求点P的坐标；（3）连接AC，过点P作直线l∥AC，交y轴于点F，连接DF．试探究：在点P 运动的过程中，是否存在点P，使得CE＝FD，若存在，请直接写出m的值；若不存在，请说明理由．【解答】解：（1）在y＝﹣x2+x+4中，令x＝0得y＝4，令y＝0得x＝8或x＝﹣2，∴A（﹣2，0），B（8，0），C（0，4），设直线BC解析式为y＝kx+4，将B（8，0）代入得：8k+4＝0，解得k＝﹣，∴直线BC解析式为y＝﹣x+4；（2）过C作CG⊥PD于G，如图：设P（m，﹣m2+m+4），∴PD＝﹣m2+m+4，∵∠COD＝∠PDO＝∠CGD＝90°，∴四边形CODG是矩形，∴DG＝OC＝4，CG＝OD＝m，∴PG＝PD﹣DG＝﹣m2+m+4﹣4＝﹣m2+m，∵CP＝CE，CG⊥PD，∴GE＝PG＝﹣m2+m，∵∠GCE＝∠OBC，∠CGE＝90°＝∠BOC，∴△CGE∽△BOC，∴＝，即＝，解得m＝0（舍去）或m＝4，∴P（4，6）；（3）存在点P，使得CE＝FD，理由如下：过C作CH⊥PD于H，如图：设P（m，﹣m2+m+4），由A（﹣2，0），C（0，4）可得直线AC解析式为y＝2x+4，根据PF∥AC，设直线PF解析式为y＝2x+b，将P（m，﹣m2+m+4）代入得：﹣m2+m+4＝2m+b，∴b＝﹣m2﹣m+4，∴直线PF解析式为y＝2x﹣m2﹣m+4，令x＝0得y＝﹣m2﹣m+4，∴F（0，﹣m2﹣m+4），∴OF＝|﹣m2﹣m+4|，同（2）可得四边形CODH是矩形，∴CH＝OD，∵CE＝FD，∴Rt△CHE≌Rt△DOF（HL），∴∠HCE＝∠FDO，∵∠HCE＝∠CBO，∴∠FDO＝∠CBO，∴tan∠FDO＝tan∠CBO，∴＝，即＝，∴﹣m2﹣m+4＝m或﹣m2﹣m+4＝﹣m，解得m＝2﹣2或m＝﹣2﹣2或m＝4或m＝﹣4，∵P在第一象限，∴m＝2﹣2或m＝4．8．（2022•东营）如图，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C．（1）求抛物线的表达式；（2）在对称轴上找一点Q，使△ACQ的周长最小，求点Q的坐标；（3）点P是抛物线对称轴上的一点，点M是对称轴左侧抛物线上的一点，当△PMB是以PB为腰的等腰直角三角形时，请直接写出所有点M的坐标．【解答】解：（1）将点A（﹣1，0），点B（3，0）代入y＝ax2+bx﹣3，∴，解得，∴y＝x2﹣2x﹣3；（2）连接CB交对称轴于点Q，∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的对称轴为直线x＝1，∵A、B关于对称轴x＝1对称，∴AQ＝BQ，∴AC+AQ+CQ＝AC+CQ+BQ≥AC+BC，当C、B、Q三点共线时，△ACQ的周长最小，∵C（0，﹣3），B（3，0），设直线BC的解析式为y＝kx+b，∴，解得，∴y＝x﹣3，∴Q（1，﹣2）；（3）当∠BPM＝90°时，PM＝PB，∴M点与A点重合，∴M（﹣1，0）；当∠PBM＝90°时，PB＝BM，如图1，当P点在M点上方时，过点B作x轴的垂线GH，过点P作PH⊥GH 交于H，过点M作MG⊥HG交于G，∵∠PBM＝90°，∴∠PBH+∠MBG＝90°，∵∠PBH+∠BPH＝90°，∴∠MBG＝∠BPH，∵BP＝BM，∴△BPH≌△MBG（AAS），∴BH＝MG，PH＝BG＝2，设P（1，t），则M（3﹣t，﹣2），∴﹣2＝（3﹣t）2﹣2（3﹣t）﹣3，解得t＝2+或t＝2﹣，∴M（1﹣，﹣2）或（1+，﹣2），∵M点在对称轴的左侧，∴M点坐标为（1﹣，﹣2）；如图2，当P点在M点下方时，同理可得M（3+t，2），∴2＝（3+t）2﹣2（3+t）﹣3，解得t＝﹣2+（舍）或t＝﹣2﹣，∴M（1﹣，2）；综上所述：M点的坐标为（1﹣，﹣2）或（1﹣，2）或（﹣1，0）．9．（2022•枣庄）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点．（1）求抛物线的关系式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出P点坐标；（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE 内（包括△OAE的边界），求h的取值范围；（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），∴，解得，∴抛物线的解析式为：y＝x2﹣4x+3；（2）如图，过P作PG∥y轴，交OE于点G，设P（m，m2﹣4m+3），∵OE平分∠AOB，∠AOB＝90°，∴∠AOE＝45°，∴△AOE是等腰直角三角形，∴AE＝OA＝3，∴E（3，3），∴直线OE的解析式为：y＝x，∴G（m，m），∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，∴S△OPE ＝S△OPG+S△EPG＝PG•AE＝×3×（﹣m2+5m﹣3）＝﹣（m2﹣5m+3）＝﹣（m﹣）2+，∵﹣＜0，∴当m＝时，△OPE面积最大，此时，P点坐标为（，﹣）；（3）由y＝x2﹣4x+3＝（x﹣2）2﹣1，得抛物线l的对称轴为直线x＝2，顶点为（2，﹣1），抛物线L向上平移h个单位长度后顶点为F（2，﹣1+h）．设直线x＝2交OE于点M，交AE于点N，则E（3，3），∵直线OE的解析式为：y＝x，∴M（2，2），∵点F在△OAE内（包括△OAE的边界），∴2≤﹣1+h≤3，解得3≤h≤4；（4）设P（m，m2﹣4m+3），分四种情况：①当P在对称轴的左边，且在x轴下方时，如图，过P作MN⊥y轴，交y轴于M，交l于N，∴∠OMP＝∠PNF＝90°，∵△OPF是等腰直角三角形，∴OP＝PF，∠OPF＝90°，∴∠OPM+∠NPF＝∠PFN+∠NPF＝90°，∴∠OPM＝∠PFN，∴△OMP≌△PNF（AAS），∴OM＝PN，∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，解得：m＝（舍）或，∴P的坐标为（，）；②当P在对称轴的左边，且在x轴上方时，同理得：2﹣m＝m2﹣4m+3，解得：m1＝（舍）或m2＝，∴P的坐标为（，）；③当P在对称轴的右边，且在x轴下方时，如图，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN＝FM，则﹣m2+4m﹣3＝m﹣2，解得：m1＝或m2＝（舍）；P的坐标为（，）；④当P在对称轴的右边，且在x轴上方时，如图，同理得m2﹣4m+3＝m﹣2，解得：m＝或（舍），P的坐标为：（，）；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．方法二：作直线DE：y＝x﹣2，E（1，﹣1）是D点（2，0）绕O点顺时针旋转45°并且OD缩小倍得到，易知直线DE即为对称轴上的点绕O点顺时针旋转45°，且到O点距离缩小倍的轨迹，联立直线DE和抛物线解析式得x2﹣4x+3＝x﹣2，解得x1＝，x2＝，同理可得x3＝或x4＝；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．10．（2023•澄城县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）、B，与y轴交于点C（0，3），直线l是抛物线的对称轴．（1）求抛物线的函数解析式；（2）在对称轴l上是否存在点M，使△MAC为等腰三角形，若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）把点A（﹣1，0）、点C（0，3）分别代入y＝﹣x2+bx+c，得．解得．故该抛物线解析式为：y＝﹣x2+2x+3；（2）由（1）知，该抛物线解析式为：y＝﹣x2+2x+3．则该抛物线的对称轴为直线x＝﹣＝1．故设M（1，m）．∵A（﹣1，0）、点C（0，3），∴AC2＝10，AM2＝4+m2，CM2＝1+（m﹣3）2．①若AC＝AM时，10＝4+m2，解得m＝±．∴点M的坐标为（1，）或（1，﹣）；②若AC＝CM时，10＝1+（m﹣3）2，解得m＝0或m＝6，∴点M的坐标为（1，0）或（1，6）．当点M的坐标为（1，6）时，点A、C、M共线，∴点M的坐标为（1，0）；③当AM＝CM时，4+m2＝1+（m﹣3）2，解得m＝1，∴点M的坐标为（1，1）．综上所述，符合条件的点M的坐标为（1，）或（1，﹣）或（1，0）或（1，1）．11．（2023•碑林区校级一模）二次函数y＝ax2+bx+2的图象交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．【解答】解：（1）将点（﹣1，0），B（4，0）代入y＝ax2+bx+2，∴a＝﹣，b＝，∴y＝﹣x2+x+2；（2）∵BM＝5﹣2t，∴M（2t﹣1，0），设P（2t﹣1，m），∵PC2＝（2t﹣1）2+（m﹣2）2，PB2＝（2t﹣5）2+m2，∵PB＝PC，∴（2t﹣1）2+（m﹣2）2＝（2t﹣5）2+m2，∴m＝4t﹣5，∴P（2t﹣1，4t﹣5），∵PC⊥PB，∴×＝﹣1，∴t＝1或t＝2，∴M（1，0）或M（3，0），∴D（1，3）或D（3，2）．12．（2023•东洲区模拟）抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，与y轴正半轴交于点C．（1）求此抛物线解析式；（2）如图①，连接BC，点P为抛物线第一象限上一点，设点P的横坐标为m，△PBC的面积为S，求S与m的函数关系式，并求S最大时P点坐标；（3）如图②，连接AC，在抛物线的对称轴上是否存在点M，使△MAC为等腰三角形？若存在，请直接写出符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，∴，解得：，∴抛物线解析式为y＝﹣x2+2x+3；（2）点P作PF⊥x轴于点F，交BC于点E，设BC直线解析式为：y＝kx+b，∵B（3，0），C（0，3），∴，解得，∴y＝﹣x+3，由题意可知P（m，﹣m2+2m+3），E（m，﹣m+3），S＝S△PBE+S△PCE，S＝PE•OB＝（﹣m2+2m+3+m﹣3）×3，，∵，∴当时，S有最大值，此时P点坐标为；（3）存在，M1（1，0），，，M4（1，1），①当AC＝AM时，如图，设对称轴l与AB交于点E，则，∵AM2＝AE2+EM2，∴，解得：，∴M点的坐标为或，②当AC＝MC时，则OC为AM的垂直平分线．因此M与E重合，因此，M点的坐标为（1，0），③当AM＝CM时，如图，设M点的坐标为（1，n），则AM2＝22+n2＝4+n2，CM2＝12+（3﹣n）2，∴4+n2＝12+（3﹣n）2，解得：n＝1，∴M点的坐标为（1，1），综上可知，潢足条件的M点共四个，其坐标为M1（1，0），，，M4（1，1）．13．（2023•三亚一模）如图，抛物线y＝ax2+3x+c（a≠0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，8），顶点为D，连接AC，CD，DB，直线BC 与抛物线的对称轴l交于点E．（1）求抛物线的解析式和直线BC的解析式；（2）求四边形ABDC的面积；（3）P是第一象限内抛物线上的动点，连接PB，PC，当S△PBC ＝S△ABC时，求点P的坐标；（4）在抛物线的对称轴l上是否存在点M，使得△BEM为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+3x+c（a≠0）过点A（﹣2，0）和C（0，8），∴，解得，∴抛物线的解析式为y＝﹣x2+3x+8．令y＝0，得．解得x1＝﹣2，x2＝8．∴点B的坐标为（8，0）．设直线BC的解析式为y＝kx+b．把点B（8，0），C（0，8）分别代入y＝kx+b，得，解得，∴直线BC的解析式为y＝﹣x+8．（2）如图1，设抛物线的对称轴l与x轴交于点H．∵抛物线的解析式为，∴顶点D的坐标为．∴S四边形ABDC ＝S△AOC+S梯形OCDH+S△BDH＝＝＝70．（3）∵．∴．如图2，过点P作PG⊥x轴，交x轴于点G，交BC于点F．设点．∵点F在直线BC上，∴F（t，﹣t+8）．∴．∴．∴．解得t1＝2，t2＝6．∴点P的坐标为（2，12）或P（6，8）．（4）存在．∵△BEM为等腰三角形，∴BM＝EM或BE＝BM或BE＝EM，设M（3，m），∵B（8，0），E（3，5），∴BE＝＝5，EM＝|m﹣5|，BM＝＝，当BM＝EM时，＝|m﹣5|，∴m2+25＝（m﹣5）2，解得：m＝0，∴M（3，0）；当BE＝BM时，5＝，∴m2+25＝50，解得：m＝﹣5或m＝5（舍去），∴M（3，﹣5）；当BE＝EM时，5＝|m﹣5|，解得：m＝5+5或m＝5﹣5，∴M（3，5+5）或（3，5﹣5），综上所述，点M的坐标为（3，0）或（3，﹣5）或（3，5+5）或（3，5﹣5）．14．（2023•南海区一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3（a ＞0）与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC 于点N．求线段PM的最大值和此时点P的坐标；（3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）将A（﹣1，0），B（3，0）代入函数y＝ax2+bx﹣3（a＞0）中，得，解得，∴解析式为y＝x2﹣2x﹣3，故抛物线解析式为y＝x2﹣2x﹣3；（2）当x＝0时，y＝3，∴C（0，﹣3），∵B（3，0），∴∠OCB＝∠OBC＝45°，∵PN∥y轴，∴∠MNP＝45°，∵PM⊥BC，∴PM＝PN，则当PN最大时，PM也最大，设BC的解析式为y＝mx+n，∴，解得，∴BC解析式为y＝x﹣3，设P（x，x2﹣2x﹣3），N（x，x﹣3），∴PN＝x﹣3﹣（x2﹣2x﹣3）＝﹣（x﹣）2+，当x＝时，PN最大，则PM＝PN＝×＝，∴P（，），故PM最大值为，P点坐标为（，﹣）；（3）存在，点E的坐标为（﹣5，0），（，0），（0，0），（，0）．∵CEQ是以CQ为斜边的等腰直角三角形，∴设Q（x，x2﹣2x﹣3），①如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，∵∠CEQ＝90°，∴∠QEM+∠CEN＝90°，∵∠QEM+∠MQE＝90°，∴∠EQM＝∠CEN，∵∠CNE＝∠QME＝90°，EC＝EQ，∴△EMQ≌△CNE（AAS），∴CN＝EM＝x2﹣2x﹣3，MQ＝EN＝3，∴|x Q|+MQ＝CN，﹣x+3＝x2﹣2x﹣3，解得x＝﹣2，x＝3（舍去），∴OE＝CM＝2+3＝5，E（﹣5，0），②如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴﹣x+x2﹣2x﹣3＝3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），③如图，点E和点O重合，点Q和点B重合，此时E（0，0），④如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴x+3＝x2﹣2x﹣3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），综上所述，点E的坐标为（﹣5，0），（，0），（0，0），（，0）41。

中考数学压轴题：二次函数综合、相似三角形存在性问题1．如图，抛物线y＝ax2+（a+3）x+3（a≠0）与x轴交于点A（4，0），与y轴交于点B，在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．（1）求a的值和直线AB的函数表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，若C1C2=65，求m的值．2．如图，抛物线y＝ax2+bx+√3与x轴交于A（﹣3，0），B（1，0）两点．与y轴交于点C．（1）求抛物线的解析式，并直接写出点D的坐标；（2）连接AC，在第二象限内存在点M，使得以M、O、A为顶点的三角形与△AOC相似．请直接写出所有符合条件的点M坐标．3．如图，二次函数y＝ax2+bx﹣3的图象与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．该抛物线的顶点为M．（1）求该抛物线的解析式；（2）判断△BCM的形状，并说明理由；（3）探究坐标轴上是否存在点P，使得以点P、A、C为顶点的三角形与△BCM相似？若存在，请直接写出点P的坐标；若不存在，请说明理由．4．如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y＝x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．5．如图，抛物线y＝ax2+bx﹣1（a≠0）经过A（﹣1，0），B（2，0）两点，与y轴交于点C．（1）求抛物线的解析式及顶点D的坐标；（2）点P在抛物线的对称轴上，当△ACP的周长最小时，求出点P的坐标；（3）点N在抛物线上，点M在抛物线的对称轴上，是否存在以点N为直角顶点的Rt△DNM与Rt△BOC相似？若存在，请求出所有符合条件的点N的坐标；若不存在，请说明理由．6．如图，已知抛物线y=13x2+bx+c经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．（1）求抛物线的解析式；（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP 的面积最大时，求点P的坐标；（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．7．如图，已知抛物线与x轴交于A（﹣1，0），B（4，0），与y轴交于C（0，﹣2）．（1）求抛物线的解析式；（2）D是C关于x轴的对称点，P是抛物线上的一点，当△PBD与△AOC相似时，求符合条件的P点的坐标．8．如图，抛物线y＝﹣x2+bx+c经过A（﹣1，0），B（4，0）两点，与y轴相交于点C，连接BC，点P为抛物线上一动点，过点P作x轴的垂线l，交直线BC于点G，交x轴于点E．（1）求抛物线的表达式；（2）当P位于y轴右边的抛物线上运动时，过点C作CF⊥直线l，F为垂足，当点P 运动到何处时，以P，C，F为顶点的三角形与△OBC相似？并求出此时点P的坐标；9．如图，已知二次函数y ＝﹣x 2+bx +c （b ，c 为常数）的图象经过点A （3，1），点C （0，4），顶点为点M ，过点A 作AB ∥x 轴，交y 轴于点D ，交该二次函数图象于点B ，连接BC ．（1）求该二次函数的解析式及点M 的坐标；（2）点P 是直线AC 上的动点，若点P ，点C ，点M 所构成的三角形与△BCD 相似，请直接写出所有点P 的坐标．10．如图，抛物线y ＝ax 2+bx 经过两点A （﹣1，1），B （2，2）．过点B 作BC ∥x 轴，交抛物线于点C ，交y 轴于点D ．（1）求此抛物线对应的函数表达式及点C 的坐标；（2）若抛物线上存在点M ，使得△BCM 的面积为72，求出点M 的坐标； （3）连接OA 、OB 、OC 、AC ，在坐标平面内，求使得△AOC 与△OBN 相似（边OA 与边OB 对应）的点N 的坐标．11．如图1，抛物线y＝ax2+1经过点A（4，﹣3），顶点为点B，点P为抛物线上的一个动点，l是过点（0，2）且垂直于y轴的直线，过P作PH⊥l，垂足为H，连接PO．（1）求抛物线的解析式，并写出其顶点B的坐标；（2）如图2，设点C（1，﹣2），问是否存在点P，使得以P，O，H为顶点的三角形与△ABC相似？若存在，求出P点的坐标；若不存在，请说明理由．。

中考数学复习之相似三角形的存在性问题（学案）知识与方法梳理：相似三角形存在性的处理思路1. 分析特征：分析背景图形中的定点、定线及不变特征，结合图形形成因素（判定等）考虑分类．注：相似三角形存在性问题主要结合对应关系及不变特征考虑分类．2. 画图求解：往往先从对应关系入手，再结合背景中的不变特征分析，综合考虑对应关系和不变特征后列方程求解． 注：相似三角形列方程往往借助对应边成比例；3. 结果验证：回归点的运动范围，画图或推理，验证结果．例1：在平面直角坐标系中，二次函数图象的顶点坐标为 C (4，，且与x 轴的两个交点间的距离为6． （1）求二次函数的解析式；（2）在x 轴上方的抛物线上，是否存在点Q ，使得以Q ，A ，B 为顶点的三角形与△ABC 相似？如果存在，请求出点Q 的坐标；如果不存在，请说明理由．第一问：研究背景图形 【思路分析】△由顶点坐标C (4，)可知对称轴为直线x =4，利用与x 轴两个交点间的距离为6，再结合抛物线的对称性可知A （1，0)，B (7，0)．△设交点式y =a (x -1)(x -7)，再代入坐标C (4，可求解出解析式2y x =-+．【过程示范】△顶点坐标为C (4，)， △抛物线对称轴为直线x =4，又△抛物线与x 轴的两个交点间的距离为6， △由抛物线的对称性可知：A (1，0)，B (7，0)． 设抛物线的解析式为y =a (x -1)(x -7)，将C (4，)代入可得，a = △所求解析式为2y x x =． 第二问：相似三角形的存在性 【思路分析】相似三角形存在性问题也是在存在性问题的框架下进行的：△分析特征：先研究定点、动点，其中A 、B 、C 为定点，点Q 为抛物线上的动点；进一步研究此△ABC ，发现其中AC=BC ；构造辅助线：CD 垂直于x 轴，能够计算出△BAC =30°，△ACB =30°；再考虑研究△QAB ，固定线段为AB ，并且由于点Q 在x 轴上方的抛物线上，所以△QAB 为钝角（填“钝角”或“直角”）三角形．△画图求解：先考虑点Q 在抛物线对称轴右侧的情况，此时△ABQ 为钝角，要想使△ABC 与△ABQ 相似，则需要△ABQ =120°，且AB=BQ ．求解时，可根据△ABQ =120°，AB =BQ =6来求出Q 点坐标．同理，考虑点Q 在抛物线对称轴左侧时的情况．△结果验证：考虑点Q 还要在抛物线上，将点Q 代入抛物线解析式验证． 【过程示范】存在点Q 使得△QAB 与△ABC 相似．由抛物线对称性可知，AC =BC ，过点C 作CD △x 轴于D ， 则AD =3，CD在Rt△ACD 中，tan△DAC，△△BAC =△ABC =30°，△ACB =120°． △当△ACB △△ABQ 1时， △ABQ 1=120°且BQ 1=AB =6． 过点Q 1作Q 1E △x 轴，垂足为E ， 则在Rt△BQ 1E 中，BQ 1=6，△Q 1BE =60°， △Q 1E =BQ 1·sin60°=62⨯=BE =3， △E (10，0)，Q 1(10，． 当x =10时，y= △点Q 1在抛物线上．△由抛物线的对称性可知，还存在AQ 2=AB ， 此时△Q 2AB △△ACB ，点Q 2的坐标为(-2，． 综上，Q 1(10，，Q 2(-2，．练习题1. 如图，抛物线2110833y x x =-+-经过A ，B ，C 三点，BC △OB ，AB =BC ，过点C 作CD ⊥x 轴于点D ．点M是直线AB 上方的抛物线上一动点，作MN ⊥x 轴于点N ，若△AMN 与△ACD 相似，则点M 的坐标为_____________________________．OB CDAxy2. 如图，已知抛物线234y x bx c =++与坐标轴交于A ，B ，C 三点，点A 的坐标为(1，0)，过点C 的直线334y x t=-与x 轴交于点Q ，点P 是线段BC 上的一个动点，过P 作PH △OB 于点H ．若PB 5t ，且0＜t ＜1．（1）点C 的坐标是____________，b _______，c ______． （2）求线段QH 的长（用含t 的代数式表示）．（3）依点P 的变化，是否存在t 的值，使以P ，H ，Q 为顶点的三角形与△COQ 相似？若存在，求出所有符合条件的t 值；若不存在，说明理由．A BCOHP QxyyxO CB A3. 如图，抛物线213222y x x =-++与x 轴交于A ，B 两点，与y 轴交于点C ，点D (1，m )在抛物线上，直线y =-x -1与抛物线交于A ，E 两点，点P 在x 轴上，且位于点B 的左侧，若以P ，B ，D 为顶点的三角形与△ABE 相似，则点P 的坐标为__________________________________．4. 如图，已知抛物线过点A (0，6)，B (2，0)，C (7，52)．（1）求抛物线的解析式．（2）若D 是抛物线的顶点，E 是抛物线的对称轴与直线AC 的交点，F 与E 关于D 对称．求证：△CFE =△AFE ． （3）在y 轴上是否存在这样的点P ，使△AFP 与△FDC 相似？若存在，请求出所有符合条件的点P 的坐标；若不存在，请说明理由．5.如图，抛物线y=ax2+bx经过两点A(-1，1)，B(2，2)．过点B作BC△x轴，交抛物线于点C，交y轴于点D．连接OA，OB，OC，AC，点N在坐标平面内，且△AOC与△OBN相似（边OA与边OB对应），则点N的坐标为_____________________________________．6.如图，抛物线y=-x2+4与x轴交于A，B两点，与y轴交于点C，连接AC．点P是第一象限内抛物线上的一个动点，过点P作x轴的垂线，垂足为D．是否存在以P，O，D为顶点的三角形与△OAC相似？若存在，请求出点P的坐标；若不存在，请说明理由．7.如图，已知抛物线y=x2-1与x轴交于A，B两点，与y轴交于点C，过点A作AP△CB交抛物线于点P．（1）求A，B，C三点的坐标．（2）在x轴上方的抛物线上是否存在一点M，过点M作MG△x轴于点G，使以A，M，G为顶点的三角形与△PCA 相似？若存在，请求出点M的坐标；若不存在，请说明理由．8.如图，抛物线y=ax2+b与x轴交于点A，B，且点A的坐标为(1，0)，与y轴交于点C(0，1)．（1）求抛物线的解析式，并求出点B的坐标．（2）过点B作BD△CA交抛物线于点D，在x轴上点A的左侧是否存在点P，使以P，A，C为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由．9. 如图，抛物线经过A (4，0)，B (1，0)，C (0，-2)三点．（1）求抛物线的解析式．（2）P 是抛物线上一动点，过点P 作PM △x 轴，垂足为M ，是否存在点P ，使得以A ，P ，M 为顶点的三角形与△OAC 相似？若存在，请求出符合条件的点P 的坐标；若不存在，请说明理由．参考答案1. 2. （1）(0，-3)，，-3；（2）；（3）存在，或． 3. 4. （1）；（3）． 5. N 1(3，4)，N 2(4，3)，N 3(-2，-1)，N 4(-1，-2)6.存在，1P ，2(12P --+．7.（1）A (-1，0)，B (1，0)，C (0，-1)；（2）存在，M 1(-2，3)，M 2(4，15)，347()39M ，． 1257111()()2424M M -，，，94-148 0218 4 12t t QH t t ⎧-<<⎪⎪=⎨⎪-<<⎪⎩（）（）73225321121322(0)(0)75P P -，，，21462y x x =-+1241(0)(02)2P P --，，，8.（1）y =-x 2+1，B (-1，0)；（2）存在，11(0)3P ，，P 2(-2，0)． 9.（1）215222y x x =-+-；（2）存在，P 1(0，-2)，P 2(-3，-14)，P 3(2，1)，P 4(5，-2)．。

九年级数学优辅专项训练题《二次函数学专项训练》二次函数中考压轴题(三角形与存在性问题)解析精选y =ax bx C 与X 轴正半轴交于 A 、B 两点，与y 轴交于点C ,直线y =X -2经过A 、C 两点，且 AB=2. (1) 求抛物线的解析式；(2) 若直线DE 平行于X 轴并从C 点开始以每秒1个单位的速度沿y 轴正方向平移，且分别交y 轴、线段BC 于点E 、D ,同时动点P 从点B 出发，沿BO 方向以每秒2个单位速度运动，(如图2);当点P运动到原点 O 时，直线 DE 与点P 都停止运动，连 DP ,若点P 运动时间为t 秒；设S = ED O P ,当 ED OPt 为何值时，S 有最小值，并求出最小值。

(3) 在(2)的条件下，是否存在 t 的值，使以P 、B 、D 为顶点的三角形与△ ABC 相似；若存在，求t的值；若不存在，请说明理由。

∙/ AB=2 ,∙∙∙ B (4, 0)。

y =a X -2 X -4 ,代入点 C ( 0,— 2)得1I O 3•抛物线的解析式为厂一4八2 X"」4X2^2。

由题意：CE=t , PB=2t , OP=4 — 2t 。

【例1 ].已知：如图一，抛物线 ∙可设抛物线的解析式为【答案]由 y=0 得 x=2 ,∙∙∙ A (2,0)。

九年级数学优辅专项训练题《二次函数学专项训练》∙.∙ED 〃BA ,•△CED -COB o ∙O D =CO ,即E 4S o∙ED =2t oED +OP_2t+(4 —2t )_ 4 _ 1^ ED OP 2t 4 —2t -4t 2+8t _ t -1 2+12•••当t=1时，—(t —1 ) +1有最大值1。

•••当t=1时，S=ED OP 的值最小，最小值是 10ED OP(3) 存在。

设 BC 所在直线的解析式为 y=kx+b ,由B (4, 0), C (0,— 2)由题意可得：D 点的纵坐标为t — 2,贝U D 点的横坐标为2to2 2 —• BD= 4 -2t t -2 = 5 2 -t 。

二次函数中考压轴题（三角形与存在性问题）解析精选【例1】. 已知：如图一，抛物线c bx ax y 2++=与x 轴正半轴交于A 、B 两点，与y 轴交于点C ，直线2x y -=经过A 、C 两点，且AB=2. （1）求抛物线的解析式；（2）若直线DE 平行于x 轴并从C 点开始以每秒1个单位的速度沿y 轴正方向平移，且分别交y 轴、线 段BC 于点E 、D ，同时动点P 从点B 出发，沿BO 方向以每秒2个单位速度运动，（如图2）；当点P 运动到原点O 时，直线DE 与点P 都停止运动，连DP ，若点P 运动时间为t 秒 ；设OPED OPED s ⋅+=，当t 为何值时，s 有最小值，并求出最小值。

（3）在（2）的条件下，是否存在t 的值，使以P 、B 、D 为顶点的三角形与△ABC 相似；若存在，求t 的值；若不存在，请说明理由。

【答案】解：（1）在y x 2=-中，由x=0得y=－2，∴C （0，－2）。

由 y=0得 x=2，∴A （2，0）。

∵AB=2，∴B （4，0）。

∴可设抛物线的解析式为()()y a x 2x 4=--，代入点C （0，－2）得1a 4=-。

∴抛物线的解析式为()()2113y x 2x 4x x 2442=---=-+-。

（2）由题意：CE=t ，PB=2t ，OP=4－2t 。

∵ED ∥BA ，∴△CED ∽△COB 。

∴ED CE OB CO =，即ED t42=。

∴ED=2t 。

∴()()()222t+42t ED OP 41s ===ED OP 2t 42t 4t +8t t 1+1-+=⋅⋅----。

∴当t=1时，()2t 1+1--有最大值1。

∴当t=1时，ED OPs ED OP+=⋅的值最小，最小值是1。

（3）存在。

设BC 所在直线的解析式为y=kx+b ，由B （4，0），C （0，－2）得4k+b=0b=2⎧⎨-⎩，解得1k=2b=2⎧⎪⎨⎪-⎩，∴C 所在直线的解析式为1y=x 22-。