天津市实验中学2018届高三上学期期中(第三阶段)考试数学(文)试题 Word版 含解析

天津实验中学2018--2018届高三数学期中考试卷（文科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷1至2页，第Ⅱ卷3至10页。

满分150分，考试时间120分钟。

第Ⅰ卷（选择题 共50分）一．选择题：(本大题共10小题，每小题5分，共50 分。

在每小题所给出的四个选项中，只有一项是符合题目要求的)1.已知集合{}512,,1,1M x x x R P xx Z x ⎧⎫=-≤∈=≥∈⎨⎬+⎩⎭，则MP 等于（ ）A.{}03,x x x Z <≤∈B.{}03,x x x Z ≤≤∈ C. {}10,x x x Z -≤≤∈ D.{}10,x x x Z -≤<∈2．某地区第一天下雨的概率是0.7，第二天下雨的概率是0.3，那么这两天该地区可能下雨的概率是（ ）Ａ．1 Ｂ．79.0 Ｃ．58.0 Ｄ．21.0 3. 若曲线4y x =的一条切线与直线480x y +-=垂直,则此切线方程为 （ ）A. 430x y --= Ｂ.450x y +-= Ｃ.430x y -+= Ｄ. 430x y ++= 4.将函数sin (0)y x ωω=>的图象按向量(,0)6a π=-平移,平移后的图象如图所示,则平移后的图象所对应的函数解析式是（ ）Ａ．sin()6y x π=+Ｂ．sin()6y x π=- Ｃ．sin(2)3y x π=+Ｄ．sin(2)3y x π=- 5. 若互不相等的实数,,a b c 成等差数列, b a c ,,成等比数列,且310,a b c a ++==则（ ）A ．4 Ｂ．2 Ｃ．-2 Ｄ．-46.已知函数()为常数）m m x x x f (16223-++=在[-2，2]上有最大值2，则此函数在[-2，2]上最小值为 （）A ．-38 Ｂ．-30 Ｃ．-6 Ｄ．-127.在给定椭圆中,焦点到相应准线的距离为1,则该椭圆的离心率为（ ）AＢ．2 Ｃ．12 Ｄ．48．函数)0(>+=a xax y 在区间[1,2]上存在反函数的充要条件是（ ） A ．10≤<a B ．4≥a C ．410><<a a 或 D ．410≥≤<a a 或9．定义在R 上的函数f(x)满足f(x)=f(x+2)，当]5,3[∈x 时，|4|2)(--=x x f ，则)6(sin ),2(cos ),1(sin πf f f 的大小关系是（ ）A.)2(cos )1(sin )6(sinf f f <<πB.)2(cos )6(sin)1(sin f f f <<πC.)6(sin)1(sin )2(cos πf f f << D ．)6(sin)2(cos )1(sin πf f f <<10．对a,b ∈R ，记max{a,b}=⎩⎨⎧<≥b a b ba a ,,，函数)|}(2||,1max{|)(R x x x x f ∈-+=的最小值是（ ） A ．0 B ．21 C ．23D ．3第Ⅱ卷（非选择题 共100分）注意事项：1．第Ⅱ卷共8页，用钢笔或圆珠笔直接答在试题卷中。

天津市实验中学2018届高三上学期期中（第三阶段）考试数学（文）试题第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设,a b 为实数，若复数121ii a bi+=++，则（ ） A ．31,22a b == B ．3,1a b == C ．13,22a b == D ．1,3a b ==2.已知直线,a b 分别在两个不同的平面,αβ内，则“直线a 和直线b 相交”是“平面α和平面β相交”的（ ） A.充分不必耍条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件3.下列命题中的假命题．．．是（ ） A ．1,20x x R -∀∈> B ．()2,10x N x +∀∈-> C ．00,lg 1x R x ∃∈< D ．00,tan 2x R x ∃∈=4.已知数列{}n a 中，111,n n a a a n +==+，利用如图所示的程序框图计算该数列的第10项，则判断框中应填的语句是（ ）A ．10n >B ．10n ≤C ．9n <D ．9n ≤5.双曲线()222210,0x y a b a b -=>>的离心率是2，则213b a+的最小值为（ ）A ．1B ．2 CD6. 已知n S 是等差数列{}n a 的前n 项和，151,25a S ==，设n T 为数列(){}11n n a +-的前n 项和，则2015T =（ ）A ．2014B ．2014-C ．2015D ．2015- 7.设抛物线22y x =的焦点为F ，过点)M的直线与抛物线相交于,A B 两点，与抛物线的准线相较于点C ，2BF =，则BCF ∆与ACF ∆的面积之BCFACFS S ∆∆=（ ） A ．23 B ．45 C ．47 D ．128.已知函数()2log ,02sin ,210,4x x f x x x π⎧<<⎪=⎨⎛⎫≤≤⎪⎪⎝⎭⎩若存在实数1234,,,x x x x ()()()()1234f x f x f x f x ===，且1234x x x x <<<，则()()341211x x x x -⋅-⋅的取值范围是（ ）A ．()9,21B ．()20,32 C.()8,24 D ．()15,25第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）13.设全集{}*lg 1U A B x N x =⋃=∈<，若(){}21,0,1,2,3,4U A C B m m n n ⋂==+=，则集合B = ．10.已知直线:,l y x m m R =+∈ .若以点()2,0M 为圆心的圆与直线l 相切于点P ，且点P 在y 轴上，则该圆的方程为 ．11.某三棱锥的三视图如图所示，该三棱锥的体积是 ．12.若函数()()212log 45f x x x =-++在区间()32,2m m -+内单调递增，则实数m 的取值范闱为 ．13.在平面直角坐标系xOy 中，设,,A B C 是圆221x y +=上相异三点，若存在正实数,λμ使得OC OA OB λμ=+，则()223λμ+-的取值范围是 ．14.已知函数()22f x x x =--，()1,041,0x x g x x x x ⎧+>⎪=⎨⎪+≤⎩，若方程()0g f x a -=⎡⎤⎣⎦的实根个数为4，则a 的取值范围是_ ．三、解答题 （本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15. ABC ∆中，角,,A B C 所对的边分别为,,a b c，已知3c C π==.（1）若2sin 3sin A B =，求,a b ； （2）若cos B ，求sin 2A . 16.,A B 是直线0y =与函数()()22cos cos 1023xf x x ωπωω⎛⎫=++-> ⎪⎝⎭图像的两个相邻的交点，且2AB π=.（1）求ω的值和函数()f x 的单调增区间；（2）将函数()y f x =的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移4π个单位，得到函数()y g x =的图象，求函数()g x 的对称轴方程. 17.某餐厅装修，需要大块胶合板20张，小块胶合板50张，已知市场出售A B 、两种不同规格的胶合板。

2018-2018学年天津一中高三（上）第三次月考数学试卷（文科）一、选择题：（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合A={x|x2﹣5x﹣6=0}，B={x|y=log2（2﹣x）}，则A∩（∁R B）=（）A．{2，3}B．{﹣1，6}C．{3}D．{6}2．下列选项叙述错误的是（）A．命题“若x≠l，则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0，则x=1”B．若p∨q为真命题，则p，q均为真命题C．若命题p：∀x∈R，x2+x+1≠0，则¬p：∃x∈R，x2+x+1=0D．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件3．阅读如图所示的程序框图，则输出的S=（）A．14 B．30 C．20 D．554．已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a=（）A．B．1 C．2 D．5．已知双曲线﹣=1（a＞0，b＞0）的左顶点与抛物线y2=2px的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1），则双曲线的焦距为（）A．2B．2C．4D．46．如图，PC与圆O相切于点C，直线PO交圆O于A，B两点，弦CD垂直AB于E．则下面结论中，错误的结论是（）A．△BEC∽△DEA B．∠ACE=∠ACP C．DE2=OEEP D．PC2=PAAB7．已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f （log25），c=f（2m），则a，b，c的大小关系为（）A．a＜b＜c B．c＜a＜b C．a＜c＜b D．c＜b＜a8．定义在（1，+∞）上的函数f（x）满足下列两个条件：（1）对任意的x∈（1，+∞）恒有f（2x）=2f（x）成立；（2）当x∈（1，2]时，f（x）=2﹣x；记函数g（x）=f（x）﹣k（x ﹣1），若函数g（x）恰有两个零点，则实数k的取值范围是（）A．[1，2）B．C．D．二、填空题：（本大题共6小题，每小题5分，共30分．把答案填在题中横线上）9．已知（a，b∈R），其中i为虚数单位，则a+b=．10．一个几何体的三视图如图所示，则该几何体的体积为．11．已知函数f（x）=x3+ax2+b2x+1，若a是从1，2，3三个数中任取的一个数，b是从0，1，2三个数中任取的一个数，则该函数有两个极值点的概率为．12．已知a＞0，b＞0，ab=8，则当a的值为时，log2alog2（2b）取得最大值．13．在平面四边形ABCD中，点E，F分别是边AD，BC的中点，且，EF=1，．若，则的值为．14．函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，记∠APB=θ，则sin2θ的值是．三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.15．某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况（如资金、劳动力）确定产品的月供应量，以使得总利润达到最大．已知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于这两种产品的有关数据如表：试问：怎样确定两种货物的月供应量，才能使总利润达到最大，最大利润是多少？16．已知△ABC的三个内角A，B，C的对边分别为a，b，c，且△ABC的面积为S=accosB．（1）若c=2a，求角A，B，C的大小；（2）若a=2，且≤A≤，求边c的取值范围．17．如图，四棱锥P﹣ABCD底面为一直角梯形，AB⊥AD，CD⊥AD，CD=2AB，PA⊥面ABCD，E为PC中点（Ⅰ）求证：平面PDC⊥平面PAD（Ⅱ）求证：BE∥平面PAD（Ⅲ）假定PA=AD=CD，求二面角E﹣BD﹣C的正切值．18．已知递增的等比数列{a n}的前n项和S n满足：S4=S1+28，且a3+2是a2和a4的等差中项．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若b n=a n log a n，T n=b1+b2+…+b n，求使T n+n2n+1=30成立的正整数n的值．19．已知椭圆C： +=1（a＞b＞0）的离心率为，椭圆短轴的一个端点与两个焦点构成的三角形的面积为．（Ⅰ）求椭圆C的方程；（Ⅱ）已知动直线y=k（x+1）与椭圆C相交于A、B两点．①若线段AB中点的横坐标为﹣，求斜率k的值；②若点M（﹣，0），求证：为定值．20．已知函数f（x）=2lnx﹣x2+ax（a∈R）．（Ⅰ）当a=2时，求f（x）的图象在x=1处的切线方程；（Ⅱ）若函数g（x）=f（x）﹣ax+m在[，e]上有两个零点，求实数m的取值范围；（Ⅲ）若函数f（x）的图象与x轴有两个不同的交点A（x1，0），B（x2，0），且0＜x1＜x2，求证：f′（）＜0（其中f′（x）是f（x）的导函数）．2018-2018学年天津一中高三（上）第三次月考数学试卷（文科）参考答案与试题解析一、选择题：（本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．设集合A={x|x2﹣5x﹣6=0}，B={x|y=log2（2﹣x）}，则A∩（∁R B）=（）A．{2，3}B．{﹣1，6}C．{3}D．{6}【考点】交、并、补集的混合运算．【分析】求出集合A，B，然后求解补集以及交集即可．【解答】解：集合A={x|x2﹣5x﹣6=0}={﹣1，6}，B={x|y=log2（2﹣x）}={x|x＜2}，则∁R B={x|x ≥2}则A∩（∁R B）={6}．故选：D．【点评】本题考查集合的补集以及交集的求法，是基础题．2．下列选项叙述错误的是（）A．命题“若x≠l，则x2﹣3x+2≠0”的逆否命题是“若x2﹣3x+2=0，则x=1”B．若p∨q为真命题，则p，q均为真命题C．若命题p：∀x∈R，x2+x+1≠0，则¬p：∃x∈R，x2+x+1=0D．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件【考点】命题的真假判断与应用．【分析】A“若p则q，“的逆否命题为“若﹣p则﹣q“．故A正确；B p∨q为真命题说明p和q 中至少有一个为真；C是全称命题与存在性命题的转化；D从充要条件方面判断．【解答】解：A原命题为“若p则q，“，则它的逆否命题为“若﹣p则﹣q“．故正确；B当p，q中至少有一个为真命题时，则p∨q为真命题．故错误．C正确．D 由x2一3x+2＞0解得x＜1或x＞2显然x＞2⇒x＜1或x＞2但x＜1或x＞2不能得到x＞2故“x＞2”是“x2一3x+2＞0”的充分不必要条件，故正确．故选B【点评】本题主要考查了四种命题的关系、充要条件的转化、全称命题与存在性命题的相互转化．3．阅读如图所示的程序框图，则输出的S=（）A．14 B．30 C．20 D．55【考点】循环结构．【分析】根据框图的流程依次计算程序运行的结果，直到满足条件i＞4，计算输出S的值即可．【解答】解：由程序框图知：第一次运行S=1，i=1+1=2，不满足条件i＞4，循环，第二次运行S=1+4=5，i=2+1=3，不满足条件i＞4，循环，第三次运行S=5+9=14，i=3+1=4，不满足条件i＞4，循环，第四次运行S=14+16=30，i=4+1=5，满足条件i＞4，终止程序，输出S=30，故选：B．【点评】本题考查了循环结构的程序框图，根据框图的流程依次计算程序运行的结果是解答此类问题的常用方法．4．已知过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，则a=（）A．B．1 C．2 D．【考点】直线与圆的位置关系；直线的一般式方程与直线的垂直关系．【分析】由题意判断点在圆上，求出P与圆心连线的斜率就是直线ax﹣y+1=0的斜率，然后求出a的值即可．【解答】解：因为点P（2，2）满足圆（x﹣1）2+y2=5的方程，所以P在圆上，又过点P（2，2）的直线与圆（x﹣1）2+y2=5相切，且与直线ax﹣y+1=0垂直，所以切点与圆心连线与直线ax﹣y+1=0平行，所以直线ax﹣y+1=0的斜率为：a==2．故选C．【点评】本题考查直线与圆的位置关系，直线与直线的垂直，考查转化数学与计算能力．5．已知双曲线﹣=1（a＞0，b＞0）的左顶点与抛物线y2=2px的焦点的距离为4，且双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1），则双曲线的焦距为（）A．2B．2C．4D．4【考点】双曲线的简单性质；直线与圆锥曲线的关系．【分析】根据题意，点（﹣2，﹣1）在抛物线的准线上，结合抛物线的性质，可得p=4，进而可得抛物线的焦点坐标，依据题意，可得双曲线的左顶点的坐标，即可得a的值，由点（﹣2，﹣1）在双曲线的渐近线上，可得渐近线方程，进而可得b的值，由双曲线的性质，可得c的值，进而可得答案．【解答】解：根据题意，双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1），即点（﹣2，﹣1）在抛物线的准线上，又由抛物线y2=2px的准线方程为x=﹣，则p=4，则抛物线的焦点为（2，0）；则双曲线的左顶点为（﹣2，0），即a=2；点（﹣2，﹣1）在双曲线的渐近线上，则其渐近线方程为y=±x，由双曲线的性质，可得b=1；则c=，则焦距为2c=2；故选B．【点评】本题考查双曲线与抛物线的性质，注意题目“双曲线的一条渐近线与抛物线的准线的交点坐标为（﹣2，﹣1）”这一条件的运用，另外注意题目中要求的焦距即2c，容易只计算到c，就得到结论．6．如图，PC与圆O相切于点C，直线PO交圆O于A，B两点，弦CD垂直AB于E．则下面结论中，错误的结论是（）A．△BEC∽△DEA B．∠ACE=∠ACP C．DE2=OEEP D．PC2=PAAB【考点】与圆有关的比例线段；命题的真假判断与应用．【分析】利用垂径定理、切割线定理及相似三角形的判定方法即可判断出结论．【解答】解：A．∵∠CEB=∠AED，∠BCE=∠DAE，∴△BEC∽△DEA，因此A正确；B．∵PC与圆O相切于点C，∴∠PCA=∠B=∠ACE，因此B正确；C．连接OC，则OC⊥PC，又CD⊥AB，∴CE2=OEEP，CE=ED，∴ED2=OEEP，因此C正确；D．由切割线定理可知：PC2=PAPB≠PAAB，因此D不正确．故选D．【点评】熟练掌握垂径定理、切割线定理及相似三角形的判定方法是解题的关键．7．已知定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，记a=f（log0.53），b=f （log25），c=f（2m），则a，b，c的大小关系为（）A．a＜b＜c B．c＜a＜b C．a＜c＜b D．c＜b＜a【考点】对数函数图象与性质的综合应用；奇偶性与单调性的综合．【分析】根据函数的奇偶性得出f（x）=2|x|﹣1=，利用单调性求解即可．【解答】解：∵定义在R上的函数f（x）=2|x﹣m|﹣1（m为实数）为偶函数，∴f（﹣x）=f（x），m=0，∵f（x）=2|x|﹣1=，∴f（x）在（0，+∞）单调递增，∵a=f（log0.53）=f（log23），b=f（log25），c=f（2m）=f（0）=0，0＜log23＜log25，∴c＜a＜b，故选：B【点评】本题考查了对数函数的性质，函数的奇偶性，单调性，计算能力，属于中档题．8．定义在（1，+∞）上的函数f（x）满足下列两个条件：（1）对任意的x∈（1，+∞）恒有f（2x）=2f（x）成立；（2）当x∈（1，2]时，f（x）=2﹣x；记函数g（x）=f（x）﹣k（x ﹣1），若函数g（x）恰有两个零点，则实数k的取值范围是（）A．[1，2）B．C．D．【考点】函数零点的判定定理．【分析】根据题中的条件得到函数的解析式为：f（x）=﹣x+2b，x∈（b，2b]，又因为f（x）=k（x﹣1）的函数图象是过定点（1，0）的直线，再结合函数的图象根据题意求出参数的范围即可【解答】解：因为对任意的x∈（1，+∞）恒有f（2x）=2f（x）成立，且当x∈（1，2]时，f （x）=2﹣x所以f（x）=﹣x+2b，x∈（b，2b]．由题意得f（x）=k（x﹣1）的函数图象是过定点（1，0）的直线，如图所示红色的直线与线段AB相交即可（可以与B点重合但不能与A点重合）所以可得k的范围为故选C．【点评】解决此类问题的关键是熟悉求函数解析式的方法以及函数的图象与函数的性质，数形结合思想是高中数学的一个重要数学思想，是解决数学问题的必备的解题工具．二、填空题：（本大题共6小题，每小题5分，共30分．把答案填在题中横线上）9．已知（a，b∈R），其中i为虚数单位，则a+b=1．【考点】复数相等的充要条件．【分析】先对等式化简，然后根据复数相等的充要条件可得关于a，b的方程组，解出可得．【解答】解：，即=2﹣ai=b +i ，由复数相等的条件，得，解得，∴a +b=1， 故答案为：1．【点评】本题考查复数相等的充要条件，属基础题，正确理解复数相等的条件是解题关键．10．一个几何体的三视图如图所示，则该几何体的体积为 80 ．【考点】由三视图求面积、体积．【分析】根据几何体的三视图得出该几何体是下部正方体，上部是四棱锥的组合体，求出它的体积即可．【解答】解：根据几何体的三视图知，该几何体是下部是楞长为4的正方体，上部是高为3的四棱锥的组合体，∴该几何体的体积是V 组合体=V 正方体+V 四棱锥=43+×42×3=80．故答案为：80．【点评】本题考查了空间几何体的三视图的应用问题，也考查了求几何体的体积的应用问题，是基础题．11．已知函数f（x）=x3+ax2+b2x+1，若a是从1，2，3三个数中任取的一个数，b是从0，1，2三个数中任取的一个数，则该函数有两个极值点的概率为．【考点】利用导数研究函数的极值；古典概型及其概率计算公式．【分析】f′（x）=x2+2ax+b2，要满足题意需x2+2ax+b2=0有两不等实根，由此能求出该函数有两个极值点的概率．【解答】解：∵f（x）=x3+ax2+b2x+1，∴f′（x）=x2+2ax+b2，要满足题意需x2+2ax+b2=0有两不等实根，即△=4（a2﹣b2）＞0，即a＞b，又a，b的取法共3×3=9种，其中满足a＞b的有（1，0），（2，0），（2，1），（3，0），（3，1），（3，2）共6种，故所求的概率为P=．故答案为：．【点评】本题考查概率的求法，是中档题，解题时要认真审题，注意导数性质、根的判别式、等可能事件概率计算公式的合理运用．12．已知a＞0，b＞0，ab=8，则当a的值为4时，log2alog2（2b）取得最大值．【考点】复合函数的单调性．【分析】由条件可得a＞1，再利用基本不等式，求得当a=4时，log2alog2（2b）取得最大值，从而得出结论．【解答】解：由题意可得当log2alog2（2b）最大时，log2a和log2（2b）都是正数，故有a＞1．再利用基本不等式可得log2alog2（2b）≤===4，当且仅当a=2b=4时，取等号，即当a=4时，log2alog2（2b）取得最大值，故答案为：4．【点评】本题主要考查基本不等式的应用，注意检查等号成立条件以及不等式的使用条件，属于中档题．13．在平面四边形ABCD中，点E，F分别是边AD，BC的中点，且，EF=1，．若，则的值为．【考点】平面向量数量积的运算．【分析】画出图形，结合图形，先求出的值，再利用=15，即可求出的值．【解答】解：如图所示，设AB∩DC=O，∵=++=+，=++=+，两式相加得=；∵AB=，EF=1，CD=，平方得1=；∴=﹣；又∵=15，即（﹣）（﹣）=15；∴﹣﹣+=15，∴+=15++，∴=（﹣）（﹣）=﹣﹣+=（15++）﹣﹣=15+（﹣）+（﹣）=15++=15+（﹣）=15+=15﹣=15﹣（﹣）=．故答案为：．【点评】本题考查了两个向量的加减运算的应用问题，也考查了平面向量的几何意义以及平面向量的数量积的应用问题，是综合性题目．14．函数y=sin（πx+φ）（φ＞0）的部分图象如图所示，设P是图象的最高点，A，B是图象与x轴的交点，记∠APB=θ，则sin2θ的值是．【考点】由y=Asin（ωx+φ）的部分图象确定其解析式．【分析】由题意，|AB|=2，P是图象的最高点，故P是纵坐标为1，设∠BAP=α，∠PBA=β，那么：θ=π﹣（α+β），过P作AB的垂线．即可求sinα，sinβ，cosα，cosβ，从而求sin2θ的值．【解答】解：由题意，函数y=sin（πx+φ），T=，∴|AB|=2，P是图象的最高点，故P是纵坐标为1，设∠BAP=α，∠PBA=β，那么：θ=π﹣（α+β），过P作AB的垂线交于C，|AC|=，|AP|=，|PC|=1，那么：sinα=，cosα=，|BC|=，|PB|=，那么：sinβ=，cosβ=，则：sin2θ=2sinθcosθ=﹣2sin（α+β）cos（α+β）=﹣2（sinαcosβ+cosαsinβ）（cosαcosβ﹣sinαsinβ）=，故答案为：．【点评】本题考查了三角函数图象及性质的运用和计算能力，属于中档题．三、解答题：本大题共6小题，共80分.解答应写出文字说明，证明过程或演算步骤.15．某公司计划在今年内同时出售变频空调机和智能洗衣机，由于这两种产品的市场需求量非常大，有多少就能销售多少，因此该公司要根据实际情况（如资金、劳动力）确定产品的月供应量，以使得总利润达到最大．已知对这两种产品有直接限制的因素是资金和劳动力，通过调查，得到关于这两种产品的有关数据如表：试问：怎样确定两种货物的月供应量，才能使总利润达到最大，最大利润是多少？【考点】简单线性规划的应用．【分析】利用线性规划的思想方法解决某些实际问题属于直线方程的一个应用．本题主要考查找出约束条件与目标函数，准确地描画可行域，再利用图形直线求得满足题设的最优解．【解答】解：设空调机、洗衣机的月供应量分别是x、y台，总利润是P，则P=6x+8y，由题意有30x+20y≤300，5x+10y≤110，x≥0，y≥0，x、y均为整数．由图知直线y=﹣x +P 过M （4，9）时，纵截距最大． 这时P 也取最大值P max =6×4+8×9=96（百元）．故当月供应量为空调机4台，洗衣机9台时，可获得最大利润9600元．【点评】用图解法解决线性规划问题时，分析题目的已知条件，找出约束条件和目标函数是关键，可先将题目中的量分类、列出表格，理清头绪，然后列出不等式组（方程组）寻求约束条件，并就题目所述找出目标函数．然后将可行域各角点的值一一代入，最后比较，即可得到目标函数的最优解．16．已知△ABC 的三个内角A ，B ，C 的对边分别为a ，b ，c ，且△ABC 的面积为S=accosB ．（1）若c=2a ，求角A ，B ，C 的大小；（2）若a=2，且≤A ≤，求边c 的取值范围．【考点】正弦定理；余弦定理．【分析】（1）法一：根据正弦定理，建立条件关系，即可求出角A ，B ，C 的大小；法二：根据余弦定理，建立条件关系，即可求出角A ，B ，C 的大小．（2）根据正弦定理表示出c ，根据三角函数的图象和性质即可得到结论．【解答】解：由已知及三角形面积公式得S=acsinB=accosB ，化简得sinB=cosB ，即tanB=，又0＜B ＜π，∴B=．（1）解法1：由c=2a ，及正弦定理得，sinC=2sinA ，又∵A +B=，∴sin （﹣A ）=2sinA ，化简可得tanA=，而0＜A ＜，∴A=，C=．解法2：由余弦定理得，b2=a2+c2﹣2accosB=a2+4a2﹣2a2=3a2，∴b=，∴a：b：c=1：，知A=，C=．（2）由正弦定理得，即c=，由C=﹣A，得===+1又由≤A≤，知1≤tanA≤，故c∈[2，]．【点评】本题主要考查正弦定理和余弦定理的应用，要求熟练掌握相应的定理．17．如图，四棱锥P﹣ABCD底面为一直角梯形，AB⊥AD，CD⊥AD，CD=2AB，PA⊥面ABCD，E为PC中点（Ⅰ）求证：平面PDC⊥平面PAD（Ⅱ）求证：BE∥平面PAD（Ⅲ）假定PA=AD=CD，求二面角E﹣BD﹣C的正切值．【考点】二面角的平面角及求法；直线与平面平行的判定；平面与平面垂直的判定．【分析】（Ⅰ）证明PA⊥DC，DC⊥AD，然后证明DC⊥面PAD，平面PDC⊥平面PAD（Ⅱ）取PD的中点F，连接EF，FA∵E为PC中点，证明四边形ABEF为平行四边形，推出BE∥AF，然后证明BE∥平面PAD（Ⅲ）连接AC，取AC中点O，连接EO．过O作OG⊥BD交BD于G，连接EG．说明∠EGO为所求二面角E﹣BD﹣C的平面角，设PA=AD=CD=2a，AB=a，连DO并延长交AB于B′，O为DB′中点，过B′作B′G′⊥DB交BD于G′，在△EOG中求解二面角E﹣BD﹣C的平面角的正切值．【解答】（Ⅰ）证明：∵PA⊥面ABCD，∴PA⊥DC，∵DC⊥AD且AD∩PA=A，∴DC⊥面PAD，∵DC⊂面PDC，∴平面PDC⊥平面PAD（Ⅱ）证明：取PD的中点F，连接EF，FA∵E为PC中点，∴在△PDC中：EF∥=，∴EF∥=AB，∴四边形ABEF为平行四边形，即BE∥AF，∵AF⊂面PAD且BE⊄面PAD，∴BE∥平面PAD．（Ⅲ）解：连接AC，取AC中点O，连接EO．在△PAC中：EO∥=，∴EO⊥面ABC，过O作OG⊥BD交BD于G，连接EG．由三垂线定理知：∠EGO为所求二面角E﹣BD﹣C的平面角，设PA=AD=CD=2a，AB=a，∴EO=a连DO并延长交AB于B′，则四边形AB′CD为正方形，且B′B=a，O为DB′中点，过B′作B′G′⊥DB交BD于G′．∴=在△EOG中：，故：二面角E﹣BD﹣C的平面角的正切值为．【点评】本题考查二倍角的平面角的求法，直线与平面平行于垂直的判定定理的应用，考查空间想象能力以及计算能力．18．已知递增的等比数列{a n}的前n项和S n满足：S4=S1+28，且a3+2是a2和a4的等差中项．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）若b n=a n log a n，T n=b1+b2+…+b n，求使T n+n2n+1=30成立的正整数n的值．【考点】等差数列与等比数列的综合．【分析】（I）由题意，得，由此能求出数列{a n}的通项公式．（Ⅱ）b n=a n log a n，T n=b1+b2+…+b n=﹣（1×2+2×22+…+n×2n），进而可得T n+n2n+1=30成立的正整数n的值．【解答】解：（I）设等比数列{a n}的公比为q，∵S4=S1+28，且a1+2是a2和a4的等差中项．∴，解得，即数列{a n}的通项公式为a n=22n﹣1=2n…（Ⅱ）b n=a n log a n，…T n=b1+b2+…+b n=﹣（1×2+2×22+…+n×2n）①则2T n=﹣（1×22+2×23+…+n×2n+1）②②﹣①，得T n=（2+22+…+2n）﹣n2n+1=2n+1﹣2﹣n2n+1即数列{b n}的前项和T n=2n+1﹣2﹣n2n+1，则T n+n2n+1=2n+1﹣2=30，即2n+1=32，解得：n=4【点评】本题考查数列的性质的应用，解题时要认真审题，注意数列与不等式的综合运用，合理地进行等价转化．19．已知椭圆C： +=1（a＞b＞0）的离心率为，椭圆短轴的一个端点与两个焦点构成的三角形的面积为．（Ⅰ）求椭圆C的方程；（Ⅱ）已知动直线y=k（x+1）与椭圆C相交于A、B两点．①若线段AB中点的横坐标为﹣，求斜率k的值；②若点M（﹣，0），求证：为定值．【考点】直线与圆锥曲线的综合问题；椭圆的标准方程．【分析】（1）根据椭圆的离心率，三角形的面积及椭圆几何量之间的关系，建立等式，即可求得椭圆的标准方程；（2）①直线方程代入椭圆方程，利用韦达定理及线段AB中点的横坐标为，即可求斜率k的值；②利用韦达定理，及向量的数量积公式，计算即可证得结论．【解答】（1）解：因为满足a2=b2+c2，，…根据椭圆短轴的一个端点与两个焦点构成的三角形的面积为，可得．从而可解得，所以椭圆方程为…（2）证明：①将y=k（x+1）代入中，消元得（1+3k2）x2+6k2x+3k2﹣5=0…△=36k4﹣4（3k2+1）（3k2﹣5）=48k2+20＞0，…因为AB中点的横坐标为，所以，解得…②由①知，所以…==…===…【点评】本题考查椭圆的标准方程，考查直线与椭圆的位置关系，考查向量的数量积，考查学生的运算能力，综合性强．20．已知函数f（x）=2lnx﹣x2+ax（a∈R）．（Ⅰ）当a=2时，求f（x）的图象在x=1处的切线方程；（Ⅱ）若函数g（x）=f（x）﹣ax+m在[，e]上有两个零点，求实数m的取值范围；（Ⅲ）若函数f（x）的图象与x轴有两个不同的交点A（x1，0），B（x2，0），且0＜x1＜x2，求证：f′（）＜0（其中f′（x）是f（x）的导函数）．【考点】导数在最大值、最小值问题中的应用．【分析】（I）利用导数的几何意义即可得出；（II）利用导数研究函数的单调性极值、最值，数形结合即可得出；（III）由于f（x）的图象与x轴交于两个不同的点A（x1，0），B（x2，0），可得方程2lnx﹣x2+ax=0的两个根为x1，x2，得到．可得=．经过变形只要证明，通过换元再利用导数研究其单调性即可得出．【解答】解：（Ⅰ）当a=2时，f（x）=2lnx﹣x2+2x，，切点坐标为（1，1），切线的斜率k=f′（1）=2，∴切线方程为y﹣1=2（x﹣1），即y=2x﹣1．（Ⅱ）g（x）=2lnx﹣x2+m，则，∵，故g′（x）=0时，x=1．当时，g′（x）＞0；当1＜x＜e时，g′（x）＜0．故g（x）在x=1处取得极大值g（1）=m﹣1．又，g（e）=m+2﹣e2，，∴，∴g（x）在上的最小值是g（e）．g（x）在上有两个零点的条件是解得，∴实数m的取值范围是．（Ⅲ）∵f（x）的图象与x轴交于两个不同的点A（x1，0），B（x2，0），∴方程2lnx﹣x2+ax=0的两个根为x1，x2，则两式相减得．又f（x）=2lnx﹣x2+ax，，则=．下证（*），即证明，令，∵0＜x1＜x2，∴0＜t＜1，即证明在0＜t＜1上恒成立．∵，又0＜t＜1，∴u′（t）＞0，∴u（t）在（0，1）上是增函数，则u（t）＜u（1）=0，从而知，故（*）式＜0，即成立．【点评】本题考查了利用导数研究函数的单调性极值与最值、导数的几何意义、切线的方程、方程实数根的个数转化为图象的交点，考查了推理能力和计算能力，属于难题．。

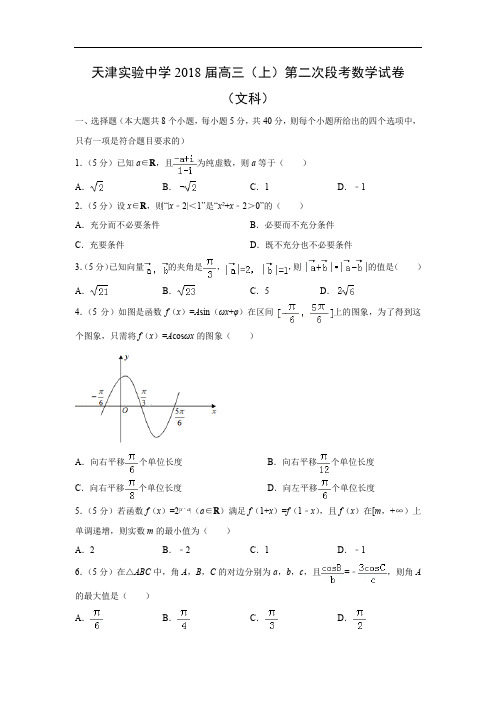
天津实验中学2018届高三（上）第二次段考数学试卷（文科）一、选择题（本大题共8个小题，每小题5分，共40分，则每个小题所给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知a∈R，且为纯虚数，则a等于（）A．B．C．1 D．﹣12．（5分）设x∈R，则“|x﹣2|＜1”是“x2+x﹣2＞0”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件3．（5分）已知向量的夹角是，，则的值是（）A．B．C．5 D．4．（5分）如图是函数f（x）=A sin（ωx+φ）在区间上的图象，为了得到这个图象，只需将f（x）=A cosωx的图象（）A．向右平移个单位长度B．向右平移个单位长度C．向右平移个单位长度D．向左平移个单位长度5．（5分）若函数f（x）=2|x﹣a|（a∈R）满足f（1+x）=f（1﹣x），且f（x）在[m，+∞）上单调递增，则实数m的最小值为（）A．2 B．﹣2 C．1 D．﹣16．（5分）在△ABC中，角A，B，C的对边分别为a，b，c，且=﹣，则角A 的最大值是（）A．B．C．D．7．（5分）若函数f（x）=sinωx+sin（ωx﹣）（ω＞0）的图象关于点（，0）对称，且在（﹣，0）内有零点，则ω的最小值是（）A．2 B．5 C．9 D．108．（5分）已知定义域为R的奇函数y=f（x）的导函数为y=f′（x），当x≠0时，f′（x）+＞0，若a=，b=﹣3f（﹣3），c=，则a，b，c的大小关系正确的是（）A．a＜b＜c B．a＜c＜b C．b＜c＜a D．c＜a＜b二、填空题（本大题共6个小题，每小题5分，共30分）9．（5分）若集合，则A∩B=．10．（5分）若圆C经过坐标原点和点（4，0），且与直线y=1相切，则圆C的方程是．11．（5分）已知为偶函数，则的单调递增区间为．12．（5分）已知各项皆为正数的等比数列{a n}（n∈N*），满足a7=a6+2a5，若存在两项a m、a n使得=4a1，则+的最小值为．13．（5分）如图，△ABC中，D，E分别为边BC，AC的中点，且与夹角120°，||=1，||=2，则=．14．（5分）已知函数，若函数g（x）=f（x）﹣log a x 有且只有三个零点，则实数a的取值范围是．三、解答题（本大题共6个小题，总分80分）15．（13分）在△ABC中，角A，B，C的对边分别为a，b，c，且3a cos A=（c cos B+b cos C）．（Ⅰ）求tan2A的值；（Ⅱ）若，求△ABC的面积．16．（13分）已知函数．（Ⅰ）求函数f（x）的最小正周期和图象的对称中心；（Ⅱ）求f（x）在区间上的最大值和最小值．17．（13分）某工艺厂有铜丝5万米，铁丝9万米，准备用这两种材料编制成花篮和花盆出售．已知编制一只花篮需要铜丝200米，铁丝300米；编制一只花盆需要铜丝100米，铁丝300米．设该厂用所有原料编制x个花篮，y个花盆．（1）列出x、y满足的关系式，并画出相应的平面区域；（2）若出售一个花篮可获利300元，出售一个花盆可获利200元，那么怎样安排花篮和花盆的编制个数，可使所得利润最大，最大利润是多少？18．（13分）已知各项均不为零的数列{a n}的前n项和S n，且满足4S n=（2n+1）a n+1，数列{b n}满足b1=1，b n+1=2b n+1．（Ⅰ）求数列{a n}，{b n}的通项公式；（Ⅱ）设c n=a n（b n+1），求数列{c n}的前n项和T n．19．（14分）已知数列{a n}的前n项和为S n，且满足．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）设，求数列{b n}的前n项和T n．20．（14分）已知函数f（x）=ax2﹣（a+2）x+ln x．（Ⅰ）当a=1时，求曲线y=f（x）在点（1，f（1））处的切线方程；（Ⅱ）当a＞0时，若f（x）在区间[1，e]上的最小值为﹣2，求a的取值范围；（Ⅲ）若对任意x1，x2＞0，x1≠x2，有恒成立，求a的取值范围．【参考答案】一、选择题1．D【解析】因为==，它是纯虚数，所以，∴a=﹣1．故选D．2．A【解析】由“|x﹣2|＜1”得1＜x＜3，由x2+x﹣2＞0得x＞1或x＜﹣2，即“|x﹣2|＜1”是“x2+x﹣2＞0”的充分不必要条件，故选：A．3．A【解析】=2×1×cos=1，（）2=+2+=4+2+1=7，（）2=+2+=4﹣2+1=3．∴||=，||=，∴=．故选：A．4．B【解析】根据函数的图象，函数的周期为：T=π，进一步求出ω=2．根据函数的图象，令（k∈Z），解得：φ=k（k∈Z），函数f（x）=A sin（ωx+φ）在区间上的图象，当k=1时，φ=，所以f（x）=A sin（2x+），为得到函数f（x）=A sin（2x+）的图象，只需将函数将f（x）=A cos2x的图象向右平移个单位，即：f（x）=A cos[2（x﹣）]=A sin（2x+）．故选：B5．C【解析】因为f（1+x）=f（1﹣x），所以，f（x）的图象关于直线x=1轴对称，而f（x）=2|x﹣a|，所以f（x）的图象关于直线x=a轴对称，因此，a=1，f（x）=2|x﹣1|，且该函数在（﹣∞，1]上单调递减，在[1，+∞）上单调递增，又因为函数f（x）在[m，+∞）上单调递增，所以，m≥1，即实数m的最小值为1．故选：C．6．A【解析】∵=﹣，∴由余弦定理可得：=﹣3×，∴解得：2a2+b2=c2，∴cos A===≥=，∵A∈（0，π），∴角A的最大值是．故选：A．7．D【解析】函数f（x）=sinωx+sin（ωx﹣）=sinωx﹣cosωx=sin（ωx﹣）且函数f（x）的图象关于点对称，∴ω﹣=kπ，k∈Z；解得ω=8k+2，k∈Z；又f（x）在内有零点，∴﹣ω﹣≤﹣π＜﹣，解得ω≥4；∴ω的最小值是8+2=10．故选：D．8．B【解析】定义域为R的奇函数y=f（x），设F（x）=xf（x），∴F（x）为R上的偶函数，∴F′（x）=f（x）+xf′（x）∵当x≠0时，f′（x）+＞0．∴当x＞0时，x•f′（x）+f（x）＞0，当x＜0时，x•f′（x）+f（x）＜0，即F（x）在（0，+∞）单调递增，在（﹣∞，0）单调递减．F（）=a=f（）=F（ln），F（﹣3）=b=﹣3f（﹣3）=F（3），F（ln）=c=（ln）f（ln）=F（ln3），∵ln＜ln3＜3，∴F（ln）＜F（ln3）＜F（3）．即a＜c＜b，故选：B．二、填空题9．（0，1]【解析】由|x﹣1|＜2，解得﹣1＜x＜3，即A=（﹣1，3），由≤0，解得0＜x≤1，即B=（0，1]，故答案为：（0，1]．10．【解析】设圆的圆心坐标（a，b），半径为r，因为圆C经过坐标原点和点（4，0），且与直线y=1相切，所以，解得，所求圆的方程为：．故答案为：．11．（5，+∞）【解析】∵为偶函数，∴f（﹣1）=f（1），∴1﹣a=1﹣2，∴a=2，则函数y=log a（x2﹣4x﹣5）即y=log2（x2﹣4x﹣5），令t=x2﹣4x﹣5，x=2是对称轴，由x2﹣4x﹣5＞0，得x＜﹣1或x＞5，由复合函数的单调性，知（5，+∞）是所求函数的递增区间．故答案为：（5，+∞）．12．【解析】设各项皆为正数的等比数列{a n}的公比为q＞0（n∈N*），∵a7=a6+2a5，∴=a5q+2a5，化为q2﹣q﹣2=0，解得q=2．∵存在两项a m、a n使得，∴=4a1，∴2m+n﹣2=24，∴m+n=6．则==≥=，当且仅当n=2m=4时取等号．∴的最小值为．故答案为：．13．﹣【解析】∵=+=+=+（﹣）=（+），①=﹣=﹣，②由①②解得=（﹣），=（2+），∴•=•（﹣）•（2+）=（2﹣﹣•）=（2﹣4+1×2×）=﹣故答案为：14．【解析】∵函数，若函数g（x）=f（x）﹣log a x有且只有三个零点，则函数y=log a x与y=f（x）有三个不同的交点，在同一坐标系内画出两个函数的图象如图所示，易得a＞1，依题意得，∴＜a＜，故答案为：．三、解答题15．解：（Ⅰ）由题意即正弦定理可得：3sin A cos A=（sin C cos B+sin B cos C）．∴3sin A cos A=sin（B+C），由A+B+C=π，A=π﹣（B+C），则3sin A cos A=sin A，由0＜A＜π，sin A≠0，则cos A=，sin A=，tan A=，则tan2A==2，∴tan2A=2；（Ⅱ）由sin（+B）=cos B=，由0＜B＜π，则sin B=，sin C=sin（A+B）=sin A cos B+cos A sin B=，由正弦定理可得a==2，∴△ABC的面积S=ac sin B=×2×2×=．△ABC的面积．16．解：（1）因为f（x）=2cos2（x﹣）+2sin（x﹣）sin（x+）=cos（2x﹣）+2sin（x﹣）sin（x+﹣）+1=cos（2x﹣）+2sin（x﹣）cos（x﹣）+1=cos2x+sin2x+sin（2x﹣）+1=cos2x+sin2x﹣cos2x+1=sin2x﹣cos2x+1=sin（2x﹣）+1，所以最小正周期T=π．由sin（2x﹣）=0得：2x﹣=kπ，所以x=+，所以函数f（x）的图象的对称中心是（+，1）（其中k∈Z）．（2）当x∈时，2x﹣∈[﹣，]，17．（1）解：由已知x、y满足的关系式为，等价于该二元一次不等式组所表示的平面区域如图中的阴影部分（2）解：设该厂所得利润为z元，则目标函数为z=300x+200y将z=300x+200y变形为，这是斜率为，在y轴上截距为、随z变化的一族平行直线．又因为x、y满足约束条件，所以由图可知，当直线经过可行域上的点M时，截距最大，即z最大解方程组得点M的坐标为（200，100）且恰为整点，即x=200，y=100所以，z max=300×200+200×100=80000答：该厂编制200个花篮，100花盆所获得利润最大，最大利润为8万元．18．解：（I）n=1，4S1=3a1+1，a1=S1⇒a1=1，n≥2，4a n=4S n﹣4S n﹣1=（2n+1）a n﹣（2n﹣1）a n﹣1，．当n=1时，a1=2•1﹣1=1，综上a n=2n﹣1．由b n+1=2b n+1⇒b n+1+1=2（b n+1），∴{b n+1}是以2位公比，2为首项的等比数列，∴，则．（II），…①…②①﹣②得：﹣T n=2+2（22+23+…+2n）﹣（2n﹣1）•2n+1=2+2×﹣（2n﹣1）•2n+1，整理为：．19．解：（Ⅰ）当n=1，2S1=2a1，a1=0，，a n=n﹣1，当n=1时，a1=1﹣1=0，所以a n=n﹣1．（Ⅱ）（k∈N+），当n为偶数时，则：T n=（b1+b3+…+b n﹣1）+（b2+b4+…+b n），=（20+22+…+2n﹣1）+（++…+），=+，当n为奇数时，综上（k∈N+）.20．解：（Ⅰ）由f（x）=x2﹣3x+ln x，则f'（1）=0，f（1）=1﹣3=﹣2，所以切线方程为y=﹣2（Ⅱ），令f'（x）=0，当a≥1时，f（x）在[1，e]上单调递增，f（x）min=f（1）=﹣2，当时，f（x）在[1，e]上单调递减，（舍），当时，f（x）在上单调递减，f（x）在上单调递增，f（x）min＜f（1）=﹣2（舍），综上，a≥1；（Ⅲ）令x1＞x2⇒x1﹣x2＞0，则，令g（x）=f（x）+2x，只要g（x）在（0，+∞）上单调递增即可．⇔g'（x）≥0在（0，+∞）上恒成立．⇔2ax2﹣ax+1≥0在（0，+∞）上恒成立．当a=0时，1≥0恒成立；当a＞0时，原不等式当时，原不等式，左边无最大值，不合题意（舍）综上，0≤a≤8．。

天津市实验中学2018-2019学年高三上学期第三次月考试卷数学含答案 班级__________ 座号_____ 姓名__________ 分数__________一、选择题（本大题共12小题，每小题5分，共60分.每小题给出的四个选项中，只有一项是符合题目要求的.）1． 设i 是虚数单位，是复数z 的共轭复数，若z=2（+i ），则z=（ ）A ．﹣1﹣iB ．1+iC ．﹣1+iD ．1﹣i2． （文科）要得到()2log 2g x x =的图象，只需将函数()2log f x x =的图象（ ）A ．向左平移1个单位B ．向右平移1个单位C ．向上平移1个单位D ．向下平移1个单位 3． 设复数1i z =-（i 是虚数单位），则复数22z z+=（ ） A.1i - B.1i + C.2i + D. 2i -【命题意图】本题考查复数的有关概念，复数的四则运算等基础知识，意在考查学生的基本运算能力．4． 已知正方体ABCD ﹣A 1B 1C 1D 1中，点E 为上底面A 1C 1的中心，若+，则x 、y 的值分别为（ ）A ．x=1，y=1B ．x=1，y=C ．x=，y=D ．x=，y=15． 已知函数f （x ）＝⎩⎨⎧a x －1，x ≤1log a1x ＋1，x ＞1（a ＞0且a ≠1），若f （1）＝1，f （b ）＝－3，则f （5－b ）＝（ ） A ．－14B ．－12C ．－34D ．－546． 二进制数）（210101化为十进制数的结果为（ ） A ．15 B ．21 C ．33 D ．417． 某几何体的三视图如下（其中三视图中两条虚线互相垂直）则该几何体的体积为（ ）A.83 B ．4 C.163D ．2038． 将函数x x f ωsin )(=（其中0>ω）的图象向右平移4π个单位长度，所得的图象经过点)0,43(π，则ω的最小值是（ ） A ．31 B ． C ．35D ．9． 设,,a b c R ∈，且a b >，则（ ）A ．ac bc >B ．11a b< C ．22a b > D ．33a b >10．函数||5y x =-的定义域为（ ）A ．{}|5x x ≠±B ．{}|4x x ≥C ．{}|45x x <<D ．{}|455x x x ≤<>或 11．已知()x f 在R 上是奇函数，且满足()()x f x f -=+5，当()5,0∈x 时，()x x x f -=2，则()=2016f （ ）A 、-12B 、-16C 、-20D 、0 12．下列命题正确的是（ ）A ．已知实数,a b ，则“a b >”是“22a b >”的必要不充分条件B ．“存在0x R ∈，使得2010x -<”的否定是“对任意x R ∈，均有210x ->”C ．函数131()()2xf x x =-的零点在区间11(,)32内D ．设,m n 是两条直线，,αβ是空间中两个平面，若,m n αβ⊂⊂，m n ⊥则αβ⊥二、填空题（本大题共4小题，每小题5分，共20分.把答案填写在横线上）13．已知1,3x x ==是函数()()()sin 0f x x ωϕω=+>两个相邻的两个极值点，且()f x 在32x =处的导数302f ⎛⎫'<⎪⎝⎭，则13f ⎛⎫= ⎪⎝⎭___________． 14．若6()mx y +展开式中33x y 的系数为160-，则m =__________．【命题意图】本题考查二项式定理的应用，意在考查逆向思维能力、方程思想．15．设x ，y 满足约束条件，则目标函数z=2x ﹣3y 的最小值是 ．16．命题：“∀x ∈R ，都有x 3≥1”的否定形式为 ．三、解答题（本大共6小题，共70分。

2018届高三第三阶段考试暨期中考试语文试卷第I卷一、选择题1.下列词语中画线的字，每对的读音都不相同的一项是A.滋润．\蕴．含赡．养\瞻．仰调．试\调．和模．样\楷模．B.对峙．\嗜．好竣．工\英俊强．．脚\别．扭．．迫\倔强蹩C.造诣．\逃逸堤．．岸\提．拔抹．黑\抹．布盘踞．\拮据．D.湖畔．\装扮怄．．然\创．伤．．气\枢．纽阻塞．\边塞怆【参考答案】D【试题分析】本题考查识记现代汉语普通话常用字的字音的能力。

A项rùn/yùn shàn/zh ān tiáo/ tiáo mú/mó；B项zhì/shìjùn/jùn qiǎng/jiàng bié/biè；C项yì/yìtī/t ímǒ/mājù/jū；D项pàn/bàn îu/shūsâ/sài chuàng/ chuāng。

【题型】语言知识基础2.下列词语完全正确的一项是A.循规蹈矩门庭若市琼楼玉宇虚无缥缈B.博闻强识积重难返揠苗助长消声匿迹C.狭路相逢妇孺皆知义愤填赝相映成趣D.绿草如荫沽名钓誉融会贯通文过饰非【参考答案】A【试题分析】本题考查识记并正确书写现代常用规范汉字的能力。

B.销声匿迹；C.义愤填膺；D.绿草如茵。

【题型】语言知识基础3.下列各句中，画线的词语使用恰当的一句是A.交际不仅是一门学问，而且是一门艺术。

只要你能够有效地运用这门艺术，便会左右逢源，无往不利．．．．，融入社会，取得成功。

B.家长不要认为拒绝孩子会造成伤害，要培养一个出色的孩子，面对他的不情之情．．．．，一定要坚决地说“不”，不能有丝毫心软。

C.《人类文明史图鉴》就人与自然、城市、家庭、战争等方面进行了具体而微．．．．的介绍，涵盖了世界各大文明，并十分重视历史的分析。

天津市实验中学2018届高三上学期期中（第三阶段）考试数学（理）试题第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合，集合，则（）A. B. C. D.【答案】C【解析】,,所以,选C.2. 已知复数，则复数的虚部是（）A. B. C. D.【答案】C【解析】,所以虚部是 ,选C.3. “”是“函数在区间上为增函数”的（）A. 充分不必耍条件B. 充要条件C. 必要不充分条件D. 既不充分也不必要条件【答案】A【解析】由函数在区间上为增函数得所以“”是“函数在区间上为增函数”的充分不必耍条件,选A.点睛：充分、必要条件的三种判断方法．1．定义法：直接判断“若则”、“若则”的真假．并注意和图示相结合，例如“⇒”为真，则是的充分条件．2．等价法：利用⇒与非⇒非，⇒与非⇒非，⇔与非⇔非的等价关系，对于条件或结论是否定式的命题，一般运用等价法．3．集合法：若⊆，则是的充分条件或是的必要条件；若＝，则是的充要条件．4. 已知为偶函数，则可以取的一个值为（）A. B. C. D.【答案】D5. 设的内角所对边的长分别为，若，则角（）A. B. C. D.【答案】B【解析】试题分析：，由正弦定理可得即；因为，所以，所以，而，所以，故选B.考点：1.正弦定理；2.余弦定理.6. 已知点，则向量在向量上的投影为（）A. B. C. D.【答案】A【解析】试题分析：由题意得，，所以向量在方向上的投影为，故选A．考点：平面向量的数量积的运算及向量的投影的概念．7. 已知是等差数列的前项和，，设为数列的前项和，则（）A. B. C. D.【答案】C【解析】,选C.点睛：本题采用分组转化法求和. 分组转化法求和的常见类型主要有分段型（如），符号型（如），周期型（如）8. 已知为偶函数，当时，，若函数恰有4个零点，则实数的取值范围（）A. B. C. D.【答案】B【解析】作图,可知恰有4个零点，所以,选B.点睛：对于方程解的个数(或函数零点个数)问题，可利用函数的值域或最值，结合函数的单调性、草图确定其中参数范围．从图象的最高点、最低点，分析函数的最值、极值；从图象的对称性，分析函数的奇偶性；从图象的走向趋势，分析函数的单调性、周期性等．第Ⅱ卷（共110分）二、填空题（每题5分，满分30分，将答案填在答题纸上）9. 已知复数是纯虚数，（为虚数单位)，则__________.【答案】【解析】所以10. 等比数列的前项和为，且成等差败列.若，则__________.【答案】15【解析】由题意得11. 设的内角，所对边的长分别是，且.则的值为__________.【答案】【解析】12. 若直线与曲线相切，则__________.【答案】【解析】即求曲线过原点切线的斜率，设切点为，斜率，切线方程为，将原点坐标代入化简得，故.13. 在平行四边形中，,为的中点，为平面内一点，若，则__________.【答案】6【解析】14. 对于函数，设，若存在，使得，则称互为“零点相邻函数”.若函数与互为“零点相邻函数”，则实数的取值范围是__________.【答案】【解析】为单调递增函数,,所以零点在[0,2]当时舍去;当时舍去;当时综上实数的取值范围是点睛：已知函数有零点求参数取值范围常用的方法和思路(1)直接讨论法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；(2)分离参数法：先将参数分离，转化成求函数值域问题加以解决；(3)数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图象，然后数形结合求解．三、解答题（本大题共6小题，共80分.解答应写出文字说明、证明过程或演算步骤.）15. 是直线与函数图像的两个相邻的交点，且.（1）求的值和函数的单调增区间（2）在锐角中，分别是角的对边，若，的面积为，求的值.【答案】(1)答案见解析；(2).【解析】试题分析：(1)首先化简三角函数式的值，然后结合周期即可求得；(2)利用题意首先求得，然后结合面积公式可得，最后由余弦定理可得.试题解析：.由函数的图像及，得到函数的周期，解得.（Ⅱ）解：因为所以.又因为是锐角三角形，所以，即，解得.由，解得.由余弦定理得，即.16. 从装有大小相同的2个红球和6个白球的袋子中，每摸出2个球为一次试验，直到摸出的球中有红球（不放回），则实验结束.（1）求第一次实验恰好摸到1个红球和1个白球的概率；（2）记实验次数为，求的分布列及数学期望.【答案】(1)；(2)答案见解析.【解析】试题分析：（1）由题意知，袋子中共有8个球，记“第一次试验恰摸到一个红球和一个白球”为事件A，则根据古典概型计算公式，得.（2）由题意知，每次试验中不放回地摸出两个球，直到摸出的球中有红球，因为袋中只有两个红球，所以最多需要进行四次试验，第一次试验的结果可能有“一个红球一个白球”或“两个红球”，第二次试验要在第一次试验没有出红球情况下进行，则袋中剩下4个白球和2个红球，结果可能为“一个红球一个白球”或“两个红球”，同理第三次试验要在前两次没有出现红球下进行，则袋中剩下2个白球和2个红球，结果能为“一个红球一个白球”或“两个红球”，第四次试验要在前三次试验没有出现红球下进行，则袋中只剩下2个红球，结果为“两个红球”，所以的值为1、2、3、4，根据古典概型的计算公式，得，，，，从而可列出的分布列，并求出其数学期望.试题解析：（1）（2）由题意可知的值分别为1、2、3、4，则，，，所以的分布列为的数学期望.考点：1.古典概率；2.随机变量的分布列、数学期望.17. 正数数列的前项和为，且，求（1）的通项公式；（2）设，数列的前项和为，求的取值范围.【答案】(1)；(2).【解析】试题分析:（1）先平方得，再根据和项与通项关系得，最后根据等差数列定义以及通项公式求解（2）因为，所以利用裂项相消法求和得，再根据数列单调性确定的取值范围.试题解析：（1）由，当带入得，两边平方得（1），时，（2），（1）-（2），得，，由正数数列，得，∴数列是以1为首项，2为公差的等差数列，∴有；（2）当，∴.点睛：裂项相消法是指将数列的通项分成两个式子的代数和的形式，然后通过累加抵消中间若干项的方法，裂项相消法适用于形如 (其中是各项均不为零的等差数列，c 为常数)的数列. 裂项相消法求和，常见的有相邻两项的裂项求和(如本例)，还有一类隔一项的裂项求和，如或.18. 等差数列的前项和为，且，数列满足：，数列的前项和为（1）求等筹数列的通项公式及前项和为；（2求数列的通项公式及前项和为（3）设集合，若的子集个数为16，求实数的取值范围.【答案】(1)..(2)，.(3).【解析】试题分析：利用等差数列的通项公式和前项和公式即可得出，先得到，再利用累乘法，得到数列的通项公式，再利用错位相减法求出前项和公式根据函数的的单调性，得到不等式继而求实数的取值范围解析：（1）设数列的公差为d，由题意知：解得，（2）由题意得：当时又也满足上式，故故——①——②①－②得：＝（3）由（1）（2）知：，令则，，，，当时，集合M的子集个数为16 中的元素个数为4的解的个数为4点睛：形如在求通项时要用累乘法，遇到通项为的数列在求和时用错位相减法，形如，其中、一个是等差数列一个是等比数列求和就用错位相减法。

一、填空题（本大题共8个小题，每小题5分，共40分，则每个小题所给出的四个选项中，只有一项是符合题目要求的）1. ，且为纯虚数，则等于A. B. C. D.【答案】D【解析】∵为纯虚数，∴-a-1=0，所以a=-1,故选D2. 已知，则“”是“”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】A【解析】若“”，则，即.所以,充分性成立；若“”，则，有或.必要性不成立.故“”是“”的充分不必要条件.故选A.3. 已知向量的夹角是，，则的值是A. B. C. D.【答案】A【解析】向量的夹角是，，所以....故选A.4. 如图是函数在区间上的图象，为了得到这个图象，只需将的图象A. 向右平移个单位长度B. 向右平移个单位长度C. 向右平移个单位长度D. 向左平移个单位长度【答案】B【解析】由图可知函数函数的周期为，解得.，解得.所以有.所以只需将右平移个单位长度.故选B.点睛：三角函数中函数图象的平移变化是常考知识点，也是易错题型.首项必须看清题目中是由哪个函数平移，平移后是哪个函数；其次，在平移时，还要注意自变量x的系数是否为1，如果x有系数，需要将系数提出来求平移量，平移时遵循“左加右减”.5. 若函数满足，且在上单调递增，则实数的最小值为A. B. C. D.【答案】C知在单调递减；在单调递增.所以.的最小值为1.故选C.6. 在中，角的对边分别为，且，则角的最大值为A. B. C. D.【答案】A【解析】由正弦定理得,所以,因此，中有一钝角, 角必为锐角,因为 ,所以,即角的最大值为,选A.点睛：在利用基本不等式求最值时，要特别注意“拆、拼、凑”等技巧，使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用，否则会出现错误.7. 若函数的图象关于点对称，且在内有零点，则的最小值是A. B. C. D.【答案】D【解析】函数.图象关于点对称,所以..当时，，令，得，.令，无解；当时，，令，得，. 令，解得，即零点为.所以的最小值是10.故选D.8. 已知定义域为的奇函数的导函数为，当时，，若，则的大小关系正确的是A. B. C. D.【答案】B【解析】定义域为R的奇函数,设,为R上的偶函数,当时，所以当时,,当时,,即在单调递增,在单调递减.；；.因为，所以.即,故选B.点睛：本题主要考查构造函数，常用的有：，构造xf(x)；2xf(x)+x2f′(x)，构造x2f(x)；，构造;，构造；，构造.等等.二、填空题（本大题共6个小题，每小题5分，共30分，请将答案填在答题卡上）9. 若集合，则________【答案】【解析】集合..10. 若圆经过坐标原点和点，且和直线相切，则圆的方程是_________【答案】【解析】设圆的圆心坐标，半径为，因为圆经过坐标原点和点，且与直线相切，所以，解得，所求圆的方程为，故答案为.11. 已知为偶函数，则的单调递增区间为_______【答案】【解析】因为为偶函数,所以,所以,解得. 则函数.令，为其对称轴.由，解得或.由复合函数的单调性知，单调递增区间为.点睛：形如的函数为,的复合函数，为内层函数,为外层函数.当内层函数单增，外层函数单增时，函数也单增；当内层函数单增，外层函数单减时，函数也单减；当内层函数单减，外层函数单增时，函数也单减；当内层函数单减，外层函数单减时，函数也单增.简称为“同增异减”.12. 已知各项都为正数的等比数列，且满足，若存在两项，使得，则的最小是为________【答案】【解析】等比数列各项都为正数，则.，则，得.；则，则故本题正确答案为13. 中，分别为边的中点，且与夹角为，则______【答案】【解析】假设为中线与的交点，则为三角形的重心。

天津大学附属中学2017—2018学年第一学期高三年级期中考试数学（文）学科试卷第Ⅰ卷一、选择题（本大题共8小题，共40分）1．设全集_，集合_，_，则_（）．A．_B．_C．_D．_【答案】A【解析】解：_，∴_，_，∴_．故选_．2．将一颗正方体型骰子投掷_次，向上的点数之和是_的概率（）．A．_B．_C．_D．_【答案】C【解析】解：点数之和为_，则两次筛子有以下几种结合，_，_，_，_,_，共有_种，则_．故选_．3．如果执行如图所示的程序框图，输入_，则输出的_值为（）．A．_B．_C．_D．__【答案】D【解析】解：_时，_，_，不满足_，_时，_，_，不满足_，_时，_，_，比满足_，_时，_，_，满足_，输出_．故选_．4．“_”是“_”的（）．A．充分不必要条件B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【答案】A【解析】解：充分性证明：由_可得_，∴_，必要性证明：_可得_，即_，即_，∴_是_的充分非必要条件．故选_．5．双曲线_的两个焦点为_、_，以线段_为边作正三角形_，若_的中点在双曲线上，则_（）．A．_B．_C．_D．_【答案】C【解析】解：即_的中点为_，由等边三角形性质可知_，且_，∴_，_，∴_，得_，∴_．故选_．6．已知函数_是定义在_上的偶函数，且在_上单调递增，若对于任意_，_恒成立，则_的取值范围是（）．A．_B．_C．_D．_【答案】B【解析】解：∵_是_上的偶函数，且_在_上递增，∴_可得_，∴_，得_，∴_．故选_．7．已知函数_，_为_的零点，_为_图像的对称轴，且_在_上单调，则_的最大值是（）．A．_B．_C．_D．_【答案】B【解析】解：设_的周期为_，则_，或_，_，又∵_，∴_．（_）当_时，_，由_可得此时_、_、_，当_时，_，则_，_，∴_在_上单调，满足题意．（_）当_，则_，由_可得此时_、_、_，当_时，_，则_，而_，∴_在_上不单调，不满足题意，_的最大值为_．故选_．8．已知函数_，则函数_的零点个数为（）．A．_B．_C．_D．_【答案】B【解析】解：_，即_，设_，_，_，_，显然_在_上单增，且_，∴_在_上有且仅有一解，而_，_，∴_在区间_上递增，注意到_，而当_时，显然_，∴_在_有且仅有一解，∴_有两解．故选_．第Ⅱ卷二、填空题（本小题共6小题，共30分）9．已知复数_，其中_为虚数单位，则复数_的模是__________．【答案】_【解析】解：_，则_．10．某校高一、高二、高三_个年级共有_名学生，其中高一年级_名，高二年级学生_名，为了解学生身体状况，现采用分层抽样方法进行调查，在抽取的样本中高二学生有_人，则该样本中高三学生人数为__________人．【答案】_【解析】解：由题意，高三学生有_人，高一、高二、高三三个年级的学生数之比为_，∴高三学生数_．11．长方体的长、宽、高分别为_，_，_，其顶点都在球_的球面上，则球_的表面积为__________．【答案】_【解析】解：设球的半径为_，∵球_是该长方体的外接球，∴_，∴_．12．已知函数_的图像在点_处的切线方程是_，则：___________．【答案】_【解析】解：∵直线_与_相切于点_，∴_，_，∴_．13．若正数_，_满足_，则_的取值范围是__________．【答案】_【解析】解：_，当且仅当_时，“_”成立，即_，得_或_（舍），∴_，_．14．如图，在平行四边形_中，_，垂直为_，且_，则___________．_【答案】_【解析】解：记_、_相交于点_，由平行四边形的性质可知_，而_，则_，又∵_且_与_共线，_，∴_．三、解答题（本大题共6小题，共80分．解答题应写出文字说明、证明过程或演算步骤）15．（本小题满分_分）在_中，已知三边_，_，_成等比数列．（_）求角_的最大值．（_）若_，求_的值．【答案】（_）_．（_）_．【解析】解：（_）∵_，_，_成等比数列，∴_，∴_，当且仅当_时，“等号成立”，∴_，即_的最大值为_．（_）当_时，由_可得_，∴_，而____，∴_．16．（本小题满分_分）某公司生产甲、乙两种桶装产品，已知生产_桶甲产品需耗_原料_千克，_原料_千克，生产_桶乙产品需耗_原料_千克，_原料_千克，每生产一桶甲产品的利润为_元，每生产一桶乙产品的利润为_元，公司在生产这两种产品的计划中，每天消耗_、_原料都不超过_千克，设公司计划每天生产_桶甲产品和_桶乙产品．（_）用_，_列出满足条件的数学关系式，并在下面的坐标系中用阴影表示相应的平面区域．（_）该公司每天需生产甲产品和乙产品各多少桶时才使所得利润最大，最大利润是多少？_【答案】（_）见解析．（_）甲、乙各生产_桶，最大利润为_元．【解析】解：（_）设每天生产甲产品_桶，乙产品_桶，则_，_满足条件的数学关系式_，该二元一次不等式组表示的平面区域（可行域）如下：_（_）设利润总额为_元，则目标函数为：_，如图，作直线_，即_，当直线_经过可行域上的点_时，截距_最大，即_最大，解方程组_，得_，即_，代入目标函数得_．17．（本小题满分_分）如图，多面体_中，四边形_是边长为_的正方形，四边形_为等腰梯形，_，_，平面_平面_．（_）证明：_平面_．（_）若梯形_的面积为_，求二面角_的余弦值．_【答案】（_）见解析．（_）_．【解析】解：（_）设_、_交于点_，则_为_中点，连接_，∵_，_，∴_，_，∴四边形_为平行四边形，得_，又∵_面_且_面_，∴_面_．（_）∵面_面_，交线为_，_，∴_面_，作_于_，连接_，∵_面_，∴_，又∵_，∴_面_，则_，∴_为二面角_的平面角，取_中点_，连接_，∵_为等腰梯形，得_，_，得_，又∵_，∴_，又∵_，得_，∴_，∴_，∴二面角_的余弦值为_．18．（本小题满分_分）已知数列_中，_，_，记_．（_）求证：数列_是等比数列，并求_．（_）求数列_的通项公式_．（_）记_，_，求_．【答案】（_）_．（_）_．（_）_．【解析】解：（_）__，又∵_，∴_．（_）_，∴_．（_）___，∴___，∴_．19．（本小题满分_分）已知椭圆_，其上顶点_与左焦点_所在的直线的倾斜角为_，_为坐标原点，三角形_的周长为_．（_）求椭圆_的方程．（_）设椭圆_的右顶点为_，不过点_的直线_与椭圆_相交于_、_两点，若以_为直径的圆经过点_，求证：直线_过定点，并求出该定点坐标．【答案】（_）_．（_）_．【解析】解：（_）由题意，_，得_，_，_，∴椭圆方程：_．（_）①当直线_的斜率_存在时，设直线_，_，_，联立_，_，∴_，_，_，得_，∵以_为直径的圆经过点_，∴_，即_，得_，∴_或_，∴直线_或_，∴直线_经过点_或_（舍去）．②当直线斜率不存在时，设直线_，_，_，此时_，∴_，得_或_（舍去），∴_经过点_，综上，直线_经过定点_．20．（本小题满分_分）已知函数_．（_）若曲线_在_处的切线与_轴平行，求实数_的值．（_）若对任意_，不等式_恒成立，求实数_的取值范围．【答案】（_）_．（_）_．【解析】解：（_）_，由题意可得_，得_．（_）由_，可得_，∴_，显然_恒成立，设_，则_，∵_，_在_上递减，∴_在_上递减，∴当_时，_，_时，_，∴_在_上递增，在_上递减，∴_，∴_．。

天津市实验中学2018届高三语文上学期期中（第三阶段）试题不分版本天津市实验中学2018届高三语文上学期期中〔第三阶段〕试题本试卷分为第I卷〔选择题〕和第II卷两局部，共150分，考试时间150分钟。

第I卷考前须知：1.每题选出答案后，用铅笔将答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

2.本卷共12小题，每题3分，共36分。

在每题给出的四个选项中，只有一项为哪一项最符合题目要求的。

一、〔18分〕1．以下词语中加点的字，每对的读音都不相同的一项为哪一项〔〕A．滋润．\蕴．含赡．养\瞻．仰调．试\调．和模．样\楷模．B．对峙．\嗜．好竣．工\英俊强．．脚\别．扭．．迫\倔强蹩C．造诣．\逃逸堤．．岸\提．拔抹．黑\抹．布盘踞．\拮据．D．湖畔．\装扮怄．．然\创．伤．．气\枢．纽阻塞．\边塞怆2．以下词语完全正确的一项为哪一项A．循规蹈矩门庭假设市琼楼玉宇虚无缥缈B．博闻强识积重难返揠苗助长消声匿迹C．狭路相逢妇孺皆知义愤填赝相映成趣D．绿草如荫沽名钓誉融会贯穿文过饰非3．以下各句中，加点的词语使用恰当的一句是〔〕A．交际不仅是一门学问，而且是一门艺术。

只要你能够有效地运用这门艺术，便会左右逢源，无往不利．．．．，融入社会，取得成功。

B．家长不要认为拒绝孩子会造成伤害，要培养一个出色的孩子，面对他的不情之情．．．．，一定要坚决地说“不〞，不能有丝毫心软。

C．《人类文明史图鉴》就人与自然、城市、家庭、战争等方面进行了具体而微．．．．的介绍，涵盖了世界各大文明，并十分重视历史的分析。

D．新星公司花重金挖来的邓一林，在近期的几次重大活动中失误不断，公司的上上下下对他另眼相看．．．．，议论纷纷。

4.以下各项中，没有语病的一项为哪一项〔〕A．许多高中毕业生填报志愿时，是优先考虑专业还是优先考虑学校，很大程度上是受市场需求、社会导向、父母意愿、个人喜好等因素的影响造成的。

B．5月4日在北京国家大剧院举行了《红色箴言》大型诗歌朗诵会，通过众多著名表演艺术家炉火纯青的朗诵表演，使在场的大学生热血沸腾，深受震撼。